Advances in Deep Learning-Driven Metasurface Design and Application in Holographic Imaging
Abstract
1. Introduction
2. Deep Learning-Based Metasurface Design
2.1. Development History of Neural Networks
2.2. Predictive Networks
Convolutional Neural Network (CNN)
2.3. Generative Networks
Generative Adversarial Network (GAN)
2.4. Sequential Networks
Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM)
3. Holographic Applications of Deep Learning-Designed Metasurfaces

4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Zeng, X.; Ma, L.; Zhang, R.; Zhan, Z.; Chen, C.; Ren, X.; He, C.; Liu, C.; Cheng, C. Manipulation for superposition of orbital angular momentum states in surface plasmon polaritons. Adv. Opt. Mater. 2019, 7, 1900372. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeng, X.; Zhang, R.; Zhan, Z.; Li, X.; Ma, L.; Liu, C.; He, C.; Cheng, C. Generation of a plasmonic radially polarized vector beam with linearly polarized illumination. Opt. Lett. 2018, 43, 4208. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, H.; Zhang, X.; Zhang, Y.; Zhang, R.; Xu, S.; Tang, Y.; Wang, X.; Zhang, J.; Ma, L.; et al. Metasurface of deflection prism phases for generating nondiffracting optical vortex lattices. Opt. Express 2018, 26, 28228–28237. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Jiang, M.; Guan, H.; Yu, J.; Lu, H.; Zhang, J.; Chen, Z. Tunable spin splitting of Laguerre–Gaussian beams in graphene metamaterials. Photonics Res. 2017, 5, 684–688. [Google Scholar] [CrossRef]
- Jiang, M.; Zhu, W.; Guan, H.; Yu, J.; Lu, H.; Tan, J.; Zhang, J.; Chen, Z. Giant spin splitting induced by orbital angular momentum in an epsilon-near-zero metamaterial slab. Opt. Lett. 2017, 42, 3259–3262. [Google Scholar] [CrossRef]
- Cheng, Y.; Cao, W.; Wang, G.; He, X.; Lin, F.; Liu, F. 3D Dirac semimetal supported thermal tunable terahertz hybrid plasmonic waveguides. Opt. Express 2023, 31, 17201–17214. [Google Scholar] [CrossRef]
- Wang, G.; Cao, W.; He, X. 3D Dirac semimetal elliptical fiber supported THz tunable hybrid plasmonic waveguides. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 8400207. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, X.; Liu, S.; Zhang, Y. Highly efficient vectorial field manipulation using a transmitted tri-layer metasurface in the terahertz band. Opto-Electron. Adv. 2023, 6, 220012. [Google Scholar]
- Du, W.; Zhu, M.; Shi, J.; Liu, T.; Sun, J.; Yi, K.; Shao, J. Effect of subsurface impurity defects on laser damage resistance of beam splitter coatings. High Power Laser Sci. Eng. 2023, 11, e61. [Google Scholar] [CrossRef]
- Howard, S.; Esslinger, J.; Wang, R.; Norreys, P.; Döpp, A. Hyperspectral compressive wavefront sensing. High Power Laser Sci. Eng. 2023, 11, e32. [Google Scholar] [CrossRef]
- Guan, H.; Hong, J.; Wang, X.; Ming, J.; Zhang, Z.; Liang, A.; Han, X.; Dong, J.; Qiu, W.; Chen, Z.; et al. Broadband, high-sensitivity graphene photodetector based on ferroelectric polarization of lithium niobate. Adv. Opt. Mater. 2021, 9, 2100245. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, M.; Li, Y.; Shang, J.; Li, K.; Qiu, W.; Dong, J.; Guan, H.; Chen, Z.; Lu, H. Highly efficient second harmonic generation of thin film lithium niobate nanograting near bound states in the continuum. Nanotechnology 2021, 32, 325207. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Jiang, W.X.; Cui, T.J. Spatial power combination for omnidirectional radiation via anisotropic metamaterials. Phys. Rev. Lett. 2012, 108, 213903. [Google Scholar] [CrossRef] [PubMed]
- Jing, X.; Gui, X.; Zhou, P.; Hong, Z. Physical Explanation of Fabry–Pérot Cavity for Broadband Bilayer Metamaterials Polarization Converter. J. Light. Technol. 2018, 36, 2322–2327. [Google Scholar] [CrossRef]
- Xia, R.; Jing, X.; Gui, X.; Tian, Y.; Hong, Z. Broadband terahertz half-wave plate based on anisotropic polarization conversion metamaterials. Opt. Mater. Express 2017, 7, 977–988. [Google Scholar] [CrossRef]
- Zhao, J.; Jing, X.; Wang, W.; Tian, Y.; Zhu, D.; Shi, G. Steady method to retrieve effective electromagnetic parameters of bianisotropic metamaterials at one incident direction in the terahertz region. Opt. Laser Technol. 2017, 95, 56–62. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C.; Cheng, H.; Fang, B.; Lu, J.; Ma, X.; Wang, L.; Hong, Z.; Jing, X. Anisotropic programmable metasurface beam splitter based on diode real-time control. Opt. Lasers Eng. 2023, 169, 107723. [Google Scholar] [CrossRef]
- Cheng, H.; Fang, B.; Huang, W.; Li, R.; Shen, C.; Ke, L.; Jing, X.; Li, C.; Hong, Z. Far-field steering of beams based on dynamic encoding metasurface. Opt. Laser Technol. 2022, 156, 108520. [Google Scholar] [CrossRef]
- Jiang, L.; Fang, B.; Yan, Z.; Fan, J.; Qi, C.; Liu, J.; He, Y.; Li, C.; Jing, X.; Gan, H.; et al. Terahertz high and near-zero refractive index metamaterials by double layer metal ring microstructure. Opt. Laser Technol. 2020, 123, 105949. [Google Scholar] [CrossRef]
- Jing, X.; Xu, Y.; Gan, H.; He, Y.; Hong, Z. High Refractive Index Metamaterials by Using Higher Order Modes Resonances of Hollow Cylindrical Nanostructure in Visible Region. IEEE Access 2019, 7, 144945–144956. [Google Scholar] [CrossRef]
- Liu, S.; Cao, W.; Jiang, S.; He, L.; Lin, F.; He, X. 3D Dirac Semimetal Supported Tunable Multi-Frequency Terahertz Metamaterial Absorbers. Adv. Quantum Technol. 2024, 7, 2300386. [Google Scholar]
- Zhang, J.; Zhang, H.; Zhang, G. Nanophononic metamaterials induced proximity effect in heat flux regulation. Front. Phys. 2024, 19, 23204. [Google Scholar] [CrossRef]
- Berhe, A.; As’ham, K.; Al-Ani, I.; Hattori, H.; Miroshnichenko, A. Strong coupling and catenary field enhancement in the hybrid plasmonic metamaterial cavity and TMDC monolayers. Opto-Electron. Adv. 2024, 7, 230181. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, Y.; Li, C.; Fang, B.; Liu, J.; Hong, Z.; Jing, X. All-dielectric double-layer honeycomb tunable metamaterial absorber with integrated gold nanoparticles. Photonics Res. 2024, 12, 2344–2353. [Google Scholar] [CrossRef]
- Zhang, R.; Guo, Y.; Zhang, F.; Pu, M.; Fan, Y.; Zhang, Q.; Li, X.; Xu, M.; Xu, J.; Luo, X. Dual-Layer Metasurface Enhanced Capacity of Polarization Multiplexing. Laser Photonics Rev. 2024, 18, 2400126. [Google Scholar] [CrossRef]
- Zeng, H.; Cong, X.; Wang, S.; Gong, S.; Huang, L.; Wang, L.; Liang, H.; Lan, F.; Cao, H.; Wang, Z.; et al. Ultrafast modulable 2DEG Huygens metasurface. Photonics Res. 2024, 12, 1004–1015. [Google Scholar]
- Wu, H.; Gao, X.; Zhang, L.; Bai, G.; Cheng, Q.; Li, L.; Cui, T. Harmonic information transitions of spatiotemporal metasurfaces. Light Sci. Appl. 2020, 9, 198. [Google Scholar] [CrossRef]
- Li, S.; Fang, Y.; Wang, J. Control of light–matter interactions in two-dimensional materials with nanoparticle-on-mirror structures. Opto-Electron. Sci. 2024, 3, 240011. [Google Scholar] [CrossRef]
- He, X.; Cao, W. Tunable terahertz hybrid metamaterials supported by 3D Dirac semimetals. Opt. Mater. Express 2023, 13, 413–422. [Google Scholar] [CrossRef]
- He, X.; Lin, F.; Liu, F.; Shi, W. 3D Dirac semimetals supported tunable terahertz BIC metamaterials. Nanophotonics 2022, 11, 4705–4714. [Google Scholar] [CrossRef]
- Peng, J.; He, X.; Shi, C.; Leng, J.; Lin, F.; Liu, F.; Zhang, H.; Shi, W. Investigation of graphene supported terahertz elliptical metamaterials. Phys. E Low-Dimens. Syst. Nanostructures 2020, 124, 114309. [Google Scholar] [CrossRef]
- Leng, J.; Peng, J.; Jin, A.; Cao, D.; Liu, D.; He, X.; Lin, F.; Liu, F. Investigation of terahertz high Q-factor of all-dielectric metamaterials. Opt. Laser Technol. 2022, 146, 107570. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zheng, C. Spectral amplitude modulation and dynamic near-field displaying of all-silicon terahertz metasurfaces supporting bound states in the continuum. Appl. Phys. Lett. 2021, 119, 241105. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zheng, C.; Yue, Z.; Wang, S.; Li, M.; Zhao, H.; Zhang, Y.; Yao, J. Active controllable spin-selective terahertz asymmetric transmission based on all-silicon metasurfaces. Appl. Phys. Lett. 2021, 118, 221110. [Google Scholar] [CrossRef]
- Li, J.; Yue, Z.; Li, J.; Zheng, C.; Wang, S.; Li, M.; Zhang, Y.; Zhang, Y.; Yao, J. Diverse terahertz wavefront manipulations empowered by the spatially interleaved metasurfaces. Sci. China Inf. Sci. 2023, 66, 132301. [Google Scholar] [CrossRef]
- Li, J.; Yue, Z.; Li, J.; Zheng, C.; Zhang, Y.; Yao, J. Ultra-narrowband terahertz circular dichroism driven by planar metasurface supporting chiral quasi bound states in the continuum. Opt. Laser Technol. 2023, 161, 109173. [Google Scholar] [CrossRef]
- Xiong, R.H.; Peng, X.Q.; Li, J.S. Graphene-metasurface for wide-incident-angle terahertz absorption. Front. Inf. Technol. Electron. Eng. 2021, 22, 334–340. [Google Scholar] [CrossRef]
- Han, H.; Zhao, J.; Zhai, W.; Xiong, Z.; Niyato, D.; Renzo, M.; Pham, Q.; Lu, W.; Lam, K. Reconfigurable Intelligent Surface Aided Power Control for Physical-Layer Broadcasting. IEEE Trans. Commun. 2021, 69, 7821–7836. [Google Scholar] [CrossRef]
- Jing, X.; Tang, X.; Tian, Y.; Kong, Z.; Li, C.; Shen, C. Enhancement of Diffraction Efficiency Based on the Addition Principle of Coded Digital Gratings. J. Light. Technol. 2022, 40, 136–142. [Google Scholar] [CrossRef]
- Wang, W.; Jing, X.; Zhao, J.; Li, Y.; Tian, Y. Improvement of accuracy of simple methods for design and analysis of a blazed phase grating microstructure. Opt. Appl. 2017, 47. [Google Scholar] [CrossRef]
- Luo, Z.; Ding, Y.; Peng, F.; Wei, G.; Wang, Y.; Wu, S.-T. Ultracompact and high-efficiency liquid-crystal-on-silicon light engines for augmented reality glasses. Opto-Electron. Adv. 2024, 7, 240039. [Google Scholar] [CrossRef]
- Rane, S.; Prabhu, S.; Chowdhury, D.R. Physics and applications of terahertz metagratings. Opto-Electron. Sci. 2024, 3, 230049. [Google Scholar]
- Jiang, J.; Fang, B.; Li, C.; Hong, Z.; Jing, X. Improvement of terahertz beam modulation efficiency for baseless all-dielectric coded gratings. Photonics Res. 2023, 11, 1738–1750. [Google Scholar]
- Alagappan, G.; Png, C.E. Deep learning models for effective refractive indices in silicon nitride waveguides. J. Opt. 2019, 21, 035801. [Google Scholar] [CrossRef]
- Kiarashinejad, Y.; Abdollahramezani, S.; Adibi, A. Deep learning approach based on dimensionality reduction for designing electromagnetic nanostructures. Npj Comput. Mater. 2020, 6, 12. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Q.; Li, Q.; Huang, Z.; Xu, L.; Quan, Y.; Zhu, Q.; Wang, B.; Chen, X.; Cui, T.; et al. Anisotropic programmable metasurfaces with individually controllable 2-bit elements. Photonics Res. 2024, 12, 2660. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, S.; Tian, Y.; Li, C.; Huang, W.; Liu, Y.; Jin, Y.; Fang, B.; Hong, Z.; Jing, X. Focus control of wide-angle metalens based on digitally encoded metasurface. Opto-Electron. Adv. 2024, 7, 240095. [Google Scholar] [CrossRef]
- Zhan, H.; Gu, M.; Tian, Y.; Feng, H.; Zhu, M.; Zhou, H.; Jin, Y.; Tang, Y.; Li, C.; Fang, B.; et al. Review for wireless communication technology based on digital encoding metasurfaces. Opto-Electron. Adv. 2025, 8, 240315. [Google Scholar]
- Cui, T.J.; Liu, S.; Zhang, L. Information metamaterials and metasurfaces. J. Mater. Chem. C 2017, 5, 3644–3668. [Google Scholar] [CrossRef]
- Geller, M.R. Fast Quantum State Discrimination with Nonlinear Positive Trace-Preserving Channels. Adv. Quantum Technol. 2023, 6, 2200156. [Google Scholar]
- Xu, Q.; Lang, Y.; Jiang, X.; Yuan, X.; Xu, Y.; Gu, J.; Tian, Z.; Ouyang, C.; Zhang, X.; Han, J.; et al. Meta-Optics Inspired Surface Plasmon Devices. Photonics Insights 2023, 2, R02. [Google Scholar] [CrossRef]
- Kang, H.; Lee, D.; Yang, Y.; Oh, D.; Seong, J.; Kim, J.; Jeon, N.; Kang, D.; Rho, J. Emerging low-cost, large-scale photonic platforms with soft lithography and self-assembly. Photonics Insights 2023, 2, R04. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Yue, Z.; Liu, J.; Li, J.; Zheng, C.; Zhang, Y.; Zhang, Y.; Yao, J. Dynamic phase assembled terahertz metalens for reversible conversion between linear polarization and arbitrary circular polarization. Opto-Electron. Adv. 2022, 5, 210062. [Google Scholar] [CrossRef]
- Gao, H.; Fan, X.; Wang, Y.; Liu, Y.; Wang, X.; Xu, K.; Deng, L.; Zeng, C.; Li, T.; Xia, J.; et al. Multi-foci metalens for spectra and polarization ellipticity recognition and reconstruction. Opto-Electron. Sci. 2023, 2, 220026. [Google Scholar] [CrossRef]
- Akram, M.; Ding, G.; Chen, K.; Feng, Y.; Zhu, W. Ultrathin Single Layer Metasurfaces with Ultra-Wideband Operation for Both Transmission and Reflection. Adv. Mater. 2020, 32, 1907308. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, X.; Rukhlenko, I.D.; Chen, H.-T.; Zhu, W. Electrically Tunable Metasurface with Independent Frequency and Amplitude Modulations. ACS Photonics 2020, 7, 265–271. [Google Scholar] [CrossRef]
- Akram, M.R.; Mehmood, M.Q.; Bai, X.; Jin, R.; Premaratne, M.; Zhu, W. High Efficiency Ultrathin Transmissive Metasurfaces. Adv. Opt. Mater. 2019, 7, 1801628. [Google Scholar] [CrossRef]
- Akram, M.R.; Bai, X.; Jin, R.; Vandenbosch, G.A.E.; Premaratne, M.; Zhu, W. Photon Spin Hall Effect-Based Ultra-Thin Transmissive Metasurface for Efficient Generation of OAM Waves. IEEE Trans. Antennas Propag. 2019, 67, 4650–4658. [Google Scholar] [CrossRef]
- Li, J.; Jin, R.; Geng, J.; Liang, X.; Wang, K.; Premaratne, M.; Zhu, W. Design of a Broadband Metasurface Luneburg Lens for Full-Angle Operation. IEEE Trans. Antennas Propag. 2019, 67, 2442–2451. [Google Scholar] [CrossRef]
- Dai, J.; Zhao, J.; Cheng, Q.; Cui, T. Independent control of harmonic amplitudes and phases via a time-domain digital coding metasurfaces. Light Sci. Appl. 2018, 7, 90. [Google Scholar] [CrossRef]
- Sakib Rahman, M.S.; Ozcan, A. Physics and artificial intelligence: Illuminating the future of optics and photonics. Adv. Photonics 2024, 6, 050500. [Google Scholar] [CrossRef]
- Zhang, Q.; Wan, X.; Liu, S.; Yin, J.Y.; Zhang, L.; Cui, T.J. Shaping electromagnetic waves using software-automatically-designed metasurfaces. Sci. Rep. 2017, 7, 3588. [Google Scholar]
- Zhou, L.; Lou, H.; Deng, Z.; Qin, X.; Pan, J.; Di, Y.; Gu, C.; Luo, D.; Li, W. Compact mid-infrared dual-comb spectrometer over 3–4 μm via intra-pulse difference frequency generation in LiNbO3 waveguides. High Power Laser Sci. Eng. 2024, 12, e23. [Google Scholar] [CrossRef]
- Zhou, J.; Yin, Y.; Tang, J.; Xia, Y.; Yin, J. Information transmission through parallel multi-task-based recognition of high-resolution multiplexed orbital angular momentum. Front. Phys. 2024, 19, 52202. [Google Scholar]
- Zheng, C.; Li, H.; Liu, J.; Wang, M.; Zang, H.; Zhang, Y.; Yao, J. Full-Stokes metasurface polarimetry requiring only a single measurement. Photonics Res. 2024, 12, 514–521. [Google Scholar]
- Zhang, Y.; Chen, Y.; Wang, T.; Zhu, Q.; Gu, M. Ultrahigh performance passive radiative cooling by hybrid polar dielectric metasurface thermal emitters. Opto-Electron. Adv. 2024, 7, 230194. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Fan, C.; Zeng, Z.; Xiong, C.; Wu, J.; Yan, Z.; Liu, D.; Sun, Q. Adaptive decentralized AI scheme for signal recognition of distributed sensor systems. Opto-Electron. Adv. 2024, 7, 240119. [Google Scholar]
- Zhang, J.C.; Chen, M.K.; Fan, Y.; Chen, Q.; Chen, S.; Yao, J.; Liu, X.Y.; Xiao, S.; Tsai, D.P. Miniature tunable Airy beam optical meta-device. Opto-Electron. Adv. 2024, 7, 230171. [Google Scholar] [CrossRef]
- Zhang, C.-L.; Hu, K.-X.; Zhang, J.; Cao, J.; Zhang, S.; Wang, H.-F. Topological Phase Transition and Edge States with Tunable Localization in the Cyclic Four-Mode Optical System. Adv. Quantum Technol. 2024, 7, 2400165. [Google Scholar] [CrossRef]
- Yu, Z.; Li, M.; Xing, Z.; Gao, H.; Liu, Z.; Pu, S.; Mao, H.; Cai, H.; Ma, Q.; Ren, W.; et al. Genetic algorithm assisted meta-atom design for high-performance metasurface optics. Opto-Electron. Sci. 2024, 3, 240016. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, Q.; Shen, B.; Tao, Y.; Zhang, X.; Tao, Z.; Xing, L.; Ge, Z.; Li, T.; Bai, B.; et al. Multifunctional mixed analog/digital signal processor based on integrated photonics. Opto-Electron. Sci. 2024, 3, 240012. [Google Scholar] [CrossRef]
- Ullah, M.; Mikki, S. Optical Nonreciprocity in a Multimode Cavity Optomechanical System Controlled by Dynamic Casimir Force. Adv. Quantum Technol. 2024, 7, 2400007. [Google Scholar] [CrossRef]
- Taha, B.A.; Addie, A.J.; Haider, A.J.; Chaudhary, V.; Apsari, R.; Kaushik, A.; Arsad, N. Exploring Trends and Opportunities in Quantum-Enhanced Advanced Photonic Illumination Technologies. Adv. Quantum Technol. 2024, 7, 2300414. [Google Scholar] [CrossRef]
- Shi, J.; Yang, C.; Chen, Y.; Wang, T.; Yu, H.; Cao, J.; Geng, Z.; Wang, Z.; Wen, H.; Tan, H.; et al. Precise mode control of mid-infrared high-power laser diodes using on-chip advanced sawtooth waveguide designs. High Power Laser Sci. Eng. 2024, 12, e42. [Google Scholar] [CrossRef]
- Roche, L.J.; Betz, F.; Yang, Y.; Limame, I.; Shih, C.-W.; Burger, S.; Reitzenstein, S. Numerical Investigation of a Coupled Micropillar—Waveguide System for Integrated Quantum Photonic Circuits. Adv. Quantum Technol. 2024, 7, 2400195. [Google Scholar] [CrossRef]
- Refaeli, Z.; Marcus, G.; Shamir, Y. A simple method for pulse contrast enhancement via self-focusing. High Power Laser Sci. Eng. 2024, 12, e18. [Google Scholar] [CrossRef]
- Nan, T.; Zhao, H.; Guo, J.; Wang, X.; Tian, H.; Zhang, Y. Generation of structured light beams with polarization variation along arbitrary spatial trajectories using tri-layer metasurfaces. Opto-Electron. Sci. 2024, 3, 230052. [Google Scholar] [CrossRef]
- Martín-Hernández, R.; Grünewald, L.; Sánchez-Tejerina, L.; Plaja, L.; Conejero Jarque, E.; Hernández-García, C.; Mai, S. Optical magnetic field enhancement using ultrafast azimuthally polarized laser beams and tailored metallic nanoantennas. Photonics Res. 2024, 12, 1078–1092. [Google Scholar] [CrossRef]
- Istokskaia, V.; Lefebvre, B.; Versaci, R.; Dreghici, D.B.; Doria, D.; Grepl, F.; Olšovcová, V.; Schillaci, F.; Stanček, S.; Tryus, M.; et al. Real-time bremsstrahlung detector as a monitoring tool for laser–plasma proton acceleration. High Power Laser Sci. Eng. 2024, 12, e57. [Google Scholar] [CrossRef]
- Hou, T.; Ge, Y.; Xue, S.; Chen, H. Curved anisotropic polaritons. Front. Phys. 2024, 19, 32201. [Google Scholar]
- Hao, Z.; Chen, H.; Yin, Y.; Qiu, C.-W.; Zhu, S.; Chen, H. Efficient conversion of acoustic vortex using extremely anisotropic metasurface. Front. Phys. 2024, 19, 42202. [Google Scholar] [CrossRef]
- Han, L.; Duan, Q.; Duan, J.; Zhu, S.; Chen, S.; Yin, Y.; Chen, H. Unidirectional propagation of water waves near ancient Luoyang Bridge. Front. Phys. 2024, 19, 32206. [Google Scholar] [CrossRef]
- Parazzoli, C.G.; Greegor, R.B.; Li, K.; Koltenbah, B.E.C.; Tanielian, M. Experimental verification and simulation of negative index of refraction using Snell’s law. Phys. Rev. Lett. 2003, 90, 107401. [Google Scholar] [CrossRef]
- Chen, X.; Luo, Y.; Zhang, J.; Jiang, K.; Pendry, J.B.; Zhang, S. Macroscopic invisibility cloaking of visible light. Nat. Commun. 2011, 2, 176. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Qin, C.B.; Liang, X.; Zhang, G.; Chen, R.; Hu, J.; Yang, Z.; Huo, J.; Xiao, L.; Jia, S. Deep learning in two-dimensional materials: Characterization, prediction, and design. Front. Phys. 2024, 19, 53601. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ryan, K.; Lengyel, J.; Shatruk, M. Crystal Structure Prediction via Deep Learning. J. Am. Chem. Soc. 2018, 140, 10158–10168. [Google Scholar] [CrossRef]
- Sato, K.; Akiyama, M.; Sakakibara, Y. RNA secondary structure prediction using deep learning with thermodynamic integration. Nat. Commun. 2021, 12, 941. [Google Scholar] [CrossRef]
- Kan, Y.H.; Zhao, C.Y.; Zhang, Z.M. Enhancement and Manipulation of Near-Field Radiative Heat Transfer Using an Intermediate Modulator. Phys. Rev. Appl. 2020, 13, 014033. [Google Scholar] [CrossRef]
- Kutz, J.N. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef]
- Qiu, T.; Shi, X.; Wang, J.; Li, Y.; Qu, S.; Cheng, Q.; Cui, T.; Sui, S. Deep Learning: A Rapid and Efficient Route to Automatic Metasurface Design. Adv. Sci. 2019, 6, 1900128. [Google Scholar] [CrossRef]
- An, S.; Fowler, C.; Zheng, B.; Shalaginov, M.Y.; Tang, H.; Li, H.; Zhou, L.; Ding, J.; Agarwal, A.M.; Rivero-Baleine, C.; et al. A Deep Learning Approach for Objective-Driven All-Dielectric Metasurface Design. ACS Photonics 2019, 6, 3196–3207. [Google Scholar] [CrossRef]
- Ma, W.; Cheng, F.; Liu, Y. Deep-Learning-Enabled On-Demand Design of Chiral Metamaterials. ACS Nano 2018, 12, 6326–6334. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef]
- Xu, Y.; Xiong, B.; Ma, W.; Liu, Y. Software-defined nanophotonic devices and systems empowered by machine learning. Prog. Quantum Electron. 2023, 89, 100469. [Google Scholar] [CrossRef]
- Kudyshev, Z.A.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Machine-learning-assisted metasurface design for high-efficiency thermal emitter optimization. Appl. Phys. Rev. 2020, 7, 021407. [Google Scholar] [CrossRef]
- Li, Y.; Deng, M.; Liu, Z.; Peng, P.; Chen, Y.; Fang, Z. Inverse Design of Unidirectional Transmission Nanostructures Based on Unsupervised Machine Learning. Adv. Opt. Mater. 2022, 10, 2200127. [Google Scholar] [CrossRef]
- Wang, L.; Ruan, Z.; Wang, H.; Shen, L.; Zhang, L.; Luo, J.; Wang, J. Deep Learning Based Recognition of Different Mode Bases in Ring-Core Fiber. Laser Photonics Rev. 2020, 14, 2000249. [Google Scholar] [CrossRef]
- Gabor, D. A New Microscopic Principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef]
- Cuche, E.; Bevilacqua, F.; Depeursinge, C. Digital holography for quantitative phase-contrast imaging. Opt. Lett. 1999, 24, 291–293. [Google Scholar] [CrossRef]
- Cuche, E.; Marquet, P.; Depeursinge, C. Spatial filtering for zero-order and twin-image elimination in digital off-axis holography. Appl. Opt. 2000, 39, 4070–4075. [Google Scholar] [CrossRef]
- Kim, Y.; Sim, M.; Moon, I. Secure storage and retrieval schemes for multiple encrypted digital holograms with orthogonal phase encoding multiplexing. Opt. Express 2019, 27, 22147–22160. [Google Scholar] [CrossRef]
- Pi, D.; Liu, J.; Kang, R.; Zhang, Z.; Han, Y. Reducing the memory usage of computer-generated hologram calculation using accurate high-compressed look-up-table method in color 3D holographic display. Opt. Express 2019, 27, 28410–28422. [Google Scholar] [CrossRef]
- Kang, R.; Liu, J.; Xue, G.; Li, X.; Pi, D.; Wang, Y. Curved multiplexing computer-generated hologram for 3D holographic display. Opt. Express 2019, 27, 14369–14380. [Google Scholar] [CrossRef]
- Yang, Y.; Forbes, A.; Cao, L. A review of liquid crystal spatial light modulators: Devices and applications. Opto-Electron. Sci. 2023, 2, 230026. [Google Scholar] [CrossRef]
- Tang, D.; Liu, J.; Chen, L.; Liu, J.; Zhang, X. Reflective plasmonic super-oscillatory metasurfaces with simultaneous phase and amplitude controls for sub-diffraction focusing. J. Phys. D Appl. Phys. 2020, 53, 154001. [Google Scholar] [CrossRef]
- Mou, Z.; Zhou, C.; Lv, H.; Bao, R.; Li, Z.; Teng, S. Uniform theory of plasmonic vortex generation based on nanoholes. Nanotechnology 2020, 31, 455301. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.-L.; Wang, Z.-Q.; Li, F.-J.; Hu, M.-X.; Li, X. Multi-freedom metasurface empowered vectorial holography. Nanophotonics 2022, 11, 1725–1739. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C.; Fang, B.; Hong, Z.; Jing, X. Flexible tuning of multifocal holographic imaging based on electronically controlled metasurfaces. Photonics Res. 2024, 12, 61–69. [Google Scholar] [CrossRef]
- Shen, C.-Y.; Li, J.; Li, Y.; Gan, T.; Bai, L.; Jarrahi, M.; Ozcan, A. Multiplane quantitative phase imaging using a wavelength-multiplexed diffractive optical processor. Adv. Photonics 2024, 6, 056003. [Google Scholar] [CrossRef]
- Sun, Z.; Yan, M.; Mupona, T.E.; Xu, B. Control Electromagnetic Waves Based on Multi-Layered Transparent Metasurface. Front. Phys. 2019, 7, 181. [Google Scholar] [CrossRef]
- Sun, Z.; Yan, M.; Xu, B. Formation of orbital angular momentum and focused beams based on chiral double-helical metamaterials. Opt. Mater. 2020, 107, 109962. [Google Scholar] [CrossRef]
- Xu, B.; Wu, C.; Wei, Z.; Fan, Y.; Li, H. Generating an orbital-angular-momentum beam with a metasurface of gradient reflective phase. Opt. Mater. Express 2016, 6, 3940–3945. [Google Scholar] [CrossRef]
- Li, Z.; Sun, J.; Fan, Y.; Jin, Y.; Shen, Q.; Trusiak, M.; Cywińska, M.; Gao, P.; Chen, Q.; Zuo, C. Deep learning assisted variational Hilbert quantitative phase imaging. Opto-Electron. Sci. 2023, 2, 220023. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Zhang, H.; Chen, S.; Bai, B.; Tan, Q.; Jin, G.; Cheah, K.-W.; Qiu, C.-W.; et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 2013, 4, 2808. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, J.; Wang, Y.; Pu, M.; Li, X.; Zhao, Z.; Gao, P.; Wang, C.; Luo, X. Metasurface-based broadband hologram with high tolerance to fabrication errors. Sci. Rep. 2016, 6, 19856. [Google Scholar] [CrossRef]
- Huang, L.; Mühlenbernd, H.; Li, X.; Song, X.; Bai, B.; Wang, Y.; Zentgraf, T. Broadband Hybrid Holographic Multiplexing with Geometric Metasurfaces. Adv. Mater. 2015, 27, 6444–6449. [Google Scholar] [CrossRef]
- Li, X.; Chen, L.; Li, Y.; Zhang, X.; Pu, M.; Zhao, Z.; Ma, X.; Wang, Y.; Hong, M.; Luo, X. Multicolor 3D meta-holography by broadband plasmonic modulation. Sci. Adv. 2016, 2, e1601102. [Google Scholar] [CrossRef]
- Wang, B.; Dong, F.; Li, Q.-T.; Yang, D.; Sun, C.; Chen, J.; Song, Z.; Xu, L.; Chu, W.; Xiao, Y.-F.; et al. Visible-Frequency Dielectric Metasurfaces for Multiwavelength Achromatic and Highly Dispersive Holograms. Nano Lett. 2016, 16, 5235–5240. [Google Scholar] [CrossRef]
- Li, Z.; Premaratne, M.; Zhu, W. Advanced encryption method realized by secret shared phase encoding scheme using a multi-wavelength metasurface. Nanophotonics 2020, 9, 3687–3696. [Google Scholar] [CrossRef]
- Huang, Y.-W.; Chen, W.T.; Tsai, W.-Y.; Wu, P.C.; Wang, C.-M.; Sun, G.; Tsai, D.P. Aluminum Plasmonic Multicolor Meta-Hologram. Nano Lett. 2015, 15, 3122–3127. [Google Scholar] [CrossRef] [PubMed]
- Min, C.; Liu, J.; Lei, T.; Si, G.; Xie, Z.; Lin, J.; Du, L.; Yuan, X. Plasmonic nano-slits assisted polarization selective detour phase meta-hologram. Laser Photonics Rev. 2016, 10, 978–985. [Google Scholar] [CrossRef]
- Mueller, J.P.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef]
- Zhou, H.; Sain, B.; Wang, Y.; Schlickriede, C.; Zhao, R.; Zhang, X.; Wei, Q.; Li, X.; Huang, L.; Zentgraf, T. Polarization-Encrypted Orbital Angular Momentum Multiplexed Metasurface Holography. ACS Nano 2020, 14, 5553–5559. [Google Scholar] [CrossRef]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.F.; Wong, P.W.H.; Cheah, K.W.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef]
- Wang, Q.; Plum, E.; Yang, Q.; Zhang, X.; Xu, Q.; Xu, Y.; Han, J.; Zhang, W. Reflective chiral meta-holography: Multiplexing holograms for circularly polarized waves. Light Sci. Appl. 2018, 7, 25. [Google Scholar] [CrossRef]
- Khalid, A.U.R.; Liu, J.; Han, Y.; Ullah, N.; Zhao, R.; Wang, Y. Multichannel polarization encoded reflective metahologram using VO2 spacer in visible regime. Opt. Commun. 2019, 451, 211–215. [Google Scholar] [CrossRef]
- Jin, J.; Li, X.; Pu, M.; Guo, Y.; Gao, P.; Xu, M.; Zhang, Z.; Luo, X. Angular-multiplexed multichannel optical vortex arrays generators based on geometric metasurface. iScience 2021, 24, 102107. [Google Scholar] [CrossRef]
- Yifat, Y.; Eitan, M.; Iluz, Z.; Hanein, Y.; Boag, A.; Scheuer, J. Highly Efficient and Broadband Wide-Angle Holography Using Patch-Dipole Nanoantenna Reflectarrays. Nano Lett. 2014, 14, 2485–2490. [Google Scholar] [CrossRef]
- Guan, C.; Ding, X.; Wang, Z.; Zhang, K.; Jin, M.; Burokur, S.N.; Wu, Q. Helicity-switched hologram utilizing a polarization-free multi-bit coding metasurface. Opt. Express 2020, 28, 22669–22678. [Google Scholar] [CrossRef] [PubMed]
- Qu, G.; Yang, W.; Song, Q.; Liu, Y.; Qiu, C.-W.; Han, J.; Tsai, D.-P.; Xiao, S. Reprogrammable meta-hologram for optical encryption. Nat. Commun. 2020, 11, 5484. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Sain, B.; Wei, Q.; Tang, C.; Li, X.; Weiss, T.; Huang, L.; Wang, Y.; Zentgraf, T. Multichannel vectorial holographic display and encryption. Light Sci. Appl. 2018, 7, 95. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Wang, Y.; Li, X.; Wang, Q.; Wei, Q.; Geng, G.; Huang, L. Switchable active phase modulation and holography encryption based on hybrid metasurfaces. Nanophotonics 2020, 9, 905–912. [Google Scholar] [CrossRef]
- Guo, X.; Zhong, J.; Li, B.; Qi, S.; Li, Y.; Li, P.; Wen, D.; Liu, S.; Wei, B.; Zhao, J. Full-Color Holographic Display and Encryption with Full-Polarization Degree of Freedom. Adv. Mater. 2022, 34, 2103192. [Google Scholar]
- Montelongo, Y.; Tenorio-Pearl, J.O.; Williams, C.; Zhang, S.; Milne, W.I.; Wilkinson, T.D. Plasmonic nanoparticle scattering for color holograms. Proc. Natl. Acad. Sci. USA 2014, 111, 12679–12683. [Google Scholar] [CrossRef]
- Huang, K.; Liu, H.; Garcia-Vidal, F.J.; Hong, M.; Luk’yanchuk, B.; Teng, J.; Qiu, C.-W. Ultrahigh-capacity non-periodic photon sieves operating in visible light. Nat. Commun. 2015, 6, 7059. [Google Scholar] [CrossRef]
- Wang, Z.X.; Wu, J.W.; Wu, L.W.; Gou, Y.; Ma, H.F.; Cheng, Q.; Cui, T.J. High Efficiency Polarization-Encoded Holograms with Ultrathin Bilayer Spin-Decoupled Information Metasurfaces. Adv. Opt. Mater. 2021, 9, 2001609. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, Y.; Chen, M.; Xu, R.; Yuan, L. Ultracompact metaimage display and encryption with a silver nanopolarizer based metasurface. Appl. Phys. Lett. 2020, 117, 021105. [Google Scholar] [CrossRef]
- Ni, X.; Kildishev, A.V.; Shalaev, V.M. Metasurface holograms for visible light. Nat. Commun. 2013, 4, 2807. [Google Scholar] [CrossRef]
- Deng, Z.L.; Jin, M.; Ye, X.; Wang, S.; Shi, T.; Deng, J.; Mao, N.; Cao, Y.; Guan, B.O.; Alù, A.; et al. Full-Color Complex-Amplitude Vectorial Holograms Based on Multi-Freedom Metasurfaces. Adv. Funct. Mater. 2020, 30, 1910610. [Google Scholar] [CrossRef]
- Sajedian, I.; Kim, J.; Rho, J. Finding the optical properties of plasmonic structures by image processing using a combination of convolutional neural networks and recurrent neural networks. Microsyst. Nanoeng. 2019, 5, 27. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zhang, Q.; Cui, T.J. Deep Learning of Reflection Phase Predection for Arbitrary Coding Metasurface Atoms. In Proceedings of the 2019 IEEE International Conference on Computational Electromagnetics (ICCEM), Shanghai, China, 20–22 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–3. [Google Scholar]
- Yuze, T.; Hai, L.; Qinglin, Z. On the application of deep learning in modeling metasurface. In Proceedings of the 2019 International Applied Computational Electromagnetics Society Symposium—China (ACES), Nanjing, China, 8–11 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–2. [Google Scholar]
- Hodge, J.A.; Mishra, K.V.; Zaghloul, A.I. RF Metasurface Array Design Using Deep Convolutional Generative Adversarial Networks. In Proceedings of the 2019 IEEE International Symposium on Phased Array System & Technology (PAST), Waltham, MA, USA, 15–18 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Han, X.; Fan, Z.; Liu, Z.; Li, C.; Guo, L. Inverse design of metasurface optical filters using deep neural network with high degrees of freedom. InfoMat 2021, 3, 432–442. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, D.; Zhang, L.; Wang, X.; Chen, X. Adaptively reverse design of terahertz metamaterial for electromagnetically induced transparency with generative adversarial network. J. Appl. Phys. 2021, 130, 033101. [Google Scholar] [CrossRef]
- Alsaedi, D.; Badawe, M.E.; Ramahi, O.M. A Breast Cancer Detection System Using Metasurfaces with a Convolution Neural Network: A Feasibility Study. IEEE Trans. Microw. Theory Tech. 2022, 70, 3566–3576. [Google Scholar] [CrossRef]
- Dai, M.; Jiang, Y.; Yang, F.; Xu, X.; Zhao, W.; Dao, M.H.; Liu, Y. SLMGAN: Single-layer metasurface design with symmetrical free-form patterns using generative adversarial networks. Appl. Soft Comput. 2022, 130, 109646. [Google Scholar] [CrossRef]
- Huang, H.; Yang, X.S. A Metasurface Modeling Method Based on Generative Adversarial Network Combined with K-Nearest Neighbor. In Proceedings of the 2022 IEEE Conference on Antenna Measurements and Applications (CAMA), Guangzhou, China, 14–17 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–2. [Google Scholar]
- Donda, K.; Zhu, Y.; Merkel, A.; Wan, S.; Assouar, B. Deep learning approach for designing acoustic absorbing metasurfaces with high degrees of freedom. Extrem. Mech. Lett. 2022, 56, 101879. [Google Scholar] [CrossRef]
- Lin, H.; Tian, Y.; Hou, J.; Xu, W.; Shi, X.; Tang, R. Fussy Inverse Design of Metamaterial Absorbers Assisted by a Generative Adversarial Network. Front. Mater. 2022, 9, 926094. [Google Scholar] [CrossRef]
- Cheng, J.; Li, R.; Wang, Y.; Yuan, Y.; Wang, X.; Chang, S. Inverse design of generic metasurfaces for multifunctional wavefront shaping based on deep neural networks. Opt. Laser Technol. 2023, 159, 109038. [Google Scholar] [CrossRef]
- Zhu, R.; Qiu, T.; Wang, J.; Sui, S.; Hao, C.; Liu, T.; Li, Y.; Feng, M.; Zhang, A.; Qiu, C.W.; et al. Phase-to-pattern inverse design paradigm for fast realization of functional metasurfaces via transfer learning. Nat. Commun. 2021, 12, 2974. [Google Scholar] [CrossRef]
- Wang, J.; Yao, B.; Niu, Y.; Ma, J.; Wang, Y.; Qu, Z.; Duan, J.; Zhang, B. Generative adversarial networks for high degree of freedom metasurface designs. Adv. Compos. Hybrid Mater. 2025, 8, 94. [Google Scholar] [CrossRef]
- Chang, Y.; Abe, K.; Yokota, H.; Sudo, K.; Nakamura, Y.; Chu, S.L. Human Induced Pluripotent Stem Cell Reprogramming Prediction in Microscopy Images using LSTM based RNN. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2416–2419. [Google Scholar]
- Liu, Y.; Bai, A.; Qiu, Y.; Zhang, Y.; Lu, Z.; Wang, H.; Tan, J. A Dual-Path Generative Adversarial Network-based inverse design method for broadband RCS reduction metasurface element patterns. Opt. Lasers Eng. 2024, 182, 108466. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Q.; Cui, D.; Li, W.; Zhao, G. Inverse design of nanohole all-dielectric metasurface based on deep convolutional neural network. Opt. Commun. 2024, 569, 130793. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Imaging Time-Series to Improve Classification and Imputation. arXiv 2015, arXiv:1506.00327. [Google Scholar] [CrossRef]
- Nezaratizadeh, A.; Hashemi, S.M.; Bod, M. Prediction of multi-layer metasurface design using conditional deep convolutional generative adversarial networks. Optik 2024, 313, 172005. [Google Scholar] [CrossRef]
- Meng, H.; Feng, H.; Liu, J.; Zhang, X.; Yang, S.; Du, H.; Jia, Y.; Lin, Y.; Gao, Y. Target-driven deep learning for optimization design of electromagnetically induced transparency metasurfaces based on lithium tantalate. Opt. Commun. 2025, 583, 131684. [Google Scholar] [CrossRef]
- Chen, Y.; Meng, T.; Wu, M.; Hu, W.; Yang, D.; Wu, W. Nucleobase discrimination based on terahertz spectroscopy using multi-scale convolutional neural network with convolutional block attention module and long short-term memory. Sens. Actuators A Phys. 2025, 387, 116434. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, C.; Wang, W.; Yang, S.; Zhou, C. Convolutional neural network-assisted design and validation of terahertz metamaterial sensor. Mater. Des. 2025, 253, 113871. [Google Scholar] [CrossRef]
- Yu, H.; Liu, Y.; Lu, X.; Zhu, Z. Inverse design of polarization-insensitive all-dielectric BIC metasurface with dual Fano-resonances by deep learning. Opt. Commun. 2025, 587, 131964. [Google Scholar] [CrossRef]
- Garibo, O.; Firbas, N.; Sebastian, L.; Conejero, J. Gramian angular fields for leveraging pretrained computer vision models with anomalous diffusion trajectories. Phys. Rev. E 2023, 107, 034138. [Google Scholar] [CrossRef]
- Yan, J.; Li, Y.; Yin, G.; Yao, S.; Peng, Y. Inverse design on customised absorption of acoustic metamaterials with high degrees of freedom by deep learning. Mech. Syst. Signal Process. 2025, 237, 112989. [Google Scholar] [CrossRef]
- Cao, H.; Cao, F.; Wang, D. Quantum artificial neural networks with applications. Inf. Sci. 2015, 290, 1–6. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Wang, Z.; Zhang, B.-L. Neuronal State Estimation for Neural Networks With Two Additive Time-Varying Delay Components. IEEE Trans. Cybern. 2017, 47, 3184–3194. [Google Scholar] [CrossRef] [PubMed]
- Cao, F.; Ye, H.; Wang, D. A probabilistic learning algorithm for robust modeling using neural networks with random weights. Inf. Sci. 2015, 313, 62–78. [Google Scholar] [CrossRef]
- Xiong, J.J.; Zhang, G.-B.; Wang, J.X.; Yan, T.H. Improved Sliding Mode Control for Finite-Time Synchronization of Nonidentical Delayed Recurrent Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2209–2216. [Google Scholar] [CrossRef]
- Jiang, X.W.; Yan, T.H.; Zhu, J.J.; He, B.; Li, W.H.; Du, H.P.; Sun, S.S. Densely Connected Deep Extreme Learning Machine Algorithm. Cogn. Comput. 2020, 12, 979–990. [Google Scholar] [CrossRef]
- Lin, S.; Cao, F. Simultaneous approximation by spherical neural networks. Neurocomputing 2016, 175, 348–354. [Google Scholar] [CrossRef]
- Meng, X.; Yan, J.; Ye, H.; Cao, F. Construction and approximation for a class of feedforward neural networks with sigmoidal function. Int. J. Wavelets Multiresolut. Inf. Process. 2023, 21, 2350028. [Google Scholar] [CrossRef]
- Cao, F.; Wang, D.; Zhu, H.; Wang, Y. An iterative learning algorithm for feedforward neural networks with random weights. Inf. Sci. 2016, 328, 546–557. [Google Scholar] [CrossRef]
- Cao, F.; Chen, B. New architecture of deep recursive convolution networks for super-resolution. Knowl. Based Syst. 2019, 178, 98–110. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Chang, H.; He, J. Optimization Design of Polar-LDPC Concatenated Scheme Based on Deep Learning. Comput. Electr. Eng. 2020, 84, 106636. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Wang, J.; Fang, X.; He, Y. Ensemble enhanced active learning mixture discriminant analysis model and its application for semi-supervised fault classification. Front. Inf. Technol. Electron. Eng. 2022, 23, 1814–1827. [Google Scholar] [CrossRef]
- He, W.; Pan, C.; Xu, W.; Zhang, N. Multi-attention embedded network for salient object detection. Soft Comput. 2021, 25, 13053–13067. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, Q.; Cao, F.; Ding, C.; Wang, L. Modeling a stochastic age-structured capital system with Poisson jumps using neural networks. Inf. Sci. 2020, 516, 254–265. [Google Scholar] [CrossRef]
- Wang, L.; Wang, B. Construction of greenhouse environment temperature adaptive model based on parameter identification. Comput. Electron. Agric. 2020, 174, 105477. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H.; Yang, X.; Gao, Y.; Cui, X.; Wang, B. Research on smooth path planning method based on improved ant colony algorithm optimized by Floyd algorithm. Front. Neurorobot. 2022, 16, 955179. [Google Scholar] [CrossRef]
- Zou, H. Clustering Algorithm and Its Application in Data Mining. Wirel. Pers. Commun. 2020, 110, 21–30. [Google Scholar] [CrossRef]
- Kong, Y.; Lu, H.J.; Xue, Y.; Xia, H.X. Terminal neural computing: Finite-time convergence and its applications. Neurocomputing 2016, 217, 133–141. [Google Scholar] [CrossRef]
- Zhang, F. Modular configuration of service elements based on the improved K-means algorithm. Expert Syst. 2019, 36, e12344. [Google Scholar] [CrossRef]
- Xiong, L.; Wang, G.Z.; Liu, H.C. New Community Estimation Method in Bipartite Networks Based on Quality of Filtering Coefficient. Sci. Program. 2019, 2019, 4310561. [Google Scholar] [CrossRef]
- Wen, C.; Qian, W.; Zhang, Q.; Cao, F. Algorithms of matrix recovery based on truncated Schatten p-norm. Int. J. Mach. Learn. Cybern. 2021, 12, 1557–1570. [Google Scholar] [CrossRef]
- Wen, C.; Huai, T.; Zhang, Q.; Song, Z.; Cao, F. A new rotation forest ensemble algorithm. Int. J. Mach. Learn. Cybern. 2022, 13, 3569–3576. [Google Scholar] [CrossRef]
- Wang, X.; Gu, R.; Li, J. Improved Reduced Latency Soft-Cancellation Algorithm for Polar Decoding. China Commun. 2020, 17, 65–77. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Z.; Li, J.; Wang, Y.; Cao, H.; Li, Z.; Shan, L. An optimized encoding algorithm for systematic polar codes. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 193. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Li, J.; Bao, X.; Xie, K. An Improved Path Splitting Decision-Aided SCL Decoding Algorithm for Polar Codes. IEEE Commun. Lett. 2021, 25, 3463–3467. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Wu, Z.; He, J.; Zhang, Y.; Shan, L. Improved NSC decoding algorithm for polar codes based on multi-in-one neural network. Comput. Electr. Eng. 2020, 86, 106758. [Google Scholar] [CrossRef]
- Wang, W.; Lou, B.; Li, X.; Lou, X.; Jin, N.; Yan, K. Intelligent maintenance frameworks of large-scale grid using genetic algorithm and K-Mediods clustering methods. World Wide Web 2020, 23, 1177–1195. [Google Scholar] [CrossRef]
- Wang, S.; Lin, C.; Yan, W.; Su, X.; Yang, L. High-order modeling of multiphase flows: Based on discrete Boltzmann method. Comput. Fluids 2023, 265, 106009. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Chang, S.; Jin, X. Time-of-arrival–based localization algorithm in mixed line-of-sight/non-line-of-sight environments. Int. J. Distrib. Sens. Netw. 2020, 16, 155014772091380. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Zhou, M. Improved Bacterial Foraging Algorithm for Cell Formation and Product Scheduling Considering Learning and Forgetting Factors in Cellular Manufacturing Systems. IEEE Syst. J. 2020, 14, 3047–3056. [Google Scholar] [CrossRef]
- Wang, G.Z.; Xiong, L.; Liu, H.C. A Bayesian Inference Method Using Monte Carlo Sampling for Estimating the Number of Communities in Bipartite Networks. Sci. Program. 2019, 2019, 9471201. [Google Scholar] [CrossRef]
- Wang, C.; Cao, F. Error analysis of distributed algorithm for large scale data classification. J. Comput. Anal. Appl. 2016, 21, 1170–1175. [Google Scholar]
- Qian, W.; Cao, F. Adaptive algorithms for low-rank and sparse matrix recovery with truncated nuclear norm. Int. J. Mach. Learn. Cybern. 2019, 10, 1341–1355. [Google Scholar]
- Luo, M.; Zhou, X. Robustness of reverse triple I algorithms based on interval-valued fuzzy inference. Int. J. Approx. Reason. 2015, 66, 16–26. [Google Scholar] [CrossRef]
- Luo, M.; Zhao, R. Fuzzy reasoning algorithms based on similarity. J. Intell. Fuzzy Syst. 2018, 34, 213–219. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, K. Robustness of full implication algorithms based on interval-valued fuzzy inference. Int. J. Approx. Reason. 2015, 62, 61–72. [Google Scholar] [CrossRef]
- Luo, M.; Wu, L.; Fu, L. Robustness analysis of the interval-valued fuzzy inference algorithms. J. Intell. Fuzzy Syst. 2020, 38, 685–696. [Google Scholar]
- Luo, M.; Wang, Y. Interval-valued fuzzy reasoning full implication algorithms based on the t-representable t-norm. Int. J. Approx. Reason. 2020, 122, 1–8. [Google Scholar]
- Luo, M.; Liu, B. Robustness of interval-valued fuzzy inference triple I algorithms based on normalized Minkowski distance. J. Log. Algebr. Methods Program. 2017, 86, 298–307. [Google Scholar]
- Luo, M.; Cheng, Z.; Wu, J. Robustness of interval-valued universal triple I algorithms. J. Intell. Fuzzy Syst. 2016, 30, 1619–1628. [Google Scholar]
- Lu, H.; Yang, L.; Yan, K.; Xue, Y.; Gao, Z. A cost-sensitive rotation forest algorithm for gene expression data classification. Neurocomputing 2017, 228, 270–276. [Google Scholar] [CrossRef]
- Lu, H.; Meng, Y.; Yan, K.; Gao, Z. Kernel principal component analysis combining rotation forest method for linearly inseparable data. Cogn. Syst. Res. 2019, 53, 111–122. [Google Scholar] [CrossRef]
- Lu, H.; Gao, H.; Ye, M.; Wang, X. A Hybrid Ensemble Algorithm Combining AdaBoost and Genetic Algorithm for Cancer Classification with Gene Expression Data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 863–870. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Du, B.; Liu, J.; Xia, H.; Yeap, W.K. A kernel extreme learning machine algorithm based on improved particle swam optimization. Memetic Comput. 2017, 9, 121–128. [Google Scholar] [CrossRef]
- Lu, H.; Chen, J.; Yan, K.; Jin, J.; Xue, Y.; Gao, Z. A hybrid feature selection algorithm for gene expression data classification. Neurocomputing 2017, 256, 56–62. [Google Scholar] [CrossRef]
- Lou, X.; Zhou, Q.; Chen, Y.; Wu, D. Research on Low Complexity K-best Sphere Decoding Algorithm for MIMO Systems. Wirel. Pers. Commun. 2015, 84, 547–563. [Google Scholar] [CrossRef]
- Lou, X.; Peng, T.; Zhou, Q.; Chen, Y. Bit-Clusters Trellis Search Based Iterative MIMO Detection Algorithm. Wirel. Pers. Commun. 2015, 81, 547–562. [Google Scholar] [CrossRef]
- Liu, H.; Sha, J.; Wang, X. An Improved Critical Set for List Decoding of Polar Codes. IEEE Commun. Lett. 2023, 27, 2269–2273. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Leung, J.Y.T. Integrated bacteria foraging algorithm for cellular manufacturing in supply chain considering facility transfer and production planning. Appl. Soft Comput. 2018, 62, 602–618. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Leung, J.Y.T. Worker assignment and production planning with learning and forgetting in manufacturing cells by hybrid bacteria foraging algorithm. Comput. Ind. Eng. 2016, 96, 162–179. [Google Scholar] [CrossRef]
- Li, W.; Jiang, S.; Jin, Q. Overlap community detection using spectral algorithm based on node convergence degree. Future Gener. Comput. Syst. 2018, 79, 408–416. [Google Scholar] [CrossRef]
- Hu, M.; Feng, X.; Ji, Z.; Yan, K.; Zhou, S. A novel computational approach for discord search with local recurrence rates in multivariate time series. Inf. Sci. 2019, 477, 220–233. [Google Scholar] [CrossRef]
- Cui, X.; Wang, B.; Wang, L.; Chen, J. Online optimal learning algorithm for Stackelberg games with partially unknown dynamics and constrained inputs. Neurocomputing 2021, 445, 1–11. [Google Scholar] [CrossRef]
- Cui, X.; Chen, J.; Wang, B.; Xu, S. Off-policy algorithm based Hierarchical optimal control for completely unknown dynamic systems. Neurocomputing 2022, 488, 669–680. [Google Scholar] [CrossRef]
- Chen, Z.; Cao, F. Approximation by Spherical de la Vallee-Poussin Mean Operators. J. Comput. Anal. Appl. 2014, 17, 539–546. [Google Scholar]
- Chai, Z. An indirect variable weights method to compute fuzzy comprehensive evaluation values. Soft Comput. 2019, 23, 12511–12519. [Google Scholar] [CrossRef]
- Cao, H.; Wang, D.; Cao, F. An adiabatic quantum algorithm and its application to DNA motif model discovery. Inf. Sci. 2015, 296, 275–281. [Google Scholar] [CrossRef]
- Cao, F.; Chen, Z. Approximation by Spherical Neural Networks with Sigmoidal Functions. J. Comput. Anal. Appl. 2015, 18, 390–396. [Google Scholar]
- Cao, F.; Liu, Y.; Zhang, W. Generalization Bounds of Regularization Algorithm with Gaussian Kernels. Neural Process. Lett. 2014, 39, 179–194. [Google Scholar]
- Wang, X.; Yan, W.Q. Human Gait Recognition Based on Frame-by-Frame Gait Energy Images and Convolutional Long Short-Term Memory. Int. J. Neural Syst. 2020, 30, 1950027. [Google Scholar]
- Wang, X.; Li, J.; Yang, L.; Mi, H. Unsupervised learning for community detection in attributed networks based on graph convolutional network. Neurocomputing 2021, 456, 147–155. [Google Scholar] [CrossRef]
- Cao, F.; Yao, K.; Liang, J. Deconvolutional neural network for image super-resolution. Neural Netw. 2020, 132, 394–404. [Google Scholar] [CrossRef] [PubMed]
- Cao, F.; Guo, W. Cascaded dual-scale crossover network for hyperspectral image classification. Knowl. Based Syst. 2020, 189, 105122. [Google Scholar] [CrossRef]
- Zhao, J.; Lv, Y.; Zhou, Z.; Cao, F. A novel deep learning algorithm for incomplete face recognition: Low-rank-recovery network. Neural Netw. 2017, 94, 115–124. [Google Scholar] [CrossRef]
- Cao, F.; Liu, H. Single image super-resolution via multi-scale residual channel attention network. Neurocomputing 2019, 358, 424–436. [Google Scholar] [CrossRef]
- Liu, H.; Cao, F. Improved dual-scale residual network for image super-resolution. Neural Netw. 2020, 132, 84–95. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, C.; Zhou, Z.; Cao, F. Single image super-resolution based on adaptive convolutional sparse coding and convolutional neural networks. J. Vis. Commun. Image Represent. 2019, 58, 651–661. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, J.; Zhou, Z. L1 model-driven recursive multi-scale denoising network for image super-resolution. Knowl. Based Syst. 2021, 225, 107115. [Google Scholar] [CrossRef]
- Miao, J.; Cao, F.; Ye, H.; Li, M.; Yang, B. Revisiting graph neural networks from hybrid regularized graph signal reconstruction. Neural Netw. 2023, 157, 444–459. [Google Scholar] [CrossRef]
- Dai, C.; Pan, C.; He, W. Feature extraction and fusion network for salient object detection. Multimed. Tools Appl. 2022, 81, 33955–33969. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, T.; Zhou, Z.; Cao, F. A Compact Recursive Dense Convolutional Network for image classification. Neurocomputing 2020, 372, 8–16. [Google Scholar] [CrossRef]
- Cao, F.; Chen, B. Densely connected network with improved pyramidal bottleneck residual units for super-resolution. J. Vis. Commun. Image Represent. 2021, 74, 102963. [Google Scholar] [CrossRef]
- Huang, G.; Yang, L.; Zhang, D.; Wang, X.; Wang, Y. Baggage Image Retrieval with Attention-Based Network for Security Checks. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2155009. [Google Scholar] [CrossRef]
- Yao, K.; Liang, J.; Liang, J.; Li, M.; Cao, F. Multi-view graph convolutional networks with attention mechanism. Artif. Intell. 2022, 307, 103708. [Google Scholar] [CrossRef]
- Liu, H.; Cao, F.; Wen, C.; Zhang, Q. Lightweight multi-scale residual networks with attention for image super-resolution. Knowl. Based Syst. 2020, 203, 106103. [Google Scholar] [CrossRef]
- Lu, J.; Zhao, J.; Cao, F. Extended feed forward neural networks with random weights for face recognition. Neurocomputing 2014, 136, 96–102. [Google Scholar] [CrossRef]
- Cao, F.; Guo, W. Deep hybrid dilated residual networks for hyperspectral image classification. Neurocomputing 2020, 384, 170–181. [Google Scholar] [CrossRef]
- Liu, Z.; Jia, X.; Xu, X. Study of shrimp recognition methods using smart networks. Comput. Electron. Agric. 2019, 165, 104926. [Google Scholar] [CrossRef]
- Dai, K.; Zhao, J.; Cao, F. A novel decorrelated neural network ensemble algorithm for face recognition. Knowl. Based Syst. 2015, 89, 541–552. [Google Scholar] [CrossRef]
- Cao, F.; Li, K. A new method for image super-resolution with multi-channel constraints. Knowl. Based Syst. 2018, 146, 118–128. [Google Scholar] [CrossRef]
- Lu, Z.; Qin, S.; Lv, P.; Sun, L.; Tang, B. Real-time continuous detection and recognition of dynamic hand gestures in untrimmed sequences based on end-to-end architecture with 3D DenseNet and LSTM. Multimed. Tools Appl. 2023, 83, 16275–16312. [Google Scholar] [CrossRef]
- Gao, C.; Ye, H.; Cao, F.; Wen, C.; Zhang, Q.; Zhang, F. Multiscale fused network with additive channel–spatial attention for image segmentation. Knowl. Based Syst. 2021, 214, 106754. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, H.; Cao, F. Image super-resolution via adaptive sparse representation. Knowl. Based Syst. 2017, 124, 23–33. [Google Scholar] [CrossRef]
- Xiang, R. Image segmentation for whole tomato plant recognition at night. Comput. Electron. Agric. 2018, 154, 434–442. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, L.; Liu, H. Emergency decision making with extended axiomatic design approach under picture fuzzy environment. Expert Syst. 2020, 37, e12482. [Google Scholar] [CrossRef]
- Zhao, R.; Luo, M.; Li, S. A Dynamic Distance Measure of Picture Fuzzy Sets and Its Application. Symmetry 2021, 13, 436. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, Y.; Fu, L. A New Similarity Measure for Picture Fuzzy Sets and Its Application to Multi-Attribute Decision Making. Informatica 2021, 32, 543–564. [Google Scholar] [CrossRef]
- Wan, W.; Zhou, Z.; Zhao, J.; Cao, F. A novel face recognition method: Using random weight networks and quasi-singular value decomposition. Neurocomputing 2015, 151, 1180–1186. [Google Scholar] [CrossRef]
- Pan, C.; Yan, W.Q. Object detection based on saturation of visual perception. Multimed. Tools Appl. 2020, 79, 19925–19944. [Google Scholar] [CrossRef]
- Luo, M.; Long, H. Picture Fuzzy Geometric Aggregation Operators Based on a Trapezoidal Fuzzy Number and Its Application. Symmetry 2021, 13, 119. [Google Scholar] [CrossRef]
- Luo, M.; Li, W. Some new similarity measures on picture fuzzy sets and their applications. Soft Comput. 2023, 27, 6049–6067. [Google Scholar] [CrossRef]
- Wang, X.; Yan, K. Immersive human–computer interactive virtual environment using large-scale display system. Future Gener. Comput. Syst. 2019, 96, 649–659. [Google Scholar] [CrossRef]
- Zheng, Z.; Wu, H.; Lv, L.; Ye, H.; Zhang, C.; Yu, G. ICCL: Independent and Correlative Correspondence Learning for few-shot image classification. Knowl. Based Syst. 2023, 266, 110412. [Google Scholar] [CrossRef]
- Ye, M.; Xu, Y.; Ji, C.; Chen, H.; Lu, H.; Qian, Y. Feature selection for cross-scene hyperspectral image classification using cross-domain ReliefF. Int. J. Wavelets Multiresolut. Inf. Process. 2019, 17, 1950039. [Google Scholar] [CrossRef]
- Zhu, W.; Peng, Y. Elastic net regularized kernel non-negative matrix factorization algorithm for clustering guided image representation. Appl. Soft Comput. 2020, 97, 106774. [Google Scholar] [CrossRef]
- He, B.; Song, Y.; Zhu, Y.; Sha, Q.; Shen, Y.; Yan, T.; Nian, R.; Lendasse, A. Local receptive fields based extreme learning machine with hybrid filter kernels for image classification. Multidimens. Syst. Signal Process. 2019, 30, 1149–1169. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Hong, R.; Li, Z.; Li, M.; Pan, W.; Glowacz, A.; He, H. Knowledge graph analysis and visualization of research trends on driver behavior. J. Intell. Fuzzy Syst. 2020, 38, 495–511. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, L.; Zhang, D.; Shen, Y.; Huang, S. Face Deduplication in Video Surveillance. Int. J. Pattern Recognit. Artif. Intell. 2018, 32, 1856001. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, G. Divergence-based distance for picture fuzzy sets and its application to multi-attribute decision-making. Soft Comput. 2024, 28, 253–269. [Google Scholar] [CrossRef]
- Cao, S.; Wang, X. Real-time dynamic gesture recognition and hand servo tracking using PTZ camera. Multimed. Tools Appl. 2019, 78, 27403–27424. [Google Scholar] [CrossRef]
- Liu, H.; Shao, M.; Wang, C.; Cao, F. Image Super-Resolution Using a Simple Transformer Without Pretraining. Neural Process. Lett. 2023, 55, 1479–1497. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, L.; Yin, H.; Lan, J.; Cao, F. An automatic 2D to 3D video conversion approach based on RGB-D images. Multimed. Tools Appl. 2021, 80, 19179–19201. [Google Scholar] [CrossRef]
- Wen, Y.; Vese, L.; Shi, K.; Guo, Z.; Sun, J. Nonlocal Adaptive Biharmonic Regularizer for Image Restoration. J. Math. Imaging Vis. 2023, 65, 453–471. [Google Scholar] [CrossRef]
- Ye, M.; Wang, C.; Meng, Z.; Xiong, F.; Qian, Y. Domain-invariant attention network for transfer learning between cross-scene hyperspectral images. IET Comput. Vis. 2023, 17, 739–749. [Google Scholar] [CrossRef]
- Lei, L.; Huang, B.; Ye, M.; Yao, F.; Qian, Y. Cross-domain residual deep NMF for transfer learning between different hyperspectral image scenes. Int. J. Wavelets Multiresolut. Inf. Process. 2023, 21, 2250046. [Google Scholar] [CrossRef]
- Zhou, Z.; Xue, B.; Wang, H.; Zhao, J. Bidirectional Multi-scale Deformable Attention for Video Super-Resolution. Multimed. Tools Appl. 2023, 83, 27809–27830. [Google Scholar] [CrossRef]
- Huang, G.; Wang, X.; Li, X.; Wang, Y. Spatiotemporal feature enhancement network for action recognition. Multimed. Tools Appl. 2023, 83, 57187–57197. [Google Scholar] [CrossRef]
- Zheng, Y.; He, L.; Wu, X.; Pan, C. Self-training and Multi-level Adversarial Network for Domain Adaptive Remote Sensing Image Segmentation. Neural Process. Lett. 2023, 55, 10613–10638. [Google Scholar] [CrossRef]
- Xiao, J.; Liu, P.; Lin, H.; Fang, H.; Xu, J.; Shan, H.; Hu, H.; Huang, Y.; Lu, H. Blockchain and UAV-Enabled Signal Source Identification with Edge Computing and Wireless Signal-Aerial Image Fusion. Wirel. Commun. Mob. Comput. 2022, 2022, 4009078. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, K.; Luo, M.; Yin, C.; Lai, X. Extreme learning machine and adaptive sparse representation for image classification. Neural Netw. 2016, 81, 91–102. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, S.; He, B.; Sha, Q.; Shen, Y.; Yan, T.; Nian, R.; Lendasse, A. Gaussian derivative models and ensemble extreme learning machine for texture image classification. Neurocomputing 2018, 277, 53–64. [Google Scholar] [CrossRef]
- Hu, T.; Zhao, J.; Zheng, R.; Wang, P.; Li, X.; Zhang, Q. Ultrasonic based concrete defects identification via wavelet packet transform and GA-BP neural network. PeerJ Comput. Sci. 2021, 7, e635. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Fan, W.; Luo, Z.; Guo, B. Soybean seed counting and broken seed recognition based on image sequence of falling seeds. Comput. Electron. Agric. 2022, 196, 106870. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, T.; Cao, F. Image super-resolution via adaptive sparse representation and self-learning. IET Comput. Vis. 2018, 12, 753–761. [Google Scholar] [CrossRef]
- Cao, F.; Feng, X.; Zhao, J. Sparse representation for robust face recognition by dictionary decomposition. J. Vis. Commun. Image Represent. 2017, 46, 260–268. [Google Scholar] [CrossRef]
- Cao, F.; Gao, C.; Ye, H. A novel method for image segmentation: Two-stage decoding network with boundary attention. Int. J. Mach. Learn. Cybern. 2022, 13, 1461–1473. [Google Scholar] [CrossRef]
- Wang, X.; Yan, K. Automatic color correction for multi-projector display systems. Multimed. Tools Appl. 2018, 77, 13115–13132. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, W.; Zhao, J. Robust visual tracking using discriminative sparse collaborative map. Int. J. Mach. Learn. Cybern. 2019, 10, 3201–3212. [Google Scholar] [CrossRef]
- Zhao, R.; Ma, L.; Li, S.; Luo, M. A Multi-Criteria Three-Way Decision Making Method in a Picture Fuzzy Probabilistic Decision System. Cogn. Comput. 2022, 14, 1924–1941. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, N.; Zhou, Z. A temporal sparse collaborative appearance model for visual tracking. Multimed. Tools Appl. 2020, 79, 14103–14125. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, J.; Sun, M.; Xiang, Z. High-density crowd behaviors segmentation based on dynamical systems. Multimed. Syst. 2017, 23, 599–606. [Google Scholar] [CrossRef]
- Yu, A.Y.; Liu, H.C.; Zhang, L.; Chen, Y. A new data envelopment analysis-based model for failure mode and effect analysis with heterogeneous information. Comput. Ind. Eng. 2021, 157, 107350. [Google Scholar] [CrossRef]
- Tan, Y.; Cao, F.; Miaomiao Cai, M.C. A New System of Face Recognition: Using Fuzziness and Sparsity. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2015, 23, 829–844. [Google Scholar] [CrossRef]
- Shi, K.; Guo, Z. Non-Gaussian Noise Removal via Gaussian Denoisers with the Gray Level Indicator. J. Math. Imaging Vis. 2023, 65, 844–860. [Google Scholar] [CrossRef]
- Shi, K. A gray level indicator-based nonlinear diffusion equation for the removal of random-valued impulse noise. Multimed. Tools Appl. 2022, 81, 10529–10544. [Google Scholar] [CrossRef]
- Qiu, G.; Tian, S.; Yuan, Q. Research of Crack Defect Detection in Metal Pipes Based on Microwave Antenna Array. Wirel. Commun. Mob. Comput. 2022, 2022, 1–8. [Google Scholar] [CrossRef]
- Liang, W.; Zhou, X.; Huang, S.; Hu, C.; Xu, X.; Jin, Q. Modeling of cross-disciplinary collaboration for potential field discovery and recommendation based on scholarly big data. Future Gener. Comput. Syst. 2018, 87, 591–600. [Google Scholar] [CrossRef]
- Li, J.; Zhuo, J.; Wu, Y.; Wang, Z.; Yao, Z.; Jia, H.; Wang, Z.; Chen, Y.; Zhou, D.; Yu, M. A Rapid Temporal Bone Localization Method Based on Machine Visual Detection Markers. Sci. Program. 2022, 2022, 7202627. [Google Scholar] [CrossRef]
- Gao, Z.; Cheng, Z.; Diao, W.; Zhang, J.; Lu, H. Identity authentication based on trajectory characteristics of mobile devices. J. Syst. Archit. 2021, 112, 101857. [Google Scholar] [CrossRef]
- Cao, S.; Shu, Z.; Xu, Z.; Xie, D.; Xu, Y. Character segmentation and restoration of Qin-Han bamboo slips using local auto-focus thresholding method. Multimed. Tools Appl. 2022, 81, 8199–8213. [Google Scholar] [CrossRef]
- Cao, F.; Zhu, L.; Ye, H.; Wen, C.; Zhang, Q. A new method for point cloud registration: Adaptive relation-oriented convolution and recurrent correspondence-walk. Knowl. Based Syst. 2024, 284, 111280. [Google Scholar] [CrossRef]
- Cao, F.; Hu, H.; Lu, J.; Zhao, J.; Zhou, Z.; Wu, J. Pose and illumination variable face recognition via sparse representation and illumination dictionary. Knowl. Based Syst. 2016, 107, 117–128. [Google Scholar] [CrossRef]
- Cao, F.; Cai, M.; Tan, Y.; Zhao, J. Image Super-Resolution via Adaptive Regularization and Sparse Representation. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1550–1561. [Google Scholar] [CrossRef]
- Jin, Y.; Lu, H.; Zhu, W.; Huo, W. Deep learning based classification of multi-label chest X-ray images via dual-weighted metric loss. Comput. Biol. Med. 2023, 157, 106683. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhao, J.; Cao, F. Diagnosis of fatigue crack growth with recursive random weight networks. Comput. Electr. Eng. 2014, 40, 2227–2235. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Yao, S.; Xu, Y.; Zhao, W.; Tong, Y.; Zhou, Z. DeepCIP: A multimodal deep learning method for the prediction of internal ribosome entry sites of circRNAs. Comput. Biol. Med. 2023, 164, 107288. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Lu, H.; Li, Z.; Wang, Y. A cross-modal deep metric learning model for disease diagnosis based on chest x-ray images. Multimed. Tools Appl. 2023, 82, 33421–33442. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Lu, H.; Zhou, R.; Yao, Y.; Zhu, W. CMFuse: Correlation-based multi-scale feature fusion network for the detection of COVID-19 from Chest X-ray images. Multimed. Tools Appl. 2023, 83, 49285–49300. [Google Scholar] [CrossRef]
- Shang, B.; Chen, R.; Yan, W.; Yu, H. GPU accelerated volumetric lattice Boltzmann model for image-based hemodynamics in portal hypertension. Comput. Fluids 2023, 266, 106038. [Google Scholar] [CrossRef]
- Li, X.; Pan, C.; He, L.; Li, X. Unsupervised Domain Adaptation for Cross-domain Histopathology Image Classification. Multimed. Tools Appl. 2023, 83, 23311–23331. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, F.; Zhao, J.; Chu, J. Segmentation of White Blood Cells Image Using Adaptive Location and Iteration. IEEE J. Biomed. Health Inform. 2017, 21, 1644–1655. [Google Scholar] [CrossRef]
- Ye, C.; Pan, J.; Jin, Q. An improved SSO algorithm for cyber-enabled tumor risk analysis based on gene selection. Future Gener. Comput. Syst. 2019, 92, 407–418. [Google Scholar] [CrossRef]
- Zheng, S.; Chang, P.; Chen, J.; Chang, Y.; Fan, H. An Investigation of Patient Decisions to Use eHealth: A View of Multichannel Services. J. Organ. End User Comput. 2021, 34, 1–24. [Google Scholar] [CrossRef]
- Wang, B.; Bao, C.; Chen, D. Identification of Axial and Radial Impacts for Pneumatic Artificial Muscles in Static and Dynamic Processes Based on Autocorrelations of Differential Pressure Signals. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2159014. [Google Scholar] [CrossRef]
- Li, S.; Li, D.; Zhang, R.; Cao, F. A novel autism spectrum disorder identification method: Spectral graph network with brain-population graph structure joint learning. Int. J. Mach. Learn. Cybern. 2024, 15, 1517–1532. [Google Scholar] [CrossRef]
- Li, J.; Li, D.; Zhuo, J.; Wang, Z. Modeling and simulation of cochlear perimodiolar electrode based on composite spring-mass model. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 290–297. [Google Scholar] [CrossRef]
- Kong, D.; Zhu, J.; Wu, S.; Duan, C.; Lu, L.; Chen, D. A novel IRBF-RVM model for diagnosis of atrial fibrillation. Comput. Methods Programs Biomed. 2019, 177, 183–192. [Google Scholar] [CrossRef]
- Ke, B.; Lu, H.; You, C.; Zhu, W.; Li, X.; Yao, Y. A semi-supervised medical image classification method based on combined pseudo-labeling and distance metric consistency. Multimed. Tools Appl. 2023, 83, 33313–33331. [Google Scholar] [CrossRef]
- Jiang, S.; Shi, H.; Lin, W.; Liu, H.-C. A large group linguistic Z-DEMATEL approach for identifying key performance indicators in hospital performance management. Appl. Soft Comput. 2020, 86, 105900. [Google Scholar] [CrossRef]
- Gou, Z.; Ruan, X.; Huang, F.; Fu, X. Effects of membrane reference state on shape memory of a red blood cell. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 465–474. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Huang, X.; Bao, Q.; Li, X.; Wang, Y. Abnormal operation recognition based on a spatiotemporal residual network. Multimed. Tools Appl. 2023, 83, 61929–61941. [Google Scholar] [CrossRef]
- Yang, B.; Xiang, X.Q.; Xu, D.Q.; Wang, X.H.; Yang, X. 3D palmprint recognition using shape index representation and fragile bits. Multimed. Tools Appl. 2017, 76, 15357–15375. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Yan, K. Hand gesture recognition based on concentric circular scan lines and weighted K-nearest neighbor algorithm. Multimed. Tools Appl. 2018, 77, 209–223. [Google Scholar] [CrossRef]
- Wang, X.; Feng, S.; Yan, W.Q. Human Gait Recognition Based on Self-Adaptive Hidden Markov Model. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 963–972. [Google Scholar]
- Wang, X.; Yan, W.Q. Non-local gait feature extraction and human identification. Multimed. Tools Appl. 2021, 80, 6065–6078. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Q.; Yan, K.; Du, Y. Deep Learning Enhanced Solar Energy Forecasting with AI-Driven IoT. Wirel. Commun. Mob. Comput. 2021, 2021, 9249387. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Y.; Wang, B.; Wang, Z. Design and analysis of associative memories based on external inputs of delayed recurrent neural networks. Neurocomputing 2014, 136, 337–344. [Google Scholar] [CrossRef]
- Lin, D.H.; Wu, J.; Li, J.N. Less conservative stability condition for uncertain discrete-time recurrent neural networks with time-varying delays. Neurocomputing 2016, 173, 1578–1588. [Google Scholar]
- Liu, Y.; Wang, J. Research on post-match score mechanism of players based on artificial intelligence and clustering regression model. J. Intell. Fuzzy Syst. 2020, 39, 4869–4879. [Google Scholar] [CrossRef]
- Zhu, W.; Peng, B. Manifold-based aggregation clustering for unsupervised vehicle re-identification. Knowl. Based Syst. 2022, 235, 107624. [Google Scholar] [CrossRef]
- Wang, L.; Li, X.; Xu, M.; Guo, Z.; Wang, B. Study on optimization model control method of light and temperature coordination of greenhouse crops with benefit priority. Comput. Electron. Agric. 2023, 210, 107892. [Google Scholar] [CrossRef]
- Zhu, W.; Chen, C.; Peng, B. Unified robust network embedding framework for community detection via extreme adversarial attacks. Inf. Sci. 2023, 643, 119200. [Google Scholar] [CrossRef]
- Zhou, Z.; Fu, Y.; Zhao, J. An efficient method for surface reconstruction based on local coordinate system transform and partition of unity. Neural Netw. World 2020, 30, 161–176. [Google Scholar] [CrossRef]
- Zhou, T.; Zhang, S.; Zhang, D.; Chan, V. Customer-oriented multi-objective optimization on a novel collaborative multi-heterogeneous-depot electric vehicle routing problem with mixed time windows. J. Intell. Fuzzy Syst. 2023, 44, 3787–3805. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Y.; Deng, G.; Yang, P.; Chen, Z.; Li, Y. An intelligently adjusted carbon price forecasting approach based on breakpoints segmentation, feature selection and adaptive machine learning. Appl. Soft Comput. 2023, 149, 110948. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, W.; Cao, F. Robust object tracking using a sparse coadjutant observation model. Multimed. Tools Appl. 2018, 77, 30969–30991. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, S.; Wu, Y.; Zhao, T.; Yan, Y.; Li, Z.; Li, Y. A new intelligent supermarket security system. Neural Netw. World 2020, 30, 113–131. [Google Scholar] [CrossRef]
- Zhang, F. Research for service flow module granularity design based on fuzzy spaces quotient theory. Clust. Comput. 2019, 22, 5825–5837. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, H. Multicultural Integration of Urban International Communities in the Innovation Ecosystem. Sci. Program. 2022, 2022, 3848088. [Google Scholar] [CrossRef]
- Tan, C. Research on the Path of Sports Sociology Curriculum from the Interdisciplinary Perspective. Mob. Inf. Syst. 2022, 2022, 3415257. [Google Scholar] [CrossRef]
- Lv, L.; Hu, P.; Zheng, Z.; Bardou, D.; Zhang, T.; Wu, H. A Community-Based Centrality Measure for Identifying Key Nodes in Multilayer Networks. IEEE Trans. Comput. Soc. Syst. 2024, 11, 2448–2463. [Google Scholar] [CrossRef]
- Luo, M.; Zhang, G.; Wu, L. A novel distance between single valued neutrosophic sets and its application in pattern recognition. Soft Comput. 2022, 26, 11129–11137. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Bao, Q.; Li, X. Behavior detection and evaluation based on multi-frame MobileNet. Multimed. Tools Appl. 2023, 83, 15733–15750. [Google Scholar] [CrossRef]
- Liu, H.; Quan, M.; Li, Z.; Wang, Z. A new integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment. Inf. Sci. 2019, 486, 254–270. [Google Scholar] [CrossRef]
- Liang, W.; Chen, X.; Huang, S.; Xiong, G.; Yan, K.; Zhou, X. Federal learning edge network based sentiment analysis combating global COVID-19. Comput. Commun. 2023, 204, 33–42. [Google Scholar] [CrossRef]
- Li, W.; Ye, Z.B.; Zhao, X.H.; Jiang, J.L.; Jin, Q. Probability Modeling and Functional Validation of Dynamic Service Composition for Location Based Services with Uncertain Factors. J. Internet Technol. 2014, 15, 635–643. [Google Scholar]
- Li, J.F.; Chen, S.P.; Duan, L.M.; Niu, L. A PR-quadtree based multi-dimensional indexing for complex query in a cloud system. Clust. Comput. 2017, 20, 2931–2942. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, X.X.; Xiu, S.W.; Zheng, D.D.; Yu, M.; Ma, D.; Huang, K.; Chen, G.; Yan, X.L. Profiling and annotation combined method for multimedia application specific MPSoC performance estimation. Front. Inf. Technol. Electron. Eng. 2015, 16, 135–151. [Google Scholar] [CrossRef]
- Huang, K.; Xiu, S.; Yu, M.; Zhang, X.; Yan, R.; Yan, X.; Liu, Z. Software Pipeline–Based Partitioning Method with Trade-Off between Workload Balance and Communication Optimization. ETRI J. 2015, 37, 562–572. [Google Scholar] [CrossRef]
- Hu, P.; Chu, X.; Lv, L.; Zuo, K.; Ni, T.; Wang, T.; Shen, Z. An efficient and secure data collection scheme for predictive maintenance of vehicles. Ad Hoc Netw. 2023, 146, 103157. [Google Scholar] [CrossRef]
- Han, Y.; Gu, P.; Gao, W.; Xu, G.; Wu, J. Aspect-level sentiment capsule network for micro-video click-through rate prediction. World Wide Web 2021, 24, 1045–1064. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, H.; Xie, Y.; Luo, Y.; Lu, H.; Yan, K. ChildGuard: A Child-Safety Monitoring System. IEEE Multimed. 2017, 24, 48–57. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, Z.; Jiang, Y.; Chen, J.; Peng, X.; Zhao, W. An Automatic RF-EMF Radiated Immunity Test System for Electricity Meters in Power Monitoring Sensor Networks. Ad Hoc Sens. Wirel. Netw. 2021, 50, 173–192. [Google Scholar]
- Yan, K.; Guo, X.; Ji, Z.; Zhou, X. Deep Transfer Learning for Cross-Species Plant Disease Diagnosis Adapting Mixed Subdomains. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 20, 2555–2564. [Google Scholar] [CrossRef]
- Xiang, R.; Jiang, H.; Ying, Y. Recognition of clustered tomatoes based on binocular stereo vision. Comput. Electron. Agric. 2014, 106, 75–90. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, X.; Shi, K. The analysis of agricultural Internet of things product marketing by deep learning. J. Supercomput. 2023, 79, 4602–4621. [Google Scholar] [CrossRef]
- Nadell, C.; Huang, B.; Malof, J.M.; Padilla, W.J. Deep learning for accelerated all-dielectric metasurface design. Opt. Express 2019, 27, 27523–27535. [Google Scholar] [CrossRef]
- Deng, Y.; Ren, S.; Fan, K.; Malof, J.M.; Padilla, W.J. Neural-adjoint method for the inverse design of all-dielectric metasurfaces. Opt. Express 2021, 29, 7526–7534. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, C.; Wan, X.; Zhang, L.; Liu, S.; Yang, Y.; Cui, T.J. Machine-Learning Designs of Anisotropic Digital Coding Metasurfaces. Adv. Theory Simul. 2019, 2, 1800132. [Google Scholar] [CrossRef]
- Socher, R.; Chen, D.; Manning, C.; Ng, A. Reasoning with neural tensor networks for knowledge base completion. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; Curran Associates Inc.: Red Hook, NY, USA, 2013; Volume 1, pp. 926–934. [Google Scholar]
- Malkiel, I.; Mrejen, M.; Nagler, A.; Arieli, U.; Wolf, L.; Suchowski, H. Plasmonic nanostructure design and characterization via Deep Learning. Light Sci. Appl. 2018, 7, 60. [Google Scholar] [CrossRef]
- Jiang, L.; Li, X.; Wu, Q.; Wang, L.; Gao, L. Neural network enabled metasurface design for phase manipulation. Opt. Express 2021, 29, 2521. [Google Scholar] [CrossRef] [PubMed]
- Mcculloch, W.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1990, 52, 99–115. [Google Scholar] [CrossRef] [PubMed]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.; Henderson, D.; Howard, R.; Hubbard, W.; Jackel, L. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, J.; Li, K.; Li, F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 2, pp. 2672–2680. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv:1411.1784. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 770–778. [Google Scholar]
- Peurifoy, J.; Shen, Y.; Li, J.; Yang, Y.; Cano-Renteria, F.; DeLacy, B.; Joannopoulos, J.; Tegmark, M.; Soljačić, M. Nanophotonic particle simulation and inverse design using artificial neural networks. Sci. Adv. 2018, 4, eaar4206. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, D.; Rodrigues, S.; Lee, K.; Cai, W. Generative Model for the Inverse Design of Metasurfaces. Nano Lett. 2018, 18, 6570–6576. [Google Scholar] [CrossRef]
- Ma, W.; Cheng, F.; Xu, Y.; Wen, Q.; Liu, Y. Probabilistic Representation and Inverse Design of Metamaterials Based on a Deep Generative Model with Semi-Supervised Learning Strategy. Adv. Mater. 2019, 31, 1901111. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Muskens, O.L. Deep Learning Meets Nanophotonics: A Generalized Accurate Predictor for Near Fields and Far Fields of Arbitrary 3D Nanostructures. Nano Lett. 2020, 20, 329–338. [Google Scholar] [CrossRef]
- Liu, Z.; Raju, L.; Zhu, D.; Cai, W. A Hybrid Strategy for the Discovery and Design of Photonic Structures. IEEE J. Emerg. Sel. Top. Circuits Syst. 2020, 10, 126–135. [Google Scholar] [CrossRef]
- Zheng, B.; Zhang, H. Deep Learning Based Multi-layer Metallic Metasurface Design. In Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Montreal, QC, Canada, 5–10 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2049–2050. [Google Scholar]
- Yeung, C.; Tsai, R.; Pham, B.; King, B.; Kawagoe, Y.; Ho, D.; Liang, J.; Knight, M.; Raman, A. Global Inverse Design across Multiple Photonic Structure Classes Using Generative Deep Learning. Adv. Opt. Mater. 2021, 9, 2100548. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, B.; Jin, F.; Zhou, G.; Lin, L. Machine Learning Approach for On-Demand Rapid Constructing Metasurface. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 4700209. [Google Scholar] [CrossRef]
- Yan, R.; Wang, T.; Jiang, X.; Zhong, Q.; Huang, X.; Wang, L.; Yue, X.; Wang, H.; Wang, Y. Efficient inverse design and spectrum prediction for nanophotonic devices based on deep recurrent neural networks. Nanotechnology 2021, 32, 335201. [Google Scholar] [CrossRef]
- Zandehshahvar, M.; Kiarashinejad, Y.; Zhu, M.; Maleki, H.; Brown, T.; Adibi, A. Manifold Learning for Knowledge Discovery and Intelligent Inverse Design of Photonic Nanostructures: Breaking the Geometric Complexity. ACS Photonics 2022, 9, 714–721. [Google Scholar] [CrossRef]
- Teng, Y.; Li, C.; Li, S.; Xiao, Y.; Jiang, L. Efficient design method for terahertz broadband metasurface patterns via deep learning. Opt. Laser Technol. 2023, 160, 109058. [Google Scholar] [CrossRef]
- Zhou, H.; Jiang, Y.; Lin, S.; Wang, J. Inverse design of cross-polarization conversion metasurfaces using convolutional neural networks. In Proceedings of the 2024 International Applied Computational Electromagnetics Society Symposium (ACES-China), Xi’an, China, 16–19 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–3. [Google Scholar]
- Xia, H.; Chen, S.; Wang, Y.; Zhao, Y.; Jia, H.; Yang, R.; Guo, Y. Deep-learning-assisted intelligent design of terahertz hybrid-functional metasurfaces with freeform patterns. Opt. Laser Technol. 2025, 181, 112041. [Google Scholar] [CrossRef]
- Wang, H.; Hu, J.; Baek, Y.; Tsuchiyama, K.; Joly, M.; Liu, Q.; Gigan, S. Optical next generation reservoir computing. Light Sci. Appl. 2025, 14, 245. [Google Scholar] [CrossRef]
- Zhu, C.; Zheng, B.; He, Z.; Gao, M.; Sun, C.; Bao, Z. State of Health Estimation of Lithium-Ion Battery Using Time Convolution Memory Neural Network. Mob. Inf. Syst. 2021, 2021, 4826409. [Google Scholar] [CrossRef]
- Wang, X.; Hu, S. Visual gait recognition based on convolutional block attention network. Multimed. Tools Appl. 2022, 81, 29459–29476. [Google Scholar] [CrossRef]
- Cao, F.; Liu, Y.; Wang, D. Efficient saliency detection using convolutional neural networks with feature selection. Inf. Sci. 2018, 456, 34–49. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Q.; Cui, X.; Guo, H.; Wang, K.; Zhu, D. High-throughput corn ear screening method based on two-pathway convolutional neural network. Comput. Electron. Agric. 2020, 175, 105525. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, Z.; Pan, J. Sensor-based fall detection using a combination model of a temporal convolutional network and a gated recurrent unit. Future Gener. Comput. Syst. 2023, 139, 53–63. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Yang, L.; Mi, H.; Yu, J. Weakly-supervised learning for community detection based on graph convolution in attributed networks. Int. J. Mach. Learn. Cybern. 2021, 12, 3529–3539. [Google Scholar] [CrossRef]
- Wang, X.; Yan, K. Gait classification through CNN-based ensemble learning. Multimed. Tools Appl. 2021, 80, 1565–1581. [Google Scholar] [CrossRef]
- Du, Z.; Ye, H.; Cao, F. A Novel Local–Global Graph Convolutional Method for Point Cloud Semantic Segmentation. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 4798–4812. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, J. Gait feature extraction and gait classification using two-branch CNN. Multimed. Tools Appl. 2020, 79, 2917–2930. [Google Scholar] [CrossRef]
- Basha, S.H.; Dubey, S.R.; Pulabaigari, V.; Mukherjee, S. Impact of fully connected layers on performance of convolutional neural networks for image classification. Neurocomputing 2020, 378, 112–119. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In Proceedings of the Computer Vision—ECCV 2016—14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Ueno, A.; Lin, H.; Yang, F.; An, S.; Martin-Monier, L.; Shalaginov, M.; Gu, T.; Hu, J. Dual-band optical collimator based on deep-learning designed, fabrication-friendly metasurfaces. Nanophotonics 2023, 12, 3491–3499. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Shalaginov, M.; Tang, H.; Li, H.; Zhou, L.; Dong, Y.; Haerinia, M.; Agarwal, A.; Rivero-Baleine, C.; et al. Deep Convolutional Neural Networks to Predict Mutual Coupling Effects in Metasurfaces. Adv. Opt. Mater. 2022, 10, 2102113. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Julian, M.; Williams, C.; Tang, H.; Gu, T.; Zhang, H.; Kim, H.; Hu, J. Deep neural network enabled active metasurface embedded design. Nanophotonics 2022, 11, 4149–4158. [Google Scholar] [CrossRef]
- Deng, Z.; Li, Y.; Li, Y.; Wang, Y.; Li, W.; Zhu, Z.; Guan, C.; Shi, J. Diverse ranking metamaterial inverse design based on contrastive and transfer learning. Opt. Express 2023, 31, 32865. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, L.; Wu, Y.; Hu, Z.; Evans, J.; Zhu, X.; Ye, G.; He, S. Utilizing Mixed Training and Multi-Head Attention to Address Data Shift in AI-Based Electromagnetic Solvers for Nano-Structured Metamaterials. Nanomaterials 2023, 13, 2778. [Google Scholar] [CrossRef]
- Liu, Z.; Dang, Z.; Liu, Z.; Li, Y.; He, X.; Dai, Y.; Chen, Y.; Peng, P.; Fang, Z. Self-design of arbitrary polarization-control waveplates via deep neural networks. Photonics Res. 2023, 11, 695. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Shalaginov, M.; Tang, H.; Li, H.; Zhou, L. A Deep Learning Approach to Explore the Mutual Coupling Effects in Metasurfaces. In Proceedings of the 2021 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 9–14 May 2021; pp. 1–2. [Google Scholar]
- Wei, H.; Bao, H.; Ruan, X. Perspective: Predicting and optimizing thermal transport properties with machine learning methods. Energy AI 2022, 8, 100153. [Google Scholar] [CrossRef]
- Lin, R.; Zhai, Y.; Xiong, C.; Li, X. Inverse design of plasmonic metasurfaces by convolutional neural network. Opt. Lett. 2020, 45, 1362. [Google Scholar] [CrossRef] [PubMed]
- Fowler, C.; An, S.; Zheng, B.; Li, H.; Tang, H.; Haerinia, M.; Dong, Y.; Zhang, Y.; Shalaginov, M.; Agarwal, A.; et al. A Deep Neural Network Near-Universal Dielectric Meta-Atom Generator. In OSA Optical Design and Fabrication 2021 (Flat Optics, Freeform, IODC, OFT); Optica Publishing Group: Washington, DC, USA, 2021. [Google Scholar]
- Dong, Y.; An, S.; Zheng, B.; Tang, H.; Huang, Y.; Haerinia, M. Data Collection and Network Design for Deep Learning Based Metasurface Design. In Proceedings of the 2023 International Applied Computational Electromagnetics Society Symposium (ACES), Seaside, CA, USA, 26–30 March 2023; pp. 1–2. [Google Scholar]
- Hegde, R. Deep neural network (DNN) surrogate models for the accelerated design of optical devices and systems. In Novel Optical Systems, Methods, and Applications XXII; Hahlweg, C.F., Mulley, J.R., Eds.; SPIE: San Diego, CA, USA, 2019; pp. 39–48. [Google Scholar]
- Yeung, C.; Pham, B.; Tsai, R.; Fountaine, K.; Raman, A. DeepAdjoint: An All-in-One Photonic Inverse Design Framework Integrating Data-Driven Machine Learning with Optimization Algorithms. ACS Photonics 2023, 10, 884–891. [Google Scholar] [CrossRef]
- Jiang, J.; Fan, J.A. Global Optimization of Dielectric Metasurfaces Using a Physics-Driven Neural Network. Nano Lett. 2019, 19, 5366–5372. [Google Scholar] [CrossRef] [PubMed]
- An, S.; Zheng, B.; Shalaginov, M.; Tang, H.; Li, H.; Zhou, L.; Ding, J.; Agarwal, A.; Rivero-Baleine, C.; Kang, M.; et al. Deep learning modeling approach for metasurfaces with high degrees of freedom. Opt. Express 2020, 28, 31932–31942. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 214–223. [Google Scholar]
- An, S.; Zheng, B.; Tang, H.; Shalaginov, M.; Zhou, L.; Li, H.; Kang, M.; Richardson, K.A.; Gu, T.; Hu, J.; et al. Multifunctional Metasurface Design with a Generative Adversarial Network. Adv. Opt. Mater. 2021, 9, 2001433. [Google Scholar] [CrossRef]
- Kudyshev, Z.; Kildishev, A.; Shalaev, V.; Boltasseva, A. Machine learning–assisted global optimization of photonic devices. Nanophotonics 2020, 10, 371–383. [Google Scholar] [CrossRef]
- Wang, H.; Cao, D.; Pang, X.; Zhang, X.; Wang, S.; Hou, W.; Nie, C.; Li, Y. Inverse design of metasurfaces with customized transmission characteristics of frequency band based on generative adversarial networks. Opt. Express 2023, 31, 37763. [Google Scholar] [CrossRef]
- Dai, P.; Sun, K.; Yan, X.; Muskens, O.L.; Groot, C.H.; Zhu, X.; Hu, Y.; Duan, H.; Huang, R. Inverse design of structural color: Finding multiple solutions via conditional generative adversarial networks. Nanophotonics 2022, 11, 3057–3069. [Google Scholar] [CrossRef]
- So, S.; Rho, J. Designing nanophotonic structures using conditional deep convolutional generative adversarial networks. Nanophotonics 2019, 8, 1255–1261. [Google Scholar] [CrossRef]
- Jiang, J.; Sell, D.; Hoyer, S.; Hickey, J.; Yang, J.; Fan, J. Free-Form Diffractive Metagrating Design Based on Generative Adversarial Networks. ACS Nano 2019, 13, 8872–8878. [Google Scholar] [CrossRef]
- Han, X.; Fan, Z.; Li, C.; Liu, Z.; Guo, L.J. High-Freedom Inverse Design with Deep Neural Network for Metasurface Filter in the Visible. arXiv 2019, arXiv:1912.03696. [Google Scholar] [CrossRef]
- Hodge, J.A.; Mishra, K.V.; Zaghloul Amir, I. Joint Multi-Layer GAN-Based Design of Tensorial RF Metasurfaces. In Proceedings of the 2019 IEEE 29th International Workshop on Machine Learning for Signal Processing (MLSP), Pittsburgh, PA, USA, 13–16 October 2019; pp. 1–6. [Google Scholar]
- Hodge, J.A.; Vijay Mishra, K.; Zaghloul Amir, I. Multi-Discriminator Distributed Generative Model for Multi-Layer RF Metasurface Discovery. In Proceedings of the 2019 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Ottawa, NA, Canada, 11–14 November 2019; pp. 1–5. [Google Scholar]
- Zhu, D.; Liu, Z.; Raju, L.; Kim, A.; Cai, W. Multifunctional Meta-Optic Systems: Inversely Designed with Artificial Intelligence. arXiv 2020, arXiv:2007.00130. [Google Scholar] [CrossRef]
- Jiang, J.; Fan, J.A. Simulator-based training of generative models for the inverse design of metasurfaces. Nanophotonics 2019, 9, 1059–1069. [Google Scholar] [CrossRef]
- Dai, M.; Jiang, Y.; Yang, F.; Chattoraj, J.; Xia, Y.; Xu, X.; Zhao, W.; Dao, M.H.; Liu, Y. A surrogate-assisted extended generative adversarial network for parameter optimization in free-form metasurface design. Neural Netw. 2024, 180, 106654. [Google Scholar] [CrossRef]
- Salehinejad, H.; Sankar, S.; Barfett, J.; Colak, E.; Valaee, S. Recent Advances in Recurrent Neural Networks. arXiv 2018, arXiv:1801.01078. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Graves, A. Long Short-Term Memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; Volume 385, pp. 37–45. [Google Scholar]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Dey, R.; Salem, F.M. Gate-variants of Gated Recurrent Unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar]
- Huang, W.; Tang, H.; Xu, P. OEC-RNN: Object-Oriented Delineation of Rooftops With Edges and Corners Using the Recurrent Neural Network from the Aerial Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5604912. [Google Scholar] [CrossRef]
- Pi, M.; Jin, N.; Chen, D. Short-Term Solar Irradiance Prediction Based on Multichannel LSTM Neural Networks Using Edge-Based IoT System. Wirel. Commun. Mob. Comput. 2022, 2022, 2372748. [Google Scholar] [CrossRef]
- Zhang, D.; Lan, H.; Ma, Z.; Yang, Z.; Wu, X.; Huang, X. Spatial-temporal gated graph convolutional network: A new deep learning framework for long-term traffic speed forecasting. J. Intell. Fuzzy Syst. 2023, 44, 10437–10450. [Google Scholar] [CrossRef]
- Wen, J.; Wang, X. Cross-view gait recognition based on residual long short-term memory. Multimed. Tools Appl. 2021, 80, 28777–28788. [Google Scholar]
- Vinayakumar, R.; Soman, K.P.; Poornachandran, P. Long short-term memory based operation log anomaly detection. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 236–242. [Google Scholar]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In Proceedings of the Interspeech 2014, Singapore, 14–18 September 2014; ISCA: Singapore, 2014; pp. 338–342. [Google Scholar]
- Sainath, T.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, Long Short-Term Memory, fully connected Deep Neural Networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 4580–4584. [Google Scholar]
- Chen, Y.; Mao, C.; Li, M.; Li, W.; Shi, M.; Wang, Q. Prediction of spectral response of all-dielectric trimer metasurface based on deep learning. Opt. Commun. 2025, 574, 131218. [Google Scholar] [CrossRef]
- Abdelraouf, O.A.M.; Mousa, A.; Ragab, M. NanoPhotoNet: AI-enhanced design tool for reconfigurable and high-performance multi-layer metasurfaces. Photonics Nanostruct.—Fundam. Appl. 2025, 64, 101379. [Google Scholar]
- Zhao, J.; Wang, Z.; Cao, F.; Wang, D. A local learning algorithm for random weights networks. Knowl. Based Syst. 2015, 74, 159–166. [Google Scholar] [CrossRef]
- Seo, J.; Jo, J.; Kim, J.; Kang, J.; Kang, C.; Moon, S.; Lee, E.; Hong, J.; Rho, J.; Chung, H. Deep-learning-driven end-to-end metalens imaging. Adv. Photonics 2024, 6, 066002. [Google Scholar] [CrossRef]
- Wei, W.; Tang, P.; Shao, J.; Zhu, J.; Zhao, X.; Wu, C. End-to-end design of metasurface-based complex-amplitude holograms by physics-driven deep neural networks. Nanophotonics 2022, 11, 2921–2929. [Google Scholar] [CrossRef]
- Wang, K.; Liao, D.S.; Wang, H.G. Origami Metasurface Hologram Based on Deep Learning. In Proceedings of the 2022 Cross Strait Radio Science & Wireless Technology Conference (CSRSWTC), Haidian, China, 17–18 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–3. [Google Scholar]
- Chen, S.; Hou, Z.; Wang, J.; Qiu, Y.; Li, Z.; Shen, J.; Li, C. Chiral Metasurface Vortex Focusing in Terahertz Band Based on Deep Learning. IEEE Photonics Technol. Lett. 2023, 35, 637–640. [Google Scholar]
- Lin, C.; Huang, S.; Lin, T.; Wu, P. Metasurface-empowered snapshot hyperspectral imaging with convex/deep (CODE) small-data learning theory. Nat. Commun. 2023, 14, 6979. [Google Scholar] [CrossRef]
- Weng, Q.; Bao, Y. Deep learning-assisted inverse design of metasurfaces for active color image tuning. Nanoscale 2024, 16, 19034–19041. [Google Scholar] [CrossRef]
- Hou, Z.; Zhang, P.; Chen, S.; Wang, J.; Qiu, Y.; Tang, T.; Li, C.; Shen, J. On-demand design of holographic metasurfaces and continuous phase and amplitude modulation method based on deep learning. Results Phys. 2024, 66, 108026. [Google Scholar] [CrossRef]
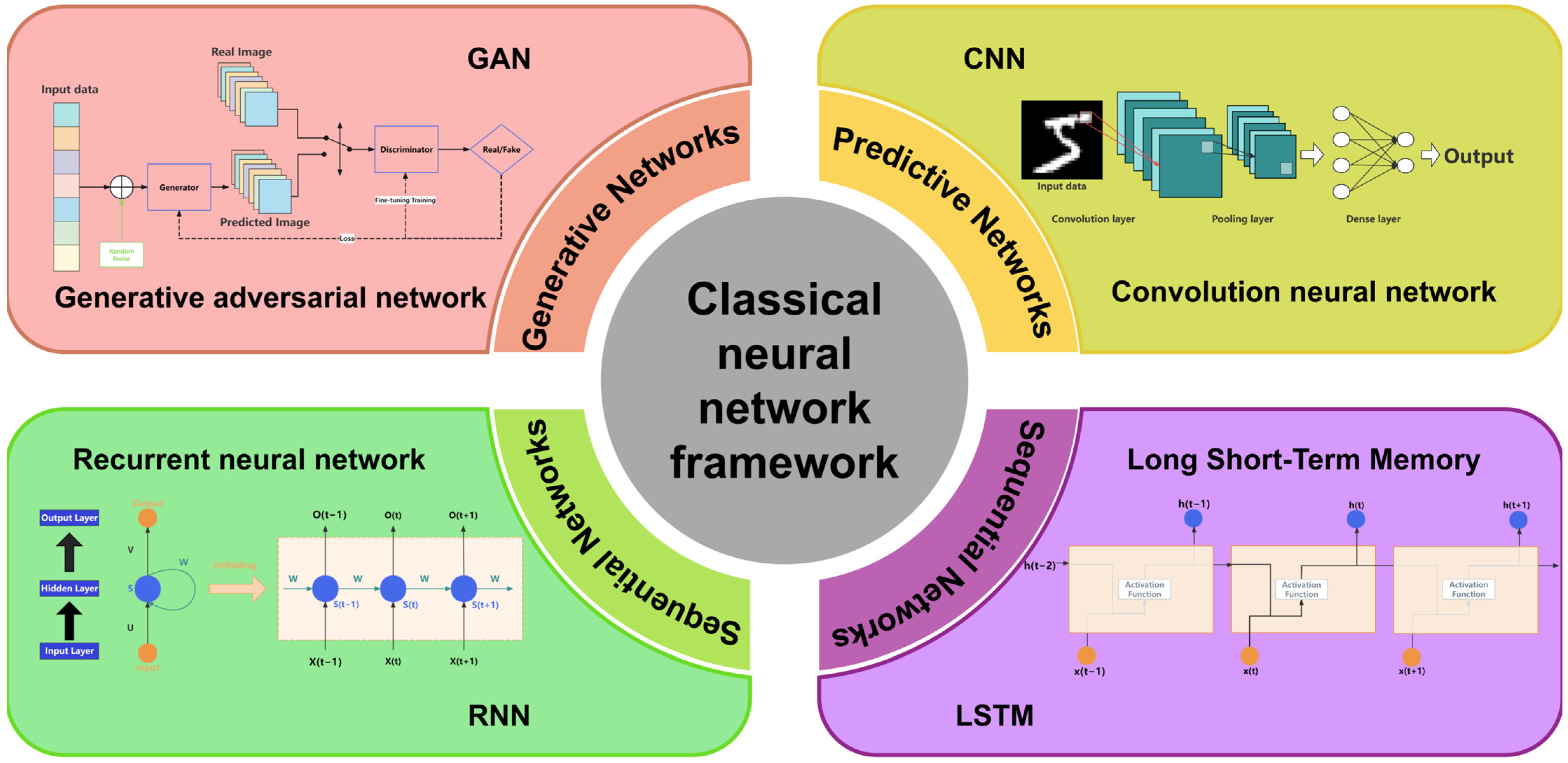
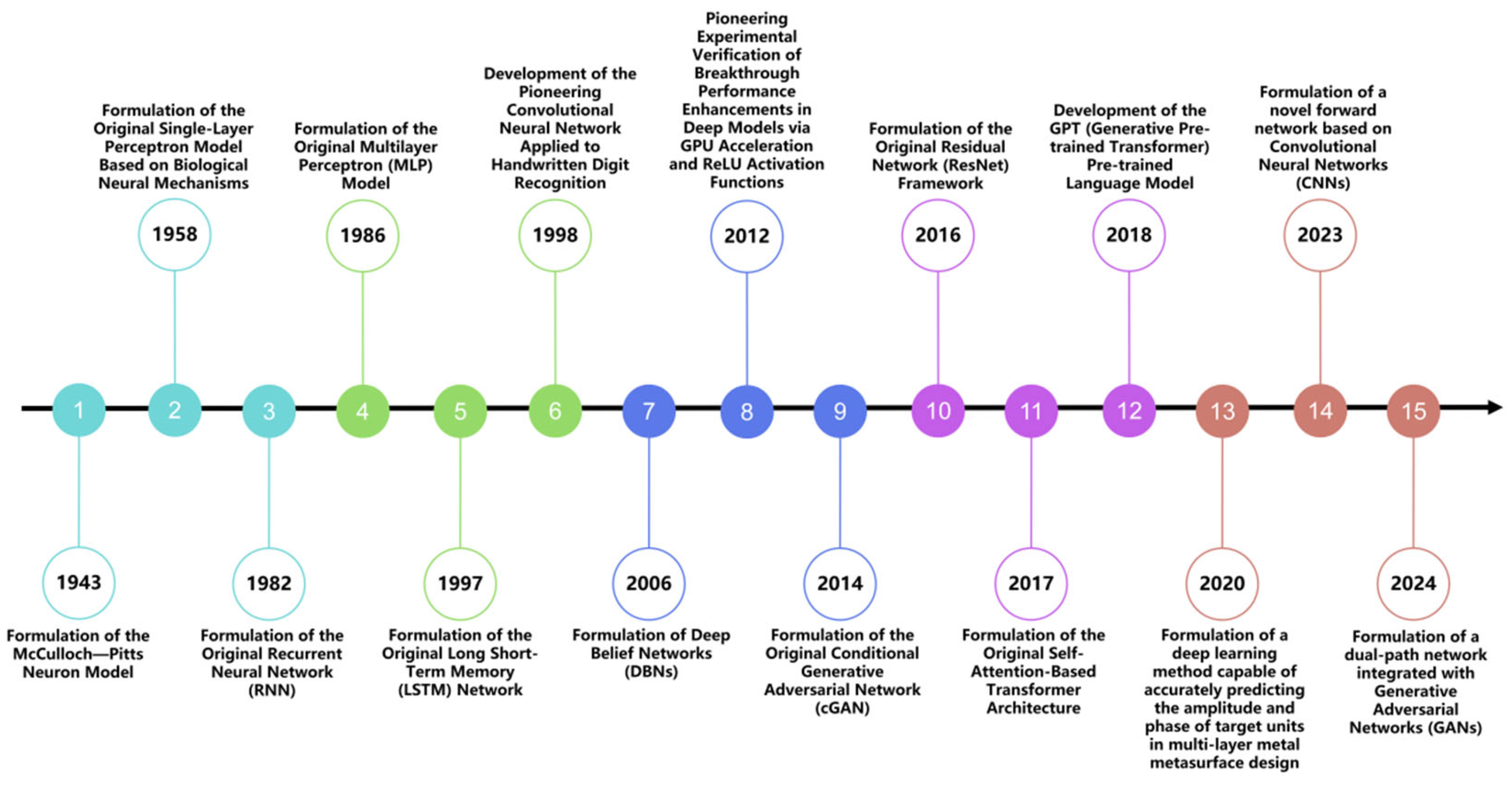

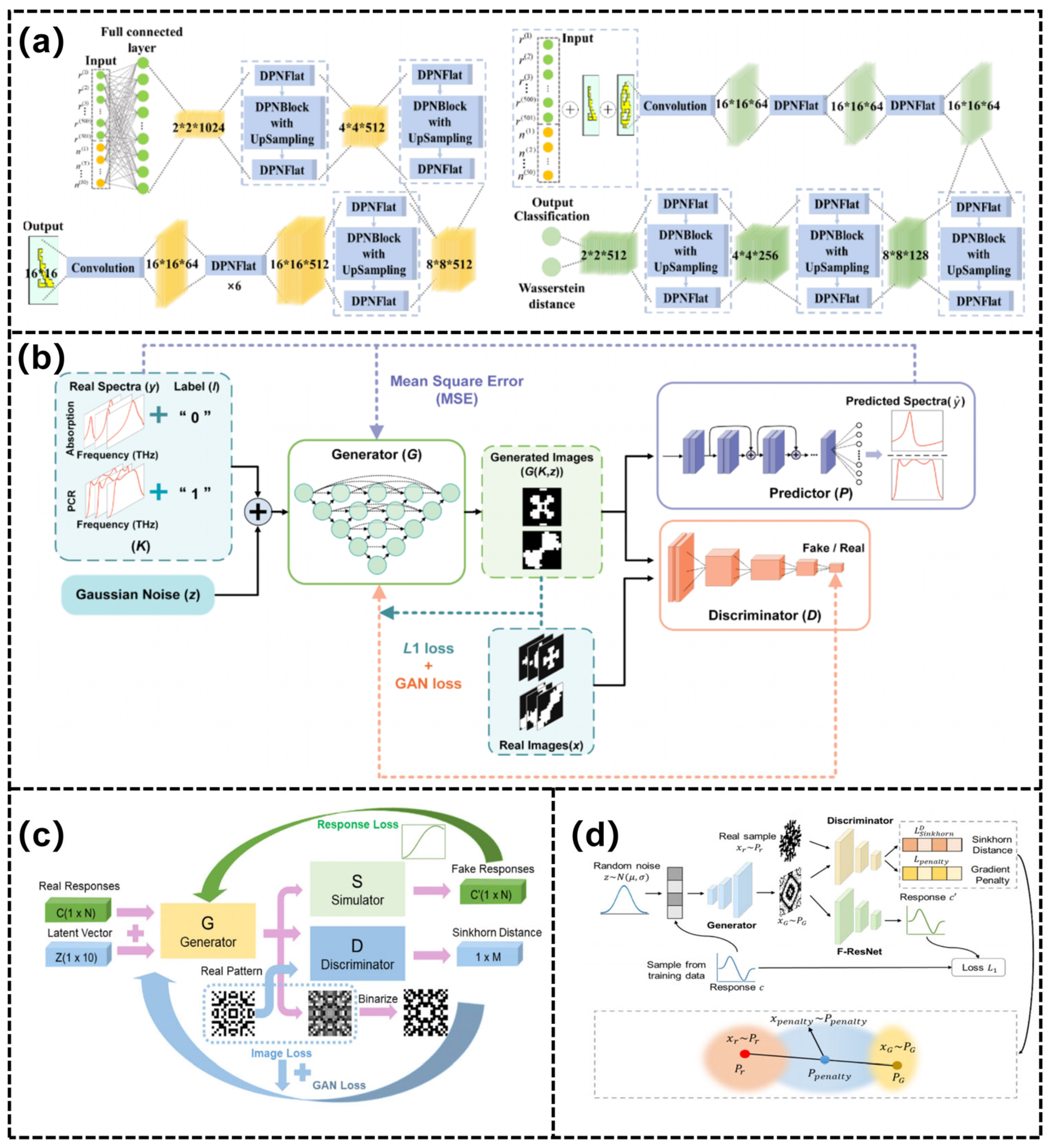

| Deep Learning Methods | Advantages and Characteristics | Limitations Analysis | Applications |
|---|---|---|---|
| Convolutional Neural Network (CNN) |
|
|
|
| Generative Adversarial Network (GAN) |
|
|
|
| Recurrent Neural Network (RNN) |
|
|
|
| Long Short-Term Memory Network (LSTM) |
|
|
|
| Algorithm | Input | Output | Working Bandwidth | Year |
|---|---|---|---|---|
| CNN [142] | Structural data | Spectral data | 800–1800 nm | 2019 |
| CNN [143] | Structural data | Spectral data | 10 GHz | 2019 |
| CNN [144] | Structural data | Spectral data | 8–13 GHz | 2019 |
| DC-GAN [145] | Target data | Structural parameters | 1–30 GHz | 2019 |
| CGAN [146] | Spectral data | Structural pattern | 400–600 nm | 2021 |
| GAN [147] | Spectral data | Structural data | 0.4–1 THz | 2021 |
| CNN [148] | Tissue data | Tissue differentiation | 1–3 GHz | 2022 |
| SLMGAN [149] | Spectral data | Structural image | 20–30 GHz | 2022 |
| KNN-GAN [150] | Spectral data | Structural image | 30–60 GHz | 2022 |
| CGAN [151] | Structural data and absorption spectrum | Structural image | 80–100 Hz | 2022 |
| GAN [152] | Target data | Structural data | 4–20 GHz | 2022 |
| CNN [153] | Structural data | Spectral data | 0.8–1.2 THz | 2023 |
| CNN [154] | Structural data | Spectral data | 650–780 nm | 2023 |
| CNN [155] | Structural data | Spectral data | 8–16 GHz | 2024 |
| XGAN [156] | Electromagnetic response | Structural image | 20–35 GHz | 2024 |
| DPN-GAN [157] | Spectral data | Structural image | 11.6–24.2 GHz | 2024 |
| GAF-CNN-LSTM [158] | 2D feature images [159] | Structural image | 1340–1400 nm | 2024 |
| cDCGAN [160] | Scattering parameters and images | Unit cell image | 4–20 GHz | 2024 |
| LSTM [161] | Target spectrum | Structural parameters | 4.5–5.6 THz | 2025 |
| RGAN [155] | Spectral data | Structural image | 2–18 GHz | 2025 |
| MsCNN-CBAM-LSTM [162] | Structural data | Spectral data | 0.2–2.0 THz | 2025 |
| CNN [163] | Structural data | Resonant frequency | 0.3–1.4 THz | 2025 |
| GAF-DCCNN-MHA [164] | 2D angular field images [165] | Structural parameters | 1300–1600 nm | 2025 |
| CGAN [166] | Target acoustic absorption spectrum | Structural image | 40–3000 Hz | 2025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, M.; Feng, H.; Jin, Y.; Tian, Y. Advances in Deep Learning-Driven Metasurface Design and Application in Holographic Imaging. Photonics 2025, 12, 947. https://doi.org/10.3390/photonics12100947
Lv M, Feng H, Jin Y, Tian Y. Advances in Deep Learning-Driven Metasurface Design and Application in Holographic Imaging. Photonics. 2025; 12(10):947. https://doi.org/10.3390/photonics12100947
Chicago/Turabian StyleLv, Manxu, Huizhen Feng, Yongxing Jin, and Ying Tian. 2025. "Advances in Deep Learning-Driven Metasurface Design and Application in Holographic Imaging" Photonics 12, no. 10: 947. https://doi.org/10.3390/photonics12100947
APA StyleLv, M., Feng, H., Jin, Y., & Tian, Y. (2025). Advances in Deep Learning-Driven Metasurface Design and Application in Holographic Imaging. Photonics, 12(10), 947. https://doi.org/10.3390/photonics12100947




