Enhanced Nanoparticle Detection Using Momentum-Space Filtering for Interferometric Scattering Microscopy (iSCAT)
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
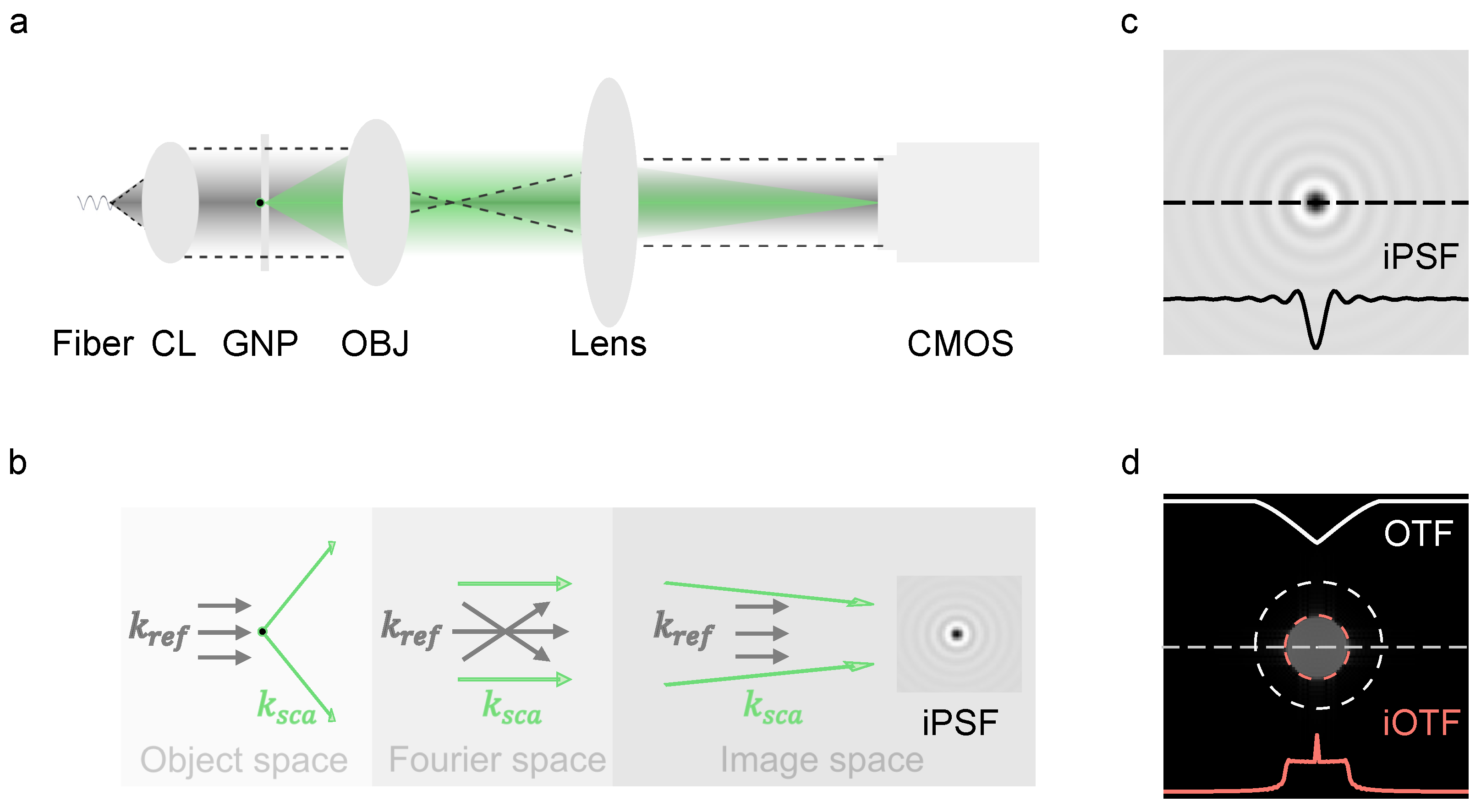
2.2. Setup
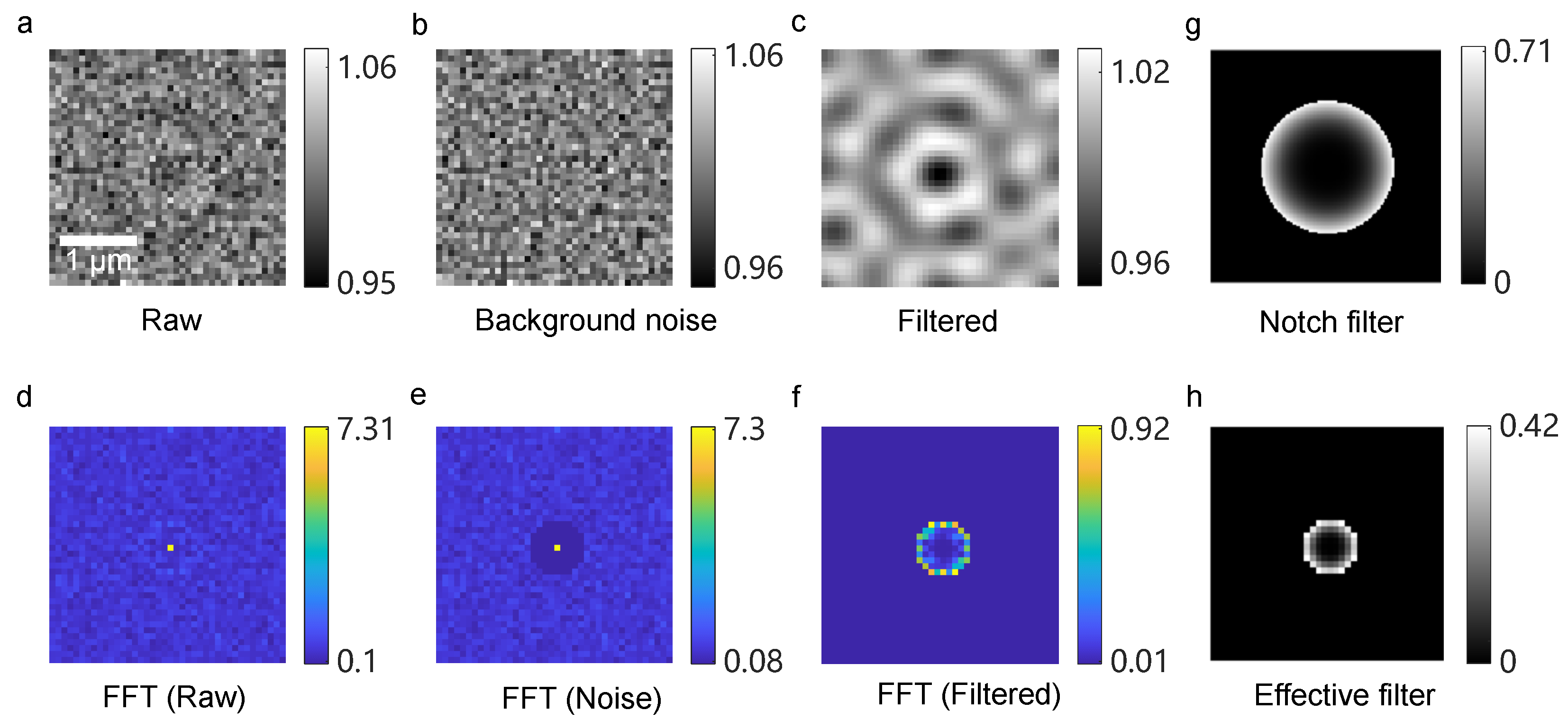
2.3. Imaging Processing
3. Results and Discussion
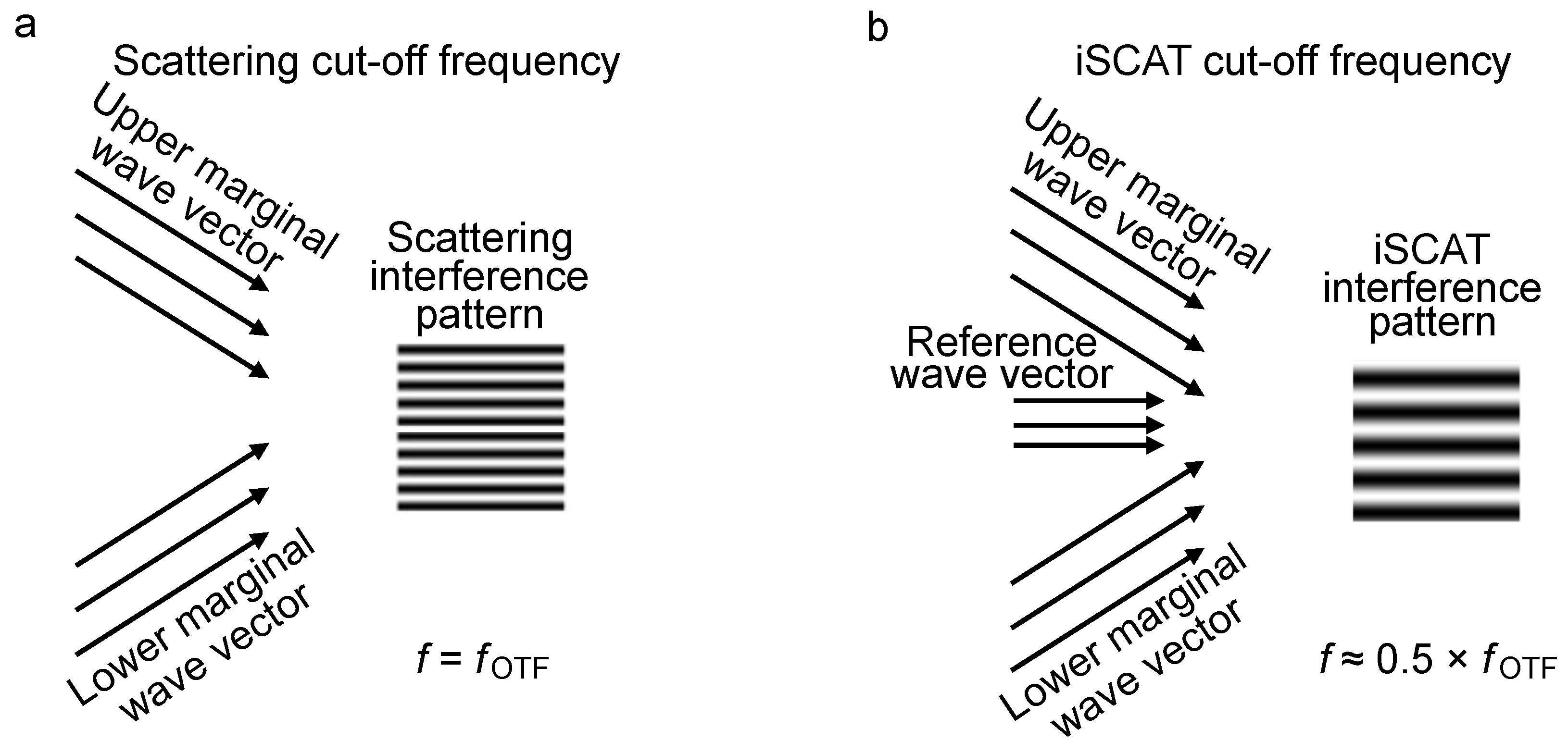
3.1. Boundary of iOTF and Frequency Components Reweighting
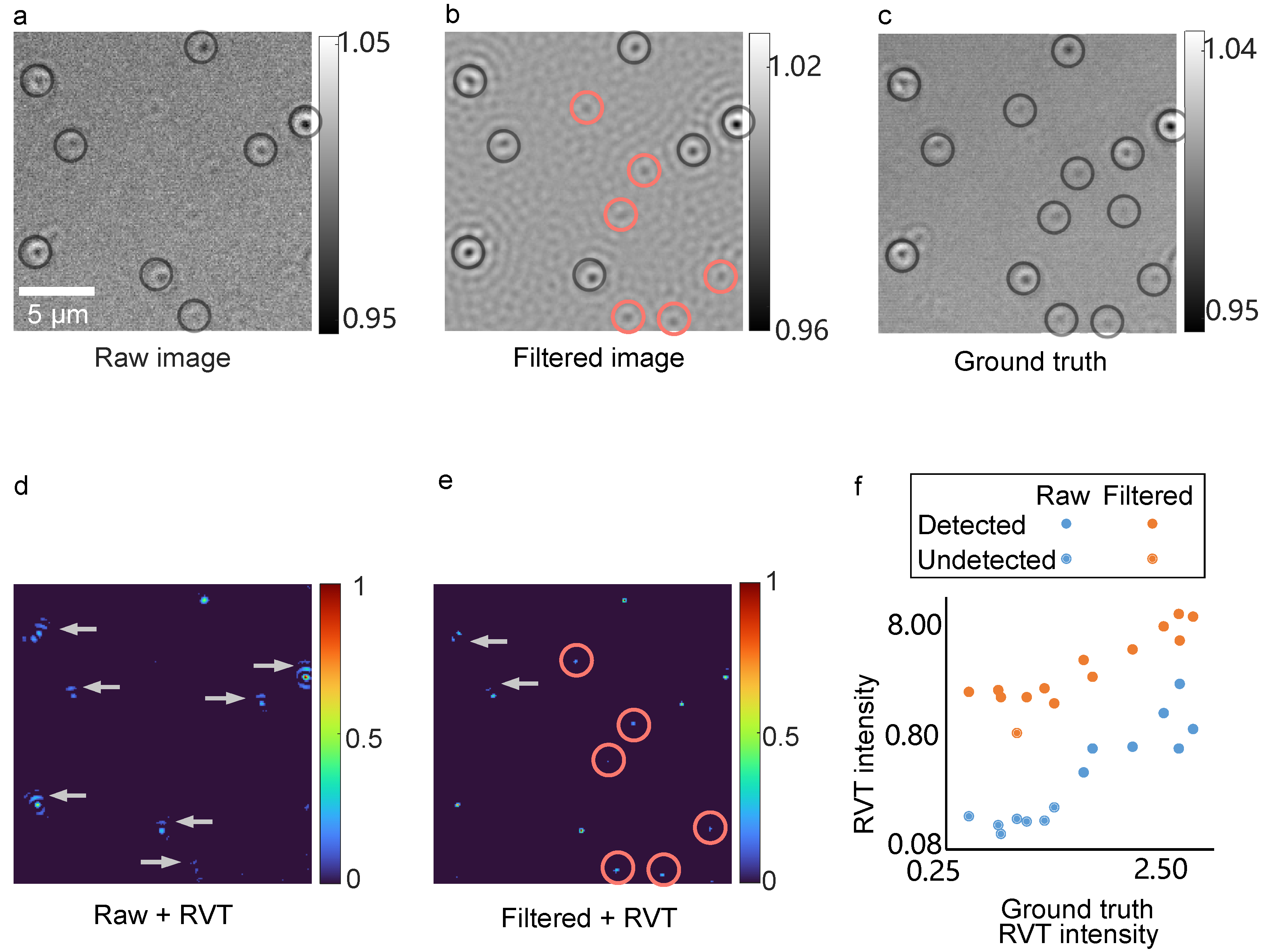
Momentum-Enhanced Particle Detection
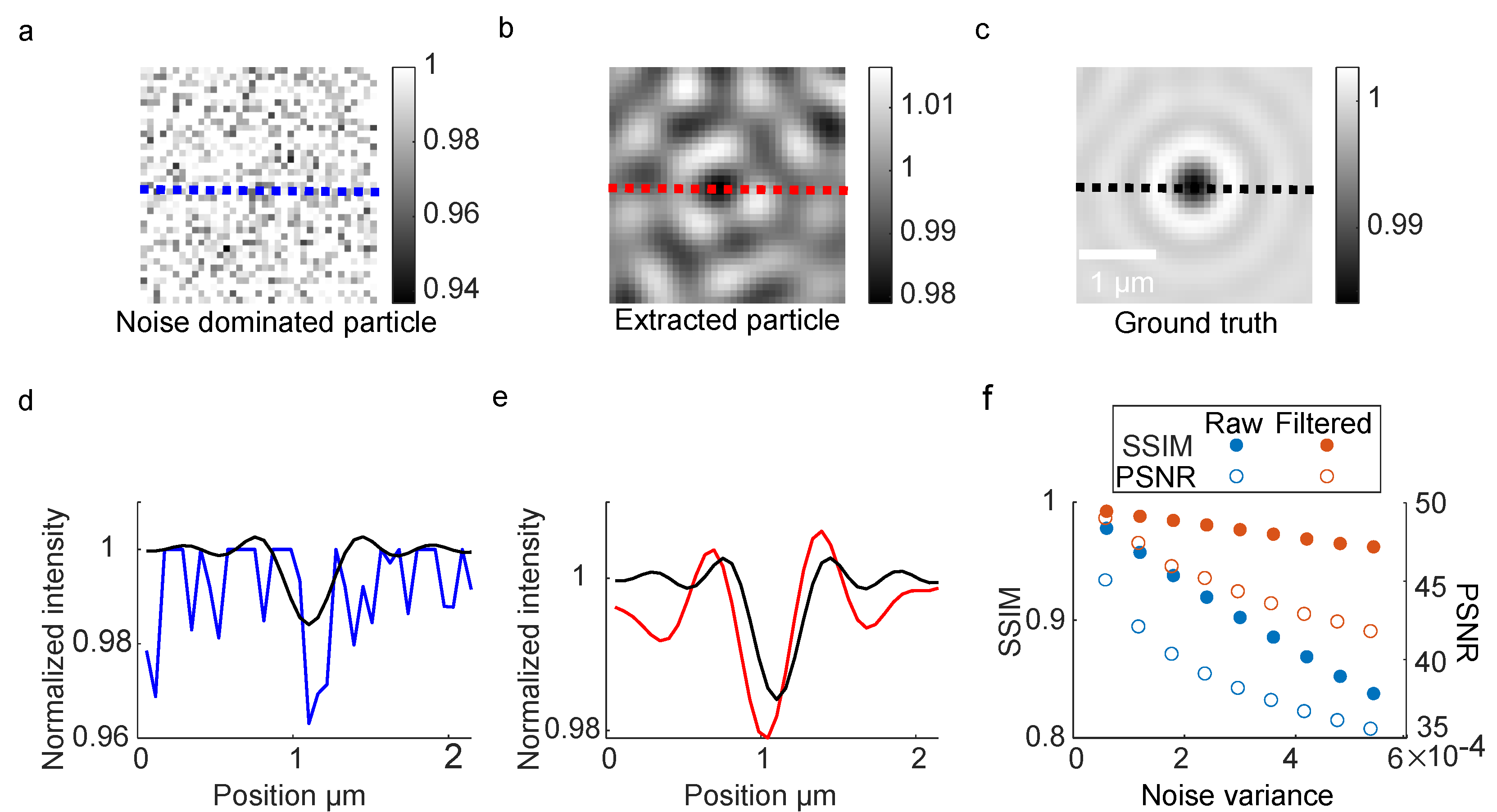
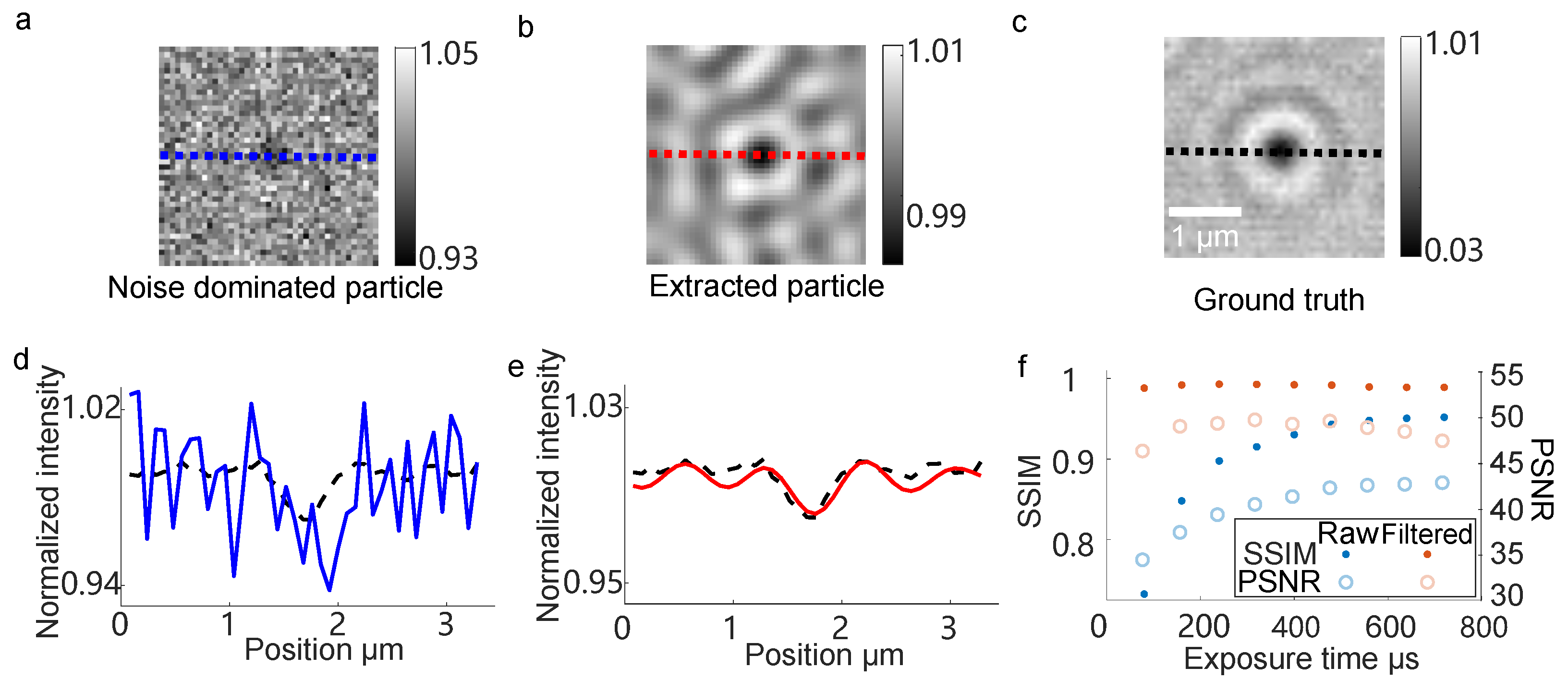
3.2. Signal Feature Enhancing Verification in Simulation
3.3. Signal Feature Enhancing Verification in Experiment
3.4. Detection Comparison of Particles with Different Contrasts
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SF | Spatial-frequency domian deconvolution |
| iSCAT | Interferometric Scattering Microscopy |
| SNR | Signal-to-noise ratios |
| PSF | Point spread function |
| iPSF | Interferometric point spread function |
| OTF | Optical transfer function |
| iOTF | Interferometric optical transfer function |
| RVT | Radial variance transfer |
| COBRI | Coherent brightfield microscopy |
| GNPs | Gold nanoparticle |
| LED | Light-Emitting Diode |
| CL | collimation lens |
| OBJ | objective |
| CMOS | Complementary Metal Oxide Semiconductor camera |
| NA | Numerical aperture |
| FFT | fast Fourier transform |
References
- Asor, R.; Kukura, P. Characterising biomolecular interactions and dynamics with mass photometry. Curr. Opin. Chem. Biol. 2022, 68, 102132. [Google Scholar] [CrossRef]
- Spindler, S.; Ehrig, J.; König, K.; Nowak, T.; Piliarik, M.; Stein, H.E.; Taylor, R.W.; Garanger, E.; Lecommandoux, S.; Alves, I.D.; et al. Visualization of lipids and proteins at high spatial and temporal resolution via interferometric scattering (iSCAT) microscopy. J. Phys. Appl. Phys. 2016, 49, 274002. [Google Scholar] [CrossRef]
- Chai, Y.J.; Cheng, C.Y.; Liao, Y.H.; Lin, C.H.; Hsieh, C.L. Heterogeneous nanoscopic lipid diffusion in the live cell membrane and its dependency on cholesterol. Biophys. J. 2022, 121, 3146–3161. [Google Scholar] [CrossRef] [PubMed]
- Ortega Arroyo, J.; Andrecka, J.; Spillane, K.M.; Billington, N.; Takagi, Y.; Sellers, J.R.; Kukura, P. Label-Free, All-Optical Detection, Imaging, and Tracking of a Single Protein. Nano Lett. 2014, 14, 2065–2070. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Wan, Z.; Yang, Y.; Zhang, P.; Wang, S.; Tao, N. Optical imaging of single-protein size, charge, mobility, and binding. Nat. Commun. 2020, 11, 4768. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, G.; Dong, W.; Wan, Z.; Wang, S.; Tao, N. Plasmonic scattering imaging of single proteins and binding kinetics. Nat. Methods 2020, 17, 1010–1017. [Google Scholar] [CrossRef]
- Liu, Y.; Sundah, N.R.; Ho, N.R.Y.; Shen, W.X.; Xu, Y.; Natalia, A.; Yu, Z.; Seet, J.E.; Chan, C.W.; Loh, T.P.; et al. Bidirectional linkage of DNA barcodes for the multiplexed mapping of higher-order protein interactions in cells. Nat. Biomed. Eng. 2024, 8, 909–923. [Google Scholar] [CrossRef]
- Ali, M.S.; Rainville, C.; Pedroza, J.; Sterner, D.E.; Wang, H.; Suresh, K.; Butt, T.R. Unraveling chain specific ubiquitination in cells using tandem ubiquitin binding entities. Sci. Rep. 2025, 15, 22961. [Google Scholar] [CrossRef]
- Gierten, J.; Welz, B.; Fitzgerald, T.; Thumberger, T.; Agarwal, R.; Hummel, O.; Leger, A.; Weber, P.; Naruse, K.; Hassel, D.; et al. Natural genetic variation quantitatively regulates heart rate and dimension. Nat. Commun. 2025, 16, 4062. [Google Scholar] [CrossRef]
- Visscher, K.; Brakenhoff, G.J.; Visser, T.D. Fluorescence saturation in confocal microscopy. J. Microsc. 1994, 175, 162–165. [Google Scholar] [CrossRef]
- Chaze, W.; Caballina, O.; Castanet, G.; Lemoine, F. The saturation of the fluorescence and its consequences for laser-induced fluorescence thermometry in liquid flows. Exp. Fluids 2016, 57, 58. [Google Scholar] [CrossRef]
- Wüstner, D. Image segmentation and separation of spectrally similar dyes in fluorescence microscopy by dynamic mode decomposition of photobleaching kinetics. Bmc Bioinform. 2022, 23, 334. [Google Scholar]
- Samantha Priyadarshani, D.M.; Stevens, A.L. Concentration-dependent nonradiative decay mechanisms in fluorescence self-quenching: Insights from azulene and 1,3-dichloroazulene. Can. J. Chem. 2025, 103, 246–251. [Google Scholar]
- Laisk, A.; Peterson, R.B.; Oja, V. Excitation transfer and quenching in photosystem II, enlightened by carotenoid triplet state in leaves. Photosynth. Res. 2024, 160, 31–44. [Google Scholar] [CrossRef]
- Fan, S.; Xu, J.; Osakada, Y.; Hashimoto, K.; Takayama, K.; Natsume, A.; Hirano, M.; Maruyama, A.; Fujitsuka, M.; Kawai, K.; et al. Electron-transfer kinetics through nucleic acids untangled by single-molecular fluorescence blinking. Chem 2022, 8, 3109–3119. [Google Scholar]
- Špačková, B.; Klein Moberg, H.; Fritzsche, J.; Tenghamn, J.; Sjösten, G.; Šípová-Jungová, H.; Albinsson, D.; Lubart, Q.; van Leeuwen, D.; Westerlund, F.; et al. Label-free nanofluidic scattering microscopy of size and mass of single diffusing molecules and nanoparticles. Nat. Methods 2022, 19, 751–758. [Google Scholar] [CrossRef]
- Huang, Y.F.; Zhuo, G.Y.; Chou, C.Y.; Lin, C.H.; Chang, W.; Hsieh, C.L. Coherent Brightfield Microscopy Provides the Spatiotemporal Resolution To Study Early Stage Viral Infection in Live Cells. ACS Nano 2017, 11, 2575–2585. [Google Scholar] [CrossRef]
- Jacobsen, V.; Stoller, P.; Brunner, C.; Vogel, V.; Sandoghdar, V. Interferometric optical detection and tracking of very small gold nanoparticles at a water-glass interface. Opt. Express 2006, 14, 405. [Google Scholar] [CrossRef]
- Piliarik, M.; Sandoghdar, V. Direct optical sensing of single unlabelled proteins and super-resolution imaging of their binding sites. Nat. Commun. 2014, 5, 4495. [Google Scholar] [CrossRef]
- Ortega Arroyo, J.; Cole, D.; Kukura, P. Interferometric scattering microscopy and its combination with single-molecule fluorescence imaging. Nat. Protoc. 2016, 11, 617–633. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Hsieh, C.L. Background Estimation and Correction for High-Precision Localization Microscopy. ACS Photonics 2017, 4, 1730–1739. [Google Scholar] [CrossRef]
- Dastjerdi, H.M.; Dahmardeh, M.; Gemeinhardt, A.; Gholami Mahmoodabadi, R.; Köstler, H.; Sandoghdar, V. Optimized analysis for sensitive detection and analysis of single proteins via interferometric scattering microscopy. J. Phys. Appl. Phys. 2021, 55, 054002. [Google Scholar] [CrossRef]
- Cole, D.; Young, G.; Weigel, A.; Sebesta, A.; Kukura, P. Label-Free Single-Molecule Imaging with Numerical-Aperture-Shaped Interferometric Scattering Microscopy. Acs Photonics 2017, 4, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Young, G.; Hundt, N.; Cole, D.; Fineberg, A.; Andrecka, J.; Tyler, A.; Olerinyova, A.; Ansari, A.; Marklund, E.G.; Collier, M.P.; et al. Quantitative mass imaging of single biological macromolecules. Science 2018, 360, 423–427. [Google Scholar] [CrossRef]
- Dahmardeh, M.; Mirzaalian Dastjerdi, H.; Mazal, H.; Köstler, H.; Sandoghdar, V. Self-supervised machine learning pushes the sensitivity limit in label-free detection of single proteins below 10 kDa. Nat. Methods 2023, 20, 442–447. [Google Scholar] [CrossRef]
- McDonald, M.P.; Gemeinhardt, A.; König, K.; Piliarik, M.; Schaffer, S.; Völkl, S.; Aigner, M.; Mackensen, A.; Sandoghdar, V. Visualizing Single-Cell Secretion Dynamics with Single-Protein Sensitivity. Nano Lett. 2017, 18, 513–519. [Google Scholar] [CrossRef]
- Stallinga, S.; Rieger, B. Accuracy of the Gaussian Point Spread Function model in 2D localization microscopy. Optics Express 2010, 18, 24461. [Google Scholar] [CrossRef]
- Liao, Y.H.; Lin, C.H.; Cheng, C.Y.; Wong, W.C.; Juo, J.Y.; Hsieh, C.L. Monovalent and Oriented Labeling of Gold Nanoprobes for the High-Resolution Tracking of a Single-Membrane Molecule. ACS Nano 2019, 13, 10918–10928. [Google Scholar] [CrossRef]
- Robert, H.M.L.; Holanová, K.; Bujak, L.; Vala, M.; Henrichs, V.; Lánský, Z.; Piliarik, M. Fast photothermal spatial light modulation for quantitative phase imaging at the nanoscale. Nat. Commun. 2021, 12, 2921. [Google Scholar] [CrossRef]
- Hsiao, Y.T.; Tsai, C.N.; Chen, T.H.; Hsieh, C.L. Label-Free Dynamic Imaging of Chromatin in Live Cell Nuclei by High-Speed Scattering-Based Interference Microscopy. ACS Nano 2021, 16, 2774–2788. [Google Scholar] [CrossRef]
- Gholami Mahmoodabadi, R.; Taylor, R.W.; Kaller, M.; Spindler, S.; Mazaheri, M.; Kasaian, K.; Sandoghdar, V. Point spread function in interferometric scattering microscopy (iSCAT). Part I: Aberrations in defocusing and axial localization. Opt. Express 2020, 28, 25969. [Google Scholar] [CrossRef]
- Kasaian, K.; Mazaheri, M.; Sandoghdar, V. Long-Range Three-Dimensional Tracking of Nanoparticles Using Interferometric Scattering Microscopy. ACS Nano 2024, 18, 30463–30472. [Google Scholar] [CrossRef]
- Huang, M.; Chen, Q.; Liu, Y.; Zhang, C.; Zhang, R.; Yuan, J.; Zhang, D. One-dimensional photonic crystal enhancing spin-to-orbital angular momentum conversion for single-particle tracking. Light. Sci. Appl. 2024, 13, 268. [Google Scholar] [CrossRef] [PubMed]
- Van den Eynde, R.; Leutenegger, M.; Lidke, D.S.; Jungmann, R.; Vandenberg, W.; Dedecker, P. Simultaneous multicolor single-molecule imaging and tracking using duplication-based PSF engineering. Biophys. J. 2024, 123, 434a. [Google Scholar] [CrossRef]
- Jouchet, P.; Roy, A.R.; Moerner, W.E. Simultaneous position and orientation measurements of single molecules using deep learning and PSF engineering approaches. Biophys. J. 2022, 121, 412a–413a. [Google Scholar] [CrossRef]
- Opatovski, N.; Nehme, E.; Zoref, N.; Barzilai, I.; Orange Kedem, R.; Ferdman, B.; Keselman, P.; Alalouf, O.; Shechtman, Y. Depth-enhanced high-throughput microscopy by compact PSF engineering. Nat. Commun. 2024, 15, 4861. [Google Scholar] [CrossRef]
- Wen, G.; Li, S.; Wang, L.; Chen, X.; Sun, Z.; Liang, Y.; Jin, X.; Xing, Y.; Jiu, Y.; Tang, Y.; et al. High-fidelity structured illumination microscopy by point-spread-function engineering. Light. Sci. Appl. 2021, 10, 70. [Google Scholar]
- Kashkanova, A.D.; Shkarin, A.B.; Mahmoodabadi, R.G.; Blessing, M.; Tuna, Y.; Gemeinhardt, A.; Sandoghdar, V. Precision Single-Particle Localization Using Radial Variance Transform. Optics Express 2021, 29, 11070. [Google Scholar] [CrossRef]
- McFarlane, N.J.B.; Schofield, C.P. Segmentation and Tracking of Piglets in Images. Mach. Vis. Appl. 1995, 8, 187–193. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Yang, Y. Enhanced Nanoparticle Detection Using Momentum-Space Filtering for Interferometric Scattering Microscopy (iSCAT). Photonics 2025, 12, 945. https://doi.org/10.3390/photonics12100945
Zhang X, Yang Y. Enhanced Nanoparticle Detection Using Momentum-Space Filtering for Interferometric Scattering Microscopy (iSCAT). Photonics. 2025; 12(10):945. https://doi.org/10.3390/photonics12100945
Chicago/Turabian StyleZhang, Xiang, and Yatao Yang. 2025. "Enhanced Nanoparticle Detection Using Momentum-Space Filtering for Interferometric Scattering Microscopy (iSCAT)" Photonics 12, no. 10: 945. https://doi.org/10.3390/photonics12100945
APA StyleZhang, X., & Yang, Y. (2025). Enhanced Nanoparticle Detection Using Momentum-Space Filtering for Interferometric Scattering Microscopy (iSCAT). Photonics, 12(10), 945. https://doi.org/10.3390/photonics12100945





