Ultrafast Airy Beam Generation with a Mode-Locked Fiber Laser
Abstract
1. Introduction
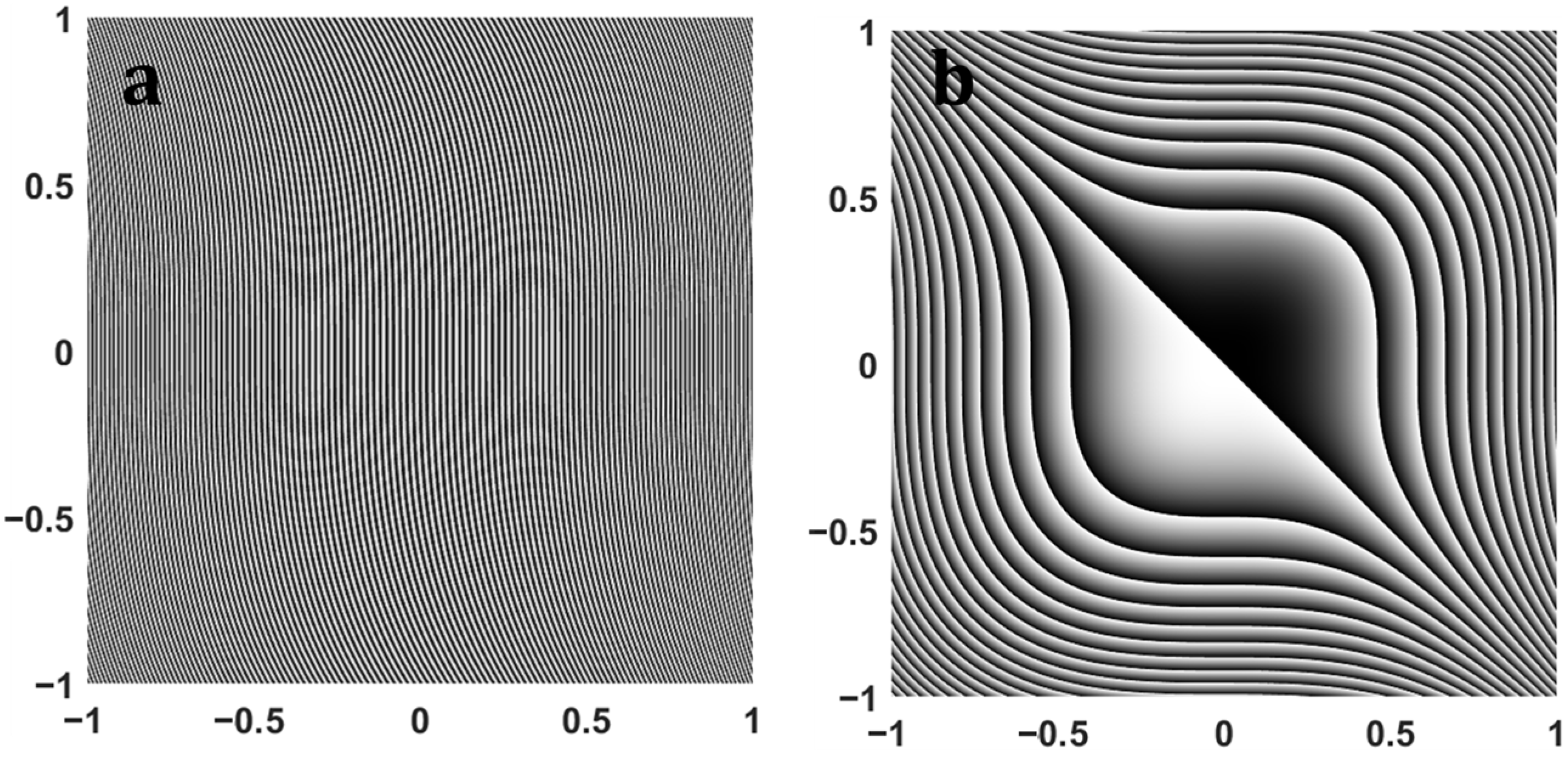
2. Theoretical Background
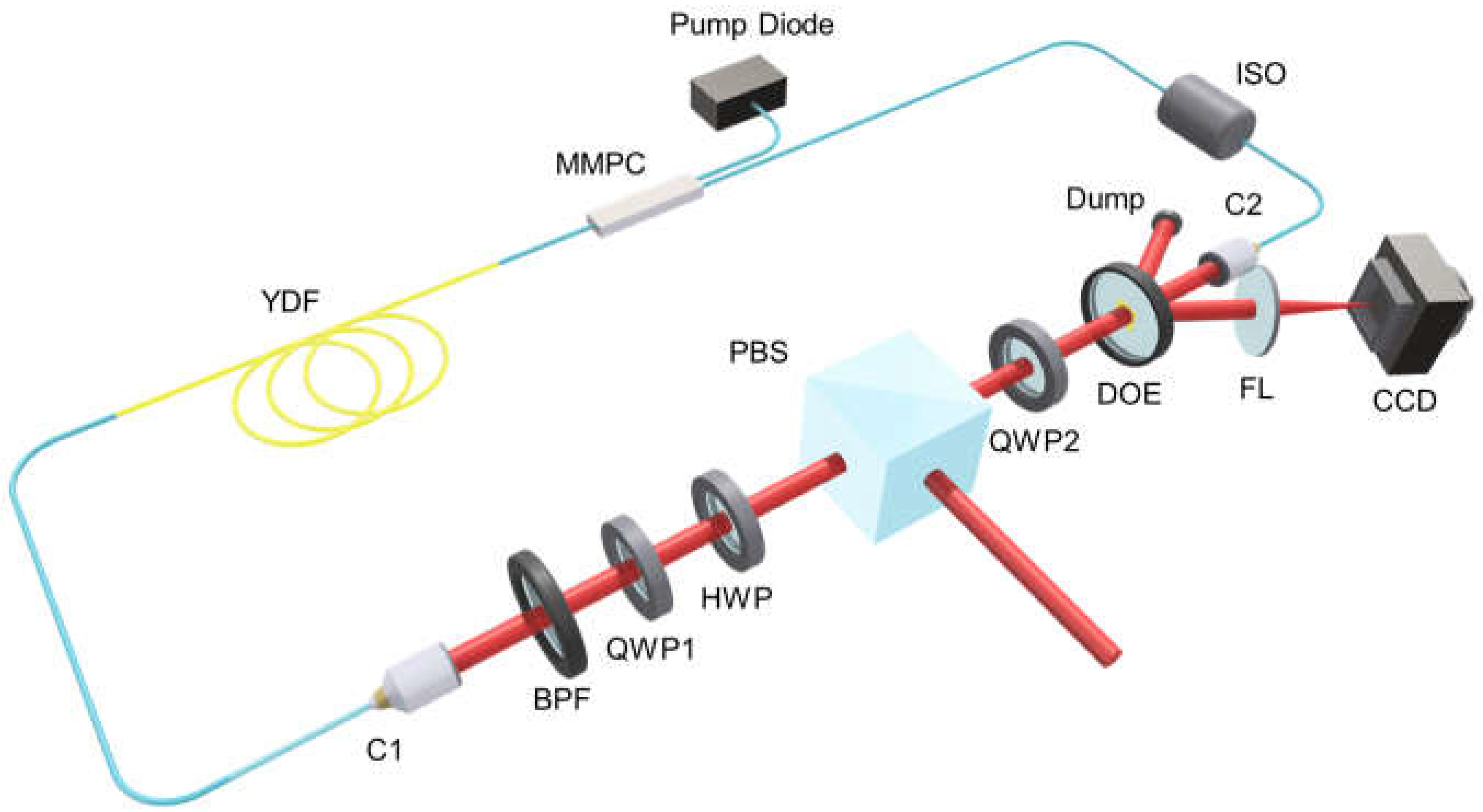
3. Experimental Setup
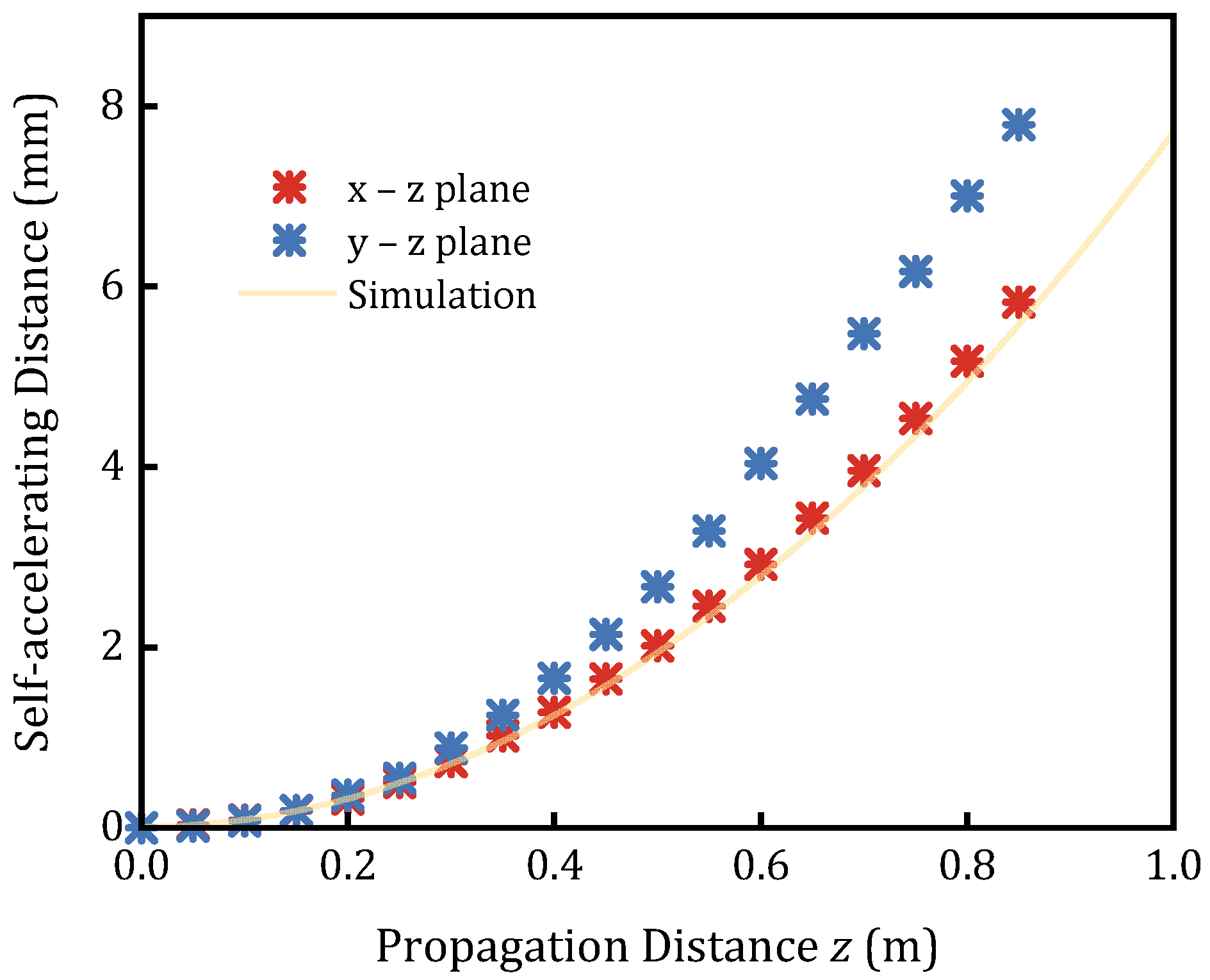
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef] [PubMed]
- Porat, G.; Dolev, I.; Barlev, O.; Arie, A. Airy beam laser. Opt. Lett. 2011, 36, 4119–4121. [Google Scholar] [CrossRef] [PubMed]
- Minovich, A.E.; Klein, A.E.; Neshev, D.N.; Pertsch, T.; Kivshar, Y.S.; Christodoulides, D.N. Airy plasmons: Non-diffracting optical surface waves. Laser Photonics Rev. 2013, 8, 221–232. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of accelerating airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef]
- Wong, C.W. Nonspreading wave packets. Am. J. Phys. 1996, 64, 792–799. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A. Airy beam with a hyperbolic trajectory. Opt. Commun. 2014, 313, 290–293. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Chen, Z.G.; Segev, M.; Christodoulides, D.N. Airy beams and accelerating waves: An overview of recent advances. Optica 2019, 6, 686–701. [Google Scholar] [CrossRef]
- Zhang, P.; Prakash, J.; Zhang, Z.; Mills, M.S.; Efremidis, N.K.; Christodoulides, D.N.; Chen, Z. Trapping and guiding microparticles with morphing autofocusing airy beams. Opt. Lett. 2011, 36, 2883–2885. [Google Scholar] [CrossRef] [PubMed]
- Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated particle clearing using airy wavepackets. Nat. Photonics 2008, 2, 675–678. [Google Scholar] [CrossRef]
- Christodoulides, D.N. Riding along an airy beam. Nat. Photonics 2008, 2, 652–653. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Z.; Prakash, J.; Huang, S.; Chen, Z. Trapping and transporting aerosols with a single optical bottle beam generated by moiré techniques. Opt. Lett. 2011, 36, 1491–1493. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.; Wang, K.; Feng, C.; Wu, T.; Zhang, Y.; Zhao, X.; Wang, J.-L. Optofluidic sorting of microparticles using airy beams. Int. J. Optomechatronics 2024, 18, 2375538. [Google Scholar] [CrossRef]
- Vettenburg, T.; Dalgarno, H.I.C.; Nylk, J.; Coll-Lladó, C.; Ferrier, D.E.K.; Čižmár, T.; Gunn-Moore, F.J.; Dholakia, K. Light-sheet microscopy using an airy beam. Nat. Methods 2014, 11, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Stegmeyer, R.I.; Stasch, M.; Olesker, D.; Taylor, J.M.; Mitchell, T.J.; Hosny, N.A.; Kirschnick, N.; Spickermann, G.; Vestweber, D.; Volkery, S. Intravital microscopy with an airy beam light sheet microscope improves temporal resolution and reduces surgical trauma. Microsc. Microanal. 2024, 30, 925–943. [Google Scholar] [CrossRef]
- Chen, L.; Gao, B.; Li, X.; Chan, C.T.; Wang, J.; Ye, L.; Wang, L.-G. Optimizing airy needle-like beams for long-range axial manipulation and super-resolution imaging. ACS Photonics 2024, 11, 3610–3620. [Google Scholar] [CrossRef]
- Abdollahpour, D.; Suntsov, S.; Papazoglou, D.G.; Tzortzakis, S. Spatiotemporal airy light bullets in the linear and nonlinear regimes. Phys. Rev. Lett. 2010, 105, 253901. [Google Scholar] [CrossRef] [PubMed]
- Chong, A.; Renninger, W.H.; Christodoulides, D.N.; Wise, F.W. Airy–bessel wave packets as versatile linear light bullets. Nat. Photonics 2010, 4, 103–106. [Google Scholar] [CrossRef]
- Mathis, A.; Courvoisier, F.; Froehly, L.; Furfaro, L.; Jacquot, M.; Lacourt, P.A.; Dudley, J.M. Micromachining along a curve: Femtosecond laser micromachining of curved profiles in diamond and silicon using accelerating beams. Appl. Phys. Lett. 2012, 101, 071110. [Google Scholar] [CrossRef]
- Götte, N.; Winkler, T.; Meinl, T.; Kusserow, T.; Zielinski, B.; Sarpe, C.; Senftleben, A.; Hillmer, H.; Baumert, T. Temporal airy pulses for controlled high aspect ratio nanomachining of dielectrics. Optica 2016, 3, 389–395. [Google Scholar] [CrossRef]
- Muhammad, I.; Jiang, R.; Lin, Y.; Zheng, X.; Dehdashti, B. Airy beams on two dimensional materials. Opt. Commun. 2018, 414, 40–44. [Google Scholar]
- Polynkin, P.; Kolesik, M.; Moloney, J.V.; Siviloglou, G.A.; Christodoulides, D.N. Curved plasma channel generation using ultraintense airy beams. Science 2009, 324, 229–232. [Google Scholar] [CrossRef]
- Li, L.; Li, T.; Wang, S.M.; Zhang, C.; Zhu, S.N. Plasmonic airy beam generated by in-plane diffraction. Phys. Rev. Lett. 2011, 107, 126804. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Neshev, D.N.; Shadrivov, I.V.; Miroshnichenko, A.E.; Kivshar, Y.S. Plasmonic airy beam manipulation in linear optical potentials. Opt. Lett. 2011, 36, 1164–1166. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, S.; Liu, Y.; Yin, X.; Lu, C.; Chen, Z.; Zhang, X. Plasmonic airy beams with dynamically controlled trajectories. Opt. Lett. 2011, 36, 3191–3193. [Google Scholar] [CrossRef]
- Gao, X.; Han, Y.; Wang, J.; Xu, S. Evolution of airy beams in turbulence plasma sheath. Photonics 2024, 11, 102. [Google Scholar] [CrossRef]
- Gao, C.; Wen, B.; Deng, Y.; Fan, Y.; Wei, J.; Chen, D. Generation and manipulation of airy breathing solitons in an inhomogeneous medium with periodic potential. Photonics 2023, 10, 486. [Google Scholar] [CrossRef]
- Courvoisier, S.; Götte, N.; Zielinski, B.; Winkler, T.; Sarpe, C.; Senftleben, A.; Bonacina, L.; Wolf, J.P.; Baumert, T. Temporal airy pulses control cell poration. APL Photonics 2016, 1, 046102. [Google Scholar] [CrossRef]
- Hu, Z.; Yang, Y.; Yang, L.; Gong, Y.; Chukwu, C.; Ye, D.; Yue, Y.; Yuan, J.; Kravitz, A.V.; Chen, H. Airy-beam holographic sonogenetics for advancing neuromodulation precision and flexibility. Proc. Natl. Acad. Sci. USA 2024, 121, e2402200121. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Liu, Z.; Wang, X. Generation of an airy-related beam from the sinusoidal dark hollow beam. Optik 2022, 251, 168477. [Google Scholar] [CrossRef]
- Voloch-Bloch, N.; Lereah, Y.; Lilach, Y.; Gover, A.; Arie, A. Generation of electron airy beams. Nature 2013, 494, 331–335. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Guo, Z.; Shi, J.; Jiang, X.; Chen, Q.; Chen, H.; He, Z.; Song, Q.; Xiao, S.; Yu, S.; et al. A metasurface-based full-color circular auto-focusing airy beam transmitter for stable high-speed underwater wireless optical communications. Nat. Commun. 2024, 15, 2944. [Google Scholar] [CrossRef]
- Ellenbogen, T.; Voloch-Bloch, N.; Ganany-Padowicz, A.; Arie, A. Nonlinear generation and manipulation of airy beams. Nat. Photonics 2009, 3, 395–398. [Google Scholar] [CrossRef]
- Khonina, S.N. Specular and vortical airy beams. Opt. Commun. 2011, 284, 4263–4271. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Schachtler, D.; Fink, H.W. Creating airy beams employing a transmissive spatial light modulator. Appl. Opt. 2016, 55, 6095–6101. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, Y.; Cannan, D.; Salandrino, A.; Li, T.; Morandotti, R.; Zhang, X.; Chen, Z. Generation of linear and nonlinear nonparaxial accelerating beams. Opt. Lett. 2012, 37, 2820. [Google Scholar] [CrossRef] [PubMed]
- Aadhi, A.; Sharma, V.; Chaitanya, N.A.; Samanta, G.K. Multi-gigahertz, femtosecond airy beam optical parametric oscillator pumped at 78 mhz. Sci. Rep. 2017, 7, 43913. [Google Scholar] [CrossRef]
- Apurv Chaitanya, N.; Kumar, S.C.; Aadhi, A.; Samanta, G.K.; Ebrahim-Zadeh, M. Ultrafast airy beam optical parametric oscillator. Sci. Rep. 2016, 6, 30701. [Google Scholar] [CrossRef] [PubMed]
- Aadhi, A.; Chaitanya, N.A.; Jabir, M.V.; Vaity, P.; Singh, R.P.; Samanta, G.K. Airy beam optical parametric oscillator. Sci. Rep. 2016, 6, 25245. [Google Scholar] [CrossRef] [PubMed]
- Valdmann, A.; Piksarv, P.; Valtna-Lukner, H.; Saari, P. Realization of laterally nondispersing ultrabroadband airy pulses. Opt. Lett. 2014, 39, 1877–1880. [Google Scholar] [CrossRef] [PubMed]
- Vallée, O.; Soares, M. Airy Functions and Applications to Physics; Imperial College Press: London, UK, 2004. [Google Scholar]
- Lee, W.H. Binary computer-generated holograms. Appl. Opt. 1979, 18, 3661–3669. [Google Scholar] [CrossRef]
- Morris, J.E.; Mazilu, M.; Baumgartl, J.; Čižmár, T.; Dholakia, K. Propagation characteristics of airy beams: Dependence upon spatial coherence and wavelength. Opt. Express 2009, 17, 13236–13245. [Google Scholar] [CrossRef]
- Lin, Y.; Huang, Z.; Huang, Q.; Dai, L.; Song, Q.; Yan, Z.; Mou, C.; Zhou, K.; Zhang, L. Pump-controlled wavelength switchable dissipative soliton mode-locked yb-doped fiber laser using a 45° tilted fiber grating. Optik 2020, 222, 165383. [Google Scholar] [CrossRef]
- Oktem, B.; Ülgüdür, C.; Ilday, F.Ö. Soliton–similariton fibre laser. Nat. Photonics 2010, 4, 307–311. [Google Scholar] [CrossRef]
- Davis, J.A.; Mitry, M.J.; Bandres, M.A.; Ruiz, I.; McAuley, K.P.; Cottrell, D.M. Generation of accelerating airy and accelerating parabolic beams using phase-only patterns. Appl. Opt. 2009, 48, 3170–3176. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Li, S.; Zhao, Y.; Du, J.; Zhu, L. Orbital angular momentum and beyond in free-space optical communications. Nanophotonics 2022, 11, 645–680. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Lou, Y.; Yue, C.; Zhang, X.; Zhang, F. Ultrafast Airy Beam Generation with a Mode-Locked Fiber Laser. Photonics 2025, 12, 9. https://doi.org/10.3390/photonics12010009
Guo S, Lou Y, Yue C, Zhang X, Zhang F. Ultrafast Airy Beam Generation with a Mode-Locked Fiber Laser. Photonics. 2025; 12(1):9. https://doi.org/10.3390/photonics12010009
Chicago/Turabian StyleGuo, Silin, Yajun Lou, Cai Yue, Xinhai Zhang, and Fan Zhang. 2025. "Ultrafast Airy Beam Generation with a Mode-Locked Fiber Laser" Photonics 12, no. 1: 9. https://doi.org/10.3390/photonics12010009
APA StyleGuo, S., Lou, Y., Yue, C., Zhang, X., & Zhang, F. (2025). Ultrafast Airy Beam Generation with a Mode-Locked Fiber Laser. Photonics, 12(1), 9. https://doi.org/10.3390/photonics12010009




