Optically Delaying a Radio Frequency–Linear Frequency-Modulated (RF-LFM) Pulse Using Kerr Comb Carriers and Off-the-Shelf Concatenation of a Linearly Chirped Fiber Bragg Grating and a Chirped-and-Sampled Fiber Bragg Grating
Abstract
1. Introduction
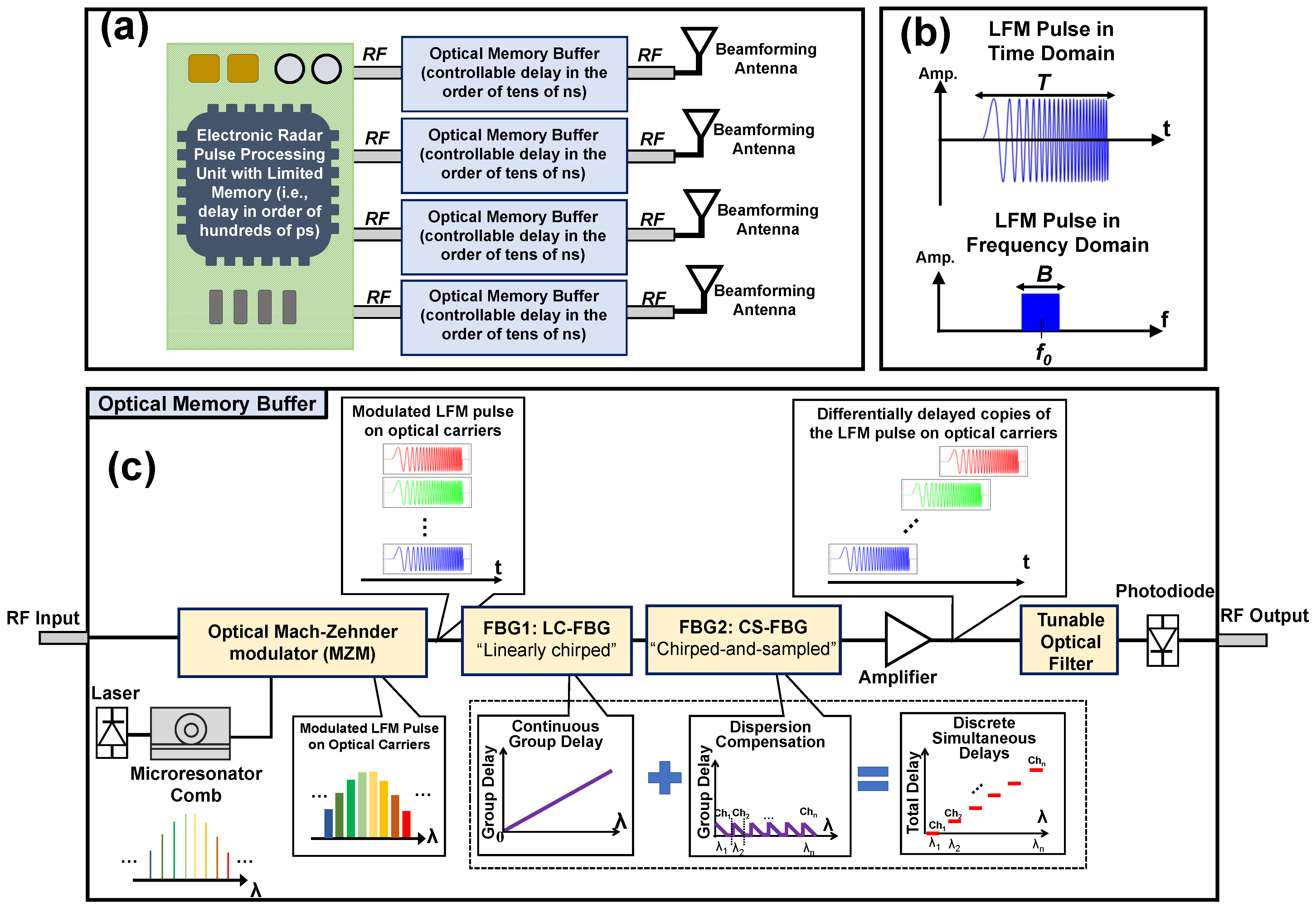
2. Concept
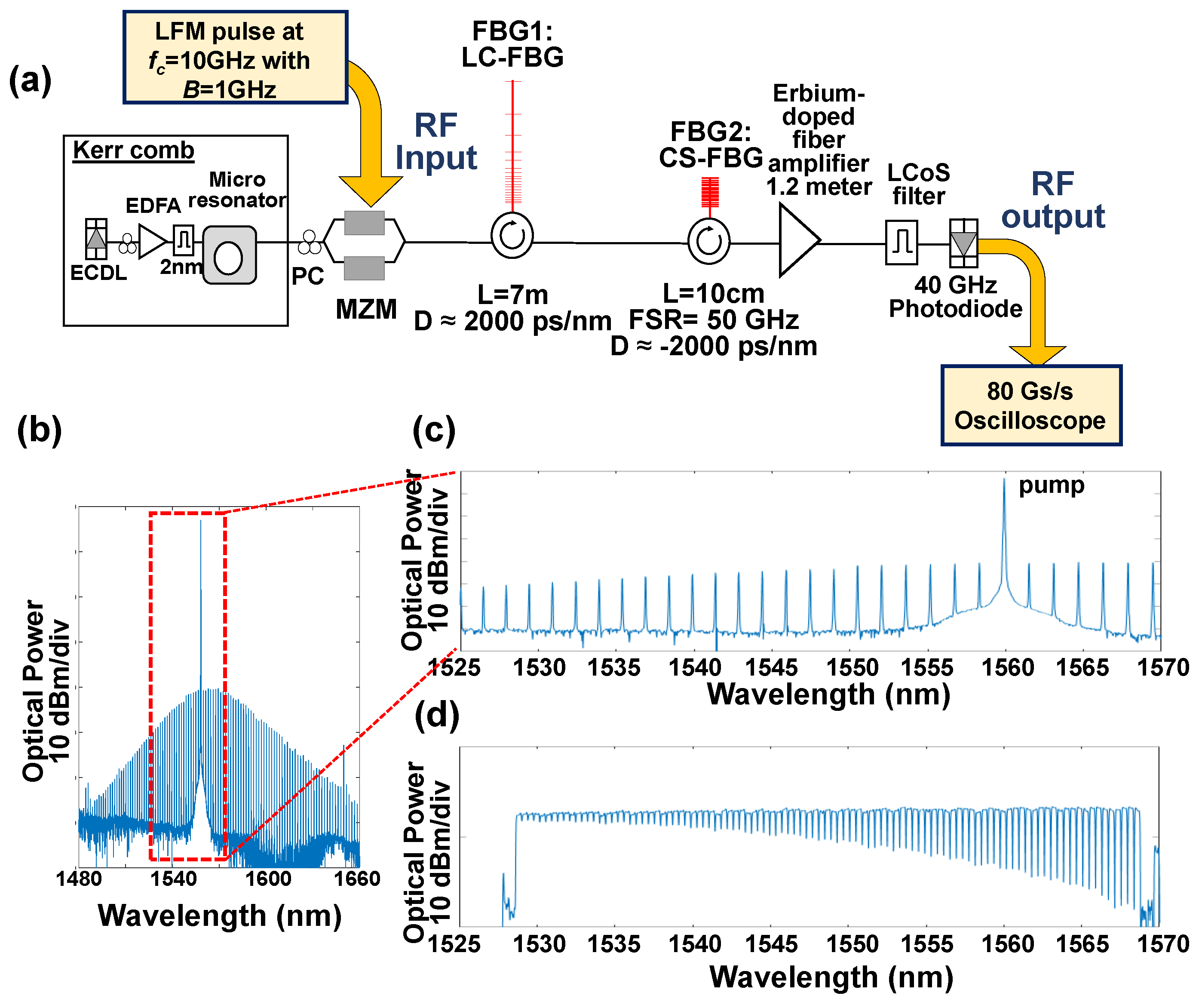
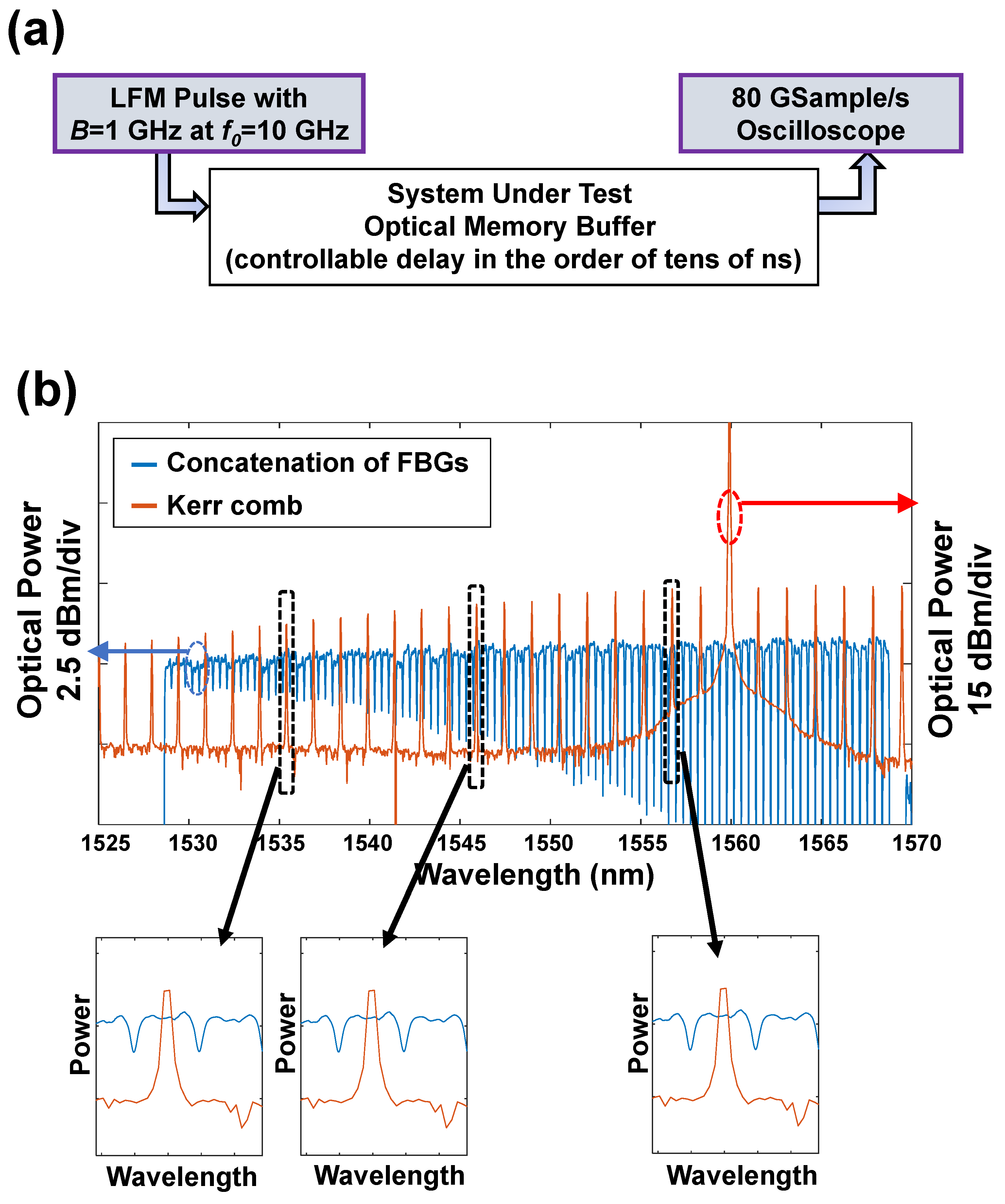
3. Experimental Setup
4. Characterization of the Optical Memory Buffer
4.1. Measuring the Delay Tuning Range
4.2. Characterizing the Latency of the Delay System
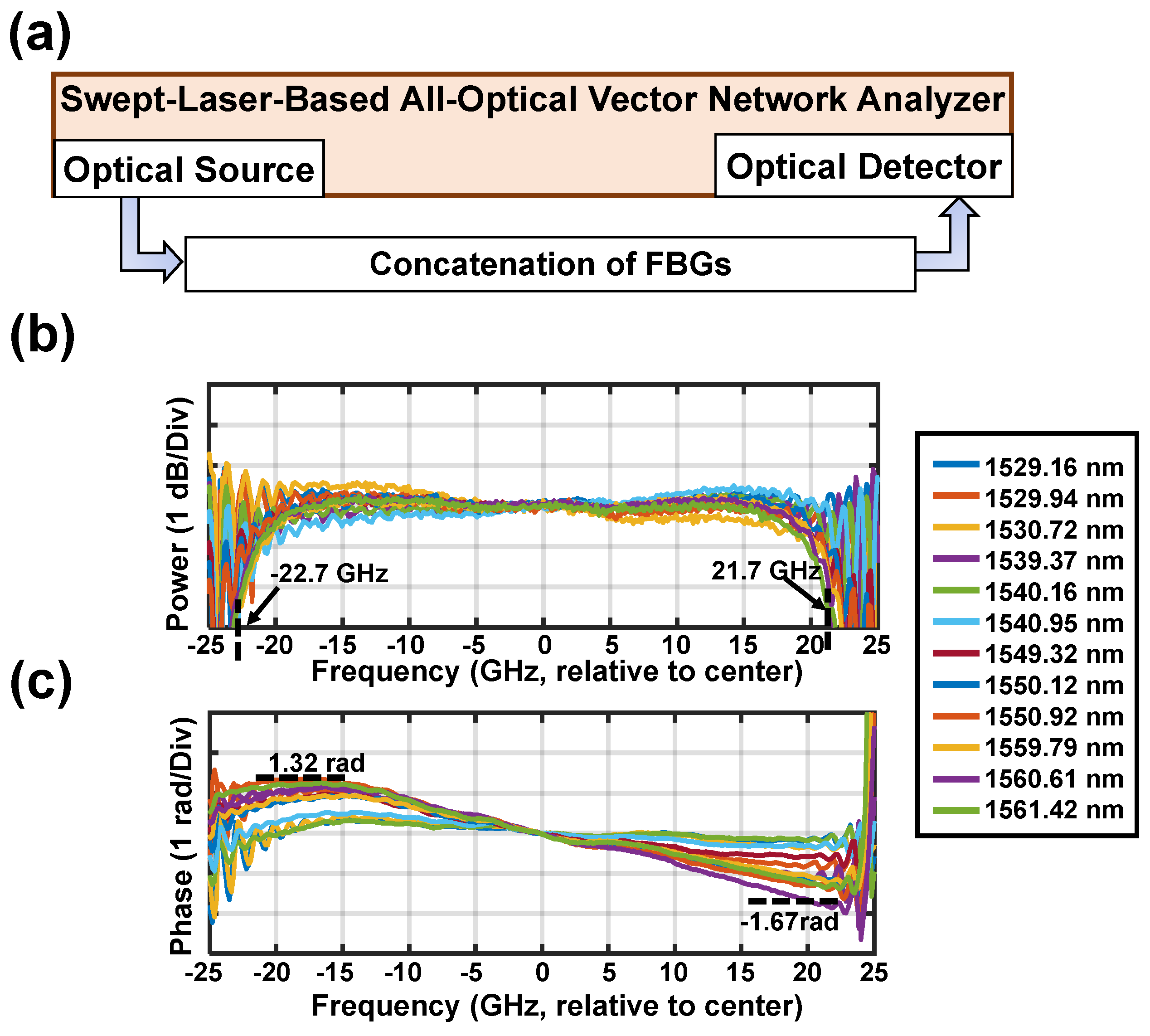
4.3. Characterizing the Bandwidth of the Delay Channels
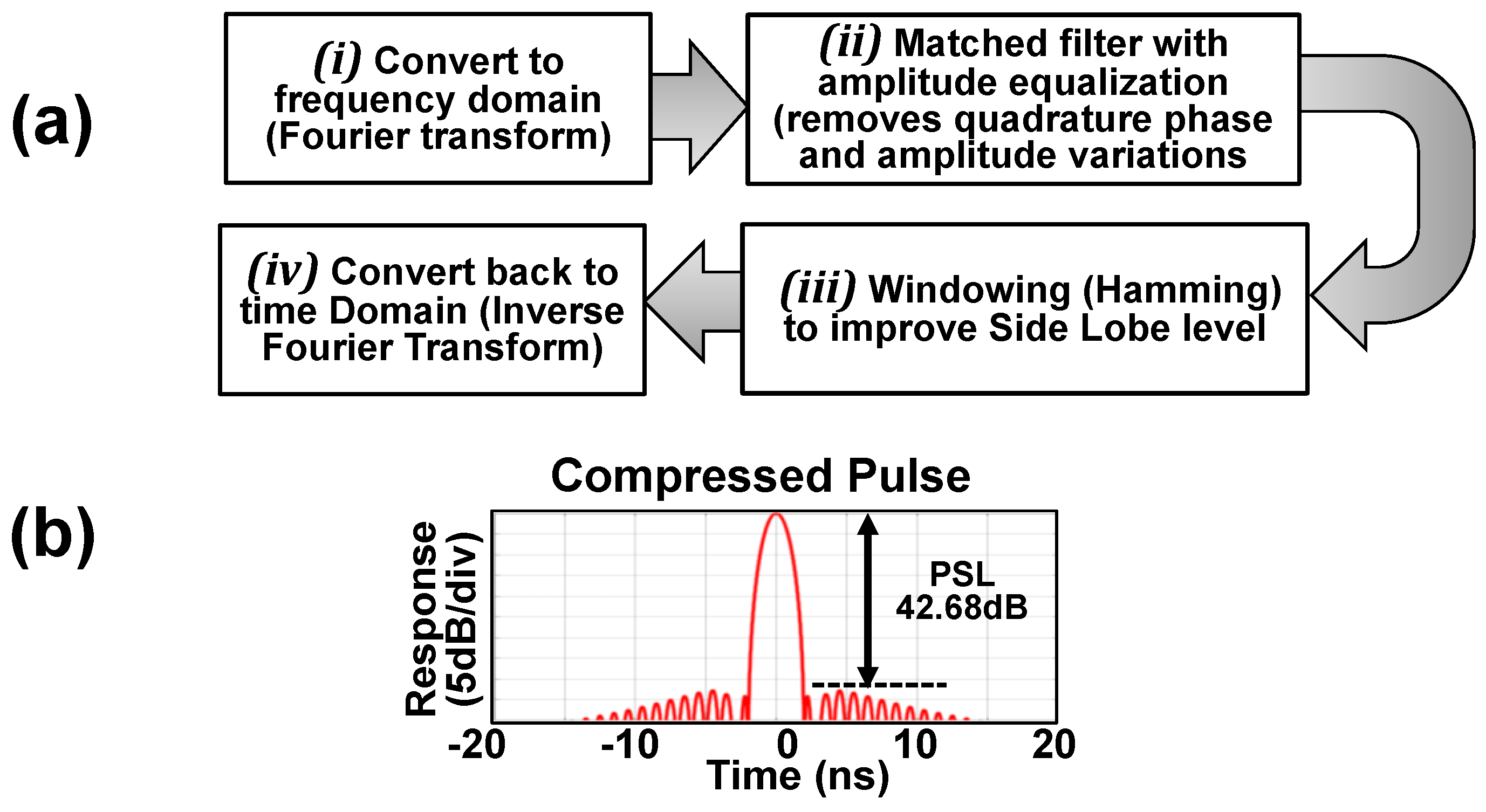
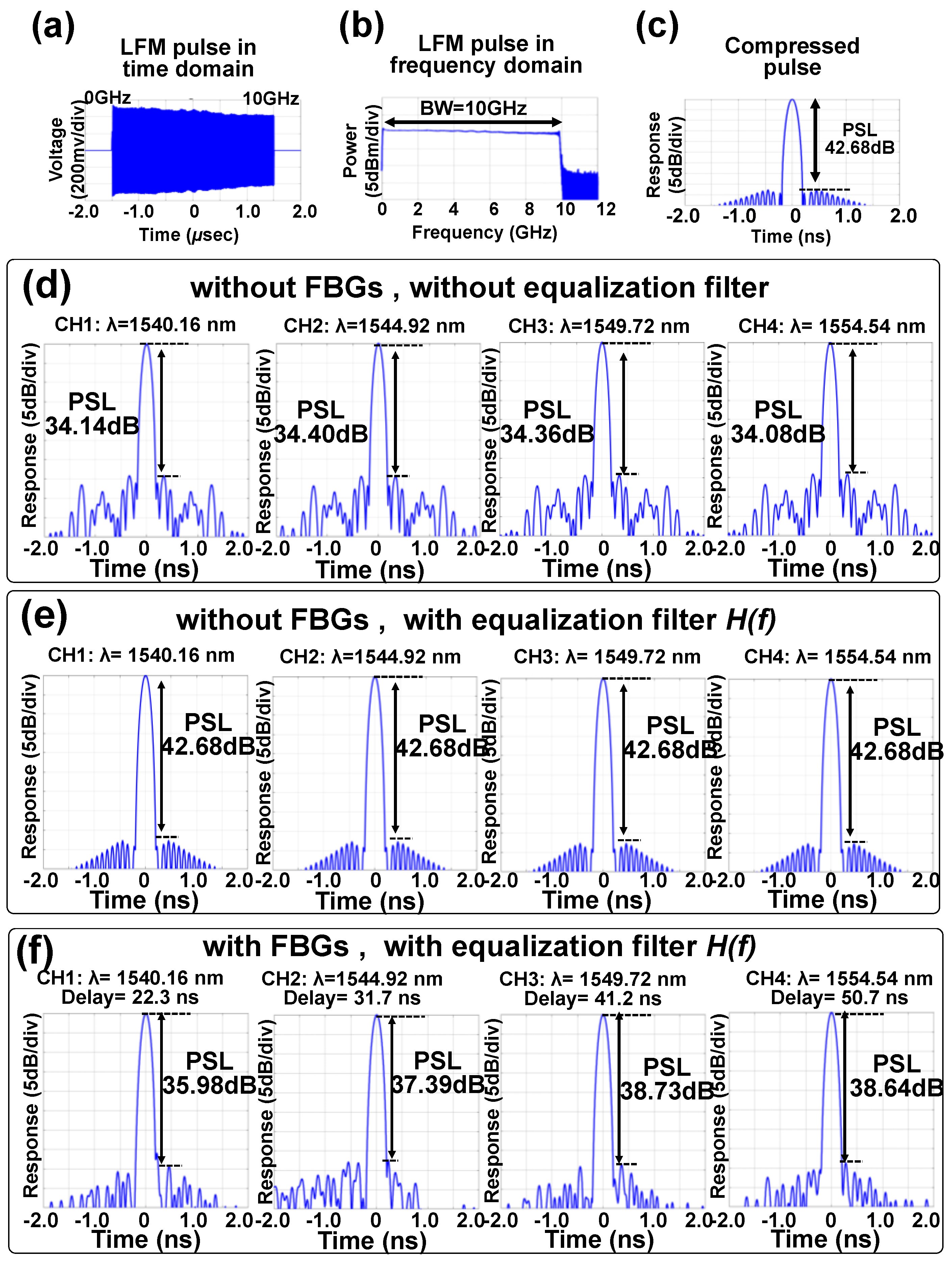
5. Experimentally Measuring the PSL of LFM Pulse
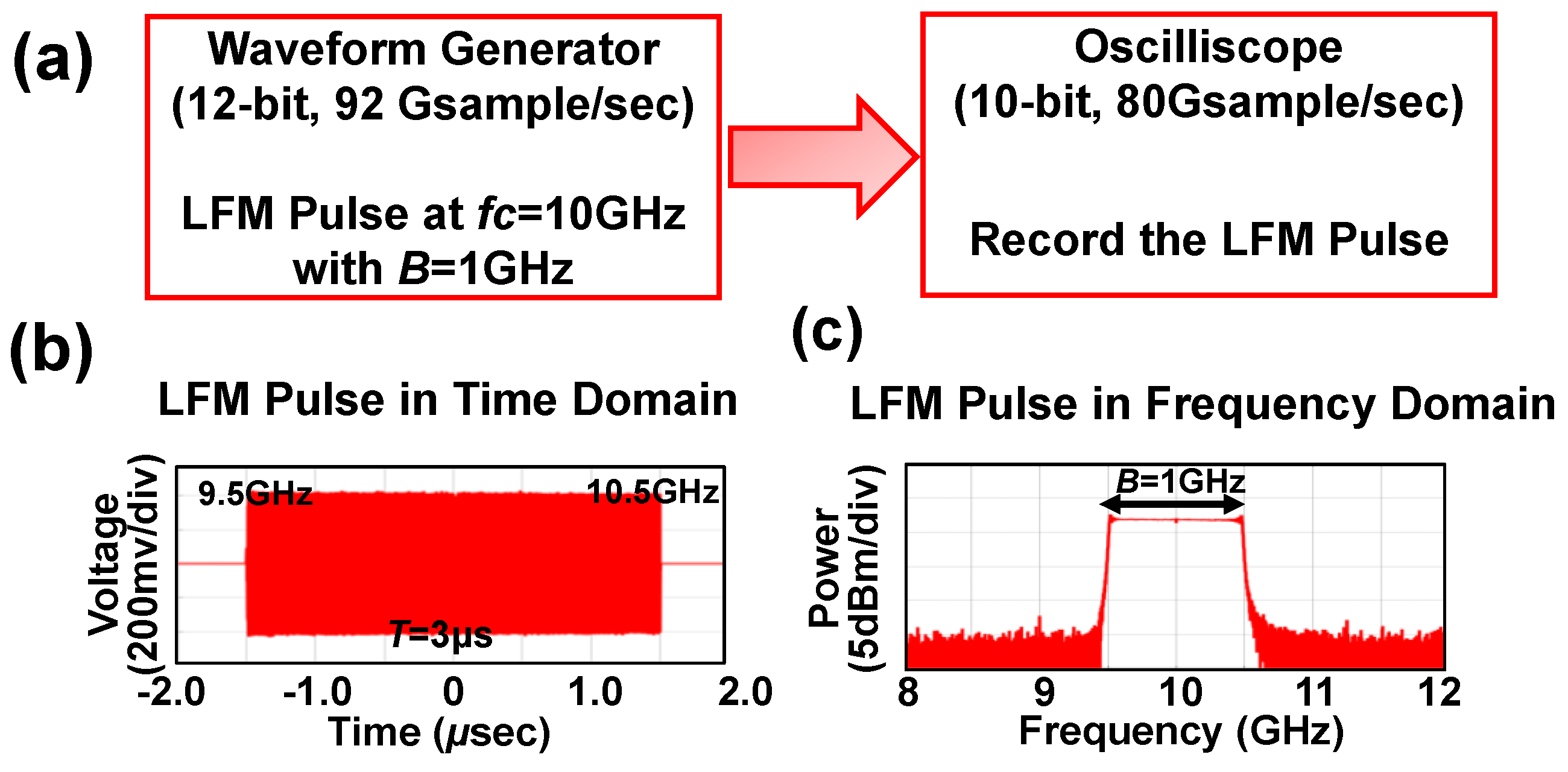
5.1. Configuration for RF-LFM Pulse Generation and Detection
5.2. The Process of Measuring the PSL
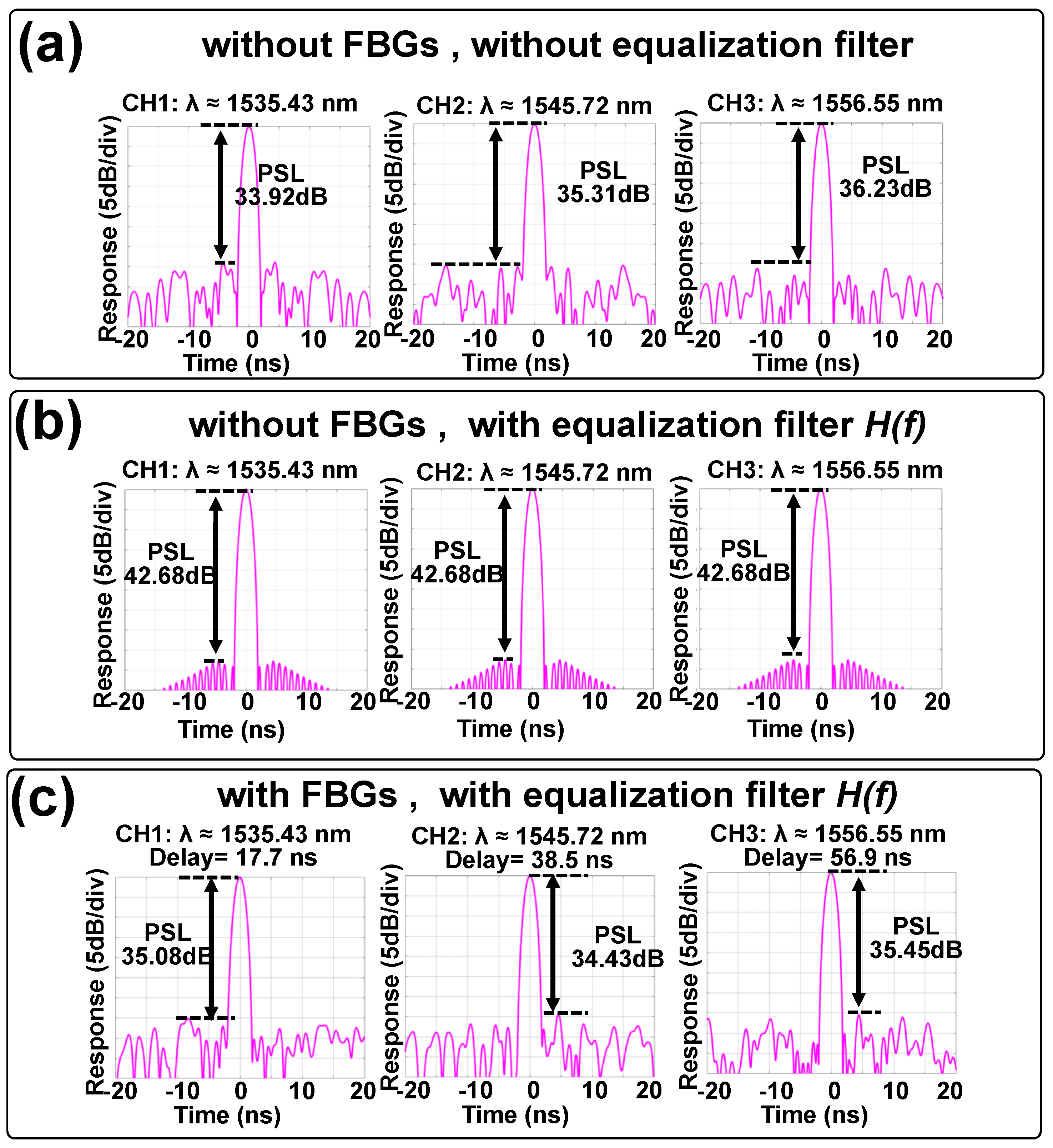
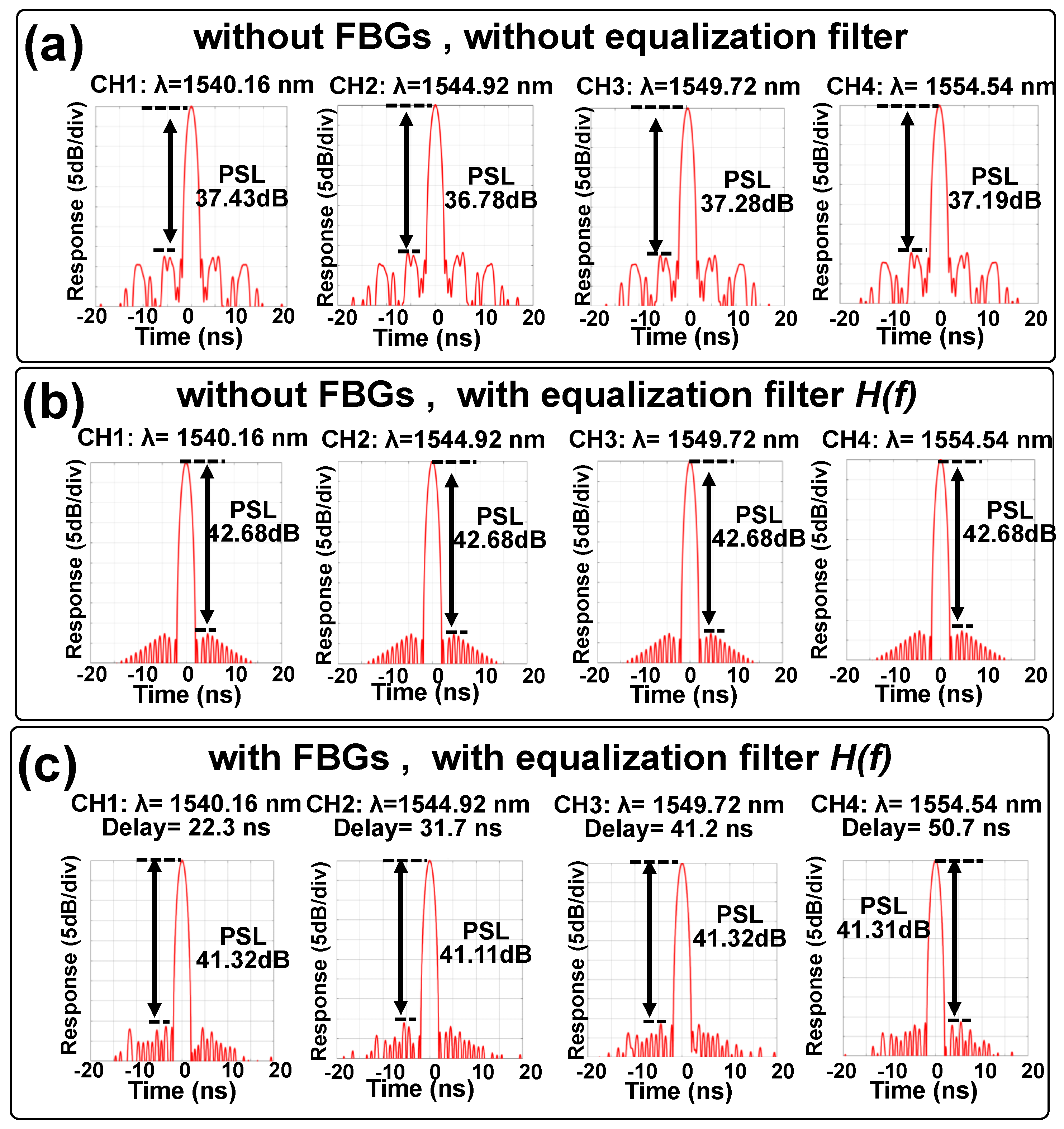
5.3. Experimentally Measuring the PSL Performance of the LFM Pulse after Delaying It Using the Optical Memory Buffer
5.4. Performance Comparison with the Buffer Made of a Bank of Lasers
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, D.H.; Lin, W.P. Phased-array beam steering using optical true time delay technique. Opt. Commun. 2015, 350, 90–96. [Google Scholar] [CrossRef]
- Tan, M.; Xu, X.; Wu, J.; Morandotti, R.; Mitchell, A.; Moss, D.J. Photonic RF and microwave filters based on 49 GHz and 200 GHz Kerr microcombs. Opt. Commun. 2020, 465, 125563. [Google Scholar] [CrossRef]
- Rotman, R.; Tur, M.; Yaron, L. True time delay in phased arrays. Proc. IEEE 2016, 104, 504–518. [Google Scholar] [CrossRef]
- Urick, V.J.; Williams, K.J.; McKinney, J.D. Fundamentals of Microwave Photonics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zhou, P.; Zhang, F.; Pan, S. Generation of linear frequency-modulated waveforms by a frequency-sweeping optoelectronic oscillator. J. Light. Technol. 2018, 36, 3927–3934. [Google Scholar] [CrossRef]
- Klinger, O.; Stern, Y.; Pederiva, F.; Jamshidi, K.; Schneider, T.; Zadok, A. Continuously variable long microwave-photonic delay of arbitrary frequency-chirped signals. Opt. Lett. 2012, 37, 3939–3941. [Google Scholar] [CrossRef] [PubMed]
- Min, S.S.; Yoo, H.; Won, Y.H. Time–wavelength hybrid optical CDMA system with tunable encoder/decoder using switch and fixed delay-line. Opt. Commun. 2003, 216, 335–342. [Google Scholar] [CrossRef]
- Yoo, S.B. Optical packet and burst switching technologies for the future photonic internet. J. Light. Technol. 2006, 24, 4468–4492. [Google Scholar] [CrossRef]
- Liu, Y.; Hill, M.; Geldenhuys, R.; Calabretta, N.; De Waardt, H.; Khoe, G.D.; Dorren, H. Demonstration of a variable optical delay for a recirculating buffer by using all-optical signal processing. IEEE Photonics Technol. Lett. 2004, 16, 1748–1750. [Google Scholar] [CrossRef]
- Tucker, R.S. The role of optics and electronics in high-capacity routers. J. Light. Technol. 2006, 24, 4655–4673. [Google Scholar] [CrossRef]
- Praena, J.Á.; Carballar, A. Chirped Integrated Bragg Grating Design. Photonics 2024, 11, 476. [Google Scholar] [CrossRef]
- Zou, X.H.; Pan, W.; Luo, B.; Qin, Z.M.; Wang, M.Y.; Zhang, W.L. Periodically chirped sampled fiber Bragg gratings for multichannel comb filters. IEEE Photonics Technol. Lett. 2006, 18, 1371–1373. [Google Scholar] [CrossRef]
- Asseh, A.; Storoy, H.; Sahlgren, B.E.; Sandgren, S.; Stubbe, R.A. A writing technique for long fiber Bragg gratings with complex reflectivity profiles. J. Light. Technol. 1997, 15, 1419–1423. [Google Scholar] [CrossRef]
- Zeitouny, A.; Stepanov, S.; Levinson, O.; Horowitz, M. Optical generation of linearly chirped microwave pulses using fiber Bragg gratings. IEEE Photonics Technol. Lett. 2005, 17, 660–662. [Google Scholar] [CrossRef]
- Ashrafi, R.; Park, Y.; Azana, J. Fiber-based photonic generation of high-frequency microwave pulses with reconfigurable linear chirp control. IEEE Trans. Microw. Theory Tech. 2010, 58, 3312–3319. [Google Scholar] [CrossRef]
- Ghelfi, P.; Scotti, F.; Laghezza, F.; Bogoni, A. Photonic generation of phase-modulated RF signals for pulse compression techniques in coherent radars. J. Light. Technol. 2012, 30, 1638–1644. [Google Scholar] [CrossRef]
- Moslemi, P.; Chen, L.R. Simultaneously generating multiple chirped microwave pulses with superimposed FBGs. IEEE Photonics Technol. Lett. 2017, 29, 1387–1390. [Google Scholar] [CrossRef]
- Wang, H.; Wu, B.; Zhou, H.; Wang, W.; Xu, G. Optical Tunable Frequency-Doubling OEO Using a Chirped FBG Based on Orthogonally Polarized Double Sideband Modulation. Photonics 2023, 10, 1002. [Google Scholar] [CrossRef]
- Jiang, Y.; Howley, B.; Shi, Z.; Zhou, Q.; Chen, R.T.; Chen, M.Y.; Brost, G.; Lee, C. Dispersion-enhanced photonic crystal fiber array for a true time-delay structured X-band phased array antenna. IEEE Photonics Technol. Lett. 2004, 17, 187–189. [Google Scholar] [CrossRef]
- Shaheen, S.; Gris-Sánchez, I.; Gasulla, I. True-time delay line based on dispersion-flattened 19-core photonic crystal fiber. J. Light. Technol. 2020, 38, 6237–6246. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, C.; Zhao, Z.; Zhang, W.; Liu, J. A Microwave Photonics True-Time-Delay System Using Carrier Compensation Technique Based on Wavelength Division Multiplexing. Photonics 2023, 10, 34. [Google Scholar] [CrossRef]
- Sun, Q.; Liu, C.; Yang, J.; Liu, J.; Dong, J.; Li, W. Phase-Derived Ranging Based Fiber Transfer Delay Measurement Using a Composite Signal for Distributed Radars with Fiber Networks. Photonics 2023, 10, 421. [Google Scholar] [CrossRef]
- Zhou, W.; Stead, M.; Weiss, S.; Okusaga, O.; Jiang, L.; Anderson, S.; Huang, Z.R. Developing an integrated photonic system with a simple beamforming architecture for phased-array antennas. Appl. Opt. 2017, 56, B5–B13. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Wu, J.; Morandotti, R.; Mitchell, A.; Moss, D.J. Microcomb-Based Photonic RF Signal Processing. IEEE Photonics Technol. Lett. 2019, 31, 1854–1857. [Google Scholar] [CrossRef]
- Hu, J.; He, J.; Liu, J.; Raja, A.S.; Karpov, M.; Lukashchuk, A.; Kippenberg, T.J.; Brès, C.S. Reconfigurable radiofrequency filters based on versatile soliton microcombs. Nat. Commun. 2020, 11, 4377. [Google Scholar] [CrossRef] [PubMed]
- Anashkina, E.A.; Marisova, M.P.; Andrianov, A.V.; Akhmedzhanov, R.A.; Murnieks, R.; Tokman, M.D.; Skladova, L.; Oladyshkin, I.V.; Salgals, T.; Lyashuk, I.; et al. Microsphere-Based Optical Frequency Comb Generator for 200 GHz Spaced WDM Data Transmission System. Photonics 2020, 7, 72. [Google Scholar] [CrossRef]
- Xu, X.; Wu, J.; Nguyen, T.G.; Shoeiby, M.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Advanced RF and microwave functions based on an integrated optical frequency comb source. Opt. Express 2018, 26, 2569–2583. [Google Scholar] [CrossRef]
- Liao, P.; Bao, C.; Kordts, A.; Karpov, M.; Pfeiffer, M.H.; Zhang, L.; Cao, Y.; Almaiman, A.; Mohajerin-Ariaei, A.; Alishahi, F.; et al. Effects of erbium-doped fiber amplifier induced pump noise on soliton Kerr frequency combs for 64-quadrature amplitude modulation transmission. Opt. Lett. 2018, 43, 2495–2498. [Google Scholar] [CrossRef] [PubMed]
- Raz, O.; Barzilay, S.; Rotman, R.; Tur, M. Submicrosecond scan-angle switching photonic beamformer with flat RF response in the C and X bands. J. Light. Technol. 2008, 26, 2774–2781. [Google Scholar] [CrossRef][Green Version]
- Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-based optical frequency combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef]
- Pan, Z.; Song, Y.; Yu, C.; Wang, Y.; Yu, Q.; Popelek, J.; Li, H.; Li, Y.; Willner, A.E. Tunable chromatic dispersion compensation in 40-Gb/s systems using nonlinearly chirped fiber Bragg gratings. J. Light. Technol. 2002, 20, 2239–2246. [Google Scholar] [CrossRef]
- Almaiman, A.; Cao, Y.; Alishahi, F.; Fallahpour, A.; Li, L.; Liao, P.; Zou, K.; Zach, S.; Cohen, N.; Tur, M.; et al. Experimental Characterization of Low-Latency Multiple and Tunable Delays of Wideband Analog LFM Signal Using Concatenated Linearly Chirped and Sampled FBGs. In Proceedings of the CLEO: Science and Innovations. Optica Publishing Group, San Jose, CA, USA, 15–20 May 2019; p. SF2N–3. [Google Scholar]
- Liu, Y.; Xuan, Y.; Xue, X.; Wang, P.H.; Chen, S.; Metcalf, A.J.; Wang, J.; Leaird, D.E.; Qi, M.; Weiner, A.M. Investigation of mode coupling in normal-dispersion silicon nitride microresonators for Kerr frequency comb generation. Optica 2014, 1, 137–144. [Google Scholar] [CrossRef]
- Kim, S.; Han, K.; Wang, C.; Jaramillo-Villegas, J.A.; Xue, X.; Bao, C.; Xuan, Y.; Leaird, D.E.; Weiner, A.M.; Qi, M. Dispersion engineering and frequency comb generation in thin silicon nitride concentric microresonators. Nat. Commun. 2017, 8, 372. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Zheng, Y.; Zhang, F.; Yang, J.; Qin, T.; Wan, W. Passive fine-tuning of microcavity whispering gallery mode for nonlinear optics by thermo-optical effect. Appl. Phys. Lett. 2019, 114, 101103. [Google Scholar] [CrossRef]
- Jin, W.; Polcawich, R.G.; Morton, P.A.; Bowers, J.E. Piezoelectrically tuned silicon nitride ring resonator. Opt. Express 2018, 26, 3174–3187. [Google Scholar] [CrossRef]
- Han, Y.G.; Dong, X.; Lee, J.; Lee, S. Simultaneous measurement of bending and temperature based on a single sampled chirped fiber Bragg grating embedded on a flexible cantilever beam. Opt. Lett. 2006, 31, 2839–2841. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Dai, Y.; Chen, X.; Zhang, Y.; Xie, S. Thermally tunable dispersion compensator in 40-Gb/s system using FBG fabricated with linearly chirped phase mask. Opt. Express 2006, 14, 44–49. [Google Scholar] [CrossRef]
- Rizzo, A.; Daudlin, S.; Novick, A.; James, A.; Gopal, V.; Murthy, V.; Cheng, Q.; Kim, B.Y.; Ji, X.; Okawachi, Y.; et al. Petabit-scale silicon photonic interconnects with integrated kerr frequency combs. IEEE J. Sel. Top. Quantum Electron. 2022, 29, 1–20. [Google Scholar] [CrossRef]
- Strain, M.J.; Sorel, M. Design and fabrication of integrated chirped Bragg gratings for on-chip dispersion control. IEEE J. Quantum Electron. 2010, 46, 774–782. [Google Scholar] [CrossRef]
- Sahin, E.; Ooi, K.; Png, C.; Tan, D. Large, scalable dispersion engineering using cladding-modulated Bragg gratings on a silicon chip. Appl. Phys. Lett. 2017, 110, 161113. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, D.; Deng, C.; Lu, M.; Huang, L.; Hu, G.; Yun, B.; Zhang, R.; Li, M.; Dong, J.; et al. Large group delay in silicon-on-insulator chirped spiral Bragg grating waveguide. IEEE Photonics J. 2021, 13, 1–5. [Google Scholar] [CrossRef]
- Hiraki, T.; Aihara, T.; Fujii, T.; Takeda, K.; Kakitsuka, T.; Tsuchizawa, T.; Matsuo, S. Membrane InGaAsP Mach–Zehnder modulator integrated with optical amplifier on Si platform. J. Light. Technol. 2020, 38, 3030–3036. [Google Scholar] [CrossRef]
- Van Gasse, K.; Wang, R.; Roelkens, G. 27 dB gain III–V-on-silicon semiconductor optical amplifier with >17 dBm output power. Opt. Express 2019, 27, 293–302. [Google Scholar] [CrossRef] [PubMed]
- Errando-Herranz, C.; Niklaus, F.; Stemme, G.; Gylfason, K.B. Low-power microelectromechanically tunable silicon photonic ring resonator add-drop filter. Opt. Lett. 2015, 40, 3556–3559. [Google Scholar] [CrossRef] [PubMed]
- Hammood, M.; Mistry, A.; Yun, H.; Ma, M.; Lin, S.; Chrostowski, L.; Jaeger, N.A. Broadband, silicon photonic, optical add–drop filters with 3 dB bandwidths up to 11 THz. Opt. Lett. 2021, 46, 2738–2741. [Google Scholar] [CrossRef] [PubMed]



| Component | Internal Element Responsible for the Latency | Measured Latency (ns) | Minimum Viable Latency (ns) |
|---|---|---|---|
| FBG1 | Fiber jumpers at the circulator ports and the FBG terminal. | 144.3 | <1 |
| FBG2 | Fiber jumpers at the circulator ports and the FBG terminal. | 11.6 | <0.5 (at zero-delay ) |
| EDFA | Fiber jumpers at the terminals of isolators and the 1.2 m erbium-doped fiber segment. | 10.1 | <2.5 |
| Optical LCoS filter | Fiber jumpers connecting input/output ports to the lenses. | 35 | <1 |
| TOTAL | 201 | <5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almaiman, A.; Cao, Y.; Liao, P.; Willner, A.; Tur, M. Optically Delaying a Radio Frequency–Linear Frequency-Modulated (RF-LFM) Pulse Using Kerr Comb Carriers and Off-the-Shelf Concatenation of a Linearly Chirped Fiber Bragg Grating and a Chirped-and-Sampled Fiber Bragg Grating. Photonics 2024, 11, 823. https://doi.org/10.3390/photonics11090823
Almaiman A, Cao Y, Liao P, Willner A, Tur M. Optically Delaying a Radio Frequency–Linear Frequency-Modulated (RF-LFM) Pulse Using Kerr Comb Carriers and Off-the-Shelf Concatenation of a Linearly Chirped Fiber Bragg Grating and a Chirped-and-Sampled Fiber Bragg Grating. Photonics. 2024; 11(9):823. https://doi.org/10.3390/photonics11090823
Chicago/Turabian StyleAlmaiman, Ahmed, Yinwen Cao, Peicheng Liao, Alan Willner, and Moshe Tur. 2024. "Optically Delaying a Radio Frequency–Linear Frequency-Modulated (RF-LFM) Pulse Using Kerr Comb Carriers and Off-the-Shelf Concatenation of a Linearly Chirped Fiber Bragg Grating and a Chirped-and-Sampled Fiber Bragg Grating" Photonics 11, no. 9: 823. https://doi.org/10.3390/photonics11090823
APA StyleAlmaiman, A., Cao, Y., Liao, P., Willner, A., & Tur, M. (2024). Optically Delaying a Radio Frequency–Linear Frequency-Modulated (RF-LFM) Pulse Using Kerr Comb Carriers and Off-the-Shelf Concatenation of a Linearly Chirped Fiber Bragg Grating and a Chirped-and-Sampled Fiber Bragg Grating. Photonics, 11(9), 823. https://doi.org/10.3390/photonics11090823






