A Three-Dimensional Reconstruction Method Based on Telecentric Epipolar Constraints
Abstract
1. Introduction
2. System Calibration
2.1. Calibration for Telecentric Lens
2.2. Projector Calibration
3. Telecentric Epipolar Constraints
3.1. Principle
3.2. Three-Dimensional Reconstruction Based on Telecentric Epipolar Constraint
3.3. Three-Dimensional Reconstruction Based on Projection Matrix
4. Experiment and Discussion
5. Conclusions
- When recovering the extrinsic parameters between the camera and the projector using the telecentric essential matrix, we ensure the intrinsic properties of the essential matrix under telecentric conditions by performing an SVD and adjusting the singular value matrix. This guarantees that the decomposed rotation matrix satisfies orthogonality constraints. Compared to the projection matrix method, the approach proposed in this paper results in smaller reconstruction standard deviations.
- It is more flexible. The equation calculating the essential matrix does not involve the extrinsic parameters of the camera. Therefore, during the camera calibration process, it is only necessary to determine the intrinsic parameters, which avoids the symbolic ambiguity of the extrinsic parameters. Additionally, in the experimental procedure, there is no need to introduce a micro-displacement platform, simplifying the process and minimizing potential errors.
- During the essential matrix estimation process, incorporating the calibration board corner data from all poses for the optimization results in a certain level of average error improvement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dai, G.; Bütefisch, S.; Pohlenz, F.; Danzebrink, H.-U. A high precision micro/nano CMM using piezoresistive tactile probes. Meas. Sci. Technol. 2009, 20, 084001. [Google Scholar] [CrossRef]
- Claverley, J.D.; Leach, R.K. A review of the existing performance verification infrastructure for micro-CMMs. Precis. Eng.-J. Int. Soc. Precis. Eng. Nanotechnol. 2015, 39, 1–15. [Google Scholar] [CrossRef]
- Hung, C.-C.; Fang, Y.-C.; Tsai, C.-M.; Lin, C.-C.; Yeh, K.-M.; Wu, J.-H. Optical design of high performance con-focal microscopy with digital micro-mirror and stray light filters. Optik 2010, 121, 2073–2079. [Google Scholar] [CrossRef]
- Kumar, U.P.; Bhaduri, B.; Kothiyal, M.P.; Mohan, N.K. Two-wavelength micro-interferometry for 3-D surface profiling. Opt. Lasers Eng. 2009, 47, 223–229. [Google Scholar] [CrossRef]
- Kumar, U.P.; Wang, H.F.; Mohan, N.K.; Kothiyal, M.P. White light interferometry for surface profiling with a colour CCD. Opt. Lasers Eng. 2012, 50, 1084–1088. [Google Scholar] [CrossRef]
- Deng, H.W.; Hu, P.Y.; Zhang, G.F.; Xia, C.S.; Cai, Y.D.; Yang, S.M. Accurate and flexible calibration method for a 3D microscopic structured light system with telecentric imaging and Scheimpflug projection. Opt. Express 2023, 31, 3092–3113. [Google Scholar] [CrossRef] [PubMed]
- Gorthi, S.S.; Rastogi, P. Fringe projection techniques: Whither we are? Opt. Lasers Eng. 2010, 48, 133–140. [Google Scholar] [CrossRef]
- Van der Jeught, S.; Dirckx, J.J.J. Real-time structured light profilometry: A review. Opt. Lasers Eng. 2016, 87, 18–31. [Google Scholar] [CrossRef]
- Mei, Q.; Gao, J.; Lin, H.; Chen, Y.; He, Y.B.; Wang, W.; Zhang, G.J.; Chen, X. Structure light telecentric stereoscopic vision 3D measurement system based on Scheimpflug condition. Opt. Lasers Eng. 2016, 86, 83–91. [Google Scholar] [CrossRef]
- Sansoni, G.; Trebeschi, M.; Docchio, F. State-of-The-Art and Applications of 3D Imaging Sensors in Industry, Cultural Heritage, Medicine, and Criminal Investigation. Sensors 2009, 9, 568–601. [Google Scholar] [CrossRef]
- Yin, Y.K.; He, D.; Liu, Z.Y.; Liu, X.L.; Peng, X. Phase aided 3D imaging and modeling: Dedicated systems and case studies. In Proceedings of the Conference on Optical Micro- and Nanometrology V, Brussels, Belgium, 15–17 April 2014. [Google Scholar]
- Yin, Y.K.; Wang, M.; Gao, B.Z.; Liu, X.L.; Peng, X. Fringe projection 3D microscopy with the general imaging model. Opt. Express 2015, 23, 6846–6857. [Google Scholar] [CrossRef]
- Windecker, R.; Fleischer, M.; Tiziani, H.J. Three-dimensional topometry with stereo microscopes. Opt. Eng. 1997, 36, 3372–3377. [Google Scholar] [CrossRef]
- Li, A.M.; Peng, X.; Yin, Y.K.; Liu, X.L.; Zhao, Q.P.; Köerner, K.; Osten, W. Fringe projection based quantitative 3D microscopy. Optik 2013, 124, 5052–5056. [Google Scholar] [CrossRef]
- Rico Espino, J.G.; Gonzalez-Barbosa, J.-J.; Gómez Loenzo, R.A.; Córdova Esparza, D.M.; Gonzalez-Barbosa, R. Vision system for 3D reconstruction with telecentric lens. In Proceedings of the Pattern Recognition: 4th Mexican Conference (MCPR 2012), Huatulco, Mexico, 27–30 June 2012; pp. 127–136. [Google Scholar]
- Miks, A.; Novák, J. Design of a double-sided telecentric zoom lens. Appl. Opt. 2012, 51, 5928–5935. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.K.; Chen, X.B.; Xi, J.T.; Wu, Z.Q. Aberration correction of double-sided telecentric zoom lenses using lens modules. Appl. Opt. 2014, 53, 6123–6132. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.S.; Kanade, T. Multiaperture telecentric lens for 3D reconstruction. Opt. Lett. 2011, 36, 1050–1052. [Google Scholar] [CrossRef] [PubMed]
- Li, B.W.; Zhang, S. Microscopic structured light 3D profilometry: Binary defocusing technique vs. sinusoidal fringe projection. Opt. Lasers Eng. 2017, 96, 117–123. [Google Scholar] [CrossRef]
- Zhang, J.K.; Chen, X.B.; Xi, J.T.; Wu, Z.Q. Paraxial analysis of double-sided telecentric zoom lenses with four components. Opt. Eng. 2014, 53, 4957–4967. [Google Scholar] [CrossRef]
- Niu, Z.Q.; Gao, N.; Zhang, Z.H.; Gao, F.; Jiang, X.Q. 3D shape measurement of discontinuous specular objects based on advanced PMD with bi-telecentric lens. Opt. Express 2018, 26, 1615–1632. [Google Scholar] [CrossRef]
- Ota, M.; Leopold, F.; Noda, R.; Maeno, K. Improvement in spatial resolution of background-oriented schlieren technique by introducing a telecentric optical system and its application to supersonic flow. Exp. Fluids 2015, 56, 48. [Google Scholar] [CrossRef]
- Marani, R.; Roselli, G.; Nitti, M.; Cicirelli, G.; D’Orazio, T.; Stella, E. A 3D vision system for high resolution surface reconstruction. In Proceedings of the 7th International Conference on Sensing Technology (ICST), Wellington, New Zealand, 3–5 December 2013; pp. 157–162. [Google Scholar]
- Baldwin-Olguin, G. Telecentric lens for precision machine vision. In Proceedings of the Second Iberoamerican Meeting on Optics, Guanajuato, Mexico, 18–22 September 1995; pp. 440–443. [Google Scholar]
- Zhang, S.F.; Li, B.; Ren, F.J.; Dong, R. High-Precision Measurement of Binocular Telecentric Vision System With Novel Calibration and Matching Methods. IEEE Access 2019, 7, 54682–54692. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Q.; Feng, S.J.; Tao, T.Y.; Asundi, A.; Zuo, C. A new microscopic telecentric stereo vision system—Calibration, rectification, and three-dimensional reconstruction. Opt. Lasers Eng. 2019, 113, 14–22. [Google Scholar] [CrossRef]
- Hu, Y.; Liang, Y.C.; Tao, T.Y.; Feng, S.J.; Zuo, C.; Zhang, Y.Z.; Chen, Q. Dynamic 3D measurement of thermal deformation based on geometric-constrained stereo-matching with a stereo microscopic system. Meas. Sci. Technol. 2019, 30, 125007. [Google Scholar] [CrossRef]
- Feng, S.J.; Zuo, C.; Zhang, L.; Tao, T.Y.; Hu, Y.; Yin, W.; Qian, J.M.; Chen, Q. Calibration of fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2021, 143, 106622. [Google Scholar] [CrossRef]
- Li, D.; Liu, C.; Tian, J. Telecentric 3D profilometry based on phase-shifting fringe projection. Opt. Express 2014, 22, 31826–31835. [Google Scholar] [CrossRef] [PubMed]
- Teng, C.H.; Chen, Y.S.; Hsu, W.H. Camera self-calibration method suitable for variant camera constraints. Appl. Opt. 2006, 45, 688–696. [Google Scholar] [CrossRef]
- Kahl, F.; Heyden, A. Affine structure and motion from points, lines and conics. Int. J. Comput. Vis. 1999, 33, 163–180. [Google Scholar] [CrossRef]
- Shapiro, L.S.; Zisserman, A.; Brady, M. 3D Motion Recovery via Affine Epipolar Geometry. Int. J. Comput. Vis. 1995, 16, 147–182. [Google Scholar] [CrossRef]
- Li, D.; Tian, J.D. An accurate calibration method for a camera with telecentric lenses. Opt. Lasers Eng. 2013, 51, 538–541. [Google Scholar] [CrossRef]
- Chen, K.P.; Shi, T.L.; Wang, X.; Zhang, Y.C.; Hong, Y.; Liu, Q.; Liao, G.L. Calibration of telecentric cameras with an improved projection model. Opt. Eng. 2018, 57, 044103. [Google Scholar] [CrossRef]
- Peng, J.Z.; Wang, M.; Deng, D.N.; Liu, X.L.; Yin, Y.K.; Peng, X. Distortion correction for microscopic fringe projection system with Scheimpflug telecentric lens. Appl. Opt. 2015, 54, 10055–10062. [Google Scholar] [CrossRef]
- Rao, L.; Da, F.P.; Kong, W.Q.; Huang, H.M. Flexible calibration method for telecentric fringe projection profilometry systems. Opt. Express 2016, 24, 1222–1237. [Google Scholar] [CrossRef] [PubMed]
- Haskamp, K.; Kästner, M.; Reithmeier, E. Accurate Calibration of a Fringe Projection System by Considering Telecentricity. In Proceedings of the Conference on Optical Measurement Systems for Industrial Inspection VII, Munich, Germany, 23–26 May 2011. [Google Scholar]
- Zhu, F.P.; Liu, W.W.; Shi, H.J.; He, X.Y. Accurate 3D measurement system and calibration for speckle projection method. Opt. Lasers Eng. 2010, 48, 1132–1139. [Google Scholar] [CrossRef]
- Feng, G.; Zhu, L.; Zou, H.; Nianxiang, W. A calibration methods for vision measuring system with large view field. In Proceedings of the 2011 4th International Congress on Image and Signal Processing, Shanghai, China, 15–17 October 2011; pp. 1377–1380. [Google Scholar]
- Tomasi, C.; Kanade, T. Shape and Motion from Image Streams under Orthography—A Factorization Method. Int. J. Comput. Vis. 1992, 9, 137–154. [Google Scholar] [CrossRef]
- Lanman, D.; Hauagge, D.C.; Taubin, G. Shape from depth discontinuities under orthographic projection. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 1550–1557. [Google Scholar]
- Liu, H.B.; Lin, H.J.; Yao, L. Calibration method for projector-camera-based telecentric fringe projection profilometry system. Opt. Express 2017, 25, 31492–31508. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Chen, Z.; Liao, H.Y.; Zhang, X.M. Telecentric stereo micro-vision system: Calibration method and experiments. Opt. Lasers Eng. 2014, 57, 82–92. [Google Scholar] [CrossRef]
- Yao, L.S.; Liu, H.B. A Flexible Calibration Approach for Cameras with Double-sided Telecentric Lenses. Int. J. Adv. Robot. Syst. 2016, 13, 82. [Google Scholar] [CrossRef]
- Chen, C.; Chen, B.; Pan, B. Telecentric camera calibration with virtual patterns. Meas. Sci. Technol. 2021, 32, 125004. [Google Scholar] [CrossRef]
- Liao, H.Y.; Chen, Z.; Zhang, X.M. Calibration of Camera with Small FOV and DOF Telecentric Lens. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013; pp. 498–503. [Google Scholar]
- Xiao, W.F.; Zhou, P.; An, S.Y.; Zhu, J.P. Constrained nonlinear optimization method for accurate calibration of a bi-telecentric camera in a three-dimensional microtopography system. Appl. Opt. 2022, 61, 157–166. [Google Scholar] [CrossRef]
- Guan, B.L.; Yao, L.S.; Liu, H.B.; Shang, Y. An accurate calibration method for non-overlapping cameras with double-sided telecentric lenses. Optik 2017, 131, 724–732. [Google Scholar] [CrossRef]
- Li, B.; Zhang, S. Flexible calibration method for microscopic structured light system using telecentric lens. Opt. Express 2015, 23, 25795–25803. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.C.; Wu, G.X.; Wu, Y.X.; Yan, J.; Luo, H.F.; Zhang, Y.N.; Liu, F. High-accuracy high-speed unconstrained fringe projection profilometry of 3D measurement. Opt. Laser Technol. 2020, 125, 106063. [Google Scholar] [CrossRef]





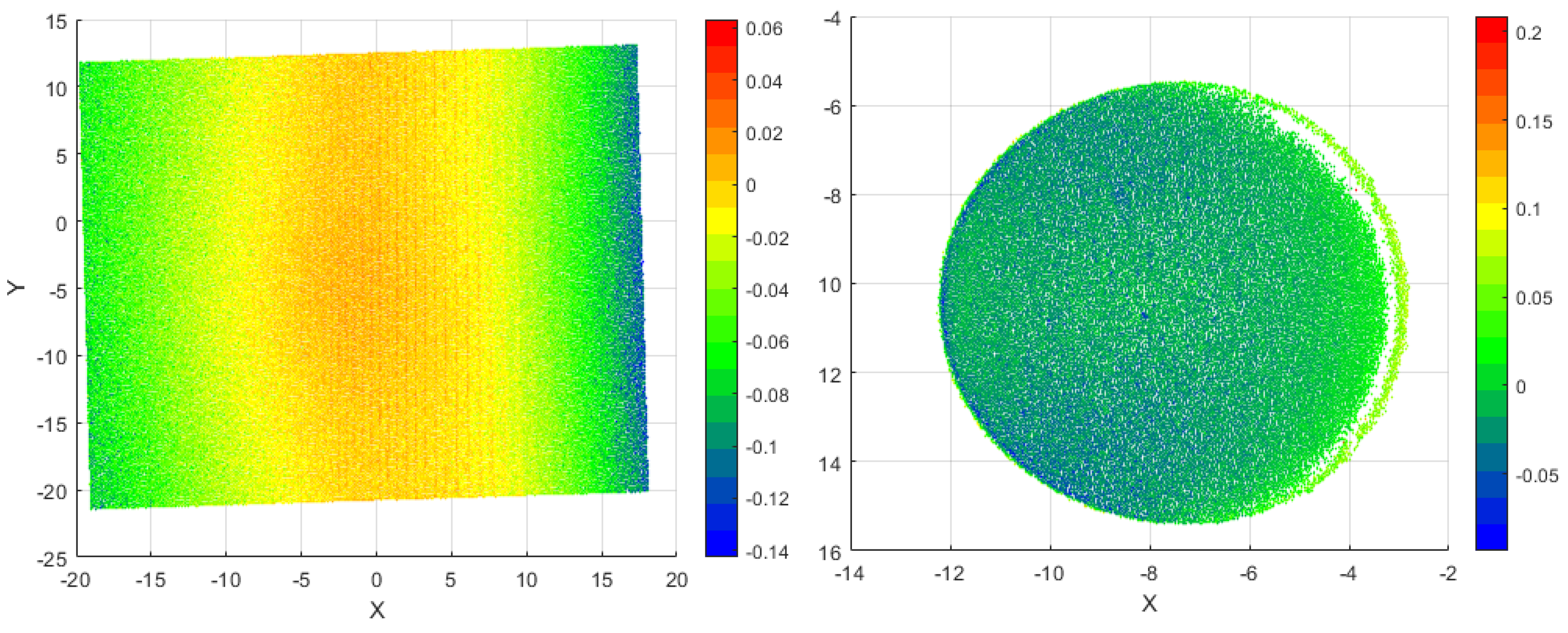

| Sphere | Position | Standard Deviation (M)/μm | Standard Deviation (E)/μm | Diameter Absolute Deviation (M)/μm | Diameter Absolute Deviation (E)/μm |
|---|---|---|---|---|---|
| S1 | upper left | 13.4 | 14.9 | 30.4 | 6.4 |
| S2 | upper right | 14.0 | 14.7 | 16.3 | 8.4 |
| S3 | middle | 13.1 | 14.6 | 25.4 | 1.0 |
| S4 | lower left | 14.1 | 15.4 | 26.3 | 9.4 |
| S5 | lower right | 13.9 | 14.8 | 14.1 | 6.3 |
| Plane | Z/mm | Standard Deviation (M)/μm | Standard Deviation (E)/μm |
|---|---|---|---|
| Plane 1 | 0.00 | 23.8 | 11.0 |
| Plane 2 | 0.75 | 21.7 | 11.1 |
| Plane 3 | 1.50 | 21.9 | 10.9 |
| Plane 4 | 2.25 | 21.8 | 9.9 |
| Plane 5 | 3.00 | 23.1 | 9.1 |
| Distance to Fitting Plane/μm | Curvature/μm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Upper Left | Upper Right | Lower Left | Lower Right | Center | Upper Left | Upper Right | Lower Left | Lower Right | AVG | |
| Plane 1 | 41.5 | 62.2 | 27.2 | 60.6 | 47.9 | 6.4 | 14.3 | 20.7 | 12.7 | 13.5 |
| Plane 2 | 39.0 | 65.2 | 28.7 | 55.5 | 47.1 | 8.1 | 18.1 | 18.4 | 8.4 | 13.3 |
| Plane 3 | 24.1 | 52.0 | 31.3 | 66.9 | 43.5 | 19.4 | 8.5 | 12.2 | 23.4 | 15.9 |
| Plane 4 | 29.4 | 63.4 | 33.9 | 61.2 | 47.0 | 17.6 | 16.4 | 13.1 | 14.2 | 15.3 |
| Plane 5 | 33.7 | 77.7 | 26.5 | 87.1 | 56.2 | 22.5 | 21.5 | 29.7 | 30.9 | 26.2 |
| Distance to Fitting Plane/μm | Curvature/μm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Upper Left | Upper Right | Lower Left | Lower Right | Center | Upper Left | Upper Right | Lower Left | Lower Right | AVG | |
| Plane 1 | 10.9 | 15.2 | 9.9 | 9.5 | 8.6 | 2.3 | 6.6 | 1.3 | 0.9 | 2.8 |
| Plane 2 | 15.0 | 16.9 | 13.1 | 12.4 | 8.2 | 6.8 | 8.7 | 4.9 | 4.2 | 6.2 |
| Plane 3 | 17.2 | 16.7 | 9.0 | 12.2 | 8.2 | 9.0 | 8.5 | 0.8 | 4.0 | 5.6 |
| Plane 4 | 8.6 | 17.2 | 10.4 | 13.0 | 8.8 | 0.2 | 8.4 | 1.6 | 4.2 | 3.6 |
| Plane 5 | 5.4 | 27.4 | 8.3 | 18.8 | 7.5 | 2.1 | 19.9 | 0.8 | 11.3 | 8.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Ge, Z.; Yang, X.; Zhu, X. A Three-Dimensional Reconstruction Method Based on Telecentric Epipolar Constraints. Photonics 2024, 11, 804. https://doi.org/10.3390/photonics11090804
Li Q, Ge Z, Yang X, Zhu X. A Three-Dimensional Reconstruction Method Based on Telecentric Epipolar Constraints. Photonics. 2024; 11(9):804. https://doi.org/10.3390/photonics11090804
Chicago/Turabian StyleLi, Qinsong, Zhendong Ge, Xin Yang, and Xianwei Zhu. 2024. "A Three-Dimensional Reconstruction Method Based on Telecentric Epipolar Constraints" Photonics 11, no. 9: 804. https://doi.org/10.3390/photonics11090804
APA StyleLi, Q., Ge, Z., Yang, X., & Zhu, X. (2024). A Three-Dimensional Reconstruction Method Based on Telecentric Epipolar Constraints. Photonics, 11(9), 804. https://doi.org/10.3390/photonics11090804




