Abstract
Electromagnetic metasurfaces have been playing exotic roles in the construction of ultracompact and versatile metadevices for wave–matter interactions. So far, multiple metasurfaces cascaded with intercouplings have been intensively investigated for extraordinary wavefront control and broadband spectral regulations. However, most cases face high structural complexity and little attention is paid to cascaded metasurfaces without interlayer couplings. In this paper, we demonstrate one type of terahertz Bragg mirror with ideally high reflectivity and ultra-broad bandwidth by simply resorting to decoupled metasurfaces. Cascaded metasurfaces with decoupled mode control prove practically straightforward for analytical design and easy to fabricate for engineering purpose in our scheme. Essentially, by flexibly tuning the decoupled metasurface mode, the middle Fabry–Perot mode that behaves like a defect mode inside the reflective passband can be eliminated for substantial band expanding. Fundamental analyses and rigorous calculations are performed to confirm the feasibility of our metasurface-based THz Bragg mirror with scalable bandgap. In comparison, our meta-mirror provides superior spectral performance of a larger bandgap and higher in-band reflectivity over that composed by ten layers of alternate dielectrics (Rogers 3003 and 3005). Finally, our analytical methodology and numerical results provide a promising way for the rapid design and fabrication of a Bragg mirror in the optical regime.
1. Introduction
For the past decades, the two-dimensional counterparts of metamaterials (MMs), i.e., the metasurfaces, have emerged as one unique type of planar optical device for exotic wave control. But different from the conventional bulky MMs, metasurfaces are usually composed of alternate meta-atoms with subwavelength periods and deep-subwavelength thicknesses that enable various ultra-compact and easy-to-integrate platforms for wave–matter interactions from the visible to infrared and THz regime. By spatially tailoring each meta-atom in a pixel-wise manner, the amplitude, wavefront and polarization state of incident waves can be modulated accordingly. By taking advantage of continuous or steep phase modulations exerted to incident waves therein, myriads of meta-devices with varied functions of passive or active control have been demonstrated, such as spectral filters [1,2], perfect absorbers [3,4,5,6], frequency-selective surfaces [7,8], meta-holograms [9,10,11], vector vortex beam generation [12,13], beam steering [14,15,16], meta-lensing [17,18,19], etc. Recently, to expand the functional dimensions, emerging types or applications of metasurface-based devices have been explored, such as hyperbolic metasurfaces (i.e., a metasurface with anisotropic hyperbolic dispersions) [20,21,22], topological metasurfaces (i.e., those with optical topological transitions) [22,23,24], and so on.
Among them, broadband spectral regulations are of great importance for many scenarios including broadband absorption or emission [25,26,27,28], photo-detection [29,30,31] and semiconductor lasers [32,33,34]. In particular, for microcavity-based photodetector or quantum photonic devices where the distributed Bragger reflectors (DBRs) are imperative, broadband spectral modulations with high passband reflectivity and ultra-low loss are significant. However, the conventional DBRs setup suffers from high complexity in the repetitious deposition of multiple films of dielectrics. Meanwhile, many metasurface-based schemes are available for broadband spectral control, such as those using composite atoms of multi-patches [35] or rings [36], cascading of multiple layers of metasurfaces [3,37,38], and so on. However, the near-field interactions caused by either intralayer couplings of adjacent atoms within a single layer of metasurface or the interlayer couplings from cascaded metasurfaces lead to destructive resonances and the undesired local minimum of reflectivity, which deteriorates the performance of a metasurface reflector.
In particular, the schemes that resort to cascaded metasurfaces have been fully explored for myriads of multifunctional control mechanisms for the past decades. To name a few, by catenary-based dispersion engineering, a broadband near-unity THz absorber is demonstrated by Zhang et al. by cascading the dual metasurfaces and separating them from a metallic ground by using the dielectric SU8 [3]. For simultaneous transmissive and reflective wavefront control, a bidirectional reflector is demonstrated by Yang et al. in the microwave region by independent tuning of the resonant and geometrical phase by cascading three functional layers of metasurfaces [39]. Further, to achieve extraordinary THz wavefront control, two dielectric all-silicon metasurfaces with independent phase profiles are cascaded and made rotatable for dynamical and flexible beam steering by Cai et al. [40]. However, the inter-couplings among cascaded metasurfaces cannot be neglected and usually need subtle engineering. Recently, the coupled-mode theory has been used to rigorously explore the intrinsic mechanism of couplings between multiple resonators [41,42]. Somehow, most methods based on cascaded metasurfaces are not analytically intuitive or practically feasible for engineering purpose or even suffer from high structural and analytical complexity, especially when more than two functional layers of metasurfaces are involved.
Therefore, to simply provide an intuitive guidance for the structural design and fundamental analyses in our work, the mechanism of two decoupled metasurfaces is explored for a strengthened Fabry–Perot (F-P) cavity that leads to a meta-mirror with a substantially expanded reflective passband. Essentially, by flexibly shifting the decoupled metasurface mode to diminish and even eliminate a middle F-P mode that behaves like a defect mode inside the reflective passband, the reflective passband of our meta-mirror is substantially expanded, i.e., almost doubled. As a result, as a proof of concept, by direct decoupling of near-field interlayer couplings between two cascaded metasurfaces, one type of metasurface-based broadband meta-mirror with ultrahigh reflectivity and ultra-low loss is demonstrated in this paper. In particular, the undesired near-field couplings between two cascaded metasurfaces are eliminated first by optimized parameter tuning, i.e., tuning the geometries of meta-atoms and thickness of the dielectric spacer sandwiched between cascaded metasurfaces. In the absence of near-field interactions or couplings, the decoupled resonance mode of multiple metasurfaces operates in an independent manner to tune the reflective spectrum for broadband purposes. Namely, the single mode of decoupled metasurfaces is tunable to overlap and eliminate one F-P mode within the reflective free special range (FSR) or passband for substantial band expanding. Further, our device is polarization-insensitive due to the structural anisotropy of our meta-units, which enables high robustness of incident angle variation for practical implementations. As a result, our numerical calculations confirm the performance and flexibility of broadband spectral tuning of the proposed THz meta-mirror. By direct cascading only two layers of metasurfaces with similarly and simply structured atoms, such a meta-mirror shows much higher reflectivity and more flexibility in broadband tuning than a conventional Bragg mirror composed of 10 alternative layers of Rogers 3003 and 3006.
2. Scheme and Analyses
To demonstrate the proposed THz meta-mirror constructed from two cascaded metasurfaces, a single layer of metasurface is constructed first by simply employing capacitive units of metal square rings, as shown in Figure 1a. Fundamentally, such a capacitive layer of metal rings shows reflective bandpass or transmissive band-stop behaviors that can be equivalently characterized by the series LC circuit with a similar spectrum of frequency selection, as shown in Figure 2a,b.
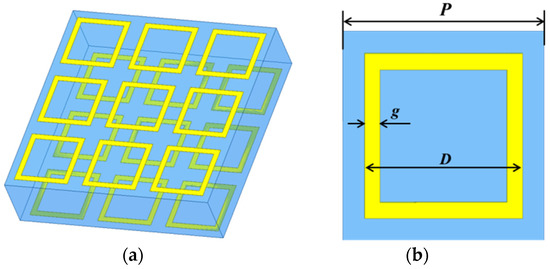
Figure 1.
(a) Schematic of the proposed THz meta-mirror composed of two metasurfaces cascaded in parallel and (b) the periodic metal (Cu) ring unit that constitutes the metasurface.
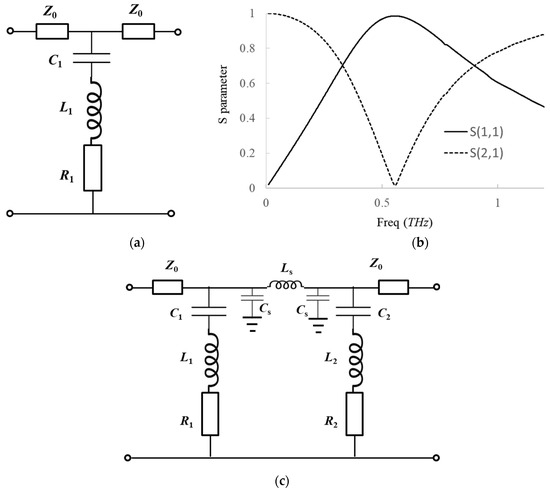
Figure 2.
The lump equivalent circuit of (a) a single layer of metasurface with (b) a low-Q resonance mode in its reflective spectrum and (c) that of two cascaded metasurfaces sandwiched by a thick spacer for independent and decoupled resonant modes.
Apparently, given the complex impedance of the series LC circuit, i.e., , a resonant frequency is equivalently located at to model the resonant behaviors of the single layer of metasurface, where C1 and L1 denote lump equivalent capacitance and inductance, respectively, and R1 is used to model the minimal ohmic loss in the impedance Z1 of a single metasurface. Herein, the characteristic impedance (Zc) and the reflection (R) coefficients of the equivalent circuit for the metasurface in Figure 1a can be approximately expressed as
where Z0 is the vacuum wave impedance and is the scattering parameter that defines the reflection coefficient herein. According to Equations (1) and (2), there is obviously a zero point for the characteristic reactance of the equivalent series LC circuit at the resonant frequency of and thus a maximum is induced in the reflective spectrum (i.e., S11 of the S parameter) of the single metasurface, as shown in Figure 2b. Herein, the equivalent capacitance and inductance can be tentatively obtained using an empirical formula [37], and the lumped elements for the equivalent impedances can be further adjusted by fitting the resonant frequency and reflection coefficients in Equations (1) and (2) with the counterparts obtained by finite element method (FEM)-based calculations.
Further, to constitute the proposed THz meta-mirror with an ultra-broad reflective band, two identical metasurfaces with optimized reflectivity at a certain frequency are cascaded in parallel with a thick dielectric spacer of Rogers 3003. Due to the large spacing between two metasurfaces, the interlayer coupling can be effectively eliminated and thus both metasurfaces work independently with the same decoupled resonant mode. In such a straightforward manner, the two decoupled metasurfaces with high reflectivity constitute an F-P cavity to first enable a cavity-strengthened broadband reflector.
In this situation, to model the behaviors of the decoupled mode of two metasurfaces cascaded in parallel, the parallel configuration of two series LC circuits can be feasibly used, as shown in Figure 2c. Here, the series inductor Ls and parallel capacitor Cs in Figure 2c denote the dielectric spacer of Rogers 3003 that is modeled as transmission line according to the Telegrapher’s equations. Apparently, Ls and Cs that determine the F-P resonance mode of the dielectric film remain as short and open circuits, respectively, (and thus can be neglected) at (and even around) the resonant frequency determined by the metasurfaces.
Otherwise, it can be interpreted by the mechanism of F-P resonance that, e.g., at the resonant mode of the top metasurface, the reflectivity from the top (close to one) dominates over that from the bottom (close to zero) even when both top and bottom reflections are out of phase by 180 degrees, and vice versa. In this situation, the metasurface mode can intrinsically approach, diminish and even eliminate one of the F-P modes for as-required spectral tuning, e.g., band expanding in our work. For decoupled metasurfaces cascaded with identical geometries, such spectral tuning is more straightforward since the two metasurface modes are already merged into one.
Otherwise, in term of the equivalent circuits in Figure 2c and previous results [37], the characteristic impedance (Zc) of cascaded metasurfaces can be modeled as
where and denote the impedance of either series LC branch in Figure 2c, denotes the mutual inductance of L1 and L2 to model the inductive intercoupling between two cascaded metasurfaces, and k denotes the coupling factor. Apparently, for , there are two zero points for the characteristic reactance in Equation (3) and thus two maxima in the reflective spectrum, i.e., two resonant modes exist for two cascaded metasurfaces with intercoupling. Meanwhile, for the metasurfaces effectively decoupled by a thick spacer, i.e., , there is only one zero point in Equation (3) and the two resonant modes merge into only one, i.e., the decoupled metasurface mode with the same frequency of .
Therefore, by flexibly tuning the decoupled mode of two cascaded metasurfaces with a reflective peak at the resonant frequency of , one middle F-P mode that acts like an undesired defect mode inside the reflective passband can be diminished and even eliminated. In such a manner, the reflective FSR with the left and right borders determined by two F-P modes is further doubled, as is discussed and confirmed in Section 3.
Further, according to Equation (3), two series LC circuits connected in parallel further reduce the total equivalent characteristic impedance in comparison to a single one, which leads to an expanded spectral range with higher reflectivity due to the superposed and decoupled modes from the two cascaded metasurfaces. Namely, the parallel impedance is approximately halved to be for two identical LC circuits around the resonant frequency range. As a result, according to Equation (2), the reflectivity is further increased inside a distinctively broadened passband. This is another feature of our scheme in addition to the advantage of band expanding.
In such a manner, based on a single layer of metasurface for as-required reflective control, two decoupled metasurfaces are cascaded in parallel distinctly to enable a THz meta-reflector with a substantially broadended passband. In particular, when a certain Fabry–Perot mode with the resonant minimum of reflectivity is superposed and thus eliminated by a metasurface mode with resonant peak of reflectivity, the reflective passband of meta-mirror is almost doubled. As a result, our scheme provides an ultra-compact platform to construct a broadband THz meta-mirror with a flexibly stretchable and scalable passband or transmissive bandgap.
3. Results and Discussion
To confirm our schemes, a model of two metasurfaces cascaded in parallel with identical geometries is constructed, as illustrated in Figure 1a, and numerical calculations are performed by using the finite element method (FEM) on the platform ANSYS Electromagnetic Suits. For a typical meta-unit illustrated in Figure 1b, the periodic boundary condition is extended to four sides or directions. The metal Cu with a skin depth of less than 100 nm in THz range is used to construct our meta-unit and taken as the dispersion-free perfect conductor in our simulations.
To typically characterize the spectral behavior of the proposed meta-mirror, both the transmission and reflection coefficients are extracted by calculating the S-parameters as indicated in Equation (2). First, the THz spectral responses are obtained by tentatively calculating the equivalent capacitance and inductance using an empirical formula in previous work [37] and then the reflection coefficient according to Equations (1) and (2). To achieve the optimal spectral response, the period (P), length (D) and width (g) of meta-units and the spacer thickness (t) are swept and adjusted for optimal spectra in the FEM calculations.
First, two metasurfaces are customized with identical geometries and cascaded in parallel by a dielectric spacer (Rogers 3003) with varied thickness. As shown in Figure 3a, the extracted transmission spectra show varied resonant frequencies of minima around 0.5 THz along with a few resonant peaks of F-P modes. In particular, for varied spacer thicknesses (t), intercoupling between two cascaded metasurfaces changes significantly to induce distinct spectral evolution.
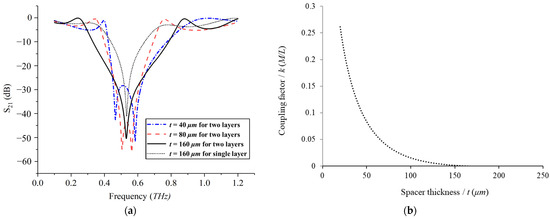
Figure 3.
(a) The transmission spectra of two identical metasurfaces cascaded in parallel with the parameters of P = 144 μm, D = 120 μm and g = 8 μm and sandwiched by a Rogers 3003 spacer with a varied thickness (t) of 40 μm, 80 μm and 160 μm in comparison with that of only one metasurface; (b) the coupling factor (k) numerically extracted for varied spacer thickness (t).
Herein, to approximately determine the spacer thickness (t) when intercoupling between two cascaded metasurfaces becomes negligible, the mutual inductance (M) or the coupling factor (k) in Equation (3) is estimated. For our case, cascaded metasurfaces with identical geometries can be characterized by the same lump equivalent inductance (L) as in Figure 2c, i.e., L1 = L2 = L and . So, the coupling strength k = M/L, i.e., the ratio of mutual inductance to self-inductance of either metasurface, is directly considered.
For approximate estimations, the mutual inductance (M) and self-inductance (L) are calculated according to a formula from the literature [43], and then the coupling factor (k) is extracted for varied spacer thickness (t), as shown in Figure 3b. Apparently, the extracted coupling strength (k) in Figure 3b rapidly approaches zeros in an asymptotic manner and becomes minimal especially when spacer thickness (t) rises beyond 150 μm, as agrees well with spectral results in Figure 3a. Therefore, in this situation, a spacer with a relatively large thickness beyond 150 μm can be used to reasonably diminish and even eliminate the intercoupling effect between cascaded metasurfaces.
As indicated in the blue and red dotted curves in Figure 3a, two resonant modes with two transmissive minima exist for the relatively small spacer thicknesses of t = 40 μm and 80 μm. However, when the spacer thickness further increases to be as large as t = 160 μm, the original two resonant modes ultimately merge into a single one with the same resonant frequency, i.e., the intercoupling effect between two cascaded metasurfaces almost disappears, in good agreement with the predictions in Figure 3b. Inversely speaking, when two metasurfaces gradually approach each other with a relatively small gap, the intercoupling effect appears to split the original single resonant mode into two. Noteworthily, when the two resonant modes due to intercouplings merge into one by decoupling, the decoupled mode ultimately assumes the same resonant frequency as that for only one single metasurface, as shown in the black doted curve in Figure 3a.
Further, other than the spacer thickness (t) that is used for direct intercoupling control, other parameters including the length (D), width (g) and period (P) also induce an indirect impact on the intercoupling effect. As indicated from the discussions about the coupling factors above, this can be also attributed to the overall balance between the intralayer couplings between neighboring meta-atoms in each metasurface versus the interlayer couplings between two cascaded metasurfaces, i.e., the self-inductance L versus mutual inductance M.
Taking the length (D) as an example, a smaller length (D) leads to a lower density of atoms arranged with the unchanged period (P), so neighboring atoms in either layer of metasurface become less closely coupled to each other, i.e., intralayer couplings become weaker. As is well confirmed by results in Figure 4, upon the decreasing length (D) from 135 μm to 110 μm, the interlayer coupling tends to be more prominent and the single resonant mode ultimately splits into two modes when the lengths become 120 μm and 110 μm. So, it can be interpreted that intralayer couplings tend to become weaker and less dominant over the interlayer couplings with a smaller length (D), i.e., the self-inductance of L becomes relatively smaller, so the coupling strength (e.g., by k = M/L) becomes larger. Inversely, the two split resonant modes due to interlayer couplings tend to merge into only one with a larger length (D), in good agreement with the spectra in Figure 4.
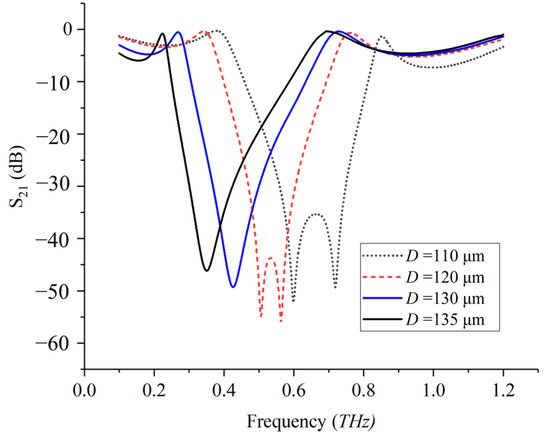
Figure 4.
The transmission spectra of two identical metasurfaces cascaded in parallel with the parameters of P = 144 μm, g = 8 μm, t = 80 μm, and the varied lengths of D = 110 μm, 120 μm and 130 μm.
Similarly, the width (g) of meta-rings also induces an indirect impact on the balance between intralayer couplings and interlayer couplings. With smaller widths (g), it is indicated that smaller areas of two cascaded metasufaces face each other, so the mutual inductance M becomes smaller and meanwhile the self-inductance (L) becomes larger. As a result, the interlayer couplings become obviously weaker and each metasurface becomes more independent and decoupled with the other, as is well confirmed by the results in Figure 5.
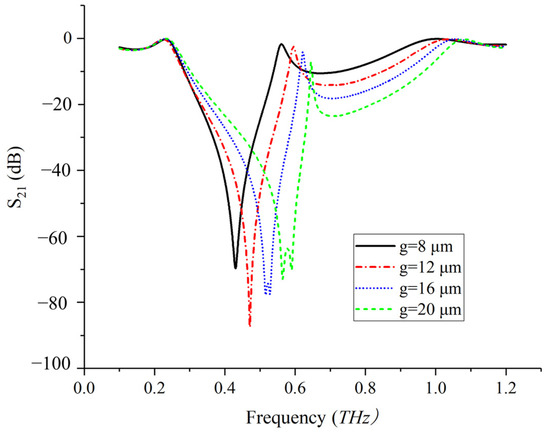
Figure 5.
Transmission spectra of two identical metasurfaces cascaded in parallel with the parameters of P = 160 μm, t = 127 μm and D = 130 μm, and the varied widths of g = 8 μm, 12 μm, 16 μm and 20 μm.
Finally, even the width (g) causes direct changes to the coupling areas and an indirect impact on the interlayer couplings of cascaded metasurfaces facing each other; the period (P) also causes an indirect impact on the interlayer couplings. In a similar manner as changing the length (D), the intralayer coupling within each metasurface can also be distinctly tuned by changing the period (P).
As an example, smaller periods (P) for fixed length (D) lead to a higher density of meta-atoms with stronger intralayer couplings, i.e., the self-inductance L becomes larger versus the mutual inductance M and the coupling factor (k) becomes smaller. Then, the two cascaded metasurfaces become more independent from each other and the decoupled mode ultimately appears instead of two split ones, as is well confirmed by the spectral results in Figure 6.
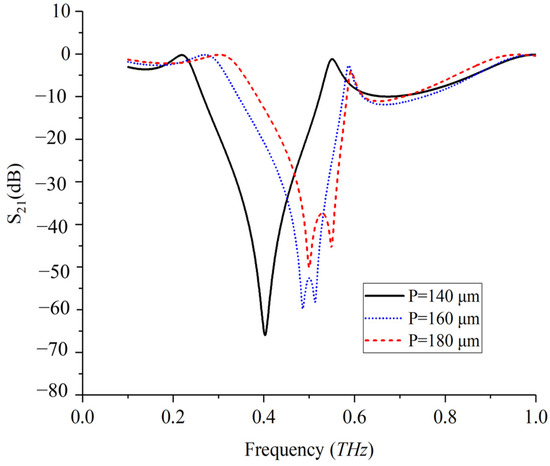
Figure 6.
The transmission spectra of two identical metasurfaces cascaded in parallel with the parameters of D = 130 μm, g = 8 μm and t = 127 μm and varied periods of P = 140 μm, 160 μm and 180 μm.
In summary, according to all results indicated in Figure 3, Figure 4, Figure 5 and Figure 6, the interlayer and intralayer couplings in the model of two cascaded metasurfaces can be deliberately regulated and balanced by tuning the parameters of spacer thickness (t), the length (D), period (P) and width (g). In particular, when the interlayer couplings are diminished, the decoupled mode with a single transmissive resonant peak is flexibly scalable to overlap with a certain F-P mode inside the original FSR for substantial band expanding.
Therefore, to directly characterize the spectral behaviors of our meta-mirror, the reflection coefficients (i.e., S11) are extracted for two metasurfaces cascaded without inter-layer coupling, as shown in Figure 7, Figure 8 and Figure 9. First, as an example, for the as-desired spectral tuning shown in Figure 7, when the length (D) decreases from 115 μm to be 102 μm, an F-P mode (blue dotted line) at ~0.6 THz is gradually approached and eliminated by the decoupled metasurface mode. Herein, the F-P-modes enabled (or strengthened) by destructive interference of reflected waves from the top and bottom metasurfaces segment the whole spectral band and constitute the passband of the meta-mirror with high reflectivity. In such a manner, by deliberately adjusting the metasurface resonance mode with peak reflectivity, the F-P-mode-segmented and -strengthened reflective band is further doubled to generate a broadband meta-mirror. Finally, by deliberately tuning the interlayer couplings between two metasurfaces, one type of broadband THz meta-mirror with a similar property as the Bragg reflector can be simply obtained, as shown in Figure 8. As discussed above, by only tuning the spacer thickness, the metasurface-based meta-mirror can be configured with an apparently scalable bandwidth or bandgap performance.
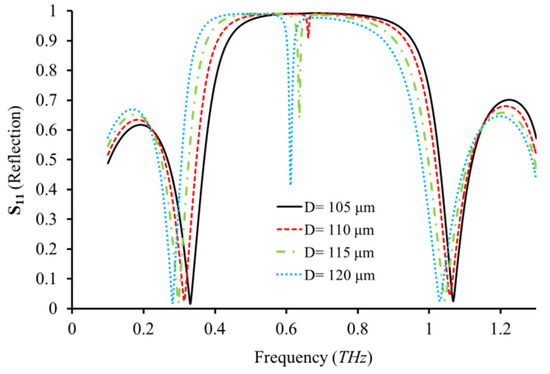
Figure 7.
The reflection spectra of two identical metasurfaces cascaded in parallel with the parameters of P = 140 μm, g = 8 μm and t = 127 μm, and varied lengths of D = 105 μm, 110 μm, 115 μm and 120 μm.
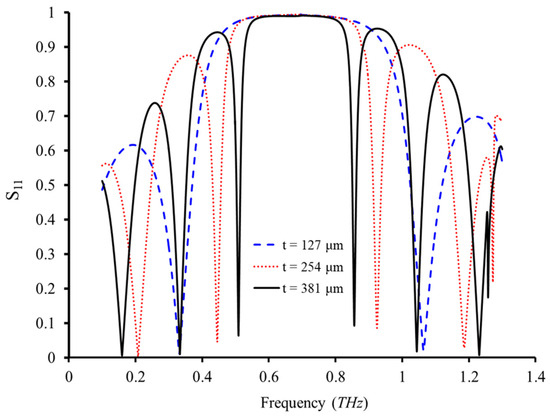
Figure 8.
The reflection spectra (or the scattering parameters of S11) of two decoupled metasurfaces cascaded in parallel with the parameters of P = 140 μm, g = 8 μm and D = 105 μm and sandwiched by spacer with the varied thicknesses of t = 127 μm, 254 μm and 381 μm.
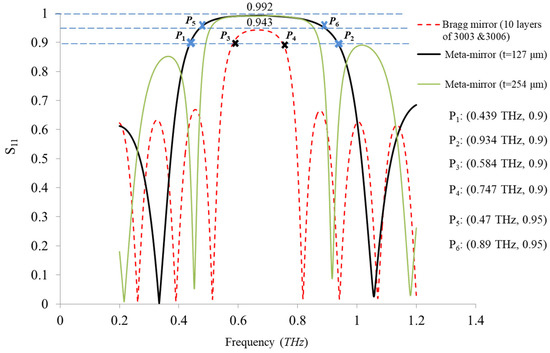
Figure 9.
The reflective spectra of meta-mirrors configured by two decoupled metasurfaces that are sandwiched by a dielectric spacer in comparison with the spectrum of a Bragg mirror composed of 10 layers or 5 pairs of Rogers 3003 and 3006. For clear analyses, critical points (P1~P6) are marked.
For further comparison, a conventional Bragg mirror is also configured and simulated here by alternatively depositing ten layers or five pairs of Rogers 3003 and 3006. Herein, the Rogers 3003 layer is configured with a dielectric constant of 3 and a loss tangent of 0.0013 and the Rogers 3006 layer is configured with a dielectric constant of 6.15 and a loss tangent of 0.0025. Both layers are set to have identical optical thicknesses of 195 μm to shift the reflective passband inside, like those of our meta-mirror constructed from cascaded metasurfaces. After a similar process of FEM-based calculations, the spectrum of the conventional Bragg mirror is extracted, as seen from the red dotted line in Figure 9. Also, the spectra of our meta-mirror constructed from two identical metasurfaces cascaded with the spacer thickness of 127 μm and 254 μm are compared with the reflective spectrum of the conventional Bragg mirror in Figure 9.
Obviously, as indicated by the critical points (P1~P2) marked in the curves of Figure 9, the maximal reflective bandwidth (>90%) of our meta-mirror with the spacer thickness of t = 127 μm is ~0.5 THz (the range determined by the points of P1 and P2), while that of the conventional Bragg mirror is only ~0.16 THz (the range determined by the points of P3 and P4). Even for a reflectivity larger than 95%, the maximal reflective bandwidth (>0.95) of our meta-mirror attains a value of ~0.4 THz (the range determined by the points of P5 and P6). Further, the largest reflectivity of proposed meta-mirror is as large as 0.992, while that of the conventional mirror constructed from ten layers of alternate dielectrics of Rogers 3003 and 3006 is only ~0.94.
Apparently, as discussed above, the proposed meta-mirror constructed from two decoupled and cascaded metasurfaces shows a much larger bandwidth and reflective passband as well as a prominently enhanced in-band performance, e.g., a higher reflectivity and a more flexibly scalable bandgap, etc. The prominent features of the scalable reflective passband and ultrahigh reflectivity of our THz meta-mirror is feasibly scalable to other regimes from microwave to optical regimes. More importantly, the meta-mirror is far more easy to fabricate due to its low structural complexity, since only two identical metasurfaces with simple isotropic meta-units are used, while the fabrication of a conventional Bragg mirror involves multiple costly steps of depositions in a vacuum environment.
4. Conclusions
In conclusion, we have proposed a scheme to construct a broadband THz meta- mirror by simply configuring two layers of metasurfaces cascaded in parallel. By deliberately customizing the geometries of the meta-rings that compose the metasurface, the intralayer couplings between neighboring meta-rings and the interlayer couplings between the two metasurfaces can be effectively balanced. In particular, for a relatively large gap between two metasurfaces, the split modes due to intercoupling can be deliberately adjusted and eliminated to merge into a single decoupled mode with a flexibly scalable resonant frequency. In such a manner, a broadband THz meta-mirror is obtained with an almost doubled bandwidth when the decoupled mode with the reflective peak is shifted to overlap a destructive mode with a reflective minimum.
Obviously, with simplicity in the structural design and fundamental analyses for engineering purposes, our scheme provides a straightforward route to construct a high-reflectivity and ultra-broad-bandwidth meta-mirror. By just cascading two identical metasurfaces with simple geometries of meta-rings, the decoupled metasurface mode can be flexibly leveraged to overlap and eliminate a middle F-P mode that behaves like a defect mode inside the photonic band for substantial band expanding. Further, by using simple and isotropic meta-units to construct the meta-surfaces, the proposed THz meta-mirror is polarization-insensitive and easy to fabricate due to the low structural complexity and high robustness to incidence angle variations. Finally, even in comparison to the conventional Bragg mirror which uses ten alternate layers or five pairs of Rogers 3003 and Rogers 3006, our meta-mirror with a much simpler architecture shows a much larger bandwidth and bandgap, a lower complexity of fabrication as well a distinctly enhanced in-band performance including higher reflectivity, band scalability and so on.
Author Contributions
Conceptualization, Z.F. and S.Z.; methodology, Z.F. and S.Z.; software, S.Z. and B.L.; validation, Z.F., S.Z. and B.L.; formal analysis, Z.F. and B.L.; investigation, Z.F. and B.L.; resources, G.H.; data curation, S.Z.; writing—original draft preparation, Z.F., B.L. and S.Z.; writing—review and editing, Z.F., B.L. and S.Z.; visualization, S.Z.; supervision, S.Z. and G.H.; project administration, G.H.; funding acquisition, G.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the construction project of Shanghai Key Laboratory of Molecular Imaging, grant number 18DZ2260400, by the research grants from the National Natural Science Foundation of China, grant number 82127807, and by the National Key Research and Development Program of China, grant number 2020YFA0909000.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data involved is contained within this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, T.; Wu, Y.-K.; Luo, X.; Guo, L.J. Plasmonic nanoresonators for high-resolution colour filtering and spectral imaging. Nat. Commun. 2010, 1, 59. [Google Scholar] [CrossRef]
- Julian, M.N.; Williams, C.; Borg, S.; Bartram, S.; Kim, H.J. Reversible optical tuning of GeSbTe phase-change metasurface spectral filters for mid-wave infrared imaging. Optica 2020, 7, 746–754. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Zhang, F.; Ou, Y.; Cai, J.; Yu, H. Broadband terahertz absorber based on dispersion-engineered catenary coupling in dual metasurface. Nanophotonics 2018, 8, 117–125. [Google Scholar] [CrossRef]
- Wu, S.; Gu, Y.; Ye, Y.; Ye, H.; Chen, L. Omnidirectional broadband metasurface absorber operating in visible to near-infrared regime. Opt. Express 2018, 26, 21479–21489. [Google Scholar] [CrossRef]
- Huo, D.; Zhang, J.; Wang, Y.; Wang, C.; Su, H.; Zhao, H. Broadband perfect absorber based on tin-nanocone metasurface. Nanomaterials 2018, 8, 485. [Google Scholar] [CrossRef]
- de Araújo, J.B.O.; Siqueira, G.L.; Kemptner, E.; Weber, M.; Junqueira, C.; Mosso, M.M. An Ultrathin and Ultrawideband Metamaterial Absorber and an Equivalent-Circuit Parameter Retrieval Method. IEEE Trans. Antennas Propag. 2020, 68, 3739–3746. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Nirantar, S.; Member, S.; Withayachumnankul, W.; Bhaskaran, M. Second-Order Terahertz Bandpass Frequency Selective Surface With Miniaturized Elements. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 761–769. [Google Scholar] [CrossRef]
- Qiao, S.; Zhang, Y.; Zhao, Y.; Zhou, Y.; Liang, S.; Yang, Z. Multiband Frequency-Selective Surface With Five Resonance Peaks in Terahertz Band. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 292–299. [Google Scholar] [CrossRef]
- Deng, Z.L.; Jin, M.; Ye, X.; Wang, S.; Shi, T.; Deng, J.; Mao, N.; Cao, Y.; Guan, B.O.; Alù, A.; et al. Full-Color Complex-Amplitude Vectorial Holograms Based on Multi-Freedom Metasurfaces. Adv. Funct. Mater. 2020, 30, 1910610. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, L.; Chen, Z.; Ansari, M.A.; Chen, X.; Chan, M. Polarization-multiplexed metaholograms with erasable functionality. J. Phys. D. Appl. Phys. 2023, 56, 155102. [Google Scholar] [CrossRef]
- Shi, H.; Wang, L.; Peng, G.; Chen, X.; Li, J.; Zhu, S.; Zhang, A.; Xu, Z. Generation of Multiple Modes Microwave Vortex Beams Using Active Metasurface. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 59–63. [Google Scholar] [CrossRef]
- Wang, E.; Shi, L.; Niu, J.; Hua, Y.; Li, H.; Zhu, X.; Xie, C.; Ye, T. Vector Vortex Beam Arrays: Multichannel Spatially Nonhomogeneous Focused Vector Vortex Beams for Quantum Experiments (Advanced Optical Materials 8/2019). Adv. Opt. Mater. 2019, 7, 1970029. [Google Scholar] [CrossRef]
- Zhou, S.; Wu, Y.; Chen, S.; Liao, S.; Zhang, H.; Xie, C.; Chan, M. Phase change induced active metasurface devices for dynamic wavefront control. J. Phys. D. Appl. Phys. 2020, 53, 204001. [Google Scholar] [CrossRef]
- de Galarreta, C.R.; Alexeev, A.M.; Au, Y.Y.; Lopez-Garcia, M.; Klemm, M.; Cryan, M.; Bertolotti, J.; Wright, C.D. Nonvolatile Reconfigurable Phase-Change Metadevices for Beam Steering in the Near Infrared. Adv. Funct. Mater. 2018, 28, 1704993. [Google Scholar] [CrossRef]
- Kita, S.; Takata, K.; Ono, M.; Nozaki, K.; Kuramochi, E.; Takeda, K.; Notomi, M. Coherent control of high efficiency metasurface beam deflectors with a back partial reflector. APL Photon. 2017, 2, 046104. [Google Scholar] [CrossRef]
- Ruirui, S.; Qinling, D.; Shaolin, Z.; Mingbo, P. Catenary-based phase change metasurfaces for mid-infrared switchable wavefront control. Opt. Express 2021, 29, 23006–23018. [Google Scholar]
- Yin, X.; Steinle, T.; Huang, L.; Taubner, T.; Wuttig, M.; Zentgraf, T.; Giessen, H. Beam switching and bifocal zoom lensing using active plasmonic metasurfaces. Light Sci. Appl. 2017, 6, e17016. [Google Scholar] [CrossRef]
- Huang, Y.; Pu, M.; Zhang, F.; Luo, J.; Li, X.; Ma, X.; Luo, X. Broadband Functional Metasurfaces: Achieving Nonlinear Phase Generation toward Achromatic Surface Cloaking and Lensing. Adv. Opt. Mater. 2019, 7, 1801480. [Google Scholar] [CrossRef]
- Huo, P.; Zhang, S.; Liang, Y.; Lu, Y.; Xu, T. Hyperbolic Metamaterials and Metasurfaces: Fundamentals and Applications. Adv. Opt. Mater. 2019, 7, 1801616. [Google Scholar] [CrossRef]
- Yang, Y.; Jing, L.; Shen, L.; Wang, Z.; Zheng, B.; Wang, H.; Li, E.; Shen, N.H.; Koschny, T.; Soukoulis, C.M.; et al. Hyperbolic spoof plasmonic metasurfaces. NPG Asia Mater. 2017, 9, e428. [Google Scholar] [CrossRef]
- Kotov, O.V.; Lozovik, Y.E. Hyperbolic hybrid waves and optical topological transitions in few-layer anisotropic metasurfaces. Phys. Rev. B 2019, 100, 165424. [Google Scholar] [CrossRef]
- You, J.W.; Lan, Z.; Ma, Q.; Gao, Z.; Yang, Y.; Gao, F.; Xiao, M.; Cui, T.J. Topological metasurface: From passive toward active and beyond. Photon. Res. 2023, 11, B65. [Google Scholar] [CrossRef]
- Yermakov, O.Y.; Permyakov, D.V.; Porubaev, F.V.; Dmitriev, P.A.; Samusev, A.K.; Iorsh, I.V.; Malureanu, R.; Lavrinenko, A.V.; Bogdanov, A.A. Effective surface conductivity of optical hyperbolic metasurfaces: From far-field characterization to surface wave analysis. Sci. Rep. 2018, 8, 14135. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Zang, X.F.; Chen, L.; Peng, Y.; Cai, B.; Nash, G.R.; Zhu, Y.M. Compact Broadband Terahertz Perfect Absorber Based on Multi-Interference and Diffraction Effects. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 40–44. [Google Scholar] [CrossRef]
- Ullah, H.; Khan, A.D.; Noman, M.; Rehman, A.U. Novel Multi-Broadband Plasmonic Absorber Based on a Metal-Dielectric-Metal Square Ring Array. Plasmonics 2018, 13, 591–597. [Google Scholar] [CrossRef]
- Grant, J.; Ma, Y.; Saha, S.; Khalid, A.; Cumming, D.R.S. Polarization insensitive, broadband terahertz metamaterial absorber. Opt. Lett. 2011, 36, 3476–3478. [Google Scholar] [CrossRef]
- Qu, Y.; Li, Q.; Du, K.; Cai, L.; Lu, J.; Qiu, M. Dynamic Thermal Emission Control Based on Ultrathin Plasmonic Metamaterials Including Phase-Changing Material GST. Laser Photon. Rev. 2017, 11, 1700091. [Google Scholar] [CrossRef]
- Furchi, M.; Urich, A.; Pospischil, A.; Lilley, G.; Unterrainer, K.; Detz, H.; Klang, P.; Andrews, A.M.; Schrenk, W.; Strasser, G.; et al. Microcavity-integrated graphene photodetector. Nano Lett. 2012, 12, 2773–2777. [Google Scholar] [CrossRef]
- Mitrofanov, O.; Hale, L.L.; Vabishchevich, P.P.; Luk, T.S.; Addamane, S.J.; Reno, J.L.; Brener, I. Perfectly absorbing dielectric metasurfaces for photodetection. APL Photon. 2020, 5, 101304. [Google Scholar] [CrossRef]
- Sobhani, A.; Knight, M.W.; Wang, Y.; Zheng, B.; King, N.S.; Brown, L.V.; Fang, Z.; Nordlander, P.; Halas, N.J. Narrowband photodetection in the near-infrared with a plasmon-induced hot electron device. Nat. Commun. 2013, 4, 1643–1646. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.Y.; Ni, P.N.; Wang, Q.H.; Kan, Q.; Briere, G.; Chen, P.P.; Zhao, Z.Z.; Delga, A.; Ren, H.R.; Chen, H.D.; et al. Metasurface-integrated vertical cavity surface-emitting lasers for programmable directional lasing emissions. Nat. Nanotechnol. 2020, 15, 125–130. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Crozier, K.B. Semiconductor lasers with integrated metasurfaces for direct output beam modulation, enabled by innovative fabrication methods. Nanophotonics 2023, 12, 1443–1457. [Google Scholar] [CrossRef]
- Spägele, C.; Tamagnone, M.; Kazakov, D.; Ossiander, M.; Piccardo, M.; Capasso, F. Multifunctional wide-angle optics and lasing based on supercell metasurfaces. Nat. Commun. 2021, 12, 3787. [Google Scholar] [CrossRef]
- Bouchon, P.; Koechlin, C.; Pardo, F.; Haïdar, R.; Pelouard, J. Wideband omnidirectional infrared absorber with a patchwork of plasmonic nanoantennas. Opt. Lett. 2012, 37, 1038–1040. [Google Scholar] [CrossRef]
- Ghosh, S.; Bhattacharyya, S.; Chaurasiya, D.; Srivastava, K.V. An Ultrawideband Ultrathin Metamaterial Absorber Based on Circular Split Rings. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1172–1175. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, L.; Deng, Q.; Liao, S.; Xue, Q.; Chan, M. Intercoupling of Cascaded Metasurfaces for Broadband Spectral Scalability. Materials 2023, 16, 2013. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.Q.; Jin, Y.; He, S. Omnidirectional, polarization-insensitive and broadband thin absorber in the terahertz regime. J. Opt. Soc. Am. B 2010, 27, 498–504. [Google Scholar] [CrossRef]
- Yang, J.; Wu, X.; Song, J.; Huang, C.; Huang, Y.; Luo, X. Cascaded metasurface for simultaneous control of transmission and reflection. Opt. Express 2019, 27, 9061–9070. [Google Scholar] [CrossRef]
- Cai, X.; Tang, R.; Zhou, H.; Li, Q.; Ma, S.; Wang, D.; Liu, T.; Ling, X.; Tan, W.; He, Q.; et al. Dynamically controlling terahertz wavefronts with cascaded metasurfaces. Adv. Photon. 2021, 3, 036003. [Google Scholar] [CrossRef]
- Li, Q.; Wang, T.; Su, Y.; Yan, M.; Qiu, M. Coupled mode theory analysis of mode-splitting in coupled cavity system. Opt. Express 2010, 18, 8367–8382. [Google Scholar] [CrossRef]
- Powell, D.A.; Lapine, M.; Gorkunov, M.V.; Shadrivov, I.V.; Kivshar, Y.S. Metamaterial tuning by manipulation of near-field interaction. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 82, 155128. [Google Scholar] [CrossRef]
- Rosa, E.B. The self and mutual-inductances of linear conductors. Bull. Bur. Stand. 1908, 4, 301. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).