Abstract
We propose a task-specific method for calculating cascaded phase diffractive optical elements (DOEs) for focusing Q incident beams with different wavelengths to Q given points. Due to the utilization of a special optimization criterion, the proposed method makes it possible to calculate the elements of the cascaded DOE in a sequential way. In addition, the calculation of the diffractive microrelief of each DOE in the cascade is reduced to solving a set of independent and computationally simple “pointwise” optimization problems. Using the proposed method, cascades of two DOEs were designed to focus radiation of 11 different wavelengths to 11 different points. The presented numerical simulation results demonstrate good performance of the method. The chosen operating wavelengths correspond to a set of widely used vegetation indices enabling monitoring the vegetation status conditions and tracking the environmental stresses. This makes the obtained results promising for the application in remote sensing and smart agriculture.
1. Introduction
In recent years, there has been a revival of interest in topics related to the design and fabrication of phase diffractive optical elements (DOEs) for solving a wide class of problems involving transforming and focusing laser radiation [1,2,3,4,5]. Among different research directions, the so-called cascaded DOEs consisting of several sequentially located diffractive elements and having significantly wider functionality compared to single DOEs attract considerable attention [2,6,7,8,9,10,11,12,13,14]. In particular, cascaded DOEs are promising for use in advanced beam shaping problems [2,6,7,8], in which, for example, it is necessary to generate different intensity distributions (potentially located in different output planes along the optical axis) for different incident beams, in machine learning problems [9,10,11,12], as well as for the optical implementation of various mathematical transformations [13,14].
In most existing works, DOEs (both single and cascaded) are designed to work with radiation of one given wavelength. At the same time, the problem of calculating the so-called spectral DOEs intended to work with radiation of several different wavelengths is of great interest. DOEs of this type can, in particular, be used for spectral filtering [15], for the formation of multispectral images [16], as well as for implementing different mathematical transformations of the incident beam at several different operating wavelengths [14]. In the problems of task-specific spectral analysis, it is necessary to design DOEs that focus radiation of several different wavelengths to different points, so that each wavelength is focused to its “own” focus of a given position [15,17,18,19]. To calculate spectral cascaded DOEs that focus radiation of different wavelengths to different points, gradient methods are used (e.g., the ADAM method [20]), which are applied in the paradigm of neural network training [15,17,18]. This approach is quite universal and can be used not only in this problem, but also in the design of cascaded DOEs for optical solution of a wide class of machine learning problems [6,7,8,9,10,11,12,13,14]. At the same time, in the opinion of the present authors, to solve the problem of focusing radiation of different wavelengths to different points, task-specific methods with better performance can be developed.
In the present work, we propose a specialized method for calculating cascaded DOEs that focus radiation of different wavelengths to different points. The distinctive features of this method are, firstly, that the calculation of the elements of the cascaded DOE is carried out sequentially, and, secondly, that the calculation of the diffractive microrelief of each DOE in the cascade is reduced to solving a set of independent computationally simple “pointwise” optimization problems. As it was mentioned above, as an important potential application of such cascaded DOEs, we consider the problems of task-specific spectral analysis [15,17,18,19]. One of the relevant problems of this kind consists in monitoring the vegetation status conditions and tracking the environmental stresses using the so-called vegetation indices [21,22,23]. These indices describe the state of vegetation cover through simple mathematical expressions depending on the reflectance in a few spectral channels, the proper choice of which enables minimizing the influence of other unwanted factors, including, for example, the soil background and the atmospheric conditions. In this regard, as a design example, we consider the calculation of a two-DOE cascade, which separates and focuses radiation of 11 wavelengths corresponding to a number of widely used vegetation indices. The results of numerical simulations of the designed DOEs demonstrate high efficiency of the proposed method.
2. Method for Calculating a Cascaded DOE
Let us consider the problem of calculating a spectral cascaded DOE focusing Q different incident beams with different wavelengths to Q different points. We assume that the cascaded DOE consists of n phase DOEs located in the planes and defined by the functions of diffractive microrelief height , where are the Cartesian coordinates in the plane (Figure 1). The incident beams are defined in the plane of the first DOE by the complex amplitude functions . The points, to which these beams have to be focused, are located in the “output” plane and have the coordinates . In this case, the problem of calculating a cascaded DOE can be considered as a problem of calculating the diffractive microrelief height functions , providing the focusing of Q given input beams with different wavelengths to Q required points .
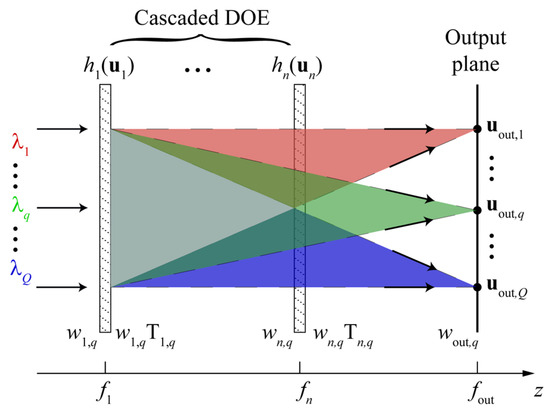
Figure 1.
Geometry of the focusing problem. Beams with different wavelengths , , and being focused are schematically shown with red, green, and blue, respectively.
We propose to solve this problem using a generalization of a method previously proposed by some of the present authors and intended for the calculation of single (non-cascaded) spectral diffractive lenses (SDLs) focusing the radiation of several different wavelengths to the same [24,25] or different [19] points. In order to calculate the SDL microrelief, a special optimization criterion was used in these works, which described the deviation of the complex amplitudes of beams generated by the SDL from the complex amplitudes of spherical beams converging to the required points. Such a criterion made it possible to reduce the SDL calculation to the solution of a set of simple “pointwise” optimization problems.
Let us show how the method for calculating a single SDL from ref. [19] can be extended to the design of cascaded DOEs. Before moving to the description of the method, let us consider the following auxiliary problem. Let a light beam with wavelength and complex amplitude pass through a phase DOE with diffractive microrelief height located in the plane . Let us establish the “best form” of the beam transmitted through the DOE for its subsequent focusing at the point of the output plane. In the thin optical element approximation, the complex amplitude of the beam impinging on the DOE will be multiplied by the complex transmission function (CTF) of the DOE, which at the wavelength has the form
where is the phase shift introduced by the DOE at the wavelength , , and is the refractive index of the DOE material. As a result, the complex amplitude of the transmitted beam takes the form
Assuming in Equation (2) that where
is the phase function of a paraxial diffractive lens calculated for the wavelength and having the focus at the point of the output plane, we obtain the transmitted beam as
where is the CTF of a diffractive lens with the phase function of Equation (3). Let us note that this CTF is defined up to a phase constant . One can easily show that in the Fresnel–Kirchhoff approximation of the scalar diffraction theory, the complex amplitude of a light beam, at which maximum possible intensity value at the desired focal point is reached, has exactly the form of Equation (4). In this regard, we will refer to the beam of Equation (4) as the “ideal” beam.
Next, in the calculation of the cascaded DOE, we will require that the fields generated by each DOE in the cascade at the considered wavelengths differ as little as possible from the “ideal” fields defined by Equation (4). This approach enables calculating the diffractive microrelief height functions of the DOEs sequentially (one after another). Indeed, let us assume that the first m − 1 DOEs are already calculated. In this case, the fields generated by the calculated m − 1 DOEs at the operating wavelengths are known. Then, the fields incident on the next (m-th) DOE will have the following form in the Fresnel–Kirchhoff approximation:
where and are the distances between the DOE planes. Let us require that the complex amplitudes of the beams transmitted through the m-th DOE and defined by Equation (2) are as close as possible to the complex amplitudes of the ideal fields [Equation (4)] at the design wavelengths. To achieve this, we will calculate the microrelief of the m-th DOE (the function ) by solving the following optimization problem:
where are certain weights and is the region defining the DOE aperture. Note that the choice of the coefficients gives additional possibilities to control the relative energies at the focusing points at different wavelengths. In the simplest case, one can assume them to be equal.
Following refs. [19,24], to solve the optimization problem of Equation (6), let us write it in a discrete form. We assume that the function of the diffractive microrelief height of the DOE is defined at the nodes of a two-dimensional grid containing N nodes by a set of values . Then, the problem of Equation (6) takes the form
where , . Thus, the function represents the sum of squared absolute values of differences between the complex amplitudes of the beams formed by the m-th DOE at the operating wavelengths, and the complex amplitudes of the ideal beams of Equation (4) at the introduced discrete grid. One can easily see that solving the problem of Equation (7) is reduced to solving N independent “pointwise” optimization problems
each of which enables finding the microrelief height at a single point . From the practical point of view, when solving the problems of Equation (8), one has to take into account the restrictions imposed by the technology that is planned to be used for the DOE fabrication. For example, one of the technologies, which is nowadays widely used for creating DOEs, is the so-called direct laser writing technique (also referred to as direct laser lithography) [4,19,24]. In contrast to the conventional photolithography, no photomasks are used in this approach, and the photoresist layer deposited on a certain substrate is directly “scanned” by a focused laser beam, which induces local changes in the resist solubility for its subsequent development, leading to the formation of a diffractive microrelief. If necessary, the relief can then be transferred to the substrate by an additional chemical etching stage. The most important restrictions in the direct laser writing technique include the maximum microrelief height and the number of microrelief height levels [4,19,24]. In our design, let us assume that the microrelief heights can take only the following L values: . In this case, the value minimizing the function can be found by a simple exhaustive search:
Thus, the calculation of the microrelief heights of the cascaded DOE includes the following steps:
- Choice of the design wavelengths, focusing points, and the geometrical and physical parameters of the cascaded DOE being designed;
- Calculation of the microrelief heights of the first DOE for the specified input beams with Q different wavelengths by solving pointwise optimization problems of Equation (9) at each point ;
- Propagation of the fields generated by the designed DOE to the plane of the next DOE in the cascade using Equation (5);
- Calculation of the microrelief heights of the next DOE by solving pointwise optimization problems of Equation (9);
- If the calculated DOE is not the last in the cascade, then return to step 2.
The present authors believe that the presented method for designing a cascaded DOE for focusing incident beams with several wavelengths to a set of points is much simpler as compared to “general” gradient algorithms for calculating cascaded DOEs [6,7,8,9,10,11,12,13,14,15]. The simplicity of the method is due to both the possibility of sequential calculation of the microrelief heights of the elements constituting the cascaded DOE as well as the reduction of the problem of calculating the microrelief height function of each DOE to a set of independent pointwise optimization problems of Equation (8).
3. Design Examples
In order to assess the efficiency of the proposed method, we designed cascades consisting of two DOEs for focusing the following 11 wavelengths defined by the vector
to 11 different points in the output plane. Let us note that the chosen wavelengths are used for the calculation of nine different vegetation indices used for monitoring forests and detecting vegetation anomalies (including, for example, the so-called water band index and several red edge indices) [21,22,23]. Let us assume that the DOEs are located in the planes and and the output plane is located at . Let the focusing points be equidistantly located on a segment [−0.8, 0.8] mm of the uout axis in the output plane: . Note that in the general case, the locations of the focusing points in the output plane can be arbitrarily chosen in the proposed method.
We will define the functions of the diffractive microrelief heights of the DOEs and on square grids with a step of 10 μm. In this case, the side of the square aperture of the DOEs amounts to 5.12 mm. We also assume that the microrelief heights can take L = 128 uniformly quantized values ranging from zero to μm. Note that these parameters are consistent with the direct laser writing technique mentioned above [4,19,24]. As the DOE material, we will consider fused silica (SiO2), the refractive index of which for the considered wavelengths varies from 1.47 at to 1.45 at . As the incident beams [having the wavelengths of Equation (10)], we will consider circular cross-section beams with a radius of R = 2.56 mm and unit amplitude , where rect(u) is the rectangular function taking the unit value at .
In the proposed method, the calculation of DOEs constituting the cascade is carried out sequentially. Figure 2a shows the diffractive microrelief height function of the first DOE calculated by pointwise optimization using Equation (9). According to the design approach, the first DOE by itself already focuses the incident beams with the given operating wavelengths (10) to the required points. In this regard, Figure 2c shows the intensity distributions generated by the first DOE along the uout axis in the output plane containing the focusing points. Let us note that here and in what follows, for the calculation of the generated distributions, the sinc-method from ref. [26] was applied with calculation grids with a step of 2.5 μm. In these calculations, each DOE pixel with the side length of 10 μm was represented as a matrix of pixels with the size of . The distributions presented in Figure 2c are normalized by the values
which correspond to the intensity values at the focusing points generated in the case of ideal beams of Equation (4) (i.e., in the case of focusing of the incident beams by diffractive lenses calculated separately for each of the design wavelengths). From Figure 2c, it is evident that the first DOE forms sharp intensity peaks at the required points . The magnitudes of the normalized peaks vary from 0.106 to 0.323, and their average value amounts to 0.154. Let us note that the widths of the peaks measured at the first minimum coincide with a good accuracy with the values describing the focal spot diameters of ideal diffractive lenses. We believe that it is due to the fact that in our design method, we minimize the differences between the complex amplitudes of the beams formed by the DOEs at the operating wavelengths, and the complex amplitudes of “ideal” beams generated by diffractive lenses designed separately for each of these wavelengths. As a result, the DOE behavior at the working wavelengths (including, e.g., the peak widths and depths of focus) becomes similar to that of the mentioned separately designed diffractive lenses.
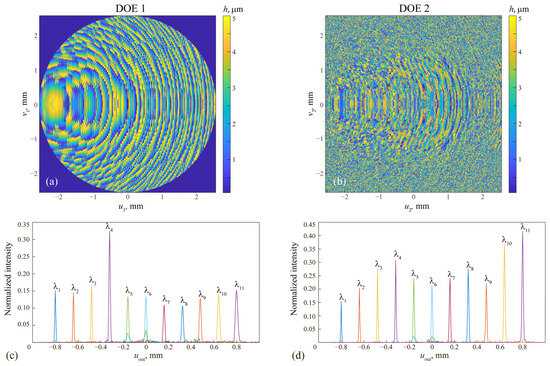
Figure 2.
(a,b) Calculated diffractive microrelief height functions of the DOEs and normalized intensity distributions generated at the design wavelengths by the first DOE (c) and the cascade of two DOEs (d).
After the calculation of the first DOE, the fields generated by it were “propagated” to the plane of the second DOE [see Equation (5)], and then for the obtained beams, the microrelief height function of the second DOE [Figure 2b] was calculated using the pointwise optimization approach [Equation (9)]. Figure 2d shows the intensity distributions generated by the cascaded DOE. As in the previous case, these distributions were normalized by the values (11) corresponding to the maximum intensities of diffractive lenses calculated separately for the design wavelengths. For the cascade of two DOEs, the average magnitude of the normalized peaks increased from 0.154 to 0.266, but the peak intensities are still significantly different.
As it was noted above, one can try to obtain a required intensity distribution between the focusing points by choosing the weights in Equations (8) and (9), which were constant in the case of DOEs shown in Figure 2. In addition, the phase constants in the CTFs of diffractive lenses in Equation (4), which can also be considered as optimization parameters, were chosen to be zero in the calculation of both DOEs constituting the cascade. In the method proposed above, the coefficients and phase constants are not considered as optimization parameters and are assumed to be given. However, taking into account the computational simplicity (the calculation of the DOEs described above at fixed and takes only several seconds on a standard desktop computer), the optimization with respect to these parameters can be performed using, for example, a genetic algorithm [25] or a gradient descent method [20]. For calculating a cascaded DOE consisting of two elements and providing a better performance, we carried out such an optimization using the genetic algorithm described in the Appendix A. The optimization of the DOEs in the cascade was performed in a sequential way, and for each DOE, the following objective function describing the minimum normalized intensity at the focusing points was maximized:
Figure 3a,b show the obtained microrelief height functions of the cascaded DOE, and Figure 3c,d show the corresponding normalized intensity distributions generated by the first DOE [Figure 3c] and the cascade of two DOEs [Figure 3d]. Figure 3c,d show that by considering the weights and phase constants as optimization parameters, one can indeed obtain an almost uniform intensity distribution between the focusing points (in the considered example, the optimization was continued until the difference between the minimum normalized peak intensity and the average normalized peak magnitude became less than 5%). It is also worth noting that for the case of a cascaded DOE, the average intensity of the peaks significantly increased (from 0.266 in the initial case to 0.318).
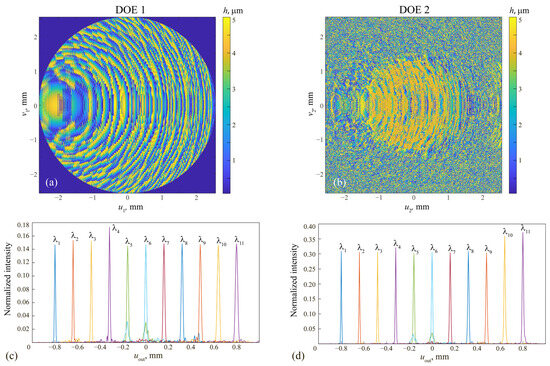
Figure 3.
(a,b) Diffractive microrelief height functions of the DOEs calculated with optimization with respect to the parameters , , and the normalized intensity distributions generated at the design wavelengths by the first DOE (c) and the cascade of two DOEs (d).
In order to better understand the efficiency of the obtained solution (Figure 3), we also calculated the two-DOE cascade using the iterative adaptive moment estimation method (ADAM) [20] implemented in the PyTorch framework. This method belongs to the family of gradient methods and is nowadays widely used in the cascaded DOE design [6,7,8,9,10,11,12,13,14,15,16,17,18]. Similarly to Equation (12), the DOE calculation was based on maximizing an objective function representing the minimum normalized intensity at the required points:
As an initial approximation for the iterative ADAM algorithm, the functions of the diffractive microrelief height shown in Figure 3a,b were taken. Let us note that these microrelief heights were calculated with an optimization with respect to the parameters and . The utilization of such an initial approximation ensured a fast convergence of the iterative method (in a few hundred iterations). The resulting microrelief height functions of the cascaded DOE and the generated intensity distributions at the operating wavelengths are shown in Figure 4. Let us note that although the obtained functions of the diffractive microrelief height [Figure 4a,b] remained visually close to the initial ones [Figure 3a,b], the average intensity at the peaks increased to 0.425 (as compared to 0.318 for the cascaded DOE shown in Figure 3). It is important to note that when random microrelief height functions (i.e., the ones having independent height values uniformly distributed in the range) were used as initial approximations, the ADAM algorithm converged to essentially inferior results, for which the average magnitude of the normalized intensity peaks was about 0.22–0.23 depending on the used random initial approximation. Moreover, for the convergence, 10,000–12,000 iterations were required. It is also worth mentioning that in the case of a single DOE, the ADAM algorithm could barely improve the initial approximation shown in Figure 3a. Thus, we can conclude that the proposed method for calculating cascaded DOEs focusing the radiation of several different wavelengths to different points presented in Section 2 is quite efficient and outperforms the iterative ADAM algorithm in the case of random initial approximation.
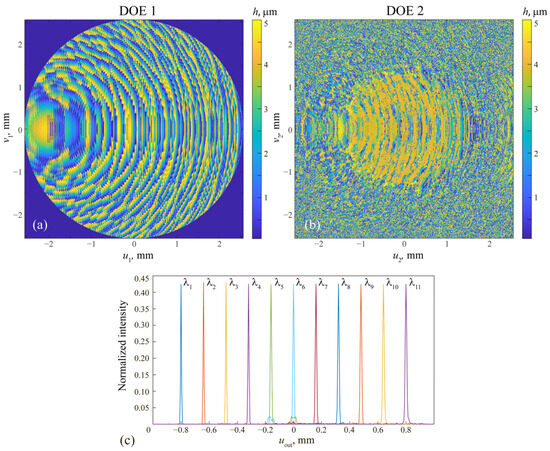
Figure 4.
(a,b) Diffractive microrelief height functions of the DOEs calculated iteratively using the ADAM method and the normalized intensity distributions generated at the design wavelengths by the cascaded DOE (c).
To conclude this section, let us note that the intensity distributions generated by the designed DOEs contain a certain “crosstalk” between the spectral channels (intensity peaks) corresponding to the wavelengths 670 nm and 680 nm, which are the closest in the operating wavelength set. For example, for single DOEs in Figure 2 and Figure 3, the average crosstalk between these channels (calculated as the ratio between the intensity of the secondary peak from the adjacent wavelength and the intensity of the main peak at the current wavelength) is about 0.22 [see Figure 2c and Figure 3c]. At the same time, in the case of a two-DOE cascade, the average crosstalk decreases to 0.1 [Figure 2d and Figure 3d] or even to 0.05 [Figure 4c]. From the physical point of view, this crosstalk is caused by the fact that two close wavelengths (with the difference of about 1.5% for the mentioned wavelengths) cannot be “processed” by the same DOE in a fully independent manner, unless its microrelief is very high [27]. In this regard, we believe that an increase in the maximum microrelief height and/or introduction of additional DOEs to the cascade will further reduce the discussed crosstalk.
4. Discussion and Conclusions
We proposed a method for calculating cascaded DOEs for focusing Q incident beams with different wavelengths to Q required points in the output plane. The method is based on the use of a special optimization criterion representing the difference between the complex amplitudes of beams formed by each element of a cascaded DOE at the design wavelengths from the complex amplitudes of “ideal beams” formed by diffraction lenses calculated separately for each of these wavelengths. This criterion makes it possible to calculate the elements of the cascaded DOE sequentially, and also enables to reduce the calculation of each DOE in the cascade to the solution of a set of independent and computationally simple “pointwise” optimization problems.
It is also important to note that the used criterion contains a set of free parameters, namely, the weights and the phase constants . The tuning of these parameters enables improving the DOE efficiency (average magnitude of the normalized intensity peaks) and controlling the intensity distribution between the focusing points corresponding to different operating wavelengths. Taking into account the computational simplicity of the method, the optimal values of the parameters and can be found by using standard optimization techniques, e.g., genetic algorithms or gradient descent methods.
Using the proposed method, cascades of two DOEs were calculated to focus radiation of 11 wavelengths corresponding to a number of widely used vegetation indices. The presented numerical simulation results demonstrate good performance of the method. In particular, for the considered parameters, the proposed method gives better results compared to the widely used ADAM method with random initial approximation. At the same time, the joint utilization of our method and ADAM enables further improving the intensity at the peaks and making them virtually uniform.
Finally, let us note that the proposed method can be easily extended to other DOE design problems. In particular, it can be generalized to the case of cascaded DOEs focusing the radiation of different wavelengths to different points in space not located in the same output plane. Moreover, instead of the complex transmission functions of ideal diffractive lenses in the optimized objective function, more sophisticated CTFs providing the generation of certain prescribed intensity patterns at the design wavelengths can be used. For example, CTFs representing DOEs with extended depth of focus [28,29,30,31] are promising for designing cascaded DOEs for utilization in microscopy and tomography systems.
Author Contributions
Conceptualization, L.L.D. and N.L.K.; methodology, L.L.D. and N.L.K.; software, D.V.S., G.A.M. and E.V.B.; validation, L.L.D., D.V.S. and G.A.M.; investigation, L.L.D., D.V.S., G.A.M., E.A.B. and D.A.B.; resources, N.L.K.; writing—original draft preparation, L.L.D. and E.A.B.; writing—review and editing, L.L.D., E.A.B., D.A.B. and N.L.K.; visualization, E.V.B., D.V.S. and G.A.M.; supervision, L.L.D. and N.L.K.; project administration, L.L.D. and N.L.K.; funding acquisition, N.L.K. and L.L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Russian Science Foundation (project 24-19-00080).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the presented results are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Description of the Genetic Algorithm
Let us consider the genetic algorithm used for the calculation of DOEs with optimization of the parameters and . Let the population consist of individuals, where the genotype of each individual is defined by the vectors and (the weights and the phase constants). At the first step, we generate a generation of with constant weights and random phase constants consisting of independent values uniformly distributed in the range. Next, the algorithm includes the following steps.
- Recombination. While there are less then individuals, we randomly choose two individuals from the previous population, from which random genes are chosen (by 50% from each individual). Using these genes, a genotype for a new individual for the next population is formed.
- Mutation. For each new individual, each gene is changed with a probability to a random value from the corresponding range.
- Selection. For each individual (pair of vectors and ), a DOE is calculated, and the objective function of Equation (12) is calculated for it. Then, best individuals (having the largest values of the objective function) are chosen.
- Then, we move to step 1 and repeat the steps, until the given number of generations passes or until a certain stopping condition is reached.
In the calculations, the following parameters of the algorithm were used: number of individuals in the population , number of the individuals kept at the selection stage , mutation probability ; number of generations . In addition, to each population, three new individuals with random genotypes were added. As a stopping condition, we used the condition of the difference between the minimum normalized intensity and the average value of the normalized peaks becoming less than 5%.
References
- Zhang, J.; Pégard, N.; Zhong, J.; Adesnik, H.; Waller, L. 3D computer-generated holography by non-convex optimization. Optica 2017, 4, 1306–1313. [Google Scholar] [CrossRef]
- Wang, H.; Piestun, R. Dynamic 2D implementation of 3D diffractive optics. Optica 2018, 5, 1220–1228. [Google Scholar] [CrossRef]
- Schmidt, S.; Thiele, S.; Toulouse, A.; Bösel, C.; Tiess, T.; Herkommer, A.; Gross, H.; Giessen, H. Tailored micro-optical freeform holograms for integrated complex beam shaping. Optica 2020, 7, 1279–1286. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Mingazov, A.A.; Byzov, E.V.; Skidanov, R.V.; Ganchevskaya, S.V.; Bykov, D.A.; Bezus, E.A.; Podlipnov, V.V.; Porfirev, A.P.; Kazanskiy, N.L. Hybrid design of diffractive optical elements for optical beam shaping. Opt. Express 2021, 29, 31875–31890. [Google Scholar] [CrossRef]
- Zhang, Q.; He, Z.; Xie, Z.; Tan, Q.; Sheng, Y.; Jin, G.; Cao, L.; Yuan, X. Diffractive optical elements 75 years on: From micro-optics to metasurfaces. Photonics Insights 2023, 2, R09. [Google Scholar] [CrossRef]
- Gülses, A.; Jenkins, B.K. Cascaded diffractive optical elements for improved multiplane image reconstruction. Appl. Opt. 2013, 52, 3608–3616. [Google Scholar] [CrossRef]
- Buske, P.; Völl, A.; Eisebitt, M.; Stollenwerk, J.; Holly, C. Advanced beam shaping for laser materials processing based on diffractive neural networks. Opt. Express 2022, 30, 22798–22816. [Google Scholar] [CrossRef]
- Soshnikov, D.V.; Doskolovich, L.L.; Motz, G.A.; Byzov, E.V.; Bezus, E.A.; Bykov, D.A.; Mingazov, A.A. Design of cascaded diffractive optical elements for optical beam shaping and image classification using a gradient method. Photonics 2023, 10, 766. [Google Scholar] [CrossRef]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef] [PubMed]
- Yan, T.; Wu, J.; Zhou, T.; Xie, H.; Xu, F.; Fan, J.; Fang, L.; Lin, X.; Dai, Q. Fourier-space diffractive deep neural network. Phys. Rev. Lett. 2019, 123, 023901. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Fang, L.; Yan, T.; Wu, J.; Li, Y.; Fan, J.; Wu, H.; Lin, X.; Dai, Q. In situ optical backpropagation training of diffractive optical neural networks. Photonics Res. 2020, 8, 940–953. [Google Scholar] [CrossRef]
- Chen, H.; Feng, J.; Jiang, M.; Wang, Y.; Lin, J.; Tan, J.; Jin, P. Diffractive deep neural networks at visible wavelengths. Engineering 2021, 7, 1483–1491. [Google Scholar] [CrossRef]
- Kulce, O.; Mengu, D.; Rivenson, Y.; Ozcan, A. All-optical synthesis of an arbitrary linear transformation using diffractive surfaces. Light Sci. Appl. 2021, 10, 196. [Google Scholar] [CrossRef]
- Li, J.; Gan, T.; Bai, B.; Luo, Y.; Jarrahi, M.; Ozcan, A. Massively parallel universal linear transformations using a wavelength-multiplexed diffractive optical network. Adv. Photonics 2023, 5, 016003. [Google Scholar] [CrossRef]
- Luo, Y.; Mengu, D.; Yardimci, N.T.; Rivenson, Y.; Veli, M.; Jarrahi, M.; Ozcan, A. Design of task-specific optical systems using broadband diffractive neural networks. Light Sci. Appl. 2019, 8, 112. [Google Scholar] [CrossRef]
- Mengu, D.; Tabassum, A.; Jarrahi, M.; Ozcan, A. Snapshot multispectral imaging using a diffractive optical network. Light Sci. Appl. 2023, 12, 86. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, Y.; Britton, W.A.; Negro, L.D. Inverse design of ultracompact multi-focal optical devices by diffractive neural networks. Opt. Lett. 2022, 47, 2842–2845. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, Y.; Negro, L.D. Design of ultracompact broadband focusing spectrometers based on diffractive optical networks. Opt. Lett. 2022, 47, 6309–6312. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Skidanov, R.V.; Blank, V.A.; Ganchevskaya, S.V.; Podlipnov, V.V.; Bykov, D.A.; Golovastikov, N.V.; Bezus, E.A. Design of multi-wavelength diffractive lenses focusing radiation of different wavelengths to different points. Photonics 2022, 9, 785. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical vegetation indices for monitoring terrestrial ecosystems globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Database for Remote Sensing Indices. Available online: https://www.indexdatabase.de/db/a-single.php?id=1 (accessed on 18 July 2024).
- Doskolovich, L.L.; Skidanov, R.V.; Bezus, E.A.; Ganchevskaya, S.V.; Bykov, D.A.; Kazanskiy, N.L. Design of diffractive lenses operating at several wavelengths. Opt. Express 2020, 28, 11705–11720. [Google Scholar] [CrossRef]
- Skinner, G.K. Design of achromatic diffractive lenses. Opt. Express 2024, 32, 230–247. [Google Scholar] [CrossRef] [PubMed]
- Cubillos, M.; Jimenez, E. Numerical simulation of optical propagation using sinc approximation. J. Opt. Soc. Am. A 2022, 39, 1403–1413. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Kazanskiy, N.L.; Soifer, V.A.; Perlo, P.; Repetto, P. Design of DOEs for wavelength division and focusing. J. Mod. Opt. 2005, 52, 917–926. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Kazanskiy, N.L.; Soifer, V.A.; Tzaregorodtzev, A.Y. Analysis of quasiperiodic and geometric optical solutions of the problem of focusing into an axial segment. Optik 1995, 101, 37–41. [Google Scholar]
- Song, W.; Guo, C.; Zhao, Y.; Wang, Y.; Zhu, S.; Min, C.; Yuan, X. Ultraviolet metasurface-assisted photoacoustic microscopy with great enhancement in DOF for fast histology imaging. Photoacoustics 2023, 32, 100525. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, R.; Xu, J.; Wang, H.; Zhu, Q.; Zhang, Y. Efficient generation of longitudinally polarized light needle with diffractive optical elements. Res. Opt. 2022, 10, 100332. [Google Scholar] [CrossRef]
- Zhao, J.; Winetraub, Y.; Du, L.; Van Vleck, A.; Ichimura, K.; Huang, C.; Aasi, S.Z.; Sarin, K.Y.; de la Zerda, A. Flexible method for generating needle-shaped beams and its application in optical coherence tomography. Optica 2022, 9, 859–867. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).