1. Introduction
Due to their exceptional time resolution and digital signal processing capabilities, SPADs have been extensively applied in various fields, including positron emission tomography [
1], quantum random number generation [
2,
3], LiDAR systems [
4,
5], and fluorescence lifetime imaging [
6,
7,
8]. In recent years, significant advancements in image sensor technology have been observed, transitioning from the popular CCD sensors of 20 years ago to the prevalent CMOS image sensors (CIS) used today. Compared to traditional cameras, SPADs typically have larger pixels and a higher tendency for dark current [
9]. However, advances in tape-out processes and 3D stacking technologies [
9] have improved the fill factor of SPADs, making them suitable for mobile devices. These enhancements enable photon counting at higher frequencies and ultra-high resolution within a single frame. SPADs’ high time resolution allows them to function in both 2D and 3D imaging modes [
10]. In 3D imaging, SPADs are utilized in applications such as autonomous driving, robotics, and facial recognition. In 2D imaging, SPADs have emerged as promising sensors due to their low readout noise and high dynamic range (HDR). Various innovative imaging technologies, such as time delay integration (TDI) imaging sensors [
11], characterized by a high modulation transfer function, have been implemented. Canon has developed a megapixel [
12] SPAD image sensor designed to eliminate dips in the signal-to-noise ratio (SNR) [
13], achieving high image quality.
A critical metric for image sensors is dynamic range, which measures the range of light intensities that can be accurately captured in an image, from the darkest shadows to the brightest highlights. The dynamic range determines the saturation limit, which is the maximum light intensity at which the sensor can record information without losing detail. As HDR display technology advances, there is an increasing demand for image sensors capable of capturing a broader range of light intensities. Below the saturation limit, the signal-to-noise ratio (SNR) of the image increases linearly with light intensity. However, once the light intensity exceeds the saturation limit, the SNR decreases because the sensor can no longer accurately record the light information. In scenes with a wide range of light intensities, low dynamic range (LDR) cameras struggle to accurately capture bright areas, resulting in a lower overall SNR and loss of detail in the brightest parts of the image. This limitation highlights the importance of developing sensors with high dynamic range capabilities to enhance image quality under various lighting conditions.
Unlike traditional CMOS image sensors (CIS), SPAD image sensors have a higher saturation limit [
14,
15]. Their high photon sensitivity enables them to perform well in low-light environments. In bright environments, SPADs exhibit a nonlinear light response, which contributes to their higher saturation limit and wide dynamic range.
Traditional cameras often require additional computing modules to achieve HDR, such as exposure bracketing [
16], coded exposure, and burst photography [
17]. These methods all require multiple exposures in different conditions, which are then merged together to form a HDR image. This process always requires a longer acquisition time. In recent years, multiple merging algorithms have been developed. Deep learning strategies provide potential future research directions for HDR imaging [
18]. However, the longer processing time and the disadvantages of dealing with unexpected saturated regions in algorithm processing have been significant issues when a fast reaction is needed. In contrast, SPADs offer a cost-effective solution for HDR imaging without the need for multiple exposures or complex merging computations, making them an excellent choice for HDR cameras.
In recent years, Quanta image sensors (QIS) have emerged as a promising technology for HDR imaging. QIS, a type of single-photon image sensor, boasts lower dark current and readout noise compared to conventional image sensors. QIS allows for shorter exposure times with higher frame rates. Additionally, various reconstruction methods are being developed for QIS to create HDR images with lower noise [
19]. Compared to QIS, SPAD can achieve HDR imaging while also providing 3D imaging capabilities. The dual-mode operability of SPAD is advantageous for applications in autonomous driving and gesture recognition. The 3D function of SPAD is a significant potential advantage over current QIS technology. The imaging processing techniques used for SPAD can also be applied to QIS [
9]. Therefore, we will address the HDR capabilities of SPAD and analyze its impact in the following sections.
The dynamic range of the SPAD image sensor is determined by both the sensor device and the calculation circuit. The device determines photon sensitivity, while the calculation circuit is responsible for converting light information into digital signals. In SPAD sensors, the most critical component affecting the dynamic range is the quenching circuit, which dictates the mode of operation and the response to photon detection.
SPAD is a photodiode that operates in Geiger mode, allowing it to detect single photons. When a photon is detected, the SPAD generates a digital pulse through a process called quenching, which involves both avalanche and recovery phases. The quench circuit, critical to this process, significantly impacts the speed and noise performance of SPAD cameras. We introduce two major categories of quenching circuits, passive quenching circuits (PQC) and active quenching circuits (AQC), and discuss their implementation in free-running and gating modes.
The passive quenching circuit is the simplest type of quenching circuit. A suitably sized resistor is sufficient for quenching. This equivalent resistance can be achieved with an MOS transistor, which can be easily integrated into chips with minimal layout area using conventional CMOS technology. When a photon is detected, the current through the diode surges, causing a voltage drop across the equivalent resistor [
20,
21]. The recovery time is determined by the total capacitance and resistance values. However, PQCs typically have long dead times, usually a few hundred nanoseconds. To address the need for higher photon detection speeds, time-gated quenching circuits [
22] have been developed. In these circuits, photon detection is controlled using a gating method, where a pulse signal regulates a gated MOS transistor. When the gate is closed, the MOS transistor functions as a resistor, and when the gate is open, the quenching process stops by connecting the SPAD to the ground. Gated quenching circuits have a fixed detection window, which is determined by the frequency of the pulse signal.
To achieve higher photon detection frequencies, active quenching circuits have been designed [
23]. These circuits accelerate both the quenching and recovery processes. They are more complex than passive circuits, incorporating feedback structures that actively restore the initial state. This active recovery minimizes dead time, allowing for higher-frequency photon detection within a single frame. Previous work has demonstrated a minimum dead time of
ns [
24]. Active quenching circuits operate in free-running mode, which features shorter dead times and discontinuous detection windows.
Both SPAD imaging modes exhibit a non-linear response to photons [
25]. Unlike conventional image sensors, which exhibit a more linear light response curve, achieving high-dynamic range images can be challenging. This paper presents a theoretical model comparing free-running and gating image modes by statistically analyzing the quenching process and photon counting. Additionally, we compare HDR SPAD sensors with conventional cameras, focusing on their photon detection capabilities, impacts on SNR, and saturation limits. This research evaluates images across different light intensities and compares the mapping processing methods in the two imaging modes, presenting both simulated and experimental imaging results. It provides insights into selecting the most appropriate imaging mode for engineering applications: the free-running imaging mode can achieve a dynamic range that is an order of magnitude higher than the gating imaging mode. Conversely, the gating mode offers lower noise, higher stability, and a smaller circuit area.
Regarding the structure, we introduce the principles of photon detection for the free-running and gating-quenching methods, as well as traditional CIS cameras, in
Section 2. Then, we depict two quenching methods using statistical models and provide a theoretical comparison of the two quenching modes. We introduce the image system and the two imaging chips in
Section 3. To support our findings, we provide visual evidence through images captured in various real-world situations and analyze the outcomes in
Section 4. This paper compares the quality of 2D imaging in both well-lit and low-light environments, where the theoretical model is validated through the analysis of imaging results. This chapter also analyzes non-ideal factors. A summary of the conclusions and future research directions is provided in
Section 5.
2. The Statistical Model of Gating and Free-Running Modes
Conventional CIS imaging sensors encode light intensity through charge accumulation. The image data are quantified by analog-to-digital converters (ADCs), and the light–response relationship is linear [
26], which causes the sensor to saturate quickly as light intensity increases. In contrast, SPAD sensors exhibit significant differences from traditional image sensors. SPAD sensors have a non-linear response to photon detection, where each captured photon is converted into a digital pulse. This character makes SPAD suitable for designing the high-dynamic range imaging sensor.
The distinction between free-running and gating modes is shown in
Figure 1. The schematic diagram illustrates scenarios under both low- and high-light conditions. In gating mode, detection cycles are determined by pulse signals and are tightly arranged without gaps. In free-running mode, detection windows are distributed according to the arrival times of photons, resulting in gaps between detection windows. This means that the free-running mode cannot fully utilize the exposure time to detect photons, whereas the gating mode can be fully active during the entire detection period. This difference affects their photon-detection capabilities.
As shown in the figure, under low-light conditions, both free-running and gating modes can detect six photons, indicating similar photon detection abilities. However, under high-light conditions, free running mode detects eight photons, while gating mode detects ten photons, demonstrating that gating mode can detect more photons. This results in a more linear light response curve and a higher saturation limit compared to free-running mode. Generally, both SPAD modes respond nonlinearly and have a higher saturation limit than traditional image sensors.
To achieve a high-dynamic range, we propose a mapping method for SPAD image processing and assessment. Typically, photon counts directly represent brightness. Inspired by the photon–response curve, each photon count corresponds to a light intensity. Therefore, we can use the count of detected photons to map the actual light intensity based on the curve. This method can extend the image’s dynamic range and enable the image to reflect light intensity more realistically. Based on the statistical model of photon counting, we can derive the SNR calculation formula, which will be detailed in the following section.
2.1. Model of the Free-Running Mode
We define as the total exposure time and T as the effective exposure time. In free-running mode, all the exposure time is effective, so . In gating mode, pixels can only detect photons during the high-level period of the square signal. Thus, the effective exposure time depends on the duty cycle D of the square signal, with . Adjusting the exposure time in both modes can make the effective exposure time the same.
The number of photons arriving within a fixed exposure time follows a Poisson distribution [
27,
28,
29]. The intervals between events in the Poisson process conform to an exponential distribution. Considering the time between two detected photons should be no shorter than the dead time, the intervals between photon pulses follow a shifted exponential distribution.
According to statistical renewal theory, the photon count can be represented with exposure-related parameters. Let
denote the luminous flux, representing the total number of photons impinging on the sensor surface in 1 ns. During the effective exposure time
T, the photon count
can be formulated as follows:
where
q denotes the photon-detection probability and
stands for the dead time. The detailed mathematical derivation process can be found in previous work by the University of Wisconsin–Madison team [
30].
In high-light intensity scenarios, the photon count converges towards a constant value:
We validated the formulas using an algorithm in MATLAB, simulating the photon-counting process in free-running mode. By randomly generating photon timestamps, we calculated the intervals between photons and the counts of the random sequence. The results were found to align with Formula (
1).
When a photon is detected, the detection process resets after the dead time. Each detection event is independent and follows the same distribution. Therefore, the photon-counting event can be modeled as an update process, with the number of photons counted following renewal theory. The standard deviation (SD) of
after a long exposure time can be expressed as Formula (
3).
Considering that the avalanche current is quantized as a pulse, the deviation also involves one bit of quantization noise [
31,
32]. The quantization noise is often considered in TDC performance evaluation, expressed as
, where
Q is the maximum difference between the analog variable and the digital variable.
Because the number of detected photons is huge, the independent and identically distributed
can be seen as normally distributed variables. Therefore, we can deduce the distribution of
using the central limit theorem [
33]. The variation of
refers to the shot noise [
34], expressed as
. Shot noise is the main factor impacting image quality [
35].
Additionally, after-pulsing noise
, caused by non-empty traps [
36], is another source of imaging distortion requiring balance with dead time [
37]. It is defined as follows:
Taking into account all these influencing factors, we can induce the SNR of a SPAD image as follows:
For the non-mapping method, the SD of
constitutes the primary source of noise, the shot noise. Thus, the non-mapping SNR is as follows:
2.2. Model of the Gating Mode
In the gating imaging mode, each cycle allows for one detection opportunity. At the end of each exposure cycle, the SPAD sensor discharges to the ground. We model photon counting using a binomial distribution [
38], with each gating detection cycle representing an independent Bernoulli trial that results in either detection or no detection. Given the Poisson distribution nature of incoming photons, the probability that
k photons arrive at the detector per unit time aligns with Equation (
8).
Considering the average photon flux per unit time
is
, the average number of detected photons is
. According to Equation (
8), the probability of photon detection within time
is
, expressed as follows:
During exposure time
T, detection events with probability
p repeat
times. According to the binomial distribution [
39,
40], the photon count
conforms to the mean of
defined as follows:
Similar to the free-running mode, photon counting in the gating mode also has a limit of
, and the SD of photon counting is conducted as follows:
In the gating mode, due to charge release in the second half of the cycle, after-pulsing is diminished, effectively reducing after-pulsing noise. Given that after-pulsing noise is the least significant noise source, we neglect it for simplification. Thus, the primary noise sources include shot noise and dark noise. Both noise sources can be derived using the central limit theorem and the cumulative distribution function (CDF) of
. For simpler calculations, we employ a Taylor approximation while preserving the first-order term in the derivation process.
We verify the model by simulating the gating imaging mode: we generate random number timestamps with a mean of
and SD of
, mapping to the corresponding light intensity using Equation (
10). We then calculate the statistical expectation and variance of the estimated light flux, finding the results consistent with theoretical derivation.
The dark noise can be deduced by replacing
with the constant dark flux
.
Using the mapping calculation method, we compute the SNR in the gating mode via Equation (
6), where
. Without the mapping method, SNR is represented by Equation (
7).
2.3. Comparison of Theoretical Curves
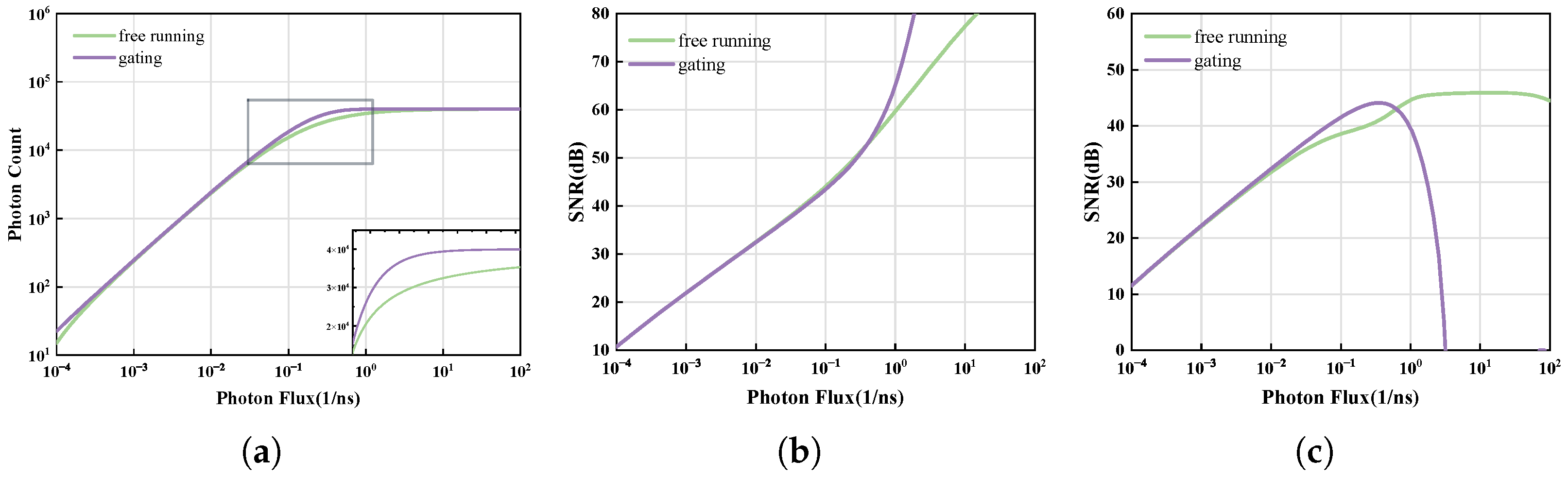
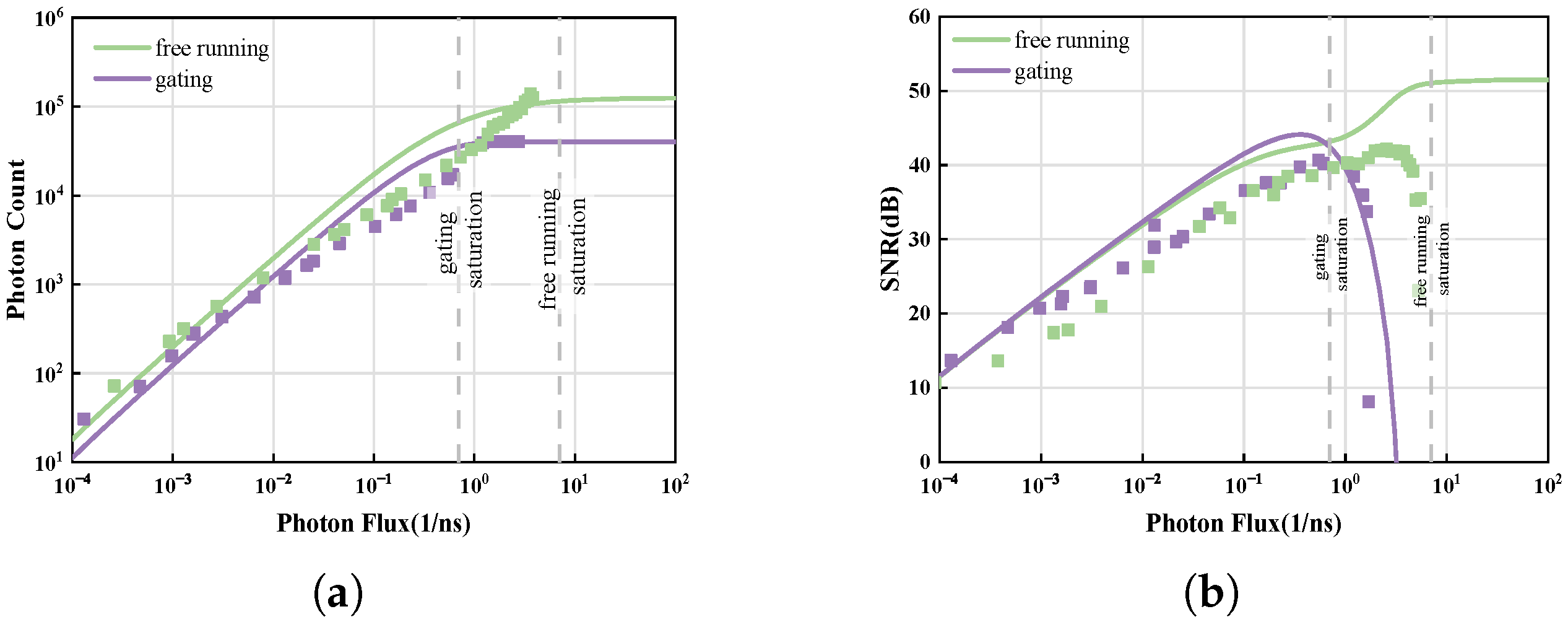
Figure 2 illustrates the photon count
and SNR under two methods. The lower green curve represents the free-running mode, while the higher purple curve represents the gating mode.
Figure 2a, generated using Formulas (
1) and (
10), indicates the number of detected photons under photon flux
. As the photon flux increases, photon counts rise sharply and then plateau. The inverse function of this mapping relationship can widen the dynamic range of the image. Before saturation, the gating mode climbs faster than the free-running mode, particularly in the highlighted curve section, suggesting that the gating mode has a greater ability to capture photons and thus achieve higher resolution.
Figure 2b shows the SNR without the mapping method. The gating mode tends to have a higher SNR compared to the free-running mode. However, SNR does not decrease after saturation due to a pole after the saturation point; only the data before this pole are valid. Thus, this method fails to depict SNR accurately, and we focus on SNR using the mapping method in subsequent sections.
Figure 2c exhibits the SNR with the mapping method. As photon flux increases, the SNR in both modes rises, peaks at the photon count curve’s inflection point, and then decreases. At low-light intensities, the gating method offers a higher SNR, making it suitable for low-light environments. At higher light intensities, the SNR of the free-running mode drops later, making it appropriate for outdoor use.
Factors such as exposure time
T, dead time
, and photon-detection probability (PDP)
p impact SNR and saturation limits. Increased exposure time can improve the SNR without affecting saturation. Therefore, we focus on the influence of
and
p.
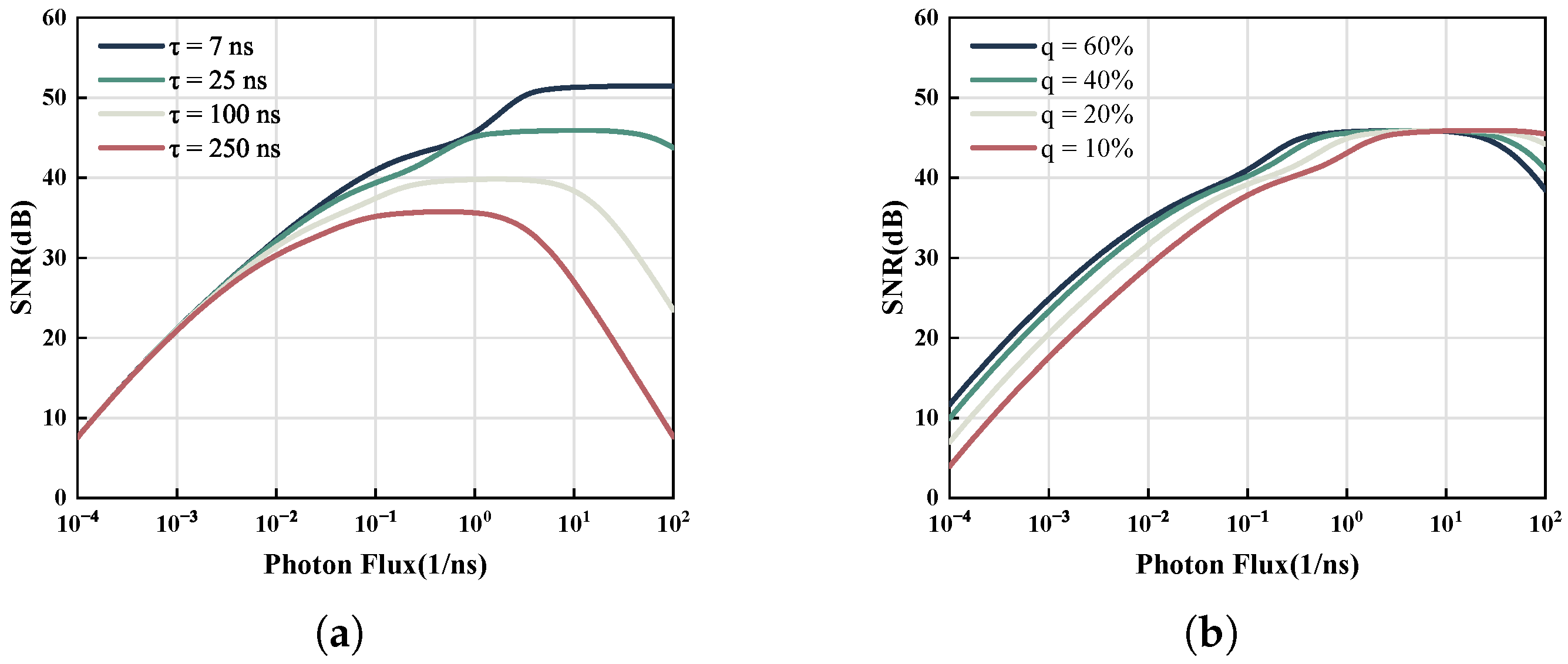
Figure 3a demonstrates the effect of
in free-running mode. The shorter the dead time, the higher the SNR, with an elevated saturation limit suggesting that faster quenching circuits saturate more slowly. As shown in
Figure 3b, enhancement in detection probability does not significantly improve the SNR. Moreover, there is minimal potential for improvement in
p within the visible light band.
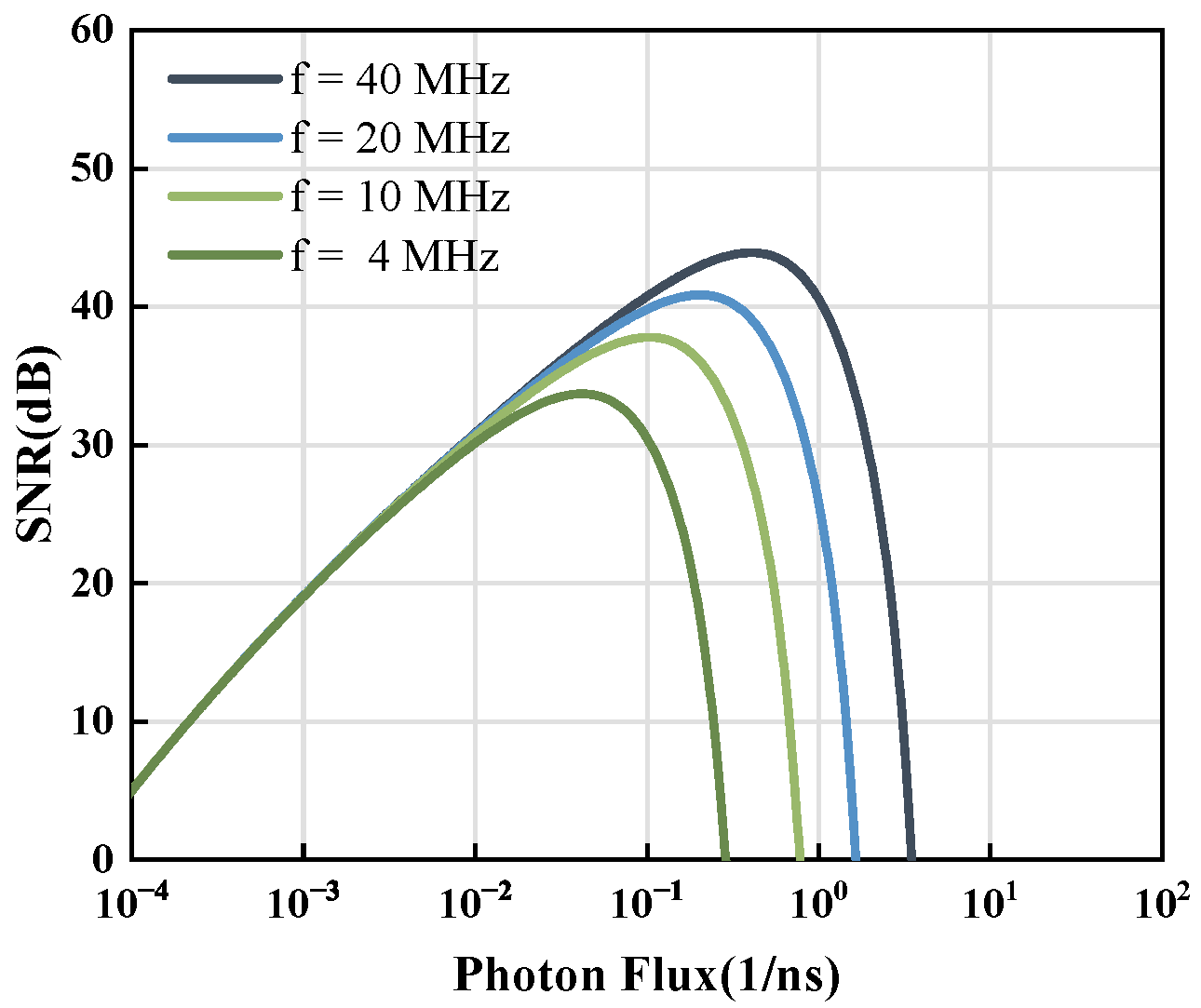
For the gating mode, we examine the effect of dead time
on the SNR. The result is depicted in
Figure 4, where
q is 23% over a period of 1 ms. The frequency of the pulse signal applied to the switching MOS tube determines the dead time: 40 MHz equates to 25 ns, 20 MHz to 50 ns, 10 MHz to 100 ns, and 4 MHz to 250 ns. At lower-light intensities, the differences among these four curves are minimal. As the light intensity increases, high-frequency quenching methods yield greater SNR and a higher saturation limit.
The dead time and photon-detection probability influence the trends of the SNR and saturation limit for both imaging modes similarly. The influence of p is less significant and can be disregarded when the difference is small.
3. Experiment System
Despite theoretical exploration, practical factors remain unaccounted for, necessitating an experimental approach to validate the theory. We designed and fabricated two chips for our experiments using 180 nm CMOS technology. One chip is equipped with free-running quenching circuits with pixels, while the other uses gating quenching circuits with pixels. To diminish the impact of differences between pixels, we used a rolling imaging strategy. Both chips function equivalently to a rolling image chip with pixels. This section introduces the two chips in terms of pixels, quenching circuits, and imaging systems.
3.1. SPAD Image Sensor Chip
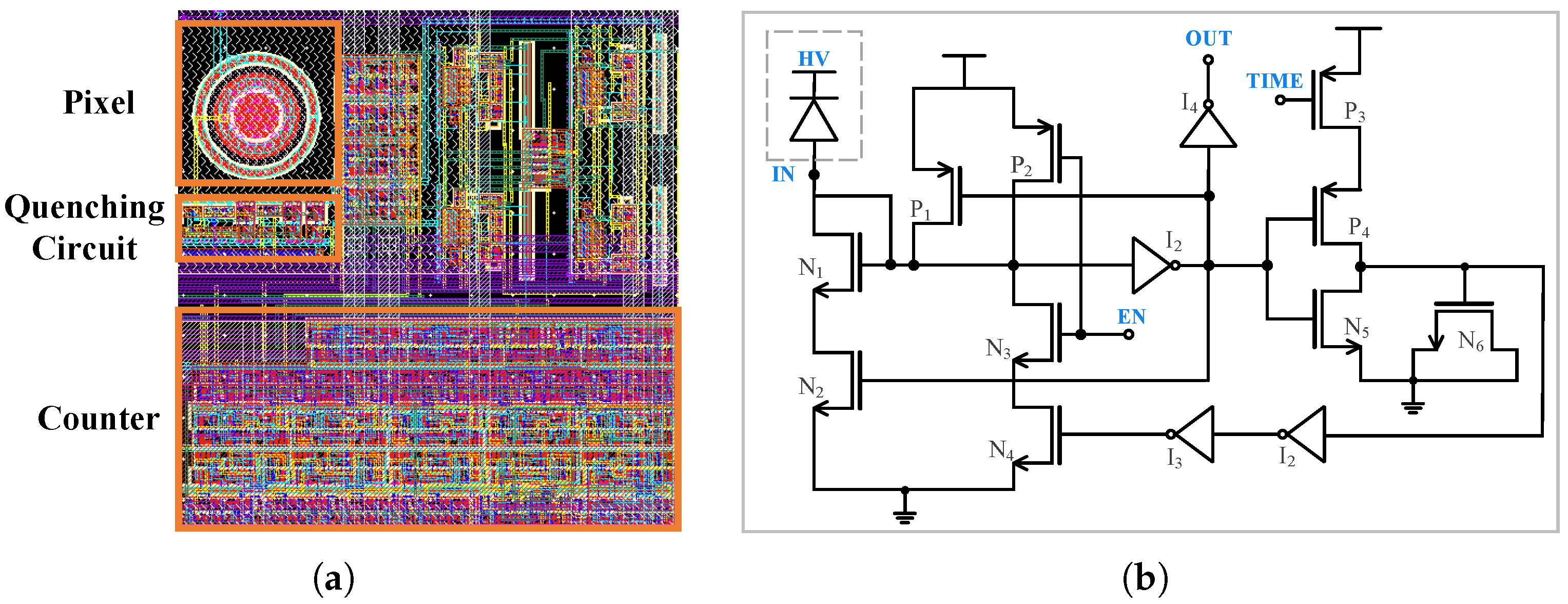
As illustrated in
Figure 5a, the free-running chip with
pixels consists of pixels, quenching circuits, photon counters, and readout circuits, which are on the periphery of the overall circuit. The other part of the circuit that is not illustrated in
Figure 5a is used for other functions not related to this article. The cathode of each pixel is connected directly to the quenching circuit, converting the light information into a digital signal. The synchronous photon counter calculates the digital pulses and locks after an exposure period. Finally, data are sent to the FIFO of the FPGA through a rolling readout system. As for the rolling imaging strategy, only one column of pixels works and is read out at a time.
The free-running chip has pixels with a diameter of 6 m. The pixels utilize a shallow junction with deep depletion to increase the probability of photon detection. The breakdown voltage is measured on a Cascade 12 semi-automated probe station as V.
The free-running chip employs active quenching circuits, as shown in
Figure 5b. This circuit connects the SPAD sensor to a photon counter, achieving a dead time of 7 ns. Signal EN activates the quenching process, while TIME controls the output pulse width. To accommodate rapid quenching,
facilitates voltage increase when the avalanche current arrives, and the circuit branch with
aids device recovery after the voltage rise. Processed digital pulses are outputted from the OUT port.
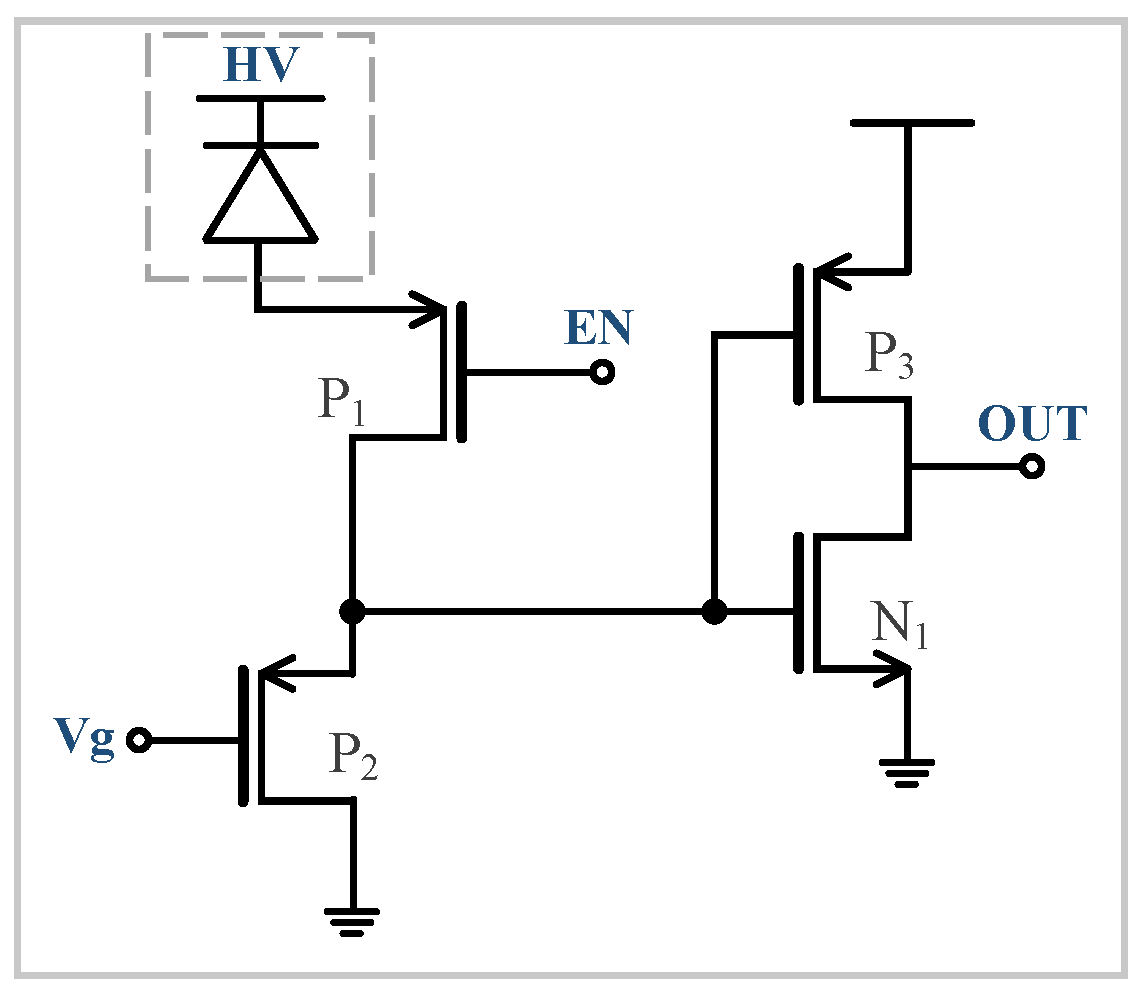
The gating chip has circuits and pixels with the same structure as the free-running chips. The gating chip uses a passive quenching circuit controlled by a gated MOS tube, as shown in
Figure 6. When the gate of
is opened by Vg, the bias voltage HV is applied to the SPAD. When
closes, the charge is released to the ground. The gating quenching circuit tolerates a gating frequency of up to 40 MHz, resulting in a detection cycle of 25 ns. For convenience, the duty cycle of the Vg pulse operates at 50%, providing an effective detection window
of
ns.
Comparing these quenching circuits, the free-running circuit uses 18 MOS tubes, while the gating circuit has only four transistors. While the free-running quenching circuit achieves a shorter dead time, which is beneficial for 3D imaging, it also consumes more layout area, leading to power consumption and fill-factor issues. The gating circuit, although not reaching the same high quenching frequency, meets the needs of chips with stringent area constraints.
Although the two types of chips have the same structure, the pixels have different doping conditions. Therefore, we introduce an experiment to measure the PDP to ensure the pixels of two chips have the same photon-detection ability.
3.2. Pixel Photon-Detection Probability
For consistency, we utilize pixels with similar effective areas and PDP. We characterize the PDP at various wavelengths to ensure minimal differences between the two chips. Photon counts are detected under a uniform laser generated through an integrating sphere, with the number and wavelength of incident photons precisely controlled by a laser source. Since photon counts are linearly proportional to the number of incident photons detected using an optical power meter, PDP [
41] is defined as the slope of photon counts
per area to the number of incident photons per area:
where
represents the frequency of light,
T is the exposure time, and
is the optical power at a specific light wavelength
.
and
are the photon-sensitive areas of the detector probe and pixel, respectively. The probe diameter is 1 cm.
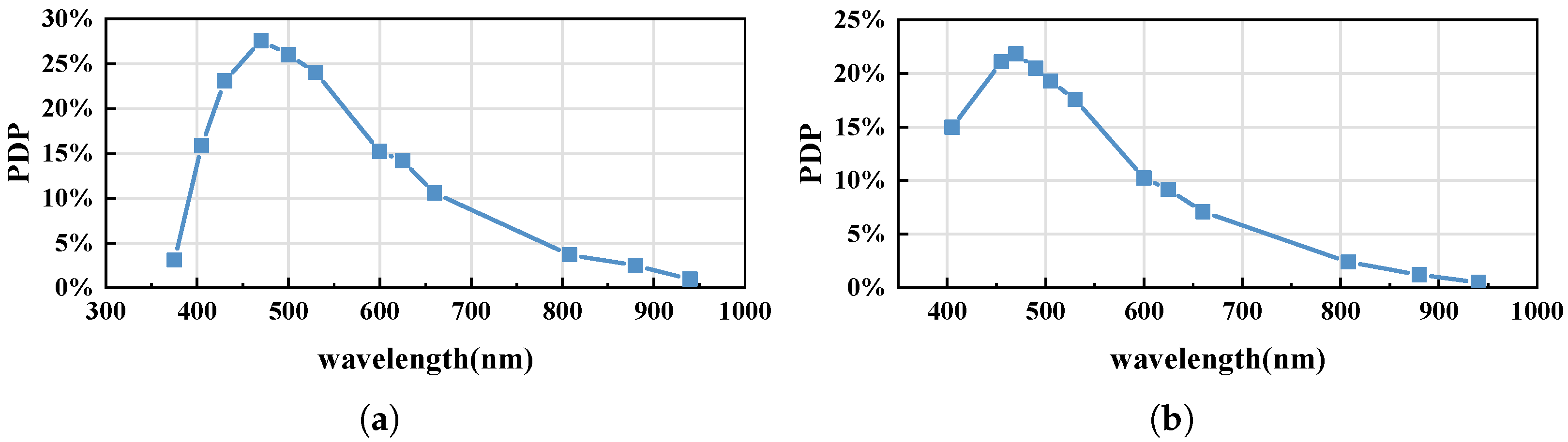
Within the wavelength range of 400 nm to 760 nm, PDP peaks around the 450 nm wavelength, as shown in
Figure 7. Given that most imaging applications operate within the visible light spectrum, we focus on this range. Free-running chip pixels offer a higher detection probability than gating chips, but the difference is less than 5%, which can be disregarded. Additionally, as demonstrated in
Figure 3, PDP has a negligible impact on the SNR, allowing us to simplify calculations by ignoring differences in detection probability
p.
3.3. Imaging System
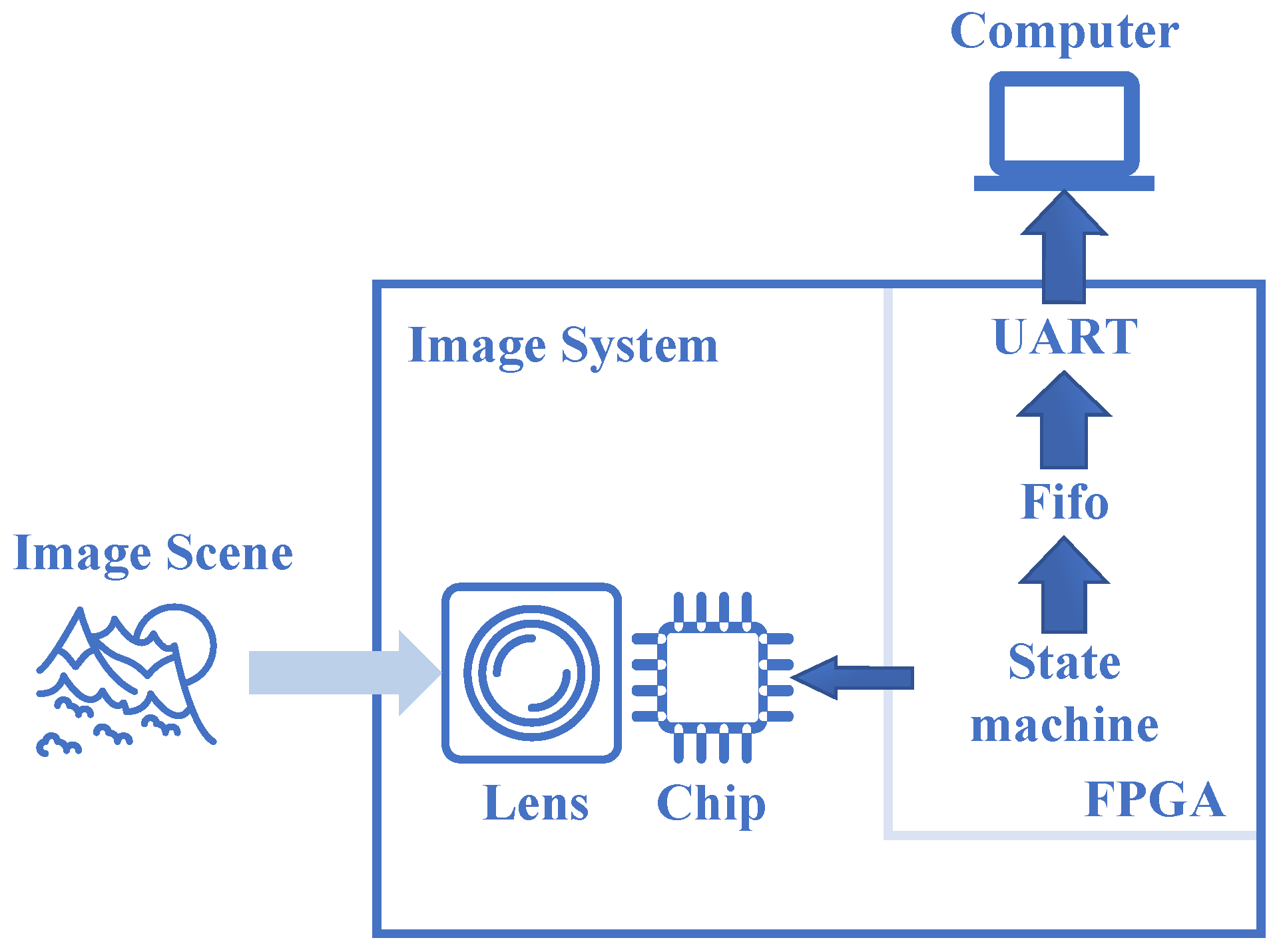
The imaging system comprises a lens, a SPAD imaging chip, and an FPGA system, as shown in
Figure 8. The chip and FPGA are connected through a PCB, which also supplies power. Data from the chip are transmitted to the FPGA, which sends control signals to the chip.
We use the Cyclone IV FPGA series designed by Altera, specifically the EP4CE15F17C8 model, which is responsible for timing control and data transfer. The FPGA’s internal control system includes several modules, such as the PLL module, state machine, asynchronous FIFO, and UART data readout module.
Figure 9a showcases the experimental imaging system, while
Figure 9b presents pictures of the gating chip (upper image) and free-running chip (lower image). The chip is placed on a turntable with a 35 mm camera lens for line scan imaging. Due to the scanning method, slight discrepancies may appear in the captured images.
5. Conclusions
SPAD sensors show great promise as image sensors due to their sensitivity at the single-photon level and in high-dynamic ranges. In SPAD imaging, photon detection is crucial. The quenching mode not only affects the photon-detection capability and power consumption but also influences the imaging SNR and dynamic range. In this study, we proposed a theoretical model for SPAD imaging, focusing on the impact of two imaging modes, the free-running and gating modes, on imaging performance.
Firstly, we derived theoretical models for the free-running and gating imaging modes based on the Poisson distribution theory of incident photons. These models reveal the nonlinear response characteristics and high-dynamic range features of SPAD imaging. Additionally, we derived and validated theoretical formulas for noise and the SNR.
Secondly, we designed and fabricated two SPAD imaging chips using 180 nm CMOS technology, equipped with free-running and gating imaging modes. A rotating imaging system was built to achieve imaging with a equivalent line array scale.
Thirdly, we conducted a comprehensive evaluation and analysis of image quality. Using mapping methods, we compared the two imaging modes under various light-intensity conditions. Experimental results validated the theoretical model and revealed that the free-running mode exhibits a higher saturation limit and is suitable for outdoor environments with high light intensity. In contrast, the gating mode demonstrates superior linearity and low noise characteristics, making it ideal for indoor imaging.
This study provides a solid foundation for a deeper understanding of the working principles and characteristics of SPAD image sensors. Furthermore, it offers theoretical guidance for optimizing and improving SPAD imaging in various academic and practical applications.