Infrared Image Enhancement Based on Adaptive Guided Filter and Global–Local Mapping

Abstract

Infrared image enhancement technology plays a crucial role in improving image quality, addressing issues like low contrast, lack of sharpness, and poor visual effects within the original images. However, existing decomposition-based algorithms struggle with balancing detail enhancement, noise suppression, and utilizing global and local information effectively. This paper proposes an innovative method for enhancing details in infrared images using adaptive guided filtering and global–local mapping. Initially, the original image is decomposed into its base layer and detail layer through the adaptive guided filter and difference of the Gaussian filter. Subsequently, the detail layer undergoes enhancement using a detail gain factor. Finally, the base layer and enhanced detail layer are merged and remapped to a lower gray level. Experimental results demonstrate significant improvements in global and local contrast, as well as sharpness, with an average gradient enhancement of nearly 3% across various scenes.

1. Introduction

The new generation of infrared (IR) imaging systems has made significant advancements, offering high resolution, dynamic range, and real-time capabilities. However, there are still various factors that impact original infrared images, including the low-pass effect by the point spread function of the optical lens, atmospheric interference, stray radiation, and air turbulence. As a result, these images exhibit poor uniformity, low contrast, weak signal strength, low sharpness, and suboptimal visual effects. To address these challenges, infrared imaging systems employ high-performance analog-to-digital converters for high dynamic range (HDR) image acquisition. Nevertheless, a disparity exists between the grayscale resolution perceivable by the human eye and standard monitors compared with the bit width of HDR infrared images. Therefore, it becomes essential to apply corrective post-processing steps such as contrast enhancement and detail enhancement, so as to enhance the visual quality such that it aligns more closely with human perception standards.

The existing literature on HDR infrared image enhancement methods can be broadly classified into three categories: mapping-based methods, decomposition-based methods, and gradient domain methods [1]. Mapping-based enhancement methods usually exhibit limited detail enhancement capabilities and are susceptible to amplifying local noise [2,3,4,5]. On the other hand, due to the straightforward principles, low computational complexity, and ease of hardware implementation, methods such as contrast limited adaptive histogram equalization (CLAHE) and plateau histogram equalization (PHE) remain prevalent in the latest generation of various infrared imaging systems. Gradient domain enhancement methods can mitigate halo artifacts and gradient reversal issues. In practice, compared with decomposition-based methods, they generally involve high complexity, exhibit poor noise reduction effects, and offer inferior detail enhancement [6,7,8].

With the advent of high-performance edge-preserving filters [9,10,11], decomposition-based enhancement methods have emerged as the predominant approach for infrared image enhancement over the past decade. Zuo et al. proposed an infrared image display and detail enhancement based on a bilateral filter (BF&DDE) [12]. This method employs the Gaussian filter to mitigate gradient artifacts caused by the bilateral filter, thus significantly improving detail enhancement capabilities. However, the high computational costs pose a significant challenge to real-time processing. Liu et al. introduced a detail enhancement method for infrared images based on a guided image filter (GF&DDE) [13]. It employs a guided filter to obtain enhanced images, resulting in a significant improvement in computational efficiency. Chen et al. proposed a real-time infrared image enhancement method based on a fast guided filter and plateau histogram equalization (FGF&PE) [14]. It strikes a good balance between detail enhancement and noise reduction while maintaining the overall grayscale distribution consistent with the original image. Ouyang et al. proposed an infrared image detail enhancement algorithm based on parameter adaptive guided filter (PAGF&IDE) [15]. It could both enhance the scene adaptation ability of detail enhancement methods and reduce noise levels while enhancing image detail information. Chen et al. proposed an ultra-fast short-wave IR image enhancement method based on the difference of Gaussian (DoG) filter [16]. This effectively highlights image details by sharpening the mask and exhibits a high operating efficiency [17]. However, this method is unsuitable for medium-wave or long-wave IR images with a lower signal-to-noise ratio. Focusing on the characteristics of infrared images such as high dynamic range, low contrast, and inconspicuous details, Zhang et al. proposed an infrared image enhancement method based on the gradient domain guided filter [18]. It incorporates adaptive double plateau histogram equalization and the edge-aware weighting factor to optimize the layer image, resulting in improved overall brightness and enhanced detail.

The decomposition-based enhancement method utilizes filters to decompose images, thereby compressing the dynamic range to improve brightness and global contrast by processing the base layer. Simultaneously, it enhances local details and reduces noise by processing the detail layer. There are three key factors in this method:

• Accurate decomposition of the base and detail layers to avoid artifacts;
• Dynamic range compression: the method should provide excellent dynamic range compression and brightness improvement while maintaining the global contrast;
• Detail layer gain factor: due to the typical blurriness of the edges in infrared images, it is necessary to create detail gain factors to enhance the detail layer and improve the visibility of local details.

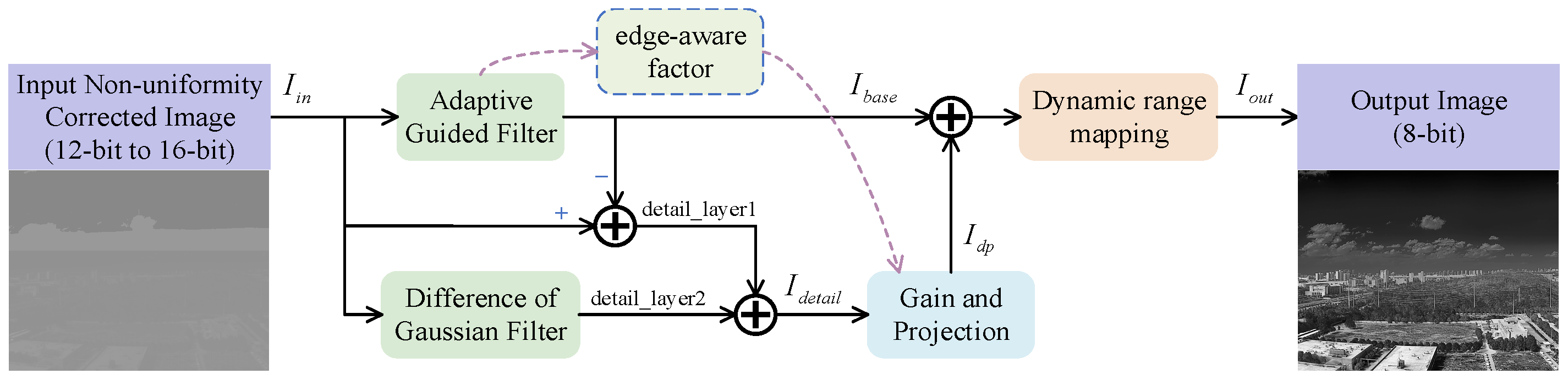
The proposed method in this paper presents a decomposition-based enhancement technique that leverages the adaptive guided filter (AGF) as the decomposition filter to enhance scene adaptability. For detail layer processing, an edge-aware factor acts as the detail gain function to subtly adjust the detail gain, so as to highlight details and reduce noise. It integrates global and local mapping using the CLAHE and Global Adaptation method to compress the dynamic range and enhance both global and local contrast. Experimental evaluations on images from diverse scenes demonstrate significant improvements in dynamic range mapping, noise reduction, detail enhancement, and adaptability.

2. Related Work

2.1. Guided Filter

The guided filter [10] is an explicit local linear filter, which applies a guided image $I$ to filter an input image $p$. Mathematically, the filter output of the pixel $i$ is defined as

$$q_{\mathrm{i}}={\displaystyle {\sum }_{\mathrm{j}}{W}_{\mathrm{ij}}\left(I\right)}{p}_{\mathrm{j}},$$

(1)

where $W_{\mathrm{ij}}$ is the filter kernel function and both $i$ and $j$ denote pixel indices. The filter can be assumed to be a linear model and the output $q$ can be expressed as

$$q_{\mathrm{i}}=a_{\mathrm{k}}{I}_{\mathrm{i}}+b_{\mathrm{k}},\forall i\in {\omega }_{\mathrm{k}},$$

(2)

where ${\omega }_{\mathrm{k}}$ is a window centered on the pixel $k$ with a radius $r$ and $\left(a_{\mathrm{k}},b_{\mathrm{k}}\right)$ is a pair of constant linear coefficients. To approximate the output image $q$ of the input image $p$, an energy function is built as follows using the least squares method:

$$E\left(a_{\mathrm{k}},b_{\mathrm{k}}\right)={\displaystyle {\sum }_{i\in {\omega }_{\mathrm{k}}}\left[{\left(a_{\mathrm{k}}{I}_{\mathrm{i}}+b_{\mathrm{k}}-p_{\mathrm{i}}\right)}^2+\epsilon a_{\mathrm{k}}^2\right]},$$

(3)

where $\epsilon$ is a regularization parameter preventing $a_{\mathrm{k}}$ from reaching an unreasonably large value. The linear coefficients can be approximated by performing a linear regression:

$$\left\{\begin{array}{c}{a}_{\mathrm{k}}={\displaystyle \frac{\frac{1}{\left|\omega \right|}{\displaystyle {\sum }_{i\in {\omega }_{\mathrm{k}}}{I}_{\mathrm{i}}{p}_{\mathrm{i}}-{\mu }_{\mathrm{k}}{\overline{p}}_{\mathrm{k}}}}{{\sigma }_{\mathrm{k}}^2+\epsilon }}\\ b_{\mathrm{k}}={\overline{p}}_{\mathrm{k}}-a_{\mathrm{k}}{\mu }_{\mathrm{k}}\end{array}\right.,$$

(4)

where $\left|\omega \right|$ represents the number of pixels within the window ${\omega }_{\mathrm{k}}$; ${\mu }_{\mathrm{k}}$ and ${\sigma }_{\mathrm{k}}$ denote the expectation and variance of the guidance image $I$ in ${\omega }_{\mathrm{k}}$, respectively; and ${\overline{p}}_{\mathrm{k}}$ is the mean of the input image $p$ in ${\omega }_{\mathrm{k}}$.

The guidance image $I$ is the same as the input image $p$ in most edge-preserving applications. Therefore, the kernel weights $W_{\mathrm{ij}}$ can be recast as:

$$\left\{\begin{array}{c}{a}_{\mathrm{k}}={\displaystyle \frac{{\sigma }_{\mathrm{k}}^2}{{\sigma }_{\mathrm{k}}^2+\epsilon }}\\ b_{\mathrm{k}}=\left(1-a_{\mathrm{k}}\right){\overline{p}}_{\mathrm{k}}\end{array}\right..$$

(5)

Since the pixel $i$ can be covered by $\left|\omega \right|$ windows, $q_i$ calculated from the $\left|\omega \right|$ window is not necessarily identical. By averaging $a_{\mathrm{k}}$ and $b_{\mathrm{k}}$ in the $\left|\omega \right|$ window, Equation (3) can be recast as:

$$q_{\mathrm{i}}={\overline{a}}_{\mathrm{i}}{I}_{\mathrm{i}}+{\overline{b}}_{\mathrm{i}},$$

(6)

where ${\overline{a}}_{\mathrm{i}}={\displaystyle \frac{1}{\left|\omega \right|}}{\displaystyle {\sum }_{i\in {\omega }_{\mathrm{k}}}{a}_{\mathrm{i}}}$ and ${\overline{b}}_{\mathrm{i}}={\displaystyle \frac{1}{\left|\omega \right|}}{\displaystyle {\sum }_{i\in {\omega }_{\mathrm{k}}}{b}_{\mathrm{i}}}$. A small change in pixel intensity in the kernel window will lead to $a_{\mathrm{k}}$ being close to 0 and $b_{\mathrm{k}}$ being close to 1 in terms of a solution to Equation (3). In contrast, an abrupt intensity change in the window will lead to $a_{\mathrm{k}}$ being close to 1 and $b_{\mathrm{k}}$ being close to 0.

2.2. Difference of Gaussian Filter

The DoG filter is commonly employed for detecting edges [19] or blobs [20]. It is mathematically defined as the disparity between two standard Gaussian filters. Specifically, the DoG filter is defined as follows:

$$DoG\left(i,j,{\sigma }_1,{\sigma }_2\right)={\displaystyle \frac{1}{2\pi {\sigma }_1^2}}{e}^{-\left(i^2+j^2\right)/2{\sigma }_1^2}-{\displaystyle \frac{1}{2\pi {\sigma }_2^2}}{e}^{-\left(i^2+j^2\right)/2{\sigma }_2^2},$$

(7)

where $\left(i,j\right)$ shows the image element coordinates and ${\sigma }_1$ and ${\sigma }_2$ are the standard deviations of the Gaussian function. The DoG filter approximates the Laplacian of Gaussian (LoG) filter when ${\sigma }_2/{\sigma }_1=1.6$, which has better edge detection performance [19]. From the signal viewpoint, the Gaussian filter passes the low-frequency signals and cuts off high-frequency information; two low-pass filters with different cutoff frequencies are then combined to form a bandpass filter. The DoG filter extracts the edge feature information that characterizes the details in this feature band, as shown in Figure 1.

2.3. Contrast Limited Adaptive Histogram Equalization

To mitigate the intrinsic limitations of the pronounced enhancement feature of the histogram equalization (HE) algorithm, alternative algorithms such as PHE, adaptive histogram equalization (AHE), and CLAHE have been devised. PE has a poor ability to highlight image details, and the platform threshold needs to be adjusted manually. AHE is prone to block effects and will amplify local noise. CLAHE can effectively improve the local contrast of the image and enhance the ability to highlight details. For an infrared image with $L$ gray levels, the histogram can be expressed as

$$H\left(l\right)=n_l,l=0,1,\cdots ,L-1,L,$$

(8)

where $n_l$ represents the number of pixels with gray level $L$ in the image. The dynamic range of the image enhanced by the HE algorithm is $R$ (256 for an 8-bit image). Therefore, the enhancement result for the gray level $l$ is

$$y_l=T\left(l\right)={\displaystyle \frac{R-1}{N}}{\displaystyle \sum _{k=0}^{l}H\left(k\right)},$$

(9)

where $T\left(l\right)$ is the mapping function that maps the gray level $l$ of the input image into $y_l$ of the output image and $N$ is the total number of image pixels.

The HE algorithm demonstrates an exaggerated amplification of high histogram values. Due to the occupation of a broad grayscale range, it is prone to excessive enhancement of infrared images. This amplification leads to heightened noise in uniform regions and impedes the realization of the desired enhancement ratio for gray levels corresponding to pixels in detailed regions. In contrast, the CLAHE algorithm effectively addresses this issue by partitioning the image into a grid of non-overlapping rectangular sub-blocks and performing HE within each sub-block. To prevent over-enhancement, the sub-histograms are adjusted by clipping and redistributing, thereby avoiding excessive enhancement in uniform areas while achieving superior contrast enhancement in detailed regions. Pixels that exceed the clipping threshold are reassigned to appropriate regions through an iterative adjustment process. The clipping threshold is calculated as follows:

$$T_{\mathrm{clip}}={\displaystyle \frac{N_{\mathrm{b}}}{L}}+\alpha \left(N_{\mathrm{b}}-{\displaystyle \frac{N_{\mathrm{b}}}{L}}\right),$$

(10)

where $N_{\mathrm{b}}$ is the number of pixels in each sub-block and $\alpha$ is a clip factor within the range $\left[0,1\right]$. Since each mapping function of the cropped histogram is independent of the others, bilinear interpolation is employed to calculate the values between blocks to eliminate block effects.

3. Proposed Method

In this section, the proposed method is described in detail. First, the original HDR infrared image is decomposed into the base layer and detail layer 1 through adaptive guided filtering. Simultaneously, the DoG filter is applied to further extract detail layer 2 that contains richer high-frequency information. Subsequently, to maintain a balance between detail enhancement and noise suppression, a detail gain function is devised based on the edge-aware weight factor of the adaptive guided filter. This function compresses the dynamic range of the weighted fusion detail layer to effectively enhance and display the detail layer. Finally, the enhanced base layer and detail layer undergo linear fusion, followed by global and local histogram mapping to improve image contrast and visual discrimination. Figure 2 illustrates the workflow of the proposed method.

3.1. Input Image Decomposition

Akin to the conventional decomposition-based approach, an edge-preserving filter is employed for image decomposition in this work. However, the optimal decomposition effect may not always be achieved across all scenes by employing a fixed filtering parameter $\epsilon$. The adaptive adjustment of parameters based on scene information is essential for enhancing the effectiveness of the decomposition. The crux of the adaptive guided filter lies in modifying the value of the parameter $\epsilon$ according to the original image $I_{\mathrm{in}}$. In Equation (5), it is evident that the local variance ${\sigma }_{\mathrm{k}}^2$ and parameter $\epsilon$ are the two variables that affect the filtering effect. Specifically, ${\sigma }_{\mathrm{k}}^2$ is determined by the grayscale of the infrared images, while the parameter $\epsilon$ greatly impacts the quality and processing effect of the detail layer. In the conventional guided filter, the calculation of $a_{\mathrm{k}}$ and $b_{\mathrm{k}}$ requires the determination of variance for each image window (i.e., local variance). The local variance ${\sigma }_{\mathrm{k}}^2$ reflects the image detail edge texture, which can significantly enhance image processing and improve the adaptability of visual masking effects. Here, the variance of each window is computed to acquire $\epsilon$, which indicates the statistical mean of the window variance:

$$\epsilon ={\displaystyle \frac{{\displaystyle \sum N_{\mathrm{n}}}\times {\sigma }_{\mathrm{k}}^2}{{\displaystyle \sum N_{\mathrm{n}}}}},$$

(11)

where $N_{\mathrm{n}}$ represents the number of the local variance ${\sigma }_{\mathrm{k}}^2$ at each level. It is worth noting that this paper only counts the local variance values that account for more than 0.1%, avoiding the influence of local variance outlier values on the value of parameter $\epsilon$. According to Equation (11), images with textured information will yield a greater $\epsilon$ in the statistical distribution of ${\sigma }_{\mathrm{k}}^2$. Conversely, for images with sparse details and texture, a lower ε is obtained adaptively to accommodate different scenes.

In this work, the original HDR infrared image $I_{\mathrm{in}}$ is decomposed into the base layer $I_{\mathrm{base}}$ and detail layer $I_{\mathrm{detail}\text{\_}1}$. The guided image $I$ is identical to $I_{\mathrm{in}}$ during the decomposition process. To obtain more edge information, the DoG filter is used to accurately extract edge features $I_{\mathrm{detail}\text{\_}2}$ from $I_{\mathrm{in}}$, which are then merged with $I_{\mathrm{detail}\text{\_}1}$ to create the final detail layer $I_{\mathrm{detail}}$:

$$I_{\mathrm{detail}}=I_{\mathrm{detail}\text{\_}1}+I_{\mathrm{detail}\text{\_}2}.$$

(12)

Figure 3a depicts the detail layer $I_{\mathrm{detail}\text{\_}1}$ obtained through AGF decomposition. In Figure 3b, the detail layer $I_{\mathrm{detail}}$ generated by superimposing the edge via DoG filtering is shown. Upon examining the image, it is evident that the superimposed detail layer texture is clear.

The edges in an image are defined by high local contrast, and the incorporation of visually distinct edges could further enhance the visual distinctiveness of the corresponding location. As mentioned above, the key parameters of the DoG filter are the standard deviations of the two Gaussian functions (${\sigma }_1$ and ${\sigma }_2$) and the filter window size $win\_size$. Under the condition of ${\sigma }_2/{\sigma }_1=1.6$, the DoG filter approaches the LoG filter, which has the highest response to edge, $edge\_size$, or spot-like targets with the size of $2\sqrt{2}\sigma$. The system of equations to calculate the two standard deviations of the DoG filter is established as follows:

$$\left\{\begin{array}{c}edge\_size=\left(2\sqrt{2}{\sigma }_1+2\sqrt{2}{\sigma }_2\right)/2\\ {\sigma }_2/{\sigma }_1=1.6\end{array}\right..$$

(13)

The edge size $edge\_size$ of infrared images typically ranges from 3 to 8 pixels. To compare the detail extraction performance of different DoG filter parameters, different pairs of $win\_size$ and $edge\_size$ are combined, and the DoG filtering results (extracted edge image) on the same image are shown in Figure 4.

The results in Figure 4 show that the window size of the DoG filter has a significantly greater impact on image sharpness than the standard deviation values, which are determined by the edge size of the image. The filter with a small window size is susceptible to noise, but a large window size will result in a wider edge transition area and cause a negative impact on image quality, so a window size of 7 is kept in the subsequent experiments. The standard deviation setting is influenced by the edge scale, and a setting of 4 works well in most of the proposed applications. As a result, the solution of Equation (13) yields ${\sigma }_1=1.088$ and ${\sigma }_2=1.7$. Multiplying these two standard deviations by $2\sqrt{2}$ gives us 3.077 and 4.923, which closely approximate the edge sizes. Consequently, the explicit array of the DoG filter with a window size of 7 is as follows:

$$G=\left[\begin{array}{rrrrrrr}\hfill -0.0029& \hfill -0.0061& \hfill -0.0090& \hfill -0.0099& \hfill -0.0090& \hfill -0.0061& \hfill -0.0029\\ \hfill -0.0061& \hfill -0.0107& \hfill -0.0088& \hfill -0.0047& \hfill -0.0088& \hfill -0.0107& \hfill -0.0061\\ \hfill -0.0090& \hfill -0.0088& \hfill 0.0168& \hfill 0.0398& \hfill 0.0168& \hfill -0.0088& \hfill -0.0090\\ \hfill -0.0099& \hfill -0.0047& \hfill 0.0398& \hfill 0.0775& \hfill 0.0398& \hfill -0.0047& \hfill -0.0099\\ \hfill -0.0090& \hfill -0.0088& \hfill 0.0168& \hfill 0.0398& \hfill 0.0168& \hfill -0.0088& \hfill -0.0090\\ \hfill -0.0061& \hfill -0.0107& \hfill -0.0088& \hfill -0.0047& \hfill -0.0088& \hfill -0.0107& \hfill -0.0061\\ \hfill -0.0029& \hfill -0.0061& \hfill -0.0090& \hfill -0.0099& \hfill -0.0090& \hfill -0.0061& \hfill -0.0029\end{array}\right].$$

(14)

As shown in Figure 5a, an original HDR infrared image is displayed by the linear mapping (LM) method. Figure 5b depicts a base layer that is obtained after decomposing the original image by the AGF. Figure 5c is the detail layer obtained by AGF and DoG filtering.

3.2. The Sharpening and Noise Reduction of the Detail Layer

The processing of the detail layer is mainly based on the human visual masking effect: the detail gain in smooth areas should be lower to avoid noise amplification; the detail gain in textured areas should be larger to enhance the visibility of the image [12,13,14]. The edge awareness factor $\overline{a}$ in the guided filter is a particularly suitable noise visibility function that can measure the richness of detailed information. In flat areas with small changes in image grayscale, the value of $a_{\mathrm{i}}$ tends to 0, while at detailed edges with large changes in image grayscale, $a_{\mathrm{i}}$ is close to 1, which can protect rich detailed edge information.

Combining with the detail gain factor $\overline{a}$, the calculation of the detail gain on the detail layer is performed by

$$I_{\mathrm{dp}}=\left(g_{\max }\times \overline{a}+g_{\min }\right)\times I_{\mathrm{detail}},$$

(15)

where $I_{\mathrm{dp}}$ represents the gained detail layer and $g_{\max }$ and $g_{\min }$ are the greatest and lowest gain value coefficients of the image, respectively, which represent the gain range of the image. In general, $g_{\min }\le 1$; in order to avoid noise amplification, $g_{\min }$ can be set as 0.2. $g_{\max }$ can be selected as needed, but the value must be greater than $g_{\min }$. A greater $g_{\max }$ allows one to generate more pronounced or even exaggerated details. In the experiments, it has been noticed that a value of $g_{\max }=10$ yields satisfactory results.

Figure 5d shows the results after processing the detail layer $I_{\mathrm{detail}}$ by Equation (15). It can be observed that the details in the detail layer have been significantly enhanced.

3.3. Dynamic Range Mapping

As illustrated in Figure 2, even after superimposing the processed detail and base layer, the image remains with a high dynamic range. It is imperative to employ appropriate mapping methods to compress the dynamic range, enhance detail information, and improve the contrast of each brightness area. As one of the most representative local mapping methods, the key idea of CLAHE is elaborated in Section 2.3. By setting a suitable clipping threshold to redistribute the redundant part of the histogram, over-enhancement is mitigated while highlighting local details and effectively improving contrast within texture detail sub-blocks. As illustrated in Figure 5e, mere CLAHE proves inadequate for addressing display issues encountered in dark and bright areas, with maintaining the overall contrast and brightness within dark areas being particularly challenging.

According to the theory of human visual brightness perception, the brightness area of infrared images can be divided into three brightness areas: under-illuminated, well-illuminated, and over-illuminated areas. It is imperative to independently enhance these different brightness areas, with a particular emphasis on enhancing the under-illuminated area to a greater extent than the well- or over-illuminated areas. In this work, the Global Adaptation method proposed by Hyunchan et al. [21] is used to remap the mapped fused image $I_{\mathrm{fc}}$

$$I_{\mathrm{out}}=255\times {\displaystyle \frac{log\left(I_{\mathrm{fc}}/{\overline{I}}_{\mathrm{fc}}+1\right)}{log\left(I_{\mathrm{fc}\text{\_}\max }/{\overline{I}}_{\mathrm{fc}}+1\right)}},$$

(16)

$${\overline{I}}_{\mathrm{fc}}=exp\left({\displaystyle \frac{1}{M\times N}}{\displaystyle \sum _{x,y}log\left(I_{\mathrm{fc}}+\mathcal{l}\right)}\right),$$

(17)

where $I_{\mathrm{out}}$ is the enhanced output image, ${\overline{I}}_{\mathrm{fc}}$ represents the logarithmic mean of the grayscale of $I_{\mathrm{fc}}$, $I_{\mathrm{fc}\text{\_}\max }$ is the maximum value of $I_{\mathrm{fc}}$, $M\times N$ is the amount of pixels, and $\mathcal{l}$ is a small constant set to avoid overflow when the pixel value is 0. As the log-average gray converges to a great value, the function converges from the shape of the logarithm function to the linear function. Thus, scenes with low log-average gray get more boosted than scenes with great values.

Figure 5f shows the resulting image processed by the proposed method. As evident from the figure, the dynamic range of the original image has been effectively compressed, the overall brightness of the image has been well adjusted, and details from dark to bright areas have been significantly enhanced.

4. Experimental Results and Discussion

To validate the effectiveness and scene adaptability of the proposed method, several comparative experiments are conducted on four real HDR infrared images from different scenes in Figure 6. These images were all captured by a mid-wave infrared camera with a resolution of $1280\times 1024$. The first image represents an indoor setting, whereas the remaining three depict outdoor scenes at varying distances.

The proposed method is qualitatively and quantitatively compared with five other state-of-the-art infrared image enhancement methods, including PE [4], BF&DDE [12], GF&DDE [13], FGF&PE [14], and PAGF&IDE [15]. For a fair comparison, the parameters within each algorithm utilize the default values that are recommended in the original work. All experiments are implemented with MATLAB and run on an Intel i5-9300H and 16 GB RAM personal computer.

4.1. Qualitative Comparison

Figure 7 shows the results of Image 1 processed by different methods. Image 1 is a 12-bit indoor image with an uncomplicated scene and a small temperature difference between the human and background objects. It is suitable for testing the contrast improvement ability and background noise reduction ability of the enhancement algorithm. As shown in Figure 7, the dynamic range compression capabilities of all comparison methods are limited, the brightness of areas other than the human body and chair in the image is insufficient, and the background information is not effectively highlighted. PE lacks the ability to highlight details. BF&DDE exhibits over-enhancement issues and introduces artifacts at edges, as indicated by the yellow arrow. Both GF&DDE and FGF&PE yield similar enhancement effects, which fail to fully capture the detailed texture. In addition, despite the fact that PAGF&IDE demonstrates improved sharpness, it also inevitably amplifies noise. In contrast, the proposed method substantially enhances the brightness and local contrast of the image while preserving global information with clarity, without significant noise amplification.

Image 2 is a 14-bit outdoor image captured under intense sunlight. The scene is intricately composed, showcasing an abundance of meticulously detailed information. As depicted in Figure 8, as a global mapping method, PE exhibits limited efficacy in enhancing contrast and highlighting details. Both BF&DDE and GF&DDE notably enhance image contrast; however, they also introduce noise amplification, resulting in a notably grainy image. Despite some fine edge details remaining blurred, FGF&PE and PAGF&IDE could enhance image details without significant noise amplification. Notably, the proposed method demonstrates substantial advantages in local contrast, image acutance, and noise reduction.

The results of Image 3 processed by different methods are presented in Figure 9. Image 3 is captured during nighttime, characterized by low scene temperature, and the grayscale range of the image is expanded due to the presence of hot sources on the ground. Among all comparison methods, PE obtains the resulting image with the lowest brightness, worst sharpness, and lowest contrast. The presence of invalid grayscales in the original image, characterized by a minimal proportion of pixels, hampers the tone mapping effect as it diminishes the dynamic range during the mapping process. The detail enhancement capability of BF&DDE is significantly better than that of PE, but the edges of the image are not clear enough and the overall visual effect is unnatural. GF&DDE and FGF&PE do not perform as well as BF&DDE in enhancing local tiny details such as leaves and eaves. PAGF&IDE highlights local details but suffers from poor local contrast effects. In contrast, the proposed method outperforms all other methods in terms of contrast, acutance, and overall visual effect.

As shown in Figure 10, Image 4 is a 16-bit image captured under sunny conditions, encompassing both distant and close targets. The image exhibits weak effective signal and low contrast. When employing PE to linearly map the original 16-bit dynamic range to an 8-bit scale, the information is compressed, which results in darker brightness and hampers detailed observation. Amongst the five compared methods, BF&DDE demonstrates superior detail enhancement capabilities. Nevertheless, as indicated by the arrow, it introduces halos along strong edges which adversely affect visual perception. GF&DDE, FGF&PE, and PAGF&IDE exhibit average overall enhancement effects with GF&DDE failing to effectively suppress noise. Both FGF&PE and PAGF&IDE yield darker grayscales overall with less pronounced contrast enhancement compared to BF&DDE. The proposed method excels in global and local contrast enhancements that surpasses all other methods while maintaining minimal graininess in the output images with clear details for easy observation. As a result, it achieves an outstanding visual effect.

4.2. Quantitative Evaluation

The average gradient (AG) [8] and the perception-based image quality evaluator (PIQE) [18,22] is introduced to quantitatively assess the performance of different methods. AG represents the average gradient magnitude across all pixels in the image, which indicates the detail level of an image. A greater AG value corresponds to better contrast and richer detail, which can be mathematically expressed as:

$$AG={\displaystyle \frac{1}{\left(M-1\right)\times \left(N-1\right)}}\times {\displaystyle \sum _{x=1}^{M-1}{\displaystyle \sum _{y=1}^{N-1}\sqrt{\frac{{\left(\frac{\partial I(x,y)}{\partial x}\right)}^2+{\left(\frac{\partial I(x,y)}{\partial y}\right)}^2}{2}}}},$$

(18)

where $M$ and $N$ denote the rows and columns of the image, respectively; $I\left(x,y\right)$ represents the grayscale value at $\left(x,y\right)$; and ${\displaystyle \frac{\partial I\left(x,y\right)}{\partial x}}$ and ${\displaystyle \frac{\partial I\left(x,y\right)}{\partial \mathrm{y}}}$ are the first-order derivatives of the image along the $x$ and $y$ directions, respectively.

PIQE is a reference-free image quality evaluation index based on perceptual features, which utilizes the block structure and noise characteristics of the image to compute its quality score:

$$PIQE={\displaystyle \frac{{\displaystyle \sum _{k=1}^{N_{\mathrm{sa}}}{D}_{\mathrm{sk}}}+C_1}{N_{\mathrm{sa}}+C_1}},$$

(19)

where $D_{\mathrm{sk}}$ is the distortion score of the $k\text{-}\mathrm{th}$ spatially active block, $N_{\mathrm{sa}}$ refers to the number of spatially active blocks within the image, and $C_1$ is a constant used for numerical stability. According to Equation (19), it can be inferred that a lower PIQE indicates better image quality.

Table 1. Results of the average gradient and the perception-based image quality evaluator.

Test Image	Index	PE	BF&DDE	GF&DDE	FGF&PE	PAGF&IDE	Proposed
Image 1	AG	4.816	4.984	3.306	7.588	5.562	9.191
	PIQE	60.884	55.021	63.564	67.448	70.283	54.670
Image 2	AG	24.489	21.451	28.745	24.929	19.356	45.091
	PIQE	34.915	35.835	38.213	32.103	34.438	30.496
Image 3	AG	14.544	9.914	11.499	13.352	12.547	34.563
	PIQE	43.142	48.261	56.488	41.182	43.223	32.914
Image 4	AG	12.918	12.458	14.059	15.348	15.446	40.924
	PIQE	54.687	45.075	53.944	47.052	49.060	47.575

presents the AG and PIQE values of four test images processed by different methods. It is evident that PE, as a global tone mapping method, yields higher overall brightness values but lacks clarity in detail. In terms of AG value, the proposed method achieves the best performance, indicating superior performance in enhancing local contrast and improving image sharpness. Moreover, the proposed method exhibits a lower PIQE value, which further verifies the elevated level of image quality.

All methods are performed 10 times, and the mean values of the running time are shown in

Table 2. Running time comparison of different methods.

Test Image	PE	BF&DDE	GF&DDE	FGF&PE	PAGF&IDE	Proposed
Image 1	0.0290	2.9155	0.5642	0.1307	0.5966	0.2076
Image 2	0.0534	3.3794	0.7610	0.1493	0.5460	0.1983
Image 3	0.0277	2.7369	0.5669	0.1378	0.5975	0.1690
Image 4	0.0285	3.2745	0.6392	0.1425	0.5345	0.1744

. It should be emphasized that the running time of BF&DDE and GF&DDE are much less than the data detailed in the recent literature [12,13] due to a powerful laptop. The running times of the proposed method are reduced compared to most decomposition-based methods, including BF&DDE, GF&DDE, and PAGF&IDE. The average running time of the proposed method is not significantly different from FGF&PE, but it performs better in detail enhancement. In addition, the adaptive guided filter and DoG filter involved in the proposed method can accelerate the operation in parallel, and the dynamic range mapping can also improve the operation efficiency of the method by constructing a lookup table.

4.3. Merits and Limitations

The proposed method achieves stable performances in different scenarios. The proposed method achieves a good balance between detail enhancement and computational cost, when compared with the other methods. Moreover, this architecture can be further accelerated by parallel computation.

However, the proposed method also has some limitations. First, the proposed method is not fast enough to meet the real-time processing requirements (≥25 fps) of images with a $1280\times 1024$ resolution, which have recently become increasingly popular. Therefore, the rapid enhancement for HDR infrared images is a very worthwhile direction for further research. Second, the proposed method cannot preserve the tiny texture details of the original HDR infrared image without generating a halo, gradient reversal, and flat area noise, such that obtaining a clean detail layer is difficult.

5. Conclusions

In light of the inherent characteristics of infrared images, such as high dynamic range, low contrast, and blurred detail information, a method is proposed in this paper that integrates both global and local mapping for enhancing HDR details.

Initially, an adaptive guided filter is used to extract coarse-level detail information, supplemented by the DoG filter for fine-level detail information, thus enhancing high-frequency content. To improve the adaptability across multiple scenes, an adaptive visual mask based on the statistical characteristics of the image variance histogram is constructed. This enables a more accurate generation of the detail gain function for processing the detail layer, thereby effectively suppressing noise and enhancing the visibility of detailed information. Finally, a combination of global and local mapping is used to map the dynamic range of the image. The CLAHE mapping method enhances contrast in local areas while a Global Adaptation method improves overall brightness.

In diverse scenarios, the enhanced images display superior grayscale utilization and substantially improved local contrast and overall brightness, effectively suppressing noise while enhancing detail information. Through both subjective and objective evaluations, the proposed method exhibits significant advantages.