Performance Investigation of Joint LUT and GS Algorithm at the Transceiver for Nonlinear and CD Compensation

Abstract

In order to meet the increasing requirements of speed and distance, an advanced digital signal processing (DSP) algorithm is preferred without changing the system structure in intensity modulation and the direct detection (IM/DD) system. As the transmission distance increases, the power fading induced by dispersion must be mitigated. In addition, linear and nonlinear inter symbol interference (ISI) introduced by bandwidth limitation and device imperfections becomes an obstacle to achieving higher capacity. The Gerchberg–Saxton (GS) algorithm was recently used to compensate for dispersion. In this paper, GS-based pre- and post-compensation schemes in the IM/DD system with nonlinearity were investigated. We investigated and compared the performance of the GS-based pre- and post-compensation algorithm in a 28 GB aud four-level pulse amplitude modulation (PAM-4) transmission over 40 km standard single-mode fiber (SSMF). The bit error rate (BER) achieved a threshold of 3.8 × 10⁻³ using look-up-table (LUT), FFE, and the GS-based pre-compensation algorithm without iterations. Turning to the GS-based post-compensation scheme, 80 iterations are needed. However, the demand for FFE is reduced. The algorithm selection depends on the tolerance of the transmitter or receiver complexity in specific scenarios. The joint LUT and GS-based pre-compensation algorithm may be a preferable approach in scenarios where a low-complexity receiver is desired.

1. Introduction

The intensity modulation and direct detection (IM/DD) system has been widely investigated because of its low cost and low power consumption. Although advanced modulation techniques increase the data rate, four-level pulse amplitude modulation (PAM-4) is preferred as the choice for IM/DD systems [1]. With the increasing demand for capacity, chromatic dispersion (CD)-induced power fading and bandwidth limitation become the main limitation of IM/DD system. In addition, nonlinear inter symbol interference (ISI) is inevitable because of the imperfect characteristic of opto-electrical components. A feedforward equalizer (FFE) is usually used to alleviate linear ISI. As for nonlinear ISI, a look-up-table (LUT) performs better due to its ability to compensate for pattern-dependent distortion.

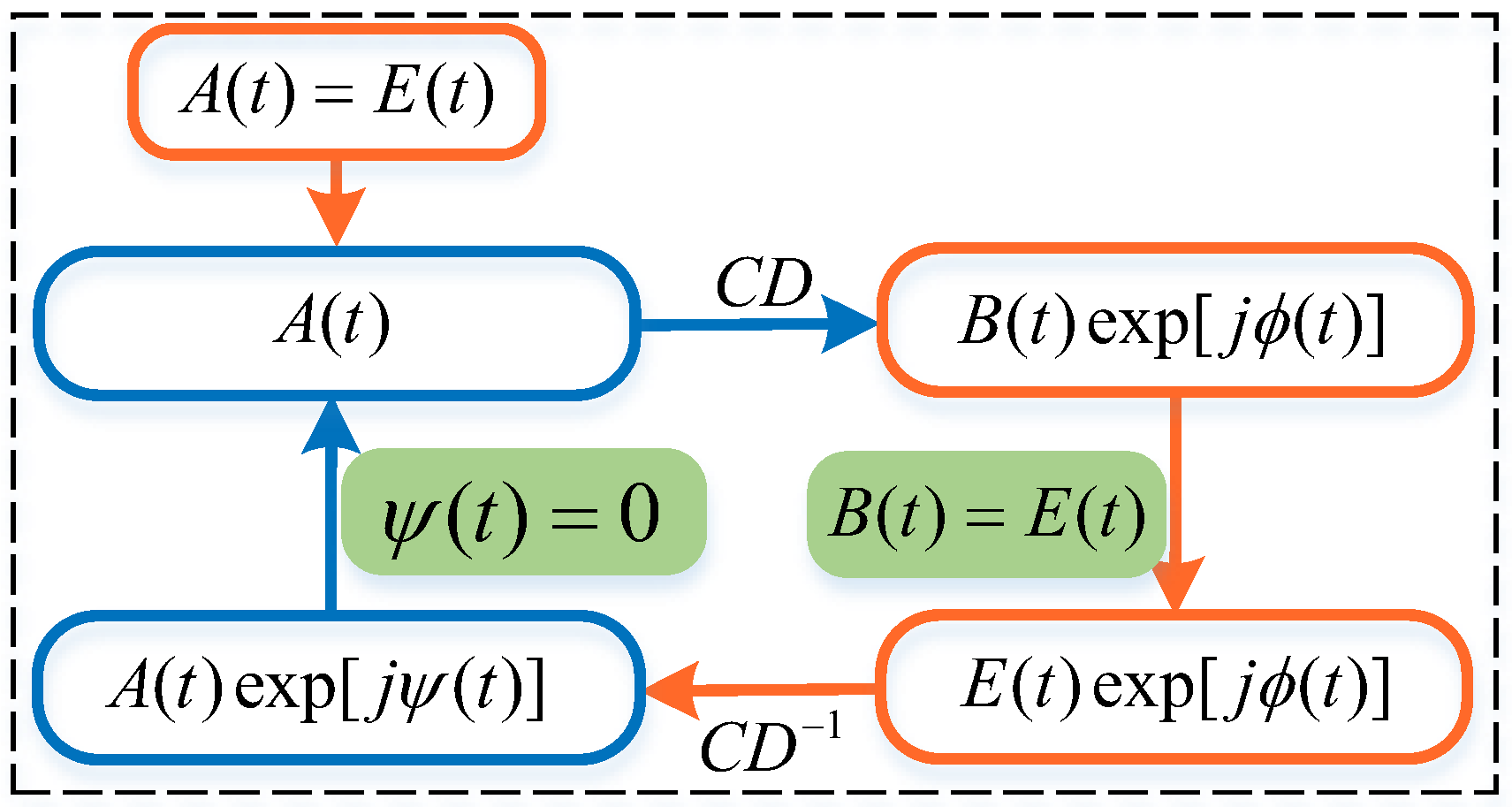
CD compensation without changing the system structure is preferred in an IM/DD system. In the field of optical communications, the Gerchberg–Saxton (GS) algorithm is firstly applied for optical field recovery. In recent years, there has been a growing interest in the field of CD pre-compensation or post-compensation based on the GS algorithm.

As for CD pre-compensation, Abdullah S. Karar proposed an iterative GS-based electrical dispersion compensation algorithm in 2020 [2]. Afterwards, the transform expression of the iterative GS algorithm was deduced in [3], which is also known as GS algorithm based on small signal analysis [4]. In [3], a 28 GBaud PAM-4 signal over 40 km standard single-mode fiber (SSMF) was realized through GS-based pre-electrical dispersion compensation (EDC) at the transmitter and FFE at the receiver. The iterative GS algorithm mitigated the effect of CD, and the FFE with 25 taps compensated for the residual ISI. After that, a series of modified GS algorithms were proposed. The phase at the transmitter and the amplitude at the receiver are regarded as the degrees of freedom, and two error-reversing factors were introduced [5,6]. Afterward, Abdullah S. Karar and Wu X. et al. summarized the theory of a GS-based finite impulse response (FIR) filter for electronic dispersion compensation and correlative experimental demonstration [7,8,9]. In this process, researchers are pursuing better performance and faster convergence of the GS algorithm. However, tens of iterations are needed for the modified GS and GS-based FIR filter. In terms of ease of implementation, the non-iterative version is preferred.

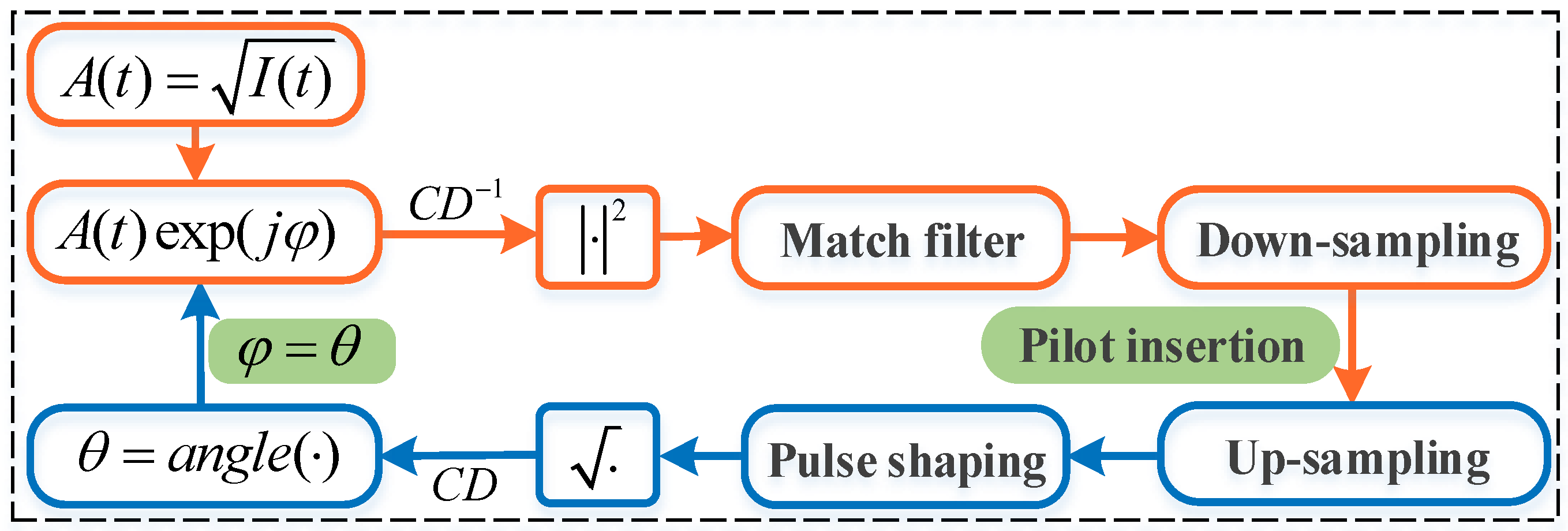
As for CD post-compensation, the GS algorithm is firstly applied for optical field recovery. Beyond that, data-aided iterative algorithm (DIA) and decision-directed DIA (DD-DIA) were proposed to increase convergence speeds and obtain a better global optimum [10]. The error-controlled iterative algorithm (ECIA) was then proposed to digitally linearize the IM/DD transmission systems. A minimum number of iterations required is reduced in comparison with DD-DIA [11]. Furthermore, the multi-constraint iterative algorithm (MCIA) was proposed to accelerate the convergence speed and realize nonlinear-equalization-free detection [12,13]. Furthermore, the adaptive hybrid MCIA improves the sensitivity and the convergence performance [14]. Considering the tradeoff between performance and complexity, DIA was selected as a representative of the GS-based post-compensation algorithm in this paper.

The CD compensation scheme based on GS at the transceiver plays a great role in alleviating power fading caused by CD. However, the current research is confined to the transmitter or the receiver. The performance comparison of the GS algorithm between the transmitter and the receiver has not been investigated. Moreover, investigation of the GS-based CD compensation scheme under nonlinearity is absent. In this paper, a GS-based CD compensation scheme at the transceiver under nonlinear condition was studied and compared. The paper is organized as follows. The principle of the GS-based CD compensation scheme at the transceiver is detailed in Section 2. In Section 3, the simulation setup and the DSP flow are introduced. In Section 4, we demonstrate the simulation results, and the comparison of the joint LUT and GS-based CD compensation scheme between transmitter and receiver is discussed. Finally, we conclude this paper.

2. Principle

The power fading induced by CD can be alleviated by the GS-based algorithm. In this section, the GS-based CD pre-compensation and post-compensation algorithms are illustrated.

2.1. GS-Based CD Pre-Compensation Algorithm at the Transmitter

Figure 1 shows the principle of the iterative GS-based CD pre-compensation algorithm. Firstly, the ideal signal E(t) is assigned to A(t) for initialization at the transmitter. The dispersion transfer module is then executed to simulate the transmission of data in the fiber. At the receiver, the phase information of the data is retained. The amplitude information is replaced by the amplitude of the ideal signal E(t) as a receiver constraint. Next, the updated data are transmitted to the transmitter by the inverse dispersion transfer function. At the transmitter, we only need to obtain the amplitude information of the data and ignore the phase information as a transmitter constraint. At this point, one whole iteration is completed. The next iteration initiates by following the steps above. It is worth mentioning that A(t) usually takes the square root of E(t). After the iteration, the GS algorithm is completed, and A(t) is squared to obtain the transmitted data.

The influence of CD can be expressed as $H_{CD}(f)=\cos (D{\lambda }^2{\omega }^{2}L/4\pi c)$, where $\lambda =1550.12$ nm, $c=3\times {10}^8$ m/s, and $D=17\times {10}^{-6}$ ps/nm/km. To simplify the description, we define $\theta =D{\lambda }^2{\omega }^{2}L/4\pi c$. According to Figure 1, the iterative GS-based CD pre-compensation algorithm process can be described by the followed expression. At the 1st iteration, the transmitted data are the ideal intensity signal without phase information. It passes through the dispersion transmission module and can be described as follows:

$$\left[\begin{array}{c}{B}^1\\ {\varphi }^1\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -2P_0\sin \theta \\ \sin \theta /2P_0& \cos \theta \end{array}\right]\left[\begin{array}{c}E\\ 0\end{array}\right]$$

(1)

Then, the amplitude of $B^1$ is replaced by $E$ as the receiver constraint. The phase of ${\varphi }^1$ is retained. It subsequently passes through the inverse dispersion transmission module and becomes the following:

$$\left[\begin{array}{c}{A}^1\\ {\psi }^1\end{array}\right]=\left[\begin{array}{cc}\cos \theta & 2P_0\sin \theta \\ -\sin \theta /2P_0& \cos \theta \end{array}\right]\left[\begin{array}{c}E\\ {\varphi }^1\end{array}\right]$$

(2)

where $A^1=\left[\cos \theta +{\sin }^2\theta \right]E$ is the desired transmitted signal at the 1st iteration. In the similar way, $A^2=\left[\cos \theta +{\sin }^2\theta \left[\cos \theta +{\sin }^2\theta \right]\right]E$ is the desired transmitted signal at the 2nd iteration. It follows that the desired transmitted signal at the nth iteration is $A^n=\left[\cos \theta +{\sin }^2\theta \left[\cos \theta +{\sin }^2\theta \left[\dots \right]\right]\right]E$. That is to say, the desired transmitted intensity signal can be achieved by multiplying the ideal signal and the function f(n). Through constructing geometric series and further deduction, the f(n) can be expressed:

$$f(n)={\sin }^{2n}\theta +{\displaystyle \frac{1-{\sin }^{2n}\theta }{\cos \theta }}$$

(3)

where $\theta$ is fixed when the transmission distance is confirmed. The only variable in f(n) is iteration number. However, the expression is the non-iterative version, and thus, the complexity is reduced.

The role of the GS-based CD pre-compensation algorithm can further be observed through the power spectrum. As shown by the blue line in the Figure 2, the transmitted signal passes through the dispersion channel and generates the spectrum nulls. The green line in the Figure 2 corresponds to the effect of f(n). It elevates the spectrum on either side of spectrum nulls. At the receiver, the received signal undergoes the combined action of dispersion and f(n). Obviously, the effect of spectrum nulls on the received signal is weakened, as shown by the orange line in the Figure 2.

2.2. GS-Based CD Post-Compensation Algorithm at the Receiver

Figure 3 illustrates the principle of iterative GS-based CD post-compensation algorithm. Firstly, the amplitude information of the received signal is obtained through a square root operation, where I(t) represents the power signal after PD detection. The phase is initialized to linearly increase from 0 to 2π. Secondly, the inverse CD transfer function, which means CD compensation, is applied following square and match filter operation. At the transmitter of the algorithm, the signal is down-sampled to 1 sps, and a pilot sequence is inserted to increase convergence speeds. Then, up-sampling and pulse-shaping operations are applied. After passing through square root and CD transfer function, the phase information is updated. Finally, the received signal is reconstructed for next iteration. As the precondition, the GS-based CD post-compensation algorithm is sensitive to ISI. As a result, it is important to add a pre-distortion process at the transmitter.

3. Simulation Setup

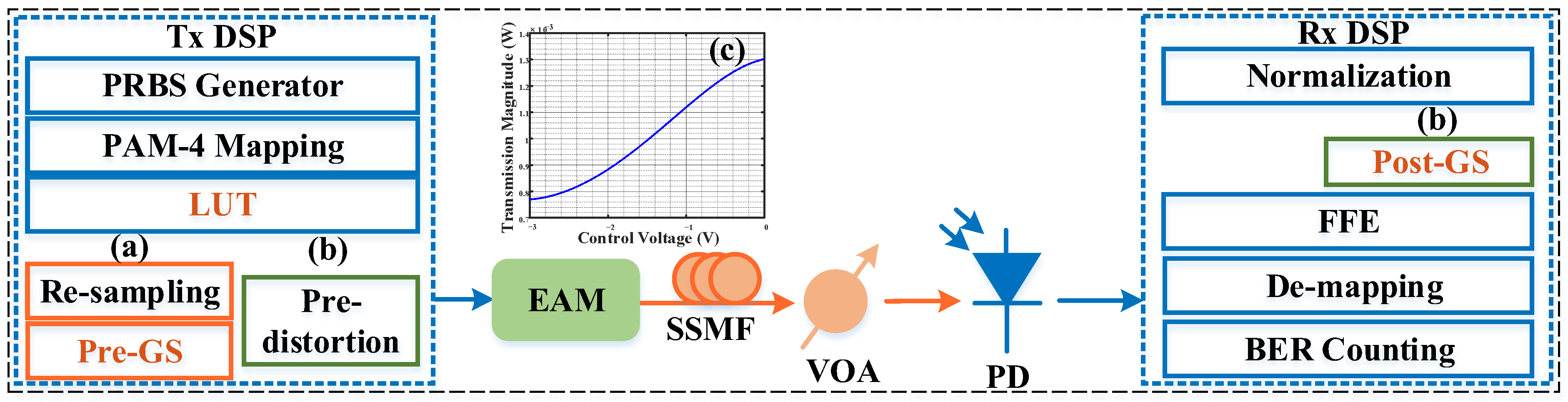
The simulation setup and the DSP flow is shown in Figure 4. Figure 4a presents the DSP scheme of the joint LUT and GS-based pre-compensation. Figure 4b shows the DSP scheme of the joint LUT and GS-based post-compensation. At the transmitter, a pseudo-random binary sequence (PRBS) with a length of 2¹⁶ was generated and used for PAM-4 mapping. The symbol was subsequently processed through the error table. When using the GS-based pre-compensation algorithm, it was resampled to the desired sampling rate and underwent the GS-based pre-compensation algorithm. In the case of using the GS-based post-compensation algorithm, the pre-distortion operation was employed at the transmitter. Then, the electro absorption modulator (EAM) was emulated by the VPI model to investigate the impact of the modulator nonlinearity. The polynomial expressed as ${\left|T(V)\right|}^2=T_0+T_{1}V+T_2{V}^2+T_3{V}^3+\dots$ was used to represent the nonlinear transfer function. Figure 4c shows the transfer curve of the modulator. After modulation by the EAM, the signal was transmitted in 40 km SSMF. The variable optical attenuator (VOA) was used to adjust the received optical power (ROP). Then, the PAM-4 signal was normalized and resampled to 2 sps for FFE. At the receiver, the normalized PAM-4 signal was firstly processed by GS-based post-compensation in the application of Figure 4b. Finally, the PAM-4 signal was de-mapped, and we calculated the bit error rate (BER) with 65,503 symbols.

4. Results and Discussions

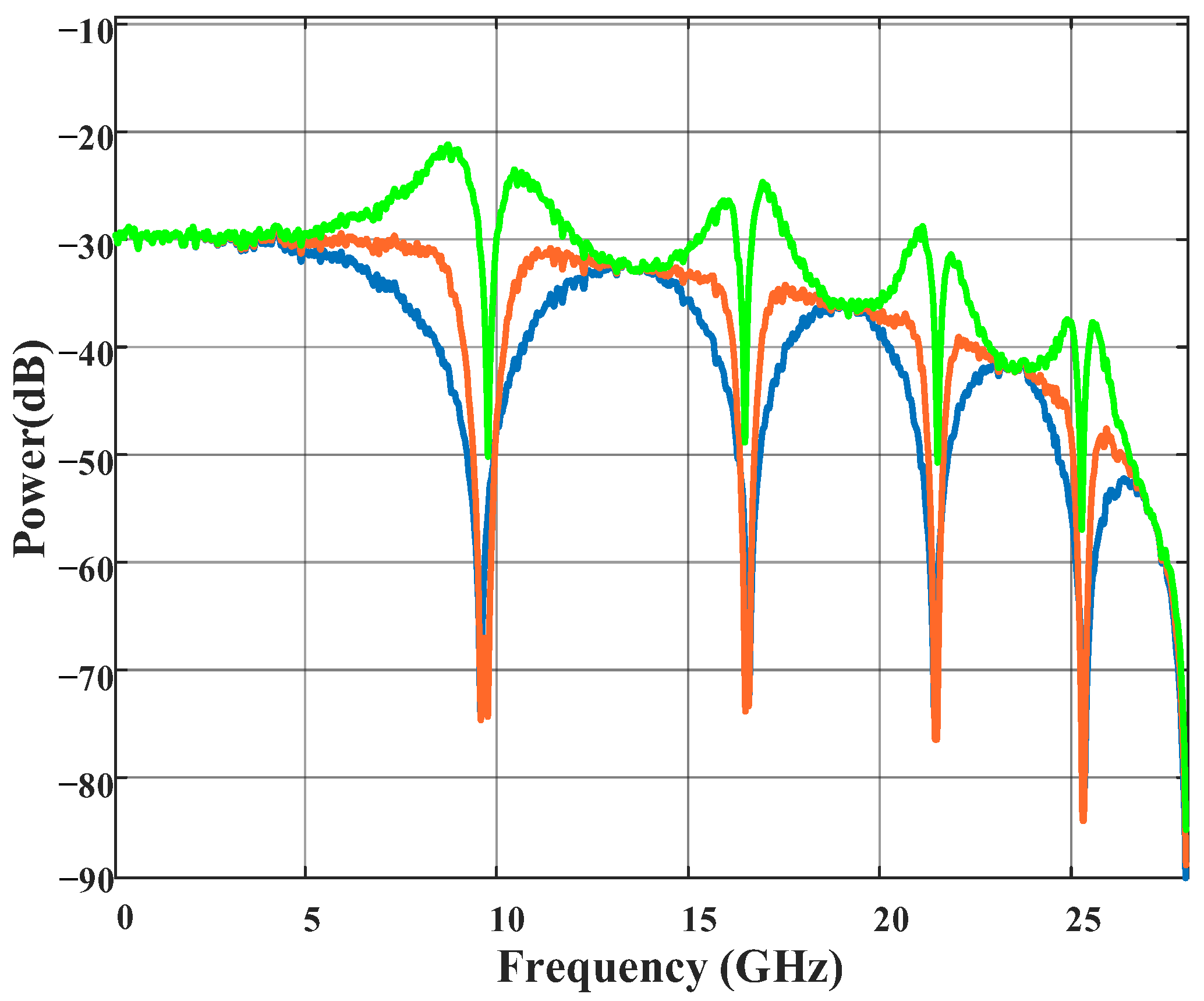
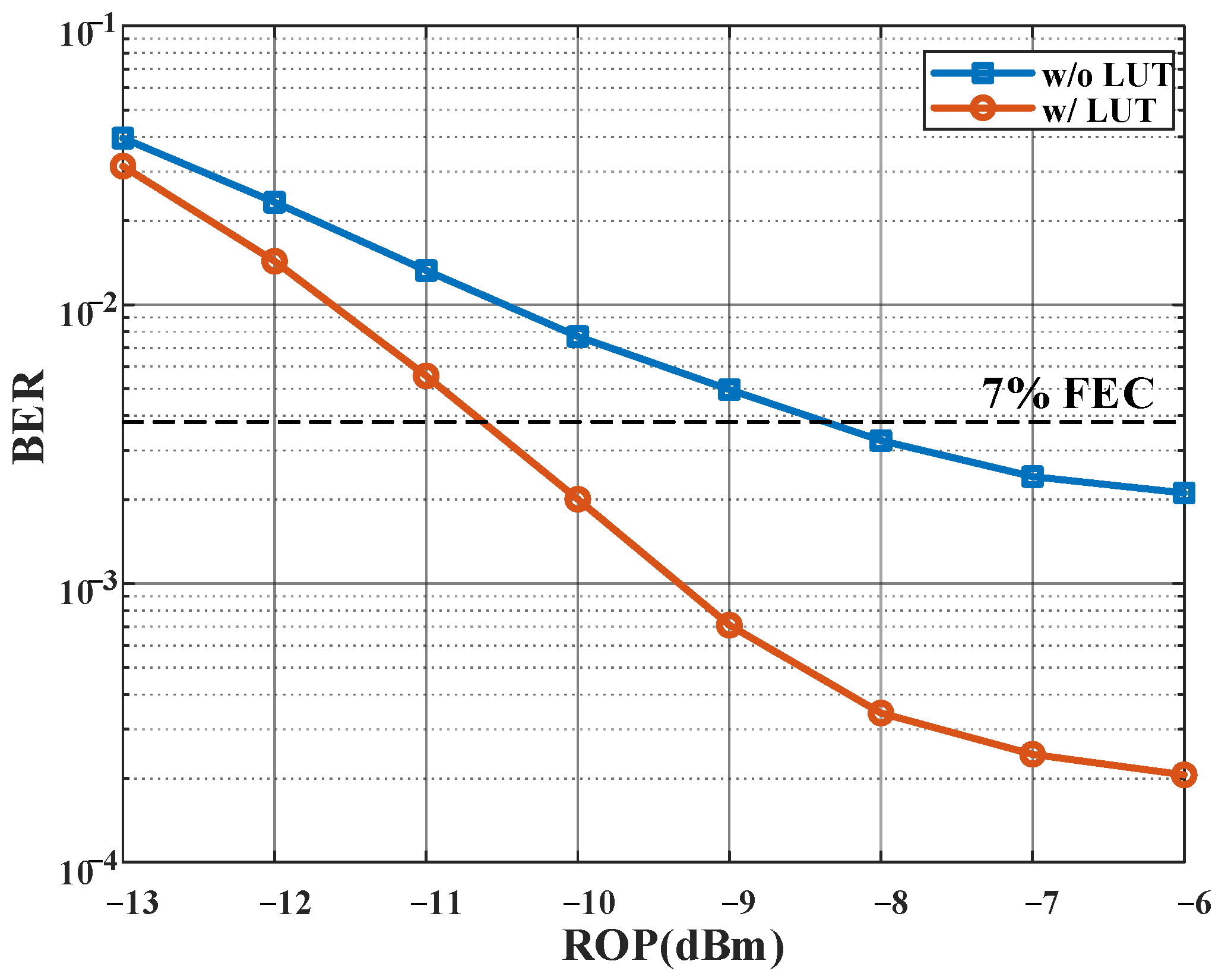
Firstly, we investigated the system performance affected by nonlinearity under the BTB case. As shown in Figure 5, a receiver sensitivity decrease of about 2 dB was observed using the LUT algorithm. That is to say, nonlinearities were present within the system, which affected the system performance. Thus, the prerequisite of nonlinearity was considered in the subsequent simulation.

4.1. Joint LUT and GS-Based CD Pre-Compensation Algorithm at the Transmitter

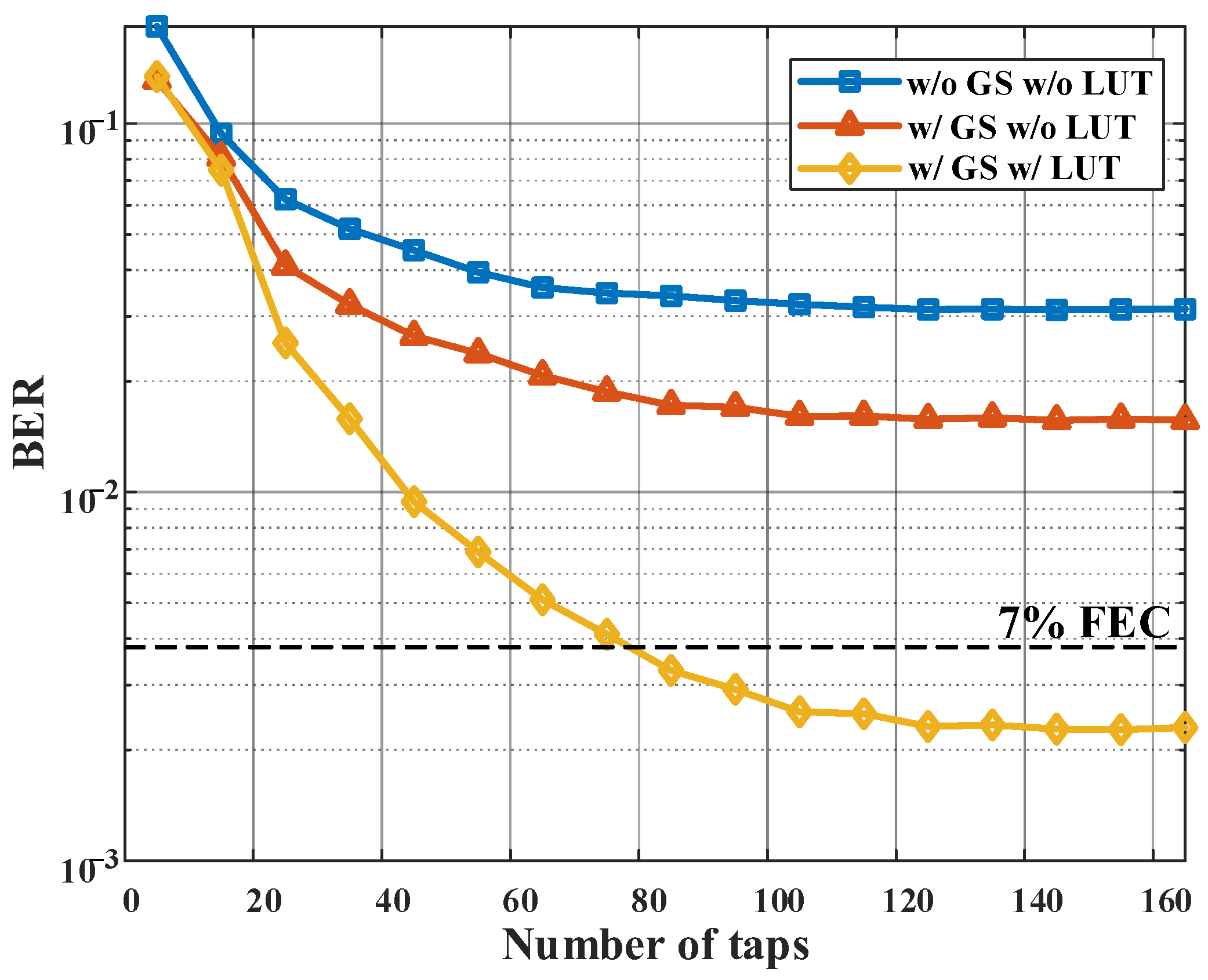
GS shows clear advantages in compensating for CD-induced power fading under 40 km SSMF transmission. As shown in Figure 6, the value of BER was reduced with the help of the GS-based CD pre-compensation algorithm. However, the BER arrived at an error floor when increasing the number of FFE taps. The reason is that FIR-based FFE algorithm is a linear equalizer. It is important to compensate for residual ISI for improving the system performance when there is no nonlinearity or weak nonlinearity. Based on the premise that dispersion and PD work together to produce nonlinear distortion, when the modulator nonlinearity is large, the GS algorithm alone cannot compensate for power fading. After using the LUT algorithm, the system nonlinearity was mostly compensated. The joint LUT and GS-based CD pre-compensation algorithm can reach the threshold of 3.8 × 10⁻³. As shown in Figure 6, the BER decreased gradually when increasing the number of taps. After 125 taps, the decreasing trend of BER was no longer obvious. Thus, we fixed the tap number at 125 in the subsequent simulations in this subsection.

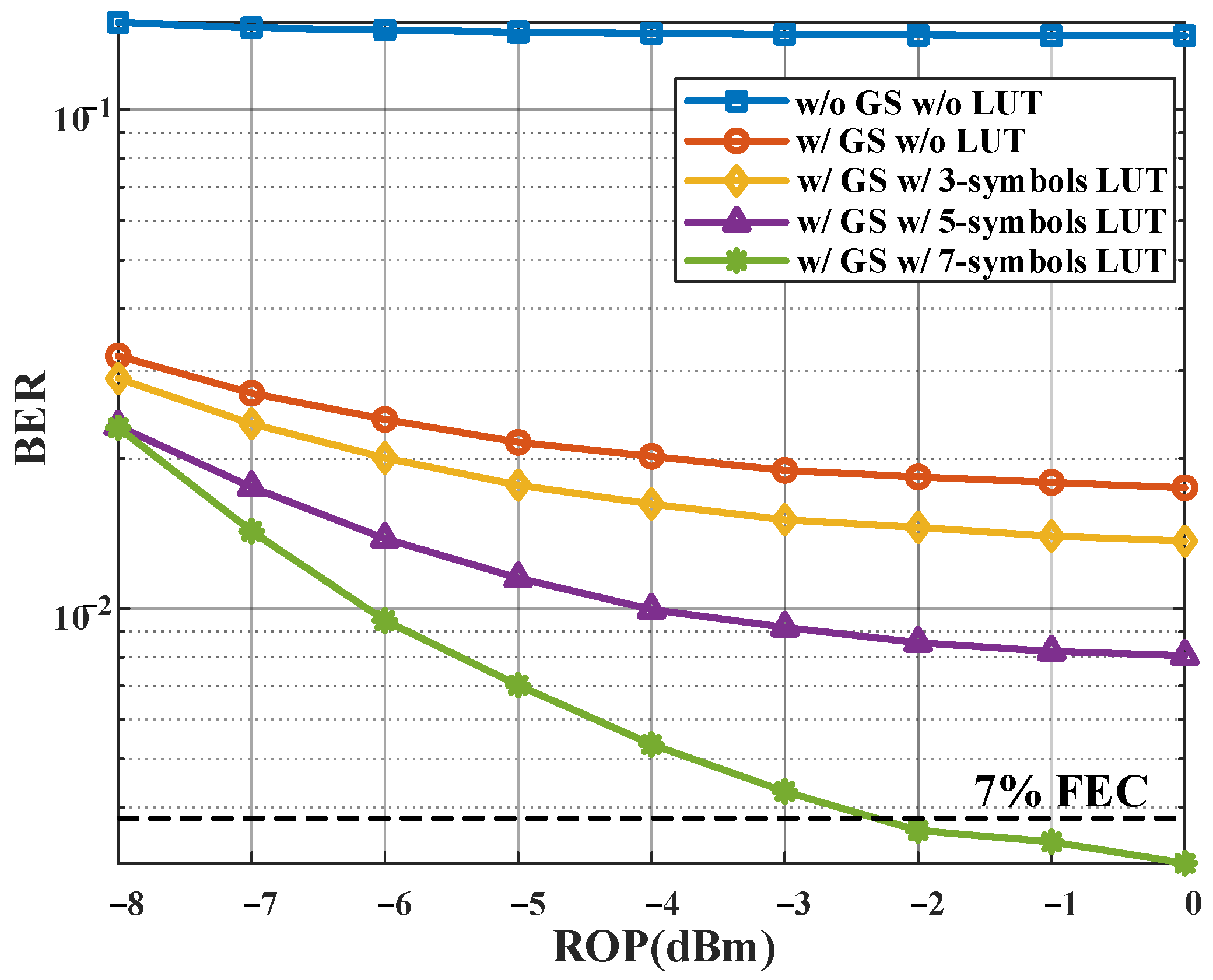
We then investigated the BER versus ROP, as shown in Figure 7. The BER was 3 × 10⁻² when the GS-based CD pre-compensation algorithm was absent. After using the GS-based CD pre-compensation algorithm, the BER dropped to 1.5 × 10⁻². However, the existence of nonlinearity seriously affected the performance of the system. The joint LUT and GS-based CD pre-compensation algorithm showed improved performance. The LUT considering more symbols performed better. The receiver sensitivity arrived at −4 dBm with the help of the 7-symbol LUT and GS-based CD pre-compensation algorithm.

4.2. Joint LUT and GS-Based CD Post-Compensation Algorithm at the Receiver

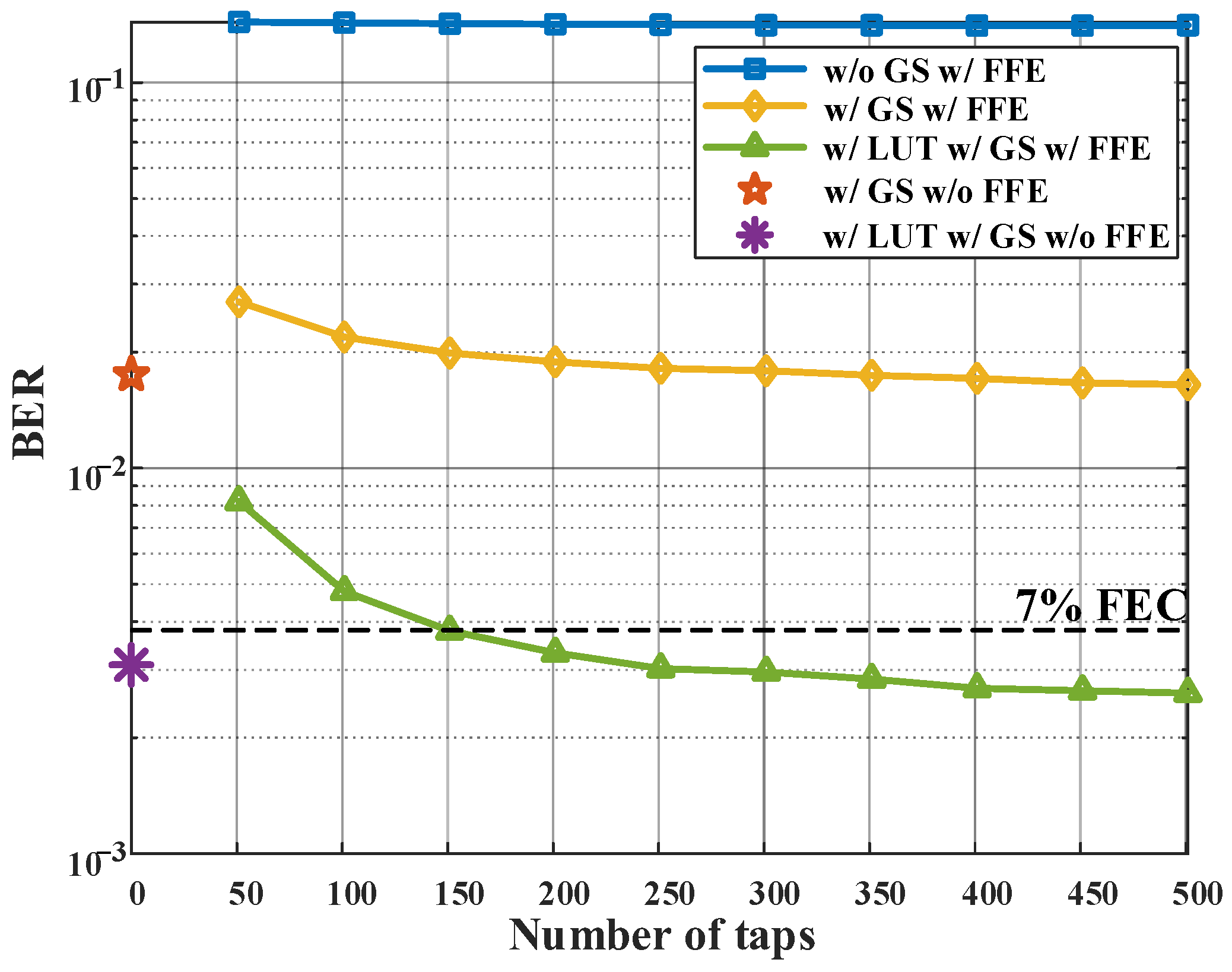
Figure 8 shows the BER of different schemes versus the number of FFE taps at an ROP of 0 dBm. No matter how much the number of taps increases, it is impossible to recover the signal in the absence of the GS-based CD post-compensation algorithm. FFE alone cannot compensate for the nonlinear impairment due to the nonlinearity of the modulator and the interaction of optical fiber dispersion and PD. The GS-based CD post-compensation algorithm with 80 iterations showed great advantages in compensating for fiber dispersion. The BER was greatly reduced. Based on the GS-based CD post-compensation algorithm, the addition of FFE showed little advantage. However, the GS-based CD post-compensation algorithm has no ability to compensate for the nonlinearity of the modulator. In order to alleviate the influence of the nonlinearity of the modulator, an error table considering 7 symbols was generated under the condition of using the GS-based CD post-compensation and FFE algorithm with 501 taps. At the transmitter, the mapped PAM-4 signal was first processed by LUT. As shown in Figure 8, the BER was below the threshold of 3.8 × 10⁻³ when using the joint LUT and GS-based CD post-compensation algorithm. Similarly, the use of FFE provided a slight performance advantage. Thus, we ignored the effect of FFE in the subsequent discussion.

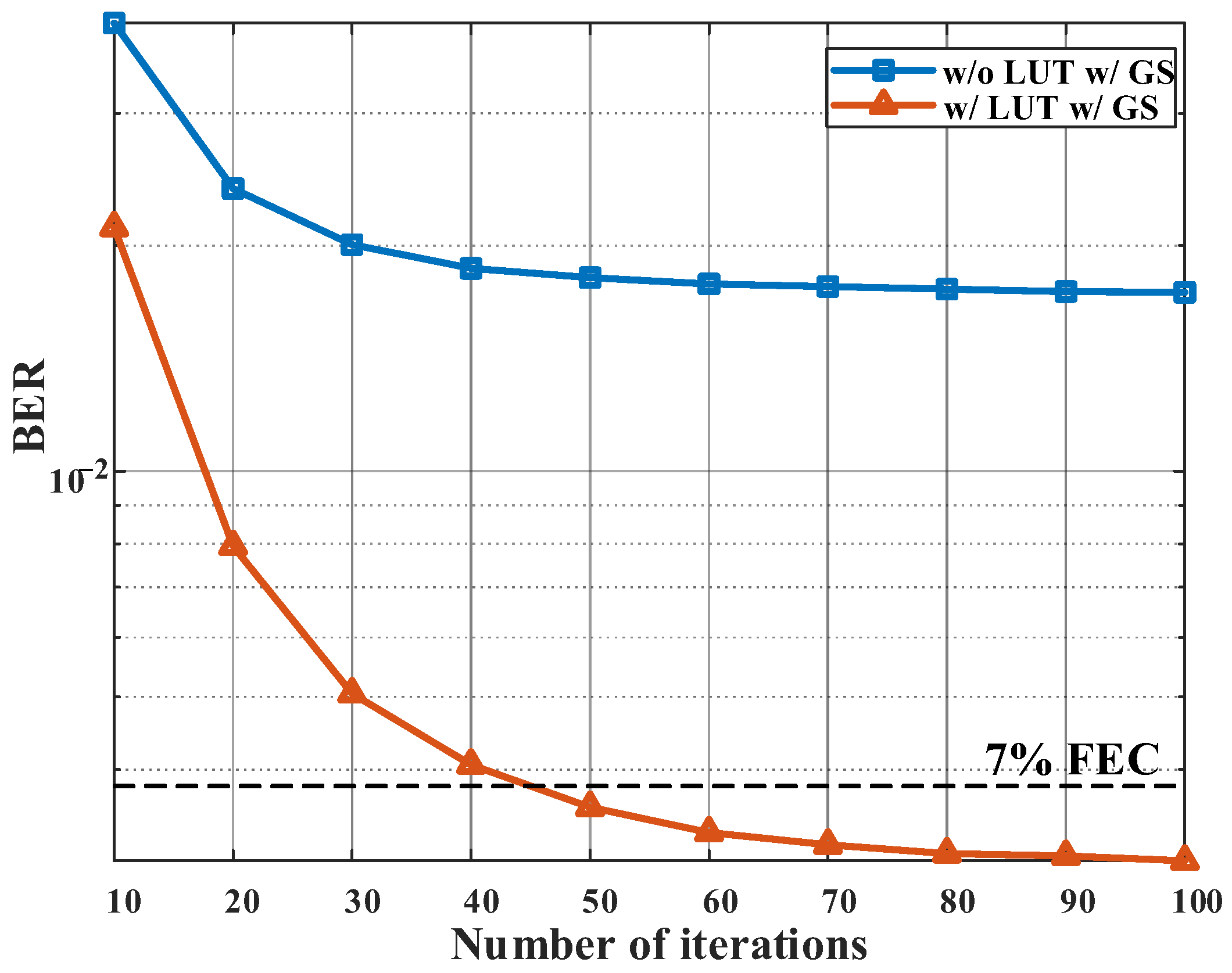
As shown in Figure 9, the effect of the iteration number of the GS-based CD post-compensation algorithm on the BER was further analyzed. The more iterations, the lower the BER. After 80 iterations, the increase in the number of iterations showed a slight improvement in performance. Considering the performance and complexity comprehensively, the number of GS iterations was fixed at 80 in subsequent simulation.

Figure 10 shows the BER versus ROP with different algorithm schemes. The deployment of the GS-based CD post-compensation algorithm brought a great performance improvement from 1.5 × 10⁻¹ to 3 × 10⁻². In the presence of system nonlinearity, the use of LUT is necessary. Furthermore, the more symbols considered in the LUT algorithm, the more obvious the improvement of system performance. At the 1 × 10⁻² threshold, a receiver sensitivity of −4 dBm was achieved by using GS-based CD post-compensation algorithm and 5-symbol LUT. When using the 7-symbol LUT, a 2 dB performance improvement was observed. Meanwhile, a receiver sensitivity of −2 dBm was achieved by using the GS-based CD post-compensation algorithm and 7-symbol LUT at the 3.8 × 10⁻³ threshold.

4.3. Comprision of GS-Based Algorithm at the Transceiver

According to the above analysis, no iteration exists in the GS-based CD pre-compensation scheme at the transmitter. That is to say, the computational complexity is lower than that at the receiver. However, FFE at the receiver is needed to compensate the residual ISI. The number of taps depend on the extent of bandwidth limitation. As for the GS-based CD post-compensation scheme at the receiver, FFE is not indispensable. It reduced the computational complexity to some extent. However, more iterations are needed to guarantee the system performance. Furthermore, the GS-based CD post-compensation algorithm is sensitive to ISI. The ISI induced by band limitation inhibited the effect of the GS-based CD post-compensation algorithm. Therefore, the pre-distortion operation is necessary, which increases the system complexity.

The latency of the whole DSP is mainly accumulated by real multiplications (RMs). Therefore, we computed the number of RMs required in different algorithm to access the real-time processing feasibility. The computational complexity of the pre- and post-compensation algorithm per symbol is shown in

Table 1. Computational Complexity of Pre- and Post-compensation algorithm per Symbol.

	Pre-Compensation	Post-Compensation
GS operation	11 RMs	23 RMs
FFE	250 RMs	0
Pre-distortion	0	14 RMs

. For the pre-compensation algorithm, it required 11 RMs per symbol in the GS algorithm and 250 RMs in FFE. However, the post-compensation algorithm needed 23 RMs per GS operation and 80 iterations at least. The computational complexity of the post-compensation algorithm is much higher than the pre-compensation algorithm.

However, in the GS-based CD pre-compensation algorithm, the algorithm parameter is determined by the channel, which needs to be known in advance. Therefore, it is only applicable to a specific fiber length. In the GS-based CD post-compensation algorithm, the CD estimation function is adaptive and can be suitable for systems of any fiber length. Generally speaking, both schemes have their advantages and disadvantages. The choice depends on the specific situation.

5. Conclusions

The GS-based CD compensation algorithm has been extensively studied in recent years. However, the performance comparison between the GS algorithm and the transmitter and the receiver has not been investigated, and it is lacking in resisting nonlinearity interference. To determine the effect of the GS-based algorithm on CD compensation in the presence of modulator nonlinearity, the IM/DD simulation system was constructed. The system performance of the joint LUT and GS-based CD compensation algorithm was verified under a 40 km SSMF transmission with 28 GBaud PAM-4. To compensate for the nonlinearity, the 7-symbol LUT is indispensable. When using the joint LUT and GS-based CD pre-compensation algorithm at the transmitter, the BER achieved a threshold of 3.8 × 10⁻³ without iterations. However, the FFE with 125 taps is needed. When turning to the joint LUT and GS-based post-compensation scheme, 80 iterations are needed, which means higher system complexity. However, the demand for FFE is reduced. Turning to practical application, the algorithm selection depends on the tolerance of the transmitter or receiver complexity in specific scenarios. The joint LUT and GS-based pre-compensation algorithm may be a preferable approach in scenarios where a low-complexity receiver is desired.