Toward Converged Satellite/Fiber 1550 nm DS-BB84 QKD Networks: Feasibility Analysis and System Requirements
Abstract
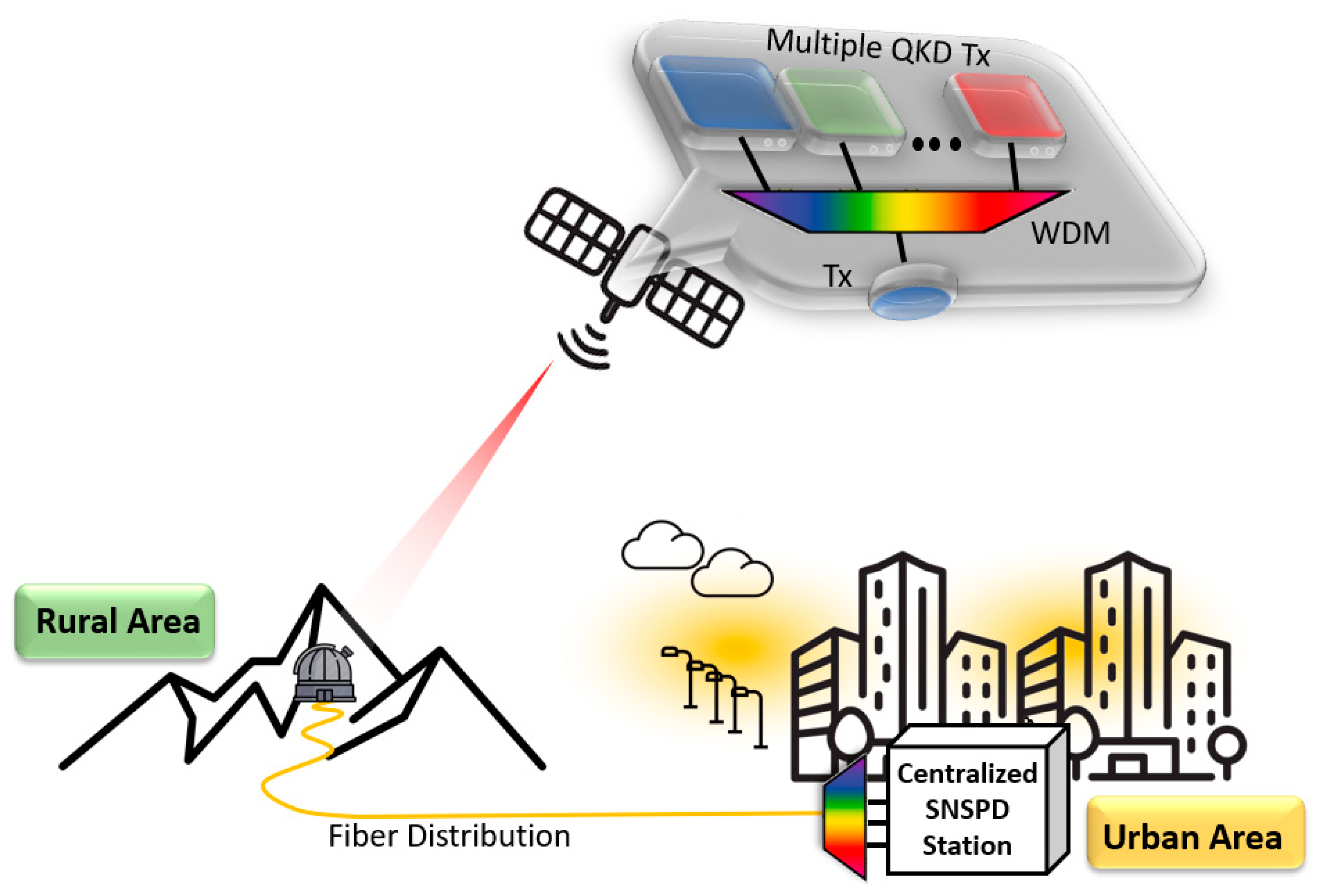
1. Introduction
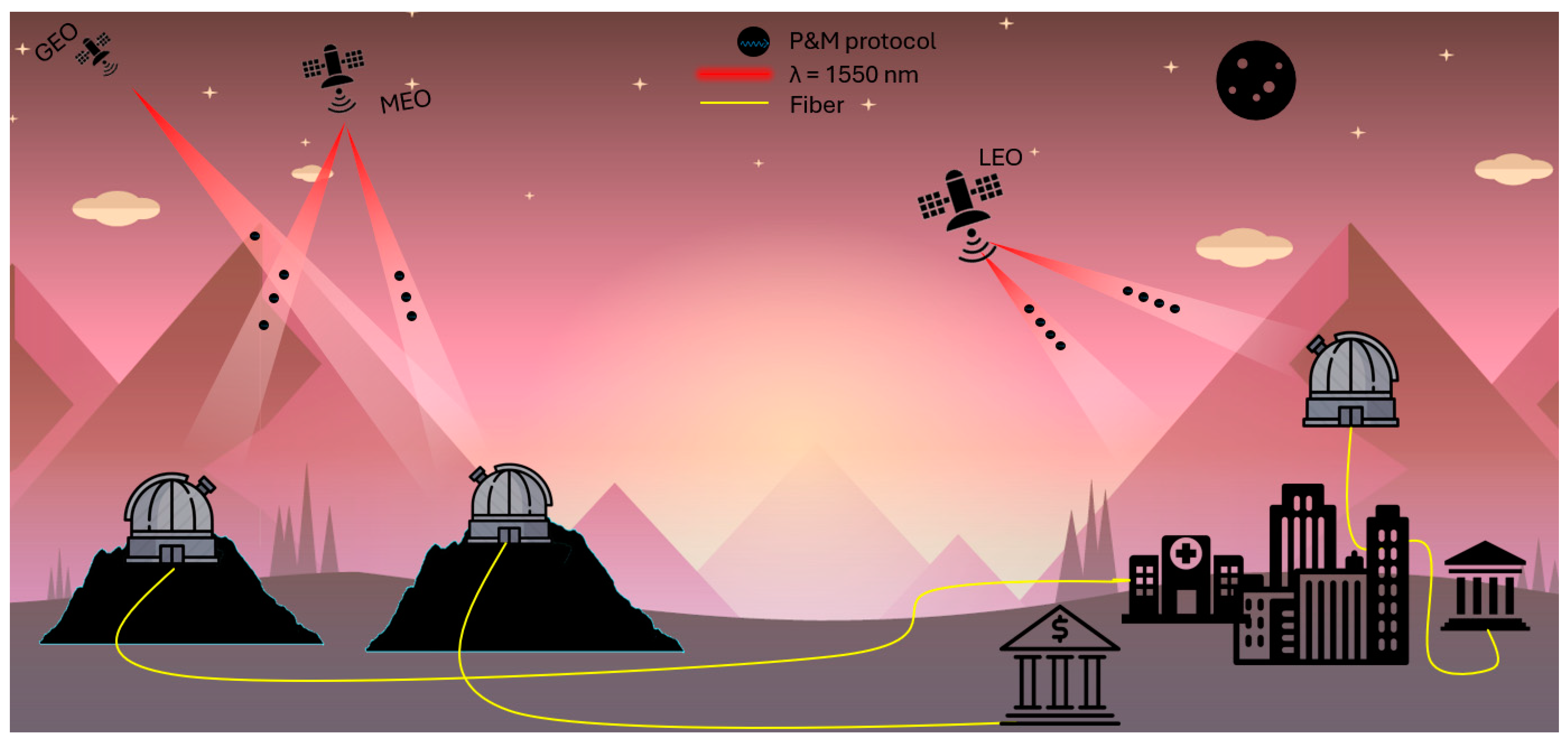
2. System Architecture and Assumptions
2.1. Orbits
2.2. Receiving Terminal
2.3. OGS-to-Detection Station Fiber Distribution
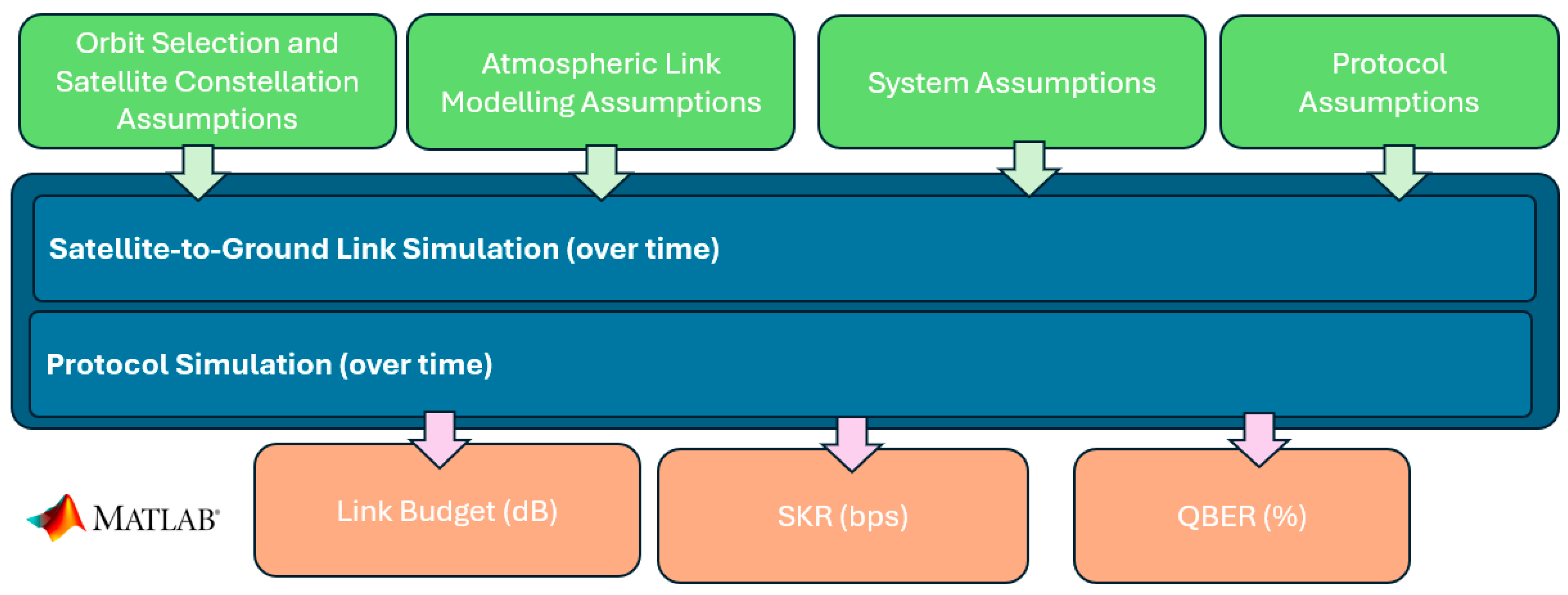
3. Satellite-to-Ground QKD Simulator
3.1. Satellite Orbits
3.2. Atmospheric Link Modeling
3.2.1. Geometrical Loss
3.2.2. Pointing Loss
3.2.3. Atmospheric Transmission
3.2.4. Turbulence
3.2.5. Night-Time Sky Radiance and Urban Background Noise
3.2.6. Fiber Coupling Efficiency
3.3. Protocol Assumptions and Finite Key Size Analysis
4. Simulation Results
4.1. Source Specification/Requirement Analysis
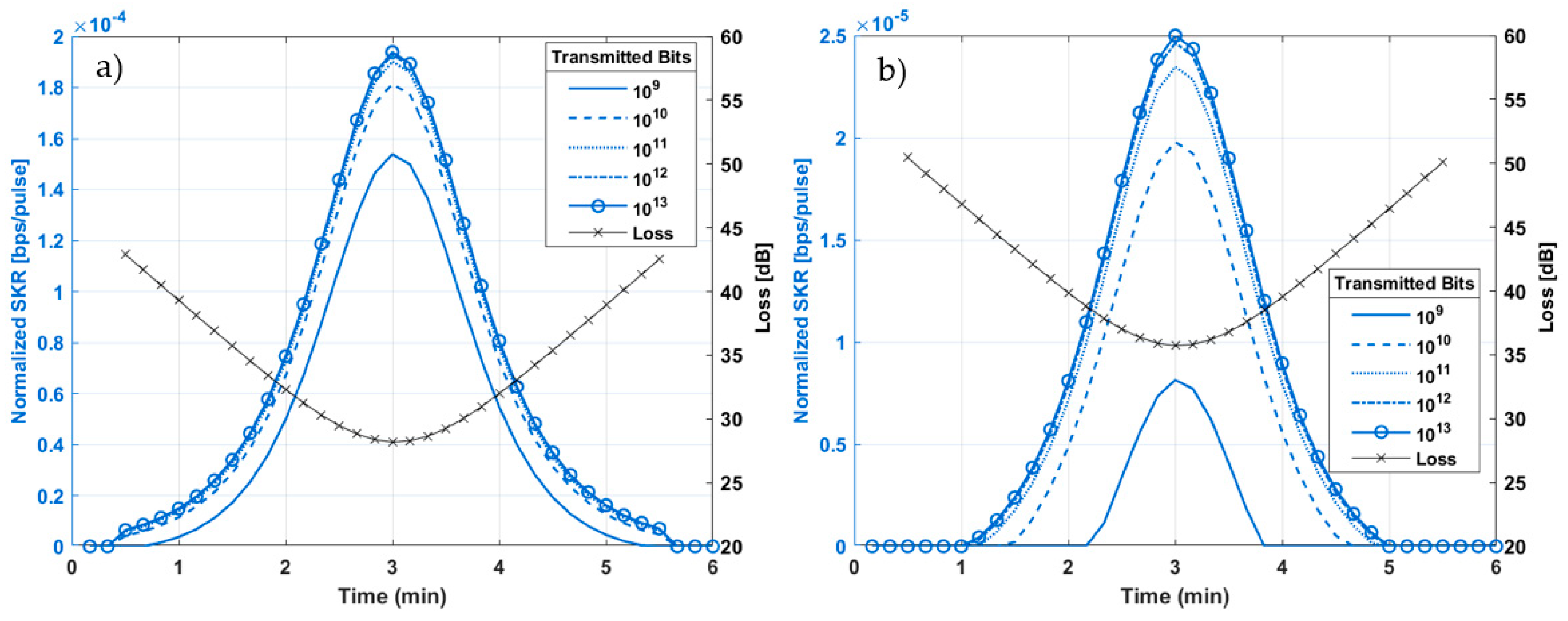
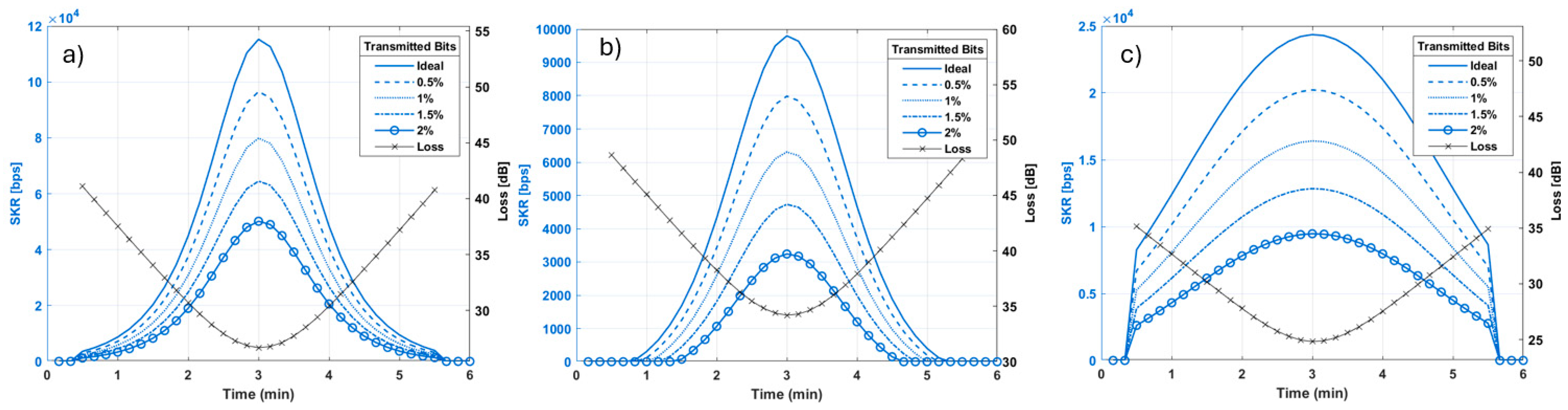
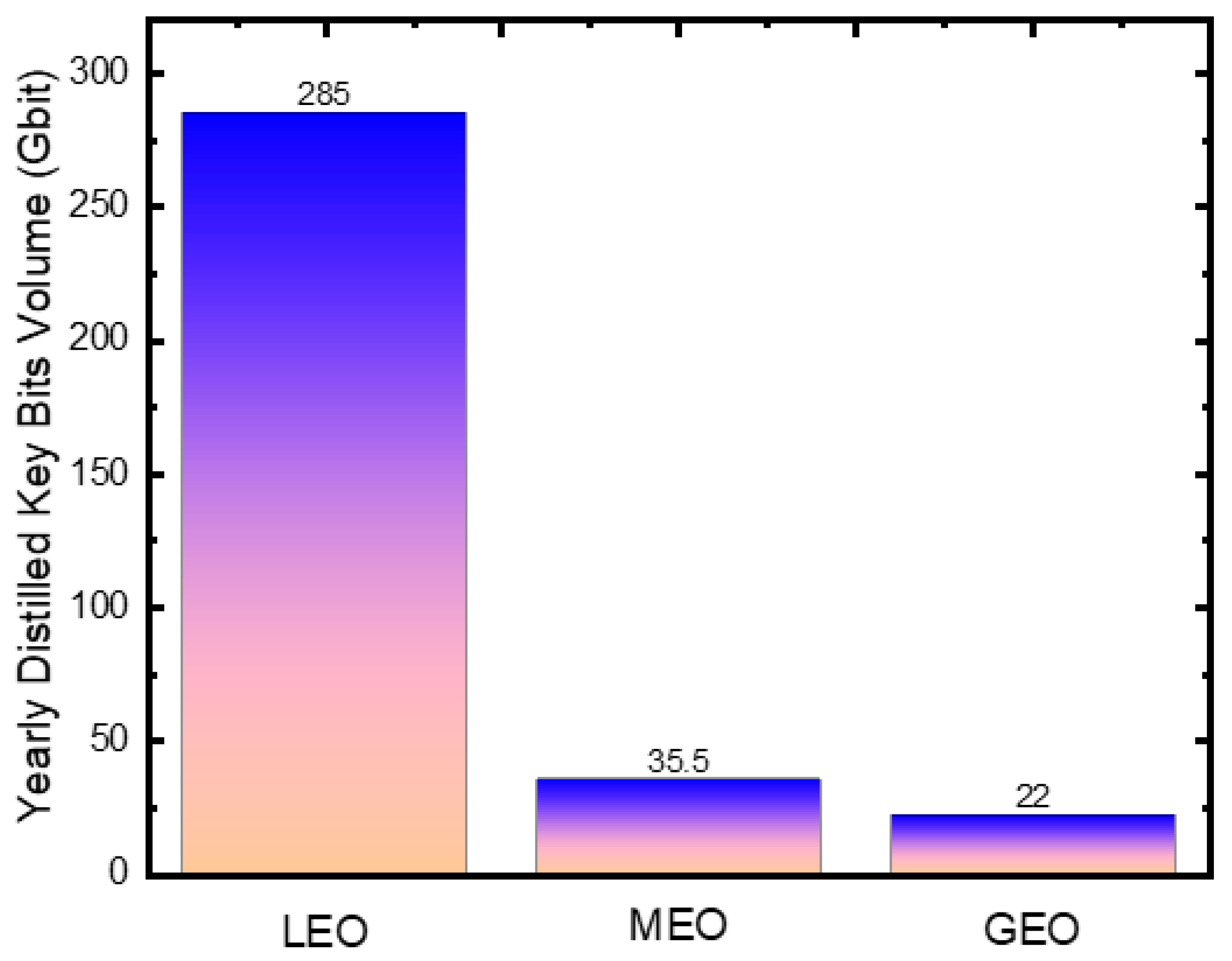
4.1.1. Emission Rate Analysis—LEO
4.1.2. Emission Rate Analysis—MEO
4.1.3. Emission Rate Analysis—GEO
4.2. iQBER Analysis
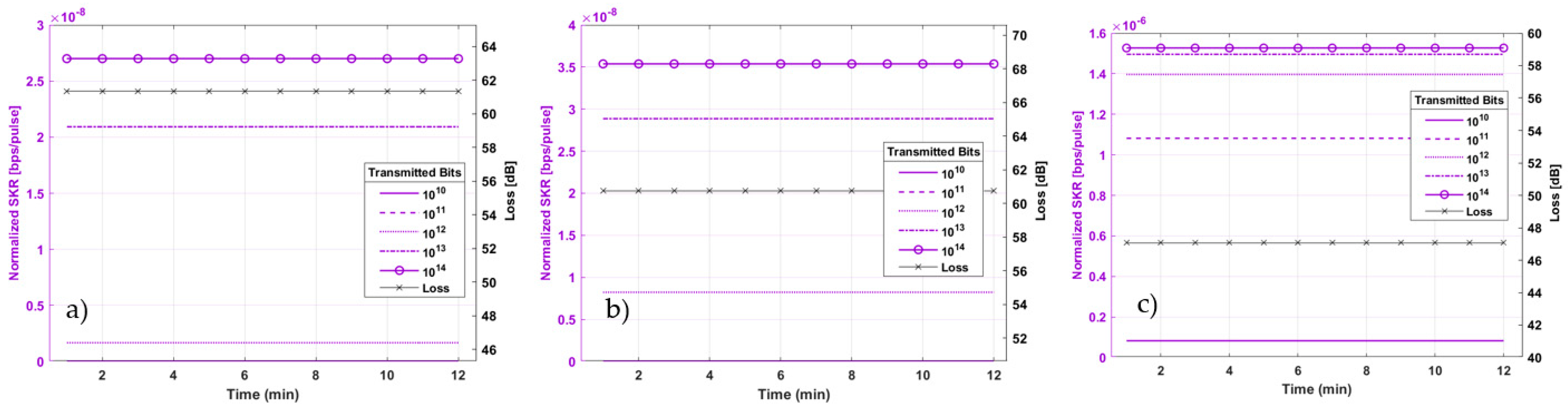
4.2.1. iQBER Analysis—LEO
4.2.2. iQBER Analysis—MEO
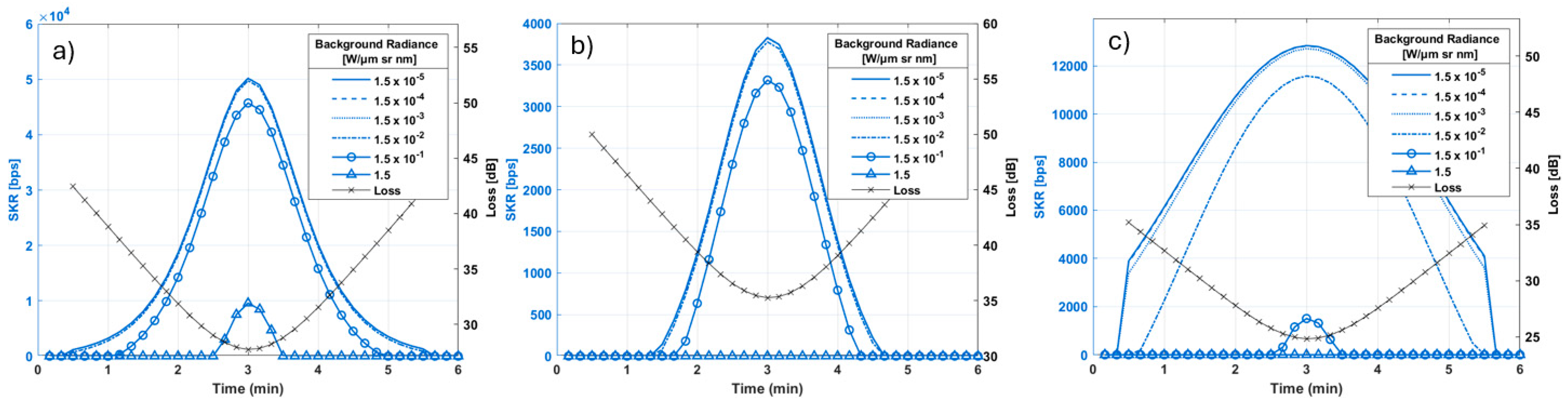
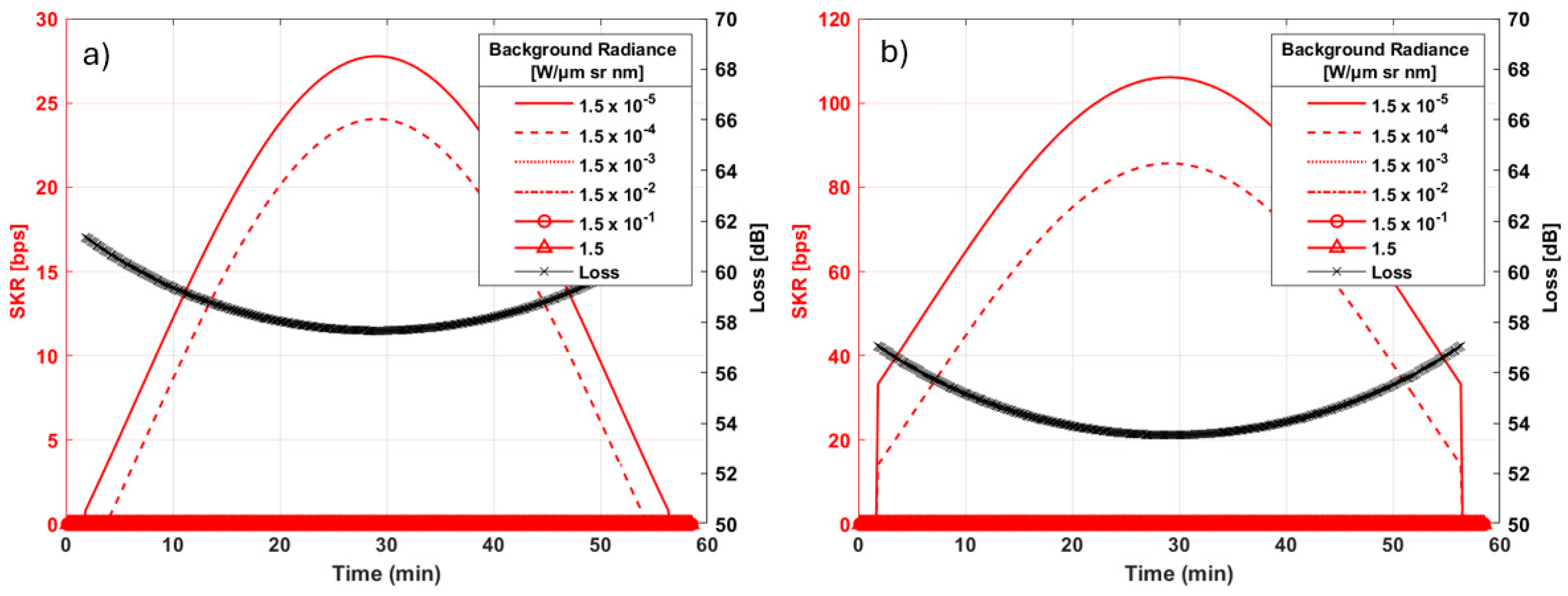
4.3. Noise Tolerance Analysis
4.3.1. Noise Tolerance—LEO
4.3.2. Noise Tolerance—MEO
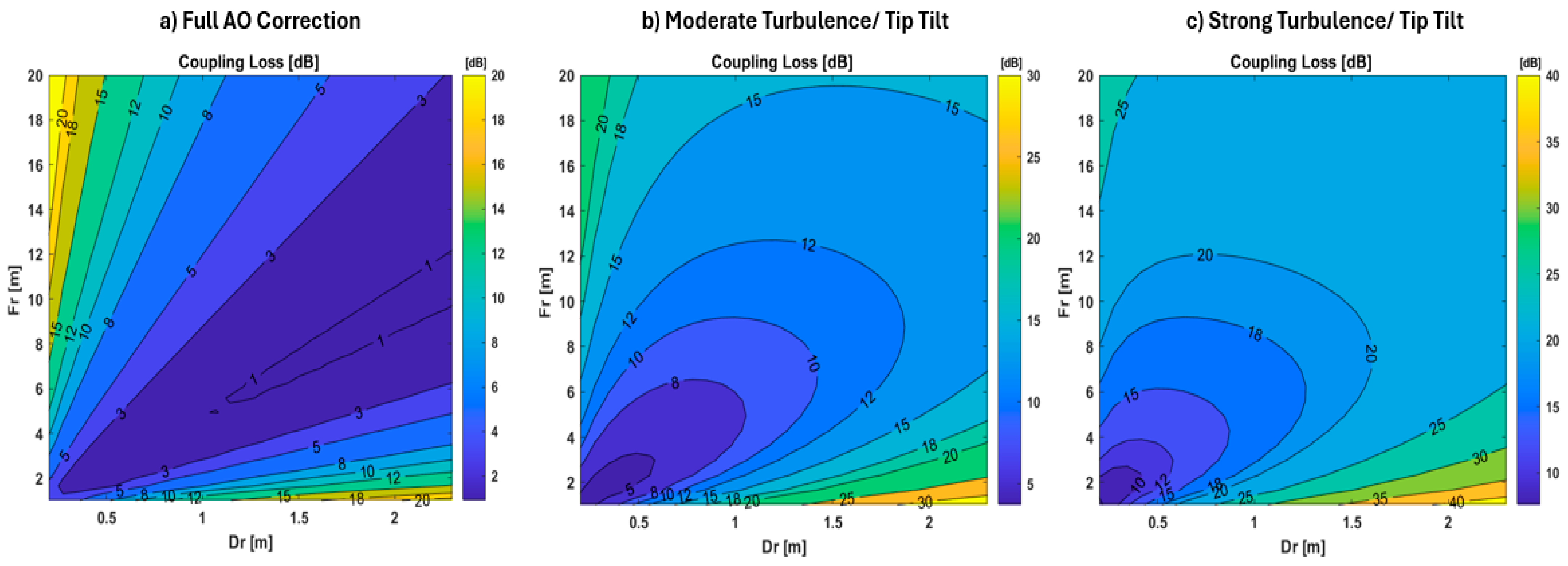
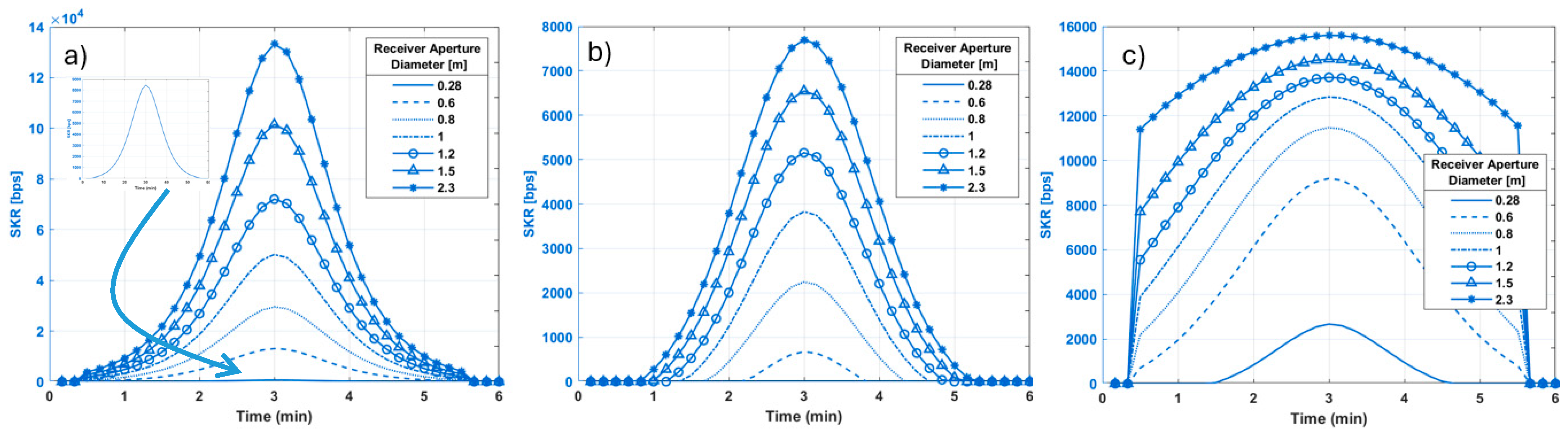
4.4. Receiver Size and Design Characteristics
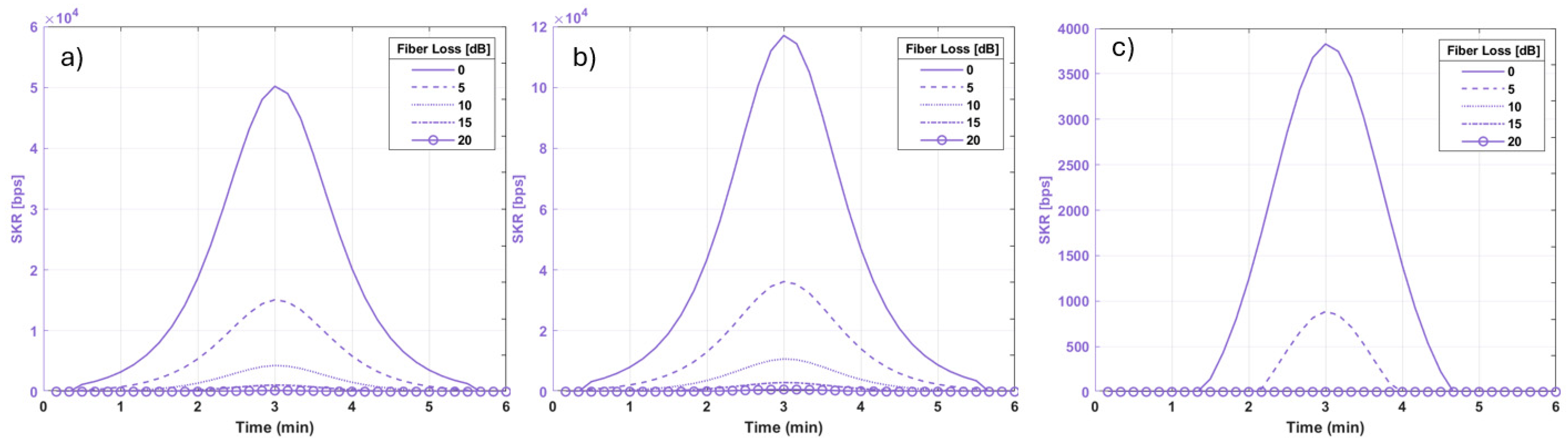
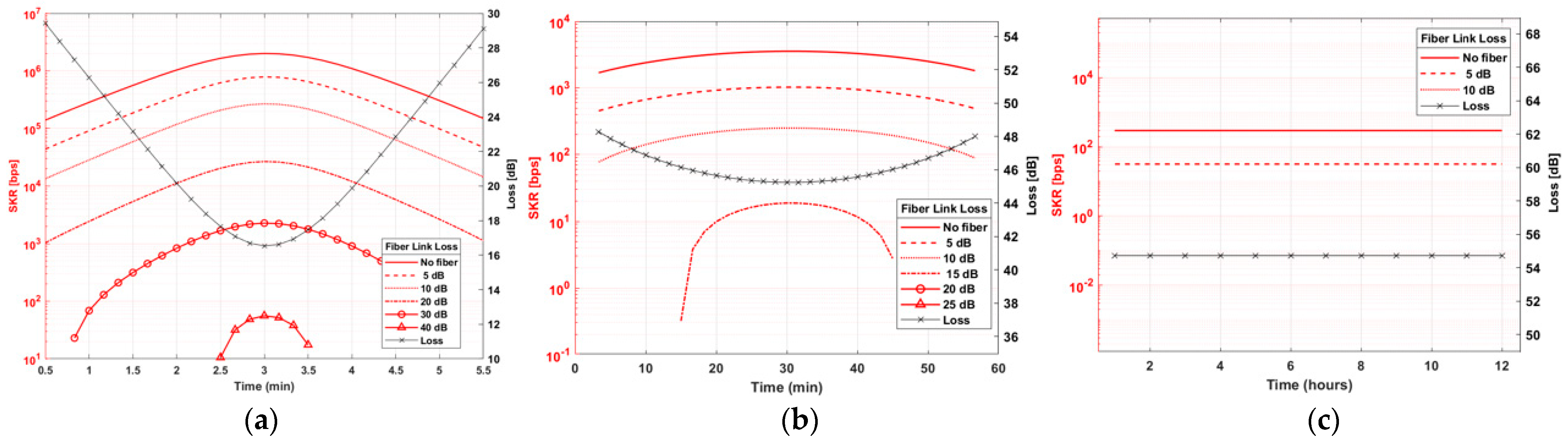
4.5. Fiber Distribution
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wehner, S.; Elkouss, D.; Hanson, R. Quantum Internet: A Vision for the Road Ahead. Science 2018, 362, eaam9288. [Google Scholar] [CrossRef] [PubMed]
- Long-Range QKD without Trusted Nodes Is Not Possible with Current Technology|Npj Quantum Information. Available online: https://www.nature.com/articles/s41534-022-00613-4 (accessed on 11 April 2024).
- Wallnöfer, J.; Hahn, F.; Wiesner, F.; Walk, N.; Eisert, J. Faithfully Simulating Near-Term Quantum Repeaters. PRX Quantum 2024, 5, 010351. [Google Scholar] [CrossRef]
- de Forges de Parny, L.; Alibart, O.; Debaud, J.; Gressani, S.; Lagarrigue, A.; Martin, A.; Metrat, A.; Schiavon, M.; Troisi, T.; Diamanti, E.; et al. Satellite-Based Quantum Information Networks: Use Cases, Architecture, and Roadmap. Commun. Phys. 2023, 6, 12. [Google Scholar] [CrossRef]
- Cuomo, D.; Caleffi, M.; Cacciapuoti, A.S. Towards a Distributed Quantum Computing Ecosystem. IET Quantum Commun. 2020, 1, 3–8. [Google Scholar] [CrossRef]
- Cavaliere, F.; Prati, E.; Poti, L.; Muhammad, I.; Catuogno, T. Secure Quantum Communication Technologies and Systems: From Labs to Markets. Quantum Rep. 2020, 2, 80–106. [Google Scholar] [CrossRef]
- Tenne, R.; Rossman, U.; Rephael, B.; Israel, Y.; Krupinski-Ptaszek, A.; Lapkiewicz, R.; Silberberg, Y.; Oron, D. Super-Resolution Enhancement by Quantum Image Scanning Microscopy. Nat. Photon. 2019, 13, 116–122. [Google Scholar] [CrossRef]
- Ansari, V.; Brecht, B.; Gil-Lopez, J.; Donohue, J.M.; Řeháček, J.; Hradil, Z.; Sánchez-Soto, L.L.; Silberhorn, C. Achieving the Ultimate Quantum Timing Resolution. PRX Quantum 2021, 2, 010301. [Google Scholar] [CrossRef]
- Liao, S.-K.; Cai, W.-Q.; Liu, W.-Y.; Zhang, L.; Li, Y.; Ren, J.-G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.-P.; et al. Satellite-to-Ground Quantum Key Distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.-K.; Lin, J.; Ren, J.-G.; Liu, W.-Y.; Qiang, J.; Yin, J.; Li, Y.; Shen, Q.; Zhang, L.; Liang, X.-F.; et al. Space-to-Ground Quantum Key Distribution Using a Small-Sized Payload on Tiangong-2 Space Lab. Chin. Phys. Lett. 2017, 34, 090302. [Google Scholar] [CrossRef]
- Jones, A. China Is Developing a Quantum Communications Satellite Network. SpaceNews, 10 March 2023. Available online: https://spacenews.com/china-is-developing-a-quantum-communications-satellite-network/ (accessed on 23 June 2024).
- Khmelev, A.; Duplinsky, A.; Bakhshaliev, R.; Ivchenko, E.; Pismeniuk, L.; Mayboroda, V.; Nesterov, I.; Chernov, A.; Trushechkin, A.; Kiktenko, E.; et al. Eurasian-Scale Experimental Satellite-Based Quantum Key Distribution with Detector Efficiency Mismatch Analysis. Opt. Express 2024, 32, 11964. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.-H.; Liao, S.-K.; Zhang, L.; Ren, J.-G.; Cai, W.-Q.; Liu, W.-Y.; Li, B.; Dai, H.; et al. Satellite-Based Entanglement Distribution over 1200 Kilometers. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.-G.; Xu, P.; Yong, H.-L.; Zhang, L.; Liao, S.-K.; Yin, J.; Liu, W.-Y.; Cai, W.-Q.; Yang, M.; Li, L.; et al. Ground-to-Satellite Quantum Teleportation. Nature 2017, 549, 70–73. [Google Scholar] [CrossRef] [PubMed]
- EAGLE-1: Advancing Europe’s Leadership in Quantum Communications|SES. Available online: https://www.ses.com/newsroom/eagle-1-advancing-europes-leadership-quantum-communications (accessed on 11 April 2024).
- SAGA for Quantum Key Distribution. Available online: https://www.esa.int/ESA_Multimedia/Images/2019/04/SAGA_for_quantum_key_distribution (accessed on 11 April 2024).
- Tricco, G. The Upcoming of Iris2: Bridging the Digital Divide and Strengthening the Role of the EU in International Space Law. J. Law. Mark. Innov. 2023, 2, 17–42. [Google Scholar] [CrossRef]
- Hutterer, M.; Auer, M.; Baliuka, A.; Marquardt, C.; Weinfurter, H.; Gall, M.; Günther, K.; Moll, F.; Papadopoulos, C.; Pudelko, J.; et al. QUBE-II—Quantum Key Distribution with a CubeSat. In Proceedings of the 73rd International Astronautical Congress, IAC 2022, Paris, France, 18–22 September 2022. [Google Scholar]
- Peev, M.; Pacher, C.; Alléaume, R.; Barreiro, C.; Bouda, J.; Boxleitner, W.; Debuisschert, T.; Diamanti, E.; Dianati, M.; Dynes, J.F.; et al. The SECOQC Quantum Key Distribution Network in Vienna. New J. Phys. 2009, 11, 075001. [Google Scholar] [CrossRef]
- García Cid, M.I.; Ortiz Martín, L.; Martín Ayuso, V. Madrid Quantum Network: A First Step to Quantum Internet. In Proceedings of the 16th International Conference on Availability, Reliability and Security, Vienna, Austria, 17–20 August 2021; Association for Computing Machinery: New York, NY, USA; pp. 1–7. [Google Scholar]
- Ribezzo, D.; Zahidy, M.; Vagniluca, I.; Biagi, N.; Francesconi, S.; Occhipinti, T.; Oxenløwe, L.K.; Lončarić, M.; Cvitić, I.; Stipčević, M.; et al. Deploying an Inter-European Quantum Network. Adv. Quantum Technol. 2023, 6, 2200061. [Google Scholar] [CrossRef]
- Brauer, M.; Vicente, R.J.; Buruaga, J.S.; Méndez, R.B.; Braun, R.-P.; Geitz, M.; Rydlichkowski, P.; Brunner, H.H.; Fung, F.; Peev, M.; et al. Linking QKD Testbeds across Europe. Entropy 2024, 26, 123. [Google Scholar] [CrossRef] [PubMed]
- Qin, H.; Haw, J.Y.; Duan, X.; Cai, Y.; Murthy, R.; Ng, N.; Sikdar, B.; Kurtsiefer, C.; Kasper, M.; Ling, A. The National Quantum-Safe Network in Singapore. In Proceedings of the 49th European Conference on Optical Communications (ECOC 2023), Glasgow, UK, 1–5 October 2023; Volume 2023, pp. 1294–1297. [Google Scholar]
- Scott, A.; Jennewein, T.; Cain, J.; D’Souza, I.; Higgins, B.; Hudson, D.; Podmore, H.; Soh, W. The QEYSSAT Mission: On-Orbit Demonstration of Secure Optical Communications Network Technologies. In Proceedings of the Environmental Effects on Light Propagation and Adaptive Systems III, Online, 21–25 September 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11532, pp. 71–76. [Google Scholar]
- Mazzarella, L.; Lowe, C.; Lowndes, D.; Joshi, S.K.; Greenland, S.; McNeil, D.; Mercury, C.; Macdonald, M.; Rarity, J.; Oi, D.K.L. QUARC: Quantum Research Cubesat—A Constellation for Quantum Communication. Cryptography 2020, 4, 7. [Google Scholar] [CrossRef]
- Lenart, A.; Sivasankaran, S.; Hidding, B.; Oi, D.; Ling, A.; Neilson, P. CubeSat In-Orbit Validation of in Situ Performance by High Fidelity Radiation Modelling. arXiv 2022, arXiv:2209.00408. [Google Scholar]
- Ahmadi, N.; Schwertfeger, S.; Werner, P.; Wiese, L.; Lester, J.; Da Ros, E.; Krause, J.; Ritter, S.; Abasifard, M.; Cholsuk, C.; et al. QUICK3^3—Design of a Satellite-Based Quantum Light Source for Quantum Communication and Extended Physical Theory Tests in Space. Adv. Quantum Technol. 2024, 7, 2300343. [Google Scholar] [CrossRef]
- Gündoğan, M.; Sidhu, J.S.; Henderson, V.; Mazzarella, L.; Wolters, J.; Oi, D.K.L.; Krutzik, M. Proposal for Space-Borne Quantum Memories for Global Quantum Networking. npj Quantum Inf. 2021, 7, 128. [Google Scholar] [CrossRef]
- Luo, W.; Li, Y.; Li, Y.; Tao, X.; Han, L.; Cai, W.; Yin, J.; Ren, J.; Liao, S.; Peng, C. Intrinsically Stable 2-GHz Polarization Modulation for Satellite-Based Quantum Key Distribution. IEEE Photonics J. 2022, 14, 1–6. [Google Scholar] [CrossRef]
- Roger, T.; Singh, R.; Perumangatt, C.; Marangon, D.G.; Sanzaro, M.; Smith, P.R.; Woodward, R.I.; Shields, A.J. Real-Time Gigahertz Free-Space Quantum Key Distribution within an Emulated Satellite Overpass. Sci. Adv. 2023, 9, eadj5873. [Google Scholar] [CrossRef] [PubMed]
- Home—QUDICE. Available online: https://qudice.eu/ (accessed on 11 April 2024).
- Press Release—LaiQa Project. Available online: https://www.Laiqa-Horizon.Eu/Press-Release/ (accessed on 23 June 2024).
- Bonato, C.; Tomaello, A.; Da Deppo, V.; Naletto, G.; Villoresi, P. Feasibility of Satellite Quantum Key Distribution. New J. Phys. 2009, 11, 045017. [Google Scholar] [CrossRef]
- Ntanos, A.; Lyras, N.K.; Zavitsanos, D.; Giannoulis, G.; Panagopoulos, A.D.; Avramopoulos, H. LEO Satellites Constellation-to-Ground QKD Links: Greek Quantum Communication Infrastructure Paradigm. Photonics 2021, 8, 544. [Google Scholar] [CrossRef]
- Scriminich, A.; Foletto, G.; Picciariello, F.; Stanco, A.; Vallone, G.; Villoresi, P.; Vedovato, F. Optimal Design and Performance Evaluation of Free-Space Quantum Key Distribution Systems. Quantum Sci. Technol. 2022, 7, 045029. [Google Scholar] [CrossRef]
- Ntanos, A.; Lyras, N.; Zavitsanos, D.; Anwar, S.; Alia, O.; Giannoulis, G.; Kanellos, G.; Panagopoulos, A.; Avramopoulos, H. MEO Satellite-to-Ground Decoy-State QKD Links Realistic Performance Analysis. In Proceedings of the International Conference on Space Optics—ICSO 2022, Dubrovnik, Croatia, 3–7 October 2022; SPIE: Bellingham, WA, USA, 2023; Volume 12777, pp. 1116–1130. [Google Scholar]
- Ntanos, A.; Lyras, N.K.; Stathis, A.; Giannoulis, G.; Panagopoulos, A.D.; Avramopoulos, H. Satellite-to-Ground QKD in Urban Environment: A Comparative Analysis of Small-Sized Optical Ground Stations. IEEE Aerosp. Electron. Syst. Mag. 2024, 39, 16–29. [Google Scholar] [CrossRef]
- Acosta, V.M.; Dequal, D.; Schiavon, M.; Montmerle-Bonnefois, A.; Lim, C.B.; Conan, J.-M.; Diamanti, E. Analysis of Satellite-to-Ground Quantum Key Distribution with Adaptive Optics. New J. Phys. 2024, 26, 023039. [Google Scholar] [CrossRef]
- Polnik, M.; Mazzarella, L.; Di Carlo, M.; Oi, D.K.; Riccardi, A.; Arulselvan, A. Scheduling of Space to Ground Quantum Key Distribution. EPJ Quantum Technol. 2020, 7, 3. [Google Scholar] [CrossRef]
- How to Choose the Best QKD Network Technology: Three Different Satellite Based Scenarios Compared. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/11852/2599218/How-to-choose-the-best-QKD-network-technology--three/10.1117/12.2599218.full#_=_ (accessed on 11 April 2024).
- Sidhu, J.S.; Brougham, T.; McArthur, D.; Pousa, R.G.; Oi, D.K.L. Finite Key Effects in Satellite Quantum Key Distribution. npj Quantum Inf. 2022, 8, 18. [Google Scholar] [CrossRef]
- Exciting News for the Greek Connectivity Optical Ground Stations—Raymetrics. 2024. Available online: https://raymetrics.com/wp-content/uploads/2024/01/Hardware-Newsletter-KOM1.pdf (accessed on 23 June 2024).
- Rattenbury, N.J.; Ashby, J.; Bennet, F.; Birch, M.; Cater, J.E.; Ferguson, K.; Giggenbach, D.; Grant, K.; Knopp, A.; Knopp, M.T.; et al. Update on the German and Australasian Optical Ground Station Networks. arXiv 2024, arXiv:2402.13282. [Google Scholar]
- Liao, S.-K.; Yong, H.-L.; Liu, C.; Shentu, G.-L.; Li, D.-D.; Lin, J.; Dai, H.; Zhao, S.-Q.; Li, B.; Guan, J.-Y.; et al. Long-Distance Free-Space Quantum Key Distribution in Daylight towards Inter-Satellite Communication. Nat. Photon. 2017, 11, 509–513. [Google Scholar] [CrossRef]
- Marsden, M.A.; Downey, J.N.; Tedder, S.A.; Vyhnalek, B.E. Testing of A Photon-Counting Optical Ground Receiver with Emulated Space-to-Ground Link Effects. In Proceedings of the SPIE Photonics West Free-Space Laser Communications XXXVI, San Francisco, CA, USA, 30–31 January 2024. [Google Scholar]
- Makarov, V.; Abrikosov, A.; Chaiwongkhot, P.; Fedorov, A.K.; Huang, A.; Kiktenko, E.; Petrov, M.; Ponosova, A.; Ruzhitskaya, D.; Tayduganov, A.; et al. Preparing a Commercial Quantum Key Distribution System for Certification against Implementation Loopholes. arXiv 2023, arXiv:2310.20107. [Google Scholar]
- Vasylyev, D.; Vogel, W.; Moll, F. Satellite-Mediated Quantum Atmospheric Links. Phys. Rev. A 2019, 99, 053830. [Google Scholar] [CrossRef]
- Bourgoin, J.-P.; Meyer-Scott, E.; Higgins, B.L.; Helou, B.; Erven, C.; Hübel, H.; Kumar, B.; Hudson, D.; D’Souza, I.; Girard, R.; et al. A Comprehensive Design and Performance Analysis of Low Earth Orbit Satellite Quantum Communication. New J. Phys. 2013, 15, 023006. [Google Scholar] [CrossRef]
- Gruneisen, M.T.; Eickhoff, M.L.; Newey, S.C.; Stoltenberg, K.E.; Morris, J.F.; Bareian, M.; Harris, M.A.; Oesch, D.W.; Oliker, M.D.; Flanagan, M.B.; et al. Adaptive-Optics-Enabled Quantum Communication: A Technique for Daytime Space-To-Earth Links. Phys. Rev. Appl. 2021, 16, 014067. [Google Scholar] [CrossRef]
- Lu, C.-Y.; Cao, Y.; Peng, C.-Z.; Pan, J.-W. Micius Quantum Experiments in Space. Rev. Mod. Phys. 2022, 94, 035001. [Google Scholar] [CrossRef]
- Li, Y.-H.; Li, S.-L.; Hu, X.-L.; Jiang, C.; Yu, Z.-W.; Li, W.; Liu, W.-Y.; Liao, S.-K.; Ren, J.-G.; Li, H.; et al. Free-Space and Fiber-Integrated Measurement-Device-Independent Quantum Key Distribution under High Background Noise. Phys. Rev. Lett. 2023, 131, 100802. [Google Scholar] [CrossRef] [PubMed]
- Ansys STK|Digital Mission Engineering Software. Available online: https://www.ansys.com/products/missions/ansys-stk (accessed on 18 April 2024).
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005; ISBN 978-0-8194-5948-0. [Google Scholar]
- Kiasaleh, K. On the Probability Density Function of Signal Intensity in Free-Space Optical Communications Systems Impaired by Pointing Jitter and Turbulence. Opt. Eng. 1994, 33, 3748–3757. [Google Scholar] [CrossRef]
- ITU-R. Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems; ITU-R 206/3; International Telecommunication Union: Geneva, Switzerland, 2015. [Google Scholar]
- Bufton, J.L. Comparison of Vertical Profile Turbulence Structure with Stellar Observations. Appl. Opt. 1973, 12, 1785–1793. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Commun. Surv. Tutor. 2017, 19, 57–96. [Google Scholar] [CrossRef]
- Giggenbach, D.; Moll, F. Scintillation Loss in Optical Low Earth Orbit Data Downlinks with Avalanche Photodiode Receivers. In Proceedings of the 2017 IEEE International Conference on Space Optical Systems and Applications (ICSOS), Naha, Japan, 14–16 November 2017; pp. 115–122. [Google Scholar] [CrossRef]
- Marsili, F.; Verma, V.B.; Stern, J.A.; Harrington, S.; Lita, A.E.; Gerrits, T.; Vayshenker, I.; Baek, B.; Shaw, M.D.; Mirin, R.P.; et al. Detecting Single Infrared Photons with 93% System Efficiency. Nat. Photon. 2013, 7, 210–214. [Google Scholar] [CrossRef]
- Er-long, M.; Zheng-fu, H.; Shun-sheng, G.; Tao, Z.; Da-sheng, D.; Guang-can, G. Background Noise of Satellite-to-Ground Quantum Key Distribution. New J. Phys. 2005, 7, 215. [Google Scholar] [CrossRef]
- Tyson, R.K.; Frazier, B.W. Principles of Adaptive Optics, 5th ed.; CRC Press: Boca Raton, FL, USA, 2022; ISBN 978-1-00-314019-1. [Google Scholar]
- Jovanovic, N.; Schwab, C.; Guyon, O.; Lozi, J.; Cvetojevic, N.; Martinache, F.; Leon-Saval, S.; Norris, B.; Gross, S.; Doughty, D.; et al. Efficient Injection from Large Telescopes into Single-Mode Fibres: Enabling the Era of Ultra-Precision Astronomy. Astron. Astrophys. 2017, 604, A122. [Google Scholar] [CrossRef]
- Bonnefois, A.M.; Velluet, M.-T.; Cissé, M.; Lim, C.B.; Conan, J.-M.; Petit, C.; Sauvage, J.-F.; Meimon, S.; Perrault, P.; Montri, J.; et al. Feasibility Demonstration of AO Pre-Compensation for GEO Feeder Links in a Relevant Environment. Opt. Express 2022, 30, 47179–47198. [Google Scholar] [CrossRef]
- Chai, G.; Huang, P.; Cao, Z.; Zeng, G. Suppressing Excess Noise for Atmospheric Continuous-Variable Quantum Key Distribution via Adaptive Optics Approach. New J. Phys. 2020, 22, 103009. [Google Scholar] [CrossRef]
- Cao, Y.; Li, Y.-H.; Yang, K.-X.; Jiang, Y.-F.; Li, S.-L.; Hu, X.-L.; Abulizi, M.; Li, C.-L.; Zhang, W.; Sun, Q.-C.; et al. Long-Distance Free-Space Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2020, 125, 260503. [Google Scholar] [CrossRef]
- Oliker, M.D.; Gruneisen, M.T. How Much Value Does Adaptive Optics Add to a Satellite QKD Uplink? In Proceedings of the Quantum Technologies and Quantum Information Science V, Strasbourg, France, 9–12 September 2019; SPIE: Bellingham, WA, USA, 2019; Volume 11167, pp. 10–19. [Google Scholar]
- TOmCAT. Available online: https://artes.esa.int/projects/tomcat (accessed on 24 March 2023).
- Ruilier, C. A Study of Degraded Light Coupling into Single-Mode Fibers. In Proceedings of the Astronomical Interferometry, Kona, HI, USA, 20–28 March 1998; SPIE: Bellingham, WA, USA, 1998; Volume 3350, pp. 319–329. [Google Scholar]
- Gruneisen, M.T.; Sickmiller, B.A.; Flanagan, M.B.; Black, J.P.; Stoltenberg, K.E.; Duchane, A.W. Adaptive Spatial Filtering for Daytime Satellite Quantum Key Distribution. In Proceedings of the Emerging Technologies in Security and Defence II; and Quantum-Physics-based Information Security III, Amsterdam, The Netherlands, 22–25 September 2014; SPIE: Bellingham, WA, USA, 2014; Volume 9254, pp. 7–20. [Google Scholar]
- Gruneisen, M.T.; Flanagan, M.B.; Sickmiller, B.A. Modeling Satellite-Earth Quantum Channel Downlinks with Adaptive-Optics Coupling to Single-Mode Fibers. Opt. Eng. 2017, 56, 126111. [Google Scholar] [CrossRef]
- Krzic, A.; Heinig, D.; Goy, M.; Steinlechner, F. Dual-Downlink Quantum Key Distribution with Entangled Photons: Prospects for Daylight Operation. In Proceedings of the Dual-Downlink Quantum Key Distribution with Entangled Photons: Prospects for Daylight Operation; International Conference on Space Optics, Dubrovnik, Croatia, 3–7 October 2022. [Google Scholar]
- Dikmelik, Y.; Davidson, F.M. Fiber-Coupling Efficiency for Free-Space Optical Communication through Atmospheric Turbulence. Appl. Opt. 2005, 44, 4946–4952. [Google Scholar] [CrossRef]
- Schmitt-Manderbach, T.; Weier, H.; Fürst, M.; Ursin, R.; Tiefenbacher, F.; Scheidl, T.; Perdigues, J.; Sodnik, Z.; Kurtsiefer, C.; Rarity, J.G.; et al. Experimental Demonstration of Free-Space Decoy-State Quantum Key Distribution over 144 Km. Phys. Rev. Lett. 2007, 98, 010504. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Qi, B.; Zhao, Y.; Lo, H.-K. Practical Decoy State for Quantum Key Distribution. Phys. Rev. A 2005, 72, 012326. [Google Scholar] [CrossRef]
- Lucamarini, M.; Patel, K.A.; Dynes, J.F.; Fröhlich, B.; Sharpe, A.W.; Dixon, A.R.; Yuan, Z.L.; Penty, R.V.; Shields, A.J. Efficient Decoy-State Quantum Key Distribution with Quantified Security. Opt. Express 2013, 21, 24550–24565. [Google Scholar] [CrossRef] [PubMed]
- Song, T.-T.; Qin, S.-J.; Wen, Q.-Y.; Wang, Y.-K.; Jia, H.-Y. Finite-Key Security Analyses on Passive Decoy-State QKD Protocols with Different Unstable Sources. Sci. Rep. 2015, 5, 15276. [Google Scholar] [CrossRef] [PubMed]
- Eraerds, P.; Walenta, N.; Legré, M.; Gisin, N.; Zbinden, H. Quantum Key Distribution and 1 Gbps Data Encryption over a Single Fibre. New J. Phys. 2010, 12, 063027. [Google Scholar] [CrossRef]
- Bellei, F.; Cartwright, A.P.; McCaughan, A.N.; Dane, A.E.; Najafi, F.; Zhao, Q.; Berggren, K.K. Free-Space-Coupled Superconducting Nanowire Single-Photon Detectors for Infrared Optical Communications. Opt. Express 2016, 24, 3248–3257. [Google Scholar] [CrossRef] [PubMed]
- Mueller, A.S.; Korzh, B.; Runyan, M.; Wollman, E.E.; Beyer, A.D.; Allmaras, J.P.; Velasco, A.E.; Craiciu, I.; Bumble, B.; Briggs, R.M.; et al. Free-Space Coupled Superconducting Nanowire Single-Photon Detector with Low Dark Counts. Optica 2021, 8, 1586–1587. [Google Scholar] [CrossRef]
- Tamura, Y.; Sakuma, H.; Morita, K.; Suzuki, M.; Yamamoto, Y.; Shimada, K.; Honma, Y.; Sohma, K.; Fujii, T.; Hasegawa, T. The First 0.14-dB/Km Loss Optical Fiber and Its Impact on Submarine Transmission. J. Light. Technol. 2018, 36, 44–49. [Google Scholar] [CrossRef]
- Clavis XG QKD System. Available online: https://www.idquantique.com/quantum-safe-security/products/clavis-xg-qkd-system/ (accessed on 26 July 2023).
- Long Distance QKD System LD—Toshiba Quantum Key Distribution. Toshiba Quantum Technology. Available online: https://www.toshiba.eu/quantum/products/quantum-key-distribution/long-distance-qkd-system-ld/ (accessed on 23 June 2024).
- Boaron, A.; Boso, G.; Rusca, D.; Vulliez, C.; Autebert, C.; Caloz, M.; Perrenoud, M.; Gras, G.; Bussières, F.; Li, M.-J.; et al. Secure Quantum Key Distribution over 421 Km of Optical Fiber. Phys. Rev. Lett. 2018, 121, 190502. [Google Scholar] [CrossRef] [PubMed]
- Toshiba Europe and Single Quantum Partner to Provide Extended Long-Distance QKD Deployment Capability. Toshiba Quantum Technology. Available online: https://www.toshiba.eu/quantum/news/toshiba-europe-and-single-quantum-partner-to-provide-extended-long-distance-qkd-deployment-capability/ (accessed on 23 June 2024).
- Influence of Satellite Motion on Polarization Qubits in a Space-Earth Quantum Communication Link. Available online: https://opg.optica.org/oe/fulltext.cfm?uri=oe-14-21-10050&id=116342 (accessed on 22 April 2024).
- Toyoshima, M.; Takenaka, H.; Shoji, Y.; Takayama, Y.; Takeoka, M.; Fujiwara, M.; Sasaki, M. Polarization-Basis Tracking Scheme in Satellite Quantum Key Distribution. Int. J. Opt. 2011, 2011, e254154. [Google Scholar] [CrossRef]
- Khanna, A.; Sakhiya, P.V.; Bhatt, J.B.; Jain, A.; Kumar, M.S.; Singh, D.K. Development of Active Polarization Tracking and Compensation System for Satellite-to-Ground QKD. In Proceedings of the 2023 IEEE Microwaves, Antennas, and Propagation Conference (MAPCON), Ahmedabad, India, 11–14 December 2023; pp. 1–6. [Google Scholar]
- Miller, A.V. Time Synchronization in Satellite Quantum Key Distribution. Probl. Inf. Transm. 2023, 59, 225–238. [Google Scholar] [CrossRef]
- Li, L.; Xuejiao, Z.; Jianhua, Z.; Changzhi, X.; Yi, J. Advanced Space Laser Communication Technology on CubeSats. ZTE Commun. 2020, 18, 45–54. [Google Scholar] [CrossRef]


| Symbol | Parameter | Value |
|---|---|---|
| Quantum channel wavelength | 1550 nm | |
| Emission rate | 40–300 MHz | |
| Transmitted block size | 1010–1013 bits | |
| Satellite orbit altitude | 550/8000/36,000 km | |
| Tx telescope aperture diameter | 0.3 m | |
| Rx telescope aperture diameter | 0.28–2.3 m | |
| Obscuration ratio | ~0.1 | |
| Focal ratio | ~f/8 | |
| ηsys | AO/tip–tilt optical transmittance | 0.9 |
| OGS Altitude | 500–2340 m | |
| Min. elevation angle | 20° | |
| Pointing error variance | 0.7 μrad | |
| Detector’s setup loss | 2 dB | |
| Refractive index structure parameter | ||
| Background solar radiance | ||
| Outage probability | 1% | |
| Receiver’s FOV | 100 μrad | |
| Filter’s spectral passband | 0.2 nm | |
| Filters efficiency | 0.7 | |
| μ | Mean signal photon/pulse | 0.7 |
| ν | Mean decoy photon/pulse | 0.1 |
| Smoothing parameter | ||
| Parameter estimation | ||
| Error correction parameter | ||
| SNSPDs detection efficiency | 0.85 | |
| SNSPDs dark count rate | 10 cps | |
| Dead time SNSPD | 30 ns | |
| SPADs detection efficiency | 0.15 | |
| SPADs dark count rate | 300 cps | |
| Dead time SPAD | 20 μs | |
| Effective gate time window | 1 ns | |
| Error probability for noise counts | 50% |
| Symbol | Parameter | Value |
|---|---|---|
| Emission rate | 1 GHz | |
| Transmitted block size | 1012 bits | |
| Satellite orbit altitude | 550/8000/36,000 km | |
| Rx telescope aperture diameter | 2.28 m | |
| Obscuration ratio | 0.32 | |
| Focal ratio | f/8 | |
| OGS altitude | 2300 m | |
| Pointing error variance | 0.7 μrad | |
| Refractive index structure parameter | ||
| Night-time Background solar radiance new moon | ||
| Effective gate time window | 0.5 ns |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stathis, A.; Ntanos, A.; Lyras, N.K.; Giannoulis, G.; Panagopoulos, A.D.; Avramopoulos, H. Toward Converged Satellite/Fiber 1550 nm DS-BB84 QKD Networks: Feasibility Analysis and System Requirements. Photonics 2024, 11, 609. https://doi.org/10.3390/photonics11070609
Stathis A, Ntanos A, Lyras NK, Giannoulis G, Panagopoulos AD, Avramopoulos H. Toward Converged Satellite/Fiber 1550 nm DS-BB84 QKD Networks: Feasibility Analysis and System Requirements. Photonics. 2024; 11(7):609. https://doi.org/10.3390/photonics11070609
Chicago/Turabian StyleStathis, Aristeidis, Argiris Ntanos, Nikolaos K. Lyras, Giannis Giannoulis, Athanasios D. Panagopoulos, and Hercules Avramopoulos. 2024. "Toward Converged Satellite/Fiber 1550 nm DS-BB84 QKD Networks: Feasibility Analysis and System Requirements" Photonics 11, no. 7: 609. https://doi.org/10.3390/photonics11070609
APA StyleStathis, A., Ntanos, A., Lyras, N. K., Giannoulis, G., Panagopoulos, A. D., & Avramopoulos, H. (2024). Toward Converged Satellite/Fiber 1550 nm DS-BB84 QKD Networks: Feasibility Analysis and System Requirements. Photonics, 11(7), 609. https://doi.org/10.3390/photonics11070609








