A Critical Analysis of the Thermo-Optic Time Constant in Si Photonic Devices
Abstract
1. Introduction
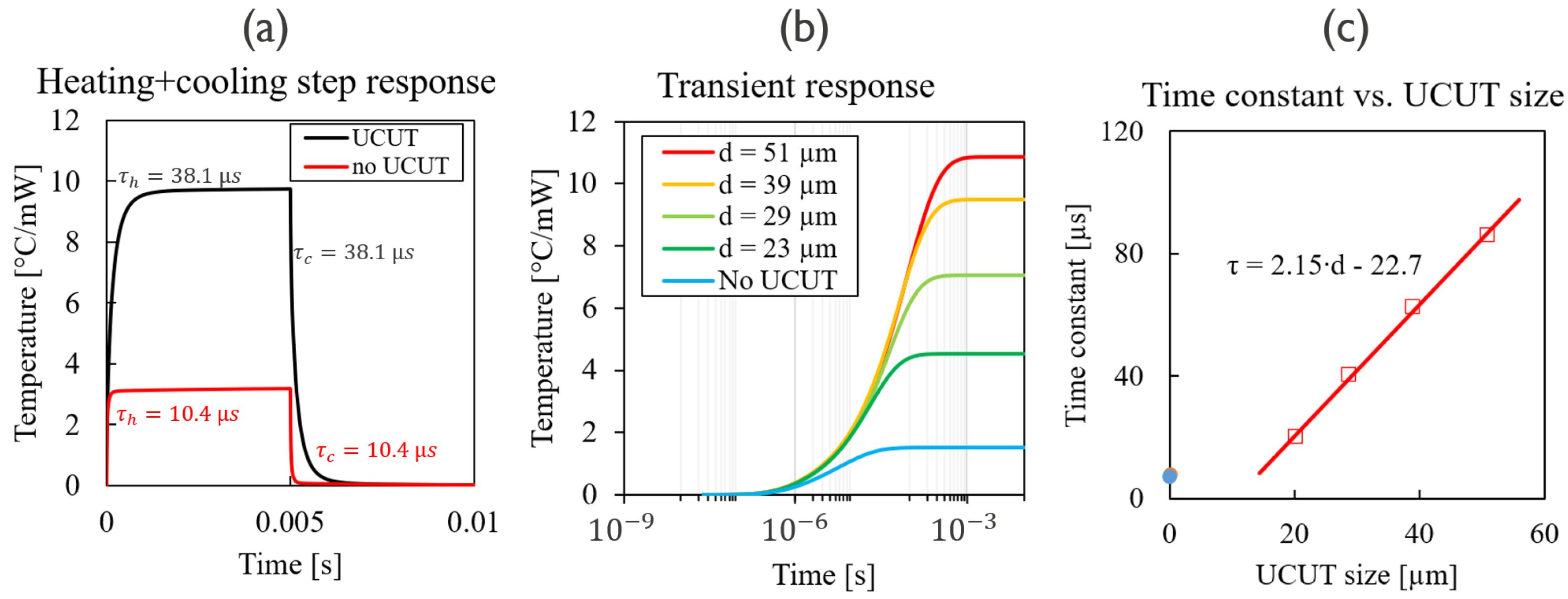
1.1. Silicon Photonic Heaters
1.2. Heat Equation and Its Solution
2. Interferometric Devices
2.1. Theoretical Description
2.2. Dynamic Characterization Method
2.2.1. Analytical Model
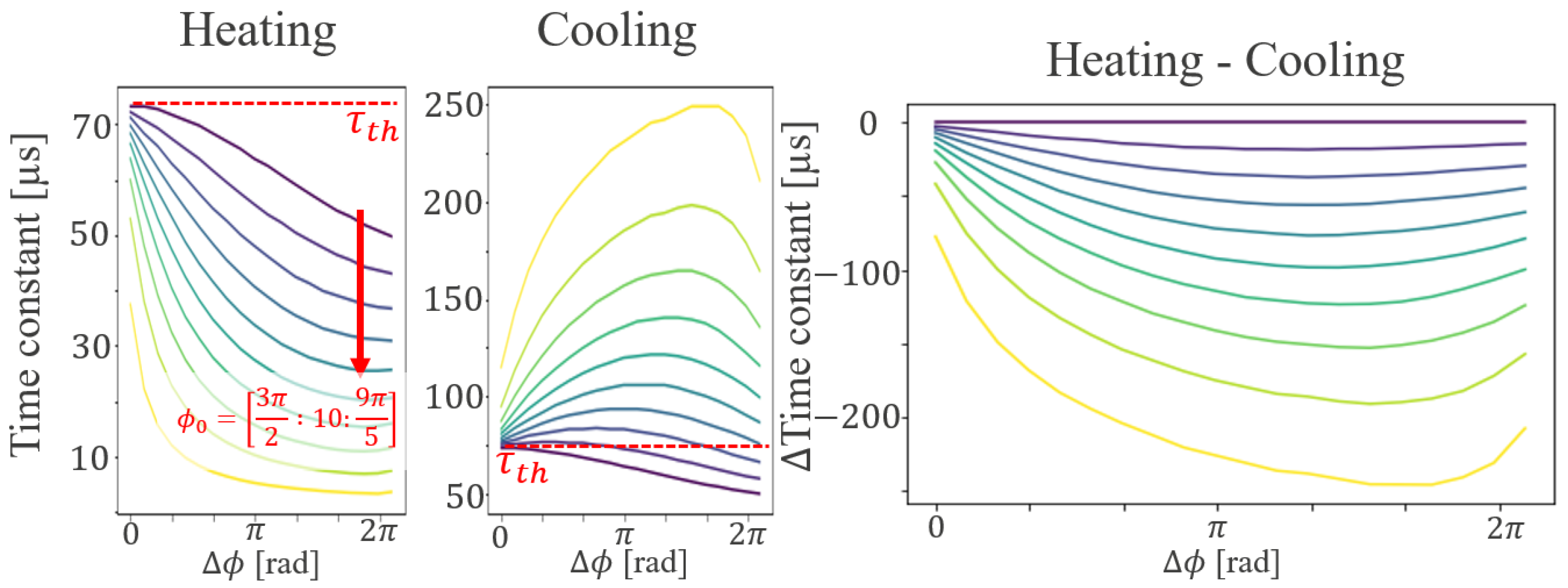
2.2.2. Impact of and on
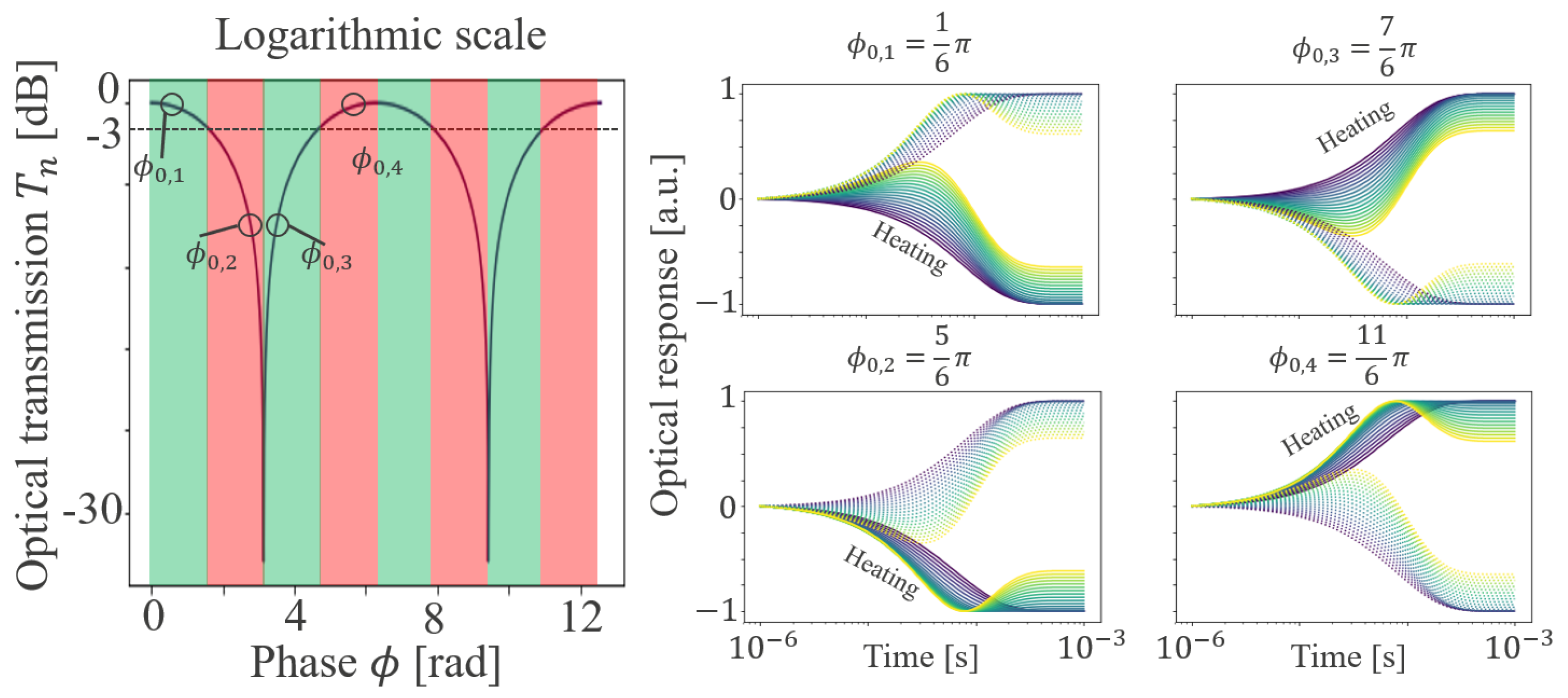
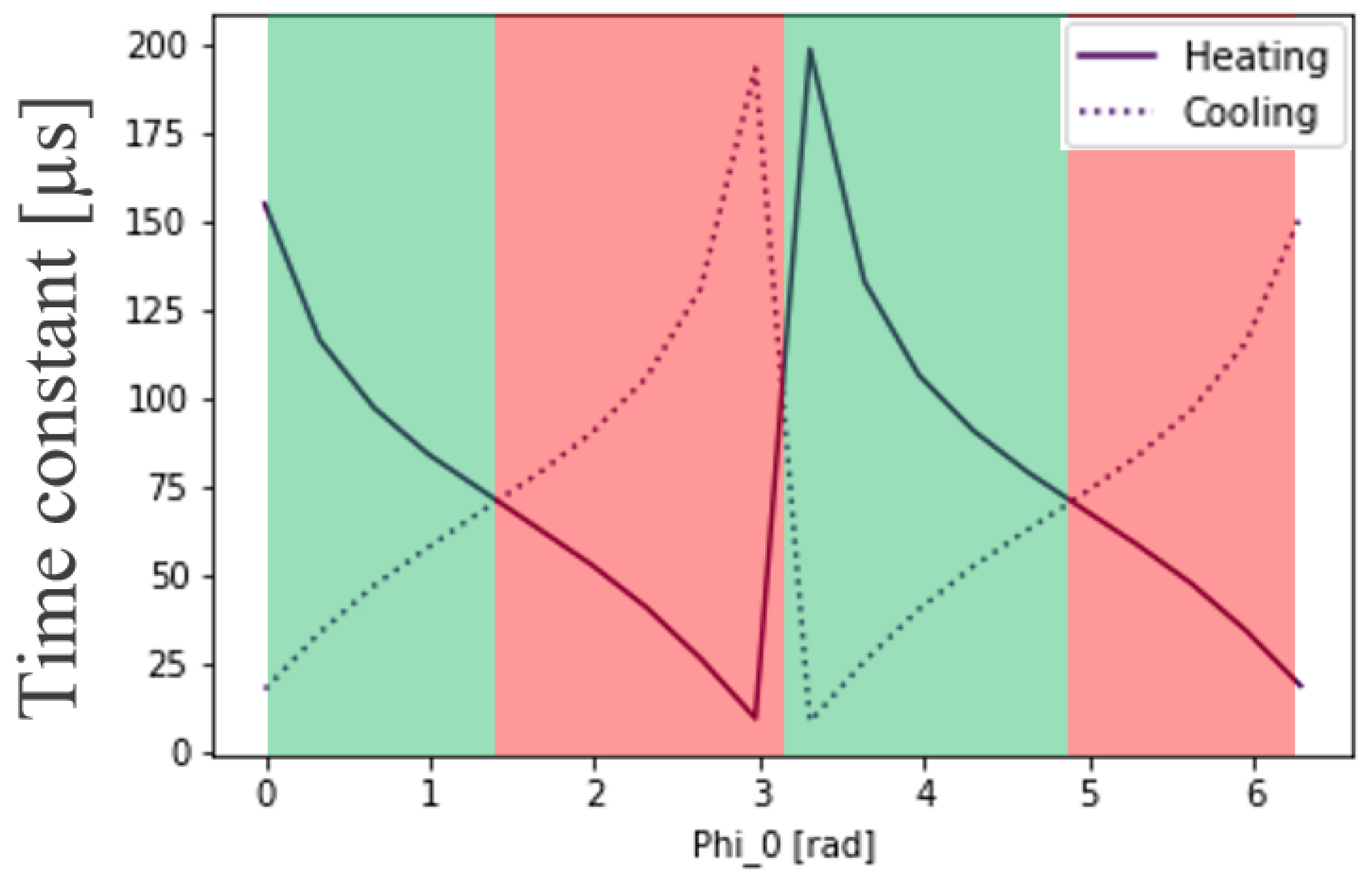
2.3. Problem Inversion
3. Resonant Devices
3.1. Theoretical Description
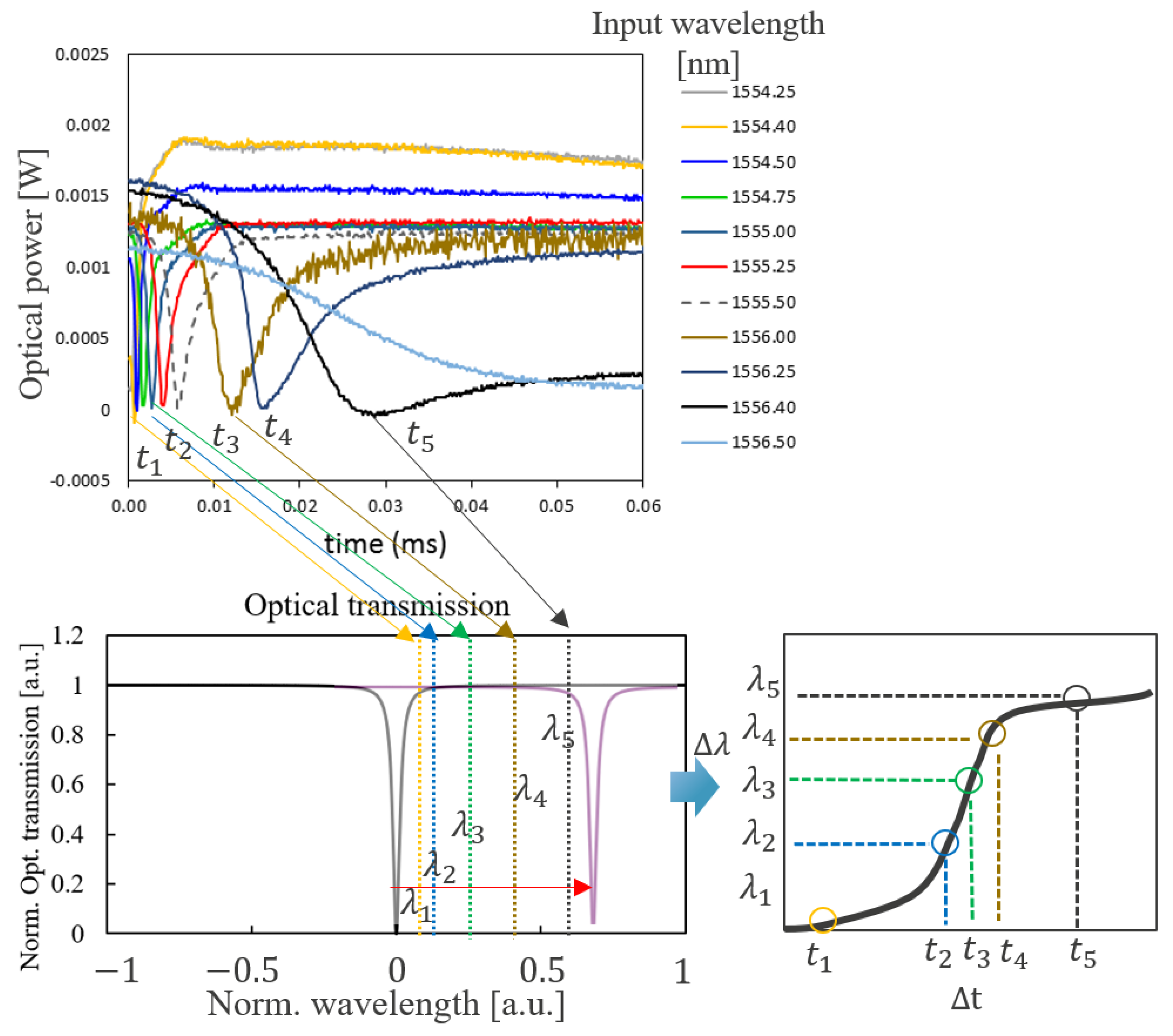
3.2. Dynamic Characterization Method
3.3. Problem Inversion
3.4. Alternative Dynamic Characterization Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SiPho | Silicon photonics |
| I/O | Input and output |
| WDM | Wavelength division multiplexing |
| BOX | Buried oxide |
| SOI | Silicon on insulator |
| RM | Ring modulator |
| TO | Thermo-optic |
| UCUT | Undercut |
| MHD | Metal heater |
| MZI | Mach–Zehnder interferometer |
References
- Rakowski, M.; Ban, Y.; De Heyn, P.; Pantano, N.; Snyder, B.; Balakrishnan, S.; Van Huylenbroeck, S.; Bogaerts, L.; Demeurisse, C.; Inoue, F.; et al. Hybrid 14 nm FinFET–Silicon Photonics Technology for Low-Power Tb/s/mm2 Optical I/O. In Proceedings of the 2018 IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 18–22 June 2018. [Google Scholar]
- Coenen, D.; Kim, M.; Oprins, H.; Ban, Y.; Velenis, D.; Van Campenhout, J.; De Wolf, I. Thermal Impact of 3D Hybrid Photonic-Electronic Integration on Ring Modulators. SPIE J. Opt. Microsyst. 2024, 4, 011004. [Google Scholar]
- Nagarajan, R.; Ding, L.; Coccioli, R.; Kato, M.; Tan, R.; Tumne, P.; Patterson, M.; Liu, L. 2.5D Heterogeneous Integration for Silicon Photonics Engines in Optical Transceivers. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 8200209. [Google Scholar] [CrossRef]
- Ferraro, F.J.; De Heyn, P.; Kim, M.; Rajasekaran, N.; Berciano, M.; Muliuk, G.; Bode, D.; Lepage, G.; Janssen, S.; Magdziak, R.; et al. Imec silicon photonics platforms: Performance overview and roadmap. In Proceedings of the SPIE 12429, Next-Generation Optical Communication: Components, Sub-Systems, and Systems XII, San Francisco, CA, USA, 31 January–2 February 2023. [Google Scholar]
- Masood, A.; Pantouvaki, M.; Goossens, D.; Lepage, G.; Verheyen, P.; Van Thourhout, D.; Absil, P.; Bogaerts, W. CMOS-compatible Tungsten heaters for silicon photonic waveguides. In Proceedings of the 9th International Conference on Group IV Photonics, San Diego, CA, USA, 29–31 August 2012. [Google Scholar]
- Masood, A.; Pantouvaki, M.; Lepage, G.; Verheyen, P.; Van Campenhout, J.; Absil, P.; Van Thourhout, D.; Bogaerts, W. Comparison of heater architectures for thermal control of silicon photonic circuits. In Proceedings of the 10th International Conference on Group IV Photonics, Seoul, Republic of Korea, 28–30 August 2013. [Google Scholar]
- Dourado, D.M.; Rocha, M.L.; Carmo, J.P.P. Mach-Zehnder modulator modeling based on imec-ePixFab ISIPP25G SiPhotonics. In Proceedings of the 2018 SBFoton International Optics and Photonics Conference (SBFoton IOPC), Campinas, Brazil, 8–10 October 2018. [Google Scholar]
- Liu, S.; Tian, Y.; Lu, Y.; Feng, J. Comparison of thermos-optic phase-shifters implemented on CUMEC silicon photonics platform. In Proceedings of the Seventh Symposium on Novel Photoelectronic Detection Technology and Application, Kunming, China, 5–7 November 2020. [Google Scholar]
- Fang, Q.; Song, J.F.; Liow, T.Y.; Cai, H.; Yu, M.B.; Lo, G.Q.; Kwong, D.L. Ultralow power silicon photonics thermo-optic switch with suspended phase arms. IEEE Photonics Technol. Lett. 2011, 23, 525–527. [Google Scholar] [CrossRef]
- Lu, Z.; Murray, K.; Jayatilleka, H.; Chrostowski, L. Michelson inter ferometer thermo-optic switch on SOI with a 50-uW power consumption. In Proceedings of the 2016 IEEE Photonics Conference (IPC), Waikoloa, HI, USA, 2–6 October 2016. [Google Scholar]
- Celo, D.; Goodwill, D.J.; Jiang, J.; Dumais, P.; Li, M.; Bernier, E. Thermo-optic silicon photonics with low power and extreme resilience to over-drive. In Proceedings of the 2016 IEEE Optical Interconnects Conference (OI), San Diego, CA, USA, 9–11 May 2016. [Google Scholar]
- Murray, K.; Lu, Z.; Jayatilleka, H.; Chrostowski, L. Dense dissimilar waveguide routing for highly efficient thermo-optic switches on silicon. Opt. Express 2015, 23, 19575–19585. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Feng, J.; Tian, Y.; Zhao, H.; Jin, L.; Ouyang, B.; Zhu, J.; Guo, J. Thermo-optic phase shifters based on silicon-on-insulator platform: State-of-the-art and a review. Front. Optoelectron. 2022, 15, 9. [Google Scholar] [CrossRef] [PubMed]
- Yue, W.; Cai, Y.; Yu, M. Review of 2 × 2 Silicon Photonic Switches. Photonics 2023, 10, 564. [Google Scholar] [CrossRef]
- Tong, W.; Wei, Y.; Zhou, H.; Dong, J.; Zhang, X. The Design of a Low-Loss, Fast-Response, Metal Thermo-Optic Phase Shifter Based on Coupled-Mode Theory. Photonics 2022, 9, 447. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer, 5th ed.; Mc Graw Hill: New York, NY, USA, 2015; pp. 74–237. [Google Scholar]
- Ducournau, G.; Latry, O.; Ketata, M. The All-fiber MZI Structure for Optical DPSK Demodulation and Optical PSBT Encoding. Syst. Inform. 2013, 4, 79–89. [Google Scholar]
- Coenen, D.; Kim, M.; Oprins, H.; Croes, K.; De Heyn, P.; Van Campenhout, J.; De Wolf, I. Static and Dynamic Thermal Modelling of Si Photonic Thermo-Optic Phase Shifter. In Proceedings of the 2024 23rd IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (iTherm), Denver, CO, USA, 28–31 May 2023. [Google Scholar]
- MSC Software Corporation, Marc: Advanced Nonlinear Simulation Solution. Available online: https://www.mscsoftware.com/product/marc (accessed on 4 May 2022).
- Coenen, D.; Oprins, H.; Ban, Y.; Ferraro, F.; Pantouvaki, M.; Van Campenhout, J.; De Wolf, I. Thermal modelling of Silicon Photonic Ring Modulator with Substrate Undercut. IEEE J. Lightwave Technol. 2022, 40, 4357–4363. [Google Scholar] [CrossRef]
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Kumar Selvaraja, S.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Coenen, D.; Kim, M.; Oprins, H.; Van Campenhout, J.; De Wolf, I. Coupled Dynamic Thermo-Optical Analysis and Compact Modelling of Self-Heating in Ring Modulator. In Proceedings of the 2023 International Conference on Photonics in Switching and Computing (PSC), Mantova, Italy, 26–29 September 2023. [Google Scholar]
- Martinez-Hernandez, H.D.; Martinez-Munoz, P.E.; Ramirez-Gutierrez, C.F.; Martinez-Ascencio, E.U.; Millan-Malo, B.M.; Rodriguez-Garcia, M.E. Effect of Intrinsic and Extrinsic Defects on the Structural, Thermal, and Electrical Properties in p-Type CZ-Si Wafers with Different Carrier Concentrations. Int. J. Thermophys. 2022, 43, 181. [Google Scholar] [CrossRef]
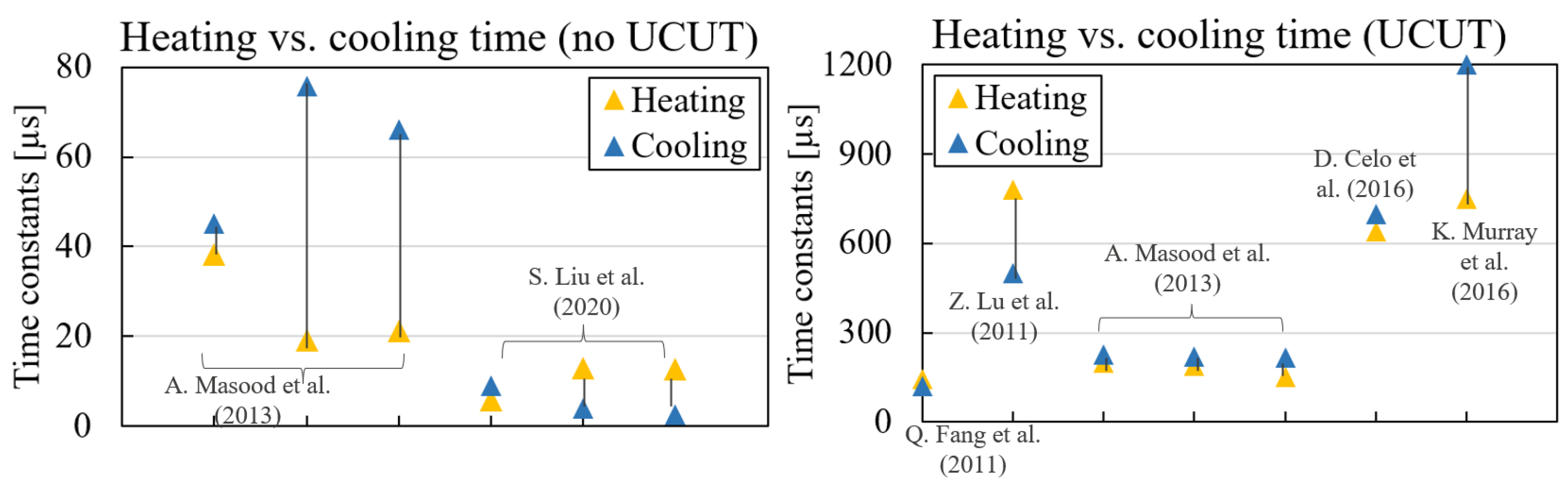
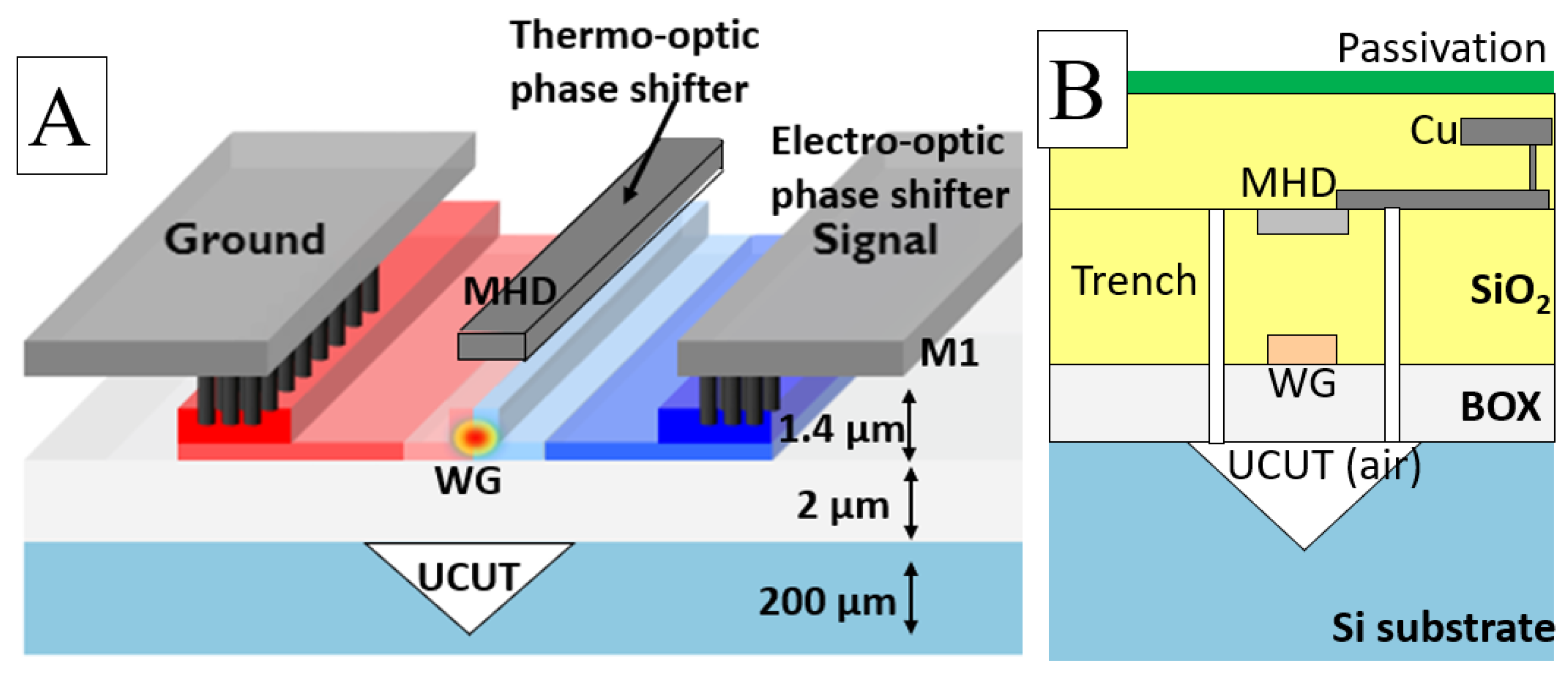
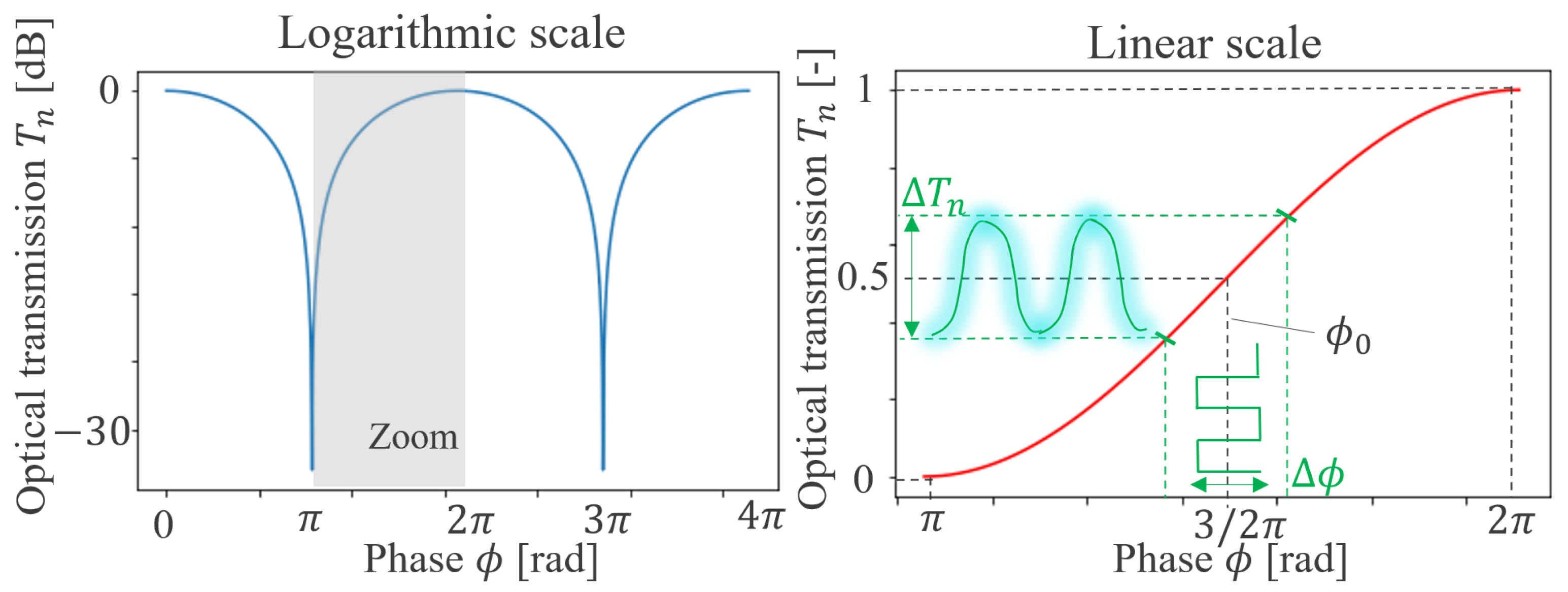

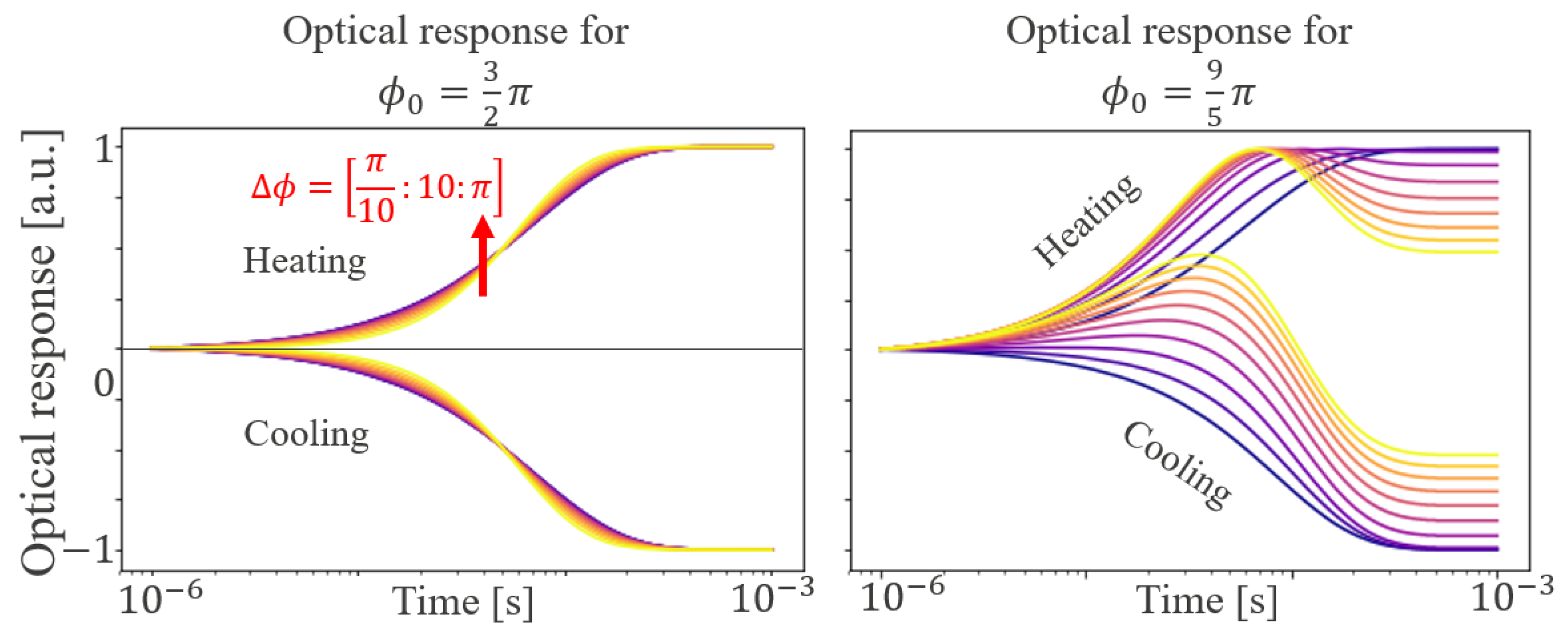


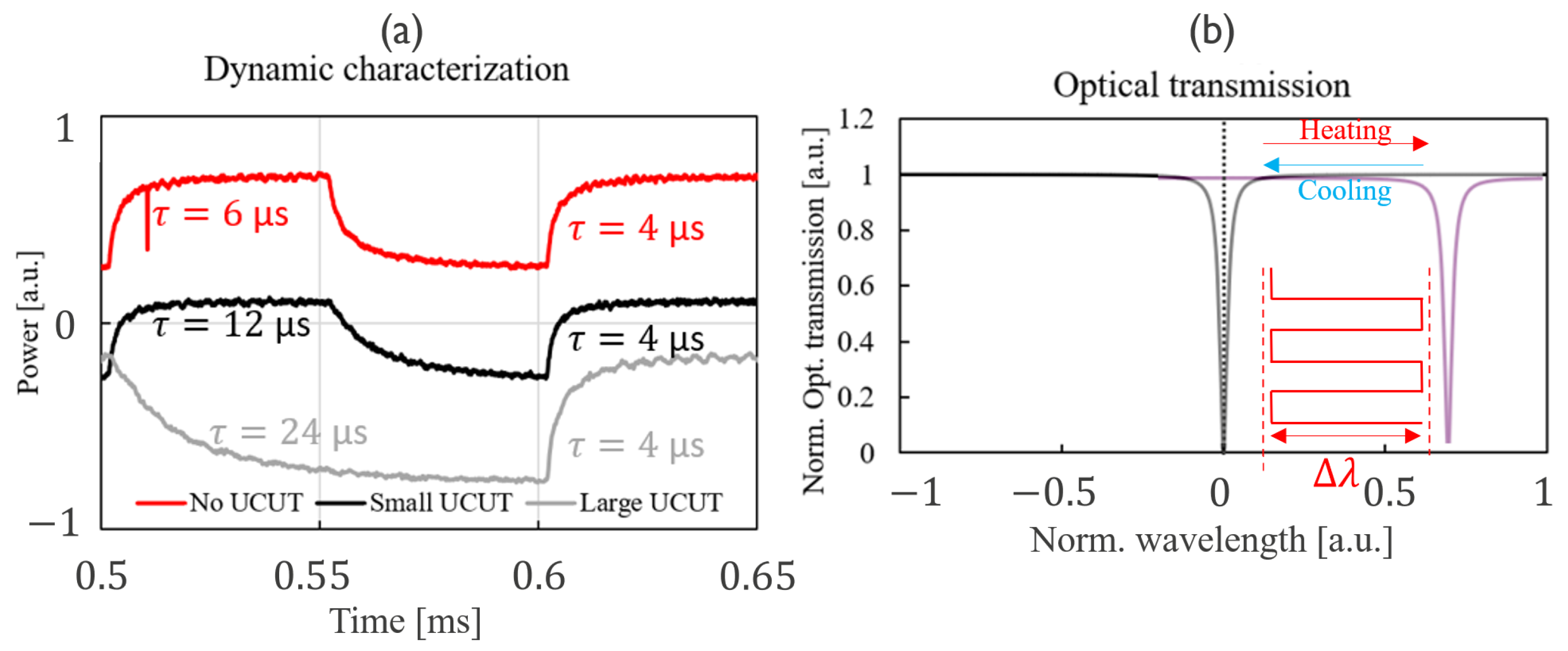

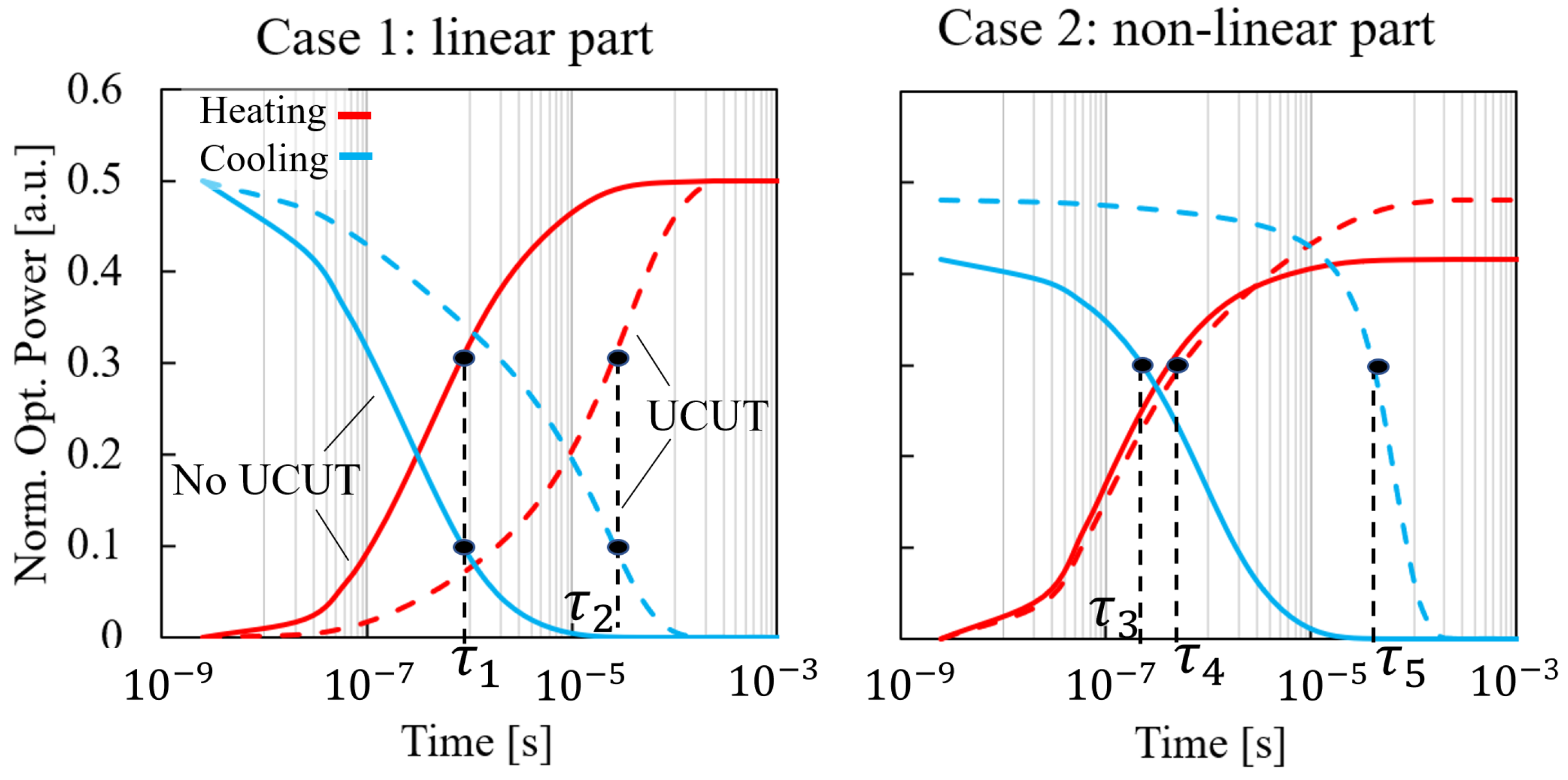
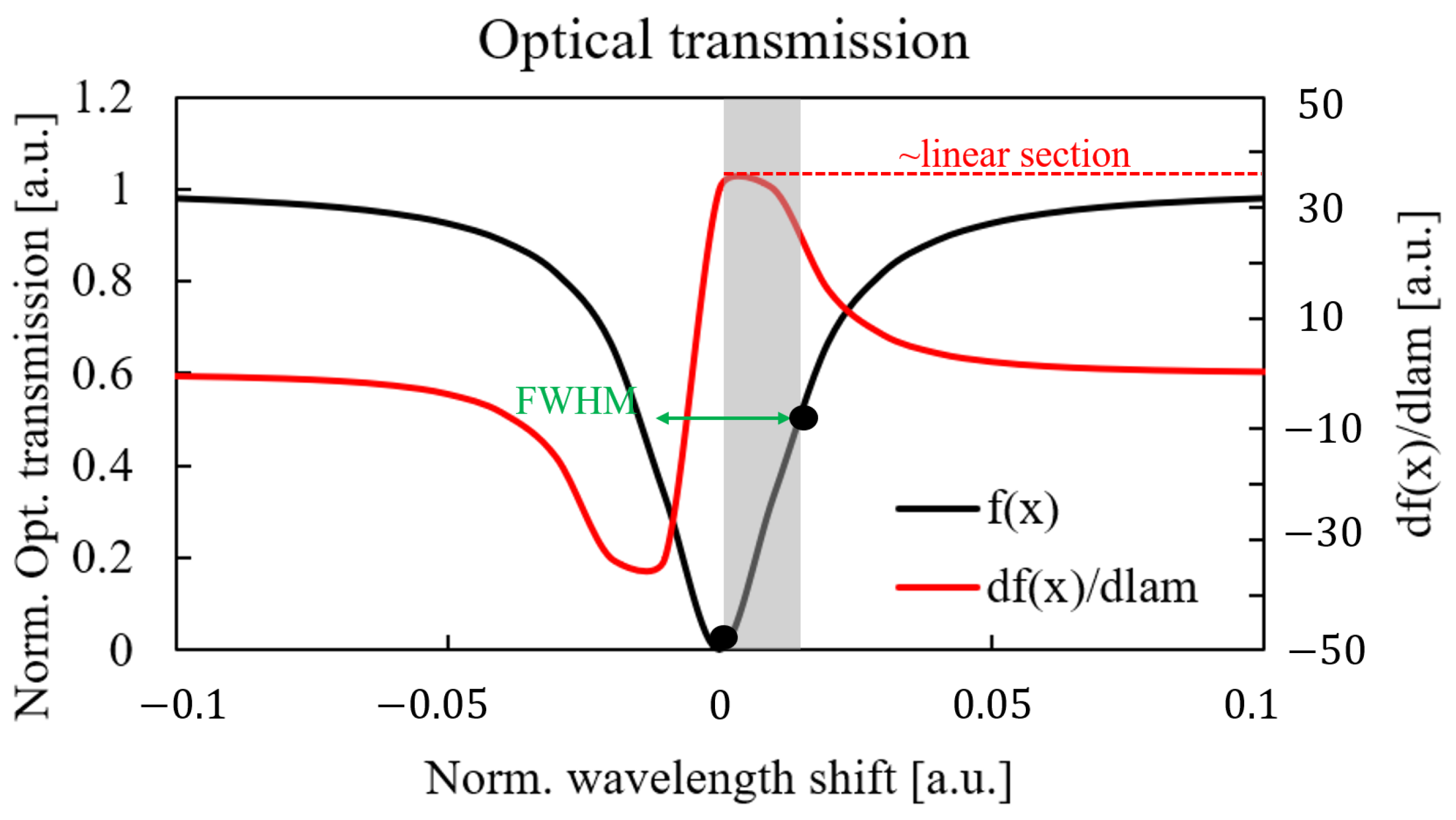
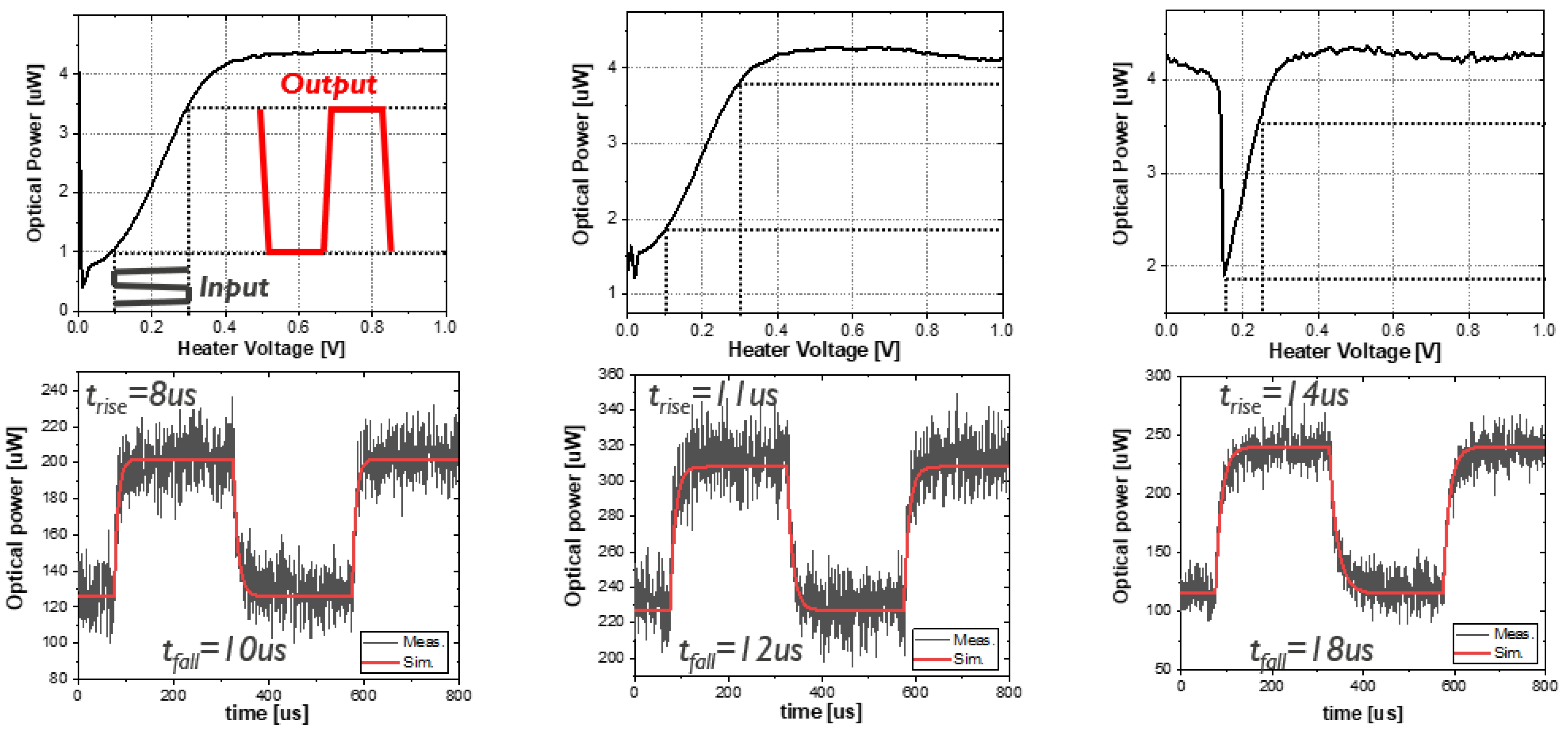
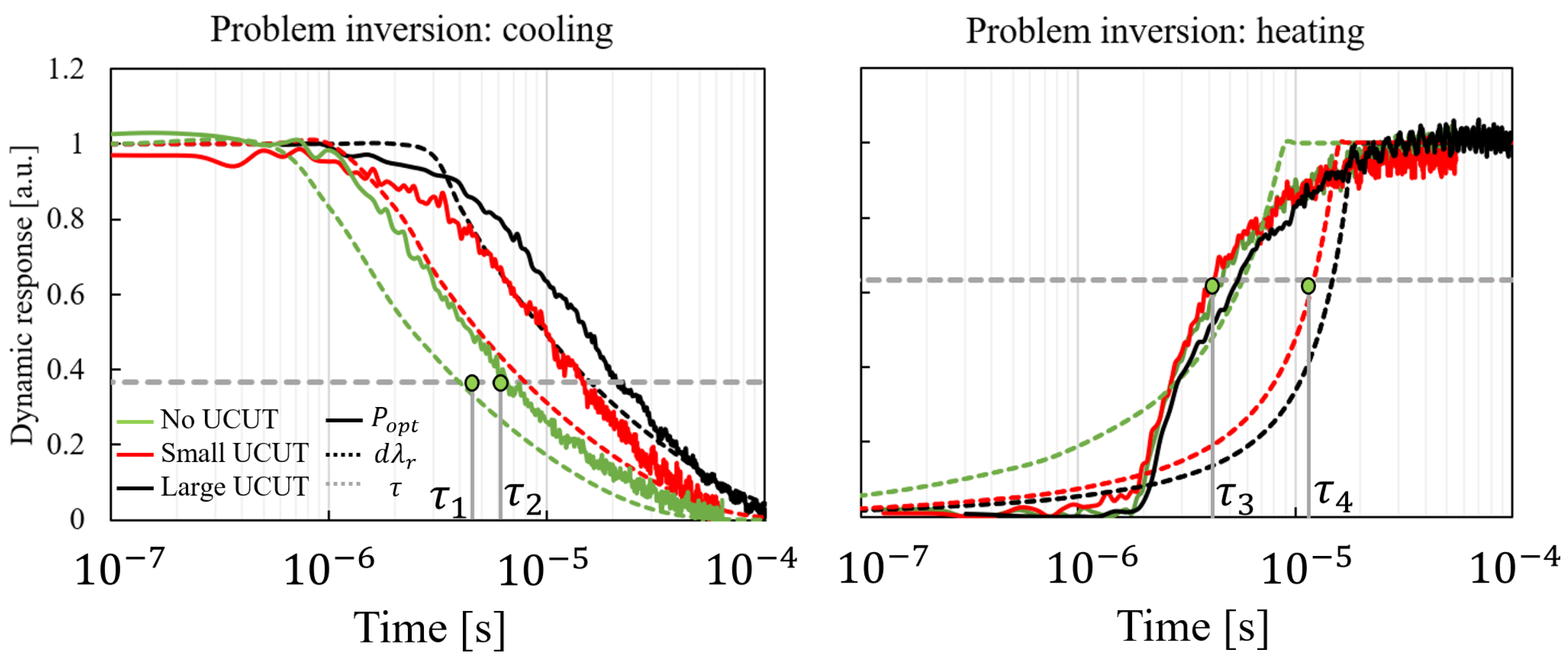
| Case 1 | Case 2 | |||
|---|---|---|---|---|
| Heating | Cooling | Heating | Cooling | |
| No UCUT | 6 | 6 | 0.3 | 4.8 |
| UCUT | 28 | 28 | 0.6 | 66.2 |
| Cooling | Heating | |||
|---|---|---|---|---|
| Exp. | Converted | Exp. | Converted | |
| No UCUT | 6 | 5 | 4 | 5 |
| Small UCUT | 12 | 9 | 4 | 9 |
| Large UCUT | 24 | 18 | 4 | 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coenen, D.; Kim, M.; Oprins, H.; Van Campenhout, J.; De Wolf, I. A Critical Analysis of the Thermo-Optic Time Constant in Si Photonic Devices. Photonics 2024, 11, 603. https://doi.org/10.3390/photonics11070603
Coenen D, Kim M, Oprins H, Van Campenhout J, De Wolf I. A Critical Analysis of the Thermo-Optic Time Constant in Si Photonic Devices. Photonics. 2024; 11(7):603. https://doi.org/10.3390/photonics11070603
Chicago/Turabian StyleCoenen, David, Minkyu Kim, Herman Oprins, Joris Van Campenhout, and Ingrid De Wolf. 2024. "A Critical Analysis of the Thermo-Optic Time Constant in Si Photonic Devices" Photonics 11, no. 7: 603. https://doi.org/10.3390/photonics11070603
APA StyleCoenen, D., Kim, M., Oprins, H., Van Campenhout, J., & De Wolf, I. (2024). A Critical Analysis of the Thermo-Optic Time Constant in Si Photonic Devices. Photonics, 11(7), 603. https://doi.org/10.3390/photonics11070603





