Study on the Robustness of an Atmospheric Scattering Model under Single Transmittance
Abstract
1. Introduction
- In a haze image, it is always possible to find a sufficiently small region in which the transmittance of the haze can be regarded as a constant. That is, any haze image can be equivalent to a combination of multiple single transmittance images. Therefore, it is of great significance to study the image dehazing model under a single transmittance to improve the dehazing model for any hazy image.
- In the usual haze image, the distance between each target and the detector is inconsistent, resulting in the transmittance of atmospheric light and haze changing with the spatial position. In this case, the error of parameter estimation at any position in the image will cause the recovery accuracy to decrease. Therefore, it is difficult to quantitatively evaluate the influence of parameter estimation bias on image restoration accuracy by using this kind of image dehazing. When a fog image with a single transmittance is used to analyze the dehazing model, the parameters in the model no longer change with space. It is helpful to quantitatively analyze the influence of atmospheric light parameters and transmittance parameters on recovery accuracy.
- Multiple target images in a haze environment with single transmittance (transmittance 0.05 to 1, step size 0.05) were obtained through laboratory experiments. The atmospheric scattering model and image degradation model were used to restore the hazed image, and the optimal restoration results of the two models were explored under the parameter range and precision settings.
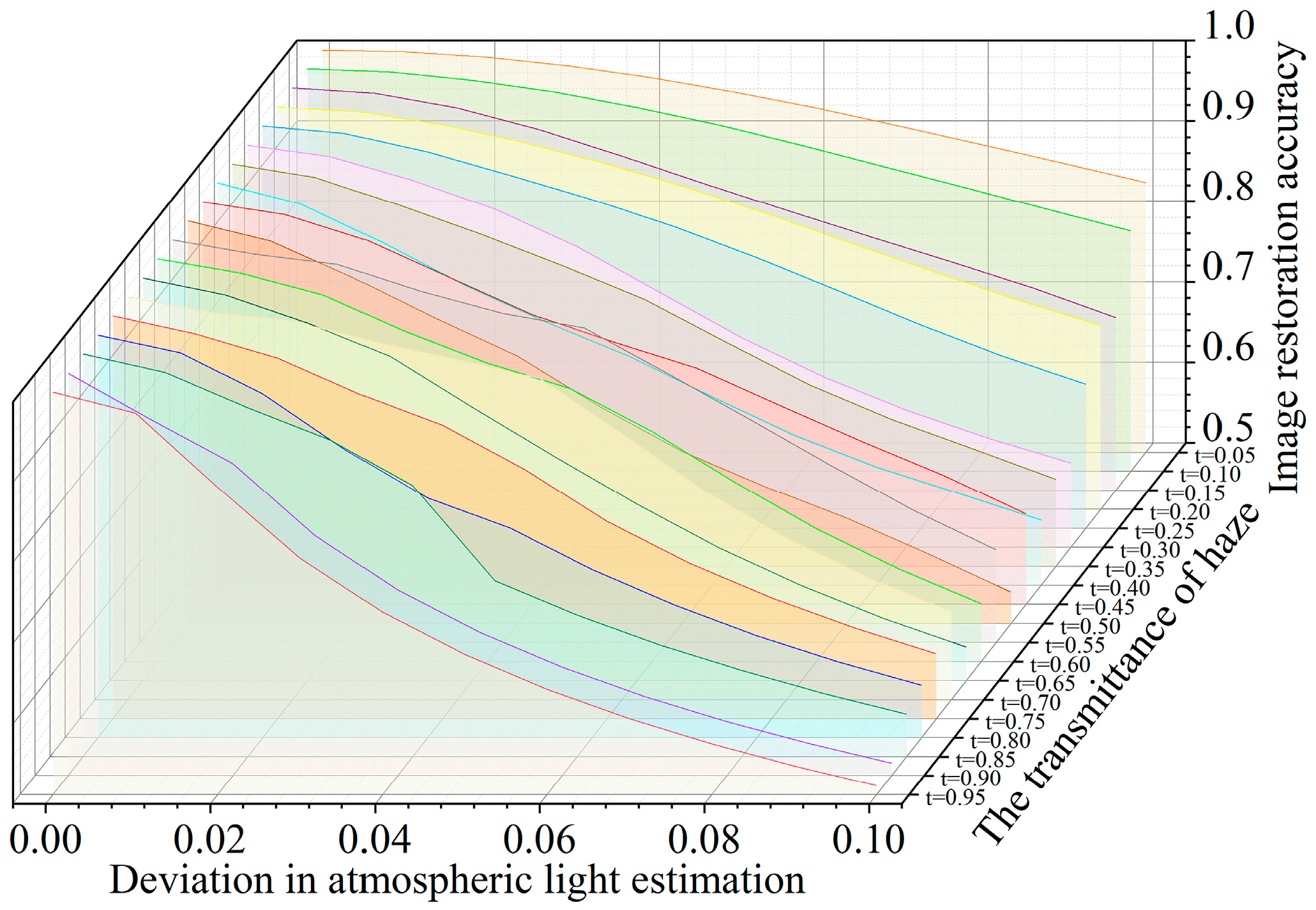
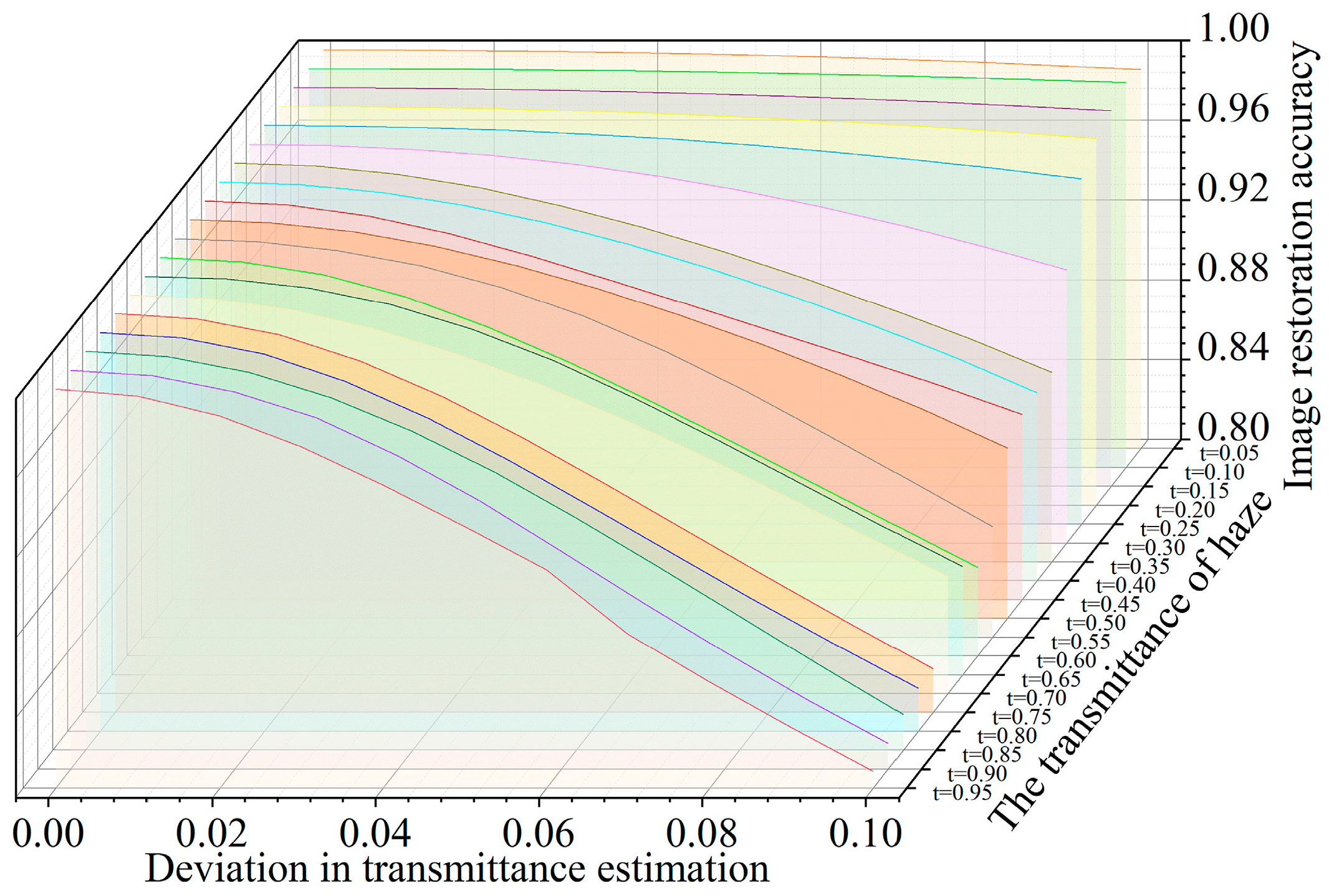
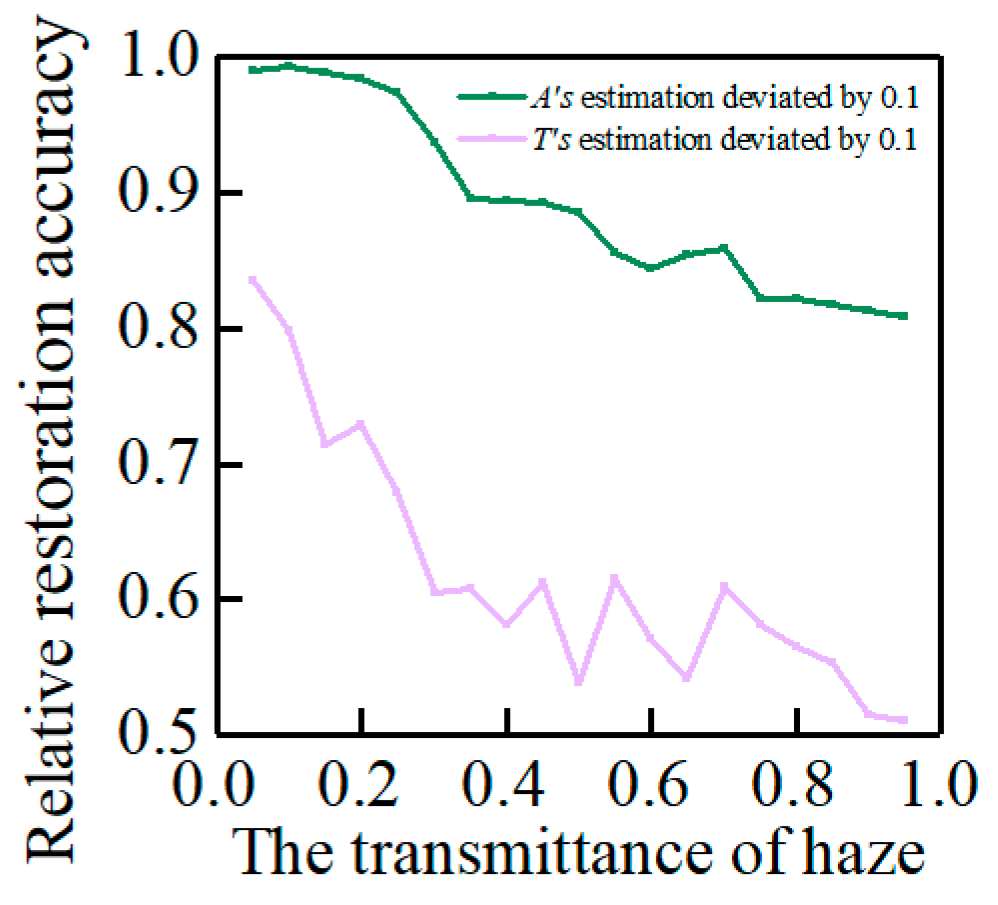
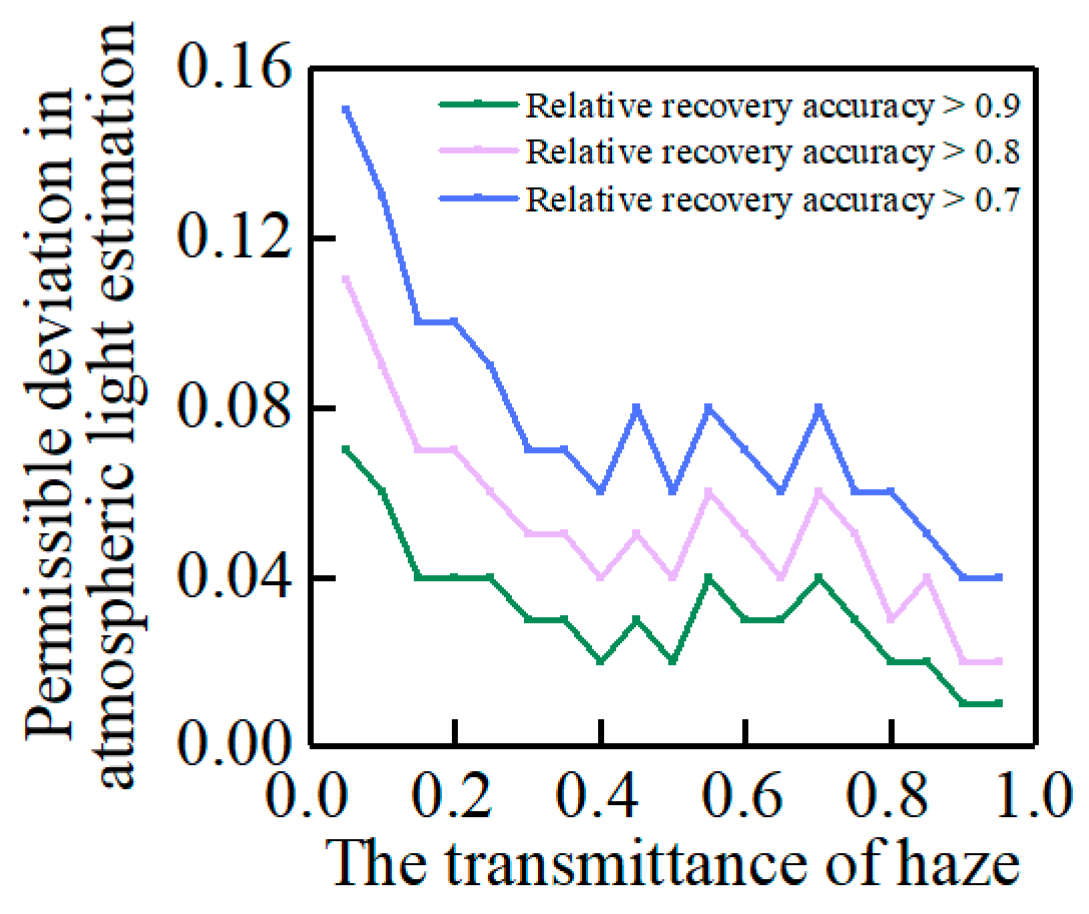
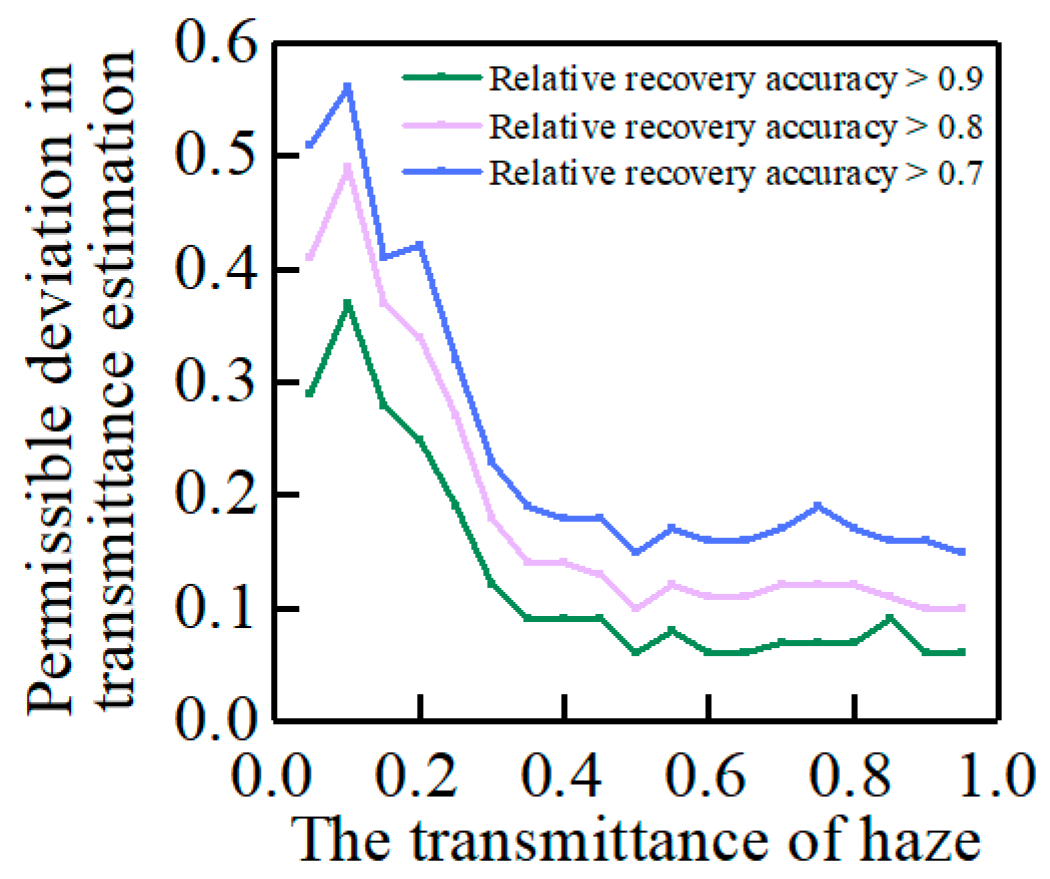
- The stability of the dehazing effect of the atmospheric scattering model under a single transmittance was studied. We studied the image recovery accuracy of atmospheric light and transmittance in an atmospheric scattering model with estimation deviation. In the case of each transmittance, the permissible deviation of parameter estimation was explored when the recovery accuracy was within 90%, 80%, and 70% of the best accuracy.
2. Methods
2.1. Linear Degradation Model of Image in Haze
2.2. Atmospheric Scattering Model
2.3. Evaluation Method of Image Dehazing
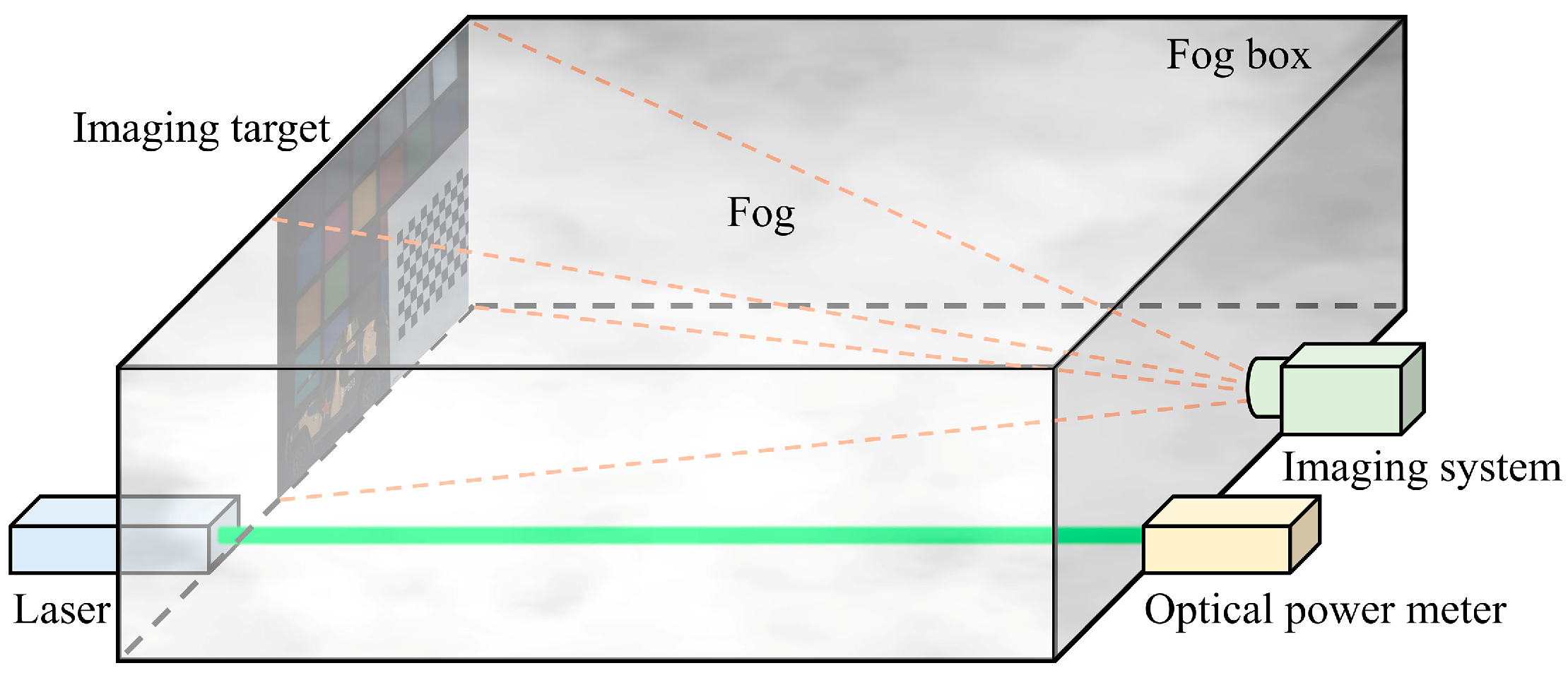
2.4. Imaging Experiment in Haze Environment with Single Transmittance
3. Results and Discussion
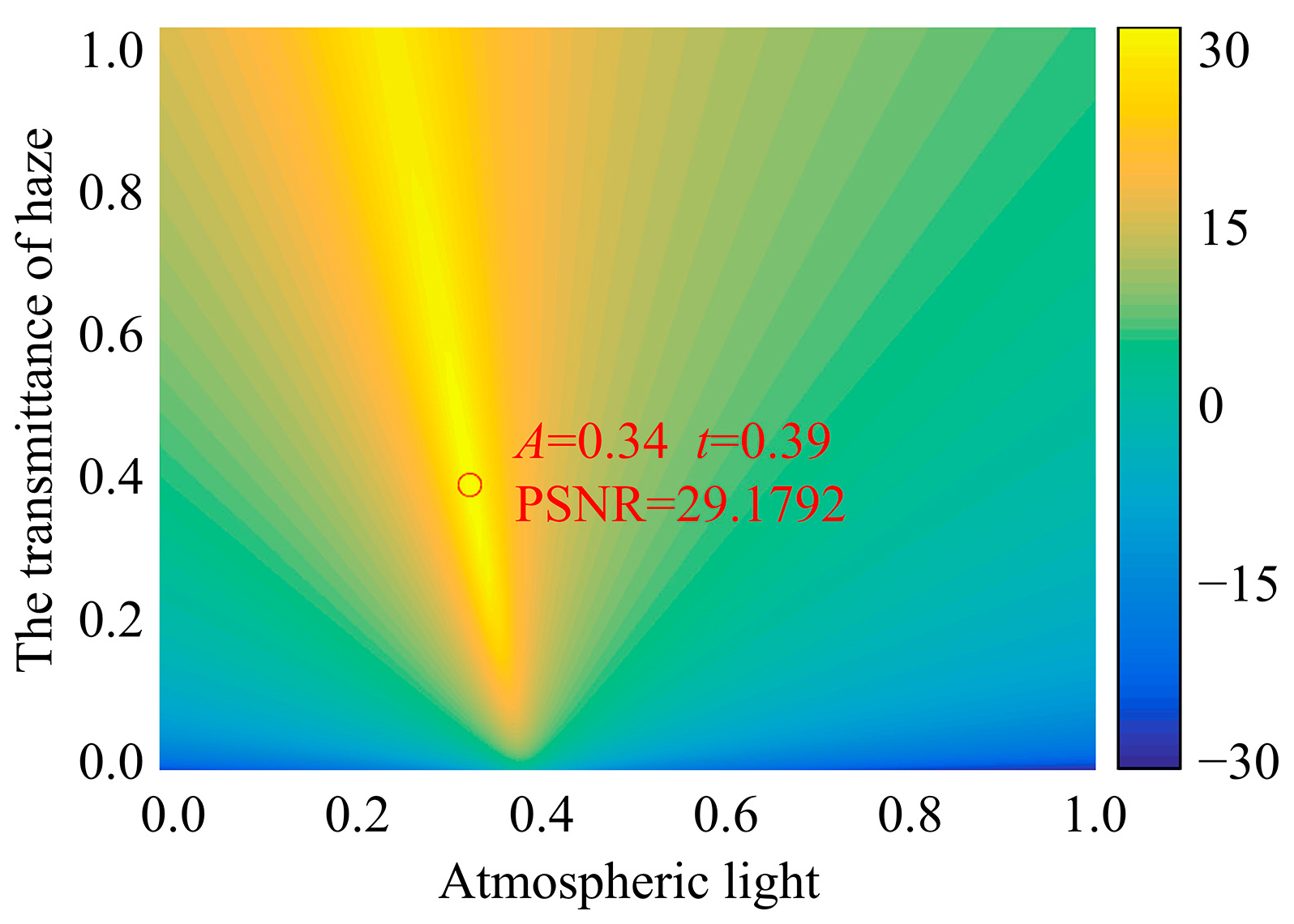
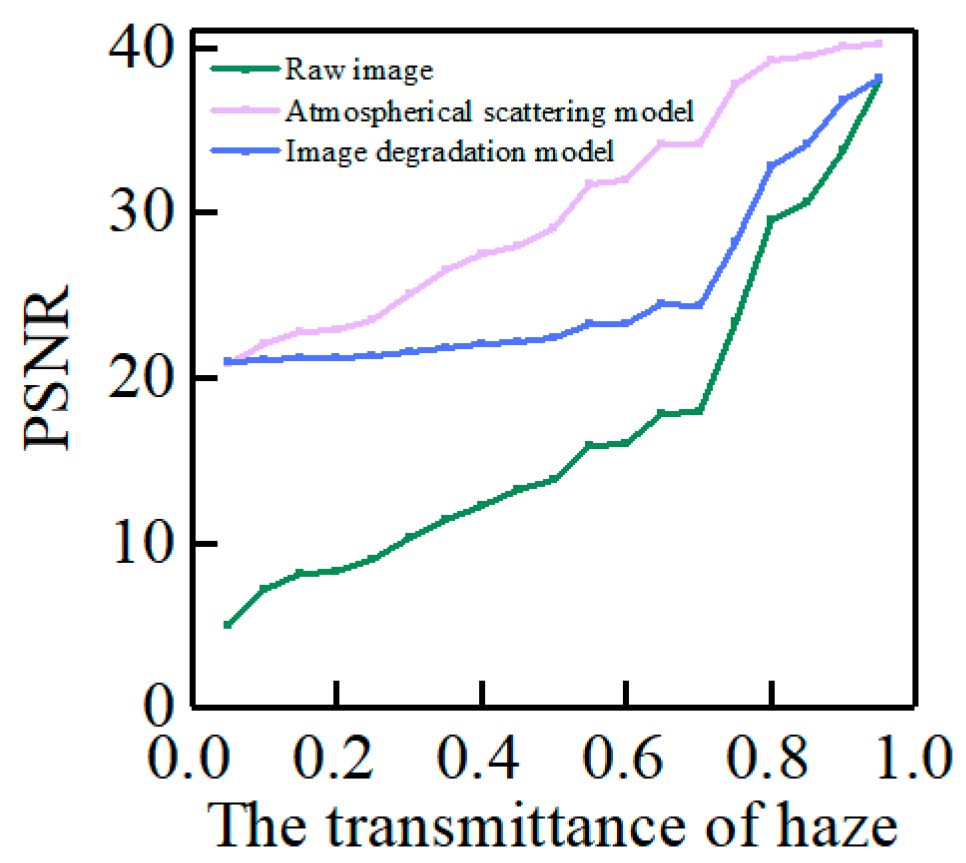
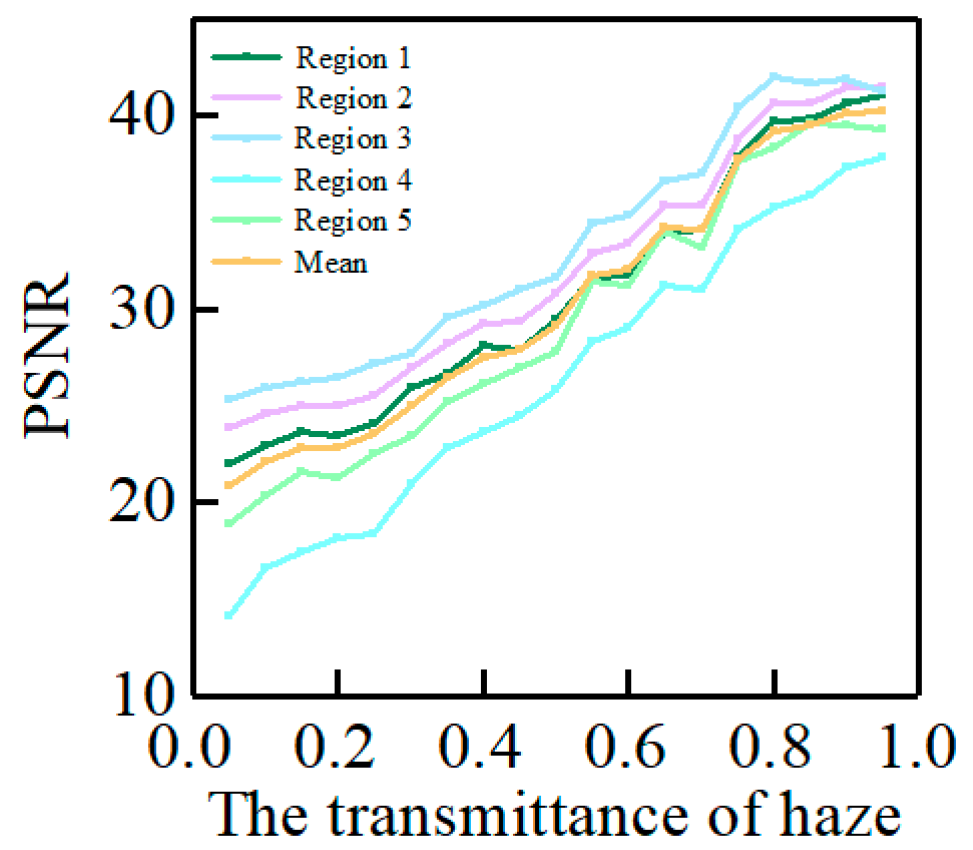
3.1. Recovery Effect of Atmospheric Scattering Model under Single Haze Transmittance
3.2. Recovery Effect of Atmospheric Scattering Model under Single Haze Transmittance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, X.; Yang, Y.; Wang, C.; Ma, J. Image dehazing via enhancement, restoration, and fusion: A survey. Inf. Fusion 2022, 87, 146–170. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, J.; Wu, X.; Huang, M. Numerical analysis of light reflection and transmission in poly-disperse sea fog. Opt. Express 2020, 28, 25410–25430. [Google Scholar] [CrossRef] [PubMed]
- Jaffe, J.S. Underwater Optical Imaging: The Past, the Present, and the Prospects. IEEE J. Ocean. Eng. 2015, 40, 683–700. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, Z.; Zhao, K.; Tian, H. Lane detection in dense fog using a polarimetric dehazing method. Appl. Opt. 2020, 59, 5702–5707. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.; Liao, T.; Fan, Z.; Zhang, X.; Wang, C. Polarization dehazing method based on separating and iterative optimizing airlight from the frequency domain for different concentrations of haze. Appl. Opt. 2022, 61, 10362–10373. [Google Scholar] [CrossRef] [PubMed]
- Qu, Y.; Zou, Z. Non-sky polarization-based dehazing algorithm for non-specular objects using polarization difference and global scene feature. Opt. Express 2017, 25, 25004–25022. [Google Scholar] [CrossRef] [PubMed]
- Fang, S.; Xia, X.; Huo, X.; Chen, C. Image dehazing using polarization effects of objects and airlight. Opt. Express 2014, 22, 19523–19537. [Google Scholar] [CrossRef] [PubMed]
- Schechner, Y.; Narasimhan, S.; Nayar, S. Polarization-based vision through haze. Appl. Opt. 2003, 42, 511–525. [Google Scholar] [CrossRef]
- Fade, J.; Panigrahi, S.; Carré, A.; Frein, L.; Hamel, C.; Bretenaker, F.; Ramachandran, H.; Alouini, M. Long-range polarimetric imaging through fog. Appl. Opt. 2014, 53, 3854–3865. [Google Scholar] [CrossRef]
- Liang, J.; Ren, L.; Ju, H.; Zhang, W.; Qu, E. Polarimetric dehazing method for dense haze removal based on distribution analysis of angle of polarization. Opt. Express 2015, 23, 26146–26157. [Google Scholar] [CrossRef]
- Wang, H.; Hu, H.; Jiang, J.; Li, X.; Zhang, W.; Cheng, Z.; Liu, T. Automatic underwater polarization imaging without background region or any prior. Opt. Express 2021, 29, 31283–31295. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar] [PubMed]
- Zhu, Q.; Mai, J.; Shao, L. A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior. IEEE Trans. Image Process. 2015, 24, 3522–3533. [Google Scholar] [PubMed]
- Cheng, S.; Yang, B. An efficient single image dehazing algorithm based on transmission map estimation with image fusion. Eng. Sci. Technol. Int. J. 2022, 35, 101190. [Google Scholar] [CrossRef]
- Zhu, Z.; Luo, Y.; Wei, H.; Li, Y.; Qi, G.; Mazur, N.; Li, Y.; Li, P. Atmospheric light estimation based remote sensing image dehazing. Remote Sens. 2021, 13, 2432. [Google Scholar] [CrossRef]
- Zhu, Z.; Wei, H.; Hu, G.; Li, Y.; Qi, G.; Mazur, N. A novel fast single image dehazing algorithm based on artificial multiexposure image fusion. IEEE Trans. Instrum. Meas. 2021, 70, 1–23. [Google Scholar] [CrossRef]
- Emberton, S.; Chittka, L.; Cavallaro, A. Underwater image and video dehazing with pure haze region segmentation. Comput. Vis. Image Underst. 2018, 168, 145–156. [Google Scholar] [CrossRef]
- Narasimhan, S.G.; Nayar, S.K. Vision and the Atmosphere. Int. J. Comput. Vis. 2002, 48, 233–254. [Google Scholar] [CrossRef]
- Shiao, Y.H.; Chen, T.J.; Chuang, K.S.; Lin, C.H.; Chuang, C.C. Quality of Compressed Medical Images. J. Digit. Imaging 2007, 20, 149–159. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a ‘Completely Blind’ Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Ming, Y.; Ju, L.; Chen, S. Study on the Robustness of an Atmospheric Scattering Model under Single Transmittance. Photonics 2024, 11, 515. https://doi.org/10.3390/photonics11060515
Shi X, Ming Y, Ju L, Chen S. Study on the Robustness of an Atmospheric Scattering Model under Single Transmittance. Photonics. 2024; 11(6):515. https://doi.org/10.3390/photonics11060515
Chicago/Turabian StyleShi, Xiaotian, Yue Ming, Lin Ju, and Shouqian Chen. 2024. "Study on the Robustness of an Atmospheric Scattering Model under Single Transmittance" Photonics 11, no. 6: 515. https://doi.org/10.3390/photonics11060515
APA StyleShi, X., Ming, Y., Ju, L., & Chen, S. (2024). Study on the Robustness of an Atmospheric Scattering Model under Single Transmittance. Photonics, 11(6), 515. https://doi.org/10.3390/photonics11060515




