Abstract
The cavity form of complex microcavity lasers predominantly relies on disordered structures, whether found in nature or artificially prepared. These structures, characterized by disorder, facilitate random lasing through the feedback effect of the cavity boundary and the internal scattering medium via various mechanisms. In this paper, we report on a random fiber laser employing a disordered scattering cladding medium affixed to the inner cladding of a hollow-core fiber. The internal flowing liquid gain establishes a stable liquid-core waveguide environment, enabling long-term directional coupling output for random laser emission. Through theoretical analysis and experimental validation, we demonstrate that controlling the disorder at the cavity boundary allows liquid-core fiber random microcavities to exhibit random lasing output with different mechanisms. This provides a broad platform for in-depth research into the generation and control of complex microcavity lasers, as well as the detection of scattered matter within micro- and nanostructures.
1. Introduction
Lasers consist of three fundamental elements: pump sources, a gain medium that amplifies stimulated radiation, and cavity structures that generate optical resonance. The conventional design of the laser cavity necessitates precise symmetrical distribution, a fixed geometrical configuration, and a stable active medium, thereby ensuring the stability and coherence of resonance mechanisms and associated output parameters [1,2]. In contrast, complex disordered systems, prevalent in both natural and artificial environments, have garnered significant attention for their potential to enable new characteristics and functions of lasers. These systems can facilitate symmetry breaking, random lasers, chaotic light sources, strange waves, and neuron-like events [3,4,5,6,7,8,9]. Such phenomena result in an unpredictable laser output and disordered parameters. However, efficient laser output characteristics can also be introduced, enabling the production of high-quality lasers with low thresholds and directional output, thereby enhancing the flexibility of the lasing control method [10,11].
When the cavity size of lasers tends to be micrometers or even sub-micrometers, microcavity lasers have emerged, in which the compact internal environment will produce rich light-matter interactions [12,13,14]. By confining the complex disordered medium inside the microcavity, the output of the microcavity laser will exhibit a variety of complex characteristics as the disorder degree of the cavity boundary and the internal medium changes [15,16,17,18]. Disordered microcavities can induce quantum and photon confinement, offering broad application prospects in optical integration, optical interconnections, optical neural networks, optical display, and optical communications [19,20,21,22,23].
For example, laser emission is usually isotropic in the plane due to the rotational symmetry of the cavity structure in whispering gallery mode (WGM) lasers, resulting in very low collection efficiency in free space. When the cavity boundaries of microcavity lasers are partially disordered, the originally closed optical systems are more prone to be excited and coupled [24,25]. During this time, the output laser modes are stable, accompanied by improved laser efficiency, directional radiation, and tunable wavelength [26,27,28]. Furthermore, when the cavity boundary reaches a completely disordered state, the complex microcavity boundary scattering system and intra-cavity gain medium lead to a resonant amplification process of free-roaming photons, which becomes the main condition for forming random lasers [29,30]. The random laser, based on the scattering system, exhibits the characteristics of high extinction cross-section and ultra-small mode volume. Therefore, random lasers with high light harvesting and scattering capabilities have excellent upfront potential in achieving ultralow threshold and high-quality factor lasing. Additionally, the laser directivity, mode characteristics, and other parameters exhibit unpredictable disordered output characteristics, providing a greater degree of freedom for the parameter control of random lasers [31,32,33].
In terms of applications, incoherent random lasers relying on a weak scattering system, which demonstrate extremely low spatial coherence [34], high spectral density, and no diffraction limitation [35], are suitable for applications such as full-field speckle-free imaging, speckle correlation imaging, and speckle-illumination imaging [36,37]. When the disorder state of the scattering system changes, multi-longitudinal mode random lasers with low temporal coherence emerge based on the coherent feedback system in a strong optical scattering environment, which is of great significance for secure communications, precision measurement, and medical diagnosis [38,39,40,41]. With the alteration of the scattering characteristics within the microcavity, the corresponding mechanism of the random laser can adeptly discern various sensitive indicators of the external environment and efficiently provide directional output, harnessing the waveguide effect of the one-dimensional carrier. This process establishes superior platforms for realizing high-sensitivity sensing applications. Nevertheless, the present solution, predicated on an integrated filling within the optical fiber, conflates scattering and gain media, impeding the exploration and application of laser characteristics sensitive to the axial environment [42,43]. Hence, further in-depth exploration and research are imperative to understand the microcavity disorder distribution and its corresponding random laser mechanism.
In this work, we report a boundary feedback fiber-type random microcavity laser with tunable coherence properties. High refractive index scattering particles are affixed to the inner wall of the hollow-core fiber (HCF), forming a disordered inner cladding structure that furnishes feedback for the multi-mechanism resonance amplification of random lasing. As the disorder of the inner cladding structure fluctuates, both theoretical and experimental results have proven that the random laser undergoes a transition from a localized regime to a diffusive regime. Microfluidic technology is used to replenish the liquid gain medium inside the random microcavity at any time, providing a gain and waveguide coupling environment for the random laser, and avoiding photobleaching. Consequently, the proposed random laser system offers a robust avenue for investigating the diverse mechanisms of the intricately stable microcavity complex laser reliant on disordered media. Complex and variable laser localization characteristics also pave the way for detecting scattered particles within micro-nano structures, which is beneficial for environmentally sensitive detection and sensing scenarios.
2. Experimental Setup and Results
The HCF chosen for the experiment features an inner diameter of 150 μm and an outer diameter of 365 μm. The optical ultraviolet glue has a refractive index of 1.5 and can solidify within 30 s under the irradiation of a 5 W UV lamp. The selected TiO2 particles with an average diameter of 50 nm were thoroughly dried and ground, and then fully mixed with UV glue to form a suspension with a ratio of 1:4. After undergoing stirring and ultra-sonic treatment for 30 min, the TiO2 nanoparticles were mixed evenly and did not form large-sized cluster structures. The suspension was subsequently applied to one end of the HCF and filled through a syringe. The microstructure is depicted in Figure 1a. The syringe was linked to an air pump with a controllable flow rate, and a significant portion of the suspension was discharged from the microcavity with a uniform airflow. The airflow inside and outside the cavity was communicated to form a wind tunnel structure.
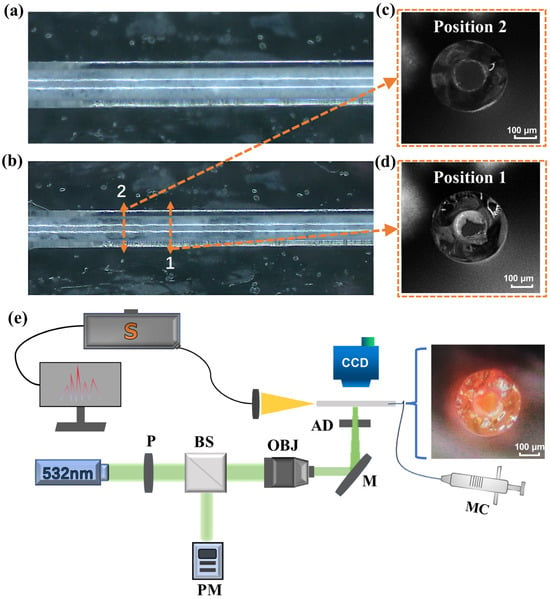
Figure 1.
Configuration and basic features of the fiber random microcavity. (a) The axial microscopic image of HCF filled with suspension. (b) The axial microscopic images of optical fiber random microcavities with different degrees of disorder formed by airflow modification. (c,d) Two random microcavity cross-sections of fiber random microcavities with different degrees of disorder. (e) Sketch of the basic experimental setup. P, polarizer. PBS, polarization beam splitter. BS, beam splitter. PM, power meter. OBJ, microscope objective. M, mirror. AD, Adjustable diaphragm. CCD, charge-coupled device, S, spectrometer. MC, microfluidic controller. The inset is a microscopic image of the end surface of the sample. From outside to inside, there are walls of HCF, disordered inner cladding, and the gain region.
At this point, a significant quantity of uniform TiO2 scattering coating remained on the cavity wall. Airflow with varying flow rates was employed to further erode the inner wall of the microcavity and modify the scattering coating into a disordered inner cladding structure with uneven thickness. The microcavity structure was subsequently solidified with an ultraviolet lamp to create an optical fiber random microcavity structure with a disordered boundary while ensuring air flow communication, as illustrated in Figure 1b. For the further examination of the cross-sectional morphology of the sample, the fiber was cut at a position where the two degrees of disorder in the fiber random microcavity were clearly distinguished, as depicted in Figure 1c,d, providing experimental support for the subsequent verification of the coherence of random lasers. In the experiment, 10 mM PM597 dye served as the gain medium of the random laser, and the peak of gain bandwidth is located near 580 nm. The microfluidic controller ensures that the gain solution is able to be replenished into the fiber random microcavity at any time, thereby mitigating solution volatilization and photobleaching induced by long-term pumping [43].
The experimental device utilized to excite the random microcavity of a liquid-core fiber random microcavity and induce the random lasing is depicted in Figure 1e. The enlarged inset depicts a microscopic image of the end surface of the liquid core microcavity, wherein the gain medium and the disordered inner cladding used for feedback are segregated to avoid crosstalk of the working medium. As the excitation pump, a 532 nm Q-switched laser with a pulse duration of 6 ns and an adjustable repetition frequency (1 to 5 Hz) is employed. The combination of a polarizer, beam splitter, objective lens group, and adjustable diaphragm facilitates the easy adjustment of the size, power, and position of the pump spot for sample excitation, as well as monitoring the power threshold of the generated laser light. A spectrometer (CHS-3000, made in Chang Hui, China, with a resolution of 0.2 nm) is used to receive random spectral information. The microfluidic controller ensures the replenishment of the liquid gain medium within the cavity.
In the experiment, the output spot diameter of the pump source was adjusted to 100 μm, and the repetition frequency was adjusted to 1 Hz. Figure 2a shows the spectrum received by the spectrometer after a single pulse excited position 1 in the fiber random microcavity. By adjusting the rotation angle of the wave plate, the pump energy used to excite the sample was gradually increased from below the random laser threshold. The pulse energy was detected by an optical power meter, and the average intensity of the single-shot spectrum peak at this time was recorded. As the pump energy increased, the spectrum evolved from amplified spontaneous emission (ASE) to random lasing with multiple longitudinal modes. This confirms that the local random microcavity can output random lasing with high coherence. The random microcavity boundary at position 1 is highly disordered and has a strong scattering feedback mechanism, i.e., a coherent random laser based on a localized regime. The relationship between the peak average photon number and the pump energy density is shown in Figure 2b. At a pump energy density of 0.35 mJ/cm2, an obvious kink in the input–output slope curve indicates the threshold point where spontaneous emission changed to stimulated emission. The full width at half-maximum (FWHM) also has an inflection point at the lasing threshold because the FWHM corresponds to the bandwidth of the ASE when working below the threshold, and it corresponds to the average linewidth of the random lasing modes when working above the threshold.
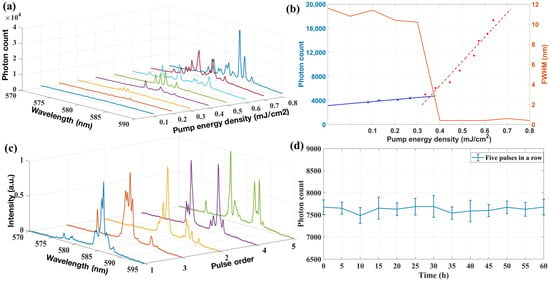
Figure 2.
The spectral properties produced by a coherent random laser based on a localized regime. (a) The spectra of random laser with different pump energy densities. (b) The average photon counts at the peaks as the pump energy density changes. (c) The excitation spectrum of five consecutive pulses during long-term segmental measurement. (d) The changing trend of the average peak photon counts of five consecutive pulses collected at different periods.
Many fluorescent dyes are susceptible to the photobleaching of the fluorescence signal during the lasing process. The photochemical destruction of a fluorophore manifests as an attenuation of the fluorescence signal due to covalent bond breakage or non-specific reactions between the fluorophore and surrounding molecules. In addition, the liquid gain medium in the cavity undergoes deactivation after long-term pumping due to the expansion and volatilization of ethanol molecules during instantaneous pumping. The above factors collectively impede the proposed random microcavity laser from producing long-term efficient lasing. In the experiment, an optical microfluidic technology was introduced to supplement and replace the deactivated gain medium. Figure 2c,d demonstrate that the random laser spectrum excited by five consecutive pulses was monitored every 5 h under stable pump energy excitation, and the average number of photons at the peak was recorded. When the microfluidic controller replenishes fresh gain media, the pump lasing of random microcavities can maintain a high-quality and stable output for dozens of hours, thus providing a method to achieve the energy robustness of random lasers.
The size of the spot remained unchanged throughout the experiment, and the pump excitation position was moved along the fiber axis to position 2. As the pump power density increases, the spectrum changes are shown in Figure 3a. Since the local inner cladding disorder at position 2 is relatively low and the corresponding scattering mechanism weakens, the random laser generated corresponds to the diffusive random laser with intensity feedback, manifested as a broadband ASE in the spectrum. However, this diffusion-based mechanism, relying on intensity feedback, still has the characteristics of random lasing, so the photon intensity shown in Figure 3b still has a threshold kink and a sudden narrowing of the FWHM. In comparison to the coherent random laser based on the localized regime discussed above, the threshold value of the diffusive random laser is elevated due to the diminished feedback mechanism.
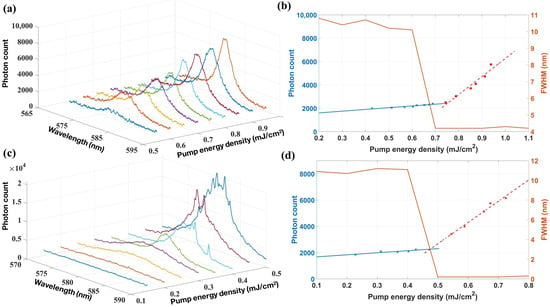
Figure 3.
The spectral properties of random laser based on diffusion and partially coherent random lasers. (a) The variation of incoherent random laser spectrum generated with pump power density at position 2. (b) The average photon counts at the peaks as the pump energy density changes. (c) The spectrum of partially coherent random laser excited with pump power density increasing. (d) The corresponding average photon counts at the peaks.
The excitation spot area also exerts a significant influence on the mechanism of the random laser. In the experiment, the pump spot size was adjusted to 200 μm to explore the random lasing situation with a more complex disorder. As shown in Figure 3c, the lasing spectrum starts in the form of ASE at lower pump energy. Then random peaks emerge at higher pump power density and are superimposed on the fluorescent substrate, indicating a tendency for both diffusion and localization mechanisms to coexist. Due to the expansion of the pump spot area, more fluorescent components in the gain medium inside the random microcavity are excited. Moreover, it shows that the disorder of the pump excitation position is complex and changeable. The lasing threshold is 0.45 mJ/cm2, lying between both diffusion and localization, as shown in Figure 3d. At the threshold, there is still a sudden narrowing of FWHM, and the change in trend is similar to Figure 2b.
3. Discussion
To further investigate the properties of the above random laser, the typical spectra obtained through excitation in position 1 and position 2 were subjected to power Fourier transform (PFT), which determined the equivalent cavity length of the lasing modes and illustrated the randomness of the mode spacing. It is obvious that the random peaks of the coherent random spectrum correspond to randomly separated harmonics in the PFT. The random peaks in PFT correspond to the Fourier component related to the optical path length, which is similar to the analysis of regular cavities [19]: , where is the order of the Fourier harmonic, is the refractive index of the gain medium, and is the equivalent optical cavity length of the random lasing modes, which is generally smaller than the overall length of the microcavity. As shown in Figure 4a, the resonant peak position corresponding to the random peak distribution with strong coherence is also relatively obvious. The first peak of PFT, , corresponds to , which is smaller than the diameter of HCF. It affirms that the local scattering envelope at position 1 can provide the coherent feedback effect of a strong localization mechanism corresponding to the closed loop of photons. In comparison, the PFT corresponding to the random laser spectrum excited in position 2 has no obvious resonance peak in Figure 4b, i.e., diffusive random lasers.
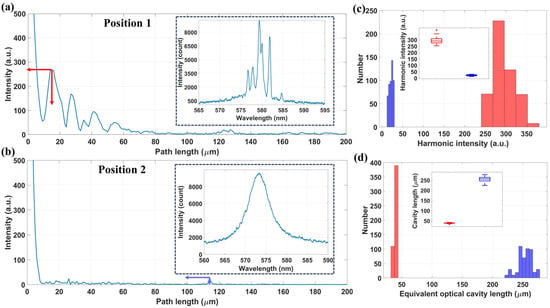
Figure 4.
The PFT properties of random lasers based on strong localization and diffusive random lasers. (a) Power Fourier transform of the output spectrum produced by pumping position 1. The inset is the corresponding spectral information of a coherent random laser. (b) Power Fourier transform of the output spectrum produced by pumping position 2. The inset is the corresponding spectral information of a diffusive random laser. (c,d) The statistical characteristics of resonance peak intensity and equivalent optical cavity length in PFT, the red represents position 1 and the blue represents position 2.
To verify the regularity of the aforementioned random systems, PFT transformation was performed on 500 sets of spectral data continuously collected at position 1/2 in the experiment to analyze the statistical distribution characteristics of the random spectrum excited at the local position of the random microcavity. As shown in Figure 4c,d, the intensity distribution of the harmonics corresponding to position 1 is between 250 and 350, much larger than the intensity distribution value corresponding to position 2. Conversely, the statistical values of the equivalent optical cavity length at position 1 are all smaller than the diameter of the HCF, while the cavity length corresponding to the weak peak at position 2 is much larger than the HCF diameter. The above statistical data indicates that the position and intensity of the resonance peaks contained in the random spectrum have stable statistical rules, and the statistics of different local microcavities vary greatly. This finding provides valuable inspiration for the application of this kind of random microcavity laser. Specifically, the localization characteristics of the spectra generated by pumping local microcavities can be used to detect the disorder of the cladding, which is also very beneficial for monitoring the types and distribution of micro-nano particles inside and outside the microcavity.
Subsequently, the method of finite difference time domain (FDTD) simulation was used to conduct mode establishment and a theoretical analysis of the optical fiber random microcavity structure based on boundary feedback. According to the specific experimental plan, it is necessary to design a fiber waveguide structure with a boundary featuring scattering and a clear separation between the scattering-free gain medium. The radial section is circular, while the axial section is rectangular. From outside to inside, the outer wall of HCF, the disordered inner cladding and the liquid core gain area were distributed. As shown in Figure 5a,d, the refractive index of the theoretical background is set to 1, and SiO2 was used as the material of the outer wall with a refractive index of 1.45. The disordered cladding forms a scattering boundary structure with a random undulating envelope. The substrate and TiO2 scattering particles with a refractive index of 1.5 and 2.1 were selected, and the number n of the scattering particles is adjustable.
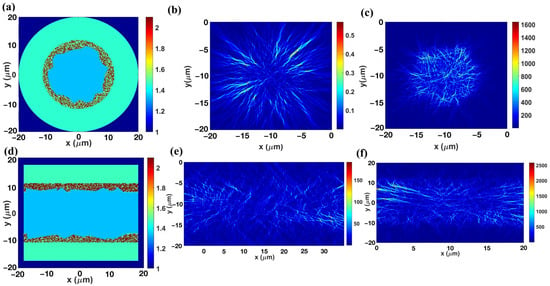
Figure 5.
The cold cavity theory analysis of boundary feedback fiber random microcavity. (a) The radial simulation structure of optical fiber random microcavity. The color scale represents the refractive index. (b,c) The change in optical power distribution in the radial section with the number of scattering particles n. The color scale represents the optical power. (b) n = 100. (c) n = 3000. (d) The axial simulation structure of optical fiber random microcavity. (e,f) The change in optical power distribution in the axial section with the number of scattering particles n, (e) n = 100. (f) n = 3000.
The light confinement effect of the two two-dimensional models described above was analyzed, and the random microcavity was excited under the conditions of a cold cavity, without adding gain inside the fiber core. The power monitor covered the entire microcavity cross-section, allowing for the monitoring of the optical power distribution in the cavity. As shown in Figure 5b, most photons escaped to areas outside the envelope when the number of scattering particles n = 100, indicating that the cold cavity has limited light confinement energy. As n increases, the stray photons are gradually captured by the disordered cavity boundaries, and the intensity range shown by the power scale bar also gradually increases. As shown in Figure 5c, most photons are concentrated inside the cavity when n reaches about 3000. Parallelly, the distribution range of the optical power matches the size of the inner cladding.
Figure 5e,f illustrate how changes in the number of scattering particles affect photons in the axial section. The waveguide confinement effect is more prominent in the axial section than in the radial section. When the number of scattering particles n changes from 100 to 3000, the disordered inner cladding not only confines the light in the middle of the fiber core, but also provides a low-dimensional waveguide channel within the core, allowing the light to efficiently propagate along the axial direction of the fiber core.
To analyze the impact of disordered boundaries on the generation mechanism of random lasers, a non-scattering gain medium is added to the fiber core. The material gain coefficient used in theoretical analysis is usually determined by the refractive index, a physical quantity related to wavelength. The Lorentz gain material suitable for PM597 was selected from the FDTD material library and added to the core part within the disordered boundary to match the PM597 dye used in the experiment. In the theoretical analysis, an electric dipole source with a central wavelength of 530 nm was used for pump excitation, and the excitation wavelength range was typically between 550 nm and 600 nm. The properties of the locally generated laser light within the microcavity can be analyzed by arranging spectrum monitors at different locations in the simulation area. The radial section structure in Figure 5a was taken as an example, and the spectral monitor data, from the core center near the light source to the excitation position, were collected. Figure 6a–c show the spectral changes throughout the whole process. The monitors received random lasing with high coherence at different monitoring positions, indicating that the strong scattering effect of the disordered boundary can provide photon localization characteristics. The photons excited by the source pass through the resonant amplification of disordered paths in the random microcavity to produce random lasing. The intensity of the random laser generated at the fiber core is higher than the monitored value near the inner cladding, which shows that most photons are confined near the fiber core and transmitted through the axial optical waveguide effect, while the photon energy leaking out of the cladding is very limited.
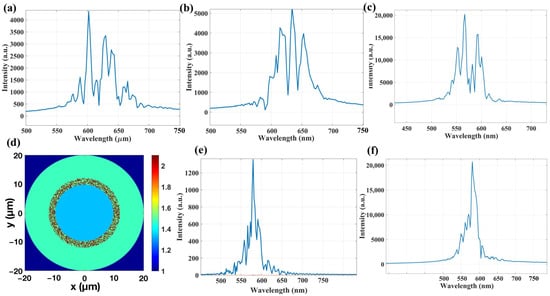
Figure 6.
The theoretical spectral analysis of boundary feedback fiber random microcavity laser. (a–c) Spectral changes monitored from the fiber core to near the scattering boundary in the radial 2D model. (d) Radial section structure of optical fiber microcavity with regular boundary feedback. The color scale represents the refractive index. (e,f) Spectral changes monitored from the fiber core to near the scattering boundary in the radial 2D model.
As shown in Figure 6d, the random laser properties transform into a diffusive mechanism when the disordered boundary of the cavity transitions into a regular state distribution. The random laser spectra, whether close to or far from the fiber core, exhibit an approximately single-peak morphology with low coherence in Figure 6e,f, similar to the results depicted in Figure 3. The above results indicate that as the disorder of the cavity boundary diminishes, the feedback ability of scattered particles to light gradually decreases, and the localization intensity of photons in the microcavity also weakens. The laser mechanism transitions to a random laser feature characterized by low coherence.
Regarding applications, random lasers, functioning as a micro-nanoscale disordered microcavity laser device, are very sensitive to changes in the external environment compared with the large-sized stable cavity structure of traditional lasers. The laser characteristics can respond to a variety of sensitive indicators to detect the external environment. The boundary feedback fiber random laser proposed in this work achieves the separation of feedback and gain media while operating independently. The statistical distribution of random spectra corresponding to two different local microcavities also indicates that the change in photon localization characteristics with the disorder of the microcavity is very beneficial for monitoring micro-nano particles in research materials.
4. Conclusions
In conclusion, a robust boundary feedback fiber random microcavity laser with multi-mechanism characteristics has been proposed and developed theoretically and experimentally. The disordered feedback medium is innovatively transferred into the inner cladding of the optical fiber, thereby achieving the physical separation and operational autonomy of the feedback and gain media for the investigation of their respective mechanism characteristics. A large amount of statistically distributed spectral data demonstrates that the coherence of the random laser can be controlled by pumping to excite the local disordered cavity boundary while the localization mechanism varies with the degree of disorder. Moreover, the cavity boundary can confine light within the cavity, thus fulfilling the role of an axial optical waveguide at the fiber core, ultimately resulting in a multi-mechanism-tunable random laser with efficient transmission. The microfluidic controller replenishes the fresh liquid gain medium into the microcavity at any time, ensuring the sustained and efficient output of random lasers. The random laser scheme proposed above can be used to detect changes in the scattering medium within the cavity wall and core.
This work would pave the way for environmentally sensitive detection and sensing solutions.
Author Contributions
H.Z. and B.Z. contributed equally to this paper. They conducted the experiment and wrote the main manuscript together. Z.H. and X.Z. conceived and guided this work. Z.L., H.G. and L.D. participated in the discussion of this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Nasim, H.; Jamil, Y. Diode lasers: From laboratory to industry. Opt. Laser Technol. 2014, 56, 211–222. [Google Scholar] [CrossRef]
- Svelto, O.; Hanna, D.C. Principles of Lasers; Springer: New York, NY, USA, 2010. [Google Scholar]
- Cao, H.; Eliezer, Y. Harnessing disorder for photonic device applications. Appl. Phys. Rev. 2022, 9, 011309. [Google Scholar] [CrossRef]
- Zaviyalov, A.; Egorov, O.; Iliew, R.; Lederer, F. Rogue waves in mode-locked fiber lasers. Phys. Rev. A 2012, 85, 013828. [Google Scholar] [CrossRef]
- Du, L.; Hasan, T.; Castellanos-Gomez, A.; Liu, G.-B.; Yao, Y.; Lau, C.N.; Sun, Z. Engineering symmetry breaking in 2D layered materials. Nat. Rev. Phys. 2021, 3, 193–206. [Google Scholar] [CrossRef]
- Gomes, A.S.; Moura, A.L.; de Araújo, C.B.; Raposo, E.P. Recent advances and applications of random lasers and random fiber lasers. Prog. Quantum Electron. 2021, 78, 100343. [Google Scholar] [CrossRef]
- Anand, V.; Ng, S.H.; Maksimovic, J.; Linklater, D.; Katkus, T.; Ivanova, E.P.; Juodkazis, S. Single shot multispectral multidimensional imaging using chaotic waves. Sci. Rep. 2020, 10, 13902. [Google Scholar] [CrossRef] [PubMed]
- Antenucci, F.; Lerario, G.; Fernandéz, B.S.; De Marco, L.; De Giorgi, M.; Ballarini, D.; Sanvitto, D.; Leuzzi, L. Demonstration of Self-Starting Nonlinear Mode Locking in Random Lasers. Phys. Rev. Lett. 2021, 126, 173901. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Zhang, W.L.; Zhang, J.C.; Chen, X.X.; Ma, R.; Rao, Y.J. Nematicon-Assisted Mode Coupling to Optical Fibers. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 4500206. [Google Scholar] [CrossRef]
- Schoenhuber, S.; Bachelard, N.; Limbacher, B.; Kainz, M.A.; Andrews, A.M.; Detz, H.; Strasser, G.; Darmo, J.; Rotter, S.; Unterrainer, K. All-optical adaptive control of quantum cascade random lasers. Nat. Commun. 2020, 11, 5530. [Google Scholar] [CrossRef]
- Yang, X.; Gong, C.; Zhang, C.; Wang, Y.; Yan, G.; Wei, L.; Chen, Y.; Rao, Y.; Gong, Y. Fiber Optofluidic Microlasers: Structures, Characteristics, and Applications. Laser Photonics Rev. 2022, 16, 2100171. [Google Scholar] [CrossRef]
- Yang, X.; Tang, S.-J.; Meng, J.-W.; Zhang, P.-J.; Chen, Y.-L.; Xiao, Y.-F. Phase-Transition Microcavity Laser. Nano Lett. 2023, 23, 3048–3053. [Google Scholar] [CrossRef] [PubMed]
- Douvidzon, M.; Maayani, S.; Nagar, H.; Admon, T.; Shuvayev, V.; Yang, L.; Deych, L.; Roichman, Y.; Carmon, T. Toward transformable photonics: Reversible deforming soft cavities, controlling their resonance split and directional emission. APL Photonics 2021, 6, 071304. [Google Scholar] [CrossRef]
- Ge, K.; Guo, D.; Niu, B.; Xu, Z.; Ruan, J.; Zhai, T. Pump-controlled RGB single-mode polymer lasers based on a hybrid 2D–3D μ-cavity for temperature sensing. Nanophotonics 2021, 10, 4591–4599. [Google Scholar] [CrossRef]
- Dai, G.; Wang, L.; Deng, L. Flexible random laser from dye doped stretchable polymer film containing nematic liquid crystal. Opt. Mater. Express 2020, 10, 68–75. [Google Scholar] [CrossRef]
- Bian, Y.; Xue, H.; Wang, Z. Programmable Random Lasing Pulses Based on Waveguide-Assisted Random Scattering Feedback. Laser Photonics Rev. 2021, 15, 2000506. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, X.; Yu, B.; Ma, J.; Xie, K.; Cheng, S.; Zhang, J.; Hu, Z. Waveguided nematic liquid crystal random lasers. Nanophotonics 2021, 10, 3541–3547. [Google Scholar] [CrossRef]
- Su, C.-Y.; Hou, C.-F.; Hsu, Y.-T.; Lin, H.-Y.; Liao, Y.-M.; Lin, T.-Y.; Chen, Y.-F. Multifunctional Random-Laser Smart Inks. ACS Appl. Mater. Interfaces 2020, 12, 49122–49129. [Google Scholar] [CrossRef]
- Du, Y.; Zou, C.-L.; Zhang, C.; Wang, K.; Qiao, C.; Yao, J.; Zhao, Y.S. Tuneable red, green, and blue single-mode lasing in heterogeneously coupled organic spherical microcavities. Light Sci. Appl. 2020, 9, 151. [Google Scholar] [CrossRef] [PubMed]
- Caselli, N.; Consoli, A.; Sánchez, M.M.; López, C. Networks of mutually coupled random lasers. Optica 2021, 8, 193–201. [Google Scholar] [CrossRef]
- Ma, R.; Luo, K.H.; Pokharel, S.; Wang, Z.; Korotkova, O.; He, J.S.; Zhang, W.L.; Fan, D.Y.; Gomes, A.S.L.; Liu, J. Orbital-angular-momentum-dependent speckles for spatial mode sorting and demultiplexing. Optica 2024, 11, 595–605. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, X.; Yan, S.; Zhang, X.; Ge, K.; Han, C.B.; Zhai, T. Single-Mode Lasing in Plasmonic-Enhanced Woven Microfibers for Multifunctional Sensing. ACS Sens. 2021, 6, 3416–3423. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.Y.; Zhang, J.C.; Zhang, W.L. Photothermal Effect Controlled Complex Lasing for Decentralized Key Distribution. ACS Photonics 2022, 9, 3600–3608. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-C.; Xiao, Y.-F.; Jiang, X.-F.; Li, B.-B.; Li, Y.; Gong, Q. Cavity-QED treatment of scattering-induced free-space excitation and collection in high-Q whispering-gallery microcavities. Phys. Rev. A 2012, 85, 013843. [Google Scholar] [CrossRef]
- Lun, Y.; Zhan, Z.; Gu, F.; Wang, P.; Yu, H.; Li, Z.-Y. Cavity mode manipulated by single gold nanoparticles. APL Photonics 2020, 5, 061304. [Google Scholar] [CrossRef]
- Jin, L.; Chen, X.; Wu, Y.; Ai, X.; Yang, X.; Xiao, S.; Song, Q. Dual-wavelength switchable single-mode lasing from a lanthanide-doped resonator. Nat. Commun. 2022, 13, 1727. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Zhao, Y.G.; Ho, S.T.; Seelig, E.W.; Wang, Q.H.; Chang, R.P.H. Random Laser Action in Semiconductor Powder. Phys. Rev. Lett. 1999, 82, 2278–2281. [Google Scholar] [CrossRef]
- Cao, H. Lasing in random media. Waves Random Media 2003, 13, R1–R39. [Google Scholar] [CrossRef]
- Wang, Z.; Meng, X.; Choi, S.H.; Knitter, S.; Kim, Y.L.; Cao, H.; Shalaev, V.M.; Boltasseva, A. Controlling Random Lasing with Three-Dimensional Plasmonic Nanorod Metamaterials. Nano Lett. 2016, 16, 2471–2477. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, H.; Wu, M.; Lin, T.; Shen, J.; Chen, Y. Stretchable and Broadband Cavity-Free Lasers Based on All 2D Metamaterials. Adv. Opt. Mater. 2020, 8, 1901326. [Google Scholar] [CrossRef]
- Hou, Y.; Zhou, Z.; Zhang, C.; Tang, J.; Fan, Y.; Xu, F.-F.; Zhao, Y.S. Full-color flexible laser displays based on random laser arrays. Sci. China Mater. 2021, 64, 2805–2812. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, W.; Yang, N.; Ma, R.; Zhang, Y.; Wang, Z.; Zhang, J.; Rao, Y. High-Power Multimode Random Fiber Laser for Speckle-Free Imaging. Ann. Phys. 2021, 533, 2100390. [Google Scholar] [CrossRef]
- Ma, R.; Wang, Z.; Zhang, H.H.; Zhang, W.L.; Rao, Y.J. Imaging through opacity using a near-infrared low-spatial-coherence fiber light source. Opt. Lett. 2020, 45, 3816–3819. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, S.; Ma, R.; Liu, Y.; Zhu, H.; Zhang, Y.; Liu, J.; Mu, Y.; Rao, Y.; Zhang, W. Near-Infrared Speckle-Illumination Imaging Based on a Multidimensionally Disordered Fiber Laser. Phys. Rev. Appl. 2022, 18, 024031. [Google Scholar] [CrossRef]
- Tong, J.; Shi, X.; Niu, L.; Zhang, X.; Chen, C.; Han, L.; Zhang, S.; Zhai, T. Dual-color plasmonic random lasers for speckle-free imaging. Nanotechnology 2020, 31, 465204. [Google Scholar] [CrossRef] [PubMed]
- Azmi, A.N.; Ismail, W.Z.W.; Abu Hassan, H.; Halim, M.M.; Zainal, N.; Muskens, O.L.; Kamil, W.M.W.A. Review of Open Cavity Random Lasers as Laser-Based Sensors. ACS Sens. 2022, 7, 914–928. [Google Scholar] [CrossRef]
- Xu, Z.; Hong, Q.; Ge, K.; Shi, X.; Wang, X.; Deng, J.; Zhou, Z.; Zhai, T. Random Lasing from Label-Free Living Cells for Rapid Cytometry of Apoptosis. Nano Lett. 2022, 22, 172–178. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, W.; Zhang, J.; Ma, R.; Wang, Z.; Rao, Y.; Li, X. Single-Shot Interaction and Synchronization of Random Microcavity Lasers. Adv. Mater. Technol. 2021, 6, 2100562. [Google Scholar] [CrossRef]
- Mendicuti, E.; Käferlein, O.; Garcia-Segundo, C. Random laser emission from whole blood as the active medium. Opt. Lett. 2021, 46, 274–277. [Google Scholar] [CrossRef]
- Wang, Z.; Cao, M.; Shao, G.; Zhang, Z.; Yu, H.; Chen, Y.; Zhang, Y.; Li, Y.; Xu, B.; Wang, Y.; et al. Coherent Random Lasing in Colloidal Quantum Dot-Doped Polymer-Dispersed Liquid Crystal with Low Threshold and High Stability. J. Phys. Chem. Lett. 2020, 11, 767–774. [Google Scholar] [CrossRef]
- de Matos, C.J.S.; Menezes, L.d.S.; Brito-Silva, A.M.; Gámez, M.A.M.; Gomes, A.S.L.; de Araújo, C.B. Random Fiber Laser. Phys. Rev. Lett. 2007, 99, 153903. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Wang, Q.; Song, B.; Zhang, C.; Liu, B.; Lin, W.; Duan, S.; Bai, H. Capillary-Fiber-Based All-in-Fiber Platform for Microfluid Sensing. IEEE Sens. J. 2021, 21, 22752–22757. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).