Influence of the Experimental Setup on Electromagnetic Pulses in the VHF Band at Relativistic High-Power Laser Facilities
Abstract
1. Introduction
2. Materials and Methods
2.1. Laser- and Target-System
2.2. Space Charge Dynamics
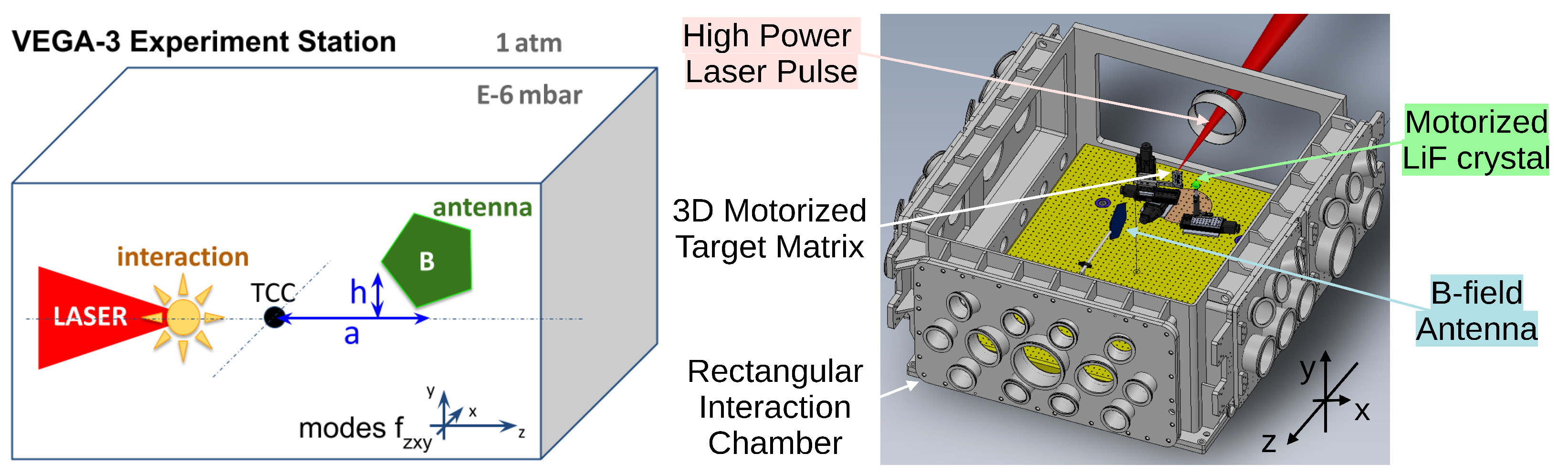
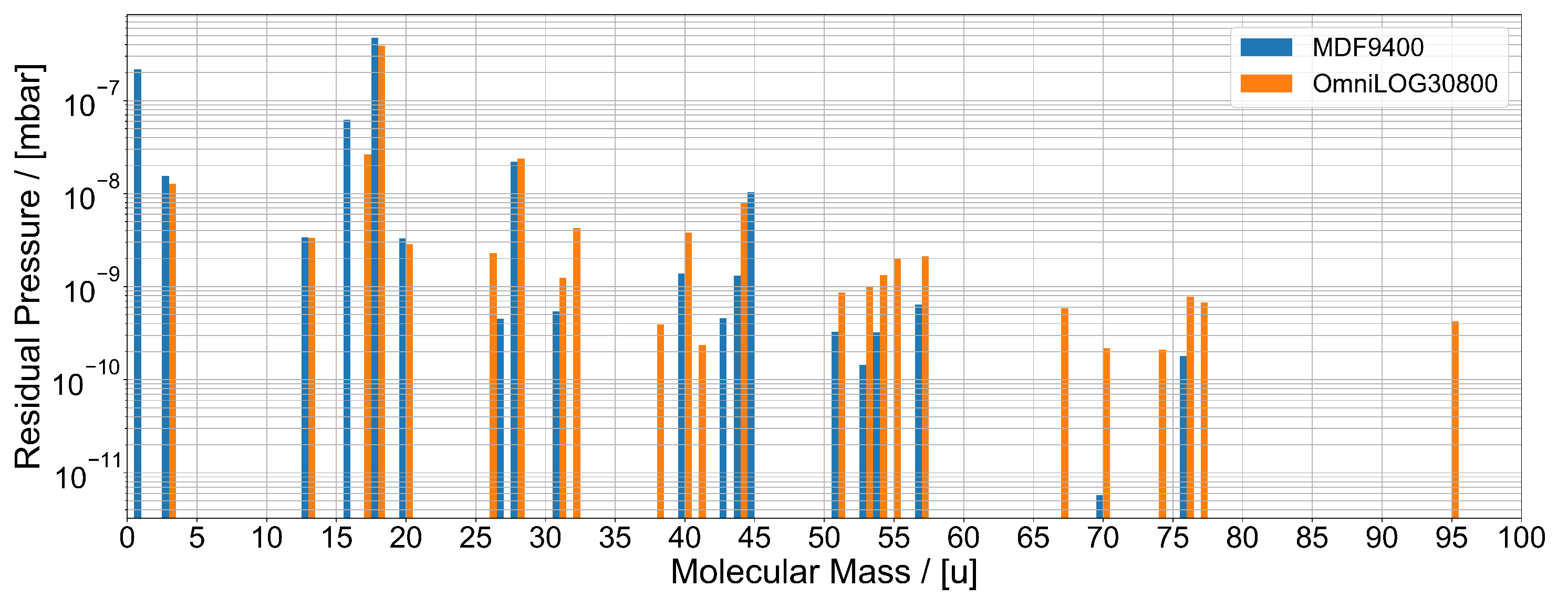
2.3. Experimental Environment
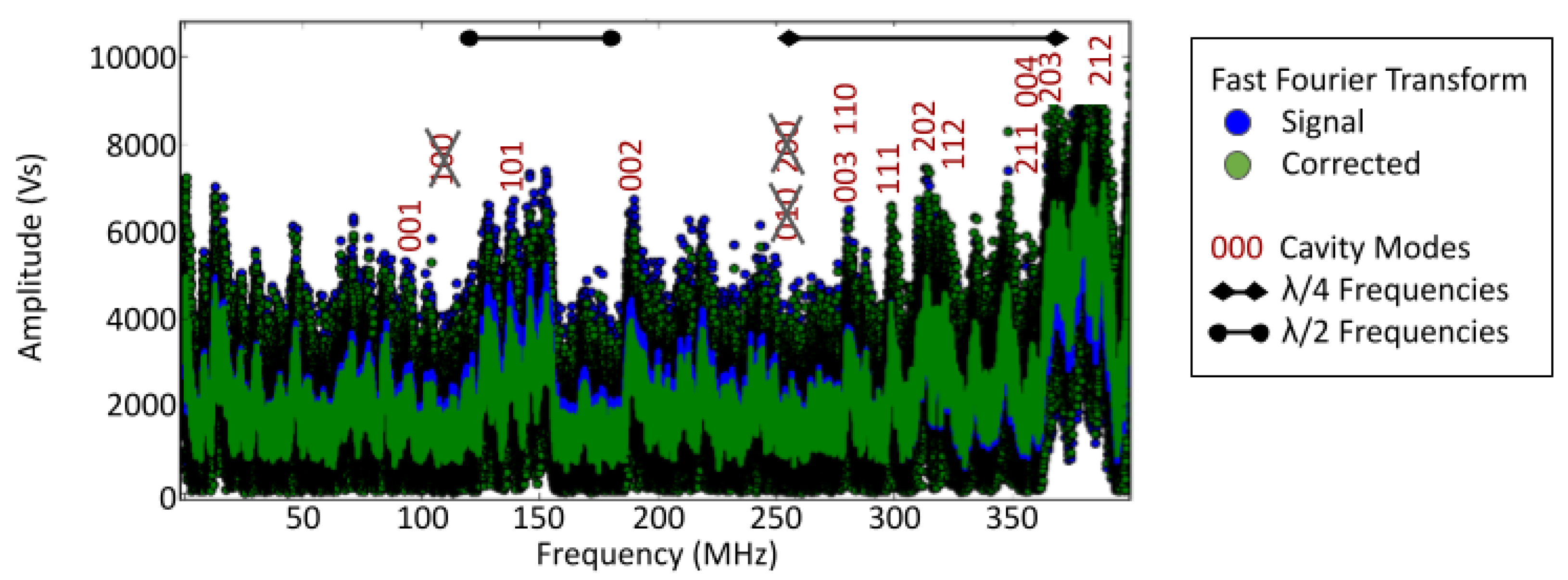
2.4. Cavity Modes
2.5. EMP Detection
3. Results
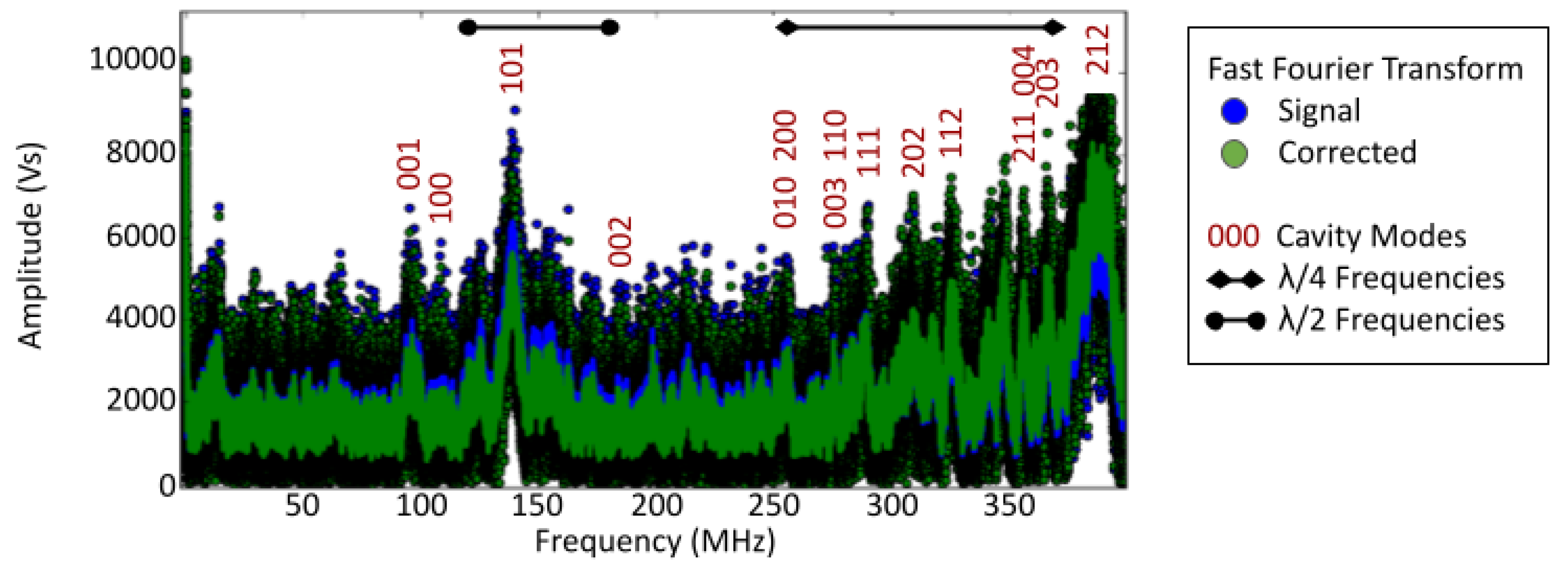
3.1. Standard Mode Structure in the VHF Band
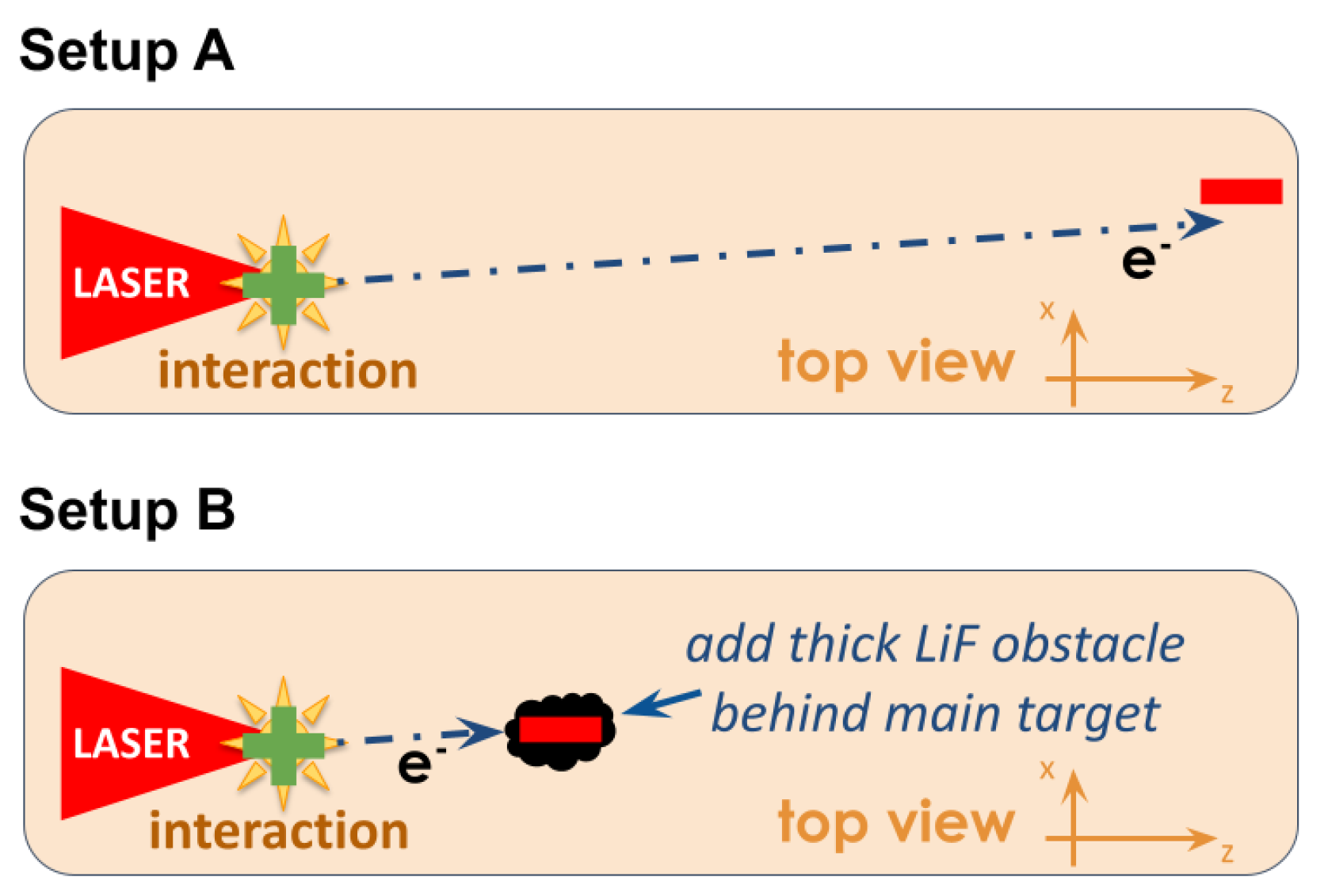
3.2. Modified Mode Structure in the VHF Band
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jeong, T.M.; Lee, J. Femtosecond petawatt laser. Ann. Phys. 2014, 526, 157. [Google Scholar] [CrossRef]
- Hooker, C.J.; Blake, S.; Chekhlov, O.; Clarke, R.J.; Collier, J.L.; Divall, E.J.; Ertel, K.; Foster, P.S.; Hawkes, S.J.; Holligan, P.; et al. Commissioning the Astra Gemini Petawatt Ti:Sapphire Laser System. In Proceedings of the Conference on Lasers and Electro-Optics/Quantum Electronics and Laser Science Conference and Photonic Applications Systems Technologies, San Jose, CA, USA, 4–9 May 2008. CLEO (OSA Technical Digest), paper JThB2 (2008). [Google Scholar]
- Yu, T.J.; Lee, S.K.; Sung, J.H.; Yoon, J.W.; Jeong, T.M.; Lee, J. Generation of high-contrast, 30 fs, 1.5 PW laser pulses from chirped-pulse amplification Ti:sapphire laser. Opt. Express 2012, 20, 10807. [Google Scholar] [CrossRef]
- Leemans, W.P.; Daniels, J.; Deshmukh, A.; Gonsalves, A.J.; Magana, A.; Mao, H.S.; Mittelberger, D.E.; Nakamura, K.; Riley, J.R.; Syversrud, D. Bella laser and operations. In Proceedings of the PAC 2013, Pasadena, CA, USA, 29 September–4 October 2013; pp. 1097–1100. [Google Scholar]
- Sung, J.H.; Lee, H.W.; Yoo, J.Y.; Yoon, J.W.; Lee, C.W.; Yang, J.M.; Son, Y.J.; Jang, Y.H.; Lee, S.K.; Nam, C.H. 4.2 PW, 20 fs Ti: Sapphire laser at 0.1 Hz. Opt. Lett. 2017, 42, 2058. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Gan, Z.; Yu, L.; Wang, C.; Liu, Y.; Guo, Z.; Xu, L.; Xu, M.; Hang, Y.; Xu, J.; et al. 339 J high-energy Ti: Sapphire chirped-pulse amplifier for 10 PW laser facility. Opt. Lett. 2018, 43, 5681. [Google Scholar] [CrossRef]
- Lureau, F.; Matras, G.; Chalus, O.; Derycke, C.; Morbieu, T.; Radier, C.; Casagrande, O.; Laux, S.; Ricaud, S.; Rey, G.; et al. High-energy hybrid femtosecond laser system demonstrating 2 × 10 PW capability. High Power Laser Sci. Eng. 2020, 8, e43. [Google Scholar] [CrossRef]
- Danson, C.; Hillier, D.; Hopps, N.; Neely, D. Petawatt class lasers worldwide. High Power Laser Sci. Eng. 2015, 3, e3. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Rockwood, A.; Luther, B.M.; Hollinger, R.; Curtis, A.; Calvi, C.; Menoni, C.S.; Rocca, J.J. 0.85 PW laser operation at 3.3 Hz and high-contrast ultrahigh-intensity λ = 400 nm second-harmonic beamline. Opt. Lett. 2017, 42, 3828–3831. [Google Scholar] [CrossRef] [PubMed]
- Daido, H.; Nishiuchi, M.; Pirozhkov, A.S. Review of laser-driven ion sources and their applications. Rep. Prog. Phys. 2012, 75, 056401. [Google Scholar] [CrossRef] [PubMed]
- Borghesi, M. Ion Acceleration: TNSA and Beyond. In Springer Proceedings in Physics; Springer: Berlin/Heidelberg, Germany, 2019; Volume 231. [Google Scholar]
- Tajima, T.; Malka, V. Laser plasma accelerators. Plasma Phys. Control. Fusion 2012, 62, 034004. [Google Scholar] [CrossRef]
- Norreys, P.A.; Santala, M.; Clark, E.; Zepf, M.; Watts, I.; Beg, F.N.; Krushelnick, K.; Tatarakis, M.; Dangor, A.E.; Fang, X.; et al. Observation of a highly directional λ-ray beam from ultrashort, ultraintense laser pulse interactions with solids. Phys. Plasmas 1999, 6, 2150–2156. [Google Scholar] [CrossRef]
- Lichters, R.; Meyer-ter-Vehn, J.; Pukhov, A. Short-pulse laser harmonics from oscillating plasma surfaces driven at relativistic intensity. Plasmas 1996, 3, 3425. [Google Scholar] [CrossRef]
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381. [Google Scholar] [CrossRef]
- Beg, F.N.; Bell, A.R.; Dangor, A.E.; Danson, C.N.; Fews, A.P.; Glinsky, M.E.; Hammel, B.A.; Lee, P.; Norreys, P.A.; Tatarakis, M. A study of picosecond laser-solid interactions up to 1019 Wcm−2. Phys. Plasmas 1997, 4, 447. [Google Scholar] [CrossRef]
- Bleko, V.; Karataev, P.; Konkov, A.; Kruchinin, K.; Naumenko, G.; Potylitsyn, A.; Vaughan, T. Coherent Cherenkov radiation as an intense THz source. J. Phys. Conf. Ser. 2016, 732, 012006. [Google Scholar] [CrossRef]
- Ehret, M.; Cikhardt, J.; Bradford, P.; Vladisavlevici, I.; Burian, T.; de Luis, D.; Henares, J.L.; Martín, R.H.; Apiñaniz, J.I.; Lera, R.; et al. High-repetition-rate source of nanosecond duration kA-current pulses driven by relativistic laser pulses. High Power Laser Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Condamine, F.P.; Jourdain, N.; Hernandez, J.-C.; Taylor, M.; Bohlin, H.; Fajstavr, A.; Jeong, T.M.; Kumar, D.; Laštovička, T.; Renner, O.; et al. High-repetition rate solid target delivery system for PW-class laser–matter interaction at ELI Beamlines. Rev. Sci. Instruments 2021, 90, 063504. [Google Scholar] [CrossRef]
- Rehwald, M.; Assenbaum, S.; Bernert, C.; Brack, F.-E.; Bussmann, M.; Cowan, T.E.; Curry, C.B.; Fiuza, F.; Garten, M.; Gaus, L.; et al. Ultra-short pulse laser acceleration of protons to 80 MeV from cryogenic hydrogen jets tailored to near-critical density. Nat. Commun. 2023, 14, 4009. [Google Scholar] [CrossRef] [PubMed]
- Snavely, R.A.; Key, M.H.; Hatchett, S.P.; Cowan, T.E.; Roth, M.; Phillips, T.W.; Stoyer, M.A.; Henry, E.A.; Sangster, T.C.; Singh, M.S.; et al. Intense High-Energy Proton Beams from Petawatt-Laser Irradiation of Solids. Phys. Rev. Lett. 2000, 85, 2945. [Google Scholar] [CrossRef]
- Wilks, S.C.; Langdon, A.B.; Cowan, T.E.; Roth, M.; Singh, M.; Hatchett, S.; Key, M.H.; Pennington, D.; MacKinnon, A.; Snavely, R.A. Energetic proton generation in ultra-intense laser–solid interactions. Phys. Plasmas 2001, 8, 542. [Google Scholar] [CrossRef]
- Esirkepov, T.; Borghesi, M.; Bulanov, S.V.; Mourou, G.; Tajima, T. Highly Efficient Relativistic-Ion Generation in the Laser-Piston Regime. Phys. Rev. Lett. 2004, 92, 175003. [Google Scholar] [CrossRef]
- Nemoto, K.; Maksimchuk, A.; Banerjee, S.; Flippo, K.; Mourou, G.; Umstadter, D.; Bychenkov, V.Y. Laser-triggered ion acceleration and table top isotope production. Appl. Phys. Lett. 2001, 78, 595–597. [Google Scholar] [CrossRef]
- Ledingham, K.W.D.; McKenna, P.; McCanny, T.; Shimizu, S.; Yang, J.M.; Robson, L.; Zweit, J.; Gillies, J.M.; Bailey, J.; Chimon, G.N.; et al. High power laser production of short-lived isotopes for positron emission tomography. J. Phys. D Appl. Phys. 2004, 37, 2341. [Google Scholar] [CrossRef]
- Santala, M.I.K.; Zepf, M.; Beg, F.N.; Clark, E.L.; Dangor, A.E.; Krushelnick, K.; Tatarakis, M.; Watts, I.; Ledingham, K.W.D.; McCanny, T.; et al. Production of radioactive nuclides by energetic protons generated from intense laser-plasma interactions. Appl. Phys. Lett. 2001, 78, 19–21. [Google Scholar] [CrossRef]
- Merrill, F.E.; Golubev, A.A.; Mariam, F.G.; Turtikov, V.I.; Varentsov, D. HEDgeHOB Collaboration Proton Microscopy at FAIR. AIP Conf. Proc. 2009, 1195, 667–670. [Google Scholar] [CrossRef]
- Mirani, F.; Maffini, A.; Casamichiela, F.; Pazzaglia, A.; Formenti, A.; Dellasega, D.; Russo, V.; Vavassori, D.; Bortot, D.; Huault, M.; et al. Integrated quantitative PIXE analysis and EDX spectroscopy using a laser-driven particle source. Sci. Adv. 2021, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Roth, M.; Cowan, T.E.; Key, M.H.; Hatchett, S.P.; Brown, C.; Fountain, W.; Johnson, J.; Pennington, D.M.; Snavely, R.A.; Wilks, S.C.; et al. Fast Ignition by Intense Laser-Accelerated Proton Beams. Phys. Rev. Lett. 2001, 86, 436–439. [Google Scholar] [CrossRef] [PubMed]
- Consoli, F.; Tikhonchuk, V.T.; Bardon, M.; Bradford, P.; Carroll, D.C.; Cikhardt, J.; Cipriani, M.; Clarke, R.J.; Cowan, T.; Danson, C.N.; et al. Laser produced electromagnetic pulses: Generation, detection and mitigation. High Power Laser Sci. Eng. 2020, 8, e22. [Google Scholar] [CrossRef]
- Brunel, F. Not-so-resonant, resonant absorption. Phys. Rev. Lett. 1987, 59, 52. [Google Scholar] [CrossRef] [PubMed]
- Wilks, C.; Kruer, W.L. Absorption of ultrashort, ultra-intense laser light by solids and overdense plasmas. IEEE J. Quantum Electron. 1997, 33, 1954. [Google Scholar] [CrossRef]
- Wilks, S.C.; Kruer, W.L.; Tabak, M.; Langdon, A.B. Absorption of ultra-intense laser pulses. Phys. Rev. Lett. 1992, 69, 1383–1386. [Google Scholar] [CrossRef]
- Pukhov, A.; Meyer-ter, V.J. Relativistic laser-plasma interaction by multi-dimensional particle-in-cell simulations. Phys. Plasmas 1998, 5, 1880–1886. [Google Scholar] [CrossRef]
- Pearlman, J.S.; Dahlbacka, G.H. Charge separation and target voltages in laser-produced plasmas. Appl. Phys. Lett. 1977, 31, 414–417. [Google Scholar] [CrossRef]
- Courtois, C.; Fontaine, A.C.L.; Landoas, O.; Lidove, G.; Méot, V.; Morel, P.; Nuter, R.; Lefebvre, E.; Boscheron, A.; Grenier, J.; et al. Effect of plasma density scale length on the properties of bremsstrahlung X-ray sources created by picosecond laser pulses. Phys. Plasmas 2009, 16, 013105. [Google Scholar] [CrossRef]
- Poyé, A.; Hulin, S.; Ribolzi, J.; Bailly-Grandvaux, M.; Lubrano-Lavaderci, F.; Bardon, M.; Raffestin, D.; Santos, J.J.; Tikhonchuk, V. Thin target charging in short laser pulse interactions. Phys. Rev. E 2018, 98, 033201. [Google Scholar] [CrossRef]
- Rusby, D.R.; Wilson, L.A.; Gray, R.J.; Dance, R.J.; Butler, N.M.H.; MacLellan, D.A.; Scott, G.G.; Bagnoud, V.; Zielbauer, B.; McKenna, P.; et al. Measurement of the angle, temperature and flux of fast electrons emitted from intense laser-solid interactions. J. Plasma Phys. 2015, 81, 5. [Google Scholar] [CrossRef]
- Dubois, J.-L.; Lubrano-Lavaderci, F.; Raffestin, D.; Ribolzi, J.; Gazave, J.; Fontaine, A.C.L.; d’Humières, E.; Hulin, S.; Nicolaï, P.; Poyé, A.; et al. Target charging in short-pulse-laser–plasma experiments. Phys. Rev. E 2014, 89, 013102. [Google Scholar] [CrossRef]
- Nelissen, K.; Liszi, M.; Marco, M.D.; Ospina, V.; Drotár, I.; Gatti, G.; Kamperidis, C.; Volpe, L. Characterisation and Modelling of Ultrashort Laser-Driven Electromagnetic Pulses. Sci. Rep. 2020, 10, 3108. [Google Scholar] [CrossRef]
- Shurenkov, V.V.; Pershenkov, V.S. Electromagnetic effects and damage mechanism on the semiconductor electronics. Facta Univ. Ser. Electron. Energetics 2016, 29, 621–629. [Google Scholar] [CrossRef]
- Volpe, L.; Fedosejevs, R.; Gatti, G.; Pérez-Hernández, J.A.; Méndez, C.; Apiñaniz, J.; Vaisseau, X.; Salgado, C.; Huault, M.; Malko, S.; et al. Generation of high energy laser-driven electron and proton sources with the 200 TW system VEGA 2 at the Centro de Laseres Pulsados. High Power Laser Sci. Eng. 2019, 7, e25. [Google Scholar] [CrossRef]
- Kluge, T.; Cowan, T.; Debus, A.; Schramm, U.; Zeil, K.; Bussmann, M. Electron Temperature Scaling in Laser Interaction with Solids. Phys. Rev. Lett. 2011, 107, 205003. [Google Scholar] [CrossRef]
- Roth, M.; Schollmeier, M. Ion Acceleration—Target Normal Sheath Acceleration. In Proceedings of the 2014 CAS-CERN Accelerator School: Plasma Wake Acceleration, Geneva, Switzerland, 23–29 November 2014. [Google Scholar] [CrossRef]
- Vertes, A.; Wolf, M.D.; Juhasz, P.; Gijbels, R. Threshold conditions of plasma ignition in laser ionization mass spectrometry of solids. Anal. Chem. 1989, 61, 1029–1035. [Google Scholar] [CrossRef]
- Drouin, D.; Couture, A.R.; Joly, D.; Tastet, X.; Aimez, V.; Gauvin, R. CASINO V2.42—A Fast and Easy-to-use Modeling Tool for Scanning Electron Microscopy and Microanalysis Users. Scanning 2007, 29, 92–101. [Google Scholar] [CrossRef] [PubMed]
- Lancaster, K.L.; Karsch, S.; Habara, H.; Beg, F.N.; Clark, E.L.; Freeman, R.; Key, M.H.; King, J.A.; Kodama, R.; Krushelnick, K.; et al. Characterization of neutron yields from laser produced ion beams for fast neutron radiography. Phys. Plasmas 2004, 11, 3404–3408. [Google Scholar] [CrossRef]
- Higginson, D.P.; McNaney, J.M.; Swift, D.C.; Petrov, G.M.; Davis, J.; Frenje, J.A.; Jarrott, L.C.; Kodama, R.; Lancaster, K.L.; Mackinnon, A.J.; et al. Production of neutrons up to 18 MeV in high-intensity short-pulse laser matter interactions. Phys. Plasmas 2011, 18, 100703. [Google Scholar] [CrossRef]
- Deng, H.X.; Sha, R.; Hu, L.X.; Jiang, X.R.; Zhao, N.; Zou, D.B.; Yu, T.P.; Shao, F.Q. Pulsed neutron source from interaction of relativistic laser pulse with micro-structure assisted pitcher-catcher target. Plasma Phys. Control. Fusion 2022, 64, 085004. [Google Scholar] [CrossRef]
- Jiang, X.R.; Shao, F.Q.; Zou, D.B.; Yu, M.Y.; Hu, L.X.; Guo, X.Y.; Huang, T.W.; Zhang, H.; Wu, S.Z.; Zhang, G.B.; et al. Energetic deuterium-ion beams and neutron source driven by multiple-laser interaction with pitcher-catcher target. Nucl. Fusion 2020, 60, 076019. [Google Scholar] [CrossRef]
- Baker, G.H. Electromagnetic Pulse Resilience of United States Critical Infrastructure: Progress and Prognostics. J. Crit. Infrastruct. Policy 2021, 2, 1. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, J.; Kim, H.; Kim, K.; Kim, H.R. Possible Effects of Radiofrequency Electromagnetic Field Exposure on Central Nerve System. Biomol. Ther. 2019, 27, 265–275. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ehret, M.; Volpe, L.; Apiñaniz, J.I.; Rodríguez-Frías, M.D.; Gatti, G. Influence of the Experimental Setup on Electromagnetic Pulses in the VHF Band at Relativistic High-Power Laser Facilities. Photonics 2024, 11, 459. https://doi.org/10.3390/photonics11050459
Ehret M, Volpe L, Apiñaniz JI, Rodríguez-Frías MD, Gatti G. Influence of the Experimental Setup on Electromagnetic Pulses in the VHF Band at Relativistic High-Power Laser Facilities. Photonics. 2024; 11(5):459. https://doi.org/10.3390/photonics11050459
Chicago/Turabian StyleEhret, Michael, Luca Volpe, Jon Imanol Apiñaniz, Maria Dolores Rodríguez-Frías, and Giancarlo Gatti. 2024. "Influence of the Experimental Setup on Electromagnetic Pulses in the VHF Band at Relativistic High-Power Laser Facilities" Photonics 11, no. 5: 459. https://doi.org/10.3390/photonics11050459
APA StyleEhret, M., Volpe, L., Apiñaniz, J. I., Rodríguez-Frías, M. D., & Gatti, G. (2024). Influence of the Experimental Setup on Electromagnetic Pulses in the VHF Band at Relativistic High-Power Laser Facilities. Photonics, 11(5), 459. https://doi.org/10.3390/photonics11050459






