Surface Plasmon Waveguide Based on Nested Dielectric Parallel Nanowire Pairs Coated with Graphene
Abstract
1. Introduction
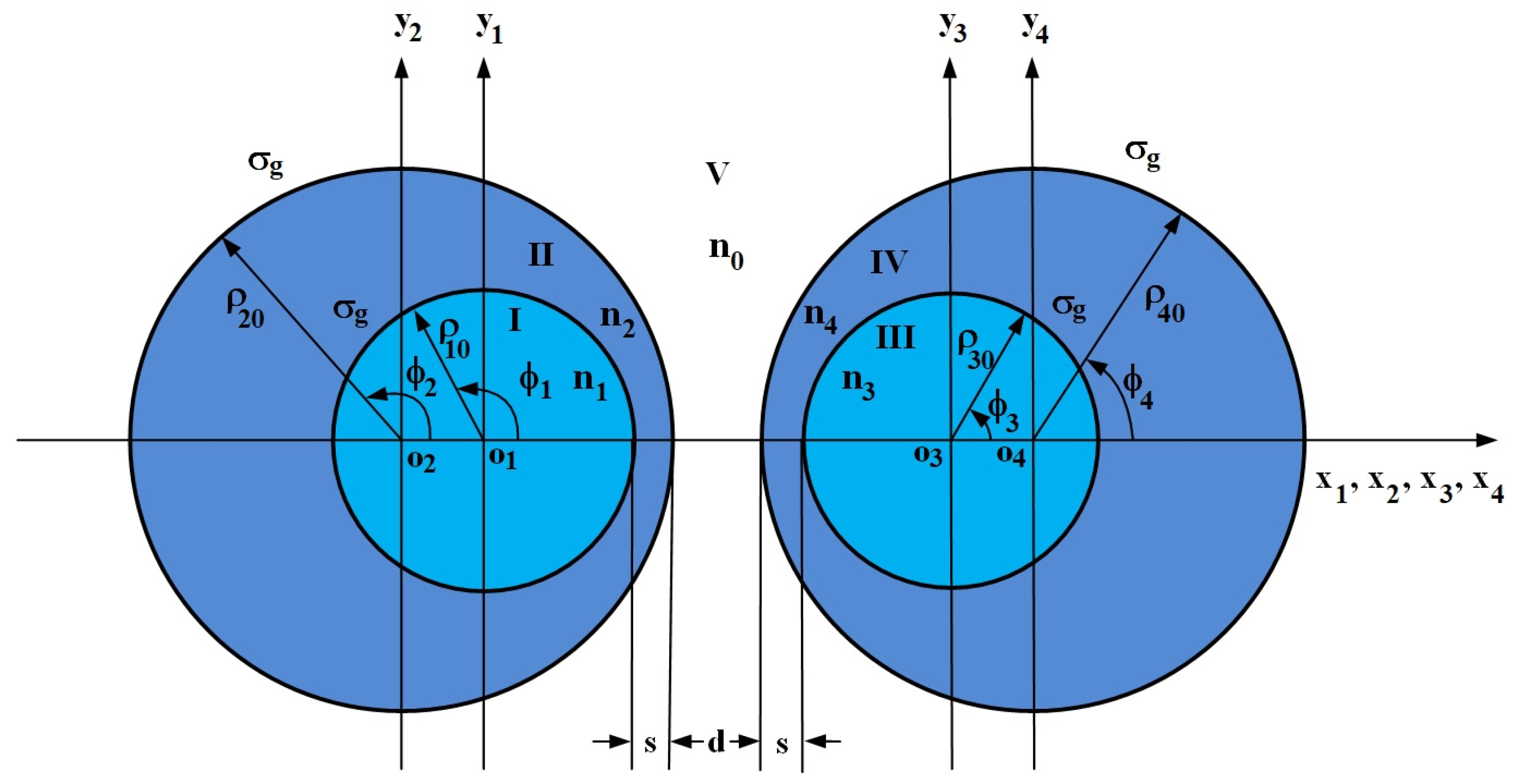
2. Waveguide Structure and Calculation Method
3. Results and Discussion
3.1. The Two Lowest-Order Modes
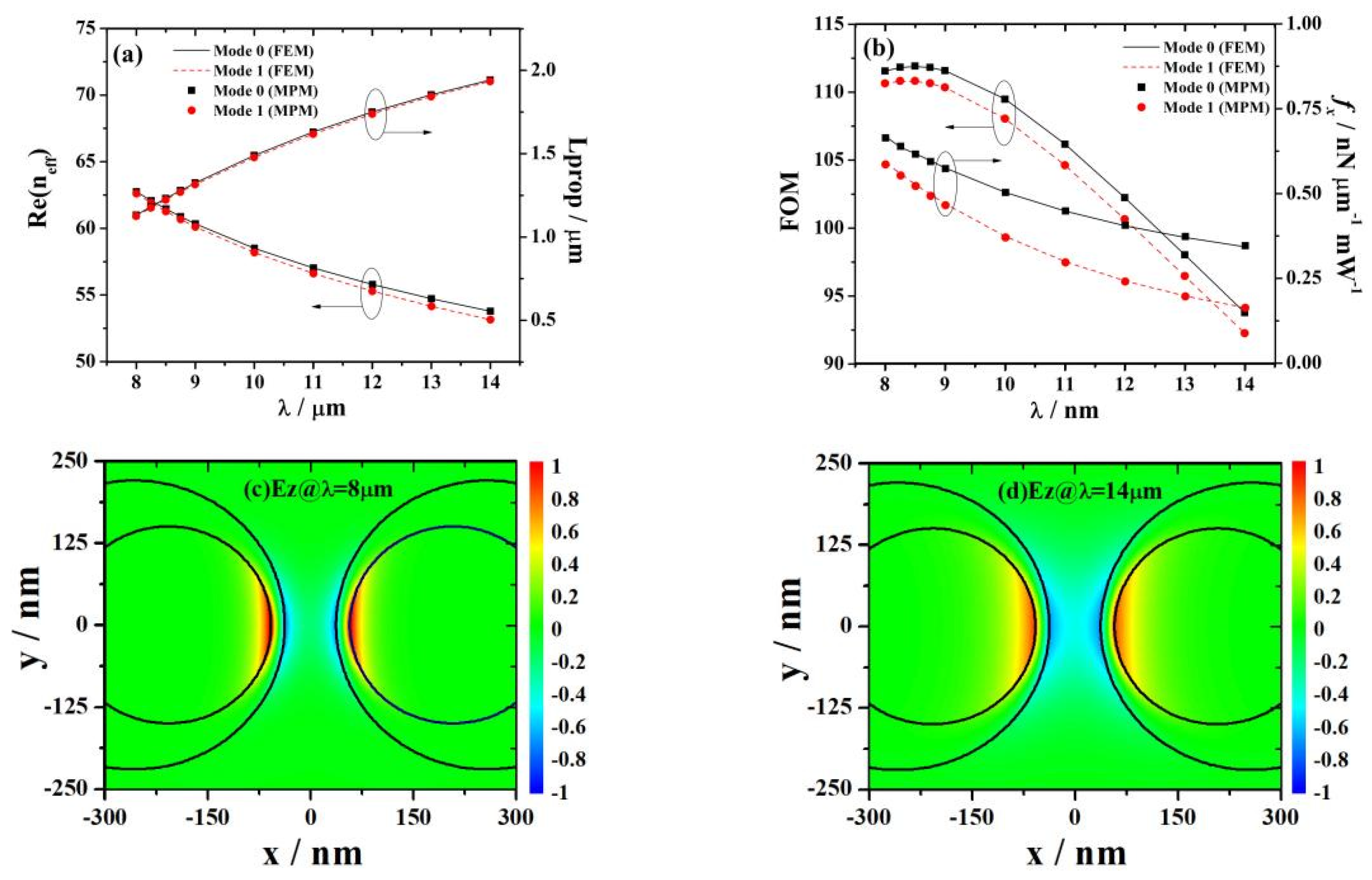
3.2. Influence of the Working Wavelength on Mode Characteristics
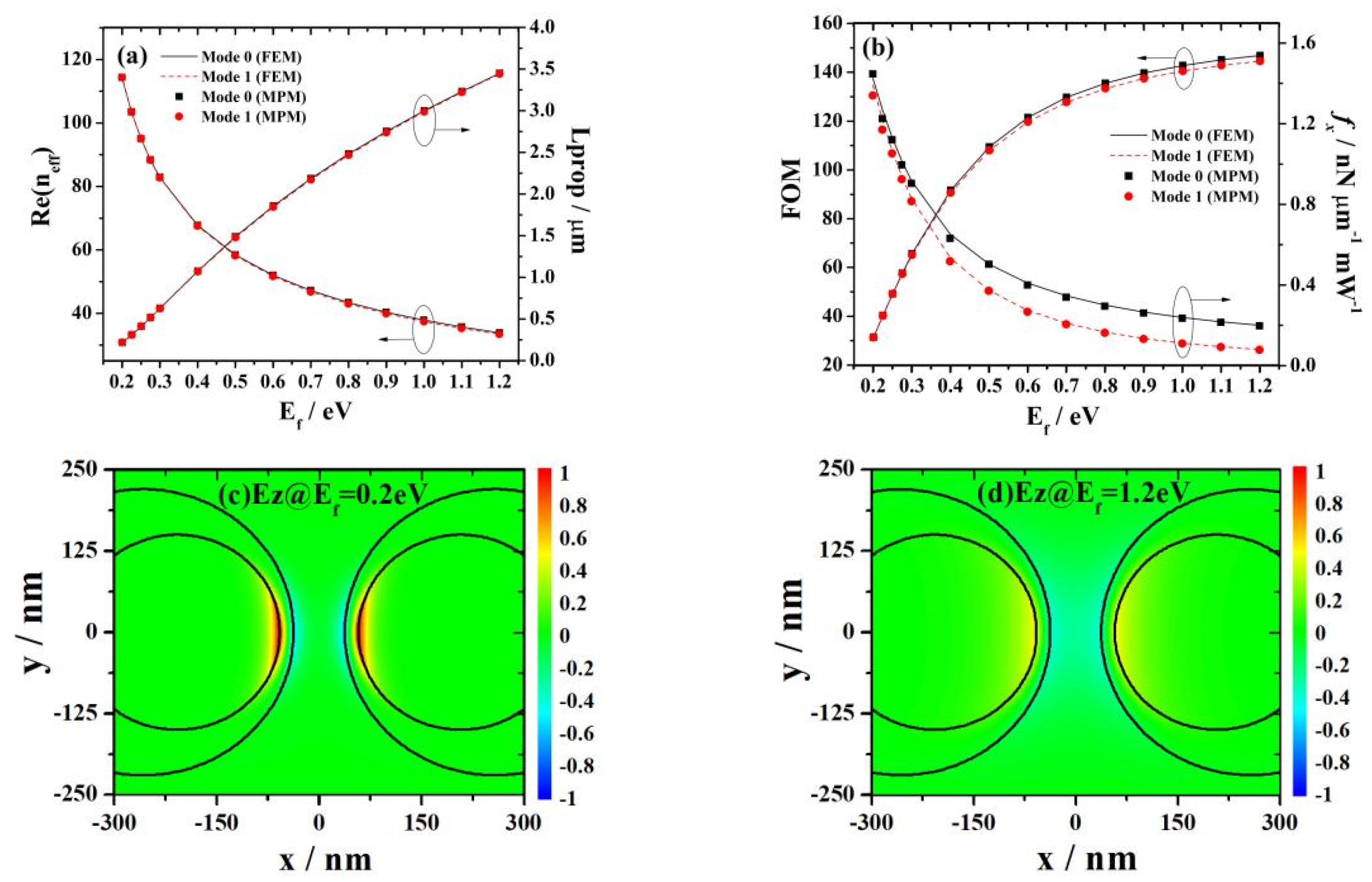
3.3. Influence of the Fermi Energy of Graphene on Mode Characteristics
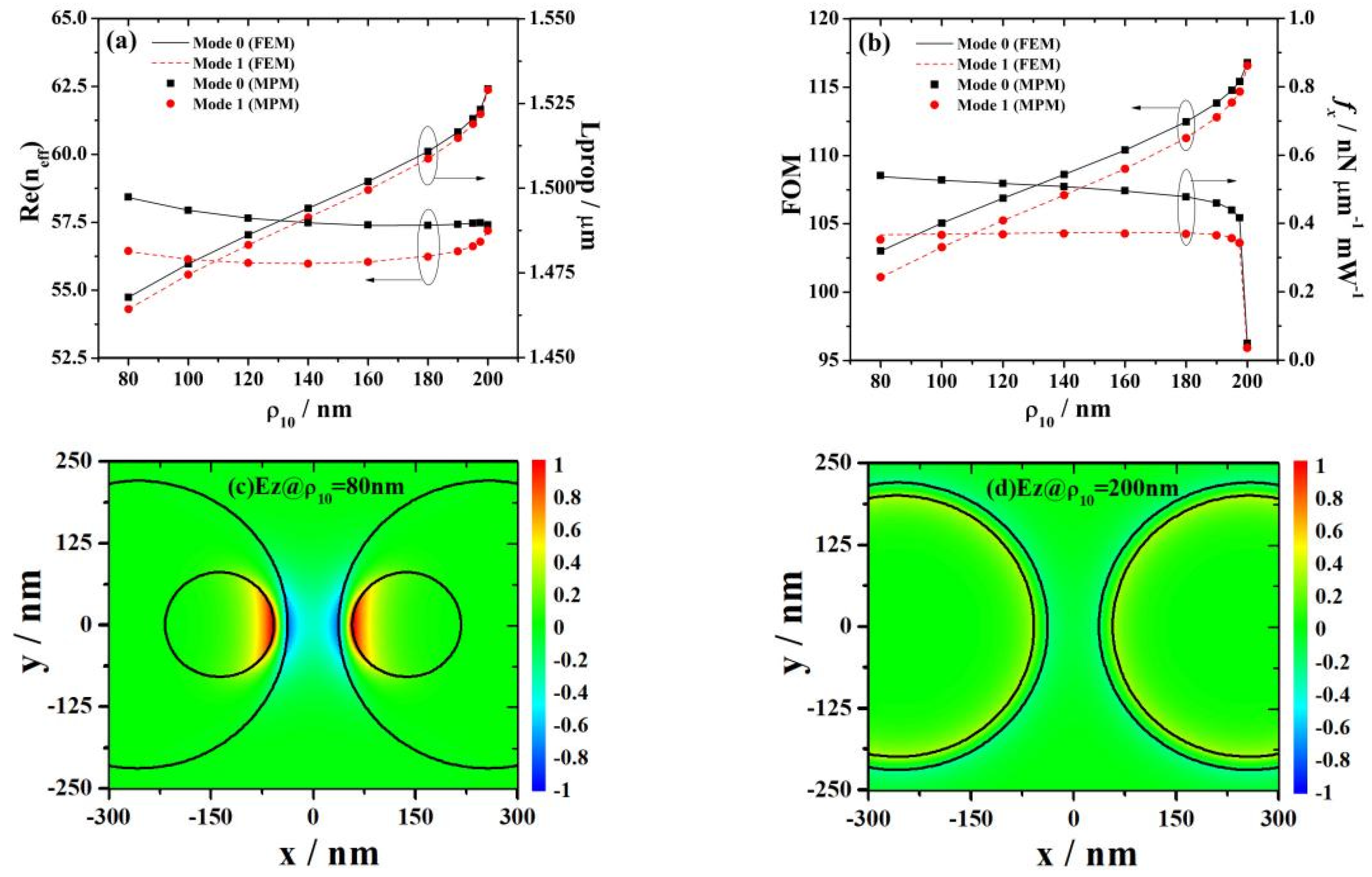
3.4. Influence of the Radii of the First Nanowire on Mode Characteristics
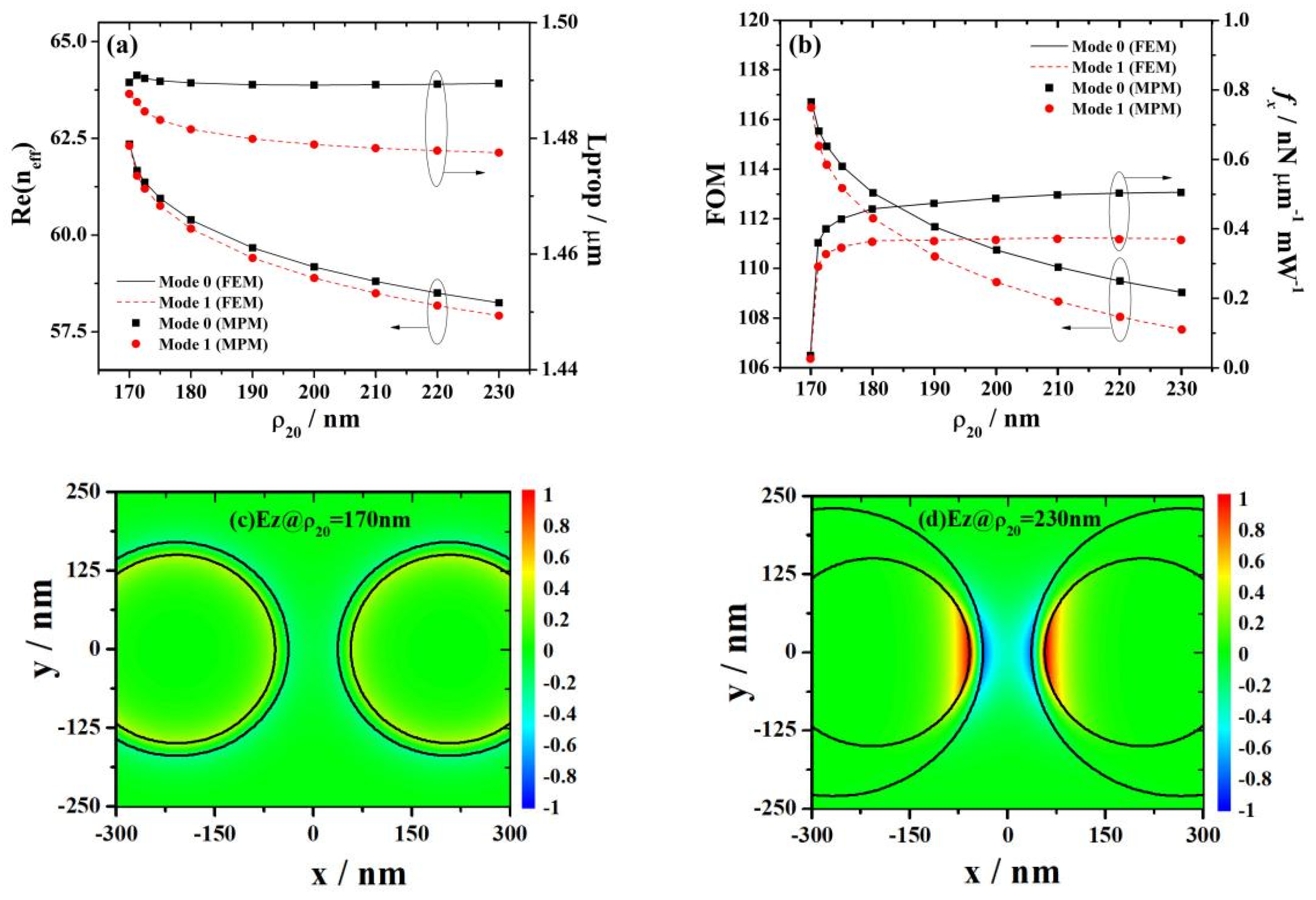
3.5. Influence of the Radii of the Second Nanowire on Mode Characteristics
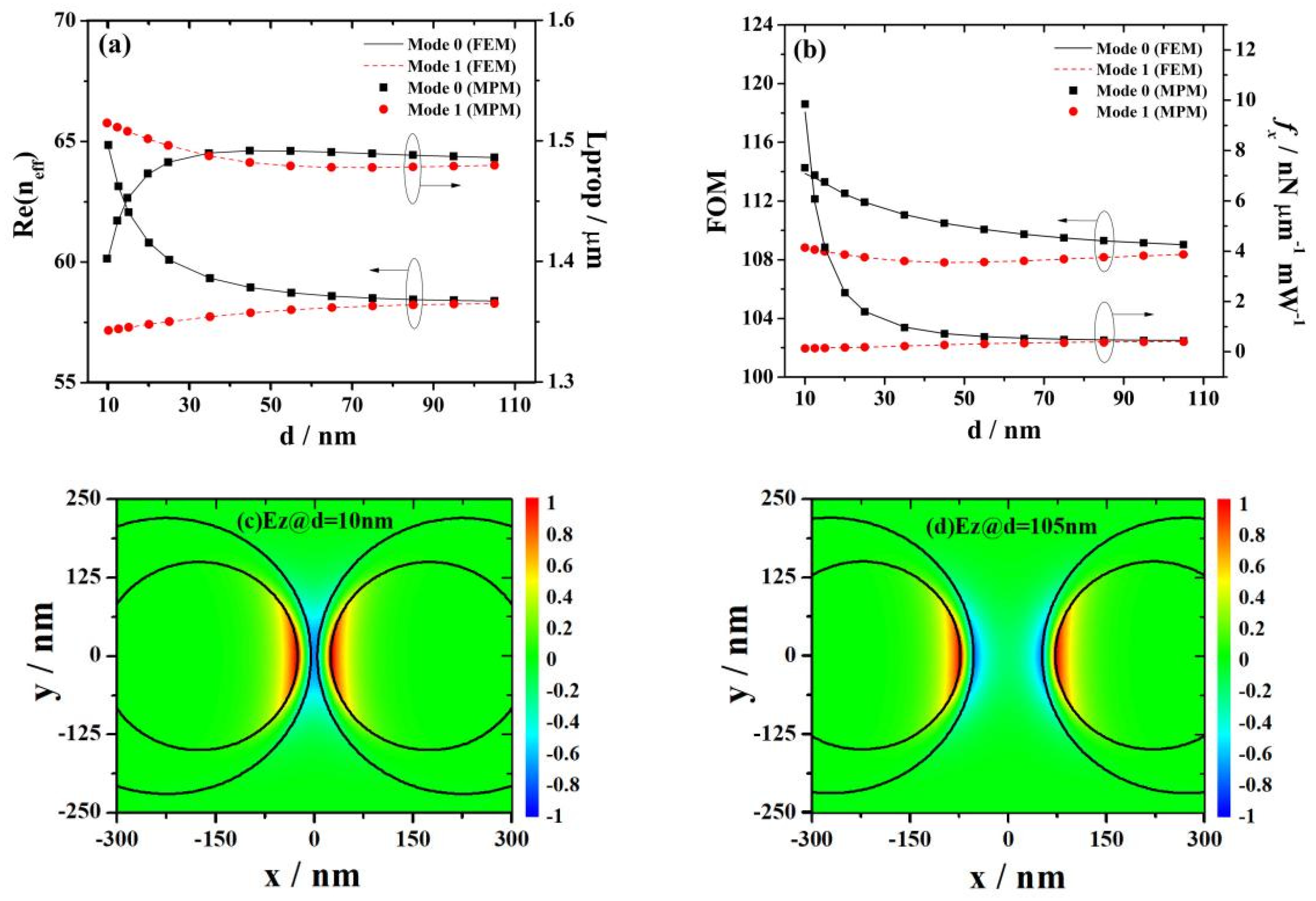
3.6. Influence of the Minimum Distance between the Outer Surfaces of Two Parallel Nanowires on Mode Characteristics
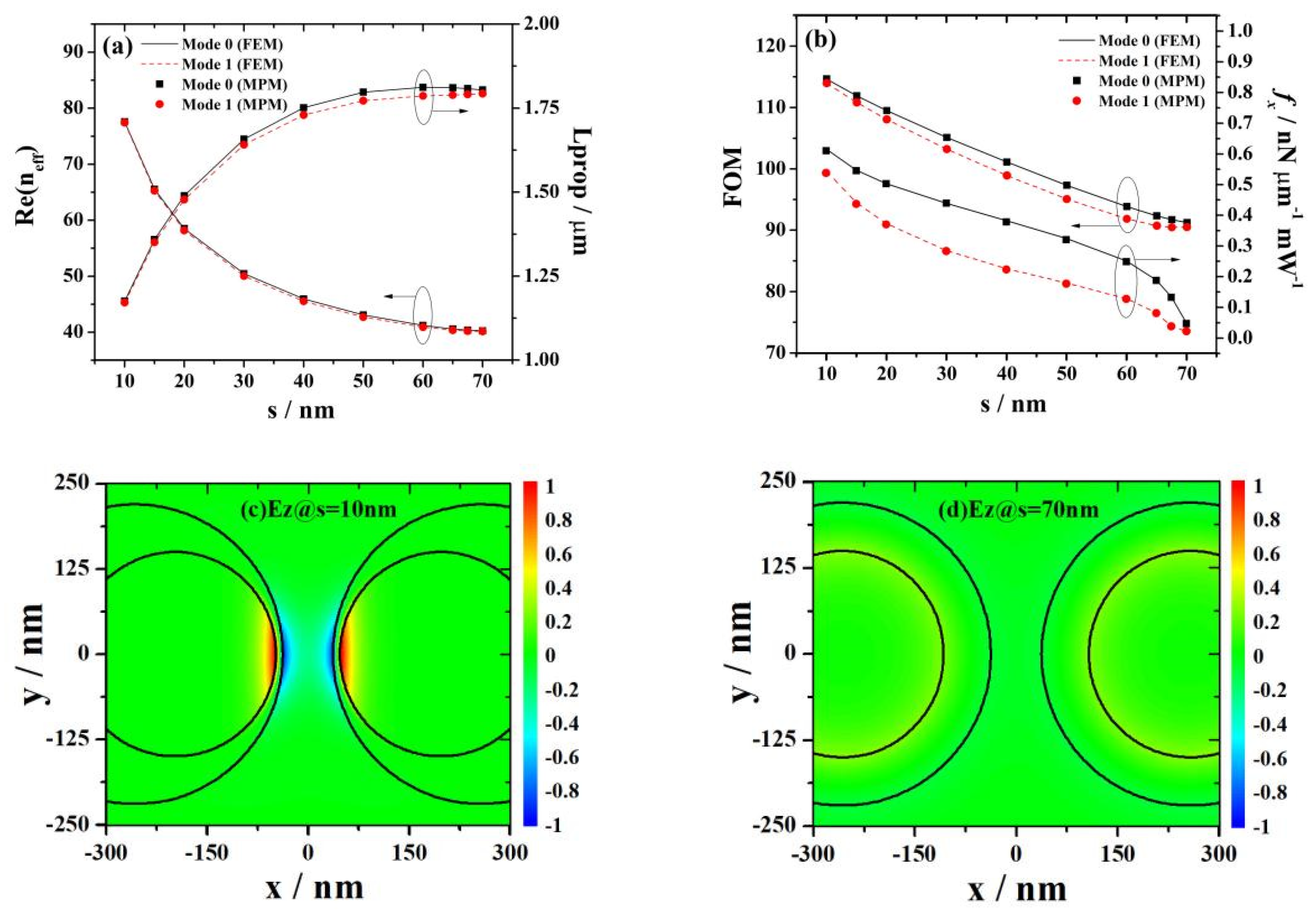
3.7. Influence of the Minimum Distance between the Surface of the Embedded Cylinder and the Surface of the Parent Cylinder on Mode Characteristics
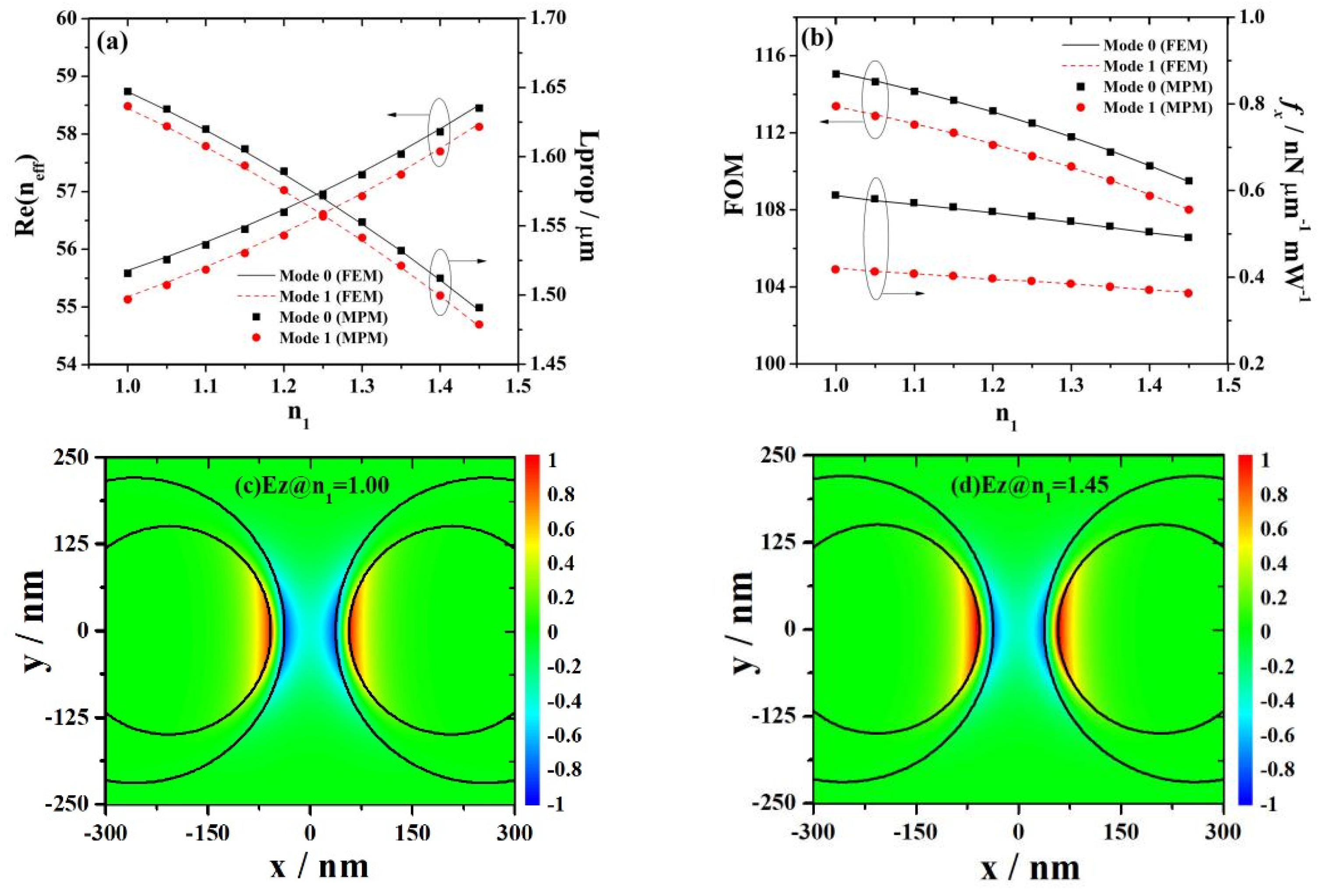
3.8. Influence of the Refractive Index of Region I (or Region III) on Mode Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, Q.; Khan, A.; Bacha, B.A.; Khan, M.; Khesro, A. Sensitivity of the surface plasmon polariton waves at the interface of metal and dielectric medium using doppler broadening effect. Plasmonics 2024, 19, 123–129. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, C.; Wang, Y.; Wang, M.; Xu, Y.; Wei, T.; Xie, Z.; Liu, S.; Lee, C.-K.; Hu, X.; et al. All-in-one, all-optical logic gates using liquid metal plasmon nonlinearity. Nat. Commun. 2024, 15, 1726. [Google Scholar] [CrossRef] [PubMed]
- Zulfajri, M.; Gedda, G.; Ulla, H.; Habibati; Gollavelli, G.; Huang, G.G. A review on the chemical and biological sensing applications of silver/carbon dots nanocomposites with their interaction mechanisms. Adv. Colloid Interface Sci. 2024, 325, 103115. [Google Scholar] [CrossRef]
- Vaidyanathan, A.; Mondal, B.; Rout, C.S.; Chakraborty, B. Plasmonic gas sensors based on nanomaterials: Mechanisms and recent developments. J. Phys. D Appl. Phys. 2024, 57, 263002. [Google Scholar] [CrossRef]
- Ramírez, M.O.; Molina, P.; Hernández-Pinilla, D.; López-Polín, G.; Ares, P.; Lozano-Martín, L.; Yan, H.; Wang, Y.; Sarkar, S.; Al Shuhaib, J.H.; et al. Integrating 2D materials and plasmonics on Lithium Niobate platforms for pulsed laser operation at the nanoscale. Laser Photonics Rev. 2024, 18, 2300817. [Google Scholar] [CrossRef]
- Fang, Y.; Sun, M. Nanoplasmonic waveguides: Towards applications in integrated nanophotonic circuits. Light Sci. Appl. 2015, 4, e294. [Google Scholar] [CrossRef]
- Boltasseva, A.; Nikolajsen, T.; Leosson, K.; Kjaer, K.; Larsen, M.; Bozhevolnyi, S. Integrated optical components utilizing long-range surface plasmon polaritons. J. Light. Technol. 2005, 23, 413–422. [Google Scholar] [CrossRef]
- Oulton, R.F.; Sorger, V.J.; Genov, D.A.; Pile, D.F.P.; Zhang, X. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation. Nat. Photonics 2008, 2, 496–500. [Google Scholar] [CrossRef]
- Kuppadakkath, A.; Najafidehaghani, E.; Gan, Z.; Tuniz, A.; Ngo, G.Q.; Knopf, H.; Löchner, F.J.F.; Abtahi, F.; Bucher, T.; Shradha, S.; et al. Direct growth of monolayer MoS2 on nanostructured silicon waveguides. Nanophotonics 2022, 11, 4397–4408. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, C.; Wan, P.; Ding, L.; Xu, W. Dielectric-loaded black phosphorus surface plasmon polariton waveguides. Opt. Express 2019, 27, 18005–18015. [Google Scholar] [CrossRef]
- Berini, P. Plasmon–polariton modes guided by a metal film of finite width. Opt. Lett. 1999, 24, 1011–1013. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Guinea, F.; Garcia-Vidal, F.J.; Martín-Moreno, L. Edge and waveguide terahertz surface plasmon modes in graphene microribbons. Phys. Rev. B 2011, 84, 161407. [Google Scholar] [CrossRef]
- Liu, L.; Han, Z.; He, S. Novel surface plasmon waveguide for high integration. Opt. Express 2005, 13, 6645–6650. [Google Scholar] [CrossRef]
- He, S.; Zhang, X.; He, Y. Graphene nano-ribbon waveguides of recordsmall mode area and ultra-high effective refractive indices for future VLSI. Opt. Express 2013, 21, 30664–30673. [Google Scholar] [CrossRef] [PubMed]
- Pile, D.F.P.; Ogawa, T.; Gramotnev, D.K.; Okamoto, T.; Haraguchi, M.; Fukui, M.; Matsuo, S. Theoretical and experimental investigation of strongly localized plasmons on triangular metal wedges for subwavelength waveguiding. Appl. Phys. Lett. 2005, 87, 061106. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, X.; Ma, Z.; Cai, W.; Wang, L.; Xu, J. Surface plasmon modes in graphene wedge and groove waveguides. Opt. Express 2013, 21, 32432–32440. [Google Scholar] [CrossRef] [PubMed]
- Gramotnev, D.K.; Pile, D.F.P. Single-mode subwavelength waveguide with channel plasmon-polaritons in triangular grooves on a metal surface. Appl. Phys. Lett. 2004, 85, 6323–6325. [Google Scholar] [CrossRef]
- Dai, D.; He, S. A silicon-based hybrid plasmonic waveguide with a metal cap for a nano-scale light confinement. Opt. Express 2009, 17, 16646–16653. [Google Scholar] [CrossRef]
- Saeed, M.; Ghaffar, A.; Rehman, S.; Naz, M.Y.; Shukrullah, S.; Naqvi, Q.A. Graphene-based plasmonic waveguides: A mini review. Plasmonics 2022, 17, 901–911. [Google Scholar] [CrossRef]
- Gao, Y.; Ren, G.; Zhu, B.; Wang, J.; Jian, S. Single-mode graphene-coated nanowire plasmonic waveguide. Opt. Lett. 2014, 39, 5909–5912. [Google Scholar] [CrossRef]
- Gao, Y.; Ren, G.; Zhu, B.; Liu, H.; Lian, Y.; Jian, S. Analytical model for plasmon modes in graphene-coated nanowire. Opt. Express 2014, 22, 24322–24331. [Google Scholar] [CrossRef]
- Liu, J.P.; Zhai, X.; Wang, L.L.; Li, H.-J.; Xie, F.; Lin, Q.; Xia, S.-X. Analysis of mid-infrared surface plasmon modes in a graphene-based cylindrical hybrid waveguide. Plasmonics 2016, 11, 703. [Google Scholar] [CrossRef]
- Yang, J.F.; Yang, J.J.; Deng, W.; Mao, F.; Huang, M. Transmission properties and molecular sensing application of CGPW. Opt. Express 2015, 23, 32289–32299. [Google Scholar] [CrossRef]
- Zhao, T.; Hu, M.; Zhong, R.; Chen, X.; Zhang, P.; Gong, S.; Zhang, C.; Liu, S. Plasmon modes of circular cylindrical doublelayer graphene. Opt. Express 2016, 24, 20461–20471. [Google Scholar] [CrossRef]
- Liu, J.P.; Zhai, X.; Xie, F.; Wang, L.-L.; Xia, S.-X.; Li, H.-J.; Luo, X.; Shang, X.-J. Analytical model of mid-infrared surface plasmon modes in a cylindrical long-range waveguide with double-layer graphene. J. Light. Technol. 2017, 35, 1971–1979. [Google Scholar] [CrossRef]
- Xing, R.; Jian, S. Numerical analysis on tunable multilayer nanoring waveguide. IEEE Photonics Technol. Lett. 2017, 29, 967–970. [Google Scholar] [CrossRef]
- Hajati, M.; Hajati, Y. High-performance and low-loss plasmon waveguiding in graphene-coated nanowire with substrate. J. Opt. Soc. Am. B 2016, 33, 2560. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Huan, Q.; Chen, W.; Li, Z. High-performance light transmission based on graphene plasmonic waveguides. J. Mater. Chem. C 2020, 8, 6832–6838. [Google Scholar] [CrossRef]
- Teng, D.; Yang, Y.; Guo, J.; Ma, W.; Tang, Y.; Wang, K. Efficient guiding mid-infrared waves with graphene-coated nanowire based plasmon waveguides. Results Phys. 2020, 17, 103169. [Google Scholar] [CrossRef]
- Zhu, B.; Ren, G.; Yang, Y.; Gao, Y.; Wu, B.; Lian, Y.; Wang, J.; Jian, S. Field enhancement and gradient force in the graphene-coated nanowire pairs. Plasmonics 2015, 10, 839–845. [Google Scholar] [CrossRef]
- Xing, R.; Jian, S. Numerical analysis on the multilayer nanoring waveguide pair. IEEE Photonics Technol. Lett. 2016, 28, 2779–2782. [Google Scholar] [CrossRef]
- Ye, S.; Wang, Z.; Sun, C.; Dong, C.; Wei, B.; Wu, B.; Jian, S. Plasmon-phonon-polariton modes and field enhancement in the graphene-coated hexagon boron nitride nanowire pairs. Opt. Express 2018, 26, 23854–23867. [Google Scholar] [CrossRef] [PubMed]
- Hajati, M.; Hajati, Y. Plasmonic characteristics of two vertically coupled graphene-coated nanowires integrated with substrate. Appl. Opt. 2017, 56, 870–875. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Huan, Q.; Zhao, Y.; Tang, Y. High-performance transmission of surface plasmons in graphene-covered nanowire pairs with substrate. Nanomaterials 2019, 9, 1594. [Google Scholar] [CrossRef] [PubMed]
- Kotsifaki, D.G.; Chormaic, S.N. Plasmonic optical tweezers based on nanostructures: Fundamentals, advances and prospects. Nanophotonics 2019, 8, 1227–1245. [Google Scholar] [CrossRef]
- Tan, H.; Hu, H.; Huang, L.; Qian, K. Plasmonic tweezers for optical manipulation and biomedical applications. Analyst 2020, 145, 5699–5712. [Google Scholar] [CrossRef]
- Hu, S.; Liao, Z.W.; Cai, L.; Jiang, X.X. Near-field optical tweezers for chemistry and biology. Phys. Status Solidi A 2020, 217, 1900604. [Google Scholar] [CrossRef]
- Li, H.; Cao, Y.; Zhou, L.; Xu, X.; Zhu, T.; Shi, Y.; Qiu, C.-W.; Ding, W. Optical pulling forces and their applications. Adv. Opt. Photonics 2020, 12, 288–366. [Google Scholar] [CrossRef]
- Zhang, Y.; Min, C.; Dou, X.; Wang, X.; Urbach, H.P.; Somekh, M.G.; Yuan, X. Plasmonic tweezers: For nanoscale optical trapping and beyond. Light Sci. Appl. 2021, 10, 59. [Google Scholar] [CrossRef]
- Zhou, L.M.; Shi, Y.; Zhu, X.; Hu, G.; Cao, G.; Hu, J.; Qiu, C.-W. Recent progress on optical micro/nanomanipulations: Structured forces, structured particles, and synergetic applications. ACS Nano 2022, 16, 13264–13278. [Google Scholar] [CrossRef]
- Samadi, M.; Alibeigloo, P.; Aqhili, A.; Khosravi, M.A.; Saeidi, F.; Vasini, S.; Ghorbanzadeh, M.; Darbari, S.; Moravvej-Farshi, M.K. Plasmonic tweezers: Towards nanoscale manipulation. Opt. Lasers Eng. 2022, 154, 107001. [Google Scholar] [CrossRef]
- Li, H.; Xue, W.; Li, N.; Du, Y.; Li, C. Mode characteristics of a graphene-coated cylindrical dielectric waveguide with a nested eccentric hollow elliptical cylinder. J. Opt. Soc. Am. B 2022, 39, 2944–2956. [Google Scholar] [CrossRef]
- Liu, J.; Yu, L.X.; Xue, W.R. Mode characteristics of nested eccentric waveguides constructed by two cylindrical nanowires coated with graphene. Chin. Phys. B 2022, 31, 036803. [Google Scholar] [CrossRef]
- Teng, D.; Wang, K.; Li, Z. Graphene-coated nanowire waveguides and their applications. Nanomaterials 2020, 10, 229. [Google Scholar] [CrossRef]
- Rezzouk, Y.; Khattou, S.; Amrani, M.; Noual, A.; El Boudouti, E.H.; Talbi, A.; Djafari-Rouhani, B. Bound states in the continuum and induced resonances in a simple plasmonic waveguide with sensing application. Photonics 2023, 10, 1284. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Guinea, F.; Garcia-Vidal, F.J.; Martin-Moreno, L. Fields radiated by a nanoemitter in a graphene sheet. Phys. Rev. B 2011, 84, 195446. [Google Scholar] [CrossRef]
- Golub, G.; van Loan, C.F. Matrix Computations, 4th ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Teng, D.; Wang, K.; Li, Z.; Zhao, Y. Graphene-coated nanowire dimers for deep subwavelength waveguiding in mid-infrared range. Opt. Express 2019, 27, 12458–12469. [Google Scholar] [CrossRef]
- He, X.Q.; Ning, T.G.; Pei, L.; Zheng, J.J.; Li, J.; Wen, X.D. Tunable hybridization of graphene plasmons and dielectric modes for highly confined light transmit at terahertz wavelength. Opt. Express 2019, 27, 5961–5972. [Google Scholar] [CrossRef]
- Hajati, M.; Hajati, Y. Deep subwavelength confinement of mid-infrared plasmon modes by coupling graphene-coated nanowire with a dielectric substrate. Plasmonics 2018, 13, 403–412. [Google Scholar] [CrossRef]
- Novotny, L.; Hecht, B. Principles of Nano-Optics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
| Mode | Combination | |
|---|---|---|
| 0 |  | 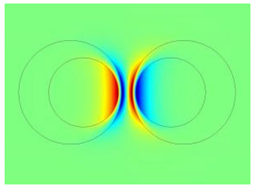 |
| 1 |  | 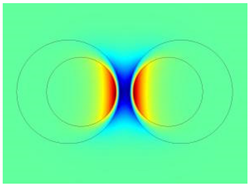 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Liu, J.; Xue, W. Surface Plasmon Waveguide Based on Nested Dielectric Parallel Nanowire Pairs Coated with Graphene. Photonics 2024, 11, 441. https://doi.org/10.3390/photonics11050441
Yu L, Liu J, Xue W. Surface Plasmon Waveguide Based on Nested Dielectric Parallel Nanowire Pairs Coated with Graphene. Photonics. 2024; 11(5):441. https://doi.org/10.3390/photonics11050441
Chicago/Turabian StyleYu, Lixia, Ji Liu, and Wenrui Xue. 2024. "Surface Plasmon Waveguide Based on Nested Dielectric Parallel Nanowire Pairs Coated with Graphene" Photonics 11, no. 5: 441. https://doi.org/10.3390/photonics11050441
APA StyleYu, L., Liu, J., & Xue, W. (2024). Surface Plasmon Waveguide Based on Nested Dielectric Parallel Nanowire Pairs Coated with Graphene. Photonics, 11(5), 441. https://doi.org/10.3390/photonics11050441





