Modulation of Second-Order Sideband Efficiency in an Atom-Assisted Optomechanical System
Abstract
1. Introduction
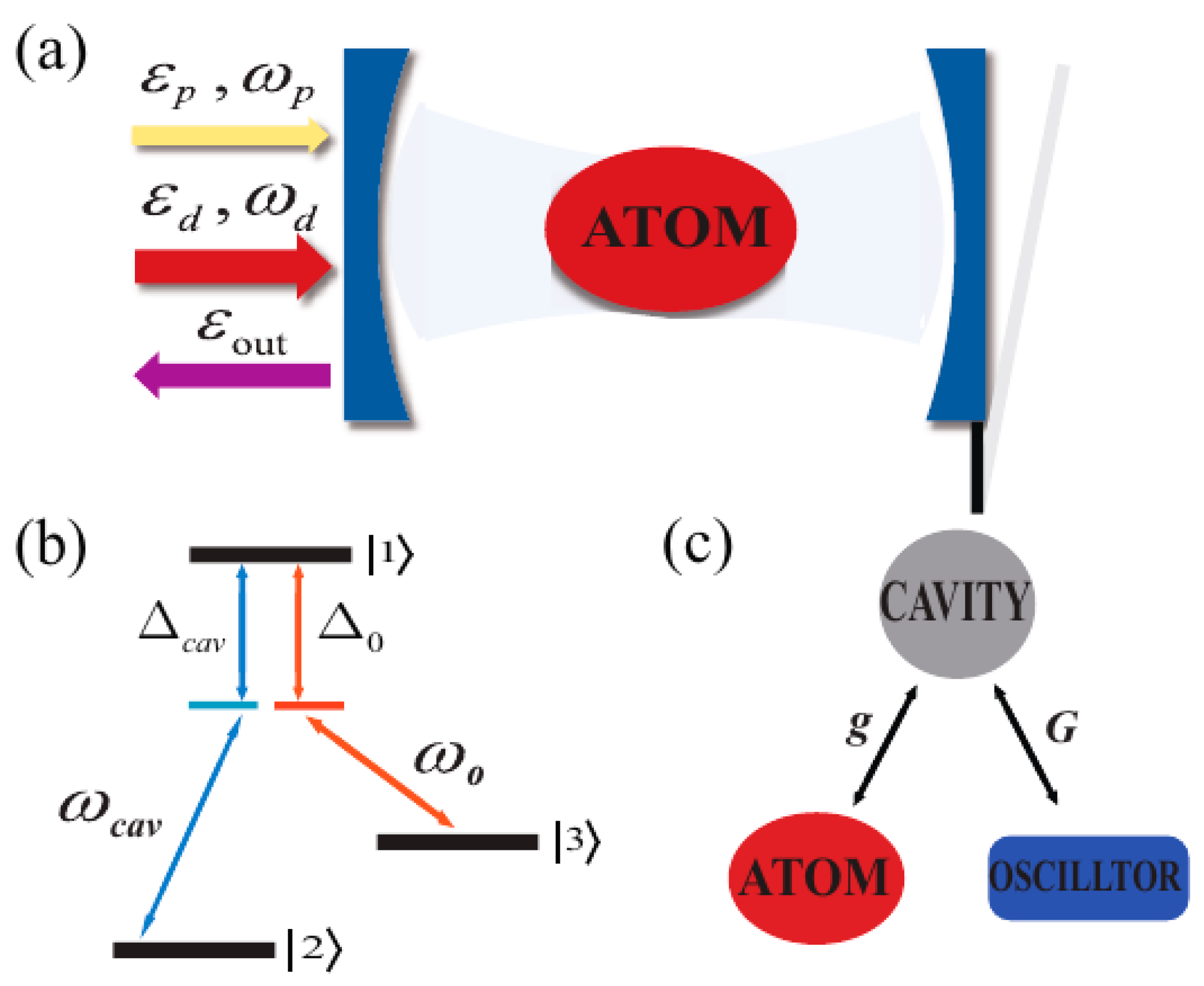
2. Theoretical Model and Equations
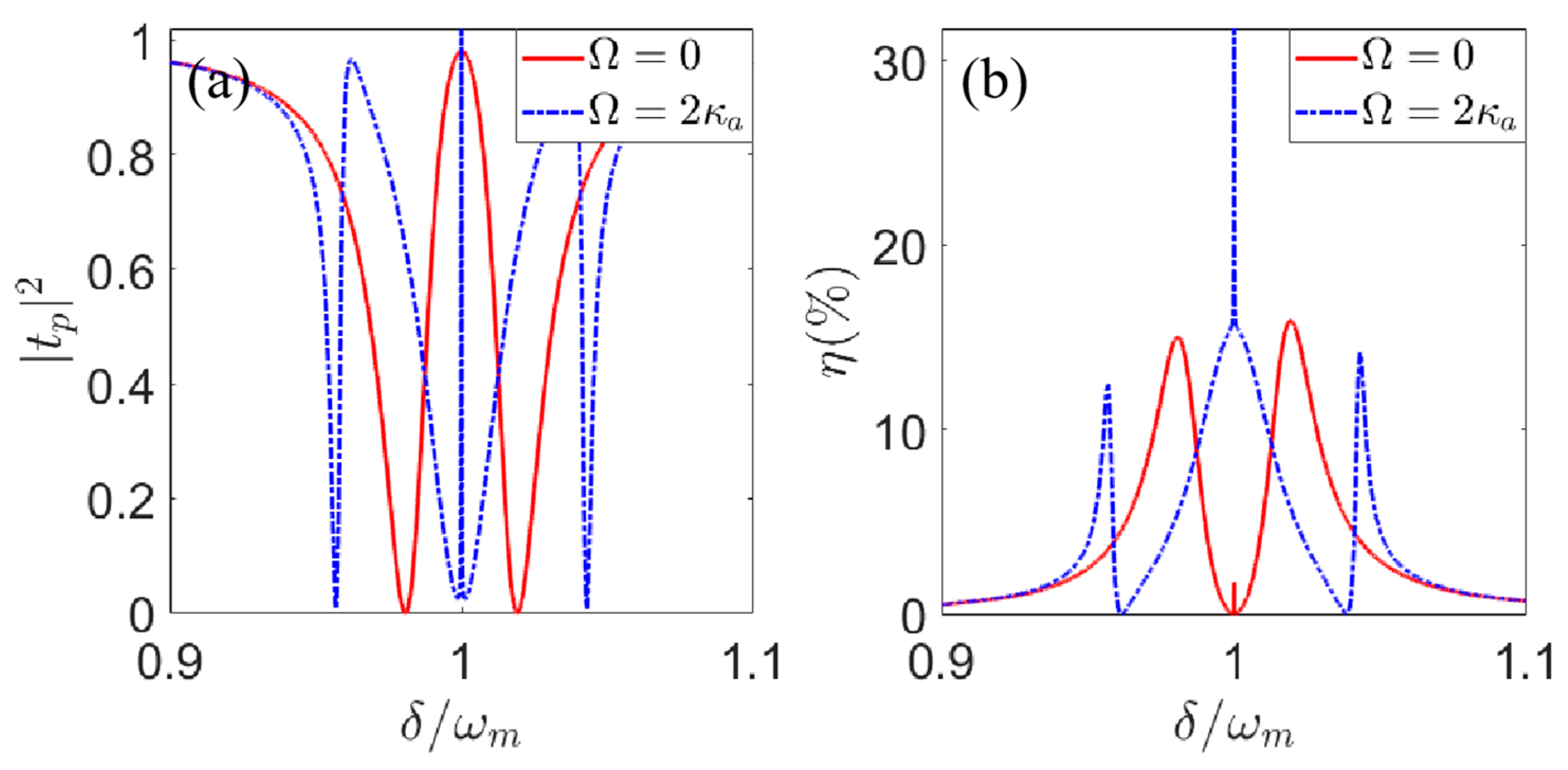
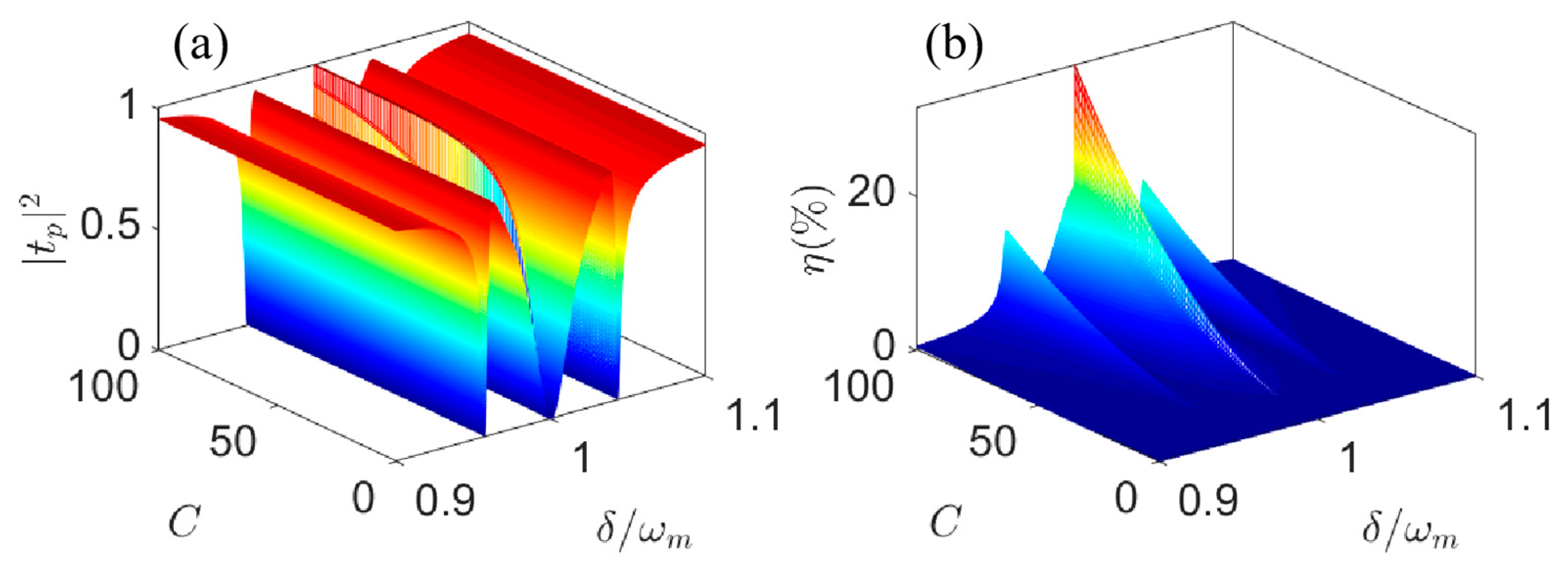
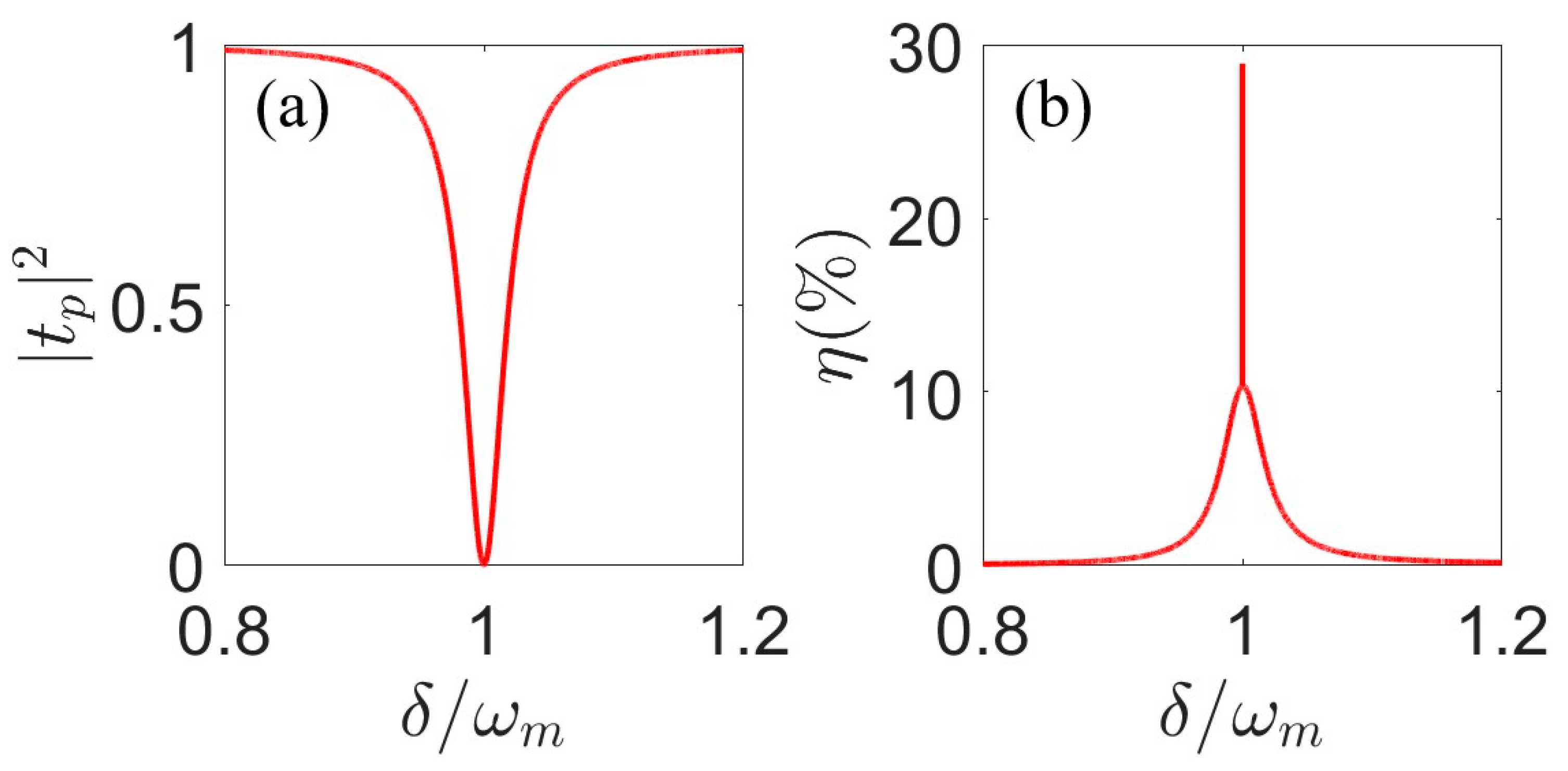
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Caves, C.M. Quantum-mechanical radiation-pressure fluctuations in an interferometer. Phys. Rev. Lett. 1980, 45, 75. [Google Scholar] [CrossRef]
- Chu, S.; Hollberg, L.; Bjorkholm, J.E.; Cable, A.; Ashkin, A. Three-dimensional viscous confinement and cooling of atoms by resonance radiation pressure. Phys. Rev. Lett. 1985, 55, 48. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Agarwal, G.S. Normal mode splitting and antibunching in stokes and anti-stokes processes in cavity optomechanics: Radiation pressure induced four-wave mixing cavity optomechanics. Phys. Rev. A 2010, 81, 76. [Google Scholar] [CrossRef]
- Huang, S.; Agarwal, G.S. Electromagnetically induced transparency with quantized fields in optocavity mechanics. Phys. Rev. A 2011, 83, 43826. [Google Scholar] [CrossRef]
- Wu, Z.; Luo, R.H.; Zhang, J.Q.; Wang, Y.H.; Yang, W.; Feng, M. Force-induced transparency and conversion between slow and fast light in optomechanics. Phys. Rev. A 2017, 96, 033832. [Google Scholar] [CrossRef]
- Liu, Q.C.; Li, T.F.; Luo, X.Q.; Zhao, H.; Xiong, W.; Zhang, Y.S.; Chen, Z.; Liu, J.S.; Chen, W.; Nori, F.; et al. Method for identifying electromagnetically induced transparency in a tunable circuit quantum electrodynamics system. Phys. Rev. A 2016, 93, 053838. [Google Scholar] [CrossRef]
- Weis, S.; Riviere, R.; Deleglise, S.; Gavartin, E.; Arcizet, O.; Schliesser, A.; Kippenberg, T.J. Optomechanically induced transparency. Science 2010, 330, 1520–1523. [Google Scholar] [CrossRef]
- Verhagen, E.; Deléglise, S.; Weis, S.; Schliesser, A.; Kippenberg, T.J. Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 2012, 482, 63–67. [Google Scholar] [CrossRef] [PubMed]
- Safavi-Naeini, A.H.; Alegre, T.M.; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J.T.; Chang, D.E.; Painter, O. Electromagneticauy induced transparency and slow light with optomechanics. Nature 2011, 472, 69–73. [Google Scholar] [CrossRef]
- Karuza, M.; Biancofiore, C.; Bawaj, M.; Molinelli, C.; Galassi, M.; Natali, R.; Tombesi, P.; Di Giuseppe, G.; Vitali, D. Optomechanically induced transparency in a membrane-in-the-middle setup at room temperature. Phys. Rev. A At. Mol. Opt. Phys. 2013, 88, 013804. [Google Scholar] [CrossRef]
- Dobrindt, J.M.; Wilson-Rae, I.; Kippenberg, T.J. Parametric normal-mode splitting in cavity optomechanics. Phys. Rev. Lett. 2008, 101, 263602. [Google Scholar] [CrossRef] [PubMed]
- Gröblacher, S.; Hammerer, K.; Vanner, M.R.; Aspelmeyer, M. Observation of strong coupling between a micromechanical resonator and an optical cavity field. Nature 2009, 60, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Nie, W.; Chen, A.; Lan, Y. Coupling mechanical motion of a single atom to a micromechanical cantilever. Opt. Express 2017, 25, 32931–32947. [Google Scholar] [CrossRef]
- Arcizet, O.; Cohadon, P.F.; Briant, T.; Pinard, M.; Heidmann, A. Radiation-pressure cooling and optomechanical instability of a micromirror. Nature 2006, 444, 71–74. [Google Scholar] [CrossRef] [PubMed]
- Bao, L.; Qi, B.; Dong, D.; Nori, F. Fundamental limits for reciprocal and nonreciprocal non-Hermitian quantum sensing. Phys. Rev. A 2021, 103, 042418. [Google Scholar] [CrossRef]
- Li, L.; Yang, W.X.; Zhang, Y.; Shui, T.; Chen, A.X.; Jiang, Z. Enhanced generation of charge-dependent second-order sideband and high-sensitivity charge sensors in a gain-cavity-assisted optomechanical system. Phys. Rev. A 2018, 98, 063840. [Google Scholar] [CrossRef]
- Jing, H.; Lü, H.; Özdemir, S.K.; Carmon, T.; Nori, F. Nanoparticle sensing with a spinning resonator. Optica 2018, 5, 1424–1430. [Google Scholar] [CrossRef]
- Liu, S.; Liu, B.; Wang, J.; Sun, T.; Yang, W.X. Realization of a highly sensitive mass sensor in a quadratically coupled optomechanical system. Phys. Rev. A 2019, 99, 033822. [Google Scholar] [CrossRef]
- Singh, S.K.; Peng, J.X.; Asjad, M.; Mazaheri, M. Entanglement and coherence in a hybrid Laguerre–Gaussian rotating cavity optomechanical system with two-level atoms. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 215502. [Google Scholar] [CrossRef]
- Lü, X.Y.; Zhang, W.M.; Ashhab, S.; Wu, Y.; Nori, F. Quantum-criticality-induced strong Kerr nonlinearities in optomechanical systems. Sci. Rep. 2013, 3, 2943. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S.; Rauschenbeutel, A.; Schneeweiss, P.; Volz, J.; Pichler, H.; Zoller, P. Chiral quantum optics. Nature 2017, 541, 473–480. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, G.S.; Huang, S. Electromagnetically induced transparency in mechanical effects of light. Phys. Rev. A 2010, 1, 041803. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, H.; Cui, Y.; Li, X.; Chen, G.; Chen, B. Electromagnetically induced transparency and slow light in two-mode optomechanics. Opt. Express 2013, 1, 12165–12173. [Google Scholar] [CrossRef] [PubMed]
- Hou, B.P.; Wei, L.F.; Wang, S.J. Optomechanically induced transparency and absorption in hybridized optomechanical systems. Phys. Rev. A 2015, 92, 033829. [Google Scholar] [CrossRef]
- Bai, C.; Hou, B.P.; Lai, D.G.; Wu, D. Tunable optomechanically induced transparency in double quadratically coupled optomechanical cavities within a common reservoir. Phys. Rev. A 2016, 93, 043804. [Google Scholar] [CrossRef]
- Suzuki, H.; Brown, E.; Sterling, R. Nonlinear dynamics of an optomechanical system with a coherent mechanical pump: Second-order sideband generation. Phys. Rev. A 2015, 92, 33823. [Google Scholar] [CrossRef]
- Xiong, H.; Si, L.G.; Zheng, A.S.; Yang, X.; Wu, Y. Higher-order sidebands in optomechanically induced transparency. Phys. Rev. A 2012, 86, 013815. [Google Scholar] [CrossRef]
- Liu, S.; Yang, W.X.; Zhu, Z.; Shui, T.; Li, L. Quadrature squeezing of a higher-order sideband spectrum in cavity optomechanics. Opt. Lett. 2018, 43, 9. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Xiao, Q.; Wu, Y. Giant enhancement of optical high-order sideband generation and their control in a dimer of two cavities with gain and loss. Phys. Rev. A 2016, 93, 063814. [Google Scholar] [CrossRef]
- Li, J.; Qu, Y.; Yu, R.; Wu, Y. Generation and control of optical frequency combs using cavity electromagnetically induced transparency. Phys. Rev. A 2018, 97, 023826. [Google Scholar] [CrossRef]
- Lü, X.Y.; Jing, H.; Ma, J.Y.; Wu, Y. PT-symmetry-breaking chaos in optomechanics. Phys. Rev. Lett. 2015, 114, 253601. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Yang, X. Strong-coupling theory of periodically driven two-level systems. Phys. Rev. Lett. 2007, 98, 013601. [Google Scholar] [CrossRef]
- Gao, Y.P.; Liu, X.F.; Wang, T.J.; Cao, C.; Wang, C. Photon excitation and photon-blockade effects in optomagnonic microcavities. Phys. Rev. A 2019, 100, 043831. [Google Scholar] [CrossRef]
- Gao, Y.P.; Cao, C.; Lu, P.F.; Wang, C. Phase-controlled photon blockade in optomechanical systems. Fundam. Res. 2023, 3, 30–36. [Google Scholar] [CrossRef]
- Xiong, H.; Si, L.-G.; Lü, X.-Y.; Yang, X.; Wu, Y. Carrier-envelope phase-dependent effect of high-order sideband generation in ultrafast driven optomechanical system. Opt. Lett. 2013, 38, 353. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.H.; Si, L.G.; Wang, X.Y.; Wu, Y. Exceptional points enhance sum sideband generation in a mechanical PT-symmetric system. Opt. Express 2021, 29, 4875–4886. [Google Scholar] [CrossRef] [PubMed]
- Hodaei, H.; Hassan, A.U.; Wittek, S.; Garcia-Gracia, H.; El-Ganainy, R.; Christodoulides, D.N.; Khajavikhan, M. Enhanced sensitivity at higher-order exceptional points. Nature 2017, 548, 187–191. [Google Scholar] [CrossRef]
- Liu, Z.X.; Xiong, H.; Wu, Y. Generation and amplification of a high-order sideband induced by two-level atoms in a hybrid optomechanical system. Phys. Rev. A 2018, 97, 013801. [Google Scholar] [CrossRef]
- Zhang, W.; Qin, L.G.; Tian, L.J.; Wang, Z.Y. Multiple induced transparency in a hybrid driven cavity optomechanical device with a two-level system. Chin. Phys. B 2021, 30, 094203. [Google Scholar] [CrossRef]
- Liu, S.; Yang, W.X.; Shui, T.; Zhu, Z.; Chen, A.X. Tunable two-phonon higher-order sideband amplification in a quadratically coupled optomechanical system. Sci. Rep. 2017, 7, 17637. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.X. Precision measurement of magnetic field based on second-order sideband generation in a hybrid electromagnetic-optomechanical system. IEEE Sens. J. 2018, 18, 9145–9150. [Google Scholar] [CrossRef]
- Jiao, Y.; Lü, H.; Qian, J.; Li, Y.; Jing, H. Nonlinear optomechanics with gain and loss: Amplifying higher-order sideband and group delay. New J. Phys. 2016, 18, 083034. [Google Scholar] [CrossRef]
- Hao, H.; Kuzyk, M.C.; Ren, J.; Zhang, F.; Gu, Y. Hybrid electromagnetically-optomechanically induced transparency in an atom-assisted optomechanical system. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 105502. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, L.-X.; Shui, T.; Li, L.; Yang, W.-X. Modulation of Second-Order Sideband Efficiency in an Atom-Assisted Optomechanical System. Photonics 2024, 11, 416. https://doi.org/10.3390/photonics11050416
Fan L-X, Shui T, Li L, Yang W-X. Modulation of Second-Order Sideband Efficiency in an Atom-Assisted Optomechanical System. Photonics. 2024; 11(5):416. https://doi.org/10.3390/photonics11050416
Chicago/Turabian StyleFan, Liang-Xuan, Tao Shui, Ling Li, and Wen-Xing Yang. 2024. "Modulation of Second-Order Sideband Efficiency in an Atom-Assisted Optomechanical System" Photonics 11, no. 5: 416. https://doi.org/10.3390/photonics11050416
APA StyleFan, L.-X., Shui, T., Li, L., & Yang, W.-X. (2024). Modulation of Second-Order Sideband Efficiency in an Atom-Assisted Optomechanical System. Photonics, 11(5), 416. https://doi.org/10.3390/photonics11050416




