A Superimposed Codebook Design for Downlink Sparse Code Multiple Access Visible Light Communication System
Abstract
1. Introduction
- We derive the analytical expression of the average SER for a shot noise-incorporated SCMA-VLC system, based on the probability density function (PDF) of the received signal. The derived analytical expression of the SER is in good agreement with the numerical simulation results.
- We propose a real, superimposed codebook design scheme for a downlink SCMA-VLC system under shot noise. The scheme adopts a separable codebook structure, which contributes to simplifying the optimization objective from minimizing the system SER to minimizing the SER of the one-dimensional components of superimposed codewords. Then, the optimization problem is formulated and solved by the differential evolution (DE) algorithm to obtain the optimal multi-user superimposed codewords for different shot noise conditions. Compared with existing works, the proposed codebooks are able to provide significant gains in BER performance, especially for higher shot noise intensities. In addition, the proposed codebook design scheme can be extended to meet the needs of higher overload factors.
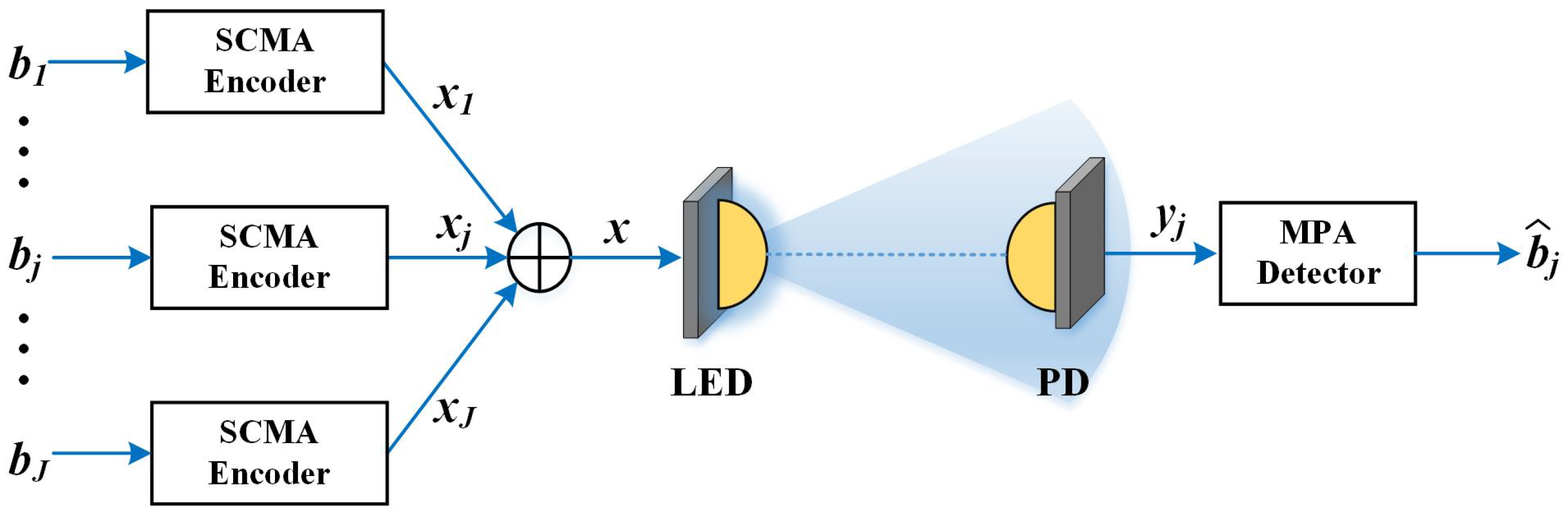
2. System Model
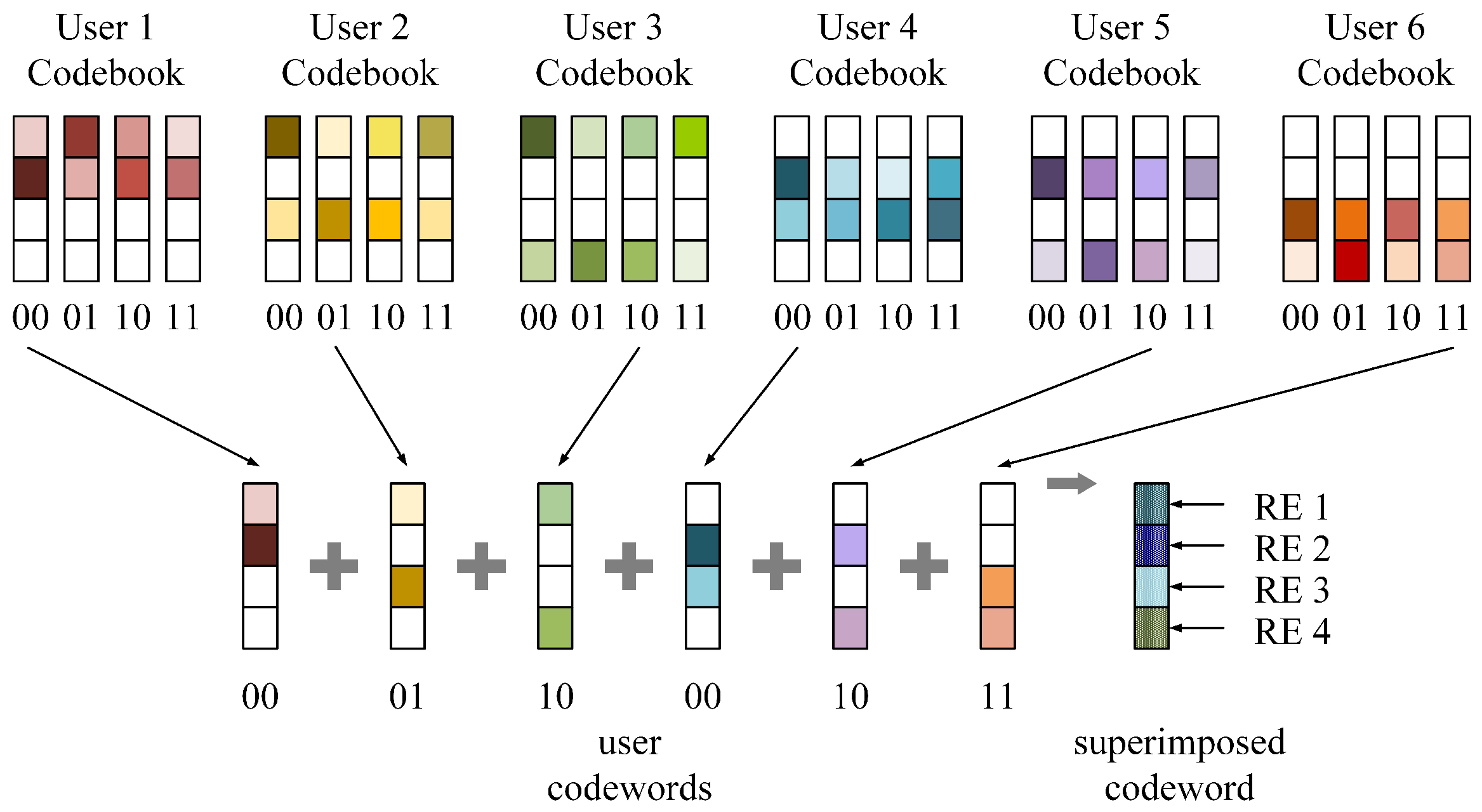
3. SCMA-VLC Codebook Design
3.1. Codebook Structure Design
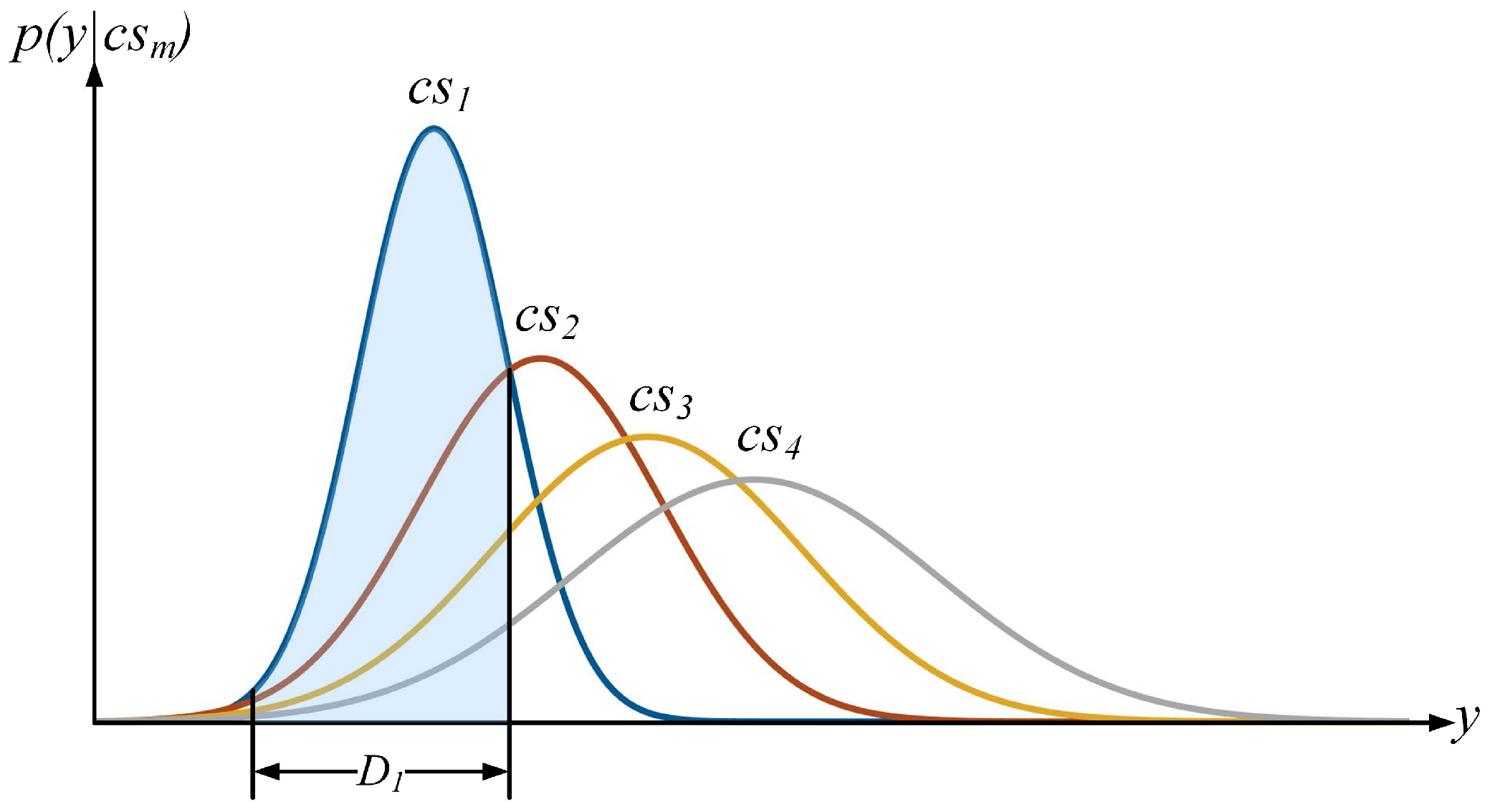
3.2. Optimization Criteria
3.3. Implementation and Analysis
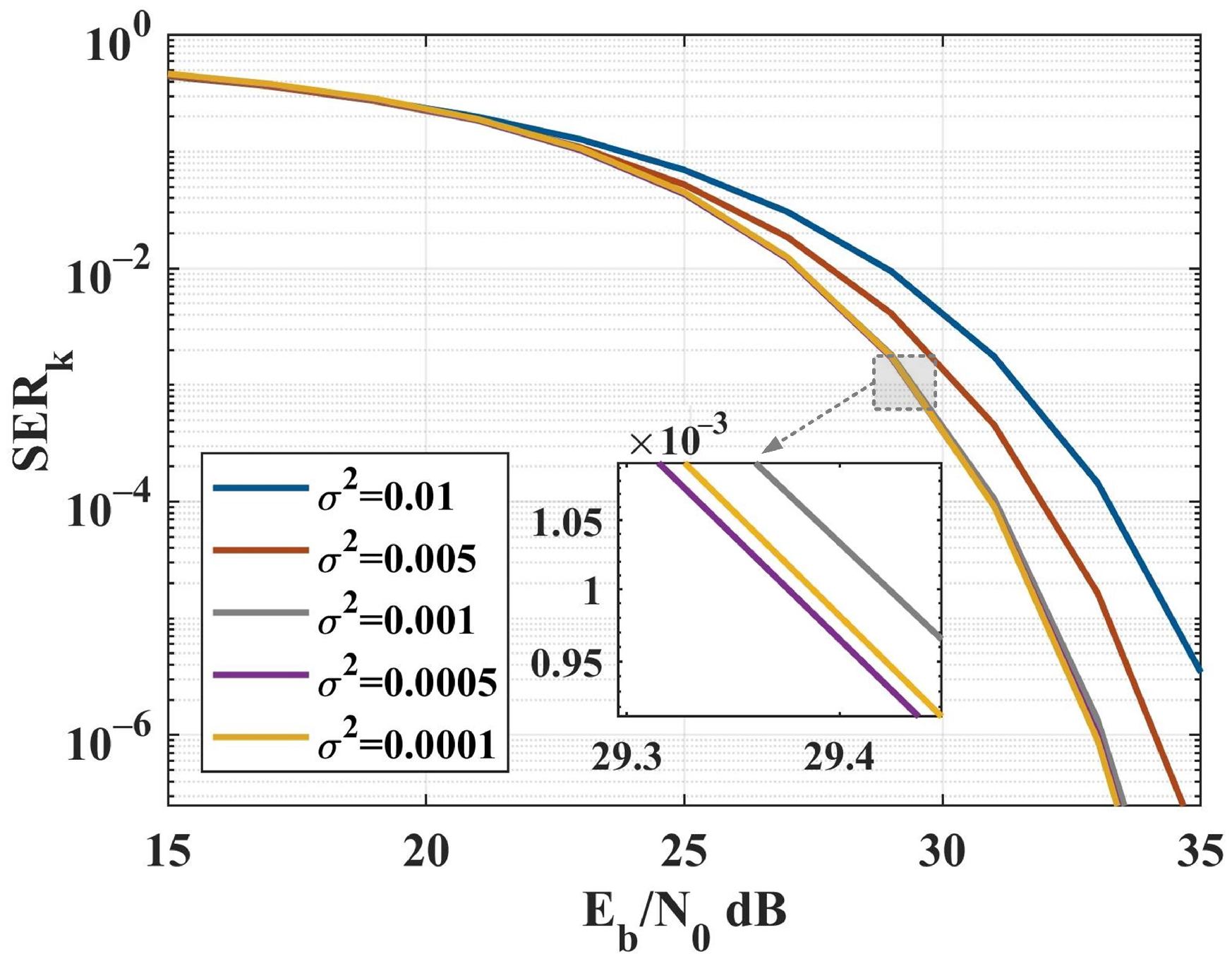
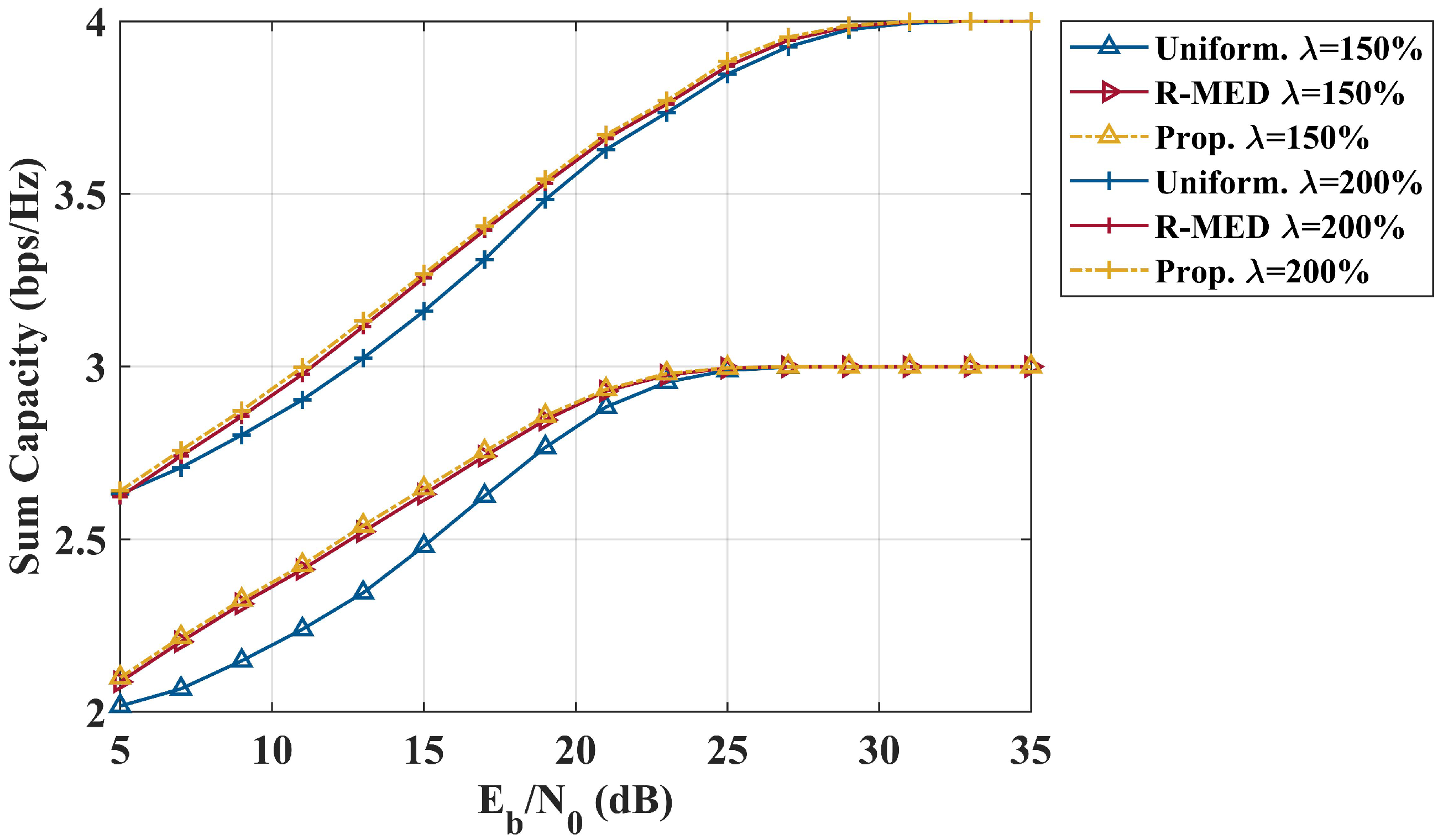
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karunatilaka, D.; Zafar, F.; Kalavally, V.; Parthiban, R. LED Based Indoor Visible Light Communications: State of the Art. IEEE Commun. Surv. Tutor. 2015, 17, 1649–1678. [Google Scholar] [CrossRef]
- Matheus, L.E.M.; Vieira, A.B.; Vieira, L.F.M.; Vieira, M.A.M.; Gnawali, O. Visible Light Communication: Concepts, Applications and Challenges. IEEE Commun. Surv. Tutor. 2019, 21, 3204–3237. [Google Scholar] [CrossRef]
- Chi, N.; Zhou, Y.; Wei, Y.; Hu, F. Visible Light Communication in 6G: Advances, Challenges, and Prospects. IEEE Veh. Technol. Mag. 2020, 15, 93–102. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A Survey of Non-Orthogonal Multiple Access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar] [CrossRef]
- Nikopour, H.; Baligh, H. Sparse code multiple access. In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 332–336. [Google Scholar]
- Taherzadeh, M.; Nikopour, H.; Bayesteh, A.; Baligh, H. SCMA Codebook Design. In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, BC, Canada, 14–17 September 2014; pp. 1–5. [Google Scholar]
- Mitra, R.; Sharma, S.; Kaddoum, G.; Bhatia, V. Color-Domain SCMA NOMA for Visible Light Communication. IEEE Commun. Lett. 2021, 25, 200–204. [Google Scholar] [CrossRef]
- Lin, B.; Tang, X.; Zhou, Z.; Lin, C.; Zabih, G. Experimental demonstration of SCMA for visible light communications. Opt. Commun. 2018, 419, 36–40. [Google Scholar] [CrossRef]
- Lin, B.; Tang, X.; Ghassemlooy, Z. A Power Domain Sparse Code Multiple Access Scheme for Visible Light Communications. IEEE Wirel. Commun. Lett. 2020, 9, 61–64. [Google Scholar] [CrossRef]
- Lou, S.; Gong, C.; Gao, Q.; Xu, Z. SCMA with Low Complexity Symmetric Codebook Design for Visible Light Communication. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Yu, L.; Qian, J.; Gui, Y.; Liu, Z.; Xiao, P.; Wang, Y.; Wang, Z. Uniform-Distributed Constellation Codebook Design for High-Capacity Visible Light Communications. IEEE Commun. Lett. 2023, 27, 2993–2997. [Google Scholar] [CrossRef]
- Hu, S.; Gao, Q.; Gong, C.; Xu, Z.; Boluda-Ruiz, R.; Qaraqe, K. Energy-efficient Modulation for Visible Light SCMA System with Signal-dependent Noise. In Proceedings of the 2018 11th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–6. [Google Scholar]
- Gao, Q.; Qaraqe, K.; Serpedin, E. Rotated Color Shift Keying for Visible Light Communications with Signal-Dependent Noise. IEEE Commun. Lett. 2020, 24, 844–848. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Anwar, D.N.; Bohara, V.A.; Srivastava, A.; Liu, Z. Low-Complexity Codebook Design for SCMA-Based Visible Light Communication. IEEE Open J. Commun. Soc. 2022, 3, 106–118. [Google Scholar] [CrossRef]
- Gao, Q.; Hu, S.; Gong, C.; Serpedin, E.; Qaraqe, K.; Xu, Z. Distance-Range-Oriented Constellation Design for VLC-SCMA Downlink With Signal-Dependent Noise. IEEE Commun. Lett. 2019, 23, 434–437. [Google Scholar] [CrossRef]
- Komine, T.; Nakagawa, M. Fundamental Analysis for Visible-Light Communication System Using LED Lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
- Moser, S.M. Capacity Results of an Optical Intensity Channel With Input-Dependent Gaussian Noise. IEEE Trans. Inf. Theory 2012, 58, 207–223. [Google Scholar] [CrossRef]
- Yaseen, M.; Alsmadi, M.; Canbilen, A.E.; Ikki, S.S. Visible Light Communication With Input-Dependent Noise: Channel Estimation, Optimal Receiver Design and Performance Analysis. J. Light. Technol. 2021, 39, 7406–7416. [Google Scholar] [CrossRef]
- Hoshyar, R.; Wathan, F.P.; Canbilen, A.E.; Tafazolli, R. Novel Low-Density Signature for Synchronous CDMA Systems Over AWGN Channel. IEEE Trans. Signal Process. 2008, 56, 1616–1626. [Google Scholar] [CrossRef]
- Zheng, Y.; Xin, J.; Wang, H.; Zhang, S.; Qiao, Y. A Low-Complexity Codebook Design Scheme for SCMA Systems Over an AWGN Channel. IEEE Trans. Veh. Technol. 2022, 71, 8675–8688. [Google Scholar] [CrossRef]
- Zhang, S.; Xiao, K.; Xiao, B.; Chen, Z.; Xia, B.; Chen, D.; Ma, S. A capacity-based codebook design method for sparse code multiple access systems. In Proceedings of the 2016 8th International Conference on Wireless Communications & Signal Processing (WCSP), Yangzhou, China, 13–15 October 2016; pp. 1–5. [Google Scholar]
- Price, K.; Storn, R.; Lampinen, J. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
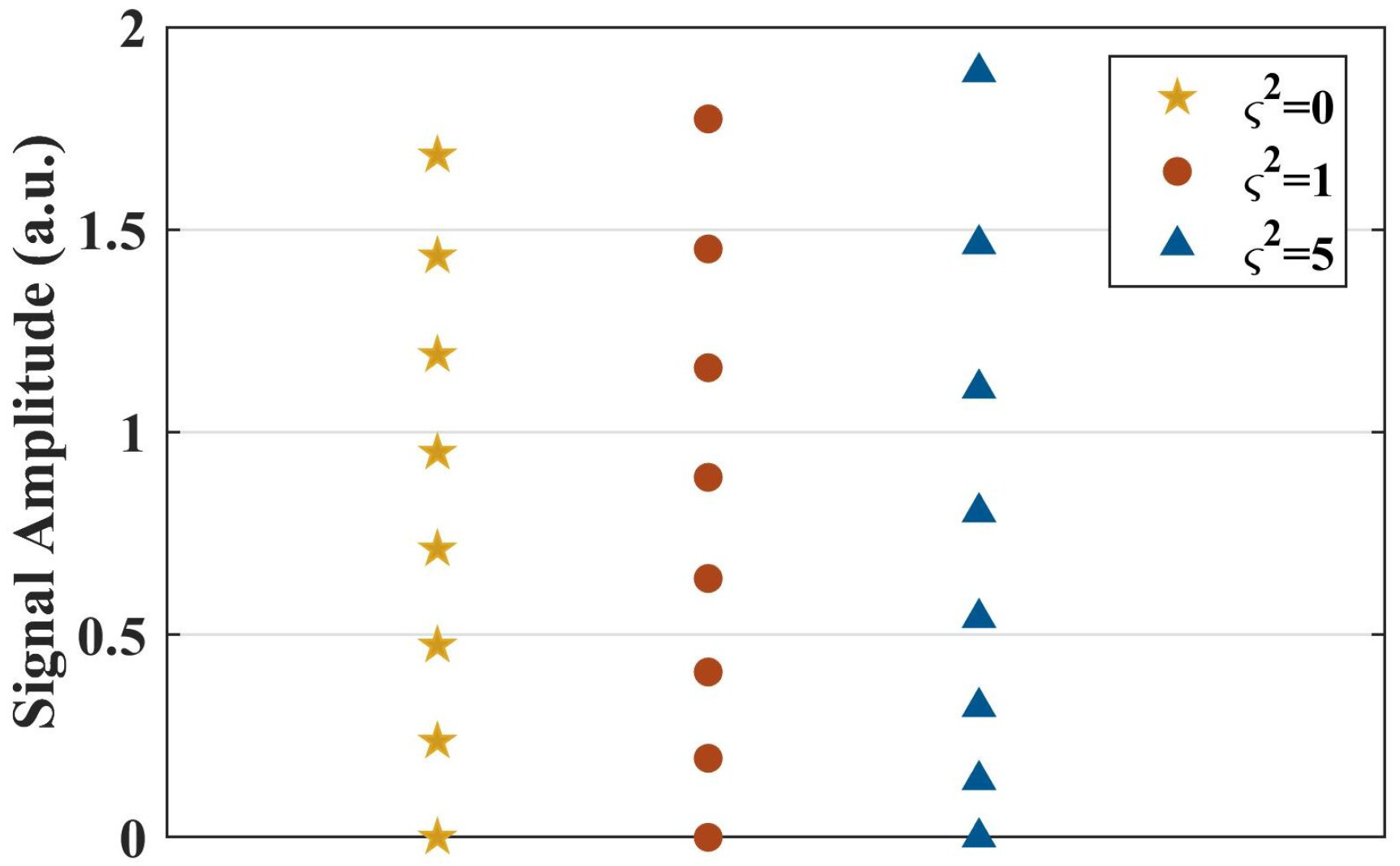



| Parameter | Value |
|---|---|
| Current-to-light conversion efficiency, | 0.2 A/W |
| Semi-angle at half power, | |
| Gain of optical filter, | 1 |
| Refractive index, | 1.5 |
| Field of view of PD, | |
| Responsivity of PD, R | 0.6 W/A |
| Active area of PD, A | 1 cm2 |
| Distance between LED and receivers, | 1 m |
| Number of iterations in MPA | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Wang, Z.; Yu, J.; Jiang, Y. A Superimposed Codebook Design for Downlink Sparse Code Multiple Access Visible Light Communication System. Photonics 2024, 11, 321. https://doi.org/10.3390/photonics11040321
Dong J, Wang Z, Yu J, Jiang Y. A Superimposed Codebook Design for Downlink Sparse Code Multiple Access Visible Light Communication System. Photonics. 2024; 11(4):321. https://doi.org/10.3390/photonics11040321
Chicago/Turabian StyleDong, Jingxuan, Zixiong Wang, Jinlong Yu, and Yang Jiang. 2024. "A Superimposed Codebook Design for Downlink Sparse Code Multiple Access Visible Light Communication System" Photonics 11, no. 4: 321. https://doi.org/10.3390/photonics11040321
APA StyleDong, J., Wang, Z., Yu, J., & Jiang, Y. (2024). A Superimposed Codebook Design for Downlink Sparse Code Multiple Access Visible Light Communication System. Photonics, 11(4), 321. https://doi.org/10.3390/photonics11040321






