Cascaded Third-Harmonic Generation in Optically Induced 3D Nonlinear Photonic Crystals
Abstract
1. Introduction
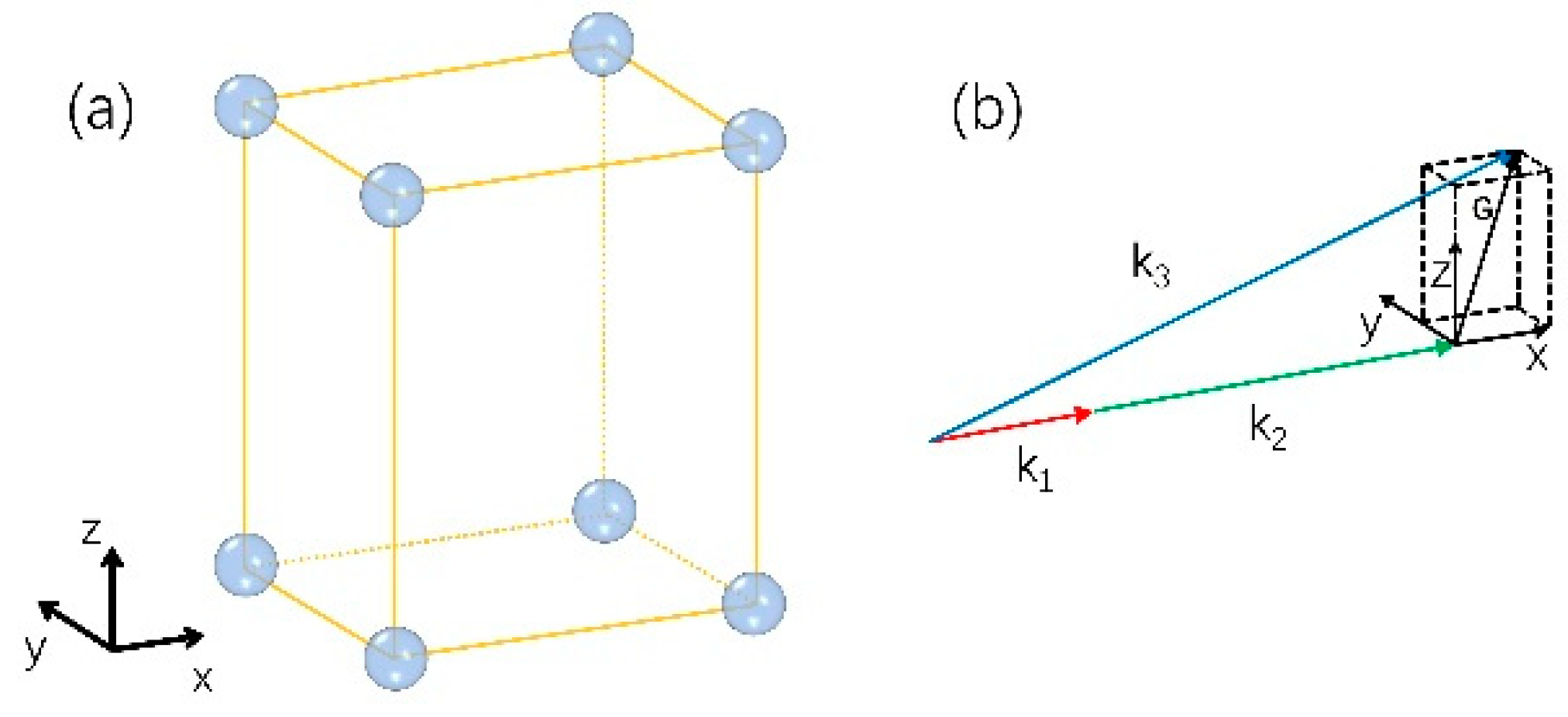
2. Structure Design
3. Experiment
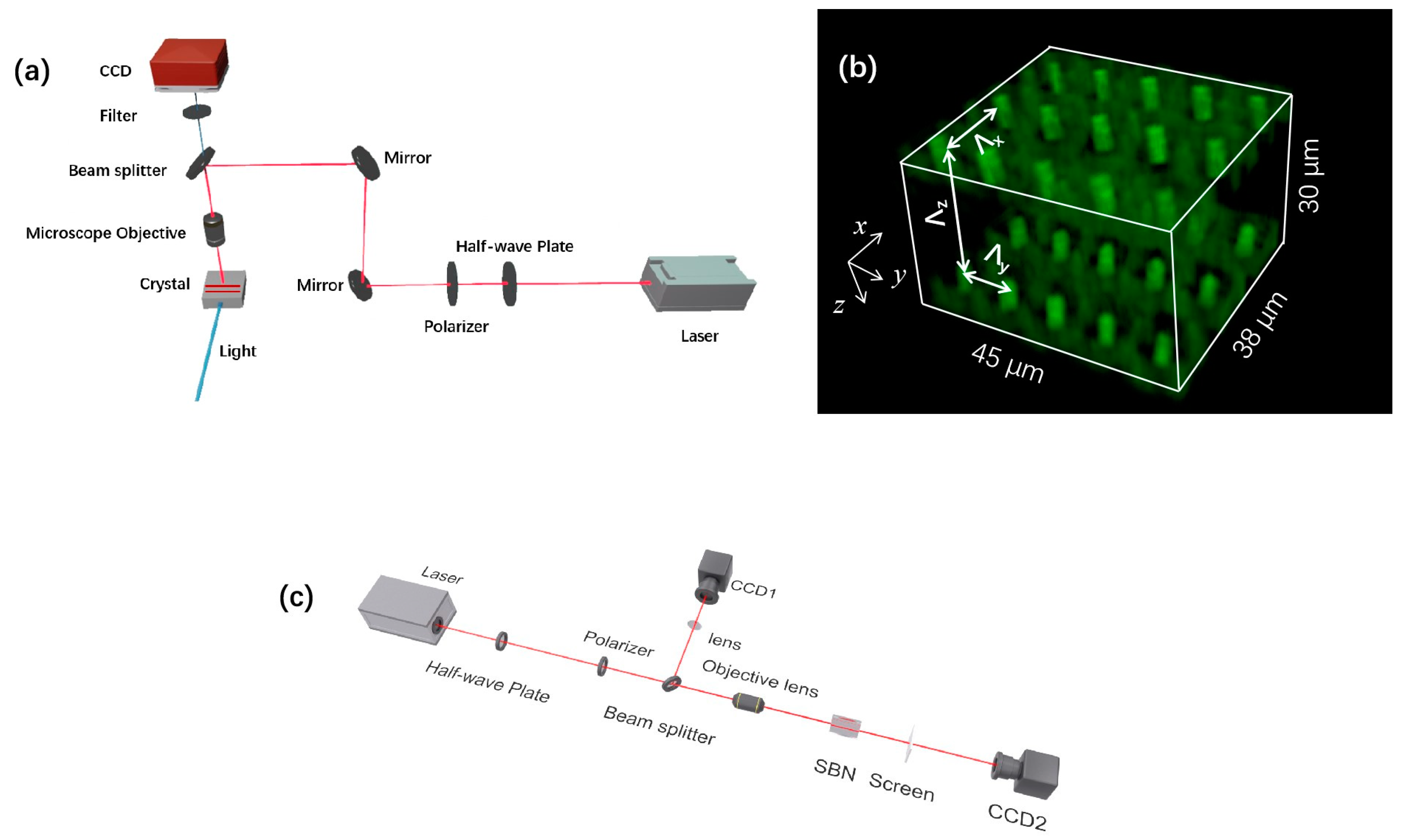
3.1. Sample Fabrication
3.2. Cascaded Third Harmonic Generation Experiment
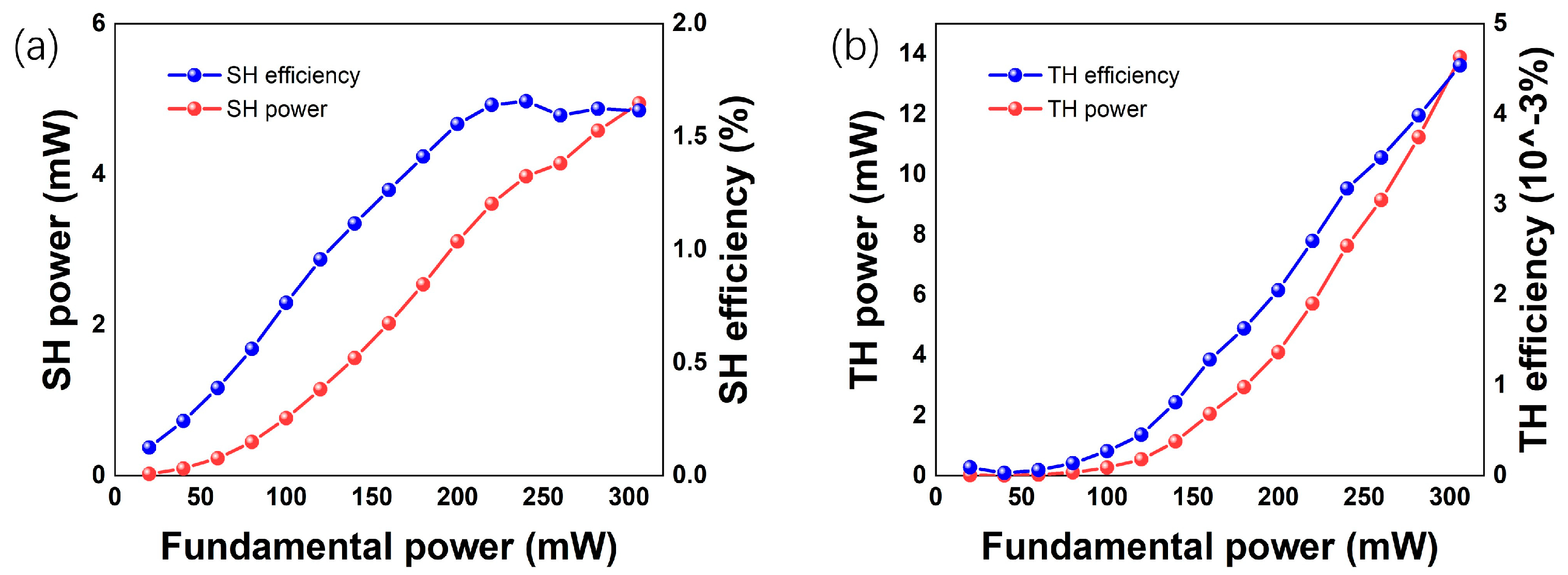
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arie, A.; Voloch, N. Periodic, quasi-periodic, and random quadratic nonlinear photonic crystals. Laser Photonics Rev. 2010, 4, 355–373. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, Y.; Wang, D.; Song, W.; Liu, X.; Pang, J.; Geng, D.; Sang, Y.; Liu, H. Microstructure and domain engineering of lithium niobate crystal films for integrated photonic applications. Light Sci. Appl. 2020, 9, 197. [Google Scholar] [CrossRef]
- Pan, J.-W.; Chen, Z.-B.; Lu, C.-Y.; Weinfurter, H.; Zeilinger, A.; Żukowski, M. Multiphoton entanglement and interferometry. Rev. Mod. Phys. 2012, 84, 777–838. [Google Scholar] [CrossRef]
- Canalias, C.; Pasiskevicius, V. Mirrorless optical parametric oscillator. Nat. Photonics 2007, 1, 459–462. [Google Scholar] [CrossRef]
- Ge, L.; Chen, Y.; Jiang, H.; Li, G.; Zhu, B.; Liu, Y.a.; Chen, X. Broadband quasi-phase matching in a MgO:PPLN thin film. Photonics Res. 2018, 6, 954. [Google Scholar] [CrossRef]
- Zhang, X.; Lytle, A.L.; Popmintchev, T.; Zhou, X.; Kapteyn, H.C.; Murnane, M.M.; Cohen, O. Quasi-phase-matching and quantum-path control of high-harmonic generation using counterpropagating light. Nature Phys. 2007, 3, 270–275. [Google Scholar] [CrossRef]
- Yamada, M.; Nada, N.; Saitoh, M.; Watanabe, K. First-order quasi-phase matched LiNbO3waveguide periodically poled by applying an external field for efficient blue second-harmonic generation. Appl. Phys. Lett. 1993, 62, 435–436. [Google Scholar] [CrossRef]
- Chen, X.; Karpinski, P.; Shvedov, V.; Koynov, K.; Wang, B.; Trull, J.; Cojocaru, C.; Krolikowski, W.; Sheng, Y. Ferroelectric domain engineering by focused infrared femtosecond pulses. Appl. Phys. Lett. 2015, 107, 141102. [Google Scholar] [CrossRef]
- Thomas, J.; Hilbert, V.; Geiss, R.; Pertsch, T.; Tünnermann, A.; Nolte, S. Quasi phase matching in femtosecond pulse volume structured x-cut lithium niobate. Laser Photonics Rev. 2013, 7, L17–L20. [Google Scholar] [CrossRef]
- Xu, X.; Wang, T.; Chen, P.; Zhou, C.; Ma, J.; Wei, D.; Wang, H.; Niu, B.; Fang, X.; Wu, D.; et al. Femtosecond laser writing of lithium niobate ferroelectric nanodomains. Nature 2022, 609, 496–501. [Google Scholar] [CrossRef]
- Xu, T.; Switkowski, K.; Chen, X.; Liu, S.; Koynov, K.; Yu, H.; Zhang, H.; Wang, J.; Sheng, Y.; Krolikowski, W. Three-dimensional nonlinear photonic crystal in ferroelectric barium calcium titanate. Nat. Photonics 2018, 12, 591–595. [Google Scholar] [CrossRef]
- Wei, D.; Wang, C.; Wang, H.; Hu, X.; Wei, D.; Fang, X.; Zhang, Y.; Wu, D.; Hu, Y.; Li, J.; et al. Experimental demonstration of a three-dimensional lithium niobate nonlinear photonic crystal. Nat. Photonics 2018, 12, 596–600. [Google Scholar] [CrossRef]
- Imbrock, J.; Wesemann, L.; Kroesen, S.; Ayoub, M.; Denz, C. Waveguide-integrated three-dimensional quasi-phase-matching structures. Optica 2020, 7, 28–34. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, H.; Chen, X. Three-dimensional nonlinear optical holograms. Phys. Rev. A 2020, 102, 063505. [Google Scholar] [CrossRef]
- Zhang, Y.; Sheng, Y.; Zhu, S.; Xiao, M.; Krolikowski, W. Nonlinear photonic crystals: From 2D to 3D. Optica 2021, 8, 372–381. [Google Scholar] [CrossRef]
- Wei, D.; Wang, C.; Xu, X.; Wang, H.; Hu, Y.; Chen, P.; Li, J.; Zhu, Y.; Xin, C.; Hu, X.; et al. Efficient nonlinear beam shaping in three-dimensional lithium niobate nonlinear photonic crystals. Nat. Commun. 2019, 10, 4193. [Google Scholar] [CrossRef]
- Chen, P.; Xu, X.; Wang, T.; Zhou, C.; Wei, D.; Ma, J.; Guo, J.; Cui, X.; Cheng, X.; Xie, C.; et al. Laser nanoprinting of 3D nonlinear holograms beyond 25000 pixels-per-inch for inter-wavelength-band information processing. Nat. Commun. 2023, 14, 5523. [Google Scholar] [CrossRef]
- Bahabad, A.; Arie, A. Generation of Optical Vortex Beams by NonlinearWave Mixing. Opt. Express 2007, 15, 17619–17624. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Mazur, L.M.; Switkowski, K.; Wang, B.; Chen, F.; Arie, A.; Krolikowski, W.; Sheng, Y. Highly Efficient 3D Nonlinear Photonic Crystals in Ferroelectrics. Adv. Opt. Mater. 2023, 11, 2300021. [Google Scholar] [CrossRef]
- Hu, X.; Liu, S.; Xu, T.; Sheng, Y.; Zhao, R.; Krolikowski, W. Nonlinear generation of an optical bottle beam in domain-engineered ferroelectric crystals. Opt. Lett. 2023, 48, 5527–5530. [Google Scholar] [CrossRef]
- Karnieli, A.; Tsesses, S.; Bartal, G.; Arie, A. Emulating spin transport with nonlinear optics, from high-order skyrmions to the topological Hall effect. Nat. Commun. 2021, 12, 1092. [Google Scholar] [CrossRef]
- Yesharim, O.; Pearl, S.; Foley-Comer, J.; Juwiler, I.; Arie, A. Direct generation of spatially entangled qudits using quantum nonlinear optical holography. Sci. Adv. 2023, 9, 7968. [Google Scholar] [CrossRef]
- Monat, C.; Grillet, C.; Collins, M.; Clark, A.; Schroeder, J.; Xiong, C.; Li, J.; O’Faolain, L.; Krauss, T.F.; Eggleton, B.J.; et al. Integrated optical auto-correlator based on third-harmonic generation in a silicon photonic crystal waveguide. Nat. Commun. 2014, 5, 3246. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, Y.; Ming, N.b. Quasi-Phase-Matched Third-Harmonic Generation in a Quasi-Periodic Optical Superlattice. Science 1997, 278, 843–846. [Google Scholar] [CrossRef]
- Mateos, L.; Molina, P.; Galisteo, J.; López, C.; Bausá, L.E.; Ramírez, M.O. Simultaneous generation of second to fifth harmonic conical beams in a two dimensional nonlinear photonic crystal. Opt. Express 2012, 20, 29940–29948. [Google Scholar] [CrossRef]
- Chen, B.Q.; Zhang, C.; Hu, C.Y.; Liu, R.J.; Li, Z.Y. High-Efficiency Broadband High-Harmonic Generation from a Single Quasi-Phase-Matching Nonlinear Crystal. Phys. Rev. Lett. 2015, 115, 083902. [Google Scholar] [CrossRef]
- Wei, D.; Guo, J.; Fang, X.; Wei, D.; Ni, R.; Chen, P.; Hu, X.; Zhang, Y.; Hu, W.; Lu, Y.Q.; et al. Multiple generations of high-order orbital angular momentum modes through cascaded third-harmonic generation in a 2D nonlinear photonic crystal. Opt. Express 2017, 25, 11556–11563. [Google Scholar] [CrossRef]
- Chen, C.; Lu, J.; Liu, Y.; Hu, X.; Zhao, L.; Zhang, Y.; Zhao, G.; Yuan, Y.; Zhu, S. Cerenkov third-harmonic generation via cascaded χ2 processes in a periodic-poled LiTaO3 waveguide. Opt. Lett. 2011, 36, 1227–1229. [Google Scholar] [CrossRef]
- Fang, X.; Wei, D.; Wang, Y.; Wang, H.; Zhang, Y.; Hu, X.; Zhu, S.; Xiao, M. Conical third-harmonic generation in a hexagonally poled LiTaO3 crystal. Appl. Phys. Lett. 2017, 110, 4978669. [Google Scholar] [CrossRef]
- Vernay, A.; Bonnet-Gamard, L.; Boutou, V.; Trajtenberg-Mills, S.; Arie, A.; Boulanger, B. High efficiency cascaded third-harmonic generation in a quasi-periodically poled KTiOPO4 crystal. OSA Continuum 2020, 3, osac.395084. [Google Scholar] [CrossRef]
- Keren-Zur, S.; Ellenbogen, T. A new dimension for nonlinear photonic crystals. Nature Photonics 2018, 12, 575–577. [Google Scholar] [CrossRef]
- Pogosian, T.; Lai, N.D. Theoretical investigation of three-dimensional quasi-phase-matching photonic structures. Phys. Rev. A 2016, 94, 063821. [Google Scholar] [CrossRef]
- Ayoub, M.; Roedig, P.; Imbrock, J.; Denz, C. Cascaded Čerenkov third-harmonic generation in random quadratic media. Appl. Phys. Lett. 2011, 99, 3670322. [Google Scholar] [CrossRef]
- Wang, W.; Roppo, V.; Kalinowski, K.; Kong, Y.; Neshev, D.N.; Cojocaru, C.; Trull, J.; Vilaseca, R.; Staliunas, K.; Krolikowski, W.; et al. Third-harmonic generation via broadband cascading in disordered quadratic nonlinear media. Opt. Express 2009, 17, 20117–20123. [Google Scholar] [CrossRef] [PubMed]
- Sheng, Y.; Best, A.; Butt, H.-J.; Krolikowski, W.; Arie, A.; Koynov, K. Three-dimensional ferroelectric domain visualization by Čerenkov-type second harmonic generation. Opt. Express 2010, 18, 16539–16545. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Chen, X. Domain wall characterization in ferroelectrics by using localized nonlinearities. Opt. Express 2010, 18, 15597–15602. [Google Scholar] [CrossRef] [PubMed]
- Ayoub, M.; Futterlieb, H.; Imbrock, J.; Denz, C. 3D Imaging of Ferroelectric Kinetics during Electrically Driven Switching. Adv. Mater. 2017, 29, 3325. [Google Scholar] [CrossRef] [PubMed]
- Kämpfe, T.; Reichenbach, P.; Schröder, M.; Haußmann, A.; Eng, L.M.; Woike, T.; Soergel, E. Optical three-dimensional profiling of charged domain walls in ferroelectrics by Cherenkov second-harmonic generation. Phys. Rev. B 2014, 89, 035314. [Google Scholar] [CrossRef]
- Yan Sheng, S.M.S.; Kaloian, K. Cascaded third-harmonic generation in a single short-range-ordered nonlinear photonic crystal. Opt. Lett. 2009, 34, 656–658. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, Z.D.; Qi, Z.; Zhu, S.N.; Ming, N.B. Nonlinear Cerenkov radiation in nonlinear photonic crystal waveguides. Phys. Rev. Lett. 2008, 100, 163904. [Google Scholar] [CrossRef]
- Saltiel, S.M.; Neshev, D.N.; Fischer, R.; Krolikowski, W.; Arie, A.; Kivshar, Y.S. Generation of second-harmonic conical waves via nonlinear bragg diffraction. Phys. Rev. Lett. 2008, 100, 103902. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Wang, S.; Zeng, J.; Liu, D.; Zhao, R.; Yao, Y.; Zhao, Y.; Zhao, H.; Xu, T.; Sheng, Y. Cascaded Third-Harmonic Generation in Optically Induced 3D Nonlinear Photonic Crystals. Photonics 2024, 11, 313. https://doi.org/10.3390/photonics11040313
Xu T, Wang S, Zeng J, Liu D, Zhao R, Yao Y, Zhao Y, Zhao H, Xu T, Sheng Y. Cascaded Third-Harmonic Generation in Optically Induced 3D Nonlinear Photonic Crystals. Photonics. 2024; 11(4):313. https://doi.org/10.3390/photonics11040313
Chicago/Turabian StyleXu, Tianxiang, Sen Wang, Jing Zeng, Dawei Liu, Ruwei Zhao, Yuming Yao, Yuhao Zhao, Hui Zhao, Tiefeng Xu, and Yan Sheng. 2024. "Cascaded Third-Harmonic Generation in Optically Induced 3D Nonlinear Photonic Crystals" Photonics 11, no. 4: 313. https://doi.org/10.3390/photonics11040313
APA StyleXu, T., Wang, S., Zeng, J., Liu, D., Zhao, R., Yao, Y., Zhao, Y., Zhao, H., Xu, T., & Sheng, Y. (2024). Cascaded Third-Harmonic Generation in Optically Induced 3D Nonlinear Photonic Crystals. Photonics, 11(4), 313. https://doi.org/10.3390/photonics11040313




