Single-Pixel Infrared Hyperspectral Imaging via Physics-Guided Generative Adversarial Networks
Abstract
1. Introduction
2. Principle and Method
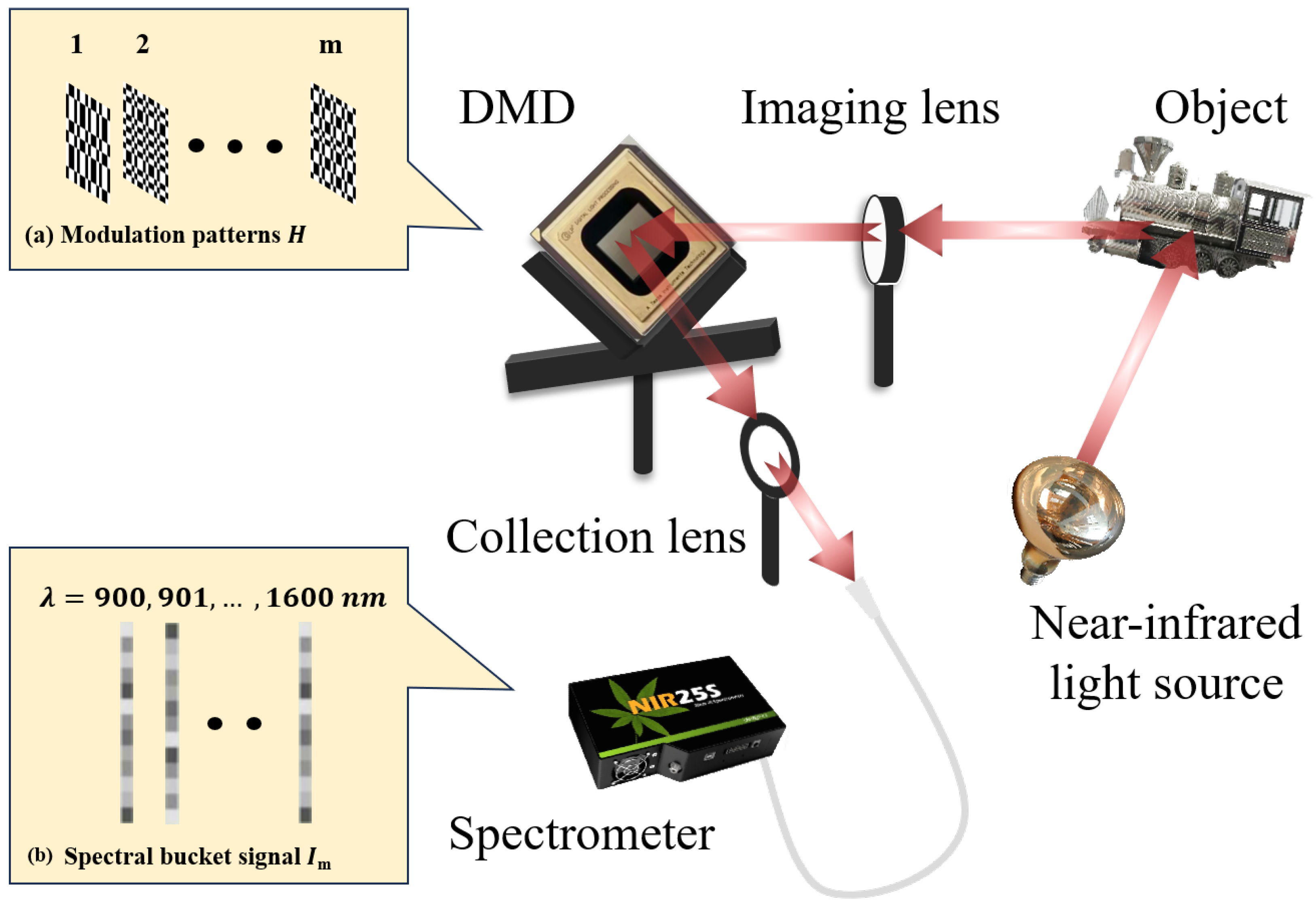
2.1. Experimental Setup
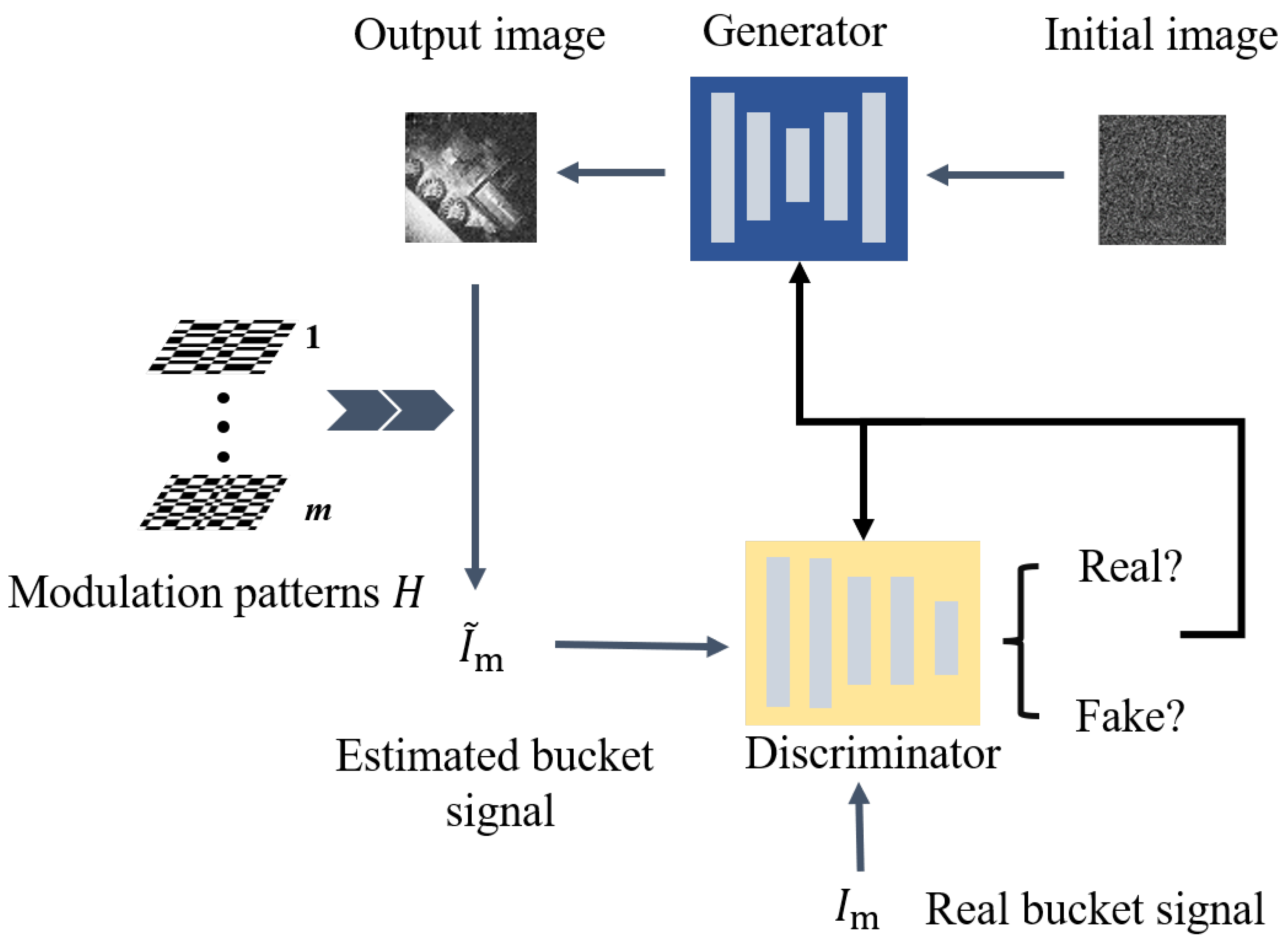
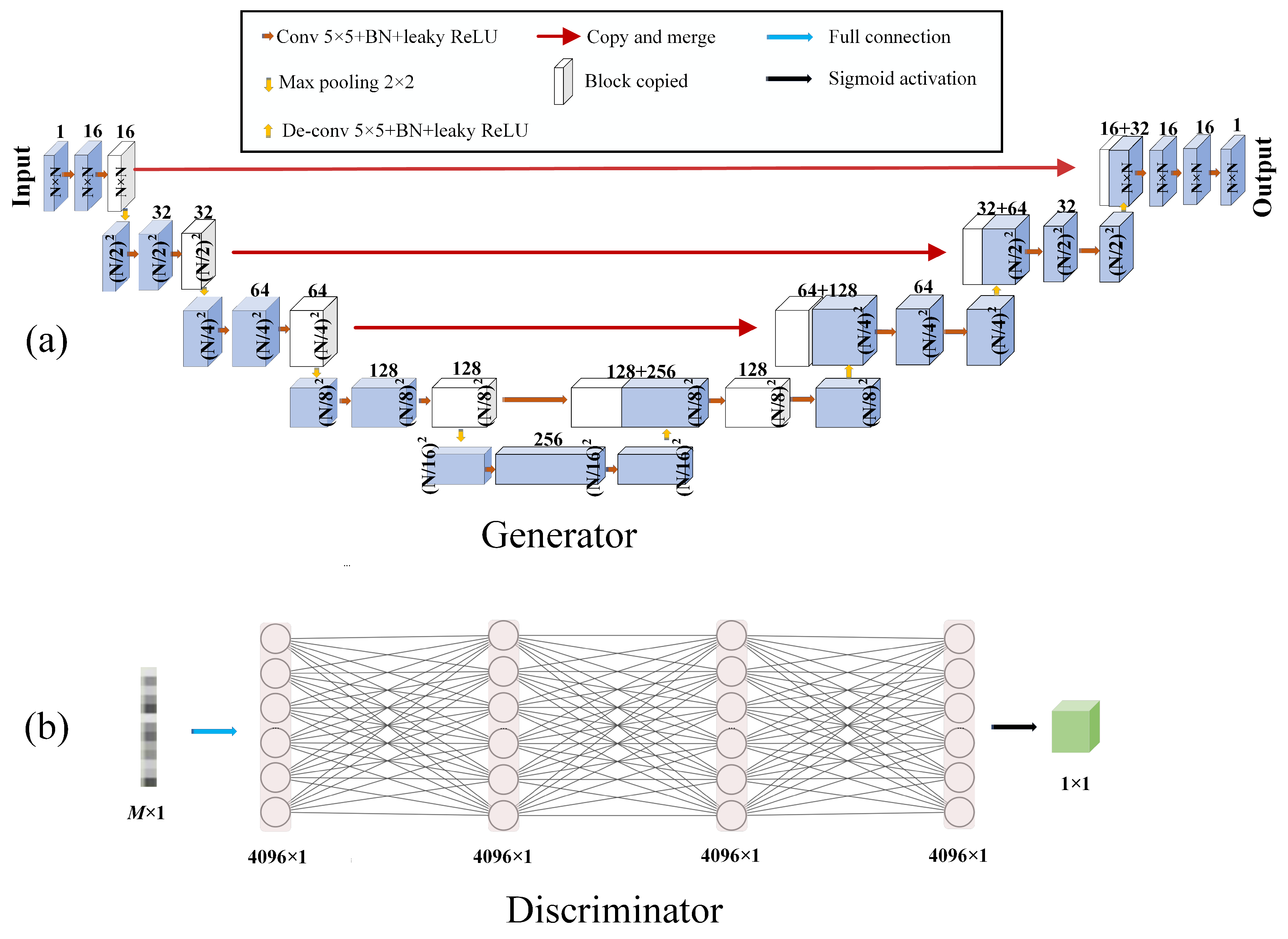
2.2. Image Reconstruction
3. Results and Discussion
3.1. Simulations
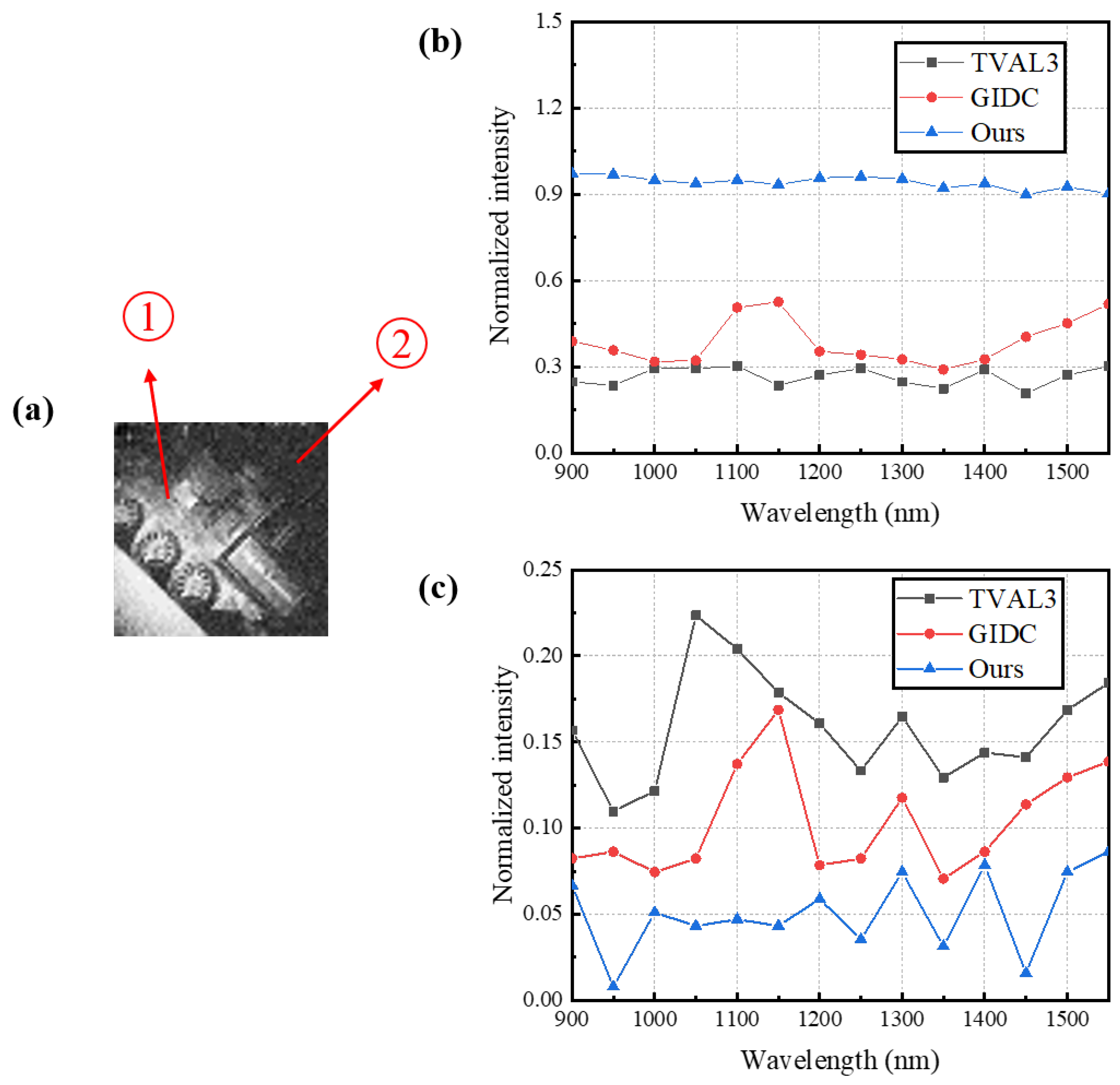
3.2. Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sarker, I.H. Deep learning: A comprehensive overview on techniques, taxonomy, applications and research directions. SN Comput. Sci. 2021, 2, 420. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Miotto, R.; Wang, F.; Wang, S.; Jiang, X.; Dudley, J.T. Deep learning for healthcare: Review, opportunities and challenges. Briefings Bioinform. 2018, 19, 1236–1246. [Google Scholar] [CrossRef]
- Rahman, A.; Hossain, M.S.; Muhammad, G.; Kundu, D.; Debnath, T.; Rahman, M.; Khan, M.S.I.; Tiwari, P.; Band, S.S. Federated learning-based AI approaches in smart healthcare: Concepts, taxonomies, challenges and open issues. Clust. Comput. 2023, 26, 2271–2311. [Google Scholar] [CrossRef]
- Lauriola, I.; Lavelli, A.; Aiolli, F. An introduction to deep learning in natural language processing: Models, techniques, and tools. Neurocomputing 2022, 470, 443–456. [Google Scholar] [CrossRef]
- Kashyap, A.A.; Raviraj, S.; Devarakonda, A.; Nayak K, S.R.; KV, S.; Bhat, S.J. Traffic flow prediction models–a review of deep learning techniques. Cogent Eng. 2022, 9, 2010510. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J.; et al. Recent advances and applications of deep learning methods in materials science. npj Comput. Mater. 2022, 8, 59. [Google Scholar] [CrossRef]
- Ragone, M.; Shahabazian-Yassar, R.; Mashayek, F.; Yurkiv, V. Deep learning modeling in microscopy imaging: A review of materials science applications. Prog. Mater. Sci. 2023, 138, 101165. [Google Scholar] [CrossRef]
- Lyu, M.; Wang, W.; Wang, H.; Wang, H.; Li, G.; Chen, N.; Situ, G. Deep-learning-based ghost imaging. Sci. Rep. 2017, 7, 17865. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Bian, Y.; Wu, K.; Liu, H.; Han, S.; Li, J.; Tian, J.; Qin, C.; Hu, J.; Xiao, L. Single-pixel imaging based on deep learning. arXiv 2023, arXiv:2310.16869v1. [Google Scholar]
- Hoshi, I.; Takehana, M.; Shimobaba, T.; Kakue, T.; Ito, T. Single-pixel imaging for edge images using deep neural networks. Appl. Opt. 2022, 61, 7793–7797. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Han, T.; Zhou, C.; Huang, J.; Ju, M.; Xu, B.; Song, L. Low sampling high quality image reconstruction and segmentation based on array network ghost imaging. Opt. Express 2023, 31, 9945–9960. [Google Scholar] [CrossRef] [PubMed]
- Rizvi, S.; Cao, J.; Hao, Q. Deep learning based projector defocus compensation in single-pixel imaging. Opt. Express 2020, 28, 25134–25148. [Google Scholar] [CrossRef] [PubMed]
- Rizvi, S.; Cao, J.; Zhang, K.; Hao, Q. Improving imaging quality of real-time Fourier single-pixel imaging via deep learning. Sensors 2019, 19, 4190. [Google Scholar] [CrossRef] [PubMed]
- Alzubaidi, L.; Bai, J.; Al-Sabaawi, A.; Santamaría, J.; Albahri, A.; Al-dabbagh, B.S.N.; Fadhel, M.A.; Manoufali, M.; Zhang, J.; Al-Timemy, A.H.; et al. A survey on deep learning tools dealing with data scarcity: Definitions, challenges, solutions, tips, and applications. J. Big Data 2023, 10, 46. [Google Scholar] [CrossRef]
- Brigato, L.; Iocchi, L. A Close Look at Deep Learning with Small Data. arXiv 2020, arXiv:2003.12843v1. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9446–9454. [Google Scholar]
- Wang, F.; Bian, Y.; Wang, H.; Lyu, M.; Pedrini, G.; Osten, W.; Barbastathis, G.; Situ, G. Phase imaging with an untrained neural network. Light. Sci. Appl. 2020, 9, 77. [Google Scholar] [CrossRef]
- Lin, J.; Yan, Q.; Lu, S.; Zheng, Y.; Sun, S.; Wei, Z. A compressed reconstruction network combining deep image prior and autoencoding priors for single-pixel imaging. Photonics 2022, 9, 343. [Google Scholar] [CrossRef]
- Gelvez-Barrera, T.; Bacca, J.; Arguello, H. Mixture-net: Low-rank deep image prior inspired by mixture models for spectral image recovery. Signal Process. 2023, 216, 109296. [Google Scholar] [CrossRef]
- Bostan, E.; Heckel, R.; Chen, M.; Kellman, M.; Waller, L. Deep phase decoder: Self-calibrating phase microscopy with an untrained deep neural network. Optica 2020, 7, 559–562. [Google Scholar] [CrossRef]
- Garini, Y.; Young, I.T.; McNamara, G. Spectral imaging: Principles and applications. Cytom. Part A J. Int. Soc. Anal. Cytol. 2006, 69, 735–747. [Google Scholar] [CrossRef]
- Deng, K.; Zhao, H.; Li, N.; Wei, W. Identification of minerals in hyperspectral imagery based on the attenuation spectral absorption index vector using a multilayer perceptron. Remote Sens. Lett. 2021, 12, 449–458. [Google Scholar] [CrossRef]
- Barberio, M.; Benedicenti, S.; Pizzicannella, M.; Felli, E.; Collins, T.; Jansen-Winkeln, B.; Marescaux, J.; Viola, M.G.; Diana, M. Intraoperative guidance using hyperspectral imaging: A review for surgeons. Diagnostics 2021, 11, 2066. [Google Scholar] [CrossRef]
- Stuart, M.B.; McGonigle, A.J.; Willmott, J.R. Hyperspectral imaging in environmental monitoring: A review of recent developments and technological advances in compact field deployable systems. Sensors 2019, 19, 3071. [Google Scholar] [CrossRef]
- Wang, C.H.; Li, H.Z.; Bie, S.H.; Lv, R.B.; Chen, X.H. Single-pixel hyperspectral imaging via an untrained convolutional neural network. Photonics 2023, 10, 224. [Google Scholar] [CrossRef]
- Magalhães, F.; Abolbashari, M.; Araújo, F.M.; Correia, M.V.; Farahi, F. High-resolution hyperspectral single-pixel imaging system based on compressive sensing. Opt. Eng. 2012, 51, 071406. [Google Scholar] [CrossRef]
- Welsh, S.S.; Edgar, M.P.; Bowman, R.; Jonathan, P.; Sun, B.; Padgett, M.J. Fast full-color computational imaging with single-pixel detectors. Opt. Express 2013, 21, 23068–23074. [Google Scholar] [CrossRef] [PubMed]
- Radwell, N.; Mitchell, K.J.; Gibson, G.M.; Edgar, M.P.; Bowman, R.; Padgett, M.J. Single-pixel infrared and visible microscope. Optica 2014, 1, 285–289. [Google Scholar] [CrossRef]
- August, Y.; Vachman, C.; Rivenson, Y.; Stern, A. Compressive hyperspectral imaging by random separable projections in both the spatial and the spectral domains. Appl. Opt. 2013, 52, D46–D54. [Google Scholar] [CrossRef] [PubMed]
- Hahn, J.; Debes, C.; Leigsnering, M.; Zoubir, A.M. Compressive sensing and adaptive direct sampling in hyperspectral imaging. Digit. Signal Process. 2014, 26, 113–126. [Google Scholar] [CrossRef]
- Tao, C.; Zhu, H.; Wang, X.; Zheng, S.; Xie, Q.; Wang, C.; Wu, R.; Zheng, Z. Compressive single-pixel hyperspectral imaging using RGB sensors. Opt. Express 2021, 29, 11207–11220. [Google Scholar] [CrossRef] [PubMed]
- Yi, Q.; Heng, L.Z.; Liang, L.; Guangcan, Z.; Siong, C.F.; Guangya, Z. Hadamard transform-based hyperspectral imaging using a single-pixel detector. Opt. Express 2020, 28, 16126–16139. [Google Scholar] [CrossRef] [PubMed]
- Gattinger, P.; Kilgus, J.; Zorin, I.; Langer, G.; Nikzad-Langerodi, R.; Rankl, C.; Gröschl, M.; Brandstetter, M. Broadband near-infrared hyperspectral single pixel imaging for chemical characterization. Opt. Express 2019, 27, 12666–12672. [Google Scholar] [CrossRef] [PubMed]
- Mur, A.L.; Montcel, B.; Peyrin, F.; Ducros, N. Deep neural networks for single-pixel compressive video reconstruction. In Unconventional Optical Imaging II; SPIE: Bellingham, WA, USA, 2020; Volume 11351, pp. 71–80. [Google Scholar]
- Kim, Y.C.; Yu, H.G.; Lee, J.H.; Park, D.J.; Nam, H.W. Hazardous gas detection for FTIR-based hyperspectral imaging system using DNN and CNN. In Electro-Optical and Infrared Systems: Technology and Applications XIV; SPIE: Bellingham, WA, USA, 2017; Volume 10433, pp. 341–349. [Google Scholar]
- Heiser, Y.; Oiknine, Y.; Stern, A. Compressive hyperspectral image reconstruction with deep neural networks. In Big Data: Learning, Analytics, and Applications; SPIE: Bellingham, WA, USA, 2019; Volume 10989, pp. 163–169. [Google Scholar]
- Itasaka, T.; Imamura, R.; Okuda, M. DNN-based hyperspectral image denoising with spatio-spectral pre-training. In Proceedings of the 2019 IEEE 8th Global Conference on Consumer Electronics (GCCE), Osaka, Japan, 15–18 October 2019; IEEE: New York, NY, USA, 2019; pp. 568–572. [Google Scholar]
- Xie, W.; Jia, X.; Li, Y.; Lei, J. Hyperspectral image super-resolution using deep feature matrix factorization. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6055–6067. [Google Scholar] [CrossRef]
- Li, C.; Sun, T.; Kelly, K.F.; Zhang, Y. A compressive sensing and unmixing scheme for hyperspectral data processing. IEEE Trans. Image Process. 2011, 21, 1200–1210. [Google Scholar]
- Wang, F.; Wang, C.; Chen, M.; Gong, W.; Zhang, Y.; Han, S.; Situ, G. Far-field super-resolution ghost imaging with a deep neural network constraint. Light. Sci. Appl. 2022, 11, 1. [Google Scholar] [CrossRef]
- Dong, Y.; Gao, D.; Qiu, T.; Li, Y.; Yang, M.; Shi, G. Residual degradation learning unfolding framework with mixing priors across spectral and spatial for compressive spectral imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 22262–22271. [Google Scholar]
- Li, J.; Li, Y.; Wang, C.; Ye, X.; Heidrich, W. Busifusion: Blind unsupervised single image fusion of hyperspectral and RGB images. IEEE Trans. Comput. Imaging 2023, 9, 94–105. [Google Scholar] [CrossRef]
- Bacca, J.; Martinez, E.; Arguello, H. Computational spectral imaging: A contemporary overview. J. Opt. Soc. Am. A 2023, 40, C115. [Google Scholar] [CrossRef]
- Edgar, M.P.; Gibson, G.M.; Padgett, M.J. Principles and prospects for single-pixel imaging. Nat. Photonics 2019, 13, 13–20. [Google Scholar] [CrossRef]
- Ferri, F.; Magatti, D.; Lugiato, L.; Gatti, A. Differential ghost imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. arXiv 2017, arXiv:1703.10593v1. [Google Scholar]
- Karim, N.; Rahnavard, N. SPI-GAN: Towards single-pixel imaging through generative adversarial network. arXiv 2021, arXiv:2107.01330. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Li, M.; Yan, L.; Yang, R.; Liu, Y. Fast single-pixel imaging based on optimized reordering Hadamard basis. Acta Phys. Sin. 2019, 68, 064202. [Google Scholar] [CrossRef]
- Li, C. An Efficient Algorithm for Total Variation Regularization with Applications to the Single Pixel Camera and Compressive Sensing. Master’s Thesis, Rice University, Houston, TX, USA, September 2010. [Google Scholar]




| Hardware | DMD (ViALUXV-2517001) |
| Imaging lens (f = 60 cm) | |
| Spectrometer (FUXIAN, NIR17+Px) |
| SR = 10% | SR = 20% | |
| Ours | 51 s | 62 s |
| GIDC | 28 s | 36 s |
| TVAL3 | 6 s | 9 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.-Y.; Bie, S.-H.; Chen, X.-H.; Yu, W.-K. Single-Pixel Infrared Hyperspectral Imaging via Physics-Guided Generative Adversarial Networks. Photonics 2024, 11, 174. https://doi.org/10.3390/photonics11020174
Wang D-Y, Bie S-H, Chen X-H, Yu W-K. Single-Pixel Infrared Hyperspectral Imaging via Physics-Guided Generative Adversarial Networks. Photonics. 2024; 11(2):174. https://doi.org/10.3390/photonics11020174
Chicago/Turabian StyleWang, Dong-Yin, Shu-Hang Bie, Xi-Hao Chen, and Wen-Kai Yu. 2024. "Single-Pixel Infrared Hyperspectral Imaging via Physics-Guided Generative Adversarial Networks" Photonics 11, no. 2: 174. https://doi.org/10.3390/photonics11020174
APA StyleWang, D.-Y., Bie, S.-H., Chen, X.-H., & Yu, W.-K. (2024). Single-Pixel Infrared Hyperspectral Imaging via Physics-Guided Generative Adversarial Networks. Photonics, 11(2), 174. https://doi.org/10.3390/photonics11020174





