A New Method for Indoor Visible Light Imaging and Positioning Based on Single Light Source
Abstract
1. Introduction
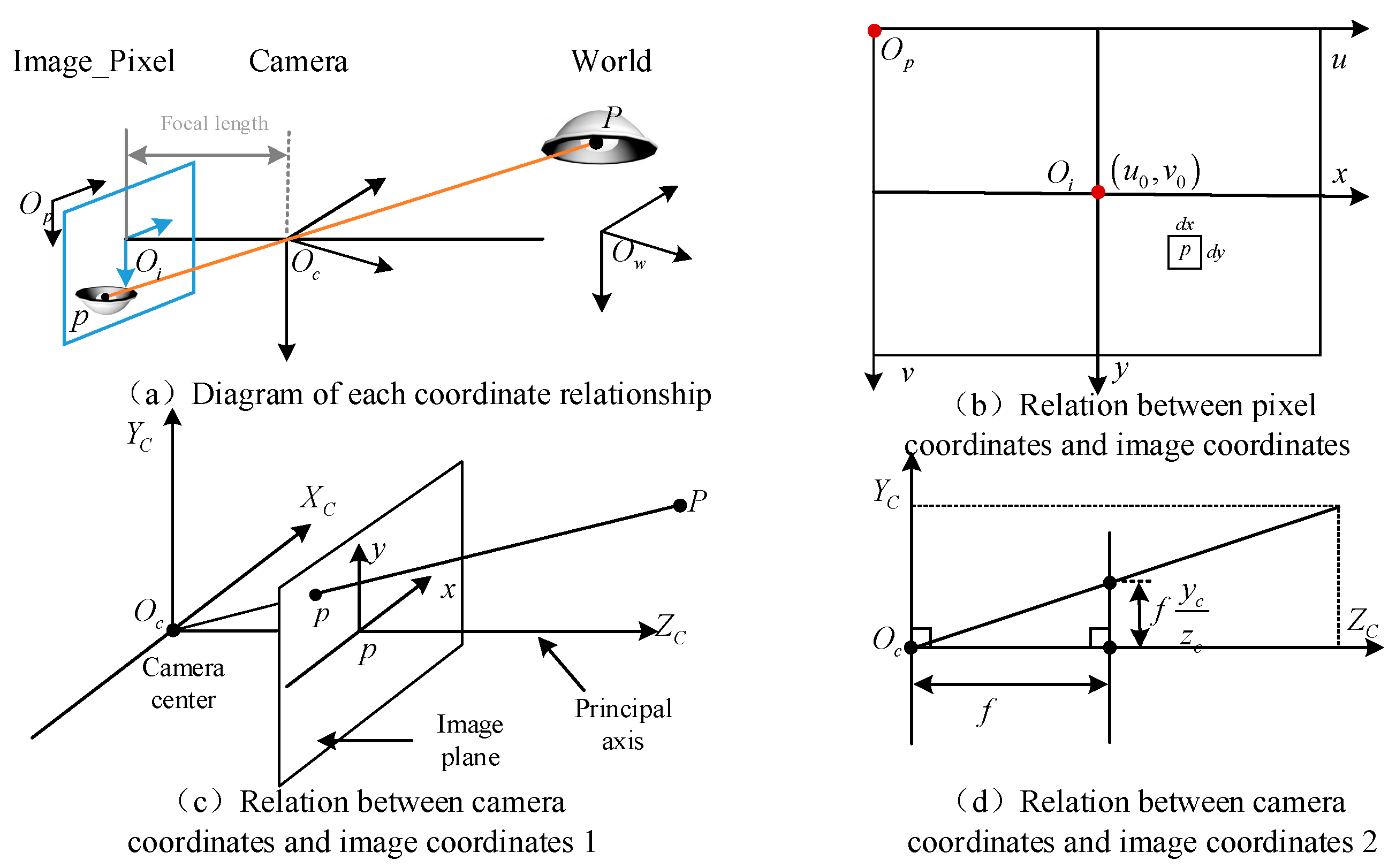
2. Positioning Principle
3. Positioning Method
3.1. System Architecture
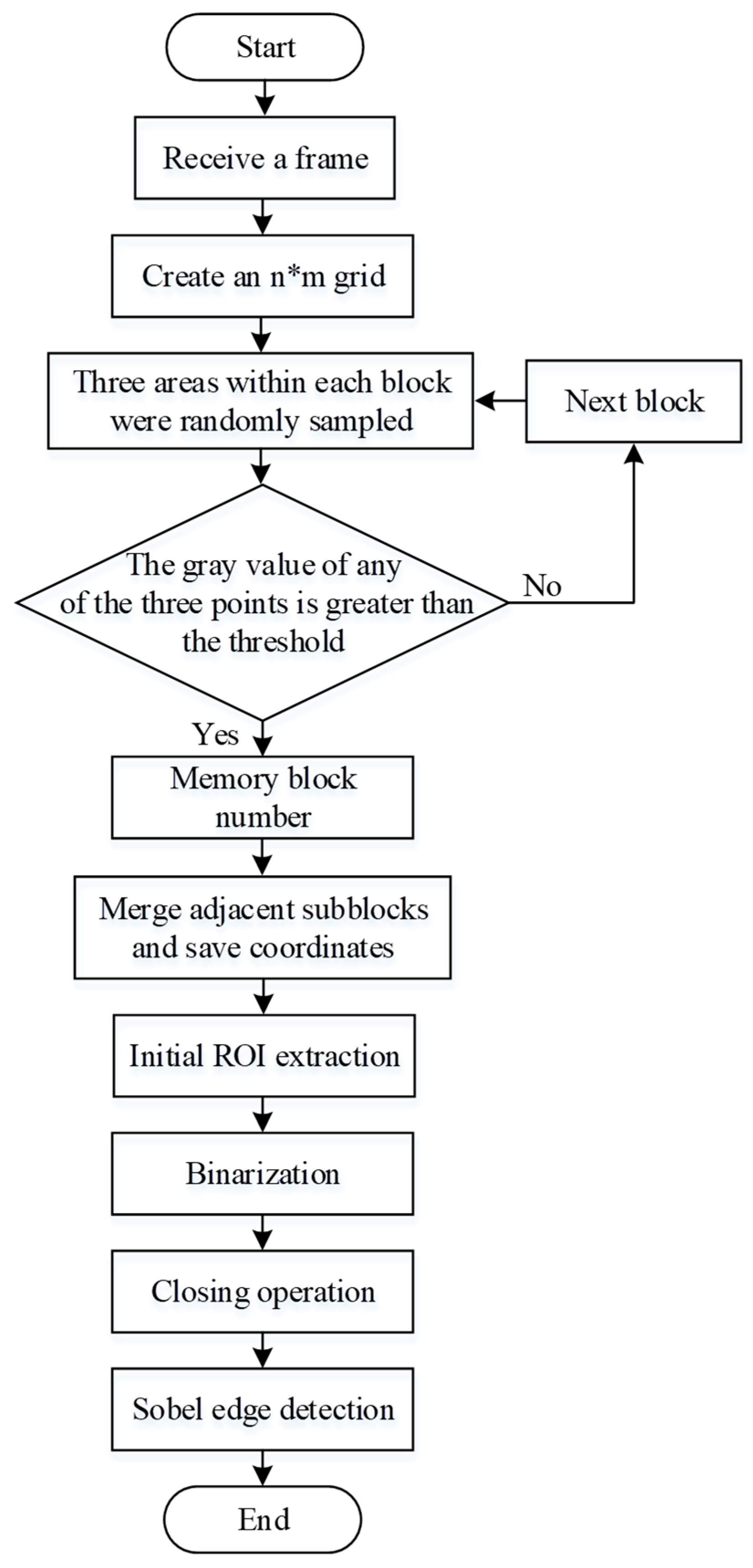
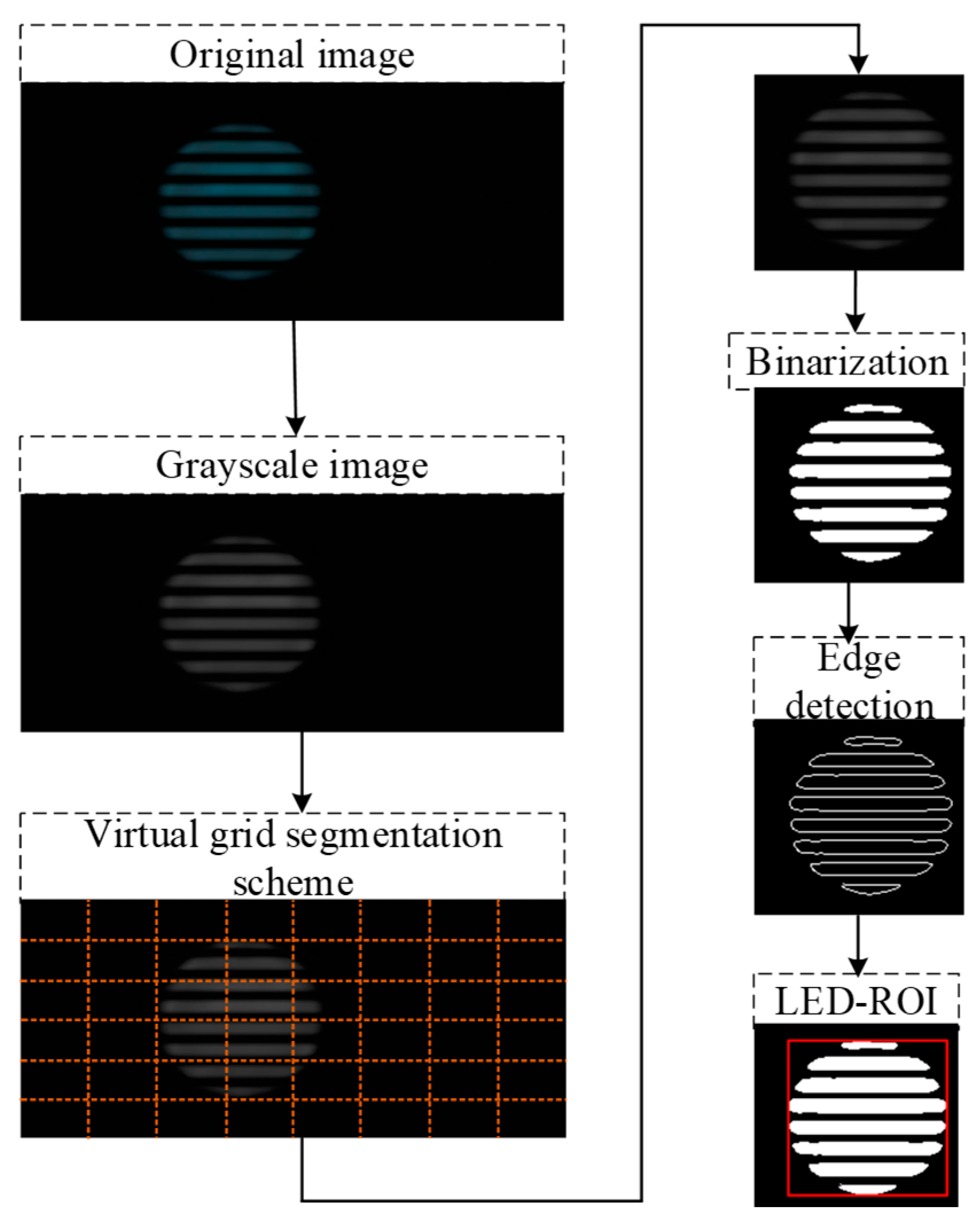
3.2. LED Image Recognition and Detection
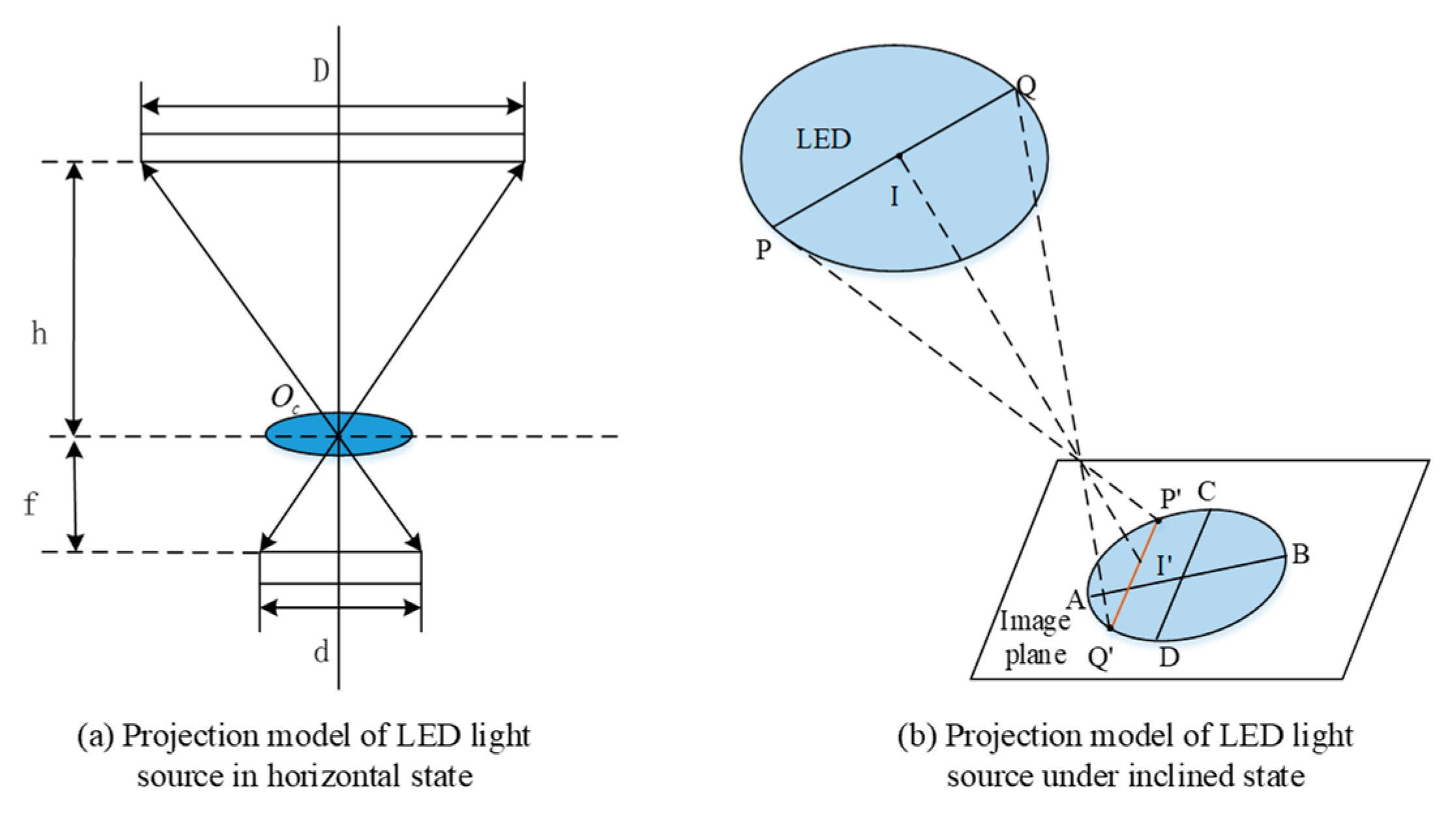
3.3. Positioning Algorithm
4. Experiment and Analysis
4.1. The Construction of the Experimental System
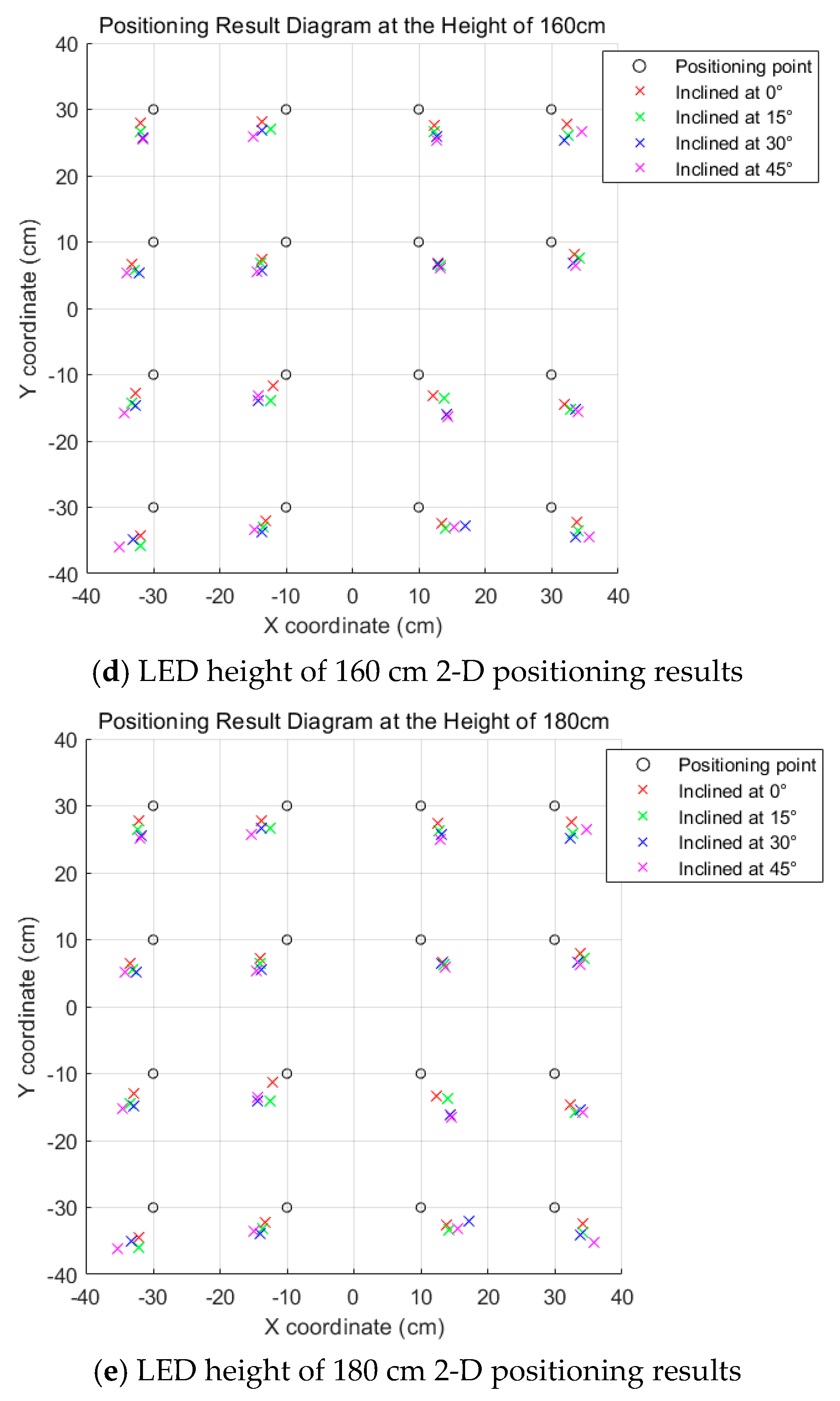
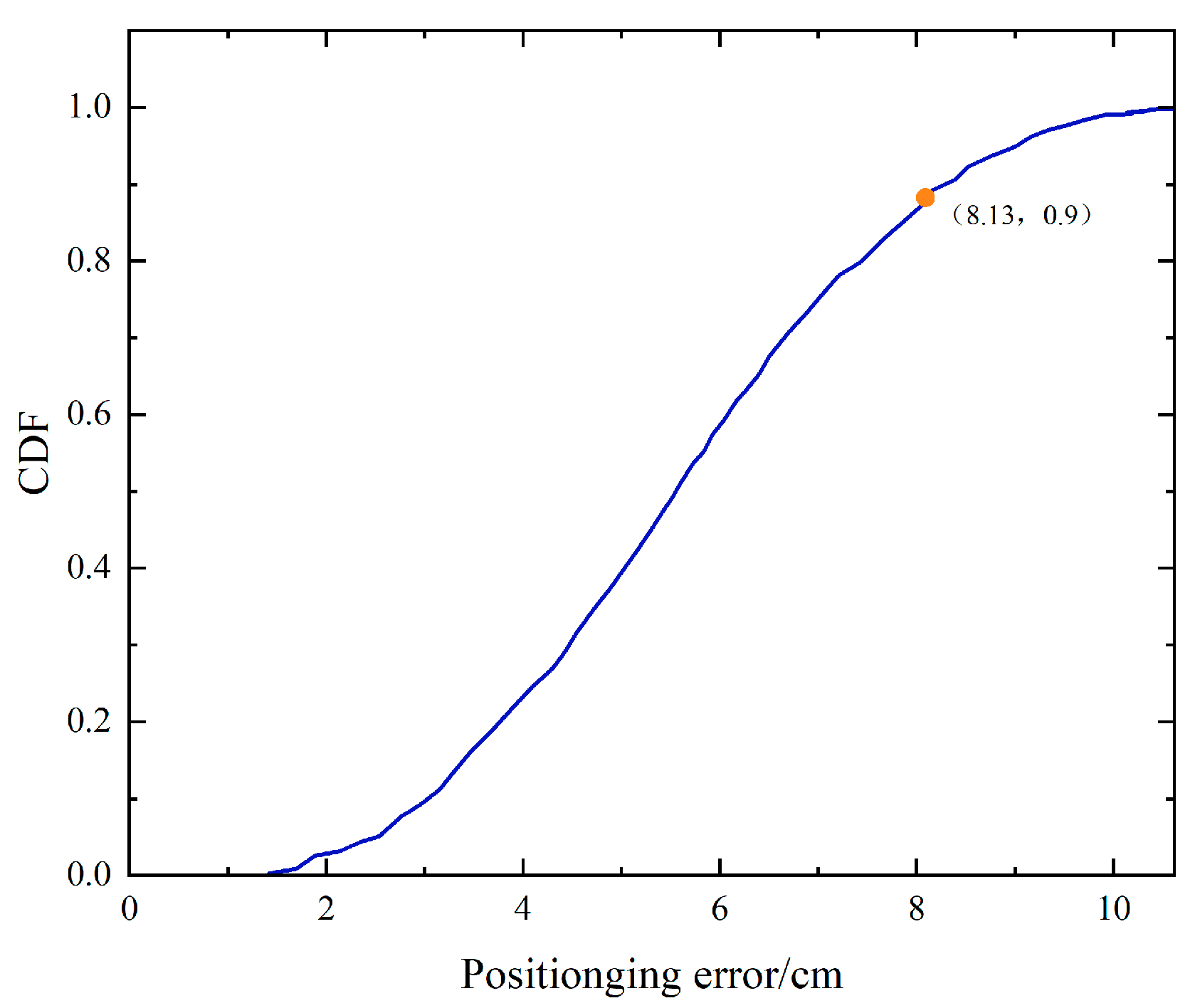
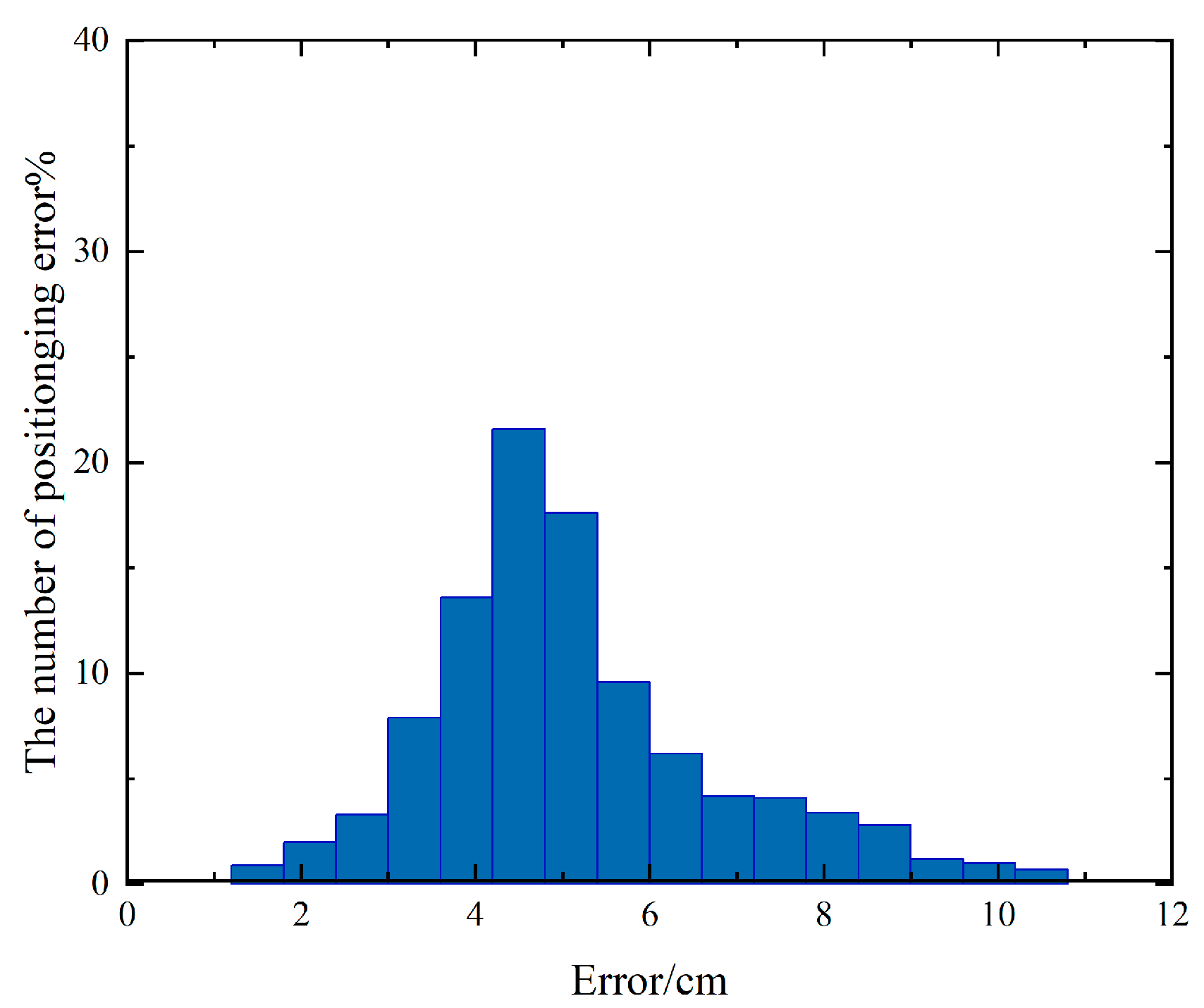
4.2. Experimental Procedure and Result Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gu, Y.; Lo, A.; Niemegeers, I. A survey of indoor positioning systems for wireless personal networks. IEEE Commun. Surv. Tutor. 2009, 11, 13–32. [Google Scholar] [CrossRef]
- Lin, P.X.; Hu, X.B.; Ruan, Y.K.; Li, H.; Fang, J.; Zhong, Y.; Zheng, H.; Fang, J.; Jiang, Z.L.; Chen, Z. Real-time visible light positioning supporting fast moving speed. Opt. Express 2020, 28, 14503–14510. [Google Scholar] [CrossRef] [PubMed]
- Zia, M.T. Visible Light Communication Based Indoor Positioning System. TEM J. 2020, 9, 30–36. [Google Scholar] [CrossRef]
- Ke, C.H.; Shu, Y.T.; Liang, J.Y. Research progress of indoor visible light localization. J. Illum. Eng. 2023, 34, 79–89. [Google Scholar]
- Xu, Y.Z.; Chen, Z. Visible light 3D positioning system based on light-emitting diode and image sensor. Laser Optoelectron. Prog. 2023, 60, 95–104. [Google Scholar]
- Guan, W.P.; Wu, Y.X.; Xie, C.Y.; Chen, H.; Cai, Y.; Chen, Y. High-precision approach to localization scheme of visible light communication based on artificial neural networks and modified genetic algorithms. Opt. Eng. 2017, 56, 106103. [Google Scholar] [CrossRef]
- Ji, Y.Q.; Xiao, C.X.; Jian, G.; Ni, J.; Cheng, H.; Zhang, P.; Sun, G. A single LED lamp positioning system based on CMOS camera and visible light communication. Opt. Commun. 2019, 443, 48–54. [Google Scholar] [CrossRef]
- Xie, C.Y.; Guan, W.P.; Wu, Y.X.; Fang, L.; Cai, Y. The LED-ID Detection and Recognition Method Based on Visible Light Positioning Using Proximity Method. IEEE Photonics J. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Hossen, M.S.; Park, Y.; Kim, K. Performance improvement of indoor positioning using light-emitting diodes and an image sensor for light-emitting diode communication. Opt. Eng. 2015, 54, 035108–035119. [Google Scholar] [CrossRef]
- Kim, J.; Yang, S.; Son, Y.; Han, S. High-resolution indoor positioning using light emitting diode visible light and camera image sensor. IET Optoelectron. 2016, 10, 184–192. [Google Scholar] [CrossRef]
- Cheng, H.; Xiao, C.X.; Ji, Y.Q.; Ni, J.; Wang, T. A Single LED Visible Light Positioning System Based on Geometric Features and CMOS Camera. IEEE Photonics Technol. Lett. 2020, 32, 1097–1100. [Google Scholar] [CrossRef]
- Jie, H.; Jing, C.; Ran, W. Visible Light Positioning Using a Single LED Luminaire. IEEE Photonics J. 2019, 11, 1–13. [Google Scholar]
- Gong, S.B.; Qian, Z.K.; Cao, B.Y. Mechanism of minimum frequency resolution in visible light positioning system. Laser Optoelectron. Prog. 2023, 60, 201–207. [Google Scholar]
- Li, H.P.; Huang, H.B.; Xu, Y.Z.; Wei, Z.; Yuan, S.; Lin, P.; Wu, H.; Lei, W.; Fang, J.; Chen, Z. A Fast and High-Accuracy Real-Time Visible Light Positioning System Based on Single LED Lamp With a Beacon. IEEE Photonics J. 2020, 12, 1–12. [Google Scholar] [CrossRef]
- Guan, W.P.; Chen, S.H.; Wen, S.S.; Tan, Z.; Song, H.; Hou, W. High-Accuracy Robot Indoor Localization Scheme based on Robot Operating System using Visible Light Positioning. IEEE Photonics J. 2020, 12, 1–16. [Google Scholar] [CrossRef]
- Xie, Z.K.; Guan, W.P.; Zheng, J.H.; Zhang, X.J.; Chen, S.H.; Chen, B.D. A High-Precision, Real-Time, and Robust Indoor Visible Light Positioning Method Based on Mean Shift Algorithm and Unscented Kalman Filter. Sensors 2019, 19, 1094. [Google Scholar] [CrossRef]
- Liu, X.Y.; Wei, X.T.; Guo, L. DIMLOC: Enabling High-Precision Visible Light Localization Under Dimmable LEDs in Smart Buildings. IEEE Internet Things J. 2019, 6, 3912–3924. [Google Scholar] [CrossRef]
- Huang, H.Q.; Lin, B.; Feng, L.H.; Lv, H.C. Hybrid indoor localization scheme with image sensor-based visible light positioning and pedestrian dead reckoning. Appl. Opt. 2019, 58, 3214–3221. [Google Scholar] [CrossRef]
- Xu, J.J.; Gong, C.; Xu, Z.Y. Experimental indoor visible light positioning systems with centimeter accuracy based on a commercial smartphone camera. IEEE Photonics J. 2018, 10, 1–17. [Google Scholar] [CrossRef]
- Liu, G. Research on 3D Sensor Calibration Algorithm and Software Design. Master’s Thesis, Nanchang University, Nanchang, China, 2015. [Google Scholar]
- Guan, W.P.; Wu, Y.X.; Xie, C.Y.; Fang, L.; Liu, X.; Chen, Y. Performance analysis and enhancement for visible light communication using CMOS sensors. Opt. Commun. 2018, 41, 531–545. [Google Scholar] [CrossRef]
- Guan, Y.; Sun, D.D.; Yin, S.G. High precision visible light indoor positioning method based on imaging communication. Chin. J. Lasers 2016, 43, 191–198. [Google Scholar]
- Zhang, Y.P.; Zhu, X.Q.; Zhu, D.Y. Train location method in visible light imaging communication based on BP neural network. Chin. J. Lasers 2023, 50, 124–134. [Google Scholar]
- Béchadergue, B.; Shen, W.-H.; Tsai, H.-M. Comparison of OFDM and OOK modulations for vehicle-to-vehicle visible light communication in real-world driving scenarios. Ad Hoc Netw. 2019, 94, 101944. [Google Scholar] [CrossRef]
- Tan, J.; Narendran, N. A driving scheme to reduce AC LED flicker. Opt. Eng. 2013, 8335, 1–6. [Google Scholar]
- Hu, X.; Zhang, P.P.; Sun, Y.M.; Deng, X.; Yang, Y.; Chen, L. High-Speed Extraction of Regions of Interest in Optical Camera Communication Enabled by Grid Virtual Division. Sensors 2022, 22, 8375. [Google Scholar] [CrossRef]
- Amsters, R.; Demeester, E.; Slaets, P.; Holm, D.; Joly, J.; Stevens, N. Towards Automated Calibration of Visible Light Positioning Systems. In Proceedings of the 2019 International Conference on Indoor Positioning and Indoor Navigation (IPIN) IEEE, Pisa, Italy, 30 September 2019; Volume 8, pp. 1–8. [Google Scholar]
- Zhang, Y.P.; Zhu, D.Y.; Ma, J.M. Subway train location based on monocular vision and visible light imaging communication. Laser Optoelectron. Prog. 2022, 59, 69–78. [Google Scholar]
- Othman, I.Y.; Neha, C.; Zabin, G. A unilateral 3D indoor positioning system employing optical Camera communications. IET Optoelectron. 2023, 4, 110–119. [Google Scholar]
- Le, N.T.; Jang, Y.M. Photography Trilateration Indoor Localization with Image Sensor Communication. Sensors 2019, 19, 3290. [Google Scholar] [CrossRef]
- Zhang, R.; Zhong, W.D.; Kemao, Q.; Zhang, S. A single LED positioning system based on circle projection. IEEE Photonics J. 2017, 9, 1–9. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| LED luminous diameter/cm | 17.4 |
| LED drive voltage/V | 30 |
| LED drive current/A | 0.1 |
| Camera resolution/pixel | 2046 × 1080 |
| Exposure time/μs | 125 |
| ISO | 50 |
| Focal length/mm | 3.6 |
| Experimental size/cm | 80 × 80 × 180 |
| LED coordinates/cm | (0, 0, 180) |
| Height/cm | 60 | 80 | 140 | 160 | 180 |
|---|---|---|---|---|---|
| Average Positioning Time/ms | 53.36 | 53.42 | 53.58 | 53.63 | 53.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.; Ke, X.; Qin, H. A New Method for Indoor Visible Light Imaging and Positioning Based on Single Light Source. Photonics 2024, 11, 1199. https://doi.org/10.3390/photonics11121199
Cheng X, Ke X, Qin H. A New Method for Indoor Visible Light Imaging and Positioning Based on Single Light Source. Photonics. 2024; 11(12):1199. https://doi.org/10.3390/photonics11121199
Chicago/Turabian StyleCheng, Xinxin, Xizheng Ke, and Huanhuan Qin. 2024. "A New Method for Indoor Visible Light Imaging and Positioning Based on Single Light Source" Photonics 11, no. 12: 1199. https://doi.org/10.3390/photonics11121199
APA StyleCheng, X., Ke, X., & Qin, H. (2024). A New Method for Indoor Visible Light Imaging and Positioning Based on Single Light Source. Photonics, 11(12), 1199. https://doi.org/10.3390/photonics11121199




