An Effective Method for Generating Isolated Attosecond Pulses from a Solid Crystal Film
Abstract
1. Introduction
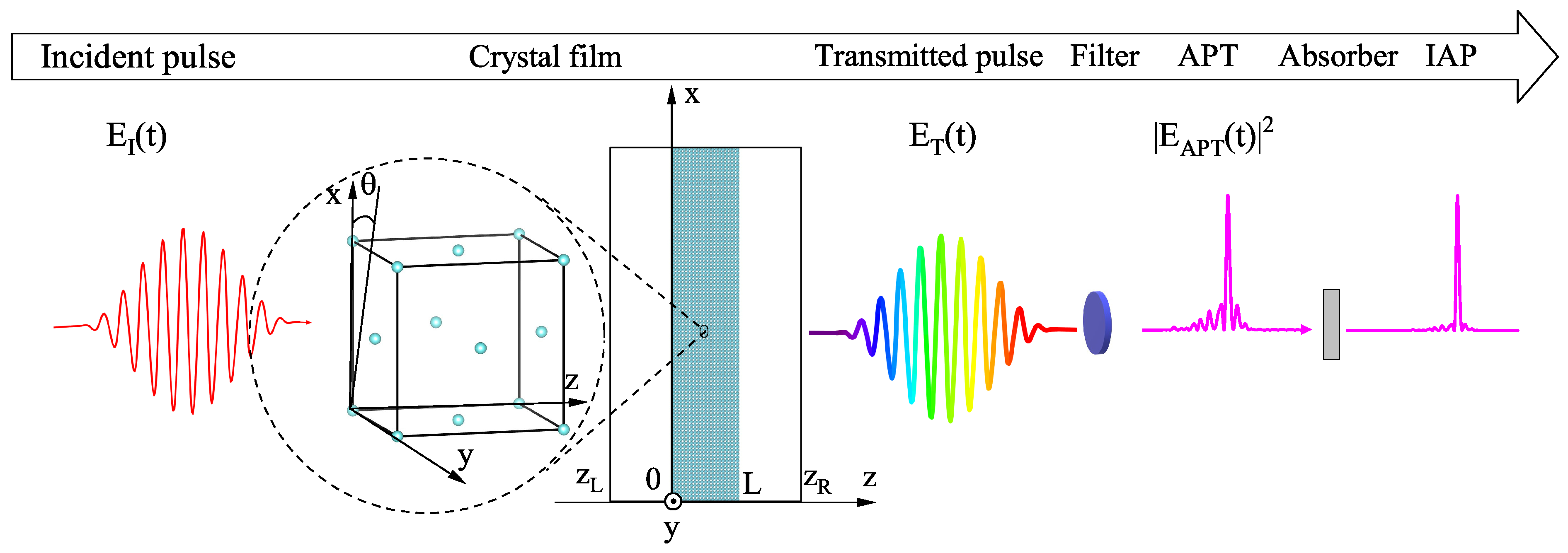
2. Materials and Methods
2.1. Light-Matter Interaction Model
2.2. Computational Details
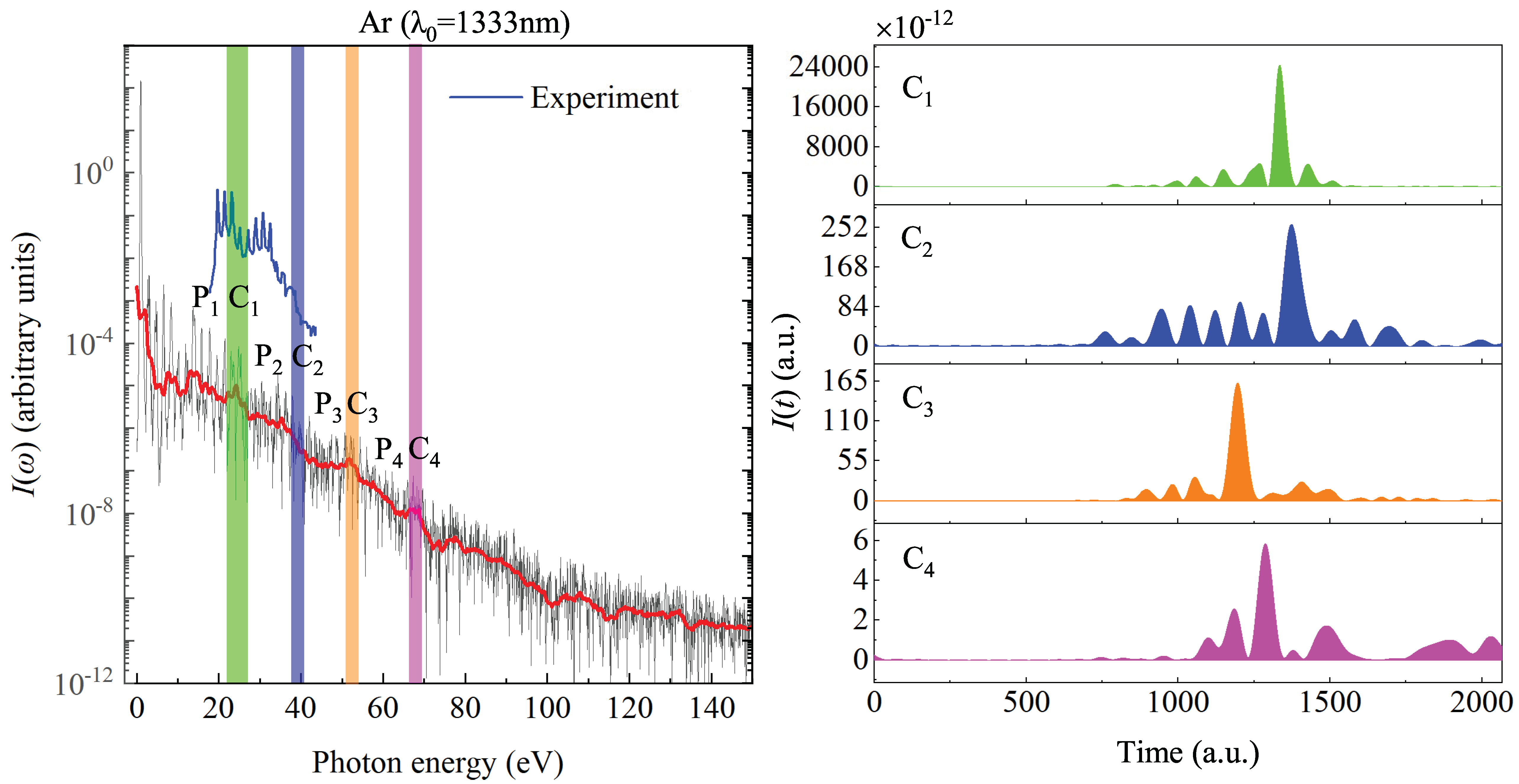
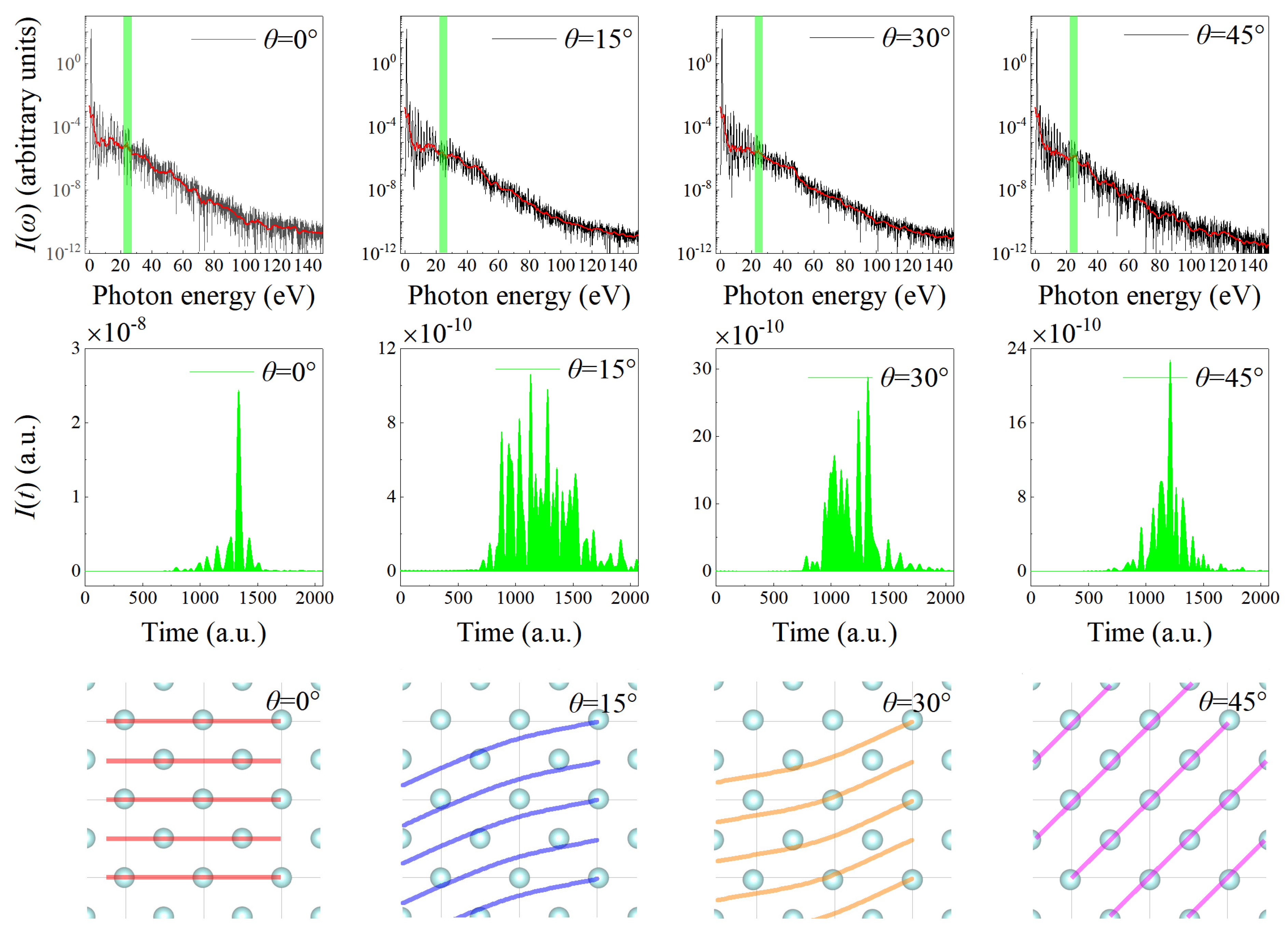
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a Train of Attosecond Pulses from High Harmonic Generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef]
- Teng, H.; He, X.K.; Zhao, K.; Wei, Z.Y. Attosecond laser station. Chin. Phys. B 2018, 27, 074203. [Google Scholar] [CrossRef]
- Agostini, P.; DiMauro, L.F. The physics of attosecond light pulses. Rep. Prog. Phys. 2004, 67, 1563. [Google Scholar] [CrossRef]
- Corkum, P.B.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 1, 163. [Google Scholar] [CrossRef]
- Duris, J.; Li, S.Q.; Driver, T.; Champenois, E.G.; MacArthur, J.P.; Lutman, A.A.; Zhang, Z.; Rosenberger, P.; Aldrich, J.W.; Coffee, R.; et al. Tunable isolated attosecond X-ray pulses with gigawatt peak power from a free-electron laser. Nat. Photonics 2020, 14, 30. [Google Scholar] [CrossRef]
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509. [Google Scholar] [CrossRef]
- Ferrari, F.; Calegari, F.; Lucchini, M.; Vozzi, C.; Stagira, S.; Sansone, G.; Nisoli, M. High-energy isolated attosecond pulses generated by above-saturation few-cycle fields. Nat. Photonics 2010, 4, 875. [Google Scholar] [CrossRef]
- Gaumnitz, T.; Jain, A.; Pertot, Y.; Huppert, M.; Jordan, I.; Ardana-Lamas, F.; Wörner, H.J. Streaking of 43-attosecond soft-X-ray pulses generated by a passively CEP-stable mid-infrared driver. Opt. Express 2017, 25, 27506. [Google Scholar] [CrossRef]
- Zhao, K.; Zhang, Q.; Chini, M.; Wu, Y.; Wang, X.; Chang, Z. Tailoring a 67 attosecond pulse through advantageous phase-mismatch. Opt. Lett. 2012, 37, 3891. [Google Scholar] [CrossRef]
- Sansone, G.; Benedetti, E.; Calegari, F.; Vozzi, C.; Avaldi, L.; Flammini, R.; Poletto, L.; Villoresi, P.; Altucci, C.; Velotta, R.; et al. Isolated single-cycle attosecond pulses. Science 2006, 314, 443. [Google Scholar] [CrossRef] [PubMed]
- Goulielmakis, E.; Schultze, M.; Hofstetter, M.; Yakovlev, V.S.; Gagnon, J.; Uiberacker, M.; Aquila, A.L.; Gullikson, E.M.; Attwood, D.T.; Kienberger, R.; et al. Single-cycle nonlinear optics. Science 2008, 320, 1614. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ren, X.M.; Yin, Y.C.; Zhao, K.; Chew, A.; Cheng, Y.; Cunningham, E.; Wang, Y.; Hu, S.Y.; Wu, Y.; et al. 53-attosecond X-ray pulses reach the carbon K-edge. Nat. Commun. 2017, 8, 186. [Google Scholar] [CrossRef]
- Takahashi, E.J.; Lan, P.F.; Mücke, O.D.; Nabekawa, Y.; Midorikawa, K. Attosecond nonlinear optics using gigawatt-scale isolated attosecond pulses. Nat. Commun. 2013, 4, 2691. [Google Scholar] [CrossRef] [PubMed]
- Hammond, T.J.; Brown, G.G.; Kim, K.T.; Villeneuve, D.M.; Corkum, P.B. Attosecond pulses measured from the attosecond lighthouse. Nat. Photonics 2016, 10, 171. [Google Scholar] [CrossRef]
- Frank, F.; Arrell, C.; Witting, T.; Okell, W.A.; McKenna, J.; Robinson, J.S.; Haworth, C.A.; Austin, D.; Teng, H.; Walmsley, I.A.; et al. Invited review article: Technology for attosecond science. Rev. Sci. Instrum. 2012, 83, 071101. [Google Scholar] [CrossRef]
- Mairesse, Y.; de Bohan, A.; Frasinski, L.J.; Merdji, H.; Dinu, L.C.; Monchicourt, P.; Breger, P.; Kovačev, M.; Auguste, T.; Carré, B.; et al. Optimization of Attosecond Pulse Generation. Phys. Rev. Lett. 2004, 93, 163901. [Google Scholar] [CrossRef]
- Cavalieri, A.; Müller, N.; Uphues, T.; Yakovlev, V.S.; Baltuška, A.; Horvath, B.; Schmidt, B.; Blümel, L.; Holzwarth, R.; Hendel, S.; et al. Attosecond spectroscopy in condensed matter. Nature 2007, 449, 1029–1032. [Google Scholar] [CrossRef]
- Lépine, F.; Ivanov, M.; Vrakking, M. Attosecond molecular dynamics: Fact or fiction? Nat. Photonics 2014, 8, 195–204. [Google Scholar] [CrossRef]
- Sola, I.J.; Mével, E.; Elouga, L.; Constant, E.; Strelkov, V.; Poletto, L.; Villoresi, P.; Benedetti, E.; Caumes, J.-P.; Stagira, S.; et al. Controlling attosecond electron dynamics by phase-stabilized polarization gating. Nat. Phys. 2006, 2, 319. [Google Scholar] [CrossRef]
- Christov, I.P.; Murnane, M.M.; Kapteyn, H.C. High-Harmonic Generation of Attosecond Pulses in the “Single-Cycle” Regime. Phys. Rev. Lett. 1997, 78, 1251. [Google Scholar] [CrossRef]
- Kienberger, R.; Goulielmakis, E.; Uiberacker, M.; Baltuska, A.; Yakovlev, V.; Bammer, F.; Scrinzi, A.; Westerwalbesloh, T.; Kleineberg, U.; Heinzmann, U.; et al. Atomic transient recorder. Nature 2004, 427, 817. [Google Scholar] [CrossRef] [PubMed]
- Oishi, Y.; Kaku, M.; Suda, A.; Kannari, F.; Midorikawa, K. Generation of extreme ultraviolet continuum radiation driven by a sub-10-fs two-color field. Opt. Express 2006, 16, 7230. [Google Scholar] [CrossRef]
- Takahashi, E.J.; Lan, P.F.; Mücke, O.D.; Nabekawa, Y.; Midorikawa, K. Infrared Two-Color Multicycle Laser Field Synthesis for Generating an Intense Attosecond Pulse. Phys. Rev. Lett. 2010, 104, 233901. [Google Scholar] [CrossRef]
- Mashiko, H.; Gilbertson, S.; Li, C.Q.; Khan, S.D.; Shakya, M.M.; Moon, E.; Chang, Z.H. Double Optical Gating of High-Order Harmonic Generation with Carrier-Envelope Phase Stabilized Lasers. Phys. Rev. Lett. 2008, 100, 103906. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.H.; Zeng, Z.N.; Li, X.F.; Chen, X.W.; Liu, P.; Xiong, H.; Lu, H.; Zhao, S.T.; Wei, P.F.; Zhang, L.; et al. Enhancement and broadening of extreme-ultraviolet supercontinuum in a relative phase controlled two-color laser field. Opt. Lett. 2008, 33, 234. [Google Scholar] [CrossRef]
- Sekikawa, T.; Kosuge, A.; Kanai, T.; Watanabe, S. Nonlinear optics in the extreme ultraviolet. Nature 2004, 423, 605. [Google Scholar] [CrossRef]
- Tzallas, P.; Skantzakis, E.; Kalpouzos, C.; Benis, E.P.; Tsakiris, G.D.; Charalambidis, D. Generation of intense continuum extreme-ultraviolet radiation by many-cycle laser fields. Nat. Phys. 2007, 3, 846. [Google Scholar] [CrossRef]
- Zhang, Q.; Lu, P.; Lan, P.; Hong, W.; Yang, Z. Multi-cycle laser-driven broadband supercontinuum with a modulated polarization gating. Opt. Express 2008, 16, 9795. [Google Scholar] [CrossRef]
- Baltuška, A.; Udem, T.; Uiberacker, M.; Hentschel, M.; Goulielmakis, E.; Gohle, C.; Holzwarth, R.; Yakovlev, V.S.; Scrinzi, A.; Hänsch, T.W.; et al. Attosecond control of electronic processes by intense light fields. Nature 2003, 421, 611. [Google Scholar] [CrossRef]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611. [Google Scholar] [CrossRef]
- Ghimire, S.; DiChiara, A.D.; Sistrunk, E.; Agostini, P.; DiMauro, L.F.; Reis, D.A. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 2011, 7, 138. [Google Scholar] [CrossRef]
- Higuchi, T.; Stockman, M.I.; Hommelhoff, P. Strong-Field Perspective on High-Harmonic Radiation from Bulk Solids. Phys. Rev. Lett. 2014, 113, 213901. [Google Scholar] [CrossRef]
- Ndabashimiye, G.; Ghimire, S.; Wu, M.X.; Browne, D.A.; Schafer, K.J.; Gaarde, M.B.; Reis, D.A. Solid-state harmonics beyond the atomic limit. Nature 2016, 534, 520. [Google Scholar] [CrossRef]
- You, Y.S.; Reis, D.A.; Ghimire, S. Anisotropic high-harmonic generation in bulk crystals. Nat. Phys. 2017, 13, 345. [Google Scholar] [CrossRef]
- Yamada, S.; Noda, M.; Nobusada, K.; Yabana, K. Time-dependent density functional theory for interaction of ultrashort light pulse with thin materials. Phys. Rev. B 2018, 98, 245147. [Google Scholar] [CrossRef]
- Wachter, G.; Lemell, C.; Burgdörfer, J.; Sato, S.A.; Tong, X.M.; Yabana, K. Ab Initio Simulation of Electrical Currents Induced by Ultrafast Laser Excitation of Dielectric Materials. Phys. Rev. Lett. 2014, 113, 087401. [Google Scholar] [CrossRef] [PubMed]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Vignale, G.; Kohn, W. Current-Dependent Exchange-Correlation Potential for Dynamical Linear Response Theory. Phys. Rev. Lett. 1996, 77, 2037. [Google Scholar] [CrossRef]
- Liu, W.J.; Liu, M.L.; Liu, B.; Quhe, R.G.; Lei, M.; Fang, S.B.; Teng, H.; Wei, Z.Y. Nonlinear optical properties of MoS2-WS2 heterostructure in fiber lasers. Opt. Express 2019, 27, 6689–6699. [Google Scholar] [CrossRef]
- Lyu, W.; Cheng, Y.; An, J.; Condorelli, M.; Pulvirenti, M.; Compagnini, G.; Wang, X.; Fu, B.; Scardaci, V. Silver Nanoplate Composites as Nonlinear Saturable Absorbers for a Q-Switched Laser. Photonics 2022, 9, 835. [Google Scholar] [CrossRef]
- Noda, M.; Sato, S.A.; Hirokawa, Y.; Uemoto, M.; Takeuchi, T.; Yamada, S.; Yamada, A.; Shinohara, Y.; Yamaguchi, M.; Iida, K.; et al. SALMON: Scalable Ab-initio Light–Matter simulator for Optics and Nanoscience. Comput. Phys. Commun. 2019, 235, 356. [Google Scholar] [CrossRef]
- Baggesen, J.C.; Madsen, L.B. On the dipole, velocity and acceleration forms in high-order harmonic generation from a single atom or molecule. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 115601. [Google Scholar] [CrossRef]
- Vampa, G.; McDonald, C.R.; Orlando, G.; Klug, D.D.; Corkum, P.B.; Brabec, T. Theoretical analysis of high-harmonic generation in solids. J. Phys. Rev. Lett. 2014, 113, 073901. [Google Scholar] [CrossRef] [PubMed]
- Vampa, G.; McDonald, C.R.; Orlando, G.; Corkum, P.B.; Brabec, T. Semiclassical analysis of high harmonic generation in bulk crystals. Phys. Rev. B 2015, 91, 064302. [Google Scholar] [CrossRef]
- Floss, I.; Lemell, C.; Wachter, G.; Smejkal, V.; Sato, S.A.; Tong, X.-M.; Yabana, K.; Burgdorfer, J. Ab initio multiscale simulation of high-order harmonic generation in solids. Phys. Rev. A 2018, 97, 011401. [Google Scholar] [CrossRef]
- Floss, I.; Lemell, C.; Yabana, K.; Burgdorfer, J. Incorporating decoherence into solid-state time-dependent density functional theory. Phys. Rev. B 2019, 99, 224301. [Google Scholar] [CrossRef]
- Lakhotia, H.; Zhan, M.; Kim, H.Y.; Goulielmakis, E. A real space perspective of high harmonic generation in crystalline solids. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 13–18 May 2018. [Google Scholar]
- Gertsvolf, M.; Jean-Ruel, H.; Rajeev, P.P.; Klug, D.D.; Rayner, D.M.; Corkum, P.B. Orientation-Dependent Multiphoton Ionization in Wide Band Gap Crystals. Phys. Rev. Lett. 2008, 101, 243001. [Google Scholar] [CrossRef]
- Ortmann, L.; Landsman, A.S. Chapter Two—High-Harmonic Generation in Solids; Academic Press: Cambridge, MA, USA, 2021; Volume 70, pp. 103–156. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, W.; Wang, F.; Gao, C. An Effective Method for Generating Isolated Attosecond Pulses from a Solid Crystal Film. Photonics 2024, 11, 1154. https://doi.org/10.3390/photonics11121154
Lv W, Wang F, Gao C. An Effective Method for Generating Isolated Attosecond Pulses from a Solid Crystal Film. Photonics. 2024; 11(12):1154. https://doi.org/10.3390/photonics11121154
Chicago/Turabian StyleLv, Wenwen, Feng Wang, and Congzhang Gao. 2024. "An Effective Method for Generating Isolated Attosecond Pulses from a Solid Crystal Film" Photonics 11, no. 12: 1154. https://doi.org/10.3390/photonics11121154
APA StyleLv, W., Wang, F., & Gao, C. (2024). An Effective Method for Generating Isolated Attosecond Pulses from a Solid Crystal Film. Photonics, 11(12), 1154. https://doi.org/10.3390/photonics11121154





