Experimental Research on the Correction of Vortex Light Wavefront Distortion
Abstract
1. Introduction
2. Basic Theory
2.1. Adaptive Optics Wavefront Correction Techniques in Vortex Beams
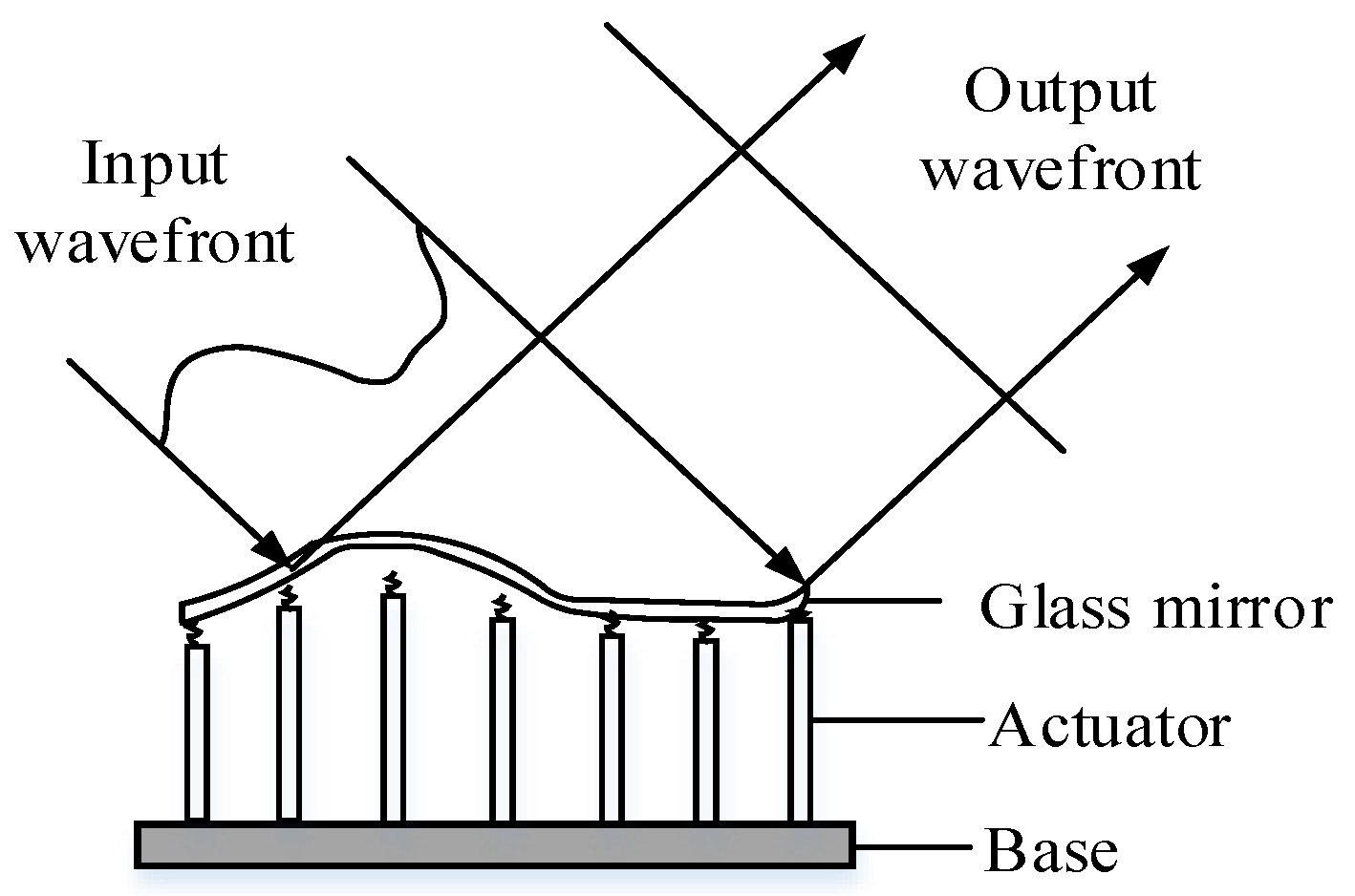
2.2. Deformable Mirror
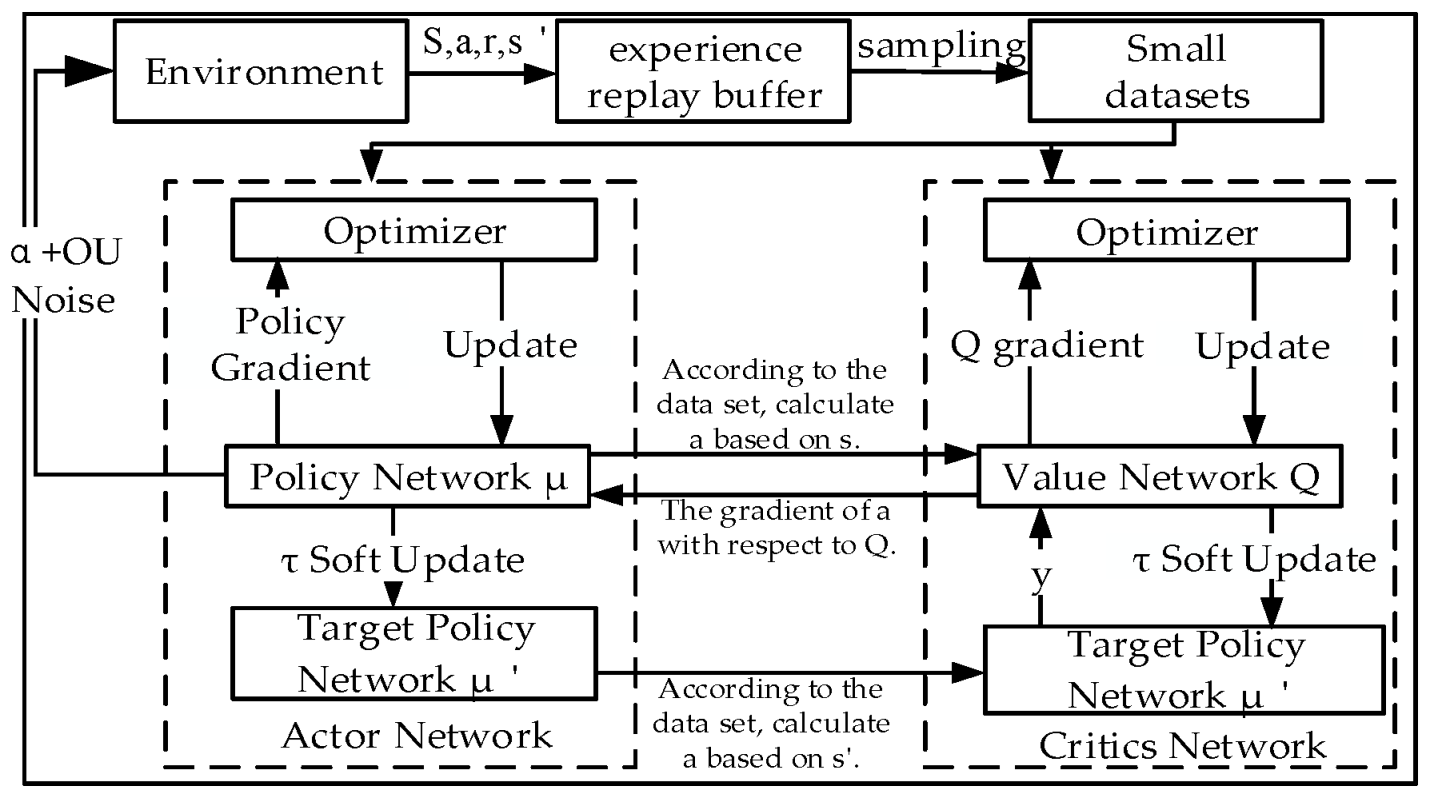
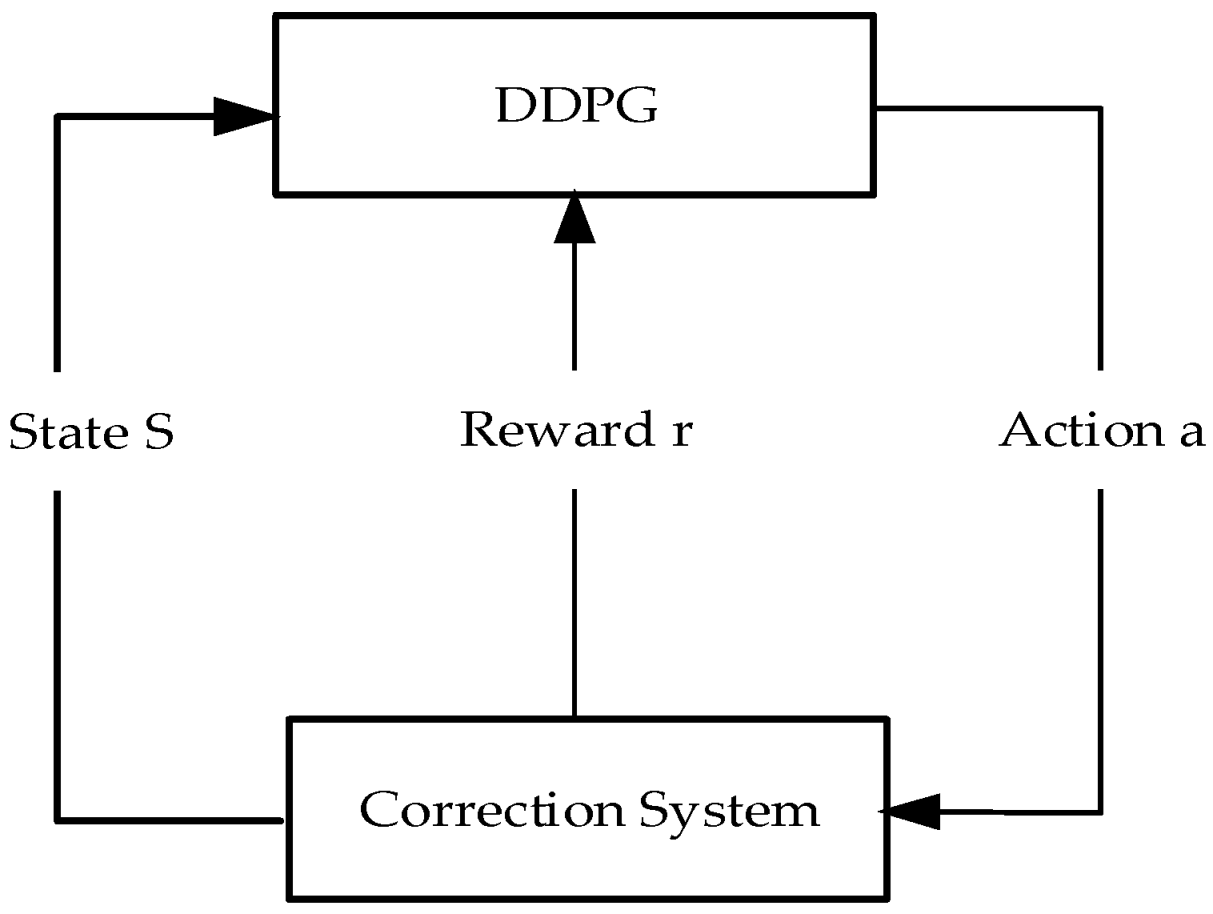
2.3. Corrective Principles of DDPG Algorithms
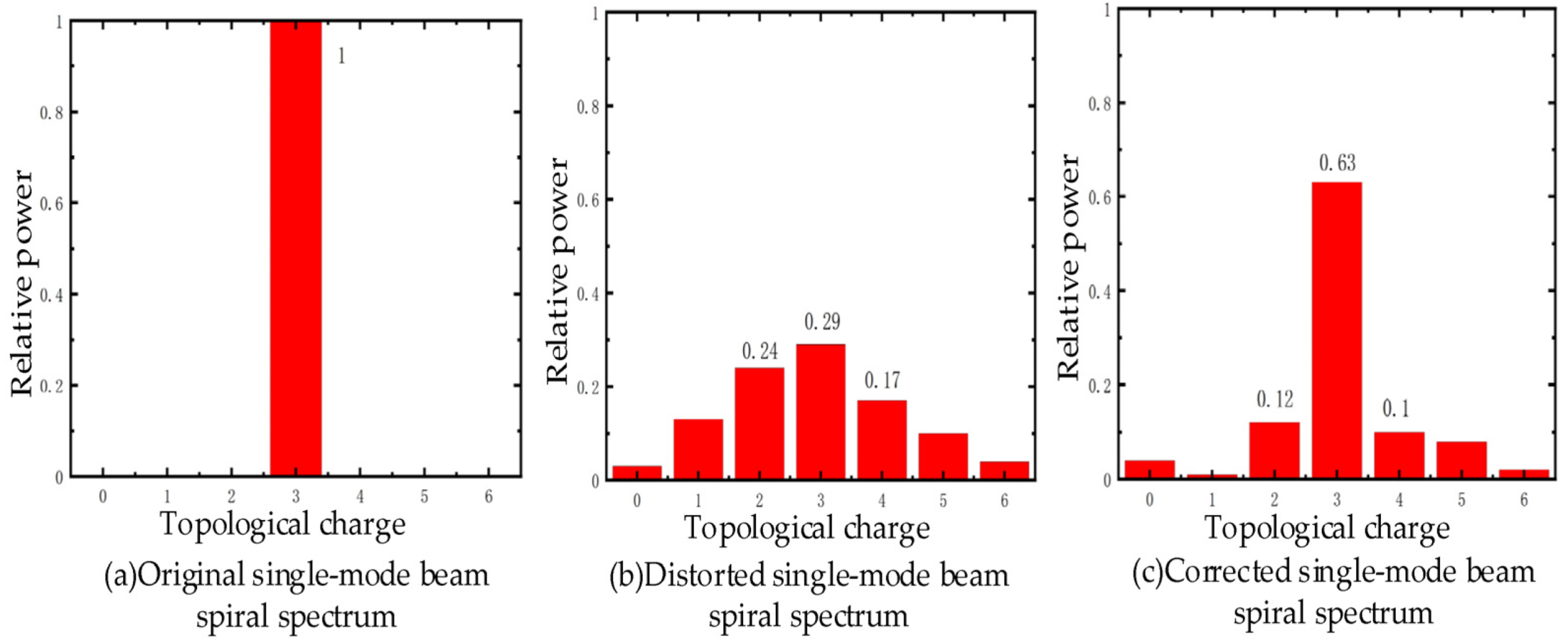
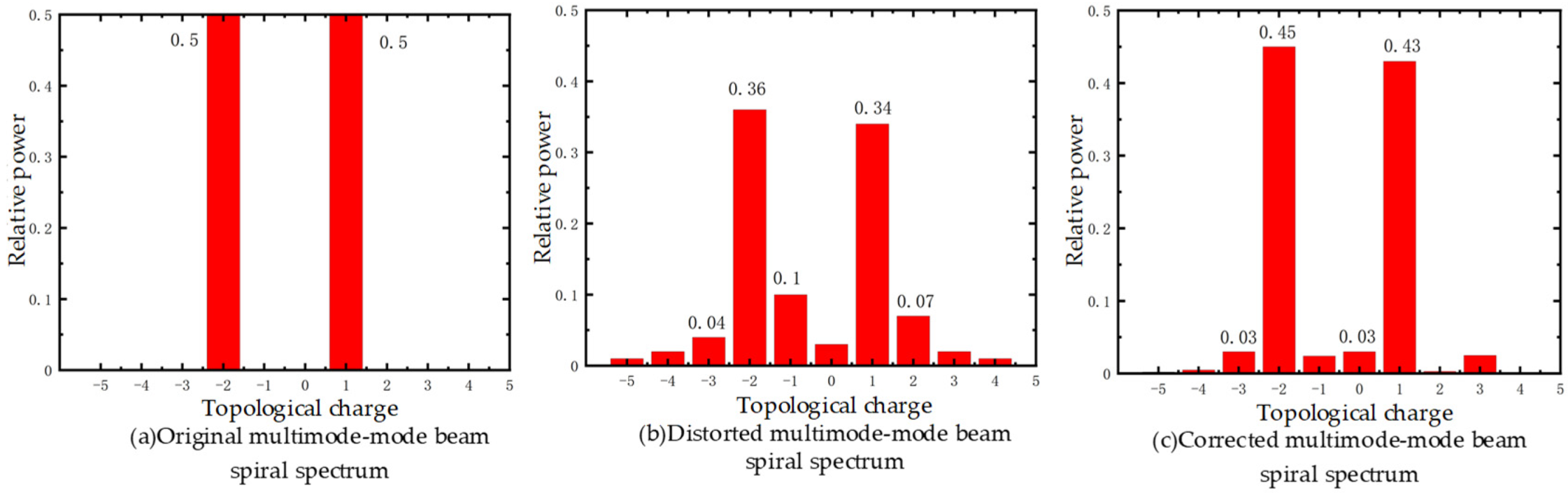
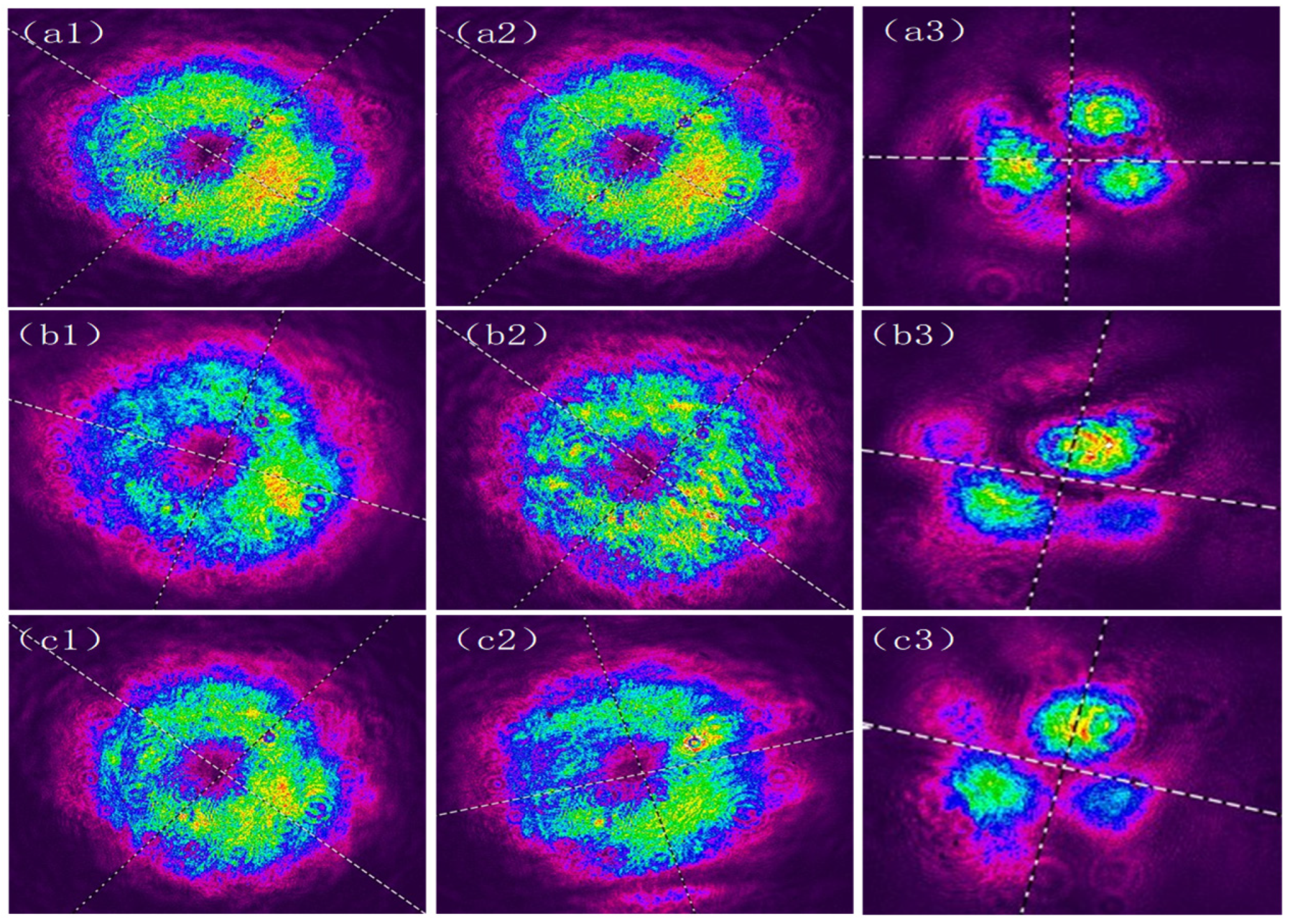
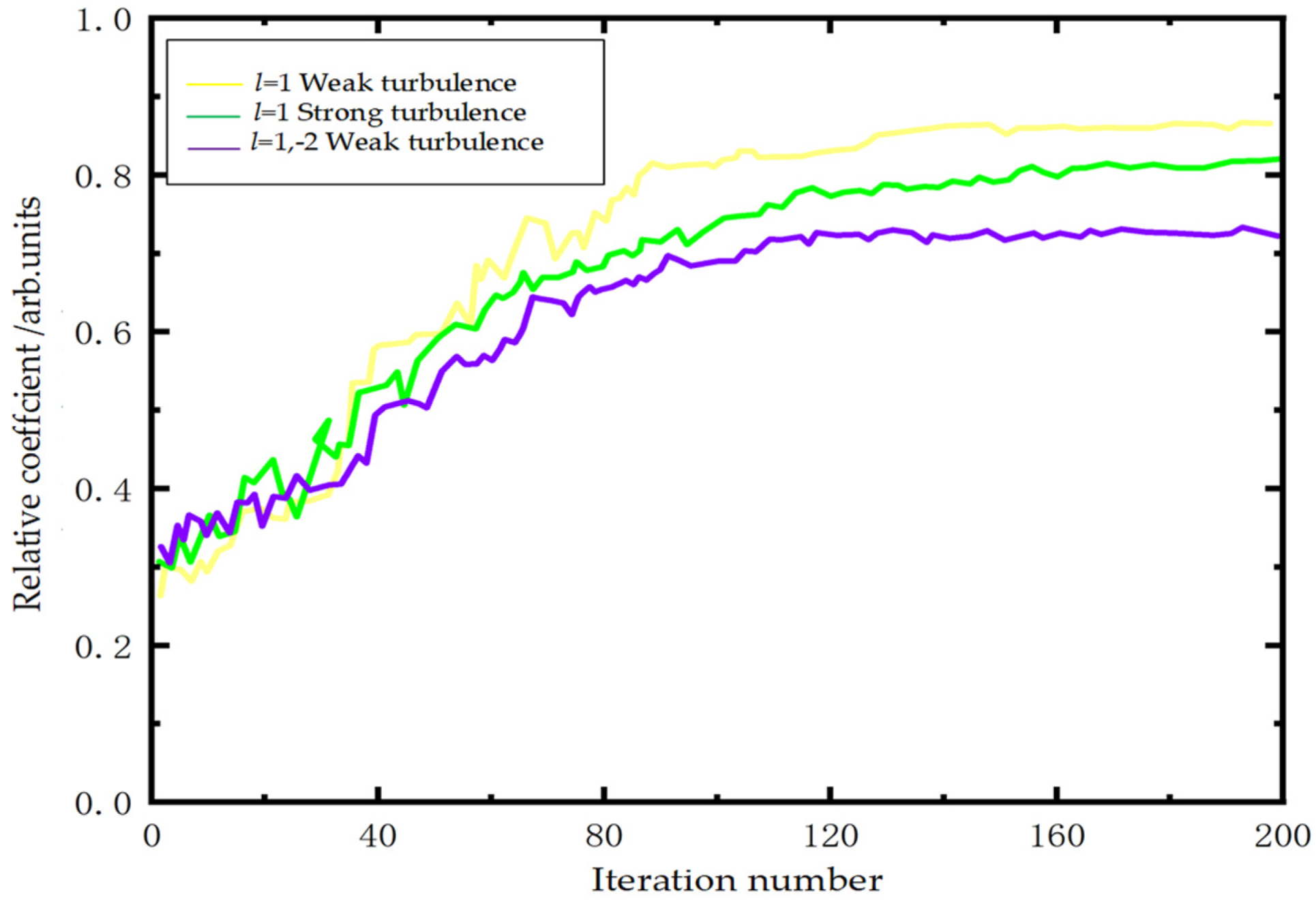
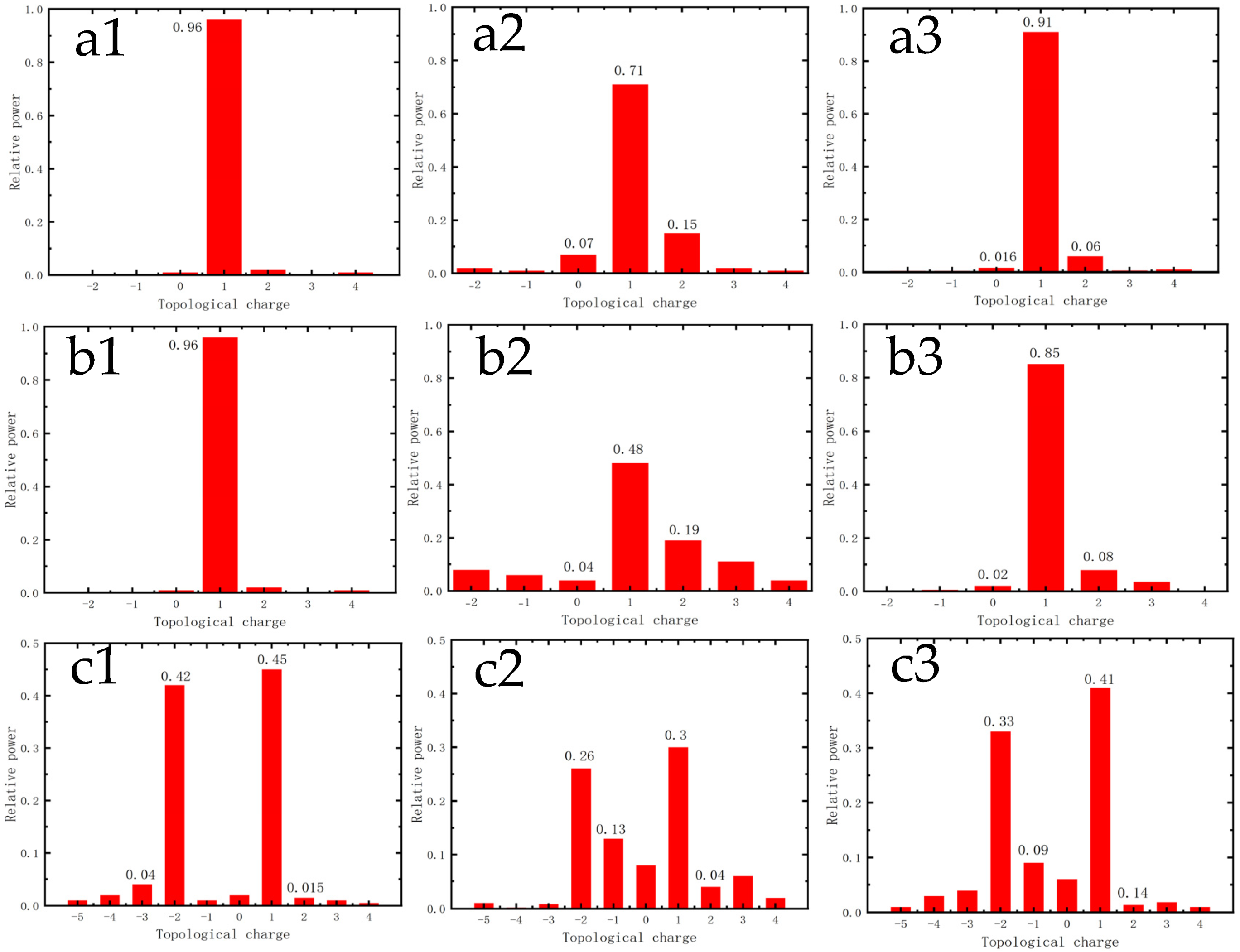
3. Results
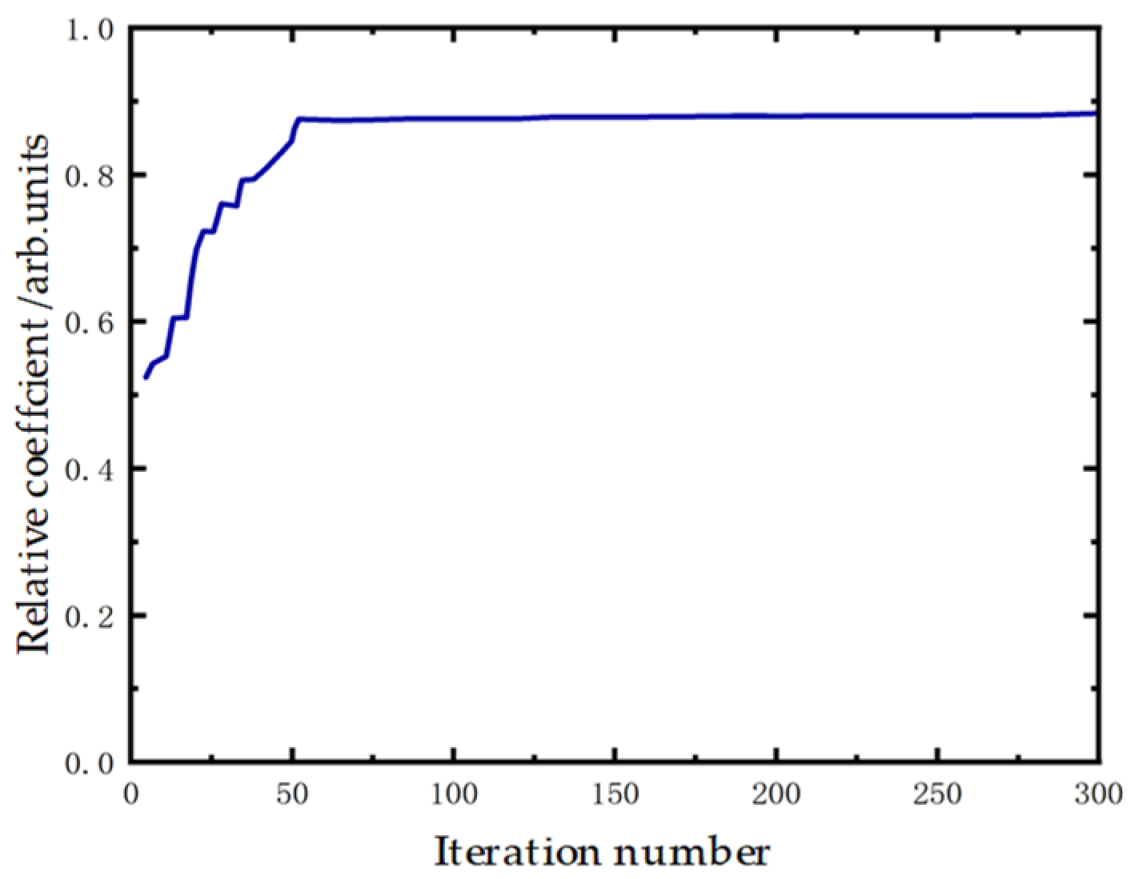
3.1. Simulation and Experimental Results
3.2. Experimental Research
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Fu, Y. The Design of a Novel Optical Communication Advance Margin Monitoring System. Chin. J. Sci. Instrum. 2006, 27, 689–690. [Google Scholar]
- Liu, Y.; Gao, C.; Qi, X.; Weber, H. Orbital angular momentum(OAM)spectrum correction in free space optical communication. Opt. Express 2008, 16, 7091–7101. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Takashima, Y.; Sun, X.; Yu, Z.; Cvijetic, M. Enhancement of channel capacity of OAM based FSO link by correction of distorted wavefront under strong turbulence. In Proceedings of the Frontiers in Optics 2014, Tucson, AZ, USA, 19–23 October 2014. [Google Scholar]
- Duan, H.; Li, E.; Wang, H.; Yang, Z. The impact of mode orthogonality on wavefront measurement by Shack-Hartmann sensors. ACTA Opt. Sin. 2003, 23, 1143–1148. [Google Scholar]
- Starikov, F.; Aksenov, V.; Atuchin, V.V.; Izmailov, I.V.; Kanev, F.Y.; Kochemasov, G.G.; Kudryashov, A.V.; Kulikov, S.M.; Malakhov, Y.I.; Manachinsky, A.N.; et al. Wave front sensing of an optical vortex and its correction in the close-loop adaptive system with bimorph mirror. In Proceedings of the Optics in Atmospheric Propagation and Adaptive Systems X, Florence, Italy, 17–20 September 2007. [Google Scholar]
- Ke, X.; Zhang, D. Fuzzy control algorithm for adaptive optical systems. Appl. Opt. 2019, 58, 9967–9975. [Google Scholar] [CrossRef] [PubMed]
- Poland, S.; Krstajić, N.; Knight, R.D.; Henderson, R.K.; Ameer-Beg, S.M. Development of a doubly weighted Gerchberg–Saxton algorithm for use in multi beam imaging applications. Opt. Lett. 2014, 39, 2431–2434. [Google Scholar] [CrossRef]
- Jesacher, A.; Schwaighofer, A.; Fürhapter, S.; Maurer, C.; Bernet, S.; Ritsch-Marte, M. Wavefront correction of spatial light modulators using an optical vortex image. Opt. Express 2007, 15, 5801–5808. [Google Scholar] [CrossRef] [PubMed]
- Baranek, M.; Behal, J.; Bouchal, Z. Optimal spiral phase modulation in Gerchberg-Saxton algorithm for wavefront reconstruction and correction. In Proceedings of the Thirteenth International Conference on Correlation Optics, Chernivtsi, Ukraine, 11–15 September 2017. [Google Scholar]
- Vorontsov, M.A.; Sivokon, V.P. Stochastic parallel-gradient-descent technique for high-resolution wave-front phase-distortion correction. J. Opt. Soc. Am. 1998, 15, 2745–2758. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Jiang, W. High resolution imaging of phase-distorted extended object using SPGD algorithm and deformable mirror. In Proceedings of the Optical Design and Testing III (Part One of Two Parts), Beijing, China, 12–15 November 2007. [Google Scholar]
- Ke, X.; Wang, X. Experimental Study on Helical Light Wavefront Deformation Correction. Acta Opt. Sin. 2018, 38, 204–210. [Google Scholar]
- Ke, X.; Zhang, Y.; Zhang, Y.; Lei, S. Graphics Processor Acceleration of Wavefront Sensing-Free Adaptive Wavefront Correction System. Laser Optoelectron. Prog. 2019, 56, 88–96. [Google Scholar]
- Jin, Y.; Zhang, Y.; Hu, L.; Huang, H.; Xu, Q.; Zhu, X.; Huang, L.; Zheng, Y.; Shen, H.L.; Gong, W.; et al. Machine learning guided rapid focusing with sensor-less aberration corrections. Opt. Express 2018, 26, 30162–30171. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Liu, H.; Qiao, Y.; Li, X.; Zhang, W. Numerical study of adaptive optics compensation based on convolutional neural networks. Opt. Commun. 2019, 433, 283–289. [Google Scholar] [CrossRef]
- Gao, J.; Anantrasirichai, N.; Bull, D. Atmospheric turbulence removal using convolutional neural network. arXiv 2019, arXiv:1912.11350. [Google Scholar] [CrossRef]
- Tian, Q.; Lu, C.; Liu, B.; Zhu, L.; Pan, X.; Zhang, Q.; Yang, L.; Tian, F.; Xin, X. DNN-based aberration correction in a wavefront sensorless adaptive optics system. Opt. Express 2019, 27, 10765–10776. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.; Hunt, J.; Pritzel, A.; Hees, N.M.O.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. CoRR 2015, 71, 1059–1062. [Google Scholar]
- Allen, L.; Beijersbergen, M.; Spreeuw, R.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185f–8189. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Ge, Y. Analysis of Vortex Shedding of Bridge Sections Based on the Modified Turbulent Freezing Hypothesis. J. Tongji Univ. 2008, 36, 1307–1313. [Google Scholar]
- Wizinowich, P.; Acton, D.; Shelton, C.; Stomski, P.; Gathright, J.; Ho, K.; Lupton, W.; Tsubota, K.; Lai, O.; Max, C.; et al. First light adaptive optics images from the Keck II telescope: A new era of high angular resolution imagery. Publ. Astron. Soc. Pac. 2000, 112, 315–319. [Google Scholar] [CrossRef]
- Pearson, J. Thermal blooming compensation with adaptive optics. Opt. Lett. 1978, 2, 7–9. [Google Scholar] [CrossRef] [PubMed]
- Liu, T. Research on LQG Wavefront Control Technology in Adaptive Optics System; Xi’an University of Technology: Xi’an, China, 2023. [Google Scholar]
- Freeman, R.; Pearson, J. Deformable mirrors for all seasons and reasons. Appl. Opt. 1982, 21, 580–588. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z. Research on Fuzz Testing Technology Based on DDPG Reinforcement Learning Algorithm; Beijing University of Posts and Telecommunications: Beijing, China, 2021. [Google Scholar]
- Sutton, R. Reinforcement Learning, 2nd ed.; Publishing House of Electronics Industry: Beijing, China, 2019. [Google Scholar]
- Guo, X.; Fang, Y. Deep Reinforcement Learning: An Introduction to the Principles; Publishing House of Electronics Industry: Beijing, China, 2019. [Google Scholar]
- Huang, H.; Ren, Y.; Yan, Y.; Ahmed, N.; Yue, Y.; Bozovich, A.; Erkmen, B.I.; Birnbaum, K.; Dolinar, S.; Tur, M.; et al. Phase-shift interference-based wavefront characterization for orbital angular momentum modes. Opt. Lett. 2013, 38, 2348–2350. [Google Scholar] [CrossRef] [PubMed]










| Driver Quantity |
Diameter of the Mirror Surface (/mm) |
Normalized Distance (/mm) |
Maximum Deformation (/) |
Stabilization Time (/) |
Bandwidth (Hz) |
|---|---|---|---|---|---|
| 69 | 10.5 | 1.5 | 60 | 800 | >750 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Y.; Ke, X. Experimental Research on the Correction of Vortex Light Wavefront Distortion. Photonics 2024, 11, 1116. https://doi.org/10.3390/photonics11121116
Ge Y, Ke X. Experimental Research on the Correction of Vortex Light Wavefront Distortion. Photonics. 2024; 11(12):1116. https://doi.org/10.3390/photonics11121116
Chicago/Turabian StyleGe, Yahang, and Xizheng Ke. 2024. "Experimental Research on the Correction of Vortex Light Wavefront Distortion" Photonics 11, no. 12: 1116. https://doi.org/10.3390/photonics11121116
APA StyleGe, Y., & Ke, X. (2024). Experimental Research on the Correction of Vortex Light Wavefront Distortion. Photonics, 11(12), 1116. https://doi.org/10.3390/photonics11121116




