A High-Speed Silicon-Photonics WDM Switch for Optical Networks Applications

Abstract

This article introduces the design of a novel high-speed silicon-photonics hitless switch that adheres to wavelength-division multiplexing (WDM) standards for channel 3 dB bandwidth, channel free spectral range, crosstalk, shape factor, and dispersion. The design combines the advantages of two structures, a compound ring resonator structure, and a Mach–Zehnder interferometer (MZI) modulator. The mathematical treatment for the proposed device is detailed, and two designs are presented. For a switch of five ring resonators, the through (drop) channel 3 dB bandwidth is 60 GHz (38 GHz), channel crosstalk is −24 dB (−24 dB), dispersion is 22 ps/nm (21 ps/nm), shape factor is 0.66 (0.5), and insertion loss is 0.3 dB (1.7 dB). For a switch of nine ring resonators, the through (drop) channel 3 dB bandwidth is 59 GHz (38 GHz), channel crosstalk is −37 dB (−24 dB), dispersion is 28.5 ps/nm (29 ps/nm), shape factor is 0.8 (0.73), and insertion loss is 0.3 dB (2.3 dB). For the five-ring design, the switch-on/off ratio is 30 dB, and for the nine-ring design, it is 31 dB. For both designs, the switching speed is 100 GHz.

1. Introduction

Progress in integrated optics hinges on the development of novel optical materials and photonic circuit designs [1,2,3], operating both in the near-infrared and mid-infrared spectra [4,5,6]. Diverse fabrication methods have been explored, such as ion exchange in glass [7], III–V semiconductors [8,9], and silicon-on-insulator (SOI) platform [2,3], in order to build such photonics circuits. Its supremacy in electronics has made SOI the center of study and investigation for the implementation of integrated optical circuits [10]. The aim is to monolithically merge photonic and electronic components to form high-speed, low-cost, and compact hybrid systems. Of special importance is the silicon-on-silica platform, which is CMOS compatible. This platform also offers a significant refractive index contrast at the C-band communications wavelength range, which enables small bending radii and high-density integration of photonic circuits [11,12,13]. Moreover, both silicon and silica exhibit minimal propagation losses at the wavelength of $1550 \mathrm{nm}$, a fact that unleashed the implementation of a wide spectrum of components, such as grating couplers [14], ring resonators [11], modulators [10,13], sensors [15], interleavers [16], and gyroscopes [17].

One more key component is optical switches. Optical switches are vital components in high-performance on-chip optical networks [18], routing, optical signal processing, information systems, large-scale programmable chips [19], and delay-line processor devices used for image processing with switchable convolution kernels [20]. Effective designs of switches with high bandwidth, low power consumption, and compact size make them vital for multi-core microprocessor systems [21].

While the trend in the literature is to design high-speed switches while maximizing the switch-on/ff ratio, unfortunately, not so much attention is given to other wavelength-division multiplexing (WDM) conditions on channel transmission. These conditions apply to the channel free spectral range ($FSR$), defined as the shift in frequency between one channel and the next for the same port; the crosstalk ($CT$), defined as the ratio of the transmission power for the two ports of the switch (through and drop); the shape factor ($S$), defined as the ratio of the $1 \mathrm{dB}$ bandwidth to the $10 \mathrm{dB}$ bandwidth for the channel power transmission; and the dispersion ($D$), defined as the ratio of the difference in the propagation delay between two successive wavelengths to the wavelength difference. The WDM requirements are $FSR=100 \mathrm{G}\mathrm{H}\mathrm{z} (\mathrm{o}\mathrm{r} \mathrm{e}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{l}\mathrm{y} 0.8 \mathrm{n}\mathrm{m})$, $CT$ $\le -23 \mathrm{d}\mathrm{B}$ within $20 \mathrm{G}\mathrm{H}\mathrm{z}$ from the channel center, $S$ $\ge 0.6$, $D$ $\le 30 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$ within $20 \mathrm{G}\mathrm{H}\mathrm{z}$ from the channel center, and, finally, $3-\mathrm{d}\mathrm{B}$ bandwidth ($BW$) $\ge 20 \mathrm{G}\mathrm{H}\mathrm{z}$ [22].

According to the switching mechanism, two big families of switch designs can be recognized in the literature. The first relies on the more easy-to-implement thermo-optic tuning mechanism. In this technique, the refractive index of the waveguide changes by heating from a nearby current-carrying conductor. As the refractive index varies, phase difference is injected between two wave signals to switch between constructive and destructive interference and, hence, on- and off-switch states. This technique relies on a large thermo-optic coefficient of the optical waveguide material. For example, for silicon, this coefficient is ${\displaystyle \frac{\mathrm{d}\mathrm{n}}{\mathrm{d}\mathrm{T}}}=1.86\times {10}^{-4}{\mathrm{K}}^{-1}$ [23]. However, the main drawback of thermo-optic switching is the slow switching speed (the speed of changing from the on to the off state). Examples of such works include the work in [24], which employs amplitude modulation in a IIIV platform switch. This design is limited to a single ring, resulting in a typical Lorentzian transmission profile that does not meet the WDM requirements, such as free spectral range, bandwidth, or shape factor. Another example is the switch design in [24] which has only one output port with a switching speed of only $1.8 \mathsf{\mu }\mathrm{s}$, significantly hindering its performance. The work in [25] utilizes thermo-optical tuning for individual rings in a multi-ring switch structure. This limits the switching speed despite a high extinction ratio of $60 \mathrm{d}\mathrm{B}$. Another switch is presented in [26], where Mach–Zehnder interferometers (MZIs) are utilized to build a wide band switch with a high extinction ratio. Reference [27] presents a quadruple silicon-on-insulator (SOI) multi-channel channel hitless switch. The operating speed is limited to $15 \mathsf{\mu }\mathrm{s}$. Despite this limitation, the use of four rings significantly improves the transmission extinction ratio to the range of $39–46 \mathrm{d}\mathrm{B}$ and reduces the crosstalk to $-24.5 \mathrm{d}\mathrm{B}$. However, the achieved maximum free spectral range of $0.5 \mathrm{n}\mathrm{m}$ falls short of the WDM specification of $0.8 \mathrm{n}\mathrm{m}$. In [28], a $4\times 4$ thermo-optic SOI hitless router is presented. The router comprises eight ring resonators of $10 \mathsf{\mu }\mathrm{m}$ in radius each. The device footprint is $0.07 {\mathrm{m}\mathrm{m}}^2$. The extinction ratio is $20.79 \mathrm{d}\mathrm{B}$, and the free spectral range is $38.5 \mathrm{G}\mathrm{H}\mathrm{z}$, with a switching speed in the range of microseconds. Again, all of these switches are slow, and their performance metrics are not WDM-compatible.

The other family of switches employs an electro-optic switching mechanism. These switches are more challenging to design and implement since, usually, a PN or a PIN junction is implanted. An alternative is to use electro-optical material as the waveguide core or as a cladding layer on top of a traditional SOI waveguide. The reward, however, is a great improvement in the switching speed. Examples of such designs include the design presented in [29] which is controlled by turning the electric current on and off through a PN junction, achieving a switching speed of $2.4 \mathrm{n}\mathrm{s}$. The drop port bandwidth is $40 \mathrm{G}\mathrm{H}\mathrm{z}$, and the extinction ratio is $25 \mathrm{d}\mathrm{B}$. The device is compact, with disk radii of $3 \mathsf{\mu }\mathrm{m}$ each. Clearly, the focus is not on meeting WDM requirements. Additionally, both the through and drop channels are switched simultaneously, making it a non-hitless switch. Reference [30] describes a PIN lateral diode used to control a 10th-order switch with a passband of $100-\mathrm{G}\mathrm{H}\mathrm{z}$ and a switch-on/off ratio of $10 \mathrm{d}\mathrm{B}$. The switching speed is $1 \mathrm{n}\mathrm{s}$. Another interesting work is presented in [31], where a PIN junction is used to control a switch with a crosstalk of less than $-20 \mathrm{d}\mathrm{B}$, bandwidth of $31 \mathrm{n}\mathrm{m}$, and switching speed in the range of $6–12 \mathrm{n}\mathrm{s}$.

In [21], a review on more recent designs is provided. The switches in this study operate using electro-optical or thermo-optical mechanisms. The switching speed ranges from $0.41 \mathrm{n}\mathrm{s}$ to $76 \mathsf{\mu }\mathrm{s}$. The footprint ranges from $0.0058 {\mathrm{m}\mathrm{m}}^2$ to $0.0225 {\mathrm{m}\mathrm{m}}^2$. The insertion loss ranges from $0.5 \mathrm{d}\mathrm{B}$ to $9 \mathrm{d}\mathrm{B}$. The crosstalk ranges from $-11.5 \mathrm{d}\mathrm{B}$ to $-41.7 \mathrm{d}\mathrm{B}$. This study shows the trade-off between design parameters, where, for example, a more box-like transmission comes at the expense of footprint.

An interesting all-optical design is given in [23], where the switch is composed of five apodized rings in the cascaded-ring optical waveguide (CROW) structure. The laser is focused on a spot in the structure to inject free carriers in order to turn the switch on and off. The footprint is $40\times 12 {\mathsf{\mu }\mathrm{m}}^2$, the switching speed is less than $2 \mathrm{n}\mathrm{s}$, and the extinction ratio is limited to $10–17 \mathrm{d}\mathrm{B}$. In addition, using a laser in tuning the switch adds more complexity to the system design.

A common theme in all of the aforementioned works, obviously, is that the progress focused only on the switching speed, device chip area, and crosstalk, with very little or no consideration paid to other WDM channel transmission specifications, especially the channel bandwidth, free spectral range, and dispersion. Therefore, in this work, we propose two designs for a switch that satisfies all WDM conditions in terms of bandwidth, free spectral range, crosstalk, dispersion, and shape factor and, at the same time, provides a high-speed hitless switching function. The switch also features a high switch-on/off ratio. The innovation in this work relies on merging a static demultiplexer that satisfies all WDM requirements with a Mach–Zehnder Interferometer (MZI)-based modulator. The demultiplexer is composed of coupled-ring resonators in a compound structure, while the modulator stage provides coupling control to one of the rings of the demultiplexer and therefore allows for control of the amount of optical power that enters into the filter. This allows for the filter to be turned on and off at a very high speed that is not limited by the photon lifetime in the resonators making up the filter [24,32,33]. The modulation is facilitated through a silicon-on-insulator (SOI) compatible tuning mechanism where a high-speed electro-optic polymer is employed as the cladding layer [34]. In addition, the switch exhibits hitless operation, wherein the drop port is switched on and off without affecting the through port’s operation. The device inherits the attractive characteristics of SOI, such as compatibility with complementary metal oxide semiconductor (CMOS) fabrication processes. Two variants of the proposed device are presented, one with five ring resonators, and the other with nine. This is helpful in highlighting the design trade-offs between different features. As will be shown, with nine rings, a more box-like transmission, i.e., a higher shape factor, is achieved with less channel crosstalk. This comes at the expense of channel dispersion, which keeps within the WDM constraints, and fabrication area.

This article is organized as follows: In Section 2, the switch design parameters are determined in a careful step-by-step approach. In Section 3, the transfer matrix analysis is presented. In Section 4, the switch performance is discussed, before we conclude in Section 5.

2. Design Parameters

The proposed device is shown in Figure 1a with five rings and in Figure 1b with nine rings. The device combines two basic structures. The first structure is composed of ring resonators that are coupled to neighboring elements, such as other rings and/or straight bus waveguides. The other structure is a MZI-based modulator that is integrated into the top ring resonator along with the top bus waveguide. This modulator consists of two waveguides sandwiched between two $3 \mathrm{d}\mathrm{B}$ couplers and is highlighted in blue.

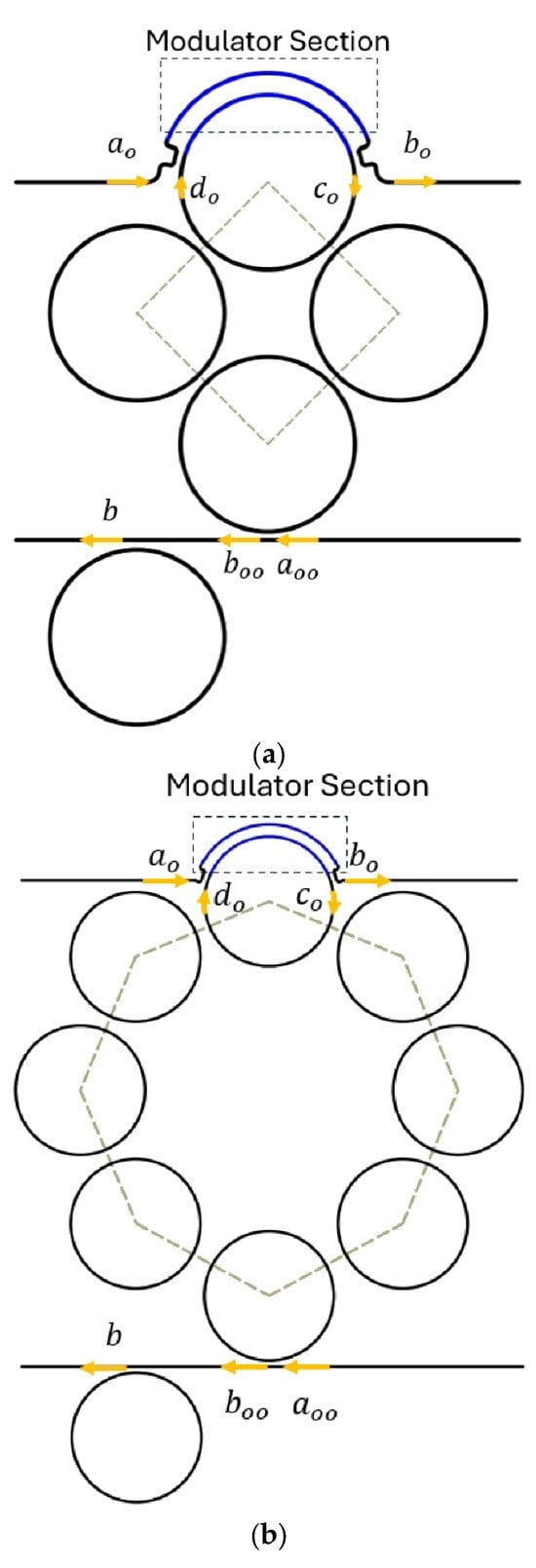
Figure 1. A schematic diagram of the proposed switch, (a) with $N=5$ and (b) with $N=9$. The MZI modulator is shown by the blue lines between two 3 dB couplers, while the significant electric field components are shown by the orange arrows. The grey dashed line indicates the uniform polygon connecting the centers of the rings. The diagrams are not drawn to scale.

The ring resonator part of the device forms a static demultiplexer that receives two interleaved data streams at its input port and splits them into two separate streams in two physically separate ports, the through port and the drop port. This demultiplexer is designed to provide transmission profiles that obey WDM conditions [16,35]. These conditions are a channel $3 \mathrm{d}\mathrm{B}$ bandwidth ($BW$) of at least $20 \mathrm{G}\mathrm{H}\mathrm{z}$, channel free spectral range ($FSR$) of $100 \mathrm{G}\mathrm{H}\mathrm{z}$ (or $0.8 \mathrm{n}\mathrm{m}$), channel crosstalk ($CT$) $\le -23 \mathrm{d}\mathrm{B}$ within a $20 \mathrm{G}\mathrm{H}\mathrm{z}$ bandwidth, dispersion ($D$) $\le 30 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$ within $20 \mathrm{G}\mathrm{H}\mathrm{z}$ bandwidth, and a shape factor ($S$) $\ge$ $0.6$ [16,35] [22]. Let $N$ be the number of rings. Then, as shown in Figure 1, there is a cluster of $N-1$ intra-coupled rings, in addition to one ring that is placed away and is coupled only to the lower bus. The main concept behind this demultiplexer design is to form a filter where there is internal feedback between the rings to provide the required poles and zeros for the desired WDM transmission characteristics [35]. To realize this internal feedback geometrically in the intra-coupled rings part, where the first and the last rings are coupled, ${\displaystyle \frac{N-1}{2}}$ must be an even number [35]. The smallest possible number is then $N-1=4$. The next more complex structure includes $N-1=8$. Unfortunately, the intra-coupled ring resonator part of the structure cannot limit the drop port dispersion to the WDM allowed value, $30 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$. Therefore an additional ring resonator is coupled to the lower bus with the task of adjusting the dispersion of the drop port signal to be below $30 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$ [35]. With one additional ring placed away from the cluster of $N-1$ rings, we then have two designs to discuss with $N=5$ and $N=9$.

In both designs, the top ring is coupled to the top bus through a MZI modulator and two $3 \mathrm{d}\mathrm{B}$ directional couplers. This modulator performs the coupling control mechanism in the switch. An interesting effort was introduced in this direction in the fundamental breakthrough work in [32,33]. In that work, the switch consisted of only one ring and one port. Coupling control is employed to drive the switch between the two states, on and off. For the on state, the power coupling between the bus and the ring is zero, which results in unity transmission. The off state is realized when the coupling is tuned to match the critical coupling condition, leading to zero transmission. The genius of this idea is that the coupling control turns the switch on and off, avoiding the slow process of building up and depleting the energy stored in the resonator. In other words, the speed limit is independent of the photon lifetime. The limit is set by the tuning mechanism, which, in our work, relies on a high-speed electro-optic polymer [34,36,37]. So, in our work, we alter this process so that it can be employed for WDM devices. Hence, the coupling changes between zero power coupling (off state for the drop port) and a certain coupling value (on state for the drop port), as found from the demultiplexer design, which is detailed below, to satisfy the WDM conditions. This way, the high-speed coupling is utilized, and the WDM transmission is preserved. In addition, the through-port transmission remains unchanged for certain wavelength bands (always on), while the drop port transmission goes on and off at other wavelength bands, providing the switch with its hitless feature [38].

The next step is to discuss the design of the demultiplexer. The main electric field components in the following analysis are indicated by arrows in Figure 1. The main input field is $a_o$, with two corresponding output fields, $b_o$ and $b_{oo}$, as the through and drop fields, respectively. The secondary input field is $a_{oo}=0$. The modulation technique for the MZI modulator in this work is adopted from [34]. In this design, a layer of the electro-optic polymer, CLD1/APC [34,36,37], resides on top of a silicon-on-silica waveguide. The three layers are squeezed between two electrodes to apply the tuning voltage, $V$ [34]. For the MZI modulator, if the voltage applied to one arm is $V$, then the voltage applied to the other arm is $-V$. This tuning mechanism supports a switching speed of up to $100 \mathrm{G}\mathrm{H}\mathrm{z}$ [34]. The optical propagation losses are given by $\mathsf{\alpha }=6 \mathrm{d}\mathrm{B}/\mathrm{c}\mathrm{m}$ [34]. In this design, at a wavelength of ${\mathsf{\lambda }}_{\mathrm{o}}=1550 \mathrm{n}\mathrm{m}$, the effective and the group refractive indices are given by $n_e=2.159$ and $n_g=4.11$, respectively [34]. The circumference, $L$, of the ring is determined using $FSR={\displaystyle \frac{c}{n_{g}L}}=100 \mathrm{G}\mathrm{H}\mathrm{z}$, which gives $L={\displaystyle \frac{c}{n_{g }\times FSR}}=729.5 \mathsf{\mu }\mathrm{m}$, where $c=3\times {10}^8 \mathrm{m}/\mathrm{s}$ is the speed of light in space. The radius of the ring is then $R={\displaystyle \frac{L}{2\pi }}=116.2 \mathsf{\mu }\mathrm{m}$. The reason for choosing this modulation technique is that the effective index of the guided mode responds to the tuning voltage, $V$, as given by ${\displaystyle \frac{d{n}_e}{dV}}\approx -2.48\times {10}^{-4}/\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}$ [34]. This is about a one order of magnitude-greater response than that of the common modulators that rely on plasma extraction [10]. Such a good response saves voltage and/or MZI arm length.

The next step in determining the structure parameters is to determine the field-coupling coefficients for every pair of neighboring elements. Let the coupling coefficient between the top ring and the top bus be $k_o$, between the bottom ring of the cluster of rings and the bottom bus be $k_{oo}$, between every two coupled rings be $k$, and, finally, between the away ring and the bottom bus be $k_{oa}$. The values for these coupling coefficients can be found in two different ways. One way, which is the most tedious, is to visualize the transmission poles and zeros on the z-plane and keep changing their values while monitoring the z-plane and the corresponding transmission characteristics until the desired transmission profile is achieved [22]. Another way is to employ an optimization technique such as the genetic algorithm [39]. So, using both methods, the coupling values are found to be $k_o=k_{oo}=0.935$, $k=0.525$, and $k_{oa}=0.952$ for $N=5$; and $k_o=0.963, k_{oo}=0.956, k=0.596$, and $k_{oa}=0.94$ for $N=9$. This variation in the coupling coefficients across the structure is a technique called ‘apodization’, which is essential to reduce side lobes in the transmission characteristics [22].

Finally, any of the field-coupling coefficients, say the ring–ring coefficient, are given by an equation like $k=\sin ({\displaystyle \frac{\pi }{2l}}{L}_c)$ [34]. Here, $l$ is the coupling length required to achieve $100\mathrm{\%}$ coupling, and $L_c$ is the coupling length to achieve a specific value, $k$. With a coupling gap between two adjacent elements of $g=0.2 \mathsf{\mu }\mathrm{m}$, we obtain $l=9.75 \mathsf{\mu }\mathrm{m}$ [34]. Therefore, the values of $L_c$, corresponding to the aforementioned coupling coefficients, are $7.5 \mathsf{\mu }\mathrm{m}$, $3.4 \mathsf{\mu }\mathrm{m}$, and $7.8 \mathsf{\mu }\mathrm{m}$, respectively, for the $N=5$ design. The $L_c$ values are $8 \mathsf{\mu }\mathrm{m},7.9 \mathsf{\mu }\mathrm{m},3.9 \mathsf{\mu }\mathrm{m}$, and $7.6 \mathsf{\mu }\mathrm{m}$, respectively, for the $N=9$ design. These values determine the length of the part of interaction of the directional couplers between two elements. As for the $3 \mathrm{d}\mathrm{B}$ couplers embedded in the MZI modulator, $L_c={\displaystyle \frac{2l}{\pi }}\mathit{asin}\sqrt{0.5}=4.9 \mathsf{\mu }\mathrm{m}$. We allow about $15 \mathsf{\mu }\mathrm{m}$ for the S-bends surrounding the directional coupler. Therefore, a $3 \mathrm{d}\mathrm{B}$ coupler occupies approximately $20 \mathsf{\mu }\mathrm{m}$ of ring circumference. We limit the modulator length, including the $3 \mathrm{d}\mathrm{B}$ couplers, to one-half of the ring circumference so that the other half is engaged with the rest of the structure. This dictates an MZI arm length of $L_{MZI}={\displaystyle \frac{\mathrm{L}}{2}}-2\times 20 \mathsf{\mu }\mathrm{m}=324.75 \mathsf{\mu }\mathrm{m}$, which can host the modulation mechanism.

3. Transfer Matrix Analysis

As shown in Figure 1, the switch receives field $a_o$ at the input port and demultiplexes it into two output fields, $b_o$ and $b_{oo}$, for the through and the drop ports, respectively. The second input field is $a_{oo}=0$. The structure should provide WDM-compatible transmission profiles with $V=0$ (on state for the drop port). Then, the right voltage value should be found to eliminate the drop-port transmission (off state for the drop port). The complex analysis for the ring resonator structure is given in [35], where the field transmission for the through and drop ports are given by ${\rho }_o={\displaystyle \frac{b_o}{a_o}}$ and ${\tau }_o={\displaystyle \frac{b_{oo}}{a_o}}$, respectively. However, this analysis should now be modified to accommodate the additional MZI modulator, as shown next.

The MZI modulator has two input fields, $a_o$ and $d_o$, and two output fields, $b_o$ and $c_o$. These fields can be related using the following [24,33]:

$$b_o={\gamma }_1{a}_o+{\gamma }_2{d}_o$$

(1)

$$c_o={\gamma }_3{a}_o+{\gamma }_4{d}_o$$

(2)

where

$${\gamma }_1=-{\gamma }_4=0.5\left(e^{-i{\eta }_1}-e^{-i{\eta }_2}\right)$$

(3)

$${\gamma }_2={\gamma }_3=-0.5i\left(e^{-i{\eta }_1}+e^{-i{\eta }_2}\right)$$

(4)

$${\eta }_1={\displaystyle \frac{2\pi }{{\lambda }_o}}{L}_{MZI}\left(V\times {\displaystyle \frac{d{n}_e}{dV}}\right)+{\mathsf{\Phi }}_1$$

(5)

$${\eta }_2={\displaystyle \frac{2\pi }{{\lambda }_o}}{L}_{MZI}\left(-V\times {\displaystyle \frac{d{n}_e}{dV}}\right)+{\mathsf{\Phi }}_2$$

(6)

Here, ${\eta }_1$ and ${\eta }_2$ represent the propagation phase change along the upper and lower arms of the MZI, respectively. Additionally, constant phase shifts are embedded in the two arms and are given by ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2$. This is different from the classical treatment in [24,33], where the phase shifts in the two arms are equal and opposite. So, with ${\mathsf{\Phi }}_1={\mathsf{\Phi }}_2=0$, the MZI parameters become ${\eta }_1=-{\eta }_4=-i\sin \left({\displaystyle \frac{2\pi }{{\lambda }_o}}{L}_{MZI}\left(V\times {\displaystyle \frac{d{n}_e}{dV}}\right)\right)$ and ${\eta }_2={\eta }_3=-i\cos \left({\displaystyle \frac{2\pi }{{\lambda }_o}}{L}_{MZI}\left(V\times {\displaystyle \frac{d{n}_e}{dV}}\right)\right)$, which share the same form as the classical result in [24]. So, with ${\mathsf{\Phi }}_1={\mathsf{\Phi }}_2=0$, there is $100\mathrm{\%}$ power coupling between the bus and the ring when $V=0$. Unfortunately, this does not match the $k_o$ value mentioned above for any of the two designs. Here comes the role of the two constant phase shifts, ${\mathsf{\Phi }}_1$ and ${\mathsf{\Phi }}_2$, as they should be designed to provide the right value of $k_o$ when $V=0$. We found that, for the $N=5$ design, ${\mathsf{\Phi }}_1=1.98 \mathrm{r}\mathrm{a}\mathrm{d}$ and ${\mathsf{\Phi }}_2=1.2 \mathrm{r}\mathrm{a}\mathrm{d}$. For the $N=9$ design, ${\mathsf{\Phi }}_1=1.87 \mathrm{r}\mathrm{a}\mathrm{d}$ and ${\mathsf{\Phi }}_2=1.27 \mathrm{r}\mathrm{a}\mathrm{d}$. Such small shifts can be implemented through small extra lengths of the MZI arms. For the $N=5$ design, the corresponding lengths are $226 \mathrm{n}\mathrm{m}$ and $137 \mathrm{n}\mathrm{m}$, respectively. For the $N=9$ design, they are $213 \mathrm{n}\mathrm{m}$ and $145 \mathrm{n}\mathrm{m},$ respectively.

We then turn our attention to merge the MZI equations above with the analysis in [35]. The symbols in the current work and in [35] have the same meanings, except for only one parameter, which is $N$. Here, $N=5$ corresponds to $N=4$ in [35], as the fifth ring is not counted in the first part of the analysis in [35]. Similarly, $N=9$ in this work is analogous to $N=8$ in [35]. Also, unless it is necessary, we will limit the discussion here to the adjustments to the mathematical treatment with respect to that in [35]. For the unaffected equations, we refer the reader to the detailed analysis in [35]. So, with the MZI equations in the current work, the following changes take place. First, the internal device field reflection and transmission coefficients are ${\rho }_i={\displaystyle \frac{b_1}{a_1}}$ and ${\tau }_i={\displaystyle \frac{c_{N-1}}{a_1}}$, with the same detailed expressions in [35], but with $c_{N-1}$ here instead of $c_N$, as explained above. Then, using ${\displaystyle \frac{d_o}{c_o}}={\tau }_i{e}^{-i{\delta }_2}$ in Equation (2), we obtain ${\displaystyle \frac{d_o}{a_o}}={\displaystyle \frac{{\tau }_i{\gamma }_3{e}^{-i{\delta }_2}}{1-{\tau }_i{\gamma }_4{e}^{-i{\delta }_2}}}$, which can then be used to find ${\displaystyle \frac{b_o}{a_o}}$ from Equation (1), and, hence,

$${\rho }_o={\displaystyle \frac{b_o}{a_o}}={\displaystyle \frac{{\gamma }_1+\left({\gamma }_2{\gamma }_3-{\gamma }_1{\gamma }_4\right){\tau }_i{e}^{-i{\delta }_2}}{1-{\gamma }_4{\tau }_i{e}^{-i{\delta }_2}}}$$

(7)

Here, $\delta ={\displaystyle \frac{2\pi n_e}{{\lambda }_o}}L-{\displaystyle \frac{i\alpha L}{2}}$ represents the complex phase change for one complete round, and ${\delta }_2$ bears the same definition as in [35]. Also, we can find ${\displaystyle \frac{a_1}{a_o}}={\displaystyle \frac{a_1}{c_o}}\times {\displaystyle \frac{c_o}{d_o}}\times {\displaystyle \frac{d_o}{a_o}}=e^{-{\displaystyle \frac{i{\delta }_2}{2}}}\times \left({\gamma }_3{\displaystyle \frac{a_o}{d_o}}+{\gamma }_4\right)\times {\displaystyle \frac{d_o}{a_o}}=e^{-{\displaystyle \frac{i{\delta }_2}{2}}}\left({\gamma }_3+{\gamma }_4\times {\displaystyle \frac{{\tau }_i{\gamma }_3{e}^{-i{\delta }_2}}{1-{\tau }_i{\gamma }_4{e}^{-i{\delta }_2}}}\right)={\displaystyle \frac{{\gamma }_3{e}^{-\frac{i{\delta }_2}{2}}}{1-{\tau }_i{\gamma }_4{e}^{-i{\delta }_2}}}$, and then

$${\tau }_o={\displaystyle \frac{b_{oo}}{a_o}}={\displaystyle \frac{-i{k}_{oo}{\gamma }_3(y_3+y_4{\rho }_i)}{e^{i{\delta }_2}-{\gamma }_4{\tau }_i}}$$

(8)

The parameters $y_3$ and $y_4$ are found using successive matrix multiplication that includes propagation phase matrices and coupling matrices, as given in [35]. Recall that the analysis in [35] is semi-analytical, where part of the analysis is based on numerical calculations and part on analytical formulae. A quick verification of the new formulae for ${\rho }_o$ and ${\tau }_o$ can be carried out by replacing both ${\gamma }_1$ and ${\gamma }_4$ with $r_o$ and replacing both ${\gamma }_2$ and ${\gamma }_3$ with $-i{k}_o$ in Equations (7) and (8) in this work to retrieve the expressions given by Equations (11) and (12) in [35]. As a matter of fact, the isolated stage ring is used to correct the dispersion of the drop-port signal, and, therefore, the actual drop-port transmission is given by $\tau$, where we have the following:

$$\tau ={\displaystyle \frac{b}{a_{oo}}}={\tau }_o\times {\displaystyle \frac{b}{b_{oo}}}={\tau }_o\times {\displaystyle \frac{\sqrt{1-k_{oa}^2}-e^{-i\delta }}{1-\sqrt{1-k_{oa}^2}{e}^{-i\delta }}}$$

(9)

4. Results and Discussion

As discussed above, the compound ring resonator structure acts as a demultiplexer that splits two data streams on one physical channel into two separate channels, the through and the drop. The role of the MZI modulator is to allow power into the demultiplexer or not. This way, the WDM constraints are satisfied through the demultiplexer, while the switching is provided through the MZI modulator.

The power transmission for the $N=5$ device is depicted in Figure 2. With $V=0$, both ports transmit optical signals with the following characteristics for the through and drop ports, respectively: a 3 dB bandwidth of $60 \mathrm{G}\mathrm{H}\mathrm{z}$ and $38 \mathrm{G}\mathrm{H}\mathrm{z}$, channel crosstalk of $-24 \mathrm{d}\mathrm{B}$ for both, dispersion of $22 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$ and $21 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$, shape factor of $0.66$ and $0.5$, and, finally, insertion loss of $0.3 \mathrm{d}\mathrm{B}$ and $1.7 \mathrm{d}\mathrm{B}$. When $V=3.7 \mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}$ is applied to the top MZI arm and $-3.7 \mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}$ to the lower, the drop port power drops by $30 \mathrm{d}\mathrm{B}$ at the central wavelength. The through port’s original transmission is not affected, thus giving the hitless feature of the switch. For the $N=9$ design, power transmission is depicted in Figure 3. With $V=0$, the through and drop signals possess, respectively, a 3 dB bandwidth of $59 \mathrm{G}\mathrm{H}\mathrm{z}$ and $38 \mathrm{G}\mathrm{H}\mathrm{z}$, channel crosstalk of $-37 \mathrm{d}\mathrm{B}$ and $-24 \mathrm{d}\mathrm{B}$ for both, dispersion of $28.5 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$ and $29 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$, shape factor of $0.8$ and $0.73$, and, finally, insertion loss of $0.3 \mathrm{d}\mathrm{B}$ and $2.3 \mathrm{d}\mathrm{B}$. When $V=3.9 \mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}$ is applied to the top MZI arm and $-3.9 \mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}$ to the lower, the drop-port power drops by $31 \mathrm{d}\mathrm{B}$ at the central wavelength. For both designs, the free spectral range is $100 \mathrm{G}\mathrm{H}\mathrm{z}$ or, equivalently, $0.8 \mathrm{n}\mathrm{m}$. Clearly, both designs satisfy the WDM conditions mentioned earlier. Recalling that the crosstalk is measured within a bandwidth of $20 \mathrm{G}\mathrm{H}\mathrm{z}$ around the central wavelength of the channel transmission.

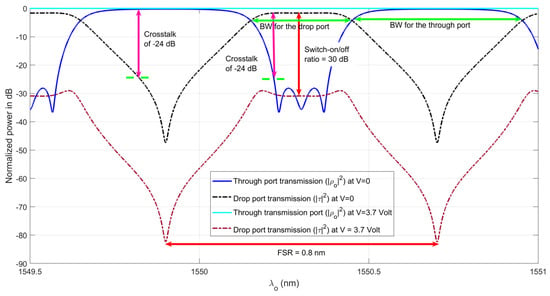
Figure 2. The $N=5$ switch transmission in the on state ($V=0$) and in the off state ($V=3.7 \mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}$).

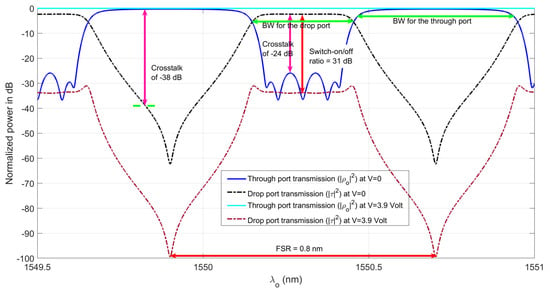
Figure 3. The $N=9$ switch transmission in the on state ($V=0$) and in the off state ($V=3.9 \mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}$).

A comparison between the performance of the proposed switch and other designs in the literature is provided in Table 1.

Table 1. A comparison between the proposed switch and other designs.

Reference	Platform	Switching Mechanism	Switching Speed	Hitless Operation	Device Footprint	Transmission Characteristics 1
[24]	IIIV semiconductors	Thermo-optic	Rise time of $1.8 \mathsf{\mu }\mathrm{s}$	Not applicable since there is only one port.	Not available	Lorentzian transmission. $\mathrm{BW}$2, $\mathrm{CT}$3, $\mathrm{FSR}$4, $\mathrm{S}$5 $\mathrm{or} \mathrm{D}$6 (NA) 7
[27]	${\mathrm{Ta}}_2{\mathsf{O}}_5-{\mathrm{SiO}}_2$ core with ${\mathrm{SiO}}_2$ cladding	Thermo-optic	Fall time of $15 \mathsf{\mu }\mathrm{s}$	Yes	Four rings of $100 \mathsf{\mu }\mathrm{m}$	$\mathrm{BW}=0.11\mathrm{nm}$ $\mathrm{CT}=-24.5\mathrm{dB}$ $\mathrm{S}=0.5$ (NC) 8 $\mathrm{FSR} \mathrm{and} \mathrm{D}$ (NA)
[28]	SOI	Thermo-optic	$1 \mathsf{\mu }\mathrm{s}$	Yes	0.$07 {\mathrm{mm}}^2$	$\mathrm{BW}=38.5 \mathrm{GHz}$ Rest of parameters (NA)
[40]	SOI	Thermo-optic	NA	No	NA	$\mathrm{BW}=0.12 \mathrm{to} 2.91 \mathrm{nm}$ Rest of parameters (NA)
[23]	SOI	Focused laser to inject free carriers	$2 \mathrm{ns}$	No	$40\times 12 {\mathsf{\mu }\mathrm{m}}^2$	$\mathrm{BW}=1.4 \mathrm{nm} \mathrm{to} 4 \mathrm{nm}$ $\mathrm{FSR}=18 \mathrm{nm}$ (NC) $\mathrm{CT}=-7 \mathrm{to}-15 \mathrm{dB}$ (NC) $\mathrm{S} \mathrm{and} \mathrm{D}$ (NA)
[29]	SOI	PN junction	$2.4 \mathrm{ns}$	No	Two rings with $3 \mathsf{\mu }\mathrm{m}$ radius	$\mathrm{BW}=40 \mathrm{GHz}$ $\mathrm{CT}=-25 \mathrm{dB}.$ $\mathrm{FSR}=4.2 \mathrm{THz}$ (NC) $\mathrm{S} \mathrm{and} \mathrm{D}$ (NA)
[31]	SOI	PIN junction	Rise time < $12.5 \mathrm{ns}$ Fall time < $6.1 \mathrm{ns}$	No	NA	$\mathrm{BW}=31 \mathrm{nm}$ $\mathrm{CT}=-20 \mathrm{dB}$ (NC) $\mathrm{FSR}, \mathrm{S} \mathrm{and} \mathrm{D}$ (NA)
[41]	SOI	PIN junction	$64 \mathrm{Gb}/s$	No	$4.6\times 2 {mm}^2$	$\mathrm{BW}=60 \mathrm{nm}$ $\mathrm{CT}=-19.4 \mathrm{dB}$ (NC) $\mathrm{FSR}, \mathrm{S} \mathrm{and} \mathrm{D}$ (NA)
This work, 5 ring design	SOI	Electro-optic polymer on SOI	$100 \mathrm{GHz}$	Yes	$0.44 {mm}^2$	$\mathrm{FSR}=100 \mathrm{GHz}$ For the through/drop channels: $\mathrm{BW}=60/38 \mathrm{GHz}$ $\mathrm{CT}=-24/-24$ $\mathrm{D}=22/21 \mathrm{ps}/\mathrm{nm}$ $\mathrm{S}=0.66/0.5$
This work, 9 ring design	SOI	Electro-optic polymer on SOI	$100 \mathrm{GHz}$	Yes	$0.995{mm}^2$	$\mathrm{FSR}=100 \mathrm{GHz}$ For the through/drop channels: $\mathrm{BW}=59/38 \mathrm{GHz}$ $\mathrm{CT}=-37/-24$ $\mathrm{D}=28.5/29 \mathrm{ps}/\mathrm{nm}$ $\mathrm{S}=0.8/0.73$

¹ WDM conditions are $\mathrm{B}\mathrm{W}\ge 20 \mathrm{G}\mathrm{H}\mathrm{z} \left(0.16 \mathrm{n}\mathrm{m}\right), \mathrm{C}\mathrm{T}\le -23 \mathrm{d}\mathrm{B}, \mathrm{F}\mathrm{S}\mathrm{R}=100 \mathrm{G}\mathrm{H}\mathrm{z} \left(0.8 \mathrm{n}\mathrm{m}\right), \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{S}\ge 0.6 \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{D}\le 30 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$. BW ², $3 \mathrm{d}\mathrm{B} \mathrm{B}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{w}\mathrm{i}\mathrm{d}\mathrm{t}\mathrm{h}$; CT ³, crosstalk; FSR ⁴, free spectral range; S ⁵, shape factor; D ⁶, dispersion; NA ⁷, (information) not available; NC ⁸, non-WDM-compatible.

Table 1 shows how advantageous the proposed design in this work is. The thermo-optic switches in [24,27,28,40] possess a switching speed in the range of microseconds, which is too slow if compared with other techniques. The thermo-optic designs are much simpler to implement, though, since implementing a heater is much less complex than implementing an electro-optic device such as a PN or a PIN junction. On the contrary, electro-optic-based switches are much faster, with a switching speed in the range of nanoseconds. Away from slow switching, not much attention was paid by many designers to meet all WDM conditions in these designs, as shown in the last column of Table 1. An exception may be the channel crosstalk. This is the difference in power transmission of the two channels of a simple switch. Yet again, achieving the WDM requiring crosstalk of $-23 \mathrm{d}\mathrm{B}$ is clearly challenging. In addition, in order to save the chip area, the trend is to implement ring resonators with a small radius. The drawback is a too-large $FSR$, such as in [29]. A too-large $FSR$ limits the number of channels in the communications band of interest. On the other hand, our designs strictly obey all of the WDM conditions, with a superior switching speed of $100 \mathrm{G}\mathrm{H}\mathrm{z}$, large and boxlike channel passband, and low dispersion.

Turning our attention now to the proposed designs in this work, we see that both designs satisfy all WDM conditions. A trade-off can be found, though. With five rings, the device’s footprint is less than half that of the nine-ring design. Also, fewer rings make the design less sensitive to fabrication tolerance. The dispersion is also less. However, the dispersion is within acceptable limits in both. On the other hand, a nine-ring design provides more boxlike transmission, as the shape factor is larger. This results in better crosstalk for the nine-ring design. Comparing both designs, there is no clear advantage regarding the bandwidth in any case, and both designs satisfy the $FSR$ condition. In both designs, a strong switch-on/off ratio is achieved as $30 \mathrm{d}\mathrm{B}$ and $31 \mathrm{d}\mathrm{B}$ for the $N=5$ and $N=9$ designs, respectively.

5. Conclusions

To the best of our knowledge, in this work, the first design of an electro-optic switch that obeys all WDM specifications is presented. The design relies on a WDM compound ring resonator wavelength demultiplexer circuit that is combined with a coupling control mechanism in the form of an MZI modulator. The mathematical treatment of the demultiplexer circuit is modified to accommodate the MZI modulator. Two flavors of the hitless switch design are presented, one with five ring resonators and the other with nine ring resonators. Both designs deliver on the bandwidth, crosstalk, free spectral range, shape factor, and dispersion requirements for WDM transmission. The switching time is not limited by the photon lifetime, which enables a speed of up to $100 \mathrm{G}\mathrm{H}\mathrm{z}$, and the switch-on/off ratio is around $30 \mathrm{d}\mathrm{B}$. With this performance, the proposed switch can play a role in many applications, such as signal-processing applications, optical networks, routing, optical signal processing, information systems, large-scale programmable chips, and delay-line processor devices used for image processing with switchable convolution kernels.