Telescope Alignment Method Using a Modified Stochastic Parallel Gradient Descent Algorithm

Abstract

To satisfy the demands of high image quality and resolutions, telescope alignment is indispensable. In this paper, a wavefront sensorless method based on a modified stochastic parallel gradient descent algorithm (SPGD) called the adaptive moment estimation SPGD (Adam SPGD) algorithm is proposed. Simulations are carried out using a four-mirror telescope, whose aperture is 6 m and fields of view are Φ2°. Three misalignments are shown as examples. Positions of the secondary mirror and third mirror are employed to compensate aberrations. The results show that merit functions and energy distributions of corrected images match with the designed ones. The mean RMS of residual wavefront errors is smaller than λ/14 (λ = 0.5 μm), indicating that the misalignments are well compensated. The results verify the effectiveness of our method.

1. Introduction

Due to the advantages of strong light collecting ability, wide detection ranges, and high resolutions, telescopes with large apertures and wide fields of view are the inevitable tendency in the fields of space debris monitoring, remote sensing, scientific observations, and so on. But misalignments between mirrors caused by machining error, mechanical deformations, operating temperature changes, deformations caused by vibrations and shock, and some other reasons can decrease the image quality and resolution, making it difficult to achieve the expected goal. As a result, telescope alignment becomes an indispensable procedure to ensure the performance of telescopes. However, for large-aperture telescopes, the primary mirrors are usually very large, heavy, and complicated, especially for segmented telescopes, making them hard to reposition. Therefore, the positions of the secondary mirror and third mirror that have a simple structure, smaller size, and relatively high sensitivity compensate aberrations caused by misalignments.

Popular methods to align telescopes can be classified into four categories, including the direct wavefront sensor method [1], the image-based wavefront sensor method, laser triangulation method [2], and wavefront sensorless method based on far-field images. The direct wavefront sensor method can recover the wavefront phase by a Shack–Hartmann wavefront sensor (SHWS) [3] and pyramid wavefront sensor (PWFS) [4]. This method needs additional elements to measure the wavefront errors, increasing the complexity of systems. Image-based wavefront sensor methods such as the phase diversity method (PD) [5,6] and phase retrieval method (PR) [7,8] can recover the wavefront using a series of focused and defocused images. On one hand, the defocused images are acquired by moving the detectors or introducing a phase modulator, which can complicate the alignment system. On the other hand, a wavefront reconstruction algorithm such as the Gerchberg–Saxton (GS) algorithm [9] should be employed to calculate the phase errors, then misalignments are corrected using a computer-aided alignment method (CAA) [10] or other methods. Both the direct wavefront sensor method and image-based wavefront sensor method need to recover the wavefront, increasing the complexity of the algorithm. The laser triangulation method [11] is a direct measurement method. The misalignments between mirrors are measured by adding sources and photodetectors such as a position sensitive detector (PSD) [12] to the edge of the reference mirror and adding small mirrors to the edge of the tested mirror [13,14] and calculated according to the changes in spot centroids obtained from photodetectors. This method introduces a measurement system installed on the edge of mirrors, increasing the complexity of the system. The wavefront sensorless method was proposed in the 1970s and used in the field of laser beam control. It flourished in the late 1990s. M. A. Vorontsov used the wavefront sensorless method combined with the SPGD algorithm to correct phase distortion in 1997 [15]. Huizhen Yang used the wavefront sensorless method combined with the SPGD algorithm to control the face of deformable mirrors [16]. Longfeng Zhou used the wavefront sensorless method combined with the SPGD algorithm to align coaxial and off-axis telescopes [17]. Compared with the other three methods, the wavefront sensorless method aligns telescopes using an optimization algorithm according to the images acquired by the far-field detector without adding elements and a recovering wavefront, having the advantages of concise measurement structure and simple algorithm. More importantly, the wavefront sensorless method can align more than one mirror at the same time without aberration decoupling.

In this paper, a wavefront sensorless method based on far-field images using a modified stochastic parallel gradient descent algorithm is proposed. Simulations are implemented by a four-mirror telescope with a 6 m aperture and Φ2° fields of view. The paper is organized as follows. Theory of the wavefront sensorless method using a modified SPGD algorithm is introduced in Section 2. Simulations and results are described in Section 3. Conclusions are given in Section 4.

2. Theory

A wavefront sensorless method can align telescopes based on images obtained from a far-field detector using optimization algorithms without adding other measurement elements. Many optimization algorithms can be employed, such as the simulated annealing algorithm (SA) [18], Newton method [19], genetic algorithm (GA) [20], ant colony algorithm (ACA) [21], stochastic parallel gradient descent algorithm (SPGD) [22], machine learning method [23], and so on. In this paper, a modified SPGD algorithm is adopted. For the traditional SPGD algorithm, the iterative formula can be expressed as Equation (1) [24].

$$u^{k+1}=u^k+\gamma g^k=u^k+\gamma \times \delta J^k\times \delta u^k$$

(1)

where γ means gain coefficient. u is a control variable. Misalignments between mirrors include six degrees of freedom, the decentrations are along x, y, z axes (dx, dy, dz) and rotations about x, y, z axes (tx, ty, tz). For coaxial telescopes, optical systems have rotational symmetry about the z axis, which is the optical axis. As a result, rotation about the z axis is usually ignored during the alignment as it has little effect on image quality. Therefore, control variables u are five-dimensional vectors, defined as follows.

$$u=[dx,dy,dz,tx,ty]$$

(2)

k is the iteration number. δu means perturbations for control variables. J is a merit function of images, and δJ is a change in merit functions. There are some popular merit functions to evaluate the quality of images, such as encircled energy, Strehl ratio, root mean square (RMS) radius, and so on. g^k is the gradient of merit functions.

There are two problems with the traditional SPGD algorithm according to our research. One is that the SPGD algorithm only takes the current gradient information into account, which is easily trapped in the local optimum and can decrease the convergence speed. The other one is that the traditional SPGD algorithm uses a settled gain coefficient, which can decrease the efficiency of alignment processes. To overcome these disadvantages, a modified SPGD algorithm called the adaptive moment estimation SPGD (Adam SPGD) algorithm [25] is implemented. For the first problem, the first moment estimation of gradient m is updated using exponential moving averages (EMAs), which set the most recent values with the highest weight, as defined in Equation (3).

$$m^k={\beta }_1{m}^{k-1}+(1-{\beta }_1)g^k$$

(3)

Here, β₁ is a parameter used to control the decay rate of EMAs. To avoid the first moment estimation biasing towards zero, the expression of first moment estimation [26] is amended as Equation (4).

$$\widehat{m^k}=m^k/(1-{\prod }_{i=1}^k{\beta }_1)$$

(4)

The first moment estimation of gradient can not only improve the convergence speed but also make the gradient smooth and reduce oscillation.

For the second problem, the second moment estimation of gradient [27] v is introduced as an adaptive gain, by which each variable can choose the proper learning rate. As a result, the convergence efficiency will be improved. It is defined as Equation (5).

$$\widehat{v^k}={[\beta }_2{v}^{k-1}+(1-{\beta }_2){(g^k)}^2]/(1-{\prod }_{i=1}^k{\beta }_2)$$

(5)

where β₂ is the parameter to control the decay factor of the EMA for second moment estimation v.

As a result, the iteration formula of the Adam SPGD algorithm can be expressed as Equation (6).

$$u^k=u^{k-1}+\alpha \widehat{m^k}/\sqrt{\widehat{v^k}+\epsilon }$$

(6)

where α is the learning rate and ε is a small constant to avoid a zero denominator.

In this paper, the root mean square radius of images is used as a merit function and defined as Equation (7) [28].

$$J={\sum }_{i=1}^M{\sum }_{j=1}^N\sqrt{{\left(x_{ij}-x_0\right)}^2+{\left(y_{ij}-y_0\right)}^2}I(x_{ij},y_{ij})/{\sum }_{i=1}^M{\sum }_{j=1}^{N}I(x_{ij},y_{ij})$$

(7)

where the image size is (M,N). The intensity of images with coordinate (x,y) is I(x,y). The centroids of images are (x₀,y₀), defined as Equation (8).

$$x_0={\displaystyle \frac{{\sum }_{i=1}^M{\sum }_{j=1}^N{x}_{ij}I(x_{ij},y_{ij})}{{\sum }_{i=1}^M{\sum }_{j=1}^{N}I(x_{ij},y_{ij})}},y_0={\displaystyle \frac{{\sum }_{i=1}^M{\sum }_{j=1}^N{y}_{ij}I(x_{ij},y_{ij})}{{\sum }_{i=1}^M{\sum }_{j=1}^{N}I(x_{ij},y_{ij})}}$$

(8)

For wide fields of view telescopes, images in both on-axis and off-axis fields should be taken into account. As a result, a multi-field wavefront sensorless method is proposed, and the merit function for multi-field images is the weighted average of merit functions corresponding to images in each field of view.

$$\overline{J^k}={\sum }_{i=1}^n{w}_i{J}_i^k/n$$

(9)

where J_i is the merit function of ith field of view, and n is the number of fields used to align telescopes. w_i is the weight of fields.

As Figure 1 shows, the alignment process of the wavefront sensorless method using the Adam SPGD algorithm can be divided into five steps.

(1)

Step 1: Parameter settings. As mentioned regarding the theory, some parameters should be given.

(2)

Step 2: Image acquisition should be carried out. Images in both on-axis and off-axis fields of view should be collected for wide fields of view telescopes, then merit functions should be calculated.

(3)

Step 3: Control variables are perturbed. In this paper, bilateral perturbation is used to improve the stability of the algorithm. Variations of merit functions are computed, according to which, the gradient of merit functions is calculated. Then, the first moment estimation and second moment estimation of the gradient are figured up.

(4)

Step 4: Merit functions of images corresponding to the new positions are calculated. The new positions of the secondary mirror or third mirror can be obtained according to the iterative formula, and images in both on-axis and off-axis fields are acquired. Then, merit functions are computed.

(5)

Step 5: Determine whether the iteration is terminated. The criterion can be iteration numbers or threshold of merit functions. If the results satisfy the criterion, the iteration is terminated, otherwise, the next iteration will be implemented until the results meet the requirements.

3. Simulations

A four-mirror telescope with a 6 m aperture and Φ2° fields of view is used to verify our method. It is composed of a primary mirror (PM), secondary mirror (SM), third mirror (TM), and fourth mirror (FM). The F number is 2.5. The optical system with light corresponding to different fields of view is shown as Figure 2.

To realize the large aperture and wide fields of view, four aspherical mirrors are used. As mentioned above, multi-field alignment is carried out. Five fields of view are adopted, including an on-axis field (0°,0°) and four off-axis fields (0°,1°), (0°,−1°), (1°,0°), (−1°,0°). Images and wavefronts corresponding to the five fields of view under the designed condition are given in Figure 3. Merit functions J and root mean square (RMS) values of wavefronts are also shown in the figure. The sizes of images are set as 200 × 200 pixels.

As we can see from Figure 3, the image in the on-axis fields of view is nearly diffraction-limited with an RMS of wavefront of 0.0173λ, where λ is set as 0.5 μm. However, images in off-axis fields of view carry aberrations, including coma, astigmatism, and spherical aberrations. Ten misalignments are simulated according to the tolerance allocation, and three of them are shown in this paper as examples. The primary mirror is a reference. Three misalignments are shown in

Table 1. Three misalignments corresponding to different mirrors.

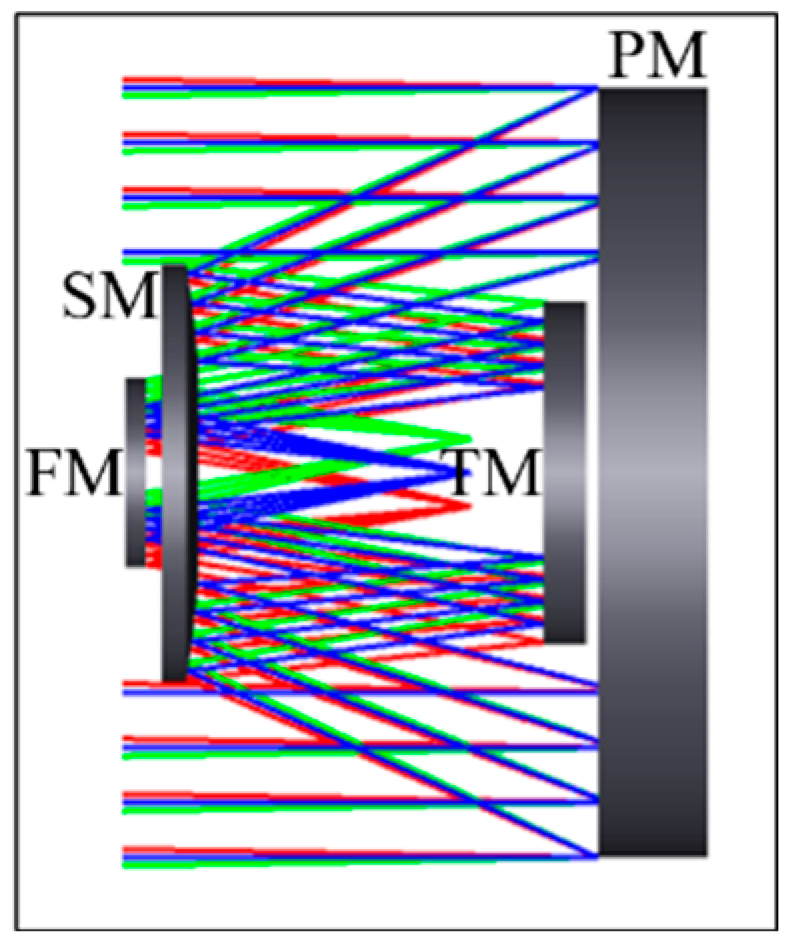
Misalignments	Mirrors	dx/mm	dy/mm	dz/mm	tx/°	ty/°
1	SM	0.1	−0.1	0.01	−0.0028	−0.0028
	TM	0.05	0.1	−0.008	0.0014	0.0022
	FM	0.08	0.01	−0.01	0.0026	−0.0018
2	SM	0.1	−0.1	0.01	−0.0028	−0.0028
	TM	0.05	−0.05	0.005	−0.0014	−0.0014
	FM	0.1	−0.1	0.01	−0.0028	−0.0028
3	SM	0.1	0.07	0.007	0.0008	0.0012
	TM	−0.03	0.1	−0.01	−0.0019	0.0021
	FM	−0.06	−0.09	0.01	0.0020	0.0017

.

Misaligned images corresponding to the three misalignments are shown in Figure 4. Misalignments of mirrors are expressed as aberrations of images, which decrease the image quality and resolution. Therefore, the misalignments have to be compensated.

3.1. Results of Secondary Mirror Alignment

Firstly, all the misalignments are compensated by the positions of the secondary mirror. The wavefront sensorless method based on far-field images using the Adam SPGD algorithm is employed to align the SM. Merit function J used in this paper is the root mean square radius of spots. The corrected images are shown as Figure 5. Merit functions of images acquired in different conditions are listed in

Table 2. Comparison of merit functions.

Conditions	Fields of View
	(0°,0°)	(0°,1°)	(0°,−1°)	(1°,0°)	(−1°,0°)	$\overline{\mathit{J}}$
Misalignment 1	0.2809	0.3326	0.3261	0.3352	0.3045	0.3159
Misalignment 2	0.4184	0.4114	0.4199	0.4241	0.4098	0.4167
Misalignment 3	0.1820	0.2434	0.1809	0.1933	0.2013	0.2002
Correction 1	0.0505	0.1346	0.1402	0.1287	0.1323	0.1173
Correction 2	0.0496	0.1345	0.1345	0.1279	0.1323	0.1158
Correction 3	0.0472	0.1401	0.1568	0.1266	0.1231	0.1188
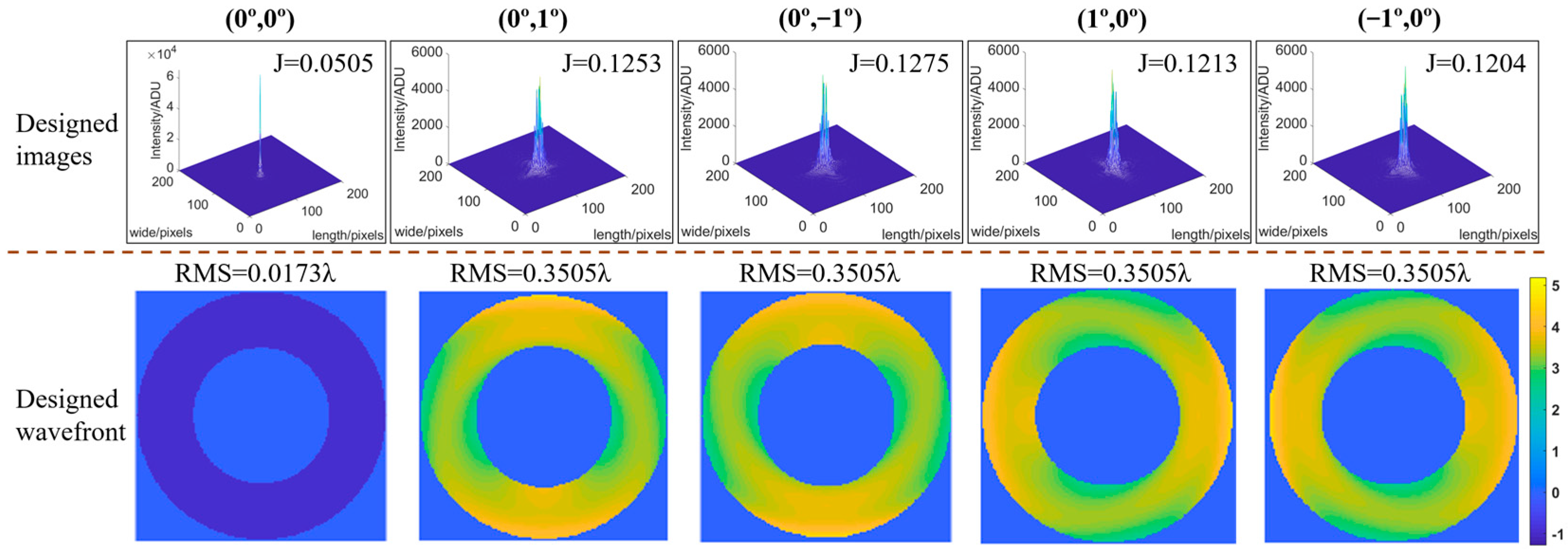
Designed images	0.0505	0.1253	0.1275	0.1213	0.1204	0.1090

, and weighted averages of merit functions are calculated. In this paper, images in each field of view have equal weight.

As we can see from Figure 5, the images after alignment which are called corrected images have a concentrated intensity distribution compared with misaligned images. But the energy distributions of corrected images do not perfectly correspond to the designed ones. Table 2 provides merit functions of misaligned images and corrected images corresponding to each misalignment. The weighted average merit functions $\overline{J}$ of corrected images are equal to 0.1173 for misalignment 1, 0.1158 for misalignment 2, and 0.1188 for misalignment 3, improving greatly compared with misaligned merit functions. But the average merit function is slightly larger than the designed ones, indicating that there are still small aberrations which are not completely corrected. To verify the precision of alignment, residual wavefront errors between corrected wavefronts and designed wavefronts are calculated and shown in Figure 6. The RMS of residual wavefront errors is computed.

As shown in Figure 6, the RMS of residual wavefront errors in the on-axis field of view is smaller than λ/30, which means the aberrations in the on-axis field are well corrected. However, the RMS of residual wavefront errors in the edge fields of view is smaller than λ/4, indicating that most of the aberrations are compensated, but there are still residual aberrations.

3.2. Results of Secondary Mirror and Third Mirror Alignment

To achieve a high resolution and better image quality, both the secondary mirror and third mirror are aligned using the method proposed in this paper. As shown in Figure 7, the corrected images have almost the same energy distributions as designed images, indicating that aberrations in both on-axis and off-axis fields of view are well compensated.

Table 3. Comparison of merit functions after alignment of the secondary mirror and third mirror.

Conditions	Fields of View
	(0°,0°)	(0°,1°)	(0°,−1°)	(1°,0°)	(−1°,0°)	$\overline{\mathit{J}}$
Correction 1	0.0528	0.1263	0.1262	0.1210	0.1222	0.1097
Correction 2	0.0512	0.1287	0.1270	0.1189	0.1250	0.1102
Correction 3	0.0529	0.1260	0.1290	0.1218	0.1217	0.1103
Designed images	0.0505	0.1253	0.1275	0.1213	0.1204	0.1090

shows the comparison of merit functions after alignment of the secondary mirror and third mirror. The average merit functions after alignment are consistent with the designed results. Residual wavefront errors between corrected wavefronts and designed wavefronts are calculated and shown in Figure 8. The RMS of residual wavefront errors is also estimated.

As we can see from Figure 8, the worst RMS of residual wavefront errors corresponding to different fields of view is smaller than 0.1λ, indicating that aberrations are well corrected. The average RMSs of residual wavefront errors obtained in the condition of secondary mirror alignment and both secondary mirror and third mirror alignment are compared in Figure 9.

As shown in Figure 9, the average RMS of residual wavefront errors for misalignment 1 after alignment of the secondary mirror is 0.1714λ, 0.1554λ for misalignment 2, and 0.1652λ for misalignment 3. However, the average RMS for misalignment 1 after alignment of the secondary mirror and third mirror is 0.0405λ, improving by 76.4% compared with the results of secondary mirror alignment. For misalignment 2, the average RMS after alignment of the secondary mirror and third mirror is 0.0704λ, improving by 54.7% compared with the results of secondary mirror alignment. For misalignment 3, the result after alignment of the secondary mirror and third mirror is 0.0488λ, improving by 70.5%. The results show that after alignment of the secondary mirror and third mirror, the average RMS of residual wavefront errors is less than λ/14, indicating that the system meets the designed requirements. The results also indicate that more than one mirror should be used to compensate aberrations for telescopes with large apertures and wide fields of view that have a high and strict requirement for image quality and resolution. Otherwise, stricter tolerances should be proposed.

4. Conclusions

To align telescopes with wide fields of view and large apertures, a multi-field wavefront sensorless method using the Adam SPGD algorithm is proposed. Simulations are carried out using a four-mirror telescope with a 6 m aperture and Φ2° fields of view. Three sets of misalignments are shown as examples in this paper. Aberrations introduced by misalignments of mirrors are compensated with positions of the secondary mirror and the third mirror. Results show that there are still small residual aberrations if only the secondary mirror is aligned with merit functions of corrected images slightly larger than the designed ones and an average RMS of residual wavefront errors smaller than λ/5. As a result, positions of the third mirror are introduced to compensate aberrations. The results show that energy distributions of corrected images are almost same as those of the designed images after alignment, and the average merit functions are consistent with the designed ones. Furthermore, the average RMS of residual wavefront errors is smaller than λ/14, indicating that aberrations are well corrected.

In conclusion, our method can align telescopes effectively and accurately with a concise system using the far-field detector without adding other measurement devices. This method has a simple principle without wavefront reconstructions. It has a broad prospect in the field of telescope alignment.