Research on Support Structure of Rectangular Cryogenic Infrared Lens with Large Aperture

Abstract

This paper presents the design and optimization of a composite flexible support structure aimed at addressing the challenges associated with maintaining the positional accuracy and surface integrity of large-aperture cryogenic infrared lenses with long focal lengths. The primary objective of the structure is to maintain precise lens alignment while preserving the surface shape under operational conditions. The design complexities and underlying principles of the flexible support structure are systematically explored. A mechanical model of the flexible support structure was derived based on its structural characteristics, and the equilibrium equation was established to ensure the lens meets thermal deformation requirements in various directions. Optimization of key design parameters was conducted for a lens operating at 200 K, measuring 304 mm × 230 mm. The gravitational deformation of the optimized lens exhibited a root mean square (RMS) surface accuracy of 7.72 nm in the X direction, 7.08 nm in the Y direction, and 9.60 nm in the Z direction for lens surface 1. For lens surface 2, RMS values were 8.62 nm in the X direction, 8.41 nm in the Y direction, and 9.64 nm in the Z direction. At 200 K and lower temperatures, the RMS values of lens surfaces 1 and 2 were 2.41 nm and 2.74 nm, respectively, with a first-order mode frequency of 143.37 Hz.

1. Introduction

Infrared detection technology, a critical component of space detection systems, finds applications in many fields, including astronomical observation and military target acquisition [1,2,3,4]. To enhance the resolution of space infrared optical systems, large-aperture optical components such as those employed in the American KH-12, GEO-5, and James Webb Space Telescope (JWST) are frequently adopted [5,6,7]. These systems operate in low-temperature environments to reduce background thermal radiation from the opto-mechanical structure, leading to improved detection sensitivity and overall performance [8,9,10,11]. However, the significant temperature differential between the assembly temperature of the optical element and its support structure and the operating environment temperature poses significant challenges in the design of the opto-mechanical structure [12,13].

In recent years, numerous scholars from within China and abroad have investigated lens support mechanisms. Kvamme proposed a flexibly bending support structure for lithium fluoride lenses used in the James Webb Telescope (JWST) [14]. Ge Huanyu, et al. adopted a dual-material support structure designed to compensate for thermal deformation by aligning the cryogenic thermal expansion coefficients of lenses with their thermal deformation, significantly enhancing the force and thermal performance of cryogenic lenses [15]. Zhao Lei, et al. proposed a multi-point uniform support structure with an overall radial flexibility for a 160 mm lens, evenly distributing the gravitational load across each support block through axial flexibility [16]. Zhang Liu, et al. utilized a three-point, six-slit, flexible support structure to mitigate thermal stress between the lens and the lens mount [17]. Wang Xiaodi, et al. proposed a composite flexible support structure for lenses with a 640 mm aperture, employing a design that separated the flexible support from the lens mount to minimize mechanical and thermal influences [18]. These studies primarily focus on support structures for circular lenses.

However, with the increasing weight and volume of space infrared cameras, the design of ultra-lightweight cameras has become a crucial consideration. One effective strategy for achieving large-aperture optics is to reduce the weight of optical components by eliminating excess material. By removing excess material, circular lenses become elongated, making the study of rectangular lens support technology particularly relevant.

In this study, a novel composite flexible support structure for rectangular lenses is presented. A comprehensive mechanical model of the flexible support structure is developed, accounting for thermal deformations of the lens in multiple directions. Equilibrium equations are then established to ensure structural integrity. Subsequently, the flexible support components are optimized, and a thorough analysis is conducted to evaluate the module’s modal performance and surface accuracy under both its own weight and temperature variations.

2. Scheme on Support Structure

2.1. Difficulties in Support Structure Design

Designing support structures for rectangular-aperture lenses in space cameras poses significant challenges.

• To prevent obstruction of the lens aperture, support points must be positioned at the periphery of the lens. However, in double convex lenses, the pronounced thickness gradient toward the edges results in increased stress at the edges [19].
• The asymmetry of circular lenses complicates the selection of optimal support locations.
• Its own weight and thermal loading of the lens can also adversely affect its surface accuracy. Ensuring precise surface accuracy under varying operational conditions requires highly sophisticated support structures [20,21].

2.2. General Structure Design

The representative lens used in this study is a concave–convex lens fabricated from silicon (Si). The lens size is 304 mm × 230 mm, and its clear aperture is 290 mm × 220 mm. Excess material was removed to achieve the required optical aperture, resulting in a significant increase in the length of the lens, as illustrated in Figure 1a. This optimization led to a substantial reduction in lens weight, decreasing from 11.78 kg to 7.19 kg, representing a 39% decrease compared to a circular lens. This reduction offers significant advantages for space cameras, where minimizing weight is crucial. The center of mass position is shown in Figure 1a. Lens position deviation and surface shape deviation requirements of the camera are shown in

Table 1. Lens position deviation and surface shape deviation requirements.

Face	Tran_x (μm)	Tran_y (μm)	Rotation_x (″)	Rotation_y (″)	RMS (nm)
Face1	30	30	20	20	18.08
Face2	30	30	20	20	18.08

.

As illustrated in Figure 1b, the lens assembly comprises a lens, mount, clips, and binder plate. A composite flexure system within the frame consists of three primary flexures and three secondary flexures. The primary flexures feature a flexible structure with fixed end beams and two sets of flexible structures with cantilever steel frames. The secondary flexures are composed of three sets of cantilever-shaped flexible structures. The lens is secured to the frame by the three primary flexures, while the outer edge of the lens is bonded to the three secondary flexures using a structural adhesive. The lens is assembled on the ground in the X direction.

By considering the lens axis as the z-axis and the plane perpendicular to the optical axis as the xy-plane, the structure depicted in Figure 1b can be simplified into the model shown in Figure 2. In this simplified model, a set of flexible structures with fixed end beams and three sets of cantilever-shaped flexible structures can be represented as springs with five degrees of rigidity. Similarly, the two sets of flexible structures with cantilever steel frames can be represented as springs with four degrees of rigidity. The primary function of the support structure is to constrain the six spatial degrees of freedom of the lens, achieving precise positioning and position retention without compromising surface accuracy. As illustrated in Figure 2, the support structure not only effectively positions the lens but also mitigates rigid body displacement in the direction of gravity, enhancing the overall dynamic performance.

The flexible support structure depicted in Figure 2 offers several advantages for rectangular-aperture lenses:

• The flexible nature of the support structure provides damping, mitigating the impact of shock, vibration, and thermal stress on the lens, thereby preventing excessive internal stresses [22,23,24].
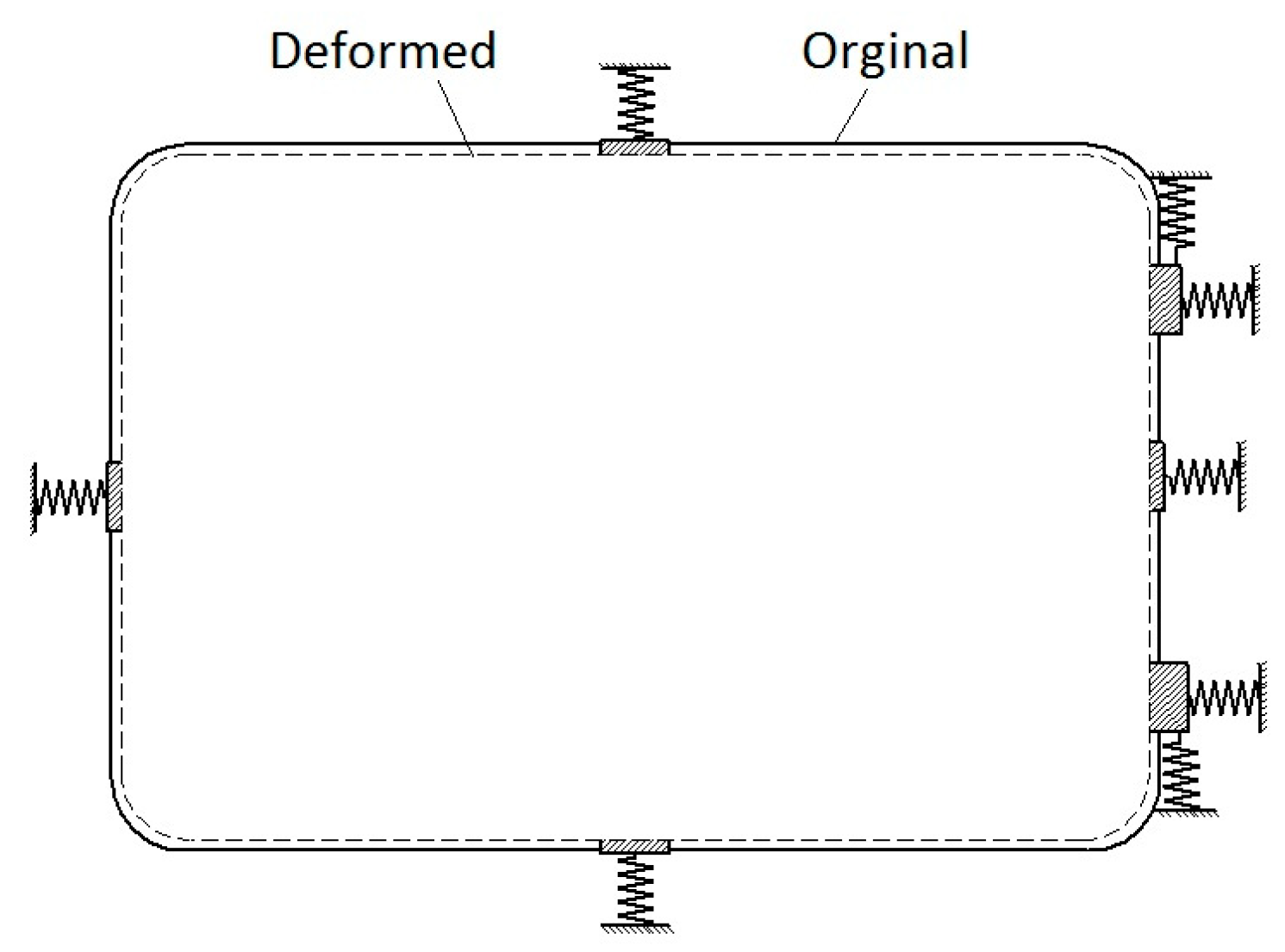
• As depicted in Figure 3, the radial flexibility of the individual flexures allows the support structure to accommodate inconsistent thermal deformations between the frame and the lens, effectively reducing thermal stress and maintaining the radial position of the lens.
• The flexible support structure can compensate for any deformations that may occur within the frame itself [25,26].

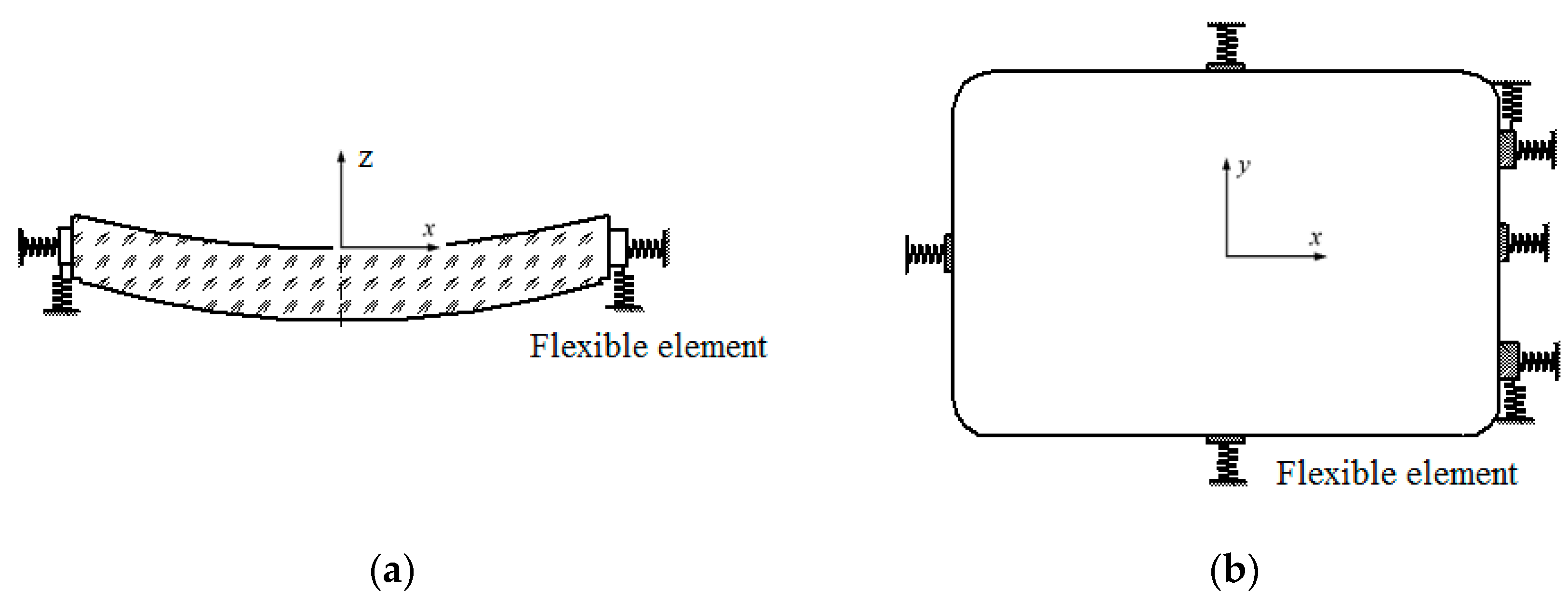
3. Mechanical Model of the Flexible Support Structure

The composite support structure illustrated in Figure 1b is comprised of three distinct types of flexible support structures. To facilitate the rational design of each individual flexible support structure, a comprehensive analysis of its mechanical model is essential. This analysis will enable the determination of appropriate structural design parameters.

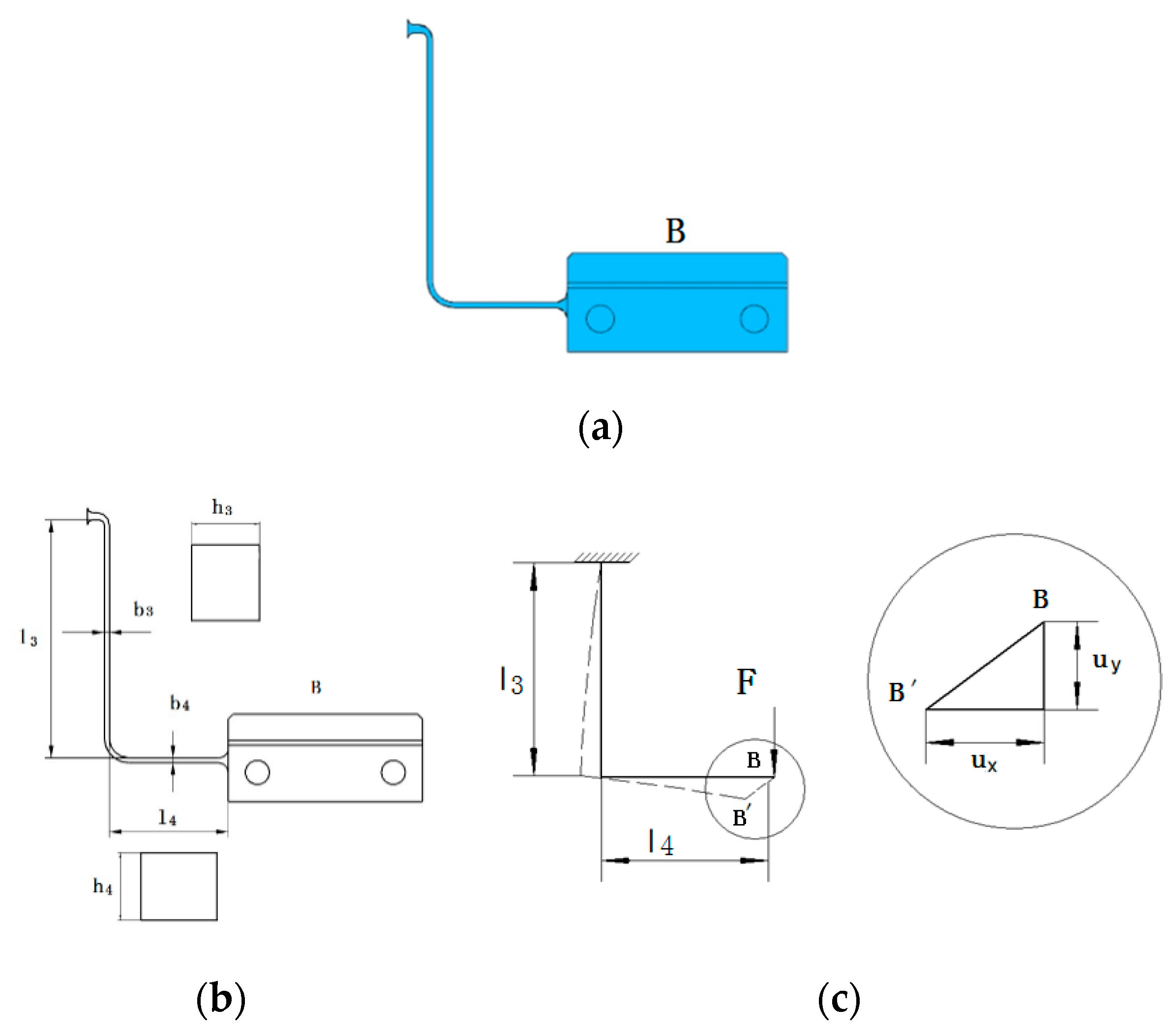
3.1. Flexible Structure in Cantilever Form

As depicted in Figure 4a, the flexibility of the cantilever-shaped flexible structure is attributed to the presence of a flexible chip. Given that both ends of the cantilever-shaped flexible structure are rigidly attached to distinct components, the conventional cantilever beam model is inappropriate for directly analyzing its deformation. A more suitable approach involves employing the half-beam model, which aligns with the deformation characteristics of the structure [27]. Figure 4b,c illustrate the equivalent model and deformation of the cantilever-shaped flexible structure [28].

The deformation along the length direction is very small, so it can be ignored. Additionally, in the half-beam theory [27], Equation (1) is employed to determine the deformation at the movable end of the flexible chip.

$$u_1={\displaystyle \frac{F{l}_1^3}{E{h}_1{b}_1^3}}$$

(1)

where E represents the elastic modulus of the flexible chip, $l_1$ denotes the length of the flexible chip, $h_1$ signifies the width of the flexible chip, and $b_1$ represents the thickness of the flexible chip.

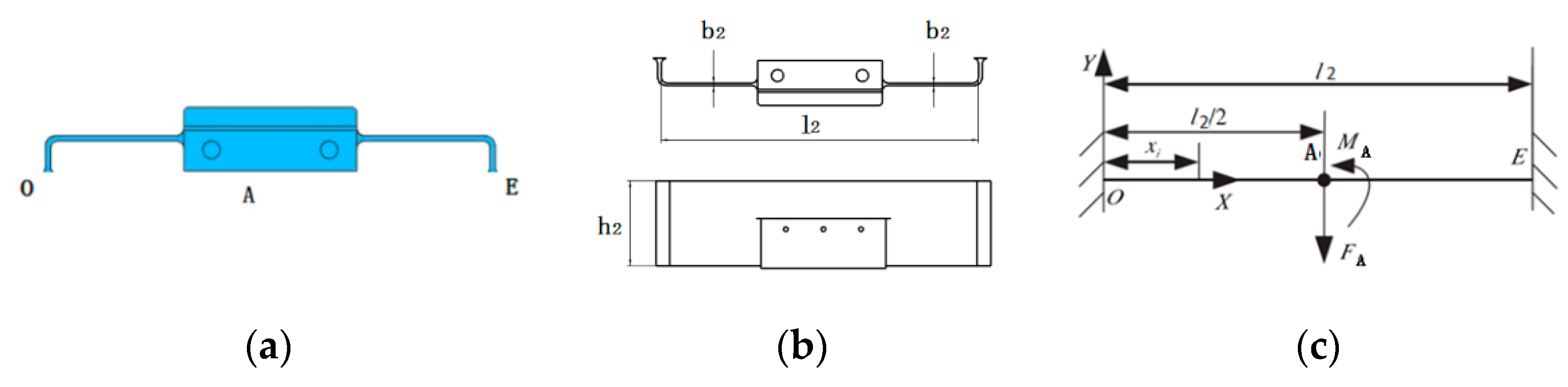
3.2. Flexible Structure with Fixed Beams at Both Ends

As depicted in Figure 5a, the flexibility of the structure with fixed beams is attributed to a flexible chip with fixed ends. The equivalent model for this structure, illustrated in Figure 5b, can be simplified into an indeterminate beam exhibiting both lateral and radial rigidity, as shown in Figure 5c [19]. In this simplified model, points O and E represent the fixed ends, while point A denotes the midpoint. The radial deformation $u_A$ of point A can be expressed as follows:

$$u_A={{\displaystyle \int }}_{l_2} {\displaystyle \frac{M\left(x\right)}{E_{2}I}}·{\displaystyle \frac{\partial M\left(x\right)}{\partial F_D}}{d}_x={\displaystyle \frac{F_A}{E_{2I}}}{{\displaystyle \int }}_0^{{\displaystyle \frac{l_2}{2}}}\left({\displaystyle \frac{x}{2}}-{\displaystyle \frac{l_2}{8}}\right)d_x+{\displaystyle \frac{F_A}{E_{2I}}}{{\displaystyle \int }}_0^{{\displaystyle \frac{l_2}{2}}}\left({\displaystyle \frac{3l_2}{8}}-{\displaystyle \frac{x}{2}}\right)d_x={\displaystyle \frac{F_A{l}_2^3}{192E_{2}I}}={\displaystyle \frac{F_A{l}_2^3}{16E_2{h}_2{b}_2^3}}$$

(2)

where $E_2$ represents the elastic modulus of the flexible chip, $I$ represents moment of inertia, $l_2$ denotes the length of the flexible chip, $h_2$ signifies the width of the flexible chip, $b_2$ represents the thickness of the flexible chip, and F_A symbolizes the force exerted at point A.

3.3. Flexible Structures with Cantilever Steel Frame

As illustrated in Figure 6a, the flexibility of the flexible structure with a cantilever steel frame is attributed to an L-shaped flexible chip. This structure can be simplified into a statically determinate beam as depicted in Figure 6b based on its structural characteristics. The deformation of this simplified beam is shown in Figure 6c. Deformation may occur at point B, with displacements possible in both the radial $u_x$ and transverse $u_y$ directions under the influence of a radial force. This deformation pattern aligns with the thermal deformation experienced by the lens mounting point B. The $u_x$ and $u_y$ deformations at point B can be expressed as follows:

$$u_y=\sum \int {\displaystyle \frac{M_{F}M}{EI}}{d}_x=\sum {\displaystyle \frac{\omega y_c}{EI}}={\displaystyle \frac{F{l}_4\times \frac{1}{2}{l}_3}{E\frac{h_3{b}_3^3}{12}}}={\displaystyle \frac{6F{l}_4{l}_3}{E{h}_3{b}_3^3}}$$

(3)

$$u_x=\sum \int {\displaystyle \frac{M_{F}M}{EI}}{d}_y=\sum {\displaystyle \frac{\omega y_c}{EI}}={\displaystyle \frac{\frac{1}{2}F{l}_4\times \frac{2}{3}{l}_4}{E\frac{h_4{b}_4^3}{12}}}+{\displaystyle \frac{F{l}_4\times \frac{1}{2}{l}_4}{E\frac{h_3{b}_3^3}{12}}}={\displaystyle \frac{4F{l}_4^2}{E{h}_4{b}_4^3}}+{\displaystyle \frac{6F{l}_4^2}{E{h}_3{b}_3^3}}$$

(4)

where $E$ represents the elastic modulus of the flexible chip, $I$ represents moment of inertia, $l_3$ and $l_4$ denote the lengths of the two sections of the flexible chip, $h_3$ and $h_4$ signify the widths of the two sections of flexible chip, $b_3$ and $b_4$ represent the thickness of the two sections of the flexible chip, and $F$ symbolizes the force exerted at point B.

3.4. Model of the Whole Support Structure

The primary function of the lens support structure is to ensure accurate lens positioning and retention (the position accuracy of the lens) within the permissible deviation range under varying lens weight and temperature fluctuations. For cryogenic lenses, temperature variation is the primary factor affecting position accuracy. Consequently, this study primarily focuses on the positional deviations ${\delta }_x$ and ${\delta }_y$ of the lens within the plane perpendicular to the optical axis. Figure 7 illustrates the force and displacement characteristics of each supporting unit. The lens is approximated as a rigid body and the equilibrium equations are established with ${\delta }_x$ and ${\delta }_y$ set to zero.

$${\delta }_x=u_{AX}+u_{BX}+u_{CX}+u_{MX}=0$$

(5)

$${\delta }_y=u_{DY}+u_{EY}+u_{BY}+u_{CY}=0$$

(6)

$$F_D+F_E=0$$

(7)

$$F_A+F_B+F_C+F_M=0$$

(8)

where $F_A$, $F_B$, $F_C$, $F_D$, $F_E$, and $F_M$ represent the force exerted on the lens mounting points. $u_{AX}$, $u_{BX}$, $u_{CX}$, and $u_{MX}$ denote the thermal deformation of the lens mounting points in the x-direction. $u_{BY}$, $u_{CY}$, $u_{DY}$, and $u_{EY}$ denote the thermal deformations of the lens mounting point in the y-direction.

By analyzing Equations (1)–(4), it becomes evident that:

$$u_{DY}=-u_{EY}={\displaystyle \frac{F_D{l}_D^3}{E{h}_D{b}_D^3}}={\displaystyle \frac{B}{2}}\left({\alpha }_{GE}-{\alpha }_{TC}\right)t$$

(9)

$$u_{BY}=-u_{CY}={\displaystyle \frac{6F_B{l}_{B4}{l}_{B3}}{E{h}_{B3}{b}_{B3}^3}}={\displaystyle \frac{B_1}{2}}\left({\alpha }_{GE}-{\alpha }_{TC}\right)t$$

(10)

$$u_{AX}={\displaystyle \frac{F_A{l}_A^3}{16E_A{h}_A{b}_A^3}}$$

(11)

$$u_{MX}={\displaystyle \frac{F_M{l}_M^3}{E{h}_M{b}_M^3}}={\displaystyle \frac{L}{2}}\left({\alpha }_{GE}-{\alpha }_{TC}\right)t$$

(12)

$$u_{BX}=u_{CX}={\displaystyle \frac{4F_B{l}_{B4}^2}{E{h}_{B4}{b}_{B4}^3}}+{\displaystyle \frac{6F{l}_{B4}^2}{E{h}_{B3}{b}_{B3}^3}}={\displaystyle \frac{L}{2}}\left({\alpha }_{GE}-{\alpha }_{TC}\right)t$$

(13)

3.5. Optimization Design of Support Structure

The relationships between the parameters of each flexible link within the lens support structure can be derived from the aforementioned equations. Building upon these relationships, the integrated optimization method is used to optimize the flexible support structure [29,30], and the ultimate goal is to find a set of optimal parameters, so that the surface accuracy RMS_X, RMS_Y, RMS_Z, RMS_T of the lens is better than 18.08 nm, and the mode is higher than 100 Hz. The range of each parameter variable can be defined according to the current processing and manufacturing capacity. The optimization model is mathematically described as Equation (14), where the $T{R}_1$ represents the values in Table 1.

Figure 8 presents the flow of integrated optimizatin. Specifically, the geometric structure model after manual intervention was established by UG, the finite element analysis model was established by Patran, the deformation of lens and support structure was calculated by Nastran, and the rigid body displacement, inclination Angle, and mirror surface profile changes of the lens were calculated by surface analysis software, and nondomination-based genetic algorithm (NSGA-II) was called to search for the global solution set.

$$\left\{\begin{array}{c}\mathrm{F}\mathrm{i}\mathrm{n}\mathrm{d}\left(\mathrm{X}\right)=\left(l_n,h_n,b_n\right) \left(\mathrm{n}=1, 2, 3, 4\right)\\ \mathrm{M}\mathrm{i}\mathrm{n} f_m({\mathrm{RMS}}_{\mathrm{X}},{\mathrm{RMS}}_{\mathrm{Y}},{\mathrm{RMS}}_{\mathrm{Z}},{\mathrm{RMS}}_{\mathrm{T}})\\ \mathrm{Min} T{R}_m\left(T_x,T_y, T_z,{\theta }_x, {\theta }_y, {\theta }_z\right)\\ \mathrm{s}.\mathrm{t}. 1\le b_n\\ 100\le \mathrm{f}\\ {\mathrm{RMS}}_{\mathrm{X}}\le 18.08 \mathrm{n}\mathrm{m}\\ {\mathrm{RMS}}_{\mathrm{Y}}\le 18.08 \mathrm{n}\mathrm{m}\\ {\mathrm{RMS}}_{\mathrm{Z}}\le 18.08 \mathrm{n}\mathrm{m}\\ {\mathrm{RMS}}_{\mathrm{T}}\le 18.08 \mathrm{n}\mathrm{m}\\ T{R}_m<T{R}_1\end{array}\right.$$

(14)

After several iterations, the structural parameters are obtained as shown in

Table 2. Optimization results of flexure hinge support structure.

Supports Position	ln/mm	hn/mm	bn/mm
A (n = 2)	40.0	34.0	2.0
D,E (n = 1)	35.0	30.0	1.0
B,C (n = 3)	35.0	34.0	2.0
B,C (n = 4)	28.0	34.0	2.0
M (n = 1)	40.0	30.0	1.0

. The optimization results meet the design objectives and consider the processing difficulty of the structure.

4. Simulation Analysis of Lens Sub-Assemblies

4.1. Modal Analysis

During transportation and launching, the lens sub-assemblies are subjected to various mechanical factors, including vibration, shock, noise, and other mechanical influences [31,32]. To ensure structural integrity and safety, these sub-assemblies must exhibit sufficient rigidity and strength. Modal analysis is conducted to evaluate the dynamic characteristics of the lens sub-assemblies. The material properties of the sub-assemblies are depicted in

Table 3. Material parameters.

Materials	Density ρ (g/cm3)	Elastic Modulus E (GPa)	Poisson’s Ratio	Thermal Expansion Coefficient α (10−6/°C)
Si	2.33	13.1	0.26	4.15
TC4	4.44	10.9	0.34	9.1

and the first three mode shapes and frequencies are depicted in

Table 4. Modal analysis results of lens sub-assembly.

Order	Frequency/Hz	Mode Shapes
1	143.37	Move along Z-axis
2	189.69	Move along Y-axis
3	200.42	Move along X-axis

and Figure 9.

4.2. Surface Shape and Rigid Body Displacement Analysis

Considering the external connection point of the lens sub-assemblies as the constrained boundary, the changes in surface shape and rigid body displacement of the lens under the influence of its own weight are illustrated in

Table 5. Surface shape and rigid body displacements of the lens under its own weight.

Load Case	Face	Tran_x (μm)	Tran_y (μm)	Rotation_x (″)	Rotation_y (″)	Rotation_z (″)	PV (nm)	RMS (nm)
Grav_Y	Face1	0.57	6.5	1.52	−1.08	0.23	29.34	7.08
	Face2	0.57	6.4	1.52	−1.07	0.39	30.52	8.41
Grav_X	Face1	7.01	−0.028	−1.12	1.05	−0.001	32.46	7.72
	Face2	7.02	−0.28	−1.11	1.06	0.29	36.56	8.62
Grav_Z	Face1	0.76	−0.43	−0.07	0.27	−0.11	40.03	9.60
	Face2	0.57	−0.35	0.1	−0.07	0.23	40.95	9.64

and Figure 10 and Figure 11. We can see from the figure that the gravitational deformation of the lens top—lens surface 2—is an astigmatis. But it is far less than the required value of optical design, so it is also a desirable result. Similarly, the changes in surface shape and rigid body displacement resulting from temperature loading are depicted in

Table 6. Surface shape and rigid body displacements of the lens sub-assemblies under temperature load.

Load Case	Face	Tran_x (μm)	Tran_y (μm)	Rotation_x (″)	Rotation_y (″)	Rotation_z (″)	PV (nm)	RMS (nm)
200k	Face1	0.3	2.6	−1.31	0.62	0.77	12.47	2.41
	Face2	−0.1	1.7	−2.11	1.05	1.41	12.96	2.74

and Figure 12. The deformation pattern does not follow the support positions. This is because the maximum deformation is very small, and this correspondence is not obvious. As shown in Figure 13, the asymmetric pattern can be reproduced by changing the size of the finite element.

5. Discussion

The results show that the composite flexible support structure explored in this paper not only guarantees the surface shape accuracy and position accuracy of the lens, but also has a high fundamental frequency of the component. The cantilever steel frame flexible element solves the problem that the support structure has bidirectional flexibility in the radial direction of the lens (X0Y plane). The mechanical model of flexible support structure and thermal deformation equilibrium equation can guide the design and optimization of support structure.

The prior studies focused on the support mode of circular aperture lenses. Kvamme proposed a flexibly bending support structure for lithium fluoride lenses [8]. Ge Huanyu, et al. adopted a dual-material support structure designed to compensate for thermal deformation by aligning the cryogenic thermal expansion coefficients of lenses with their thermal deformation [9]. Wang Xiaodi, et al. proposed a composite flexible support structure for lenses with a 640 mm aperture, employing a design that separated the flexible support [12]. Consistent with the prior studies, our study on the support structure of rectangular aperture lenses can realize the lightweight design of a lens, which is very beneficial to reducing the weight and volume of space infrared cameras.

This paper demonstrated the capability of the lens support scheme and theoretical analysis process for the design of a large aperture strip lens support structure, which can be one of the effective measures for the lightweight design of space cameras. The results of a lens with a size of 304 mm × 230 mm show that the weight is reduced by 39% compared with the circular diameter, the maximum deformation (RMS) of the lens under its own weight is 9.64 nm, the maximum deformation (RMS) at low temperature of 200 k is 2.74 nm, and the first mode is 143.37 Hz.

Research on the support structure of rectangular aperture lenses belongs to the forefront of the industry. In the future, the global optimization of flexible structure size and the combination of flexible structures can be explored, along with the alignment of the lens and the flexible support structure, and the centering alignment between multiple rectangular cryogenic lens components.