Research on Resource Allocation Algorithm for Non-Orthogonal Multiple Access Visible Light Communication

Abstract

In order to satisfy the large-scale access of visible light communication (VLC) users, as well as the demand for user request rate, the resource allocation problem of visible light communication with drone-assisted non-orthogonal multiple access (NOMA) technique is investigated. An efficient scheme for joint optimization of power allocation and access point (AP) location is proposed. According to the state of user channel information, a user pairing strategy with uniform channel gain difference for any number of users is designed, and an objective function of maximizing the average user data rate with constraints is constructed. For this non-convex NP-hard problem, the optimization problem with constraints is transformed into an optimization problem without constraints by introducing the idea of a penalty function and then solved by the Harris Hawk Optimization (HHO) algorithm based on the nonlinear energy convergence factor, and ultimately, the optimal user power allocation factor, as well as the location of the AP, are found. The simulation results show that the scheme in this paper can improve the average user data rate better compared to other classical schemes. The system performance of the HHO algorithm is improved by about 20.31% compared to the Particle Swarm Optimization (PSO) algorithm. The HHO algorithm based on the nonlinear energy convergence factor improves the convergence speed by about 50% compared to the classical HHO algorithm.

1. Introduction

With the increasing scarcity of spectrum resources, radio frequency (RF) communications can no longer meet the growing bandwidth demands [1,2]. VLC, as a new high-speed data transmission technology that uses a low-power light-emitting diode (LED) as a light source, taking into account both illumination and communication [3], is gradually gaining widespread attention. In addition, VLC has the advantages of high security and no RF radiation [4], and VLC technology is expected to be an alternative to RF communication in many applications [5]. In VLC systems, since LEDs can only support modulation bandwidths of tens of MHz, the traditional orthogonal multiple access scheme can no longer satisfy the status quo of large-scale user access and the scarcity of spectrum resources [6]. NOMA technology allows multiple users to share the same time and frequency resources, which can provide access to large-scale users, offering greater spectral efficiency [7]. The NOMA technique is an emerging multiple access scheme for wireless communication networks, which can be combined with drone-assisted communication to ensure higher spectral efficiency and lower communication delay [8]. In addition, the NOMA technique has also been shown to be suitable for VLC systems, providing high spectral efficiency and system throughput [9,10].

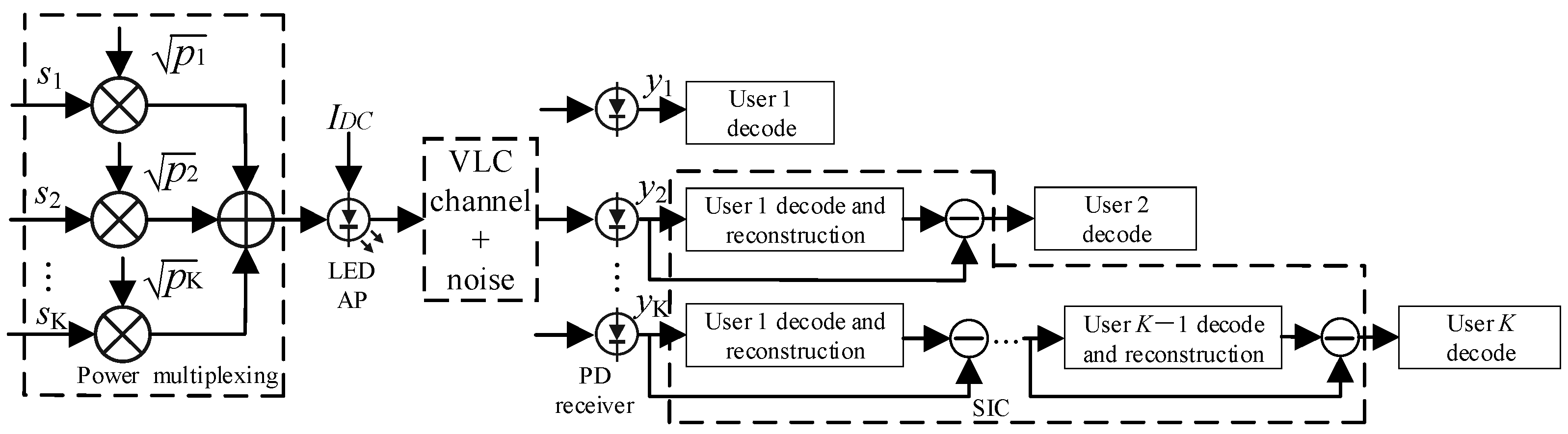
In the NOMA-VLC system, the data of different users are superimposed by different power levels at the transmitter side and decoded at the receiver side to obtain the original user data by the successive interference cancellation (SIC) technique [10]. Power allocation and user grouping are two important issues that affect the transmission of user data. Reference [10] proposed a gain ratio power allocation (GRPA) strategy that takes into account the user channel conditions to ensure efficient and fair power allocation, and this method improves the throughput of the system. Reference [11] investigated the sum log user rate maximization problem for the NOMA-VLC downlink and proposed a low complexity optimal power allocation algorithm, which compared to the traditional orthogonal frequency division multiplexing access (OFDMA) scheme, the proposed scheme has a higher system and rate. Reference [12] used a meta-heuristic optimization algorithm to compute the power allocation coefficients of the users in a NOMA-VLC-based system, which provided a significant improvement in the summation rate under fairness and light intensity constraints. References [10,11,12] adopted different power allocation methods to obtain good system performance gains, but these studies did not take into account the problem of NOMA user grouping. Grouping NOMA users can improve the SIC decoding performance of the receiver and further improve the system performance. Therefore, Reference [13] studied the user grouping and power allocation problems in 3D NOMA-VLC systems, considering the problem of different heights of user locations, and the proposed scheme resulted in an effective improvement of the average user data rate performance of the system. Reference [14] proposed a joint user grouping and power allocation scheme, designed a low-complexity dynamic user grouping algorithm, and derived a closed-form optimal power allocation expression for maximizing energy efficiency using Dinkelbach’s method and Lagrange’s pairwise decomposition method, and the proposed method can effectively improve the energy efficiency of the NOMA-VLC system.

In most existing studies, LED AP is fixed to the ceiling, without considering the quality of service for users at the edge of the communication cell. The study of LED AP position optimization is the key to further improve the performance of the NOMA-VLC system. In recent years, drones have been widely used in communication, monitoring, military, and other fields due to their advantages of lightness, flexibility, strong mobility, and wide coverage [15]. Drone-assisted VLC is gradually emerging, and drones can carry LEDs for flexible communication and dual functions of lighting [16]. At present, studies on drone-assisted VLC mainly focus on the analysis and improvement of the communication network performance [17].

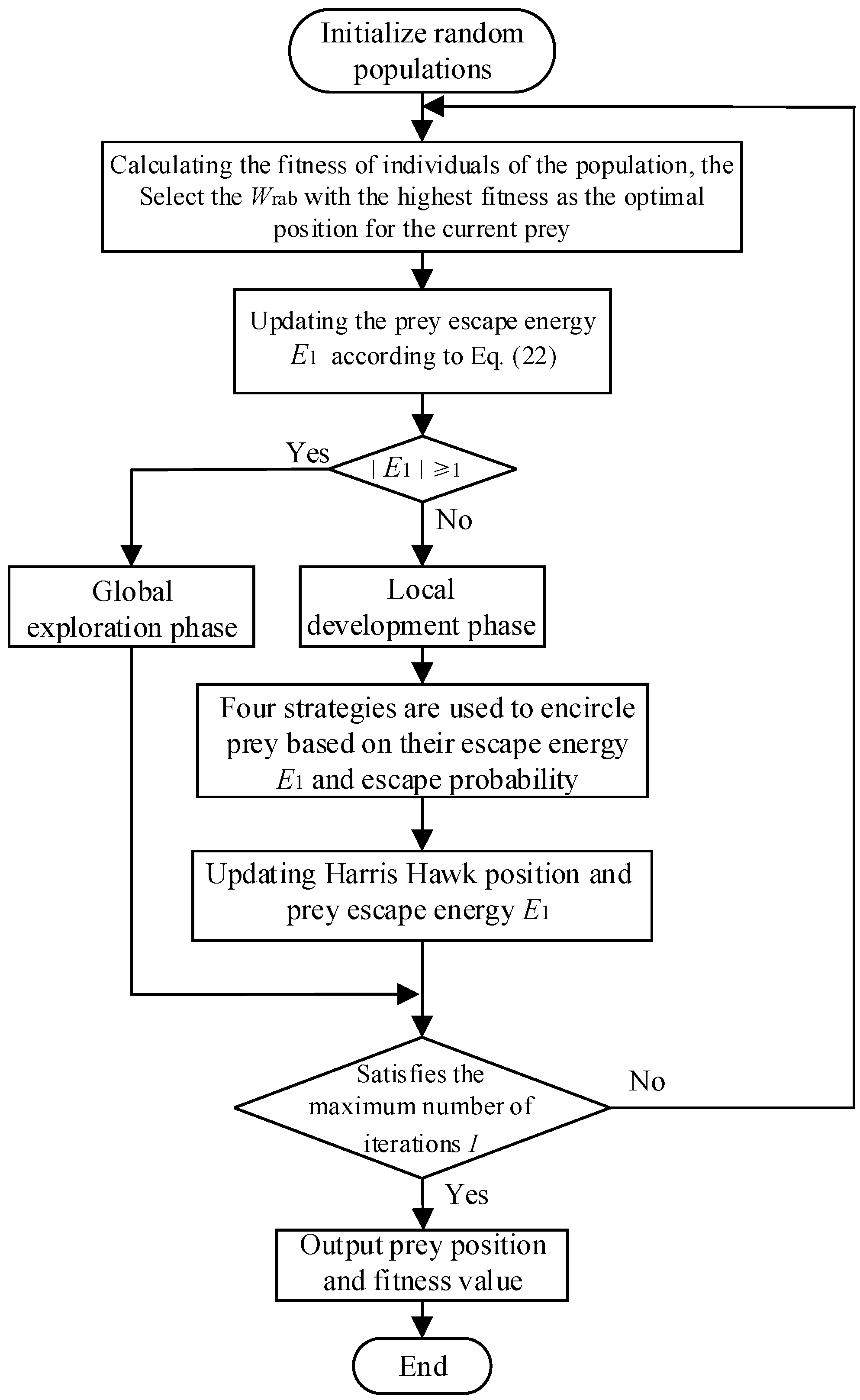
In this paper, the performance of the drone-assisted NOMA-VLC system is investigated. While taking into account the problems of user pairing, power allocation, and AP location, a user pairing strategy with uniform channel gain difference for any number of users is designed, and based on the user pairing, an effective scheme for the joint optimization of the power allocation and the LED AP location based on the NOMA technique is proposed. This scheme constructs a target function with constraints to maximize the average user data rate, introduces the idea of penalty functions, and transforms the optimization problem with constraints into an optimization problem without constraints. Then, the HHO algorithm based on the nonlinear energy convergence factor is used to solve the problem, and the optimal user power allocation factor and the location of the AP are finally obtained. The simulation results show that the proposed NOMA-based VLC resource allocation scheme can better improve the average user data rate performance, as well as satisfy the user’s quality of service, compared to other classical schemes. It is verified that the HHO algorithm based on the nonlinear energy convergence factor has faster convergence speed.

2. System Model and Problem Description

As shown in Figure 1, the NOMA-VLC system is modeled by considering N users randomly distributed in a unit cell with radius r. A drone carries a LED as an AP for communication, and the vertical height of the AP from the ground is L. The bandwidth of the system is $B_{VLC}$, which is divided into T groups, according to the channel gains of the users, and the K users in each group share the spectral resources with a bandwidth of $B=B_{VLC}/T$. Inter-group users adopt the method of orthogonal multiple access, so there is no interference between different groups of users. The users in the group adopt the NOMA method, perform superposition in the power domain, and carry out SIC decoding after receiving optical signals through their respective Photoelectric Detectors (PDs) to obtain the required information. The indices for teams and users are defined as $t\in \{\mathrm{1,2},\dots ,T\}$ and $k\in \{\mathrm{1,2},\dots ,K\}$, respectively.

2.1. VLC Channel Model

According to the characteristics of a LED, LEDs can be regarded as point light sources in the Lambertian radiation model, and the signals received by the user are mainly provided by the line-of-sight link; then, the channel gain of the user can be expressed as [18]

$$h_k=\left\{\begin{array}{c}{\displaystyle \frac{\left(m+1\right)A_p}{2\pi d_k^2}}{\mathrm{c}\mathrm{o}\mathrm{s}}^m\left({\theta }_k\right)T_{f}G\left({\phi }_k\right)cos\left({\phi }_k\right), {\phi }_k\le FOV\\ 0,{\phi }_k>FOV\end{array}\right.$$

(1)

where $m=-\mathrm{l}\mathrm{n}2/\mathrm{l}\mathrm{n}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left({\psi }_{1/2}\right)\right]$ represents the Lambert emission order, where ${\psi }_{1/2}$ is the half-power angle, $A_p$ is the receiving area of the PD, and ${\theta }_k$ and ${\phi }_k$ denote the transmitting angle and receiving angle, respectively, $T_f$ is the optical filter gain, d_k is the distance from the transmitting end to the receiving end, and $G\left({\phi }_k\right)$ is the condenser gain that can be expressed in Equation (2), where n is the refractive index coefficient, and FOV is the receiving field of view (FOV).

$$G\left({\phi }_k\right)=\left\{\begin{array}{c}{\displaystyle \frac{n^2}{{\mathrm{s}\mathrm{i}\mathrm{n}}^2\left(FOV\right)}}{, 0\le \phi }_k\le FOV\\ 0, {\phi }_k>FOV\end{array}\right.$$

(2)

2.2. NOMA Principle

NOMA technology transmits signals from multiple users superimposed on the same subcarrier at the transmitter side by using power multiplexing techniques. In power multiplexing, according to the user’s channel gain, more power is allocated to the user with small channel gain and less power is allocated to the user with large channel gain. At the receiving end, the superimposed signals are demodulated using SIC technology, and the power between users needs to ensure a certain difference to ensure the decoding performance of SIC. The NOMA technology makes the power allocated to the user less but allows the user to occupy a larger spectrum resource, which can increase the user’s data transmission rate and improve the throughput of the system and other system performances.

As shown in Figure 2, it is the realization process of NOMA for K users in the group, and the channel gains of the corresponding users are calculated according to Equation (1). Here, we assume that the channel gains of the users increase sequentially, i.e., ${h_1<h_2<\cdots <h}_K$, and according to the NOMA principle, the power assigned by the user is ${p_1,p_2,\dots ,p}_K$ and ${p_1>p_2>\cdots >p}_K$. The allocated power satisfies ${p_1+p_2+\cdots +p}_K=P$, and P is the carrier transmit power. The specific power size needs to adopt a reasonable power allocation strategy, and the superimposed signal at the transmitter side can be expressed as

$$x^{\prime }=\sqrt{p_1}{s}_1+\sqrt{p_2}{s}_2+\cdots +\sqrt{p_K}{s}_K$$

(3)

where $s_K$ is the modulation symbol of the user. In the VLC system, the nonnegativity of the signal must be ensured, so it is necessary to add a direct current (DC) bias $I_{DC}$ at the transmitting end. At the receiving end, the PD acts as the receiver, and after photoelectric conversion, the received signal of the user can be expressed as

$$\left\{\begin{array}{c}{y}_1=\epsilon h_1{x}^{\prime }+n_1\\ y_2=\epsilon h_2{x}^{\prime }+n_2\\ \dots \\ y_K=\epsilon h_K{x}^{\prime }+n_K\end{array}\right.$$

(4)

where $\epsilon$ is the responsivity of the PD, and $n_K$ is additive white Gaussian noise with a mean of 0 and variance ${\mathsf{\sigma }}^2=N_{0}B$, where $N_0$ is the noise power spectral density, and B is the carrier bandwidth of the signal. Since the NOMA technique is coded by superposition at the transmitter side, the signals received by the user are all superimposed signals $x^{\prime }$ at the transmitter side, so, at the receiver side, it is necessary to separate the signals by using SIC techniques and decode their desired signals individually. The order of decoding is related to the magnitude of the channel gain, and the user with the smallest channel gain is prioritized for demodulation. The dotted line on the right in Figure 2 shows the process of SIC, which mainly utilizes signal decoding and signal reconstruction to gradually eliminate the co-channel interference generated by weak users until the last user.

In order to realize SIC, it is necessary to reasonably allocate the user’s power; then, the power allocation needs to satisfy the following conditions in order to realize efficient SIC [19]. The power constraint required for SIC for K users in a group can be expressed as

$$P_i{\left(\epsilon h_{i+1}\right)}^2-{\left(\epsilon h_{i+1}\right)}^2\sum _{j=i+1}^K{P}_j\ge P_{tol},i=1,2,\dots ,K-1$$

(5)

where $P_{tol}$ denotes the minimum power difference required to distinguish the signal to be decoded from the remaining undecoded message signals. Equation (5) shows that the transmit power of any user must be greater than the sum of the transmit powers of all users with relatively strong channel gains.

2.3. NOMA-VLC Downlink

In the downlink of a NOMA-VLC system, considering a NOMA group with K users, and assuming that the channel gains of the users are sorted in ascending order, the superimposed signal at the transmitter side, after the DC bias $I_{DC}$ is added at the transmitter side to ensure that the transmitted signal is positive, can be represented as

$$x=\sum _{i=1}^K\sqrt{{\alpha }_{i}P}{s}_i+I_{DC}$$

(6)

where $P$ is the carrier transmit power, s_i is the modulation symbol of the user on the carrier, ${\alpha }_i$ is the power allocation factor of the user, and ${\alpha }_1+{\alpha }_2+\cdots {\alpha }_K=1$. After removing the DC component at the receiving end, the signal received by user k is

$$y_k=\epsilon h_k\sum _{i=1}^K\sqrt{{\alpha }_{i}P}{s}_i+n_k$$

(7)

where $n_k$ is the noise of the system with variance ${\mathsf{\sigma }}^2$. Since the channel gains and the allocated power of the users are known, the signal received by user k can be further expressed as

$$y_k=\epsilon h_k\sum _{m=1}^{k-1}\sqrt{{\alpha }_{m}P}{s}_m+\epsilon h_k\sqrt{{\alpha }_{k}P}{s}_k+\epsilon h_k\sum _{n=k+1}^K\sqrt{{\alpha }_{n}P}{s}_n+n_k$$

(8)

The first term on the right side of the equation indicates the signals of weak users, which need to be demodulated preferentially by SIC, and the third term indicates the signals of users with strong channel conditions, which are treated as interference noise. The SIC technique is mainly to gradually eliminate the co-channel interference generated by users with weak channel conditions. Therefore, the last user with the strongest channel condition is interference-free. Then, the signal-to-interference plus noise ratio (SINR) of user k in demodulating its own symbols can be expressed as

$$\mathrm{SIN}{\mathrm{R}}_k=\left\{\begin{array}{c}{\displaystyle \frac{{\alpha }_{k}P(\epsilon h_k{)}^2}{(\epsilon h_k{)}^2{\sum }_{j=k+1}^{K-1}{\alpha }_{j}P+{\sigma }^2}},k\ne K\\ {\displaystyle \frac{{\alpha }_{k}P(\epsilon h_k{)}^2}{{\sigma }^2}},k=K\end{array}\right.$$

(9)

According to the NOMA principle and Shannon’s theory [14], the data transmission rate of user k can be expressed as

$$R_k=B{\log }_2(1+\mathrm{SIN}{\mathrm{R}}_k)$$

(10)

2.4. Description of the Problem

Based on the above analysis, the average user data rate of the NOMA-VLC system can be expressed as

$$R_{\mathrm{avg}}={\displaystyle \frac{1}{N}}\sum _{t=1}^T\sum _{k=1}^K{R}_{t,k}$$

(11)

where N denotes the total number of users, and $R_{t,k}$ is the transmission rate of the kth user in the tth group. In order to further improve the access amount and transmission rate of NOMA-VLC users, the decoding complexity of the receiving end is reduced. In this paper, users are paired, and the improved HHO algorithm is used to solve the optimal power allocation factor and AP position to improve the performance of the system. Considering the case of two users in each user group, the transmission rates of the user with weak channel conditions and the user with strong channel conditions in group t are expressed as, respectively,

$$R_{t,w}=B{\log }_2(1+\mathrm{SIN}{\mathrm{R}}_{t,w})$$

(12)

$$R_{t,s}=B{\log }_2(1+\mathrm{SIN}{\mathrm{R}}_{t,s})$$

(13)

where $\mathrm{SIN}{\mathrm{R}}_{t,w}$ and $\mathrm{SIN}{\mathrm{R}}_{t,s}$ denote the SINR of the user with weak channel conditions and the user with strong channel conditions, respectively:

$$\mathrm{SIN}{\mathrm{R}}_{t,w}={\displaystyle \frac{(1-{\alpha }_{t,s})P(\epsilon h_{t,w}{)}^2}{{\alpha }_{t,s}P(\epsilon h_{t,w}{)}^2+{\sigma }^2}}$$

(14)

$$\mathrm{SIN}{\mathrm{R}}_{t,s}={\displaystyle \frac{{\alpha }_{t,s}P(\epsilon h_{t,s}{)}^2}{{\sigma }^2}}$$

(15)

where ${\alpha }_{t,s}$ is the power allocation factor of the strong user, $h_{t,w}$ is the channel gain of the weak user, and $h_{t,s}$ is the channel gain of the strong user, and since there are only two users in the group, the power allocation factor of the user with the weak channel condition is $1-{\alpha }_{t,s}$. The problem of the average user data rate of the system can be expressed as

$$\begin{array}{cc}& \underset{\left\{x,y,{\alpha }_{t,s}\right\}}{\max }{\displaystyle \frac{1}{N}}{\displaystyle \sum _{t=1}^T}\left(R_{t,w}+R_{t,s}\right)\hfill \\ \hfill s.t.& \mathrm{C}1: {\displaystyle \sum _{t=1}^T}P\le P_{\mathrm{m}\mathrm{a}\mathrm{x}}\hfill \\ & \mathrm{C}2: 0\le {\alpha }_{t,s}\le 0.5\hfill \\ & \mathrm{C}3: R_{t,w}\ge R_{\min }, R_{t,s}\ge R_{\min }\hfill \\ & \mathrm{C}4: (1{-\alpha }_{t,s}\left)P\right(\epsilon h_{t,s}{)}^2-{\alpha }_{t,s}P(\epsilon h_{t,s}{)}^2\ge P_{tol}\hfill \\ & \mathrm{C}5: x^2+y^2\le r^2\hfill \end{array}$$

(16)

where constraint C1 is the sum of the transmit power and does not exceed the LED maximum transmit power $P_{\mathrm{m}\mathrm{a}\mathrm{x}}$. Constraint C2 is the power allocation factor of the strong user and is limited to 0 to 0.5 to ensure the fairness of power allocation. Constraint C3 in $R_{\min }$ is the minimum request rate of the user to ensure the quality of service of the user. Constraint C4 ensures SIC at the receiving end, where $P_{tol}$ denotes the minimum power difference required to distinguish the signal to be decoded from the undecoded message signal. Constraint C5 is where x and y denote the location coordinates of the AP, and r is the cell radius. This constraint ensures that the AP is within the radius of the communication cell.

3. User Pairing and Power Allocation

Since Problem (16) is a non-convex NP-hard problem, it is difficult to obtain an optimal solution. To solve the problem, this paper solves the optimization problem by pairing the users and then using the improved HHO algorithm to solve the problem in order to solve the difficulty of solving the problem and to further improve the transmission rate of the communication users and the throughput of the system.

3.1. User Pairing Algorithm

In the NOMA-VLC system, signals from different users are superimposed at different power levels, and the data are recovered from the received signals at the receiving end by employing a SIC. If the number of superimposed signals at the receiving end is high and the channel gain difference between the superimposed signals is low, this leads to the phenomenon of error code propagation, which degrades the decoding performance of the SIC at the receiving end and reduces the transmitted data rate of the user. Therefore, pairing users with higher channel gain differences together results in higher user transmission data rates. Considering the case where the number of users is odd and even, the user pairing scheme in this paper is shown in Figure 3.

N users are randomly distributed in the communication cell, and their channel gains are computed based on the positions of the APs and the users and are arranged in ascending order, i.e., ${h_1<h_2<\cdots <h}_N$. When the number of users is even, all users are divided into two groups: ${\mathrm{G}}_n=\{{\mathrm{U}}_1,{\mathrm{U}}_2,\dots {,\mathrm{U}}_{N/2}\}$ and ${\mathrm{G}}_f=\{{\mathrm{U}}_{(N/2)+1},{\mathrm{U}}_{(N/2)+2},\dots {,\mathrm{U}}_N\}$, i.e., the first N/2 stronger users are divided into one group, and the remaining weaker users are divided into one group, and then, the users in the two groups are paired two by two in the order of their channel gains. When the number of users is odd, the middle (N + 1)/2th user is divided into a separate group, occupying an orthogonal subcarrier alone, and this user does not carry out the optimization of the next power allocation factor, and the other users are paired according to the pairing scheme for even numbers. This pairing scheme takes into account the channel gain difference between users, which ensures the comparability of the channel gain difference between different paired users and also ensures the fairness of power allocation between users. The flowchart of the user pairing algorithm is shown in Figure 4.

3.2. HHO-Based Power Allocation and AP Location Optimization Algorithm

The HHO algorithm is a meta-heuristic optimization algorithm for stochastic swarm search proposed by Heidari et al. [20] in 2019, which can be used to solve any continuous and unconstrained optimization problem. The HHO algorithm has the advantages of few tuning parameters, simple principles, and fast convergence.

3.2.1. Penalty Function Handling Constraints

Since the HHO algorithm is used to solve unconstrained optimization problems and there are constraints in optimization Problem (16), in this paper, by introducing the idea of penalty function [21], the constrained problems of Problem (16) are merged and the fitness function is defined, which transforms the constrained optimization problem into an unconstrained optimization problem to be solved. Constructing the objective function with penalty function can be expressed as

$$\min f\left(X,\lambda \right)=f_i\left(X\right)+\lambda M\left(X\right)$$

(17)

where $X$ is the optimization parameter, $\lambda$ is the penalty factor, $f_i\left(\mathrm{X}\right)$ is the objective function of the original optimization problem, and $M\left(X\right)$ is the penalty function term. Since the optimization problem in this paper is to maximize the average user’s transmission rate, the optimization objective function in this paper can be constructed as

$$\max f\left(X\right)={\displaystyle \frac{1}{N}}\sum _{t=1}^T(R_{t,w}+R_{t,s})-\lambda M\left(X\right)$$

(18)

For the maximization problem, a common practice is to subtract the penalty term from the objective function, thus transforming the minimization problem into a maximization problem, where the optimization parameters $X=\left\{x,y,{\alpha }_{1,s},{\alpha }_{2,s},\dots ,{\alpha }_{T,s}\right\}$ are the position coordinates of the AP and the power allocation factor, respectively, where the penalty function can be expressed as

$$\begin{array}{cc}\hfill M\left(X\right)& ={\left[\mathrm{m}\mathrm{a}\mathrm{x}\left\{0,{\displaystyle \sum _{t=1}^T}P-P_{max}\right\}\right]}^2+{\displaystyle \sum _{t=1}^T}{\left[\max \left\{0,{\alpha }_{t,s}-0.5\right\}\right]}^2+{\displaystyle \sum _{t=1}^T}{\left[\max \left\{0,-{\alpha }_{t,s}\right\}\right]}^2\hfill \\ & +{\displaystyle \sum _{t=1}^T}{\left[\max \left\{0,P_{tol}-(1-{\alpha }_{t,s})P{\left(\epsilon h_{t,s}\right)}^2+{\alpha }_{t,s}P{\left(\epsilon h_{t,s}\right)}^2\right\}\right]}^2+{\left[\max \left\{0,x^2+y^2-r^2\right\}\right]}^2\hfill \\ & +{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{k=1}^K}{\left[\mathrm{m}\mathrm{a}\mathrm{x}\left\{0,R_{\mathrm{m}\mathrm{i}\mathrm{n}}-R_{t,k}\right\}\right]}^2\hfill \end{array}$$

(19)

where the penalty function $M\left(X\right)$ is composed of constraints, and $\max \left\{·\right\}$ means to take the maximum value in the set, that is to say, when the constraints are satisfied, the penalty function term takes 0, and when the constraints are not satisfied, the penalty function term will be multiplied by a very large penalty factor $\lambda$, so as to “penalty” those solutions that do not satisfy the constraints. Thus, by introducing the penalty function, the constrained optimization problem is transformed into an unconstrained optimization problem, which can be solved using the HHO algorithm.

3.2.2. HHO Algorithm for Nonlinear Energy Convergence Factors

The design of the HHO algorithm is inspired by the cooperative behavior of the Harris Hawk during prey hunting and the hunting style of sudden attacks. Its principles can be summarized in three main phases: the exploration phase, the exploration-to-exploitation transition, and the exploitation phase.

Exploration phase. This phase performs an equal probability global search for prey through two strategies.

Transition from the exploration phase to development phase. The HHO algorithm transforms from exploration to development according to the escape energy E of the prey. During the escape process of the prey, E decreases linearly, and its expression is

$$E=2E_{0}a\left(i\right)$$

(20)

$$a\left(i\right)=1-i/I$$

(21)

where $E_0$ is the initial escape energy of the prey, which is a random number between $(-1,1)$, $a\left(i\right)$ is the linear convergence factor, i is the current number of iterations, and I is the maximum number of iterations, and the algorithm enters into the exploratory phase when $\left|E\right|$ is greater than or equal to 1. Conversely, it enters into the development phase and adopts different update strategies.

Since the HHO algorithm with a linear convergence factor [22] has the drawbacks of low convergence accuracy and being easy to fall into the local optimum, this paper improves the convergence factor by adopting the logarithmic nonlinear convergence factor instead of the original convergence factor in order to strengthen the algorithm’s global searching ability and avoid falling into the local optimum. The new escape energy expression is

$$E_1=2E_0{a}_1\left(i\right)$$

(22)

$$a_1\left(i\right)=1-\lg (1+9i/I)$$

(23)

Shown in Figure 5 are the variation curves of different convergence factors with the number of iterations. It can be seen from the figure that the nonlinear variation of $a_1\left(i\right)$ decreases rapidly in the early stage of the iteration compared to the linear convergence factor, while it slows down gradually in the later stage. This precisely adapts the HHO algorithm to utilize the higher population diversity for rapid exploration in the early stage, while the local exploitation ability needs to be strengthened in the later stage.

Development phase. In this phase, the Harris Hawk adopts four different strategies to encircle the prey based on the prey’s escape energy $E_1$ and escape probability: soft encirclement, hard encirclement, soft encirclement with progressive fast dive, and hard encirclement with progressive fast dive.

In this paper, the upper and lower bounds of the search space are set as the maximum and minimum emission power of the LED and the distribution range of the AP location, the maximum number of iterations I is set to 500, the population size H is set to 30, the fitness function of the algorithm is Equation (18), and the optimization parameters include the positional coordinates of the AP $(x,y)$ and the power allocation factor.

In the optimization process, the location of the users is known and does not change, the channel gain is calculated based on the AP location, and the users are paired according to the user grouping algorithm in this paper. Subsequently, the HHO algorithm is executed to allocate power to the users, and the optimal AP location and power allocation factor are solved to maximize the average user data transfer rate of the system, subject to the satisfaction of various constraints. Figure 6 shows the flowchart of power allocation and AP position optimization based on the improved HHO algorithm, which first initializes the random population and calculates the fitness values of all individuals in the population and the optimal solution of the current iterative optimization problem, i.e., the position of the prey. Then, the escape energy $E_1$ of the prey is calculated according to Equation (22), and the global exploration phase or local development phase is executed according to the escape energy $E_1$ of the prey, and the position of the individual is updated through different phases until the maximum number of iterations of the problem is satisfied, and finally, the optimal fitness value and the position of the prey are outputted, i.e., the optimal solution globally.

3.3. Complexity Analytics

The computational complexity of the algorithm in this paper includes the computation of user pairing and the computation of the HHO algorithm, and the computational complexity of the user pairing algorithm is O(T), while T is the number of user groups. The computational complexity of the HHO algorithm is O(HI(D + M)), where H denotes the size of the population, I denotes the number of iterations, and D denotes the dimension of the optimization problem, and since the optimization parameters in this paper include the positional coordinates of the AP and the power allocation factor, the dimension of the optimization problem in this paper is D = T + 2. M denotes the number of constraints in the penalty function, and M = 5T + 2. Therefore, the total computational complexity of the algorithm in this paper is O(T) + O(HI(6T + 4)).

4. Results and Analysis

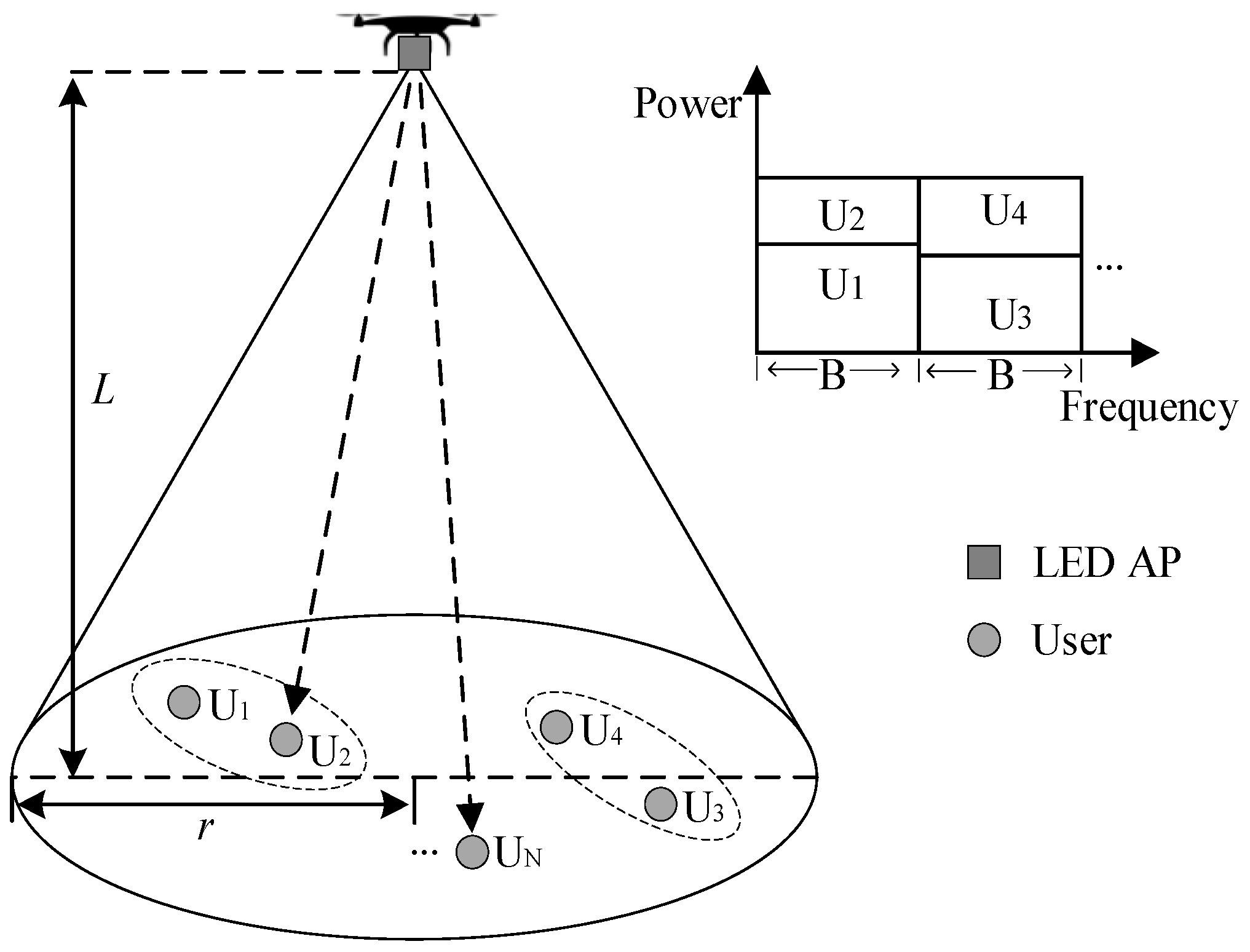
In this paper, the Monte Carlo method is used to perform extensive simulations of the proposed optimization problem to demonstrate the effectiveness of the proposed algorithm, and the system model is shown in Figure 1. In the system, a drone carries a LED as an AP for communication, and the users are randomly distributed in a small area with radius r. The drone can be moved to ensure the quality of service for each VLC communication user. The other system simulation parameters are shown in

Table 1. Simulation parameters.

Parameter	Meaning	Value
$B_{VLC}$	VLC system bandwidth	20 MHz
N	Number of users	16
r	Cell radius	4 m
L	LED AP vertical height	3 m
$P_{\mathrm{m}\mathrm{a}\mathrm{x}}$	LED total emission power	0.1 W
${\psi }_{1/2}$	LED half power angle	60°
FOV	Receiving field of view	50°
$A_p$	PD receiving area	1 cm2
$T_f$	Optical Filter Gain	1
$\epsilon$	PD responsivity	0.53 A/W
$R_{\min }$	Minimum user request rate	5 Mbps
N0	Noise power spectrum density	10−21 A2/Hz

.

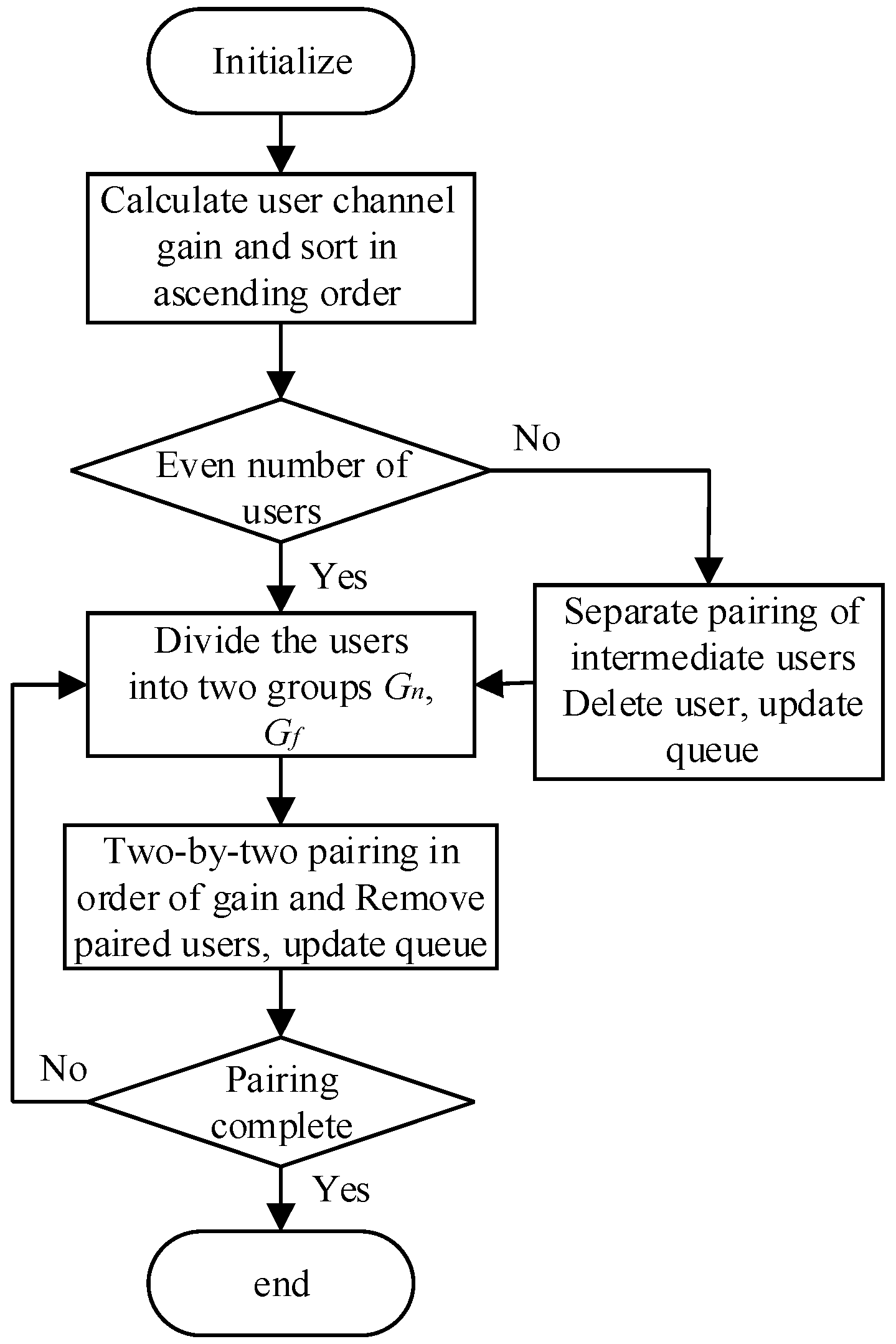
In order to demonstrate the performance of the user pairing (UGDUP) and HHO algorithms proposed in this paper, different pairing algorithms and power allocation algorithms are used as comparative algorithms, such as the Random Users Pairing (RUP) algorithm [1] and the Near-Far Pairing (NFP) algorithm [1], as well as the classical NOMA-based Fixed Power Allocation (FPA) algorithm [23] and GRPA algorithm [10]. Additionally, this paper also includes a comparison of the HHO scheme that does not consider user pairing and a NOMA scheme with a Fixed Access Point (FAP) that allocates power solely through the HHO algorithm, using them as contrasting algorithms. The OFDMA scheme used in the literature [24] is also compared to show the performance advantages of the NOMA scheme.

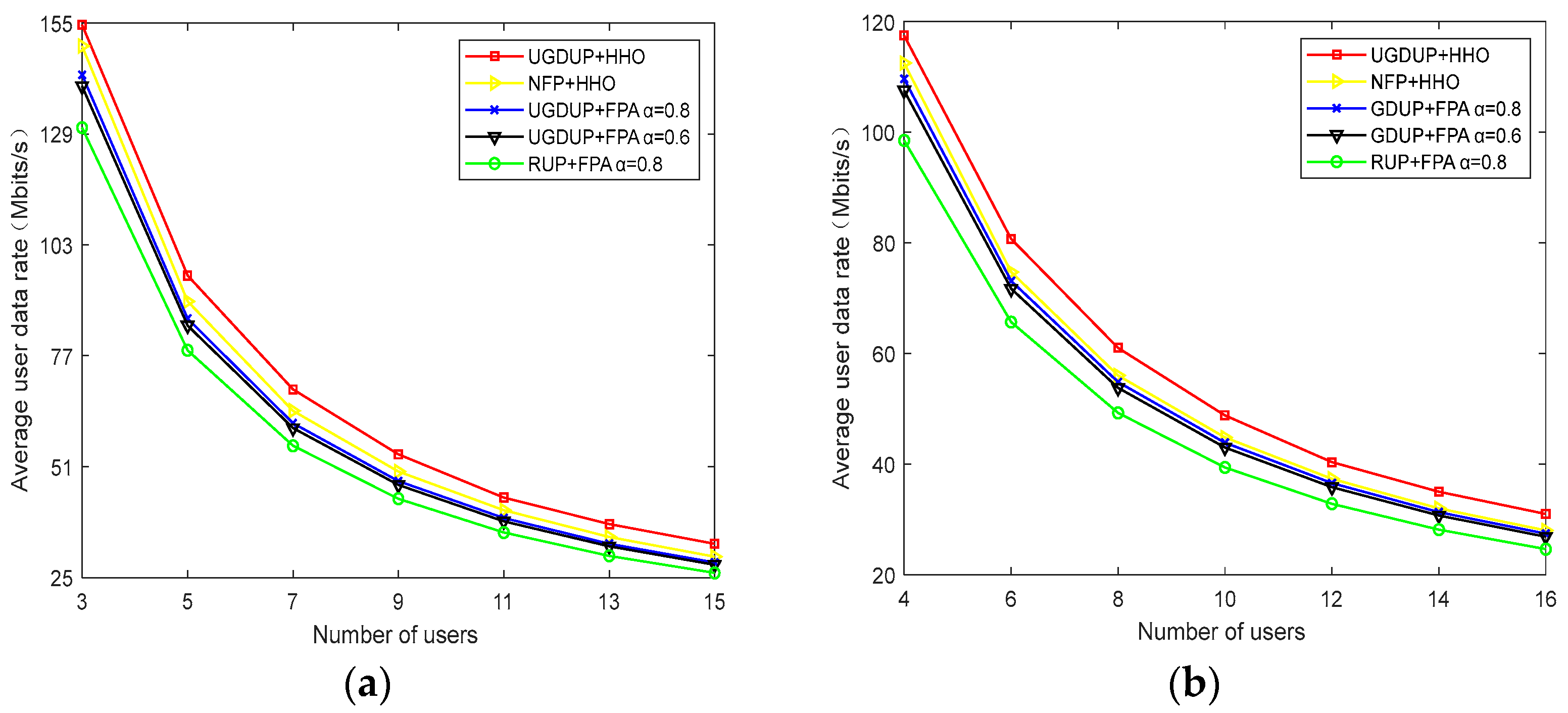
Figure 7 shows the relationship between the average user data rate and the number of users for different user pairing algorithms and power allocation algorithms. It can be found that the average user data rate decreases with the increase in the number of users, no matter whether it is the number of odd or even users. This is due to the fact that, in the case of a small number of users, each user occupies more band resources and allocated power, so there is a better data transmission rate. When the number of users is small, the difference between the user data transmission rates under different algorithms is large, and as the number of number of users becomes more, the performance difference between different algorithms becomes less. Among them, the performance obtained by the UGDUP and HHO algorithms proposed in this paper is better, and the performance obtained by the RUP algorithm and FPA algorithm is the worst. With the same user pairing algorithm, the performance obtained with HHO algorithm is better than the performance obtained with FPA algorithm with power allocation factors $\alpha =0.8$ and $\alpha =0.6$. This is due to the fact that the power allocation to users using the HHO algorithm makes the power allocation factor inconsistent between different user pairs, maximizing the user data rate within each user pair as much as possible based on the user’s request rate. This power allocation method is more flexible. By dynamically adjusting the power allocation factor to find the optimal solution of the problem, i.e., it ensures the fairness of the power allocation and improves the performance gain of the system. When both HHO algorithms are used, the UGDUP algorithm outperforms the performance obtained by the NFP algorithm, due to the fact that the use of the NFP algorithm makes the channel gain difference between different user pairs non-uniform, resulting in a lesser rate gain being obtained by the user pairs with a relatively small channel gain difference. Under the FPA algorithm, both with an power allocation factor $\alpha$ of 0.8, the UGDUP algorithm outperforms the RUP algorithm. This is due to the fact that the RUP algorithm has a random nature of user pairing that does not take into account the channel conditions of the users, which makes the fairness of the power allocation decrease and fails to satisfy the quality of service of the individual users, which leads to a reduction in the data transmission rate obtained by the users.

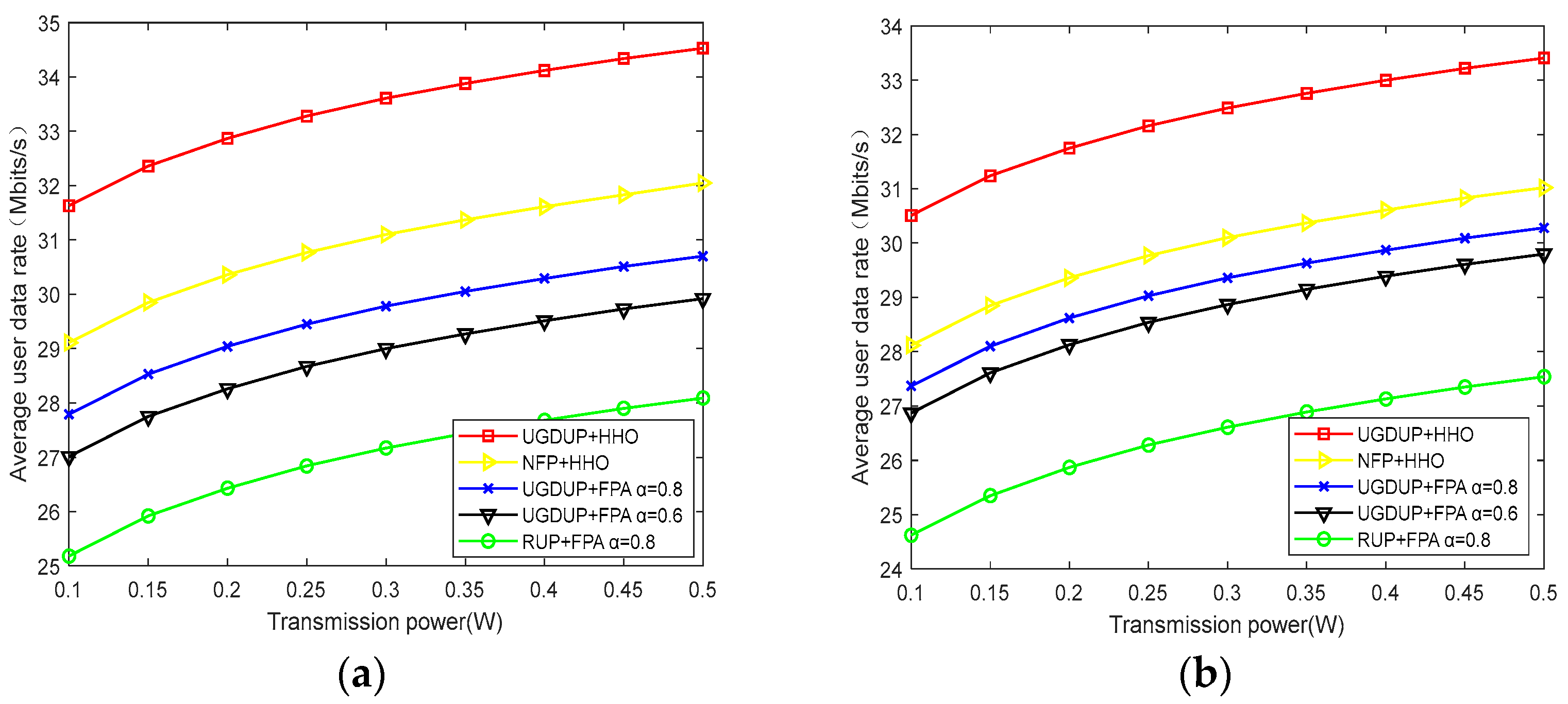
Figure 8 shows the relationship between the average user data rate and transmission power for different user pairing algorithms and power allocation algorithms. It can be seen that, as the transmission power increases, the average user data rate also increases, and the increase gradually becomes slower. This is because the increase in transmission power allows the users to allocate more power to gain a better transmission rate. Among them, the UGDUP and HHO algorithms proposed in this paper have the best performance. 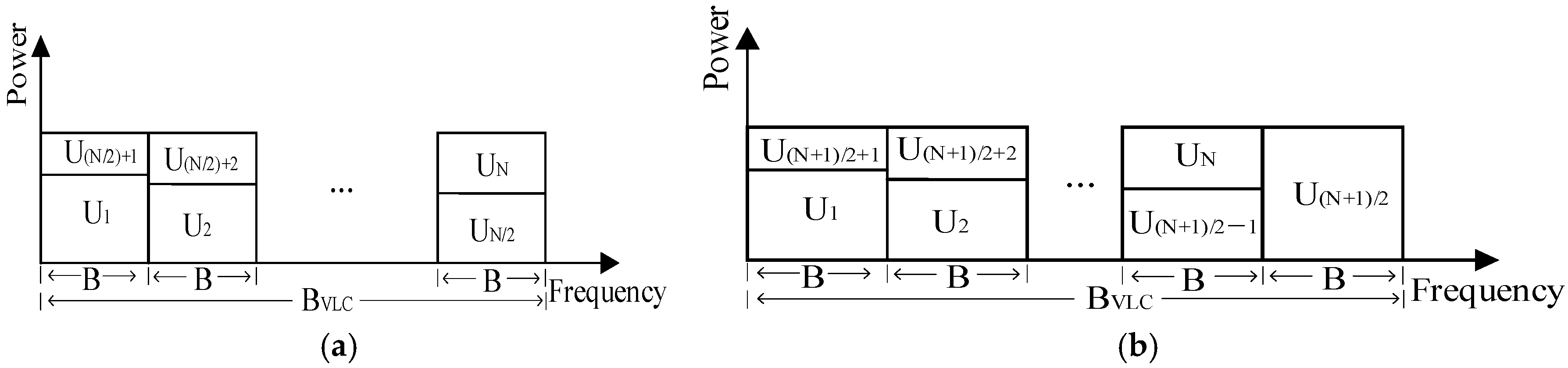When the UGDUP and FPA algorithms are used, the performance obtained when the power allocation factor $\alpha$ is 0.8 is better than that obtained when the power allocation factor $\alpha$ is 0.6. The RUP algorithm and FPA algorithm have the worst performance. It can also be observed from the graph that, under the same algorithm, the performance achieved with 15 users is overall better than that with 16 users. This is because, in the case of an odd number of users, the middle user occupies the same frequency band resources separately from the users in other groups, which allows for a better transmission rate and thus enhances the overall system performance.

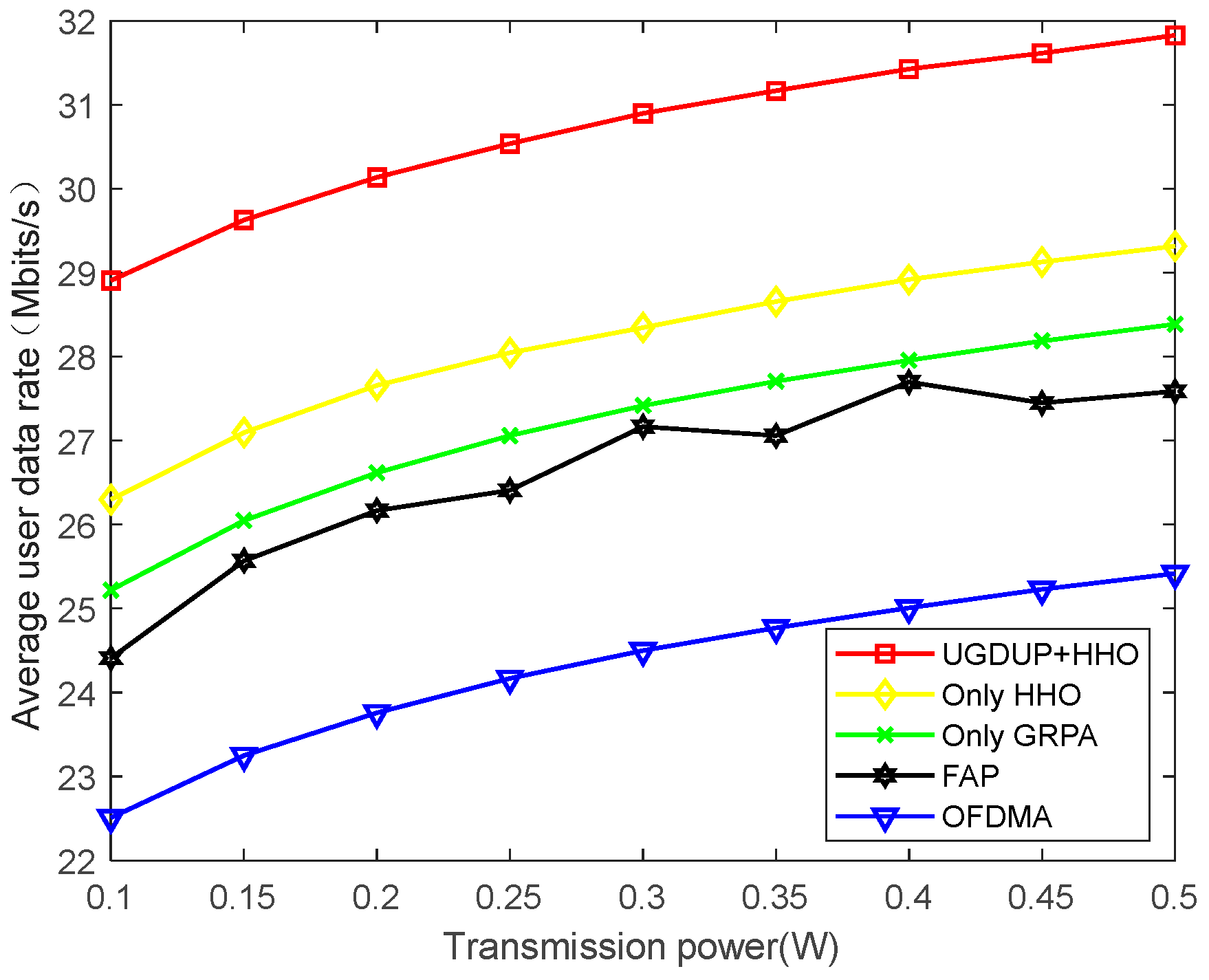
In order to verify the importance of user grouping and the performance of the algorithm proposed in this paper, Figure 9, Figure 10, Figure 11 and Figure 12 show the relationship between different parameters and the average user data rate of the system. Figure 9 shows the relationship between the average user data rate and the transmission power under different algorithms, from which it can be seen that the average user data rate shows an increasing trend as the transmission power increases, and the performance obtained by the four NOMA schemes in the figure is better than that obtained by the OFDMA scheme. It shows that NOMA technology enables multiple users to share spectrum resources and has higher spectrum efficiency compared to the OFDMA scheme, while NOMA users can occupy more spectrum resources than OFDMA users for a certain system bandwidth and number of users, thus obtaining a higher transmission rate. Among the four NOMA schemes, the best performance is obtained using the UGDUP and HHO algorithms of this paper, the second best performance is obtained by the Only HHO algorithm, followed by the Only GRPA algorithm, and the worst performance is obtained by the FAP algorithm. This is due to the fact that all users share the same spectrum resources without considering user grouping, and under the guarantee of SIC decoding performance, according to Equation (9), it can be seen that the weak users are subjected to a greater amount of co-channel interference, which leads to a decrease in the user’s SINR and makes the user’s transmission rate lower. Therefore, in NOMA systems with a large number of users, the scheme proposed in this paper simultaneously considers the issues of user pairing, power allocation, and AP location, resulting in an effective improvement in the system performance. It can also be seen in Figure 9 that the performance obtained by the Only HHO algorithm is better than the performance obtained by the FAP algorithm. This is due to the fact that the FAP algorithm only optimizes the power allocation to the users, and the position of the drone is randomly fixed in the air without taking into account the optimization of the AP position, which does not guarantee the quality of service to all the users, thus making the performance of the average user data rate decrease.

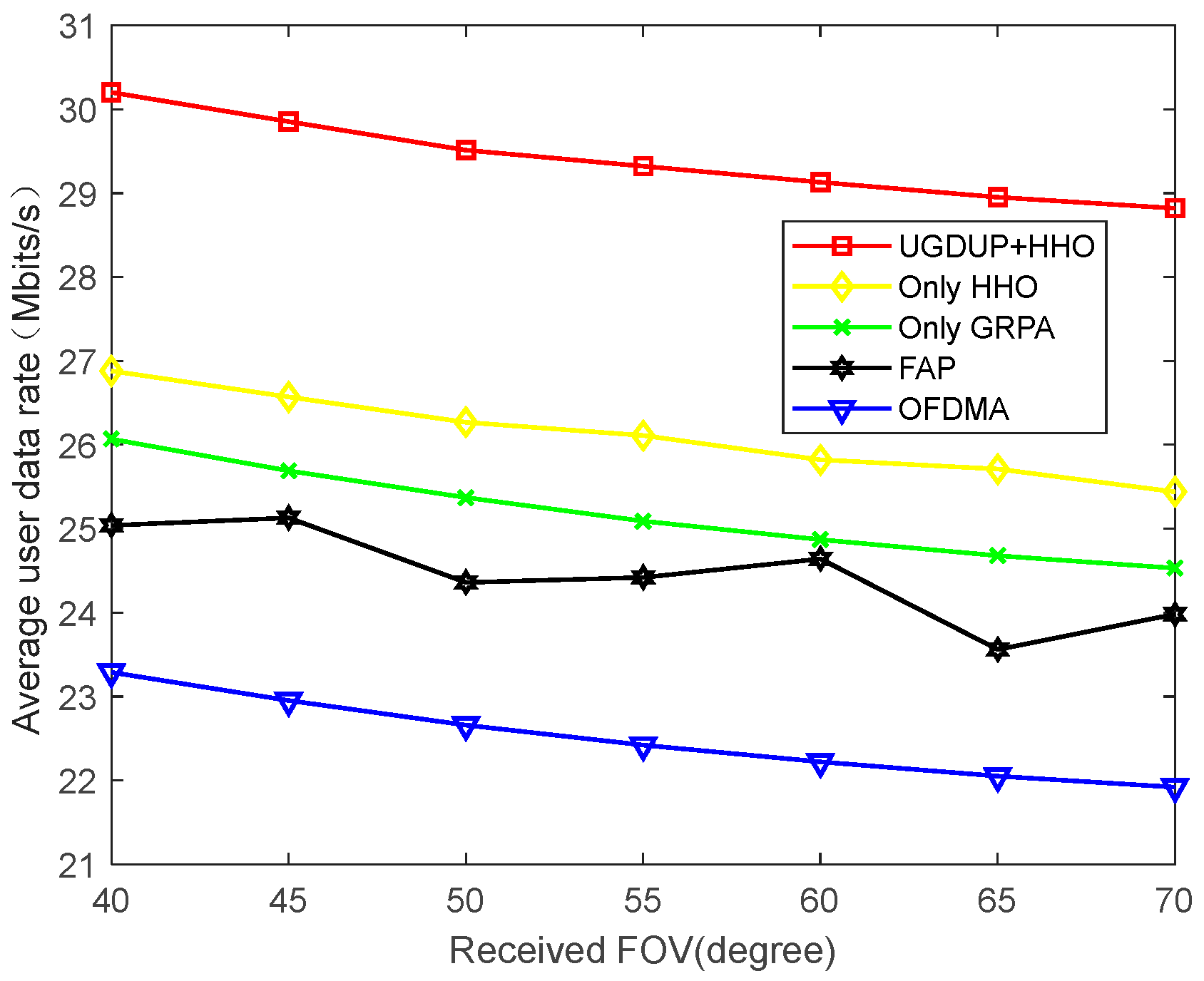
Figure 10 shows the relationship between the user’s received FOV angle and the average user data rate, and it can be seen that, as the user’s received FOV angle increases, the average user data rate exhibits a decreasing trend, which is due to the fact that the increase in the FOV angle makes it impossible for the concentrator to maintain the optimal convergence in all directions, which leads to a decrease in the efficiency of the convergence of the optical signals in some areas, which, in turn, affects the concentrator gain. Equation (2) demonstrates the relationship between the FOV angle and the concentrator gain $G\left({\phi }_k\right)$. The FOV angle is in the range of 0 degrees to 90 degrees, and as the FOV angle of the field of view increases, the concentrator gain decreases, causing the channel gain of the user to decrease, which, in turn, leads to a decrease in the average user data rate performance. The proposed algorithm also takes into account the user pairing situation, AP location, and power allocation factor and shows a better average user transmission rate performance than the other algorithms. Through the above analysis, increasing the user’s field of view angle will have a certain impact on the gain of the condenser, so, in practical applications, detailed system design and testing should be carried out according to the specific needs and scenarios to obtain the best communication performance and effect.

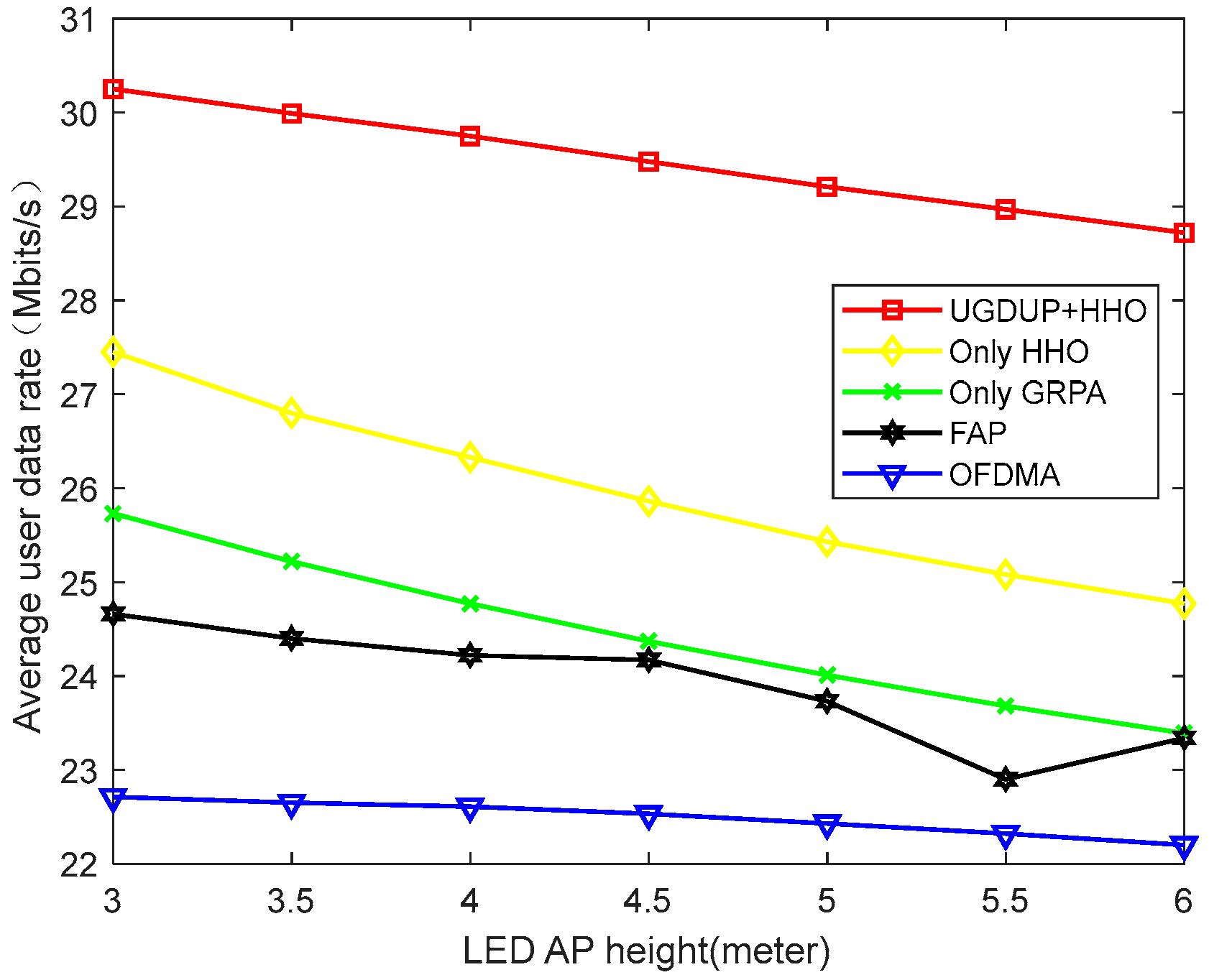
Figure 11 shows the relationship between the AP height and the average user data rate, and it can be seen that, as the AP height increases, the average user data rate shows a decreasing trend, which is due to the fact that the increase in the AP height makes the distance between the user and the AP larger, and the channel gain of the user decreases consequently, leading to a decrease in the transmission rate of the user. The algorithm in this paper takes into account the optimization of the AP location and improves the performance by about 23.17% compared to the FAP algorithm, and the system performance degradation is small as the AP height increases, indicating that user grouping can lead to a higher performance gain. The performance improvement of the Only HHO algorithm without considering the pairing is not obvious, which is because the high AP height makes the channel gain of the users smaller, and the channel gain difference between users also decreases. It is difficult to further improve the data transmission rate of users only through power allocation optimization. Therefore, this paper conducted user pairing according to the channel gain difference between users. Combined with the AP location and power allocation optimization, the data rate performance of the average user is greatly improved.

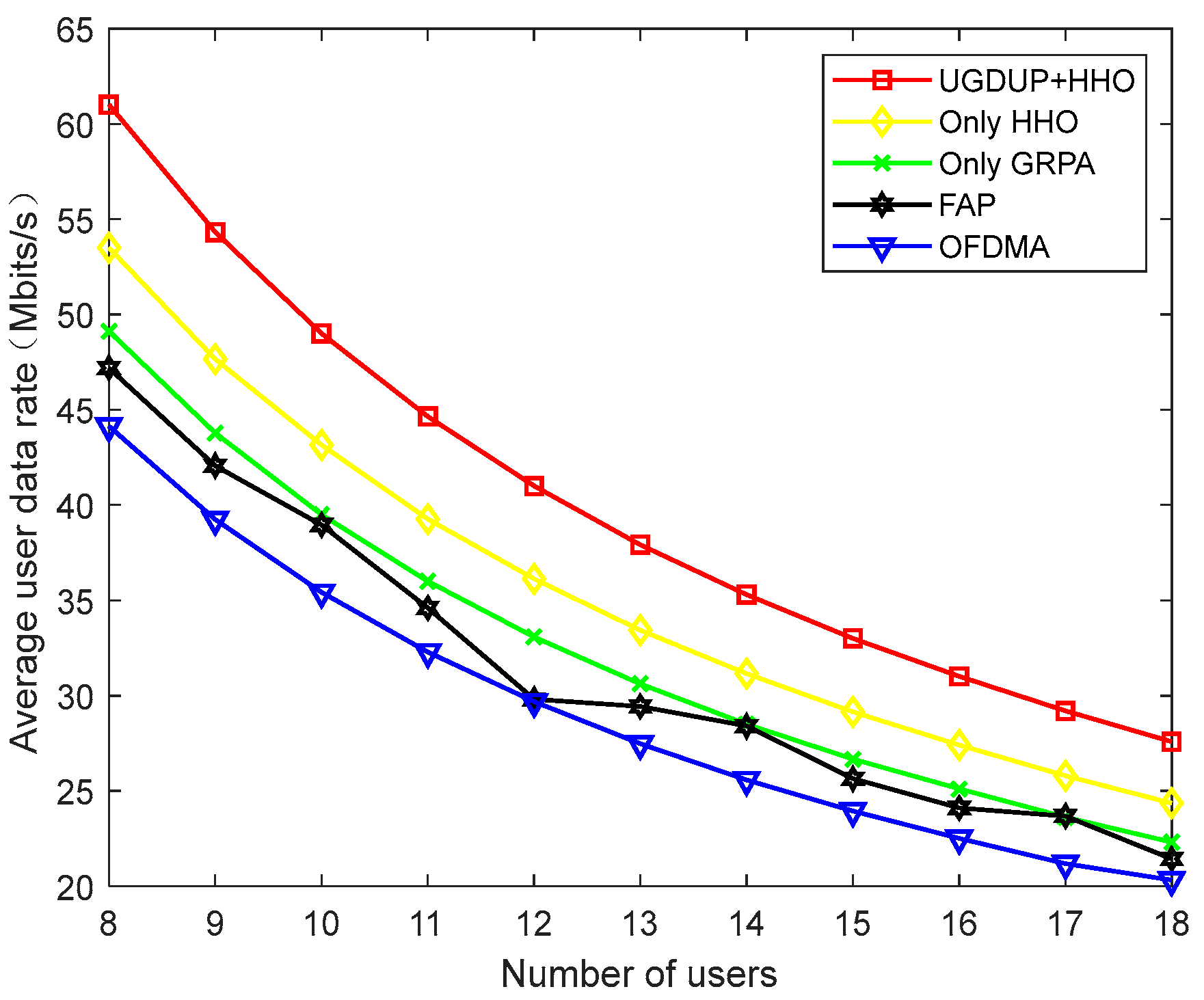
Figure 12 shows the relationship between the number of users and the average user data rate for different algorithms, and it can be seen that an increase in the number of access users leads to a decrease in the average user data rate. This is due to the fact that the spectral resources and transmit power of the system are certain, and an increase in the number of users reduces the data rate. The scheme proposed in this paper takes into account the user pairing problem and reduces the interference between users within the NOMA group, so the performance obtained by the scheme in this paper is better than that obtained by the Only HHO algorithm. The HHO scheme achieves better performance than the GRPA scheme, because the GRPA scheme only considers the fairness of power allocation without considering the overall system performance, while the HHO scheme optimizes the system performance while carrying out power allocation. The FAP algorithm does not take into account the optimization of the AP location, which may lead to obtaining a performance close to that of the OFDMA scheme, while the other three NOMA schemes obtain a performance superior to that of the OFDMA scheme.

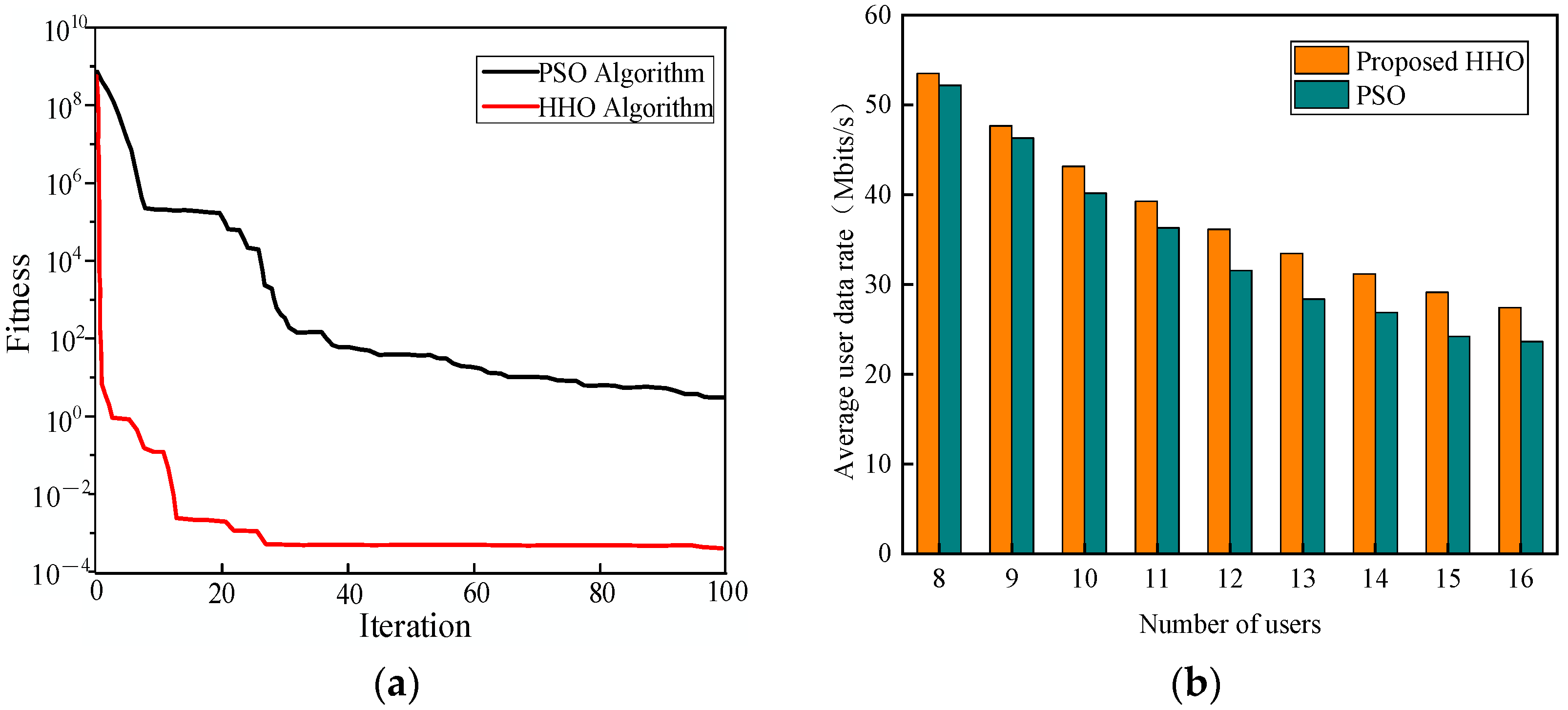
In order to demonstrate the advantages of the HHO algorithm proposed in this paper, Figure 13 shows a comparison between the HHO algorithm and the PSO algorithm [17]. Figure 13a shows the curve of the number of iterations versus the value of the fitness function, which shows that the HHO algorithm has a faster convergence speed and has a stronger ability to find the optimal solution than the PSO algorithm. This is due to the fact that the HHO algorithm has the ability to search globally to a certain extent, while the PSO algorithm is prone to fall into local optimal solutions during the search process. Figure 13b shows the change between the number of users and the average user data rate under the two intelligent optimization algorithms. It can be observed that the performance obtained by the HHO algorithm is superior to that of the PSO algorithm. When the number of users is small, the performance gap between the two algorithms is not significant. However, as the number of users increases, the HHO algorithm demonstrates better system performance. This is because the increasing number of users elevates the complexity of the optimization problem, allowing HHO to exhibit superior global search capability. Nevertheless, this also leads to a reduction in the optimization ability of the PSO algorithm. The performance gap between the HHO algorithm and the PSO algorithm obtained is the largest when the number of users is 15, and the HHO algorithm improves the performance by about 20.31% compared to the PSO algorithm.

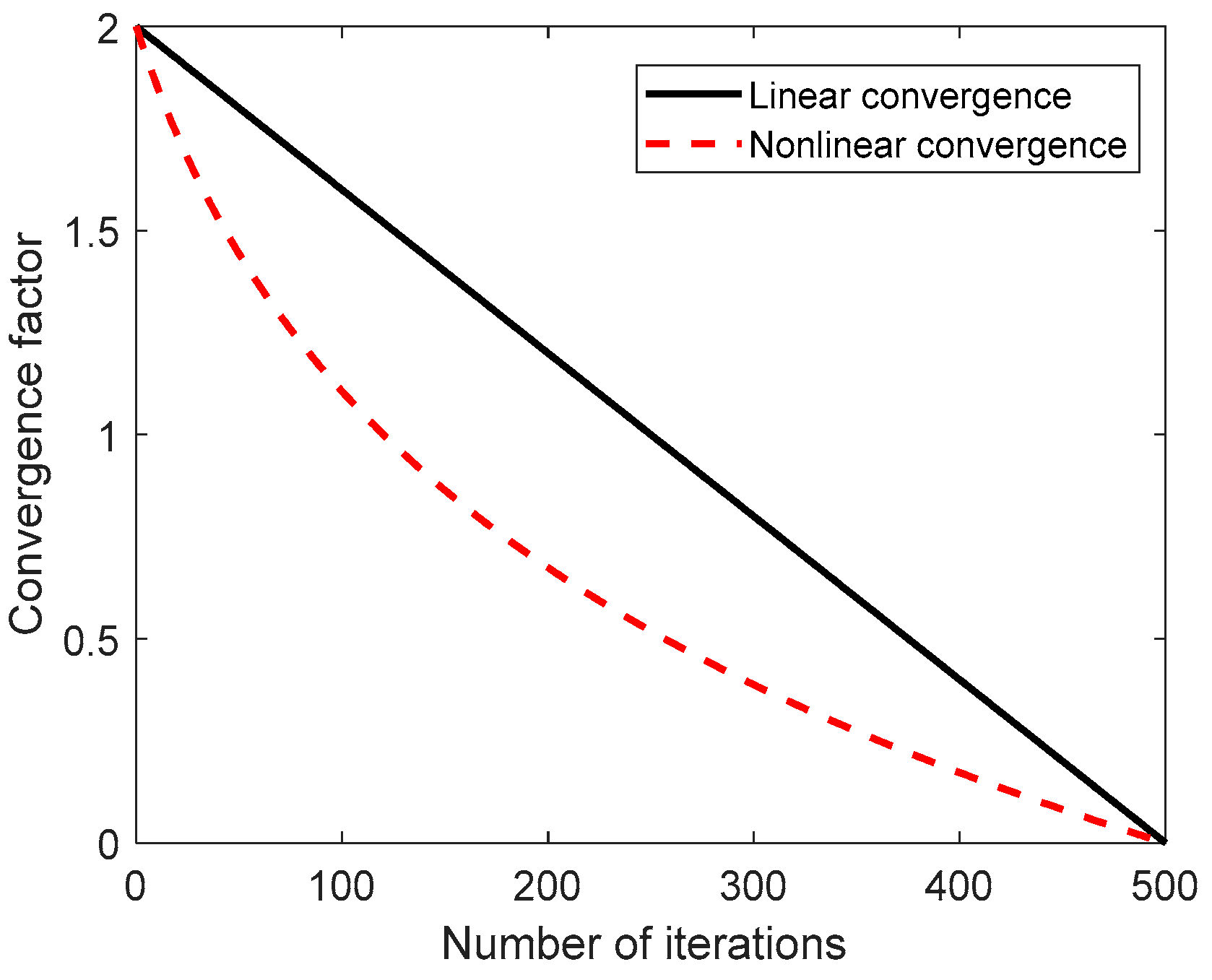
Figure 14 shows the convergence relationship between the number of iterations and the average user data rate for different convergence factors, and it can be seen that the HHO algorithm with nonlinear convergence factor $a_1\left(i\right)$ used in this paper reaches convergence at about 50 iterations, and the HHO algorithm with linear convergence factor $a\left(i\right)$ reaches convergence at about 100 iterations. It shows that the nonlinear convergence factor HHO algorithm adopted in this paper has a faster convergence speed, which, in turn, proves that the parameter tuning scheme proposed in this paper effectively facilitates the smooth transition of the HHO algorithm from the pre-exploration to the post-exploitation development and maintains the equilibrium between the two, which, in turn, accelerates the convergence of the HHO algorithm and improves the solution accuracy.

5. Conclusions

In this paper, we investigate the resource allocation problem of a NOMA-VLC system assisted by drones, taking into account the user pairing, power allocation, and AP location in the system, aiming to improve the average user data transmission rate of the system and to satisfy the user’s service requirements. A user pairing algorithm with uniform channel gain difference for an arbitrary number of users is proposed under the condition that the user channel gains are known, and then, the HHO algorithm based on the nonlinear energy convergence factor is used to solve for the optimal power allocation factor and the location of the AP. The simulation results show that the scheme in this paper can improve the average user data rate better compared to other classical schemes. The performance obtained using the HHO algorithm is improved by about 20.31% over the performance obtained by the PSO algorithm. The HHO algorithm based on the nonlinear energy convergence factor improves the convergence speed by about 50% compared to the classical HHO algorithm.

The research in this paper provides a valuable reference for the development of NOMA-VLC, as well as drone-assisted communication technology, and in a subsequent work, we should consider more advanced adaptive user grouping methods and intelligent optimization algorithms to further improve the performance of the system.