The Design of Highly Reflective All-Dielectric Metasurfaces Based on Diamond Resonators
Abstract
1. Introduction
2. The Principles for Designing the Perfect Reflector
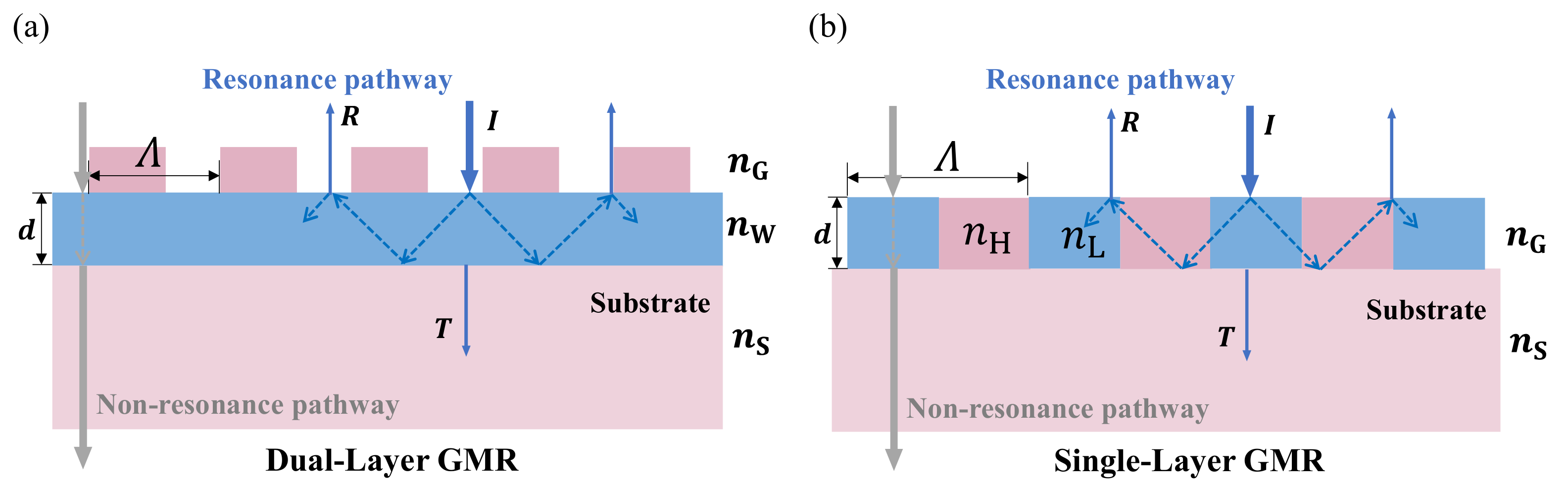
2.1. Guided-Mode Resonance
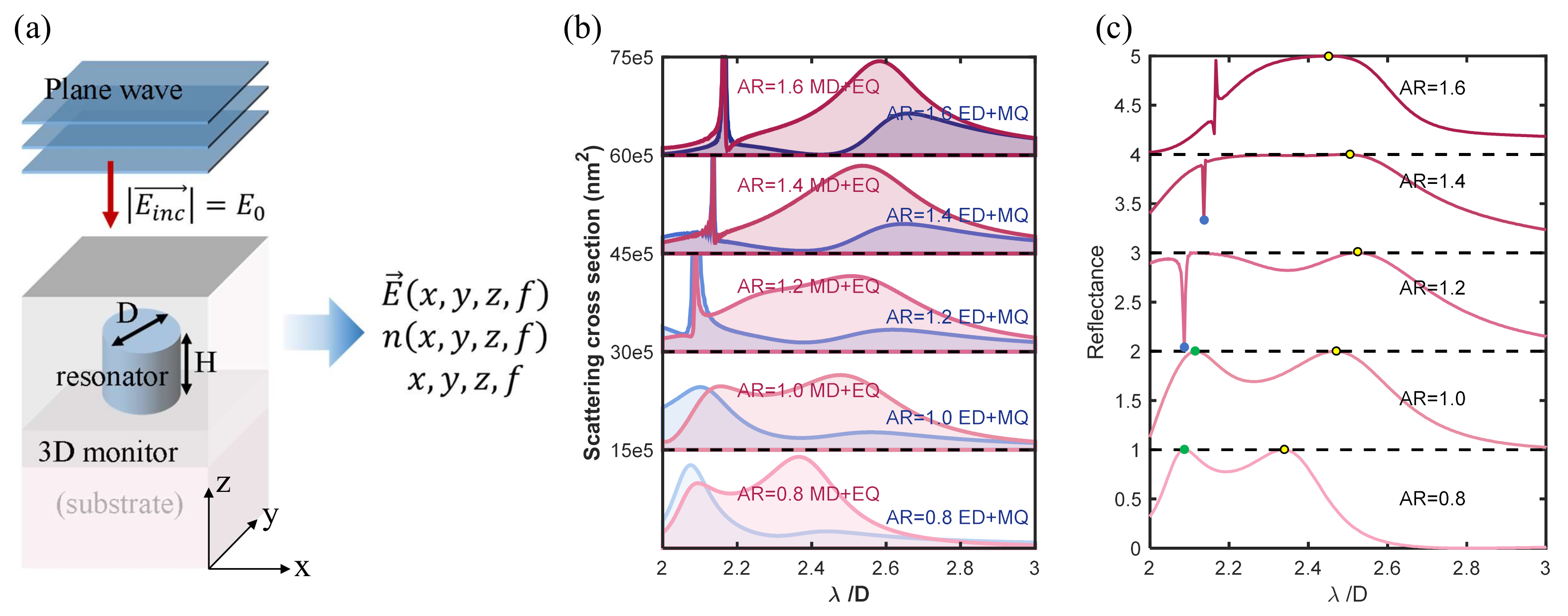
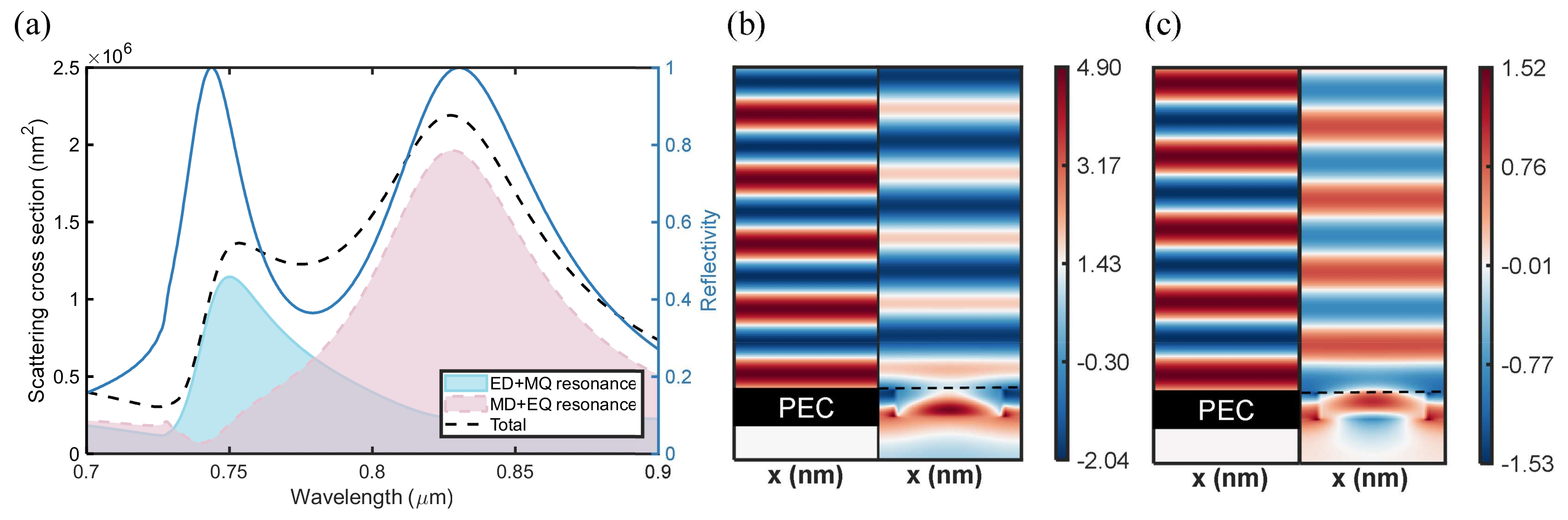
2.2. The Multipole Decomposition
3. Results and Analysis
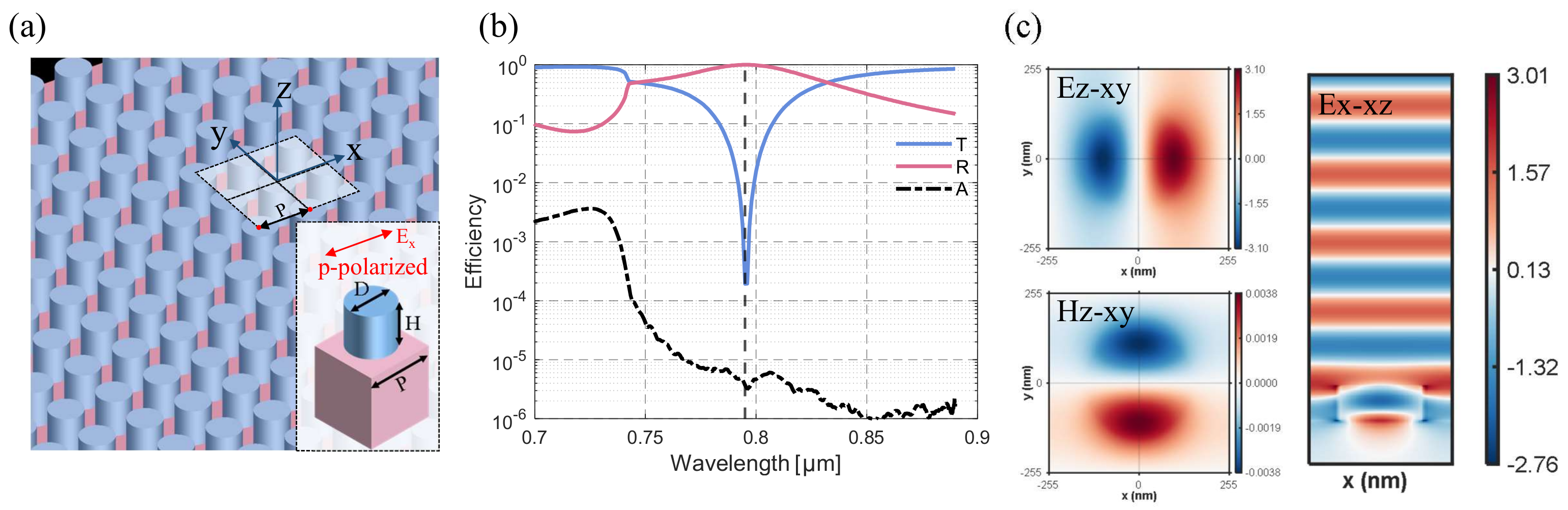
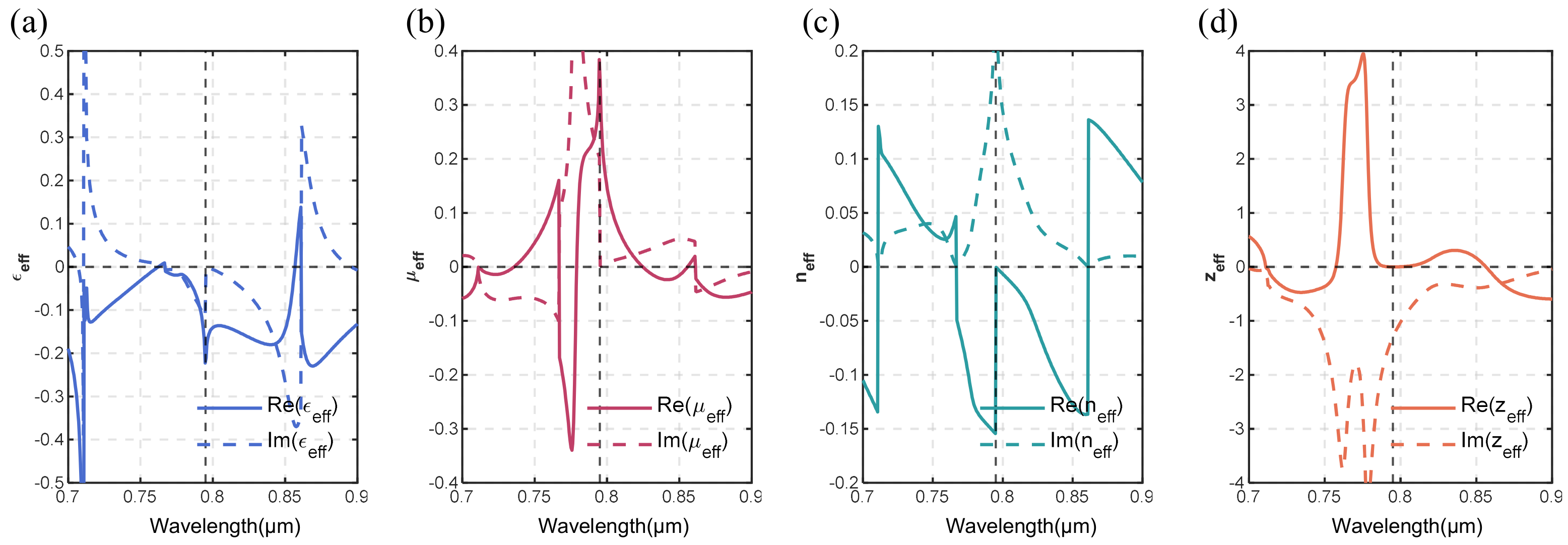
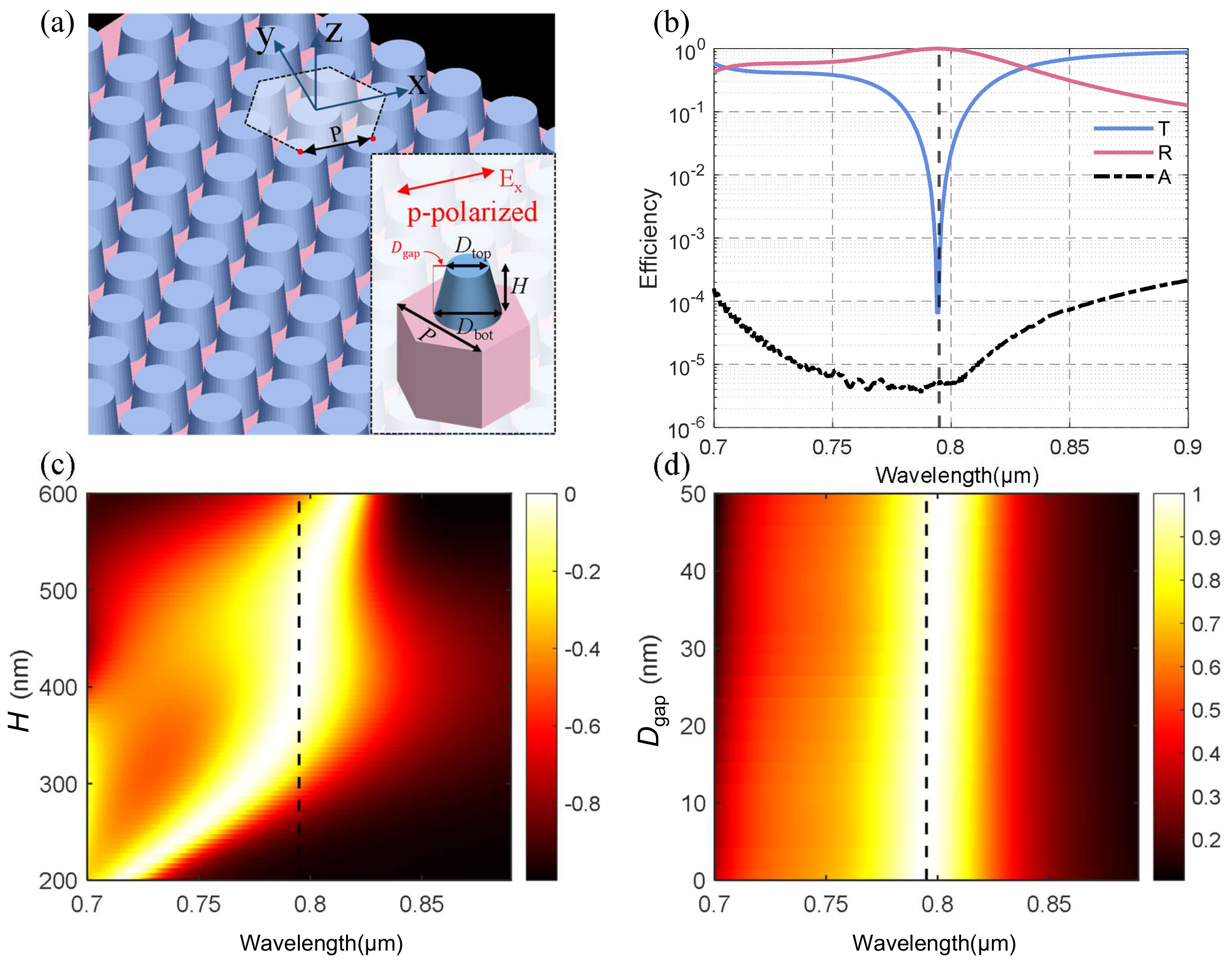
3.1. Cylindrical Resonators in Square Lattices
3.2. Frustums in Hexagonal Lattices
3.3. Dual-Band High Reflectivity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GMR | Guided Mode Resonance |
| FDTD | Finite-Difference Time-Domain |
| SCD | Single-Crystal Diamond |
| ED | Electric Dipole |
| MD | Magnetic Dipole |
| EQ | Electric Quadrupole |
| MQ | Magnetic Quadrupole |
| TFSF | Total Field Scattered Field |
| AR | Aspect Ratio |
| SCS | Scattering Cross-Section |
| PEC | Perfect Electron Crystallograph |
References
- Zheludev, N.I.; Kivshar, Y.S. From Metamaterials to Metadevices. Nat. Mater. 2012, 11, 917–924. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, X. Metamaterials: A New Frontier of Science and Technology. Chem. Soc. Rev. 2011, 40, 2494. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Zhu, A.Y.; Capasso, F. Flat Optics with Dispersion-Engineered Metasurfaces. Nat. Rev. Mater. 2020, 5, 604–620. [Google Scholar] [CrossRef]
- Chen, H.T.; Taylor, A.; Nanfang, Y. A Review of Metasurfaces: Physics and Applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef] [PubMed]
- Quan, Y.; Qin, G.; Linsen, C.; Yi, Z.; Yuhang, Y.; Xun, C.; Shuming, W.; Shining, Z.; Zhenlin, W. Recent Advanced Applications of Metasurfaces in Multi-dimensions. Nanophotonics 2023, 12, 2295–2315. [Google Scholar]
- Fröch, J.E.; Huang, L.; Tanguy, Q.A.; Colburn, S.; Zhan, A.; Ravagli, A.; Seibel, E.J.; Böhringer, K.F.; Majumdar, A. Real Time Full-color Imaging in a Meta-optical Fiber Endoscope. eLight 2023, 3, 13. [Google Scholar] [CrossRef]
- Ren, H.R.; Fang, X.Y.; Jang, J.; Burger, J.; Rho, J.; Maier, S.A. Complex-Amplitude Metasurface-Based Orbital Angular Momentum Holography in Momentum Space. Nat. Nanotechnol. 2020, 15, 948. [Google Scholar] [CrossRef]
- Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary Spin-to–Orbital Angular Momentum Conversion of Light. Science 2017, 358, 896–901. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Wang, Z.; Zhang, Y.; Guo, X.; Xiao, S.; Xu, K.; Song, Q. Folded Digital Meta-Lenses for On-Chip Spectrometer. Nano Lett. 2023, 23, 3459–3466. [Google Scholar] [CrossRef]
- Ni, Y.; Chen, S.; Wang, Y.; Tan, Q.; Xiao, S.; Yang, Y. Metasurface for Structured Light Projection over 120° Field of View. Nano Lett. 2020, 20, 6719–6724. [Google Scholar] [CrossRef]
- Joo, D.H.; Kang, M.S.; Park, S.J.; Yu, S.A.; Park, W.T. Fabrication Method of Flexible Strain Sensors with CNTs and Solvents. Sens. Actuators A Phys. 2022, 345, 113775. [Google Scholar] [CrossRef]
- Zuraiqi, K.; Zavabeti, A.; Allioux, F.M.; Tang, J.; Nguyen, C.K.; Tafazolymotie, P.; Mayyas, M.; Ramarao, A.V.; Spencer, M.; Shah, K.; et al. Liquid Metals in Catalysis for Energy Applications. Joule 2020, 4, 2290–2321. [Google Scholar] [CrossRef]
- Mostafavi, E.; Iravani, S. MXene-Graphene Composites: A Perspective on Biomedical Potentials. Nano-Micro Lett. 2022, 14, 130. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Lan, L.; Liu, X.; Ying, Y.; Ping, J. Spontaneous Growth and Regulation of Noble Metal Nanoparticles on Flexible Biomimetic MXene Paper for Bioelectronics. Biosens. Bioelectron. 2020, 148, 111799. [Google Scholar] [CrossRef]
- Kouediatouka, A.N.; Liu, Q.; Mawignon, F.J.; Wang, W.; Wang, J.; Ruan, C.; Yeo, K.F.H.; Dong, G. Sensing Characterization of an Amorphous PDMS/Ecoflex Blend Composites with an Improved Interfacial Bonding and Rubbing Performance. Appl. Surf. Sci. 2023, 635, 157675. [Google Scholar]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically Resonant Dielectric Nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef]
- Slovick, B.; Yu, Z.G.; Berding, M.; Krishnamurthy, S. Perfect Dielectric-Metamaterial Reflector. Phys. Rev. B 2013, 88, 165116. [Google Scholar] [CrossRef]
- Moitra, P.; Slovick, B.A.; Gang Yu, Z.; Krishnamurthy, S.; Valentine, J. Experimental Demonstration of a Broadband All-Dielectric Metamaterial Perfect Reflector. Appl. Phys. Lett. 2014, 104, 171102. [Google Scholar] [CrossRef]
- Moitra, P.; Slovick, B.A.; Li, W.; Kravchencko, I.I.; Briggs, D.P.; Krishnamurthy, S.; Valentine, J. Large-Scale All-Dielectric Metamaterial Perfect Reflectors. ACS Photonics 2015, 2, 692–698. [Google Scholar]
- Atikian, H.A.; Sinclair, N.; Latawiec, P.; Xiong, X.; Meesala, S.; Gauthier, S.; Wintz, D.; Randi, J.; Bernot, D.; DeFrances, S.; et al. Diamond Mirrors for High-Power Continuous-Wave Lasers. Nat. Commun. 2022, 13, 2610. [Google Scholar] [CrossRef]
- Doiron, C.F.; Brener, I.; Cerjan, A. Realizing Symmetry-Guaranteed Pairs of Bound States in the Continuum in Metasurfaces. Nat. Commun. 2022, 13, 7534. [Google Scholar] [CrossRef] [PubMed]
- Magnusson, R.; Wang, S.S. New Principle for Optical Filters. Appl. Phys. Lett. 1992, 61, 1022–1024. [Google Scholar] [CrossRef]
- Wei, C.; Liu, S.; Deng, D.; Shen, J.; Shao, J.; Fan, Z. Electric Field Enhancement in Guided-mode Resonance Filters. Opt. Lett. 2006, 31, 1223–1225. [Google Scholar] [CrossRef] [PubMed]
- Sang, T.; Wang, Z. Study on Guided-Mode Resonance Optical Devices; Tongji University Press: Shanghai, China, 2020. [Google Scholar]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric Gradient Metasurface Optical Elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef]
- Liu, W.; Kivshar, Y.S. Generalized Kerker Effects in Nanophotonics and Meta-Optics [Invited]. Opt. Express 2018, 26, 13085. [Google Scholar] [CrossRef]
- Liu, W. Generalized Magnetic Mirrors. Phys. Rev. Lett. 2017, 119, 123902. [Google Scholar] [CrossRef]
- Smith, D.R.; Schultz, S.; Markoš, P.; Soukoulis, C.M. Determination of Effective Permittivity and Permeability of Metamaterials from Reflection and Transmission Coefficients. Phys. Rev. B 2002, 65, 195104. [Google Scholar] [CrossRef]
- Smith, D.R.; Schurig, D. Electromagnetic Wave Propagation in Media with Indefinite Permittivity and Permeability Tensors. Phys. Rev. Lett. 2003, 90, 77. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic Parameter Retrieval from Inhomogeneous Metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef]
- Arslanagic, S.; Hansen, T.V.; Mortensen, N.A.; Gregersen, A.H.; Sigmund, O.; Ziolkowski, R.W.; Breinbjerg, O. A Review of the Scattering-Parameter Extraction Method with Clarification of Ambiguity Issues in Relation to Metamaterial Homogenization. IEEE Antennas Propag. Mag. 2013, 55, 91–106. [Google Scholar] [CrossRef]
- Hinamoto, T.; Fujii, M. MENP: An Open-Source MATLAB Implementation of Multipole Expansion for Nanophotonics. OSA Contin. 2021, 4, 1640. [Google Scholar] [CrossRef]
- Alaee, R.; Rockstuhl, C.; Fernandez-Corbaton, I. An Electromagnetic Multipole Expansion beyond the Long-Wavelength Approximation. Opt. Commun. 2018, 407, 17–21. [Google Scholar] [CrossRef]
- Terekhov, P.D.; Babicheva, V.E.; Baryshnikova, K.V.; Shalin, A.S.; Karabchevsky, A.; Evlyukhin, A.B. Multipole Analysis of Dielectric Metasurfaces Composed of Nonspherical Nanoparticles and Lattice Invisibility Effect. Phys. Rev. B 2019, 99, 045424. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Evlyukhin, A.B.; Yu, Y.F.; Bakker, R.M.; Chipouline, A.; Kuznetsov, A.I.; Luk’yanchuk, B.; Chichkov, B.N.; Kivshar, Y.S. Nonradiating Anapole Modes in Dielectric Nanoparticles. Nat. Commun. 2015, 6, 8069. [Google Scholar] [CrossRef]
- Conteduca, D.; Brunetti, G.; Barth, I.; Quinn, S.D.; Ciminelli, C.; Krauss, T.F. Multiplexed Near-Field Optical Trapping Exploiting Anapole States. ACS Nano 2023, 17, 16695–16702. [Google Scholar] [CrossRef]
- Tripathi, A.; Kim, H.R.; Tonkaev, P.; Lee, S.J.; Makarov, S.V.; Kruk, S.S.; Rybin, M.V.; Park, H.-G.; Kivshar, Y. Lasing Action from Anapole Metasurfaces. Nano Lett. 2021, 21, 6563–6568. [Google Scholar] [CrossRef]
- Holly, C.; Traub, M.; Hoffmann, D.; Widmann, C.; Brink, D.; Nebel, C.E.; Gotthardt, T.; Sözbir, M.C.; Wenzel, C. Monocrystalline CVD-Diamond Optics for High-Power Laser Applications. In Proceedings of the High-Power Laser Materials Processing: Lasers, Beam Delivery, Diagnostics, and Applications V, San Francisco, CA, USA, 13–18 February 2016. [Google Scholar]
- Krupke, W.F. Diode Pumped Alkali Lasers (DPALs)—A Review (Rev1). Prog. Quantum Electron. 2012, 36, 4–28. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Yang, Z.; Hua, W. Signal Broad Area High Power Laser Diode with Narrowed Linewidth. Laser Optoelectron. Prog. 2011, 48, 36–39. [Google Scholar]
- Cheng, H.; Wang, Z.; Zhang, F.; Tian, Z.; Cui, D.; Xu, Z. Research Development of Alkali Vapor Lasers. Laser Optoelectron. Prog. 2015, 52, 020002. [Google Scholar] [CrossRef]
- Magnusson, R.; Ding, Y. Spectral-Band Engineering with Interacting Resonant Leaky Modes in Thin Periodic Films. Proc. SPIE 2004, 5720, 119–129. [Google Scholar]
- Sang, T.; Wang, Z.; Wang, L.; Wu, Y.; Chen, L. Resonant Excitation Analysis of Sub-Wavelength Dielectric Grating. J. Opt. A: Pure Appl. Opt. 2006, 8, 62–66. [Google Scholar] [CrossRef]
- Lalanne, P.; Lemercier-Lelanne, D. Depth Dependence of the Effective Properties of Subwavelength Gratings. J. Opt. Soc. Am. A 1997, 14, 450–458. [Google Scholar] [CrossRef]
- Yu, X.; Yang, W.; Shen, C.; Tao, W.; Deng, X. Polarization Beam Combining by Fused Silica Subwavelength Grating. Opt. Commun. 2024, 554, 130135. [Google Scholar] [CrossRef]
- Li, Y.; Hao, X.; Dai, B.; Shu, G.; Zhao, J.; Zhang, S.; Liu, X.; Wang, W.; Liu, K.; Cao, W.; et al. Research Progress on High Rate and High Quality Growth of MPCVD Single Crystal Diamond. J. Synth. Cryst. 2020, 49, 979–989. [Google Scholar]
- Kruk, S.; Kivshar, Y. Tailoring Transmission and Reflection with Metasurfaces. In Dielectric Metamaterials; Elsevier: Amsterdam, The Netherlands, 2020; pp. 145–174. [Google Scholar]
- Savinov, V.; Fedotov, V.A.; Zheludev, N.I. Toroidal Dipolar Excitation and Macroscopic Electromagnetic Properties of Metamaterials. Phys. Rev. B 2014, 89, 205112. [Google Scholar] [CrossRef]
- Campione, S.; Liu, S.; Basilio, L.I.; Warne, L.K.; Langston, W.L.; Luk, T.S.; Wendt, J.R.; Reno, J.L.; Keeler, G.A.; Brener, I.; et al. Broken Symmetry Dielectric Resonators for High Quality Factor Fano Metasurfaces. ACS Photonics 2016, 3, 2362–2367. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound States in the Continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Vaidya, S.; Benalcazar, W.A.; Cerjan, A.; Rechtsman, M.C. Point-Defect-Localized Bound States in the Continuum in Photonic Crystals and Structured Fibers. Phys. Rev. Lett. 2021, 127, 023605. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Zhao, X.; Shi, L.; Zi, J. Realizing Tunable Evolution of Bound States in the Continuum and Circularly Polarized Points by Symmetry Breaking. ACS Photonics 2023, 10, 2316–2322. [Google Scholar] [CrossRef]
- Bustamante, C.J.; Chemla, Y.R.; Liu, S.; Wang, M.D. Optical Tweezers in Single-Molecule Biophysics. Nat. Rev. Methods Primers 2021, 1, 25. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Z.; Liao, J.; Xu, Z.; Cheng, X.; Zhang, J. The Design of Highly Reflective All-Dielectric Metasurfaces Based on Diamond Resonators. Photonics 2024, 11, 1015. https://doi.org/10.3390/photonics11111015
Xing Z, Liao J, Xu Z, Cheng X, Zhang J. The Design of Highly Reflective All-Dielectric Metasurfaces Based on Diamond Resonators. Photonics. 2024; 11(11):1015. https://doi.org/10.3390/photonics11111015
Chicago/Turabian StyleXing, Zhongyang, Jiahui Liao, Zhongjie Xu, Xiang’ai Cheng, and Jiangbin Zhang. 2024. "The Design of Highly Reflective All-Dielectric Metasurfaces Based on Diamond Resonators" Photonics 11, no. 11: 1015. https://doi.org/10.3390/photonics11111015
APA StyleXing, Z., Liao, J., Xu, Z., Cheng, X., & Zhang, J. (2024). The Design of Highly Reflective All-Dielectric Metasurfaces Based on Diamond Resonators. Photonics, 11(11), 1015. https://doi.org/10.3390/photonics11111015




