Feature Vector Effectiveness Evaluation for Pattern Selection in Computational Lithography
Abstract
1. Introduction
2. Materials and Methods
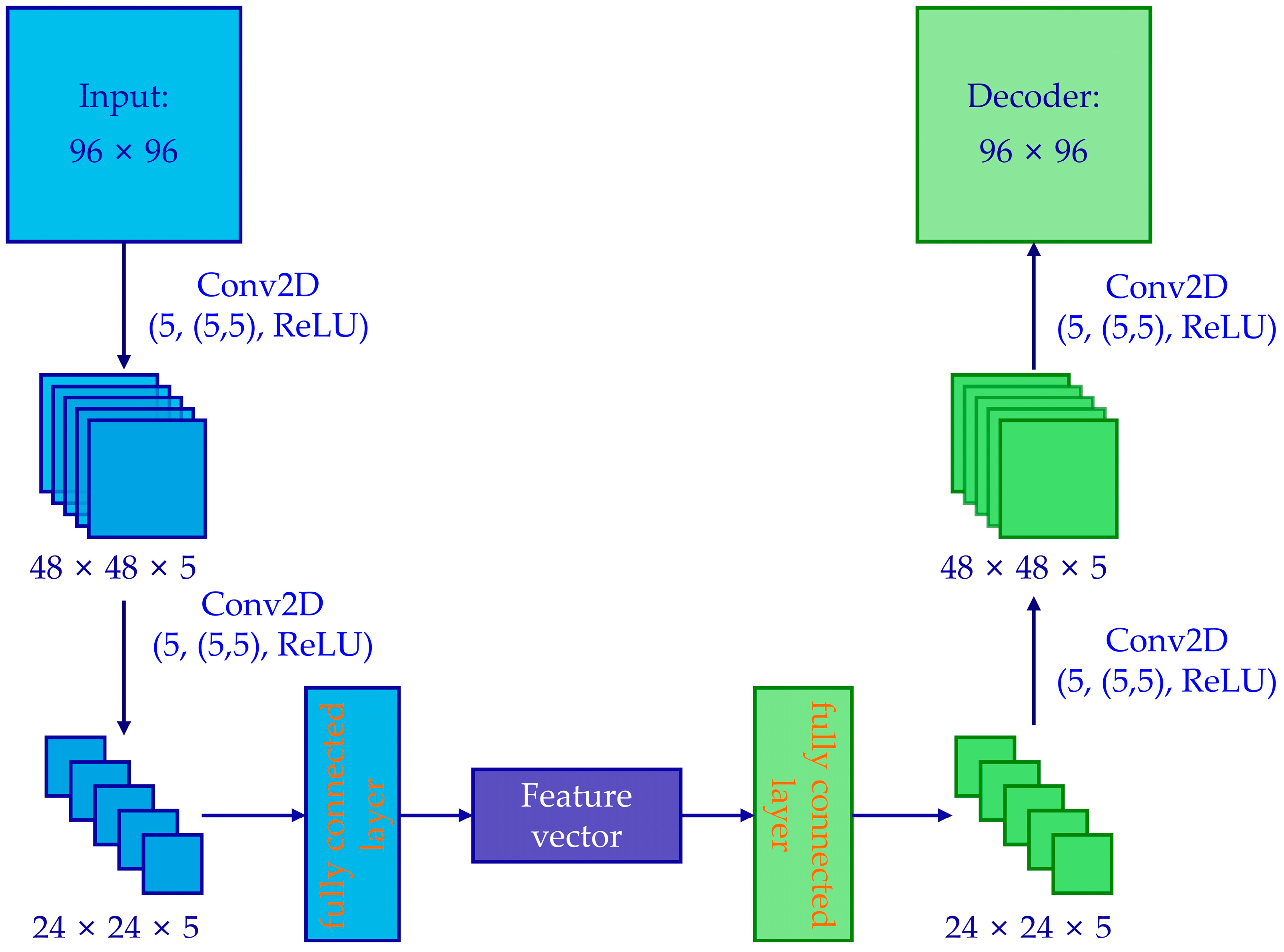
2.1. Two KPIs for Feature Vector Effectiveness Evaluation
2.2. Experiment Case
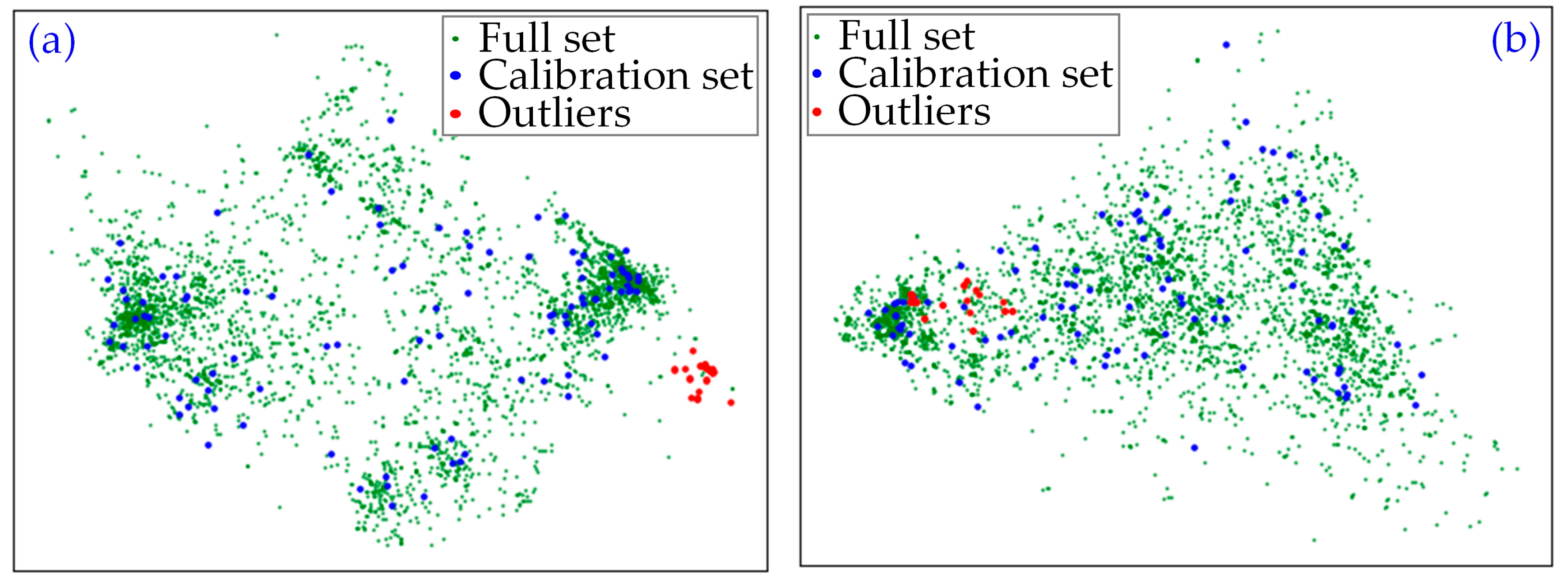
2.3. Outlier Identification
- (a)
- The outliers show a significant gap in the lithography domain to the calibration set, and thus cannot be generalized by the baseline model.
- (b)
- Special lithography effects exist in the outliers, and the lithography model lacks the fitting power to fit on these outliers.
- (c)
- The SEM metrology quality is poor on the outliers, and the “wafer CD” collected for the calibration/verification is not the actual wafer CD.
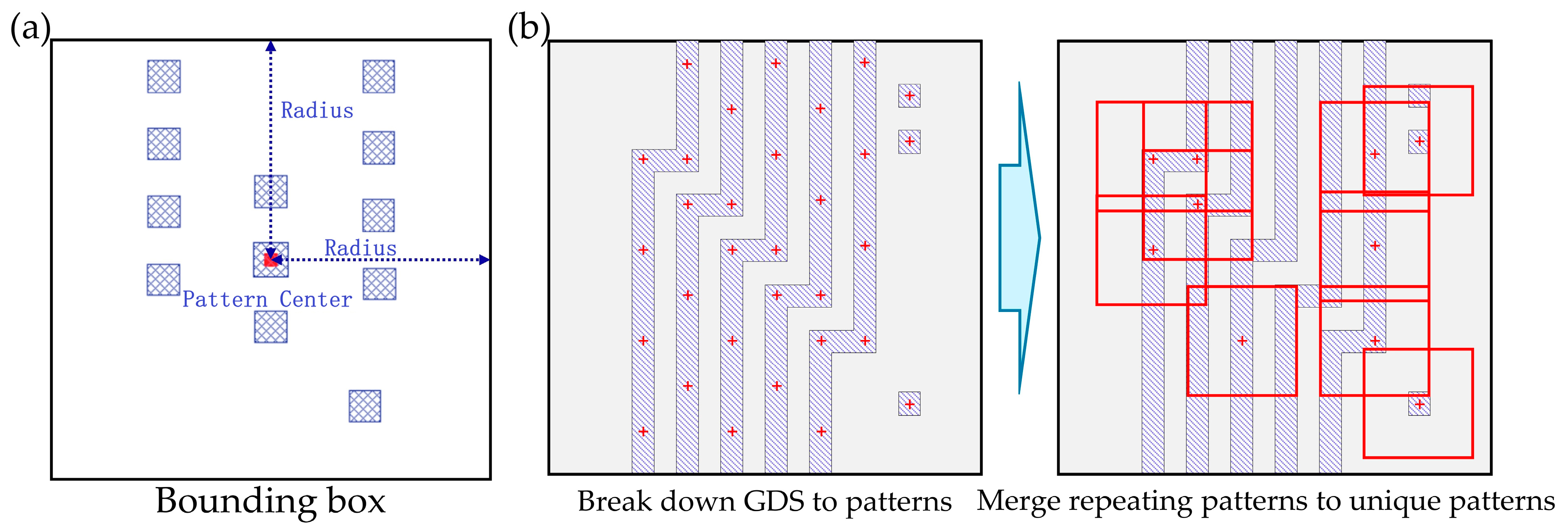
2.4. Three Feature Vector Generation Methods
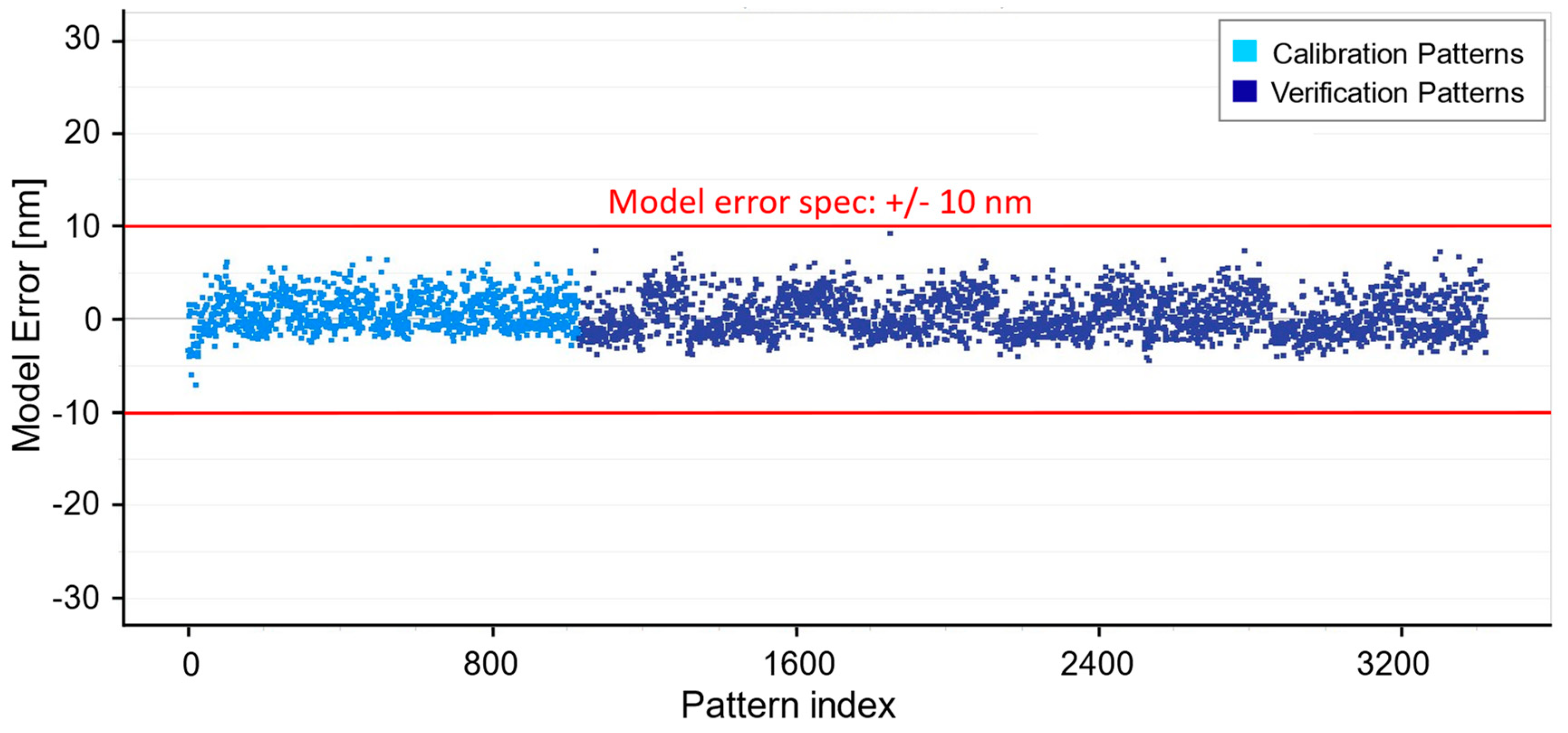
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Bisschop, P. How to make lithography patterns print: The role of OPC and pattern layout. Adv. Opt. Technol. 2015, 4, 253–284. [Google Scholar] [CrossRef]
- Schlief, R.E. Effect of data selection and noise on goodness of OPC model fit. In Optical Microlithography XVIII, Proceedings of the Microlithography 2005, San Jose, CA, USA, 27 February–4 March 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5754, p. 5754. [Google Scholar]
- Vengertsev, D.; Kim, K.; Yang, S.H.; Shim, S.; Moon, S.; Shamsuarov, A.; Lee, S.; Choi, S.W.; Choi, J.; Kang, H.K. The new test pattern selection method for OPC model calibration, based on the process of clustering in a hybrid space. In Photomask Technology 2012, Proceedings of the SPIE Photomask Technology, Monterey, CA, USA, 11–13 September 2012; SPIE: Bellingham, WA, USA, 2012; Volume 8522, pp. 387–394. [Google Scholar]
- Sun, R.C.; Kang, D.K.; Jia, C.; Liu, M.; Shao, D.B.; Kim, Y.S.; Shin, J.; Simmons, M.; Zhao, Q.; Feng, M.; et al. Enhancing model accuracy and calibration efficiency with image-based pattern selection using machine learning techniques. In Optical Microlithography XXXIV, Proceedings of the SPIE Advanced Lithography, Online Only, CA, USA, 22–27 February 2021; SPIE: Bellingham, WA, USA, 2021; Volume 11613, pp. 214–222. [Google Scholar]
- Zhang, W.; Pang, B.; Ma, Y.; Li, X.; Bai, F.; Wang, Y. Modeling sampling strategy optimization by machine learning based analysis. In Proceedings of the 2021 International Workshop on Advanced Patterning Solutions (IWAPS), Foshan, China, 12–13 December 2021; IEEE: New York, NY, USA, 2021; pp. 1–4. [Google Scholar]
- Feng, Y.; Song, Z.; Liu, J.; Li, Z.; Yang, F.; Jiang, H.; Liu, S. Layout pattern analysis and coverage evaluation in computational lithography. Opt. Express 2023, 31, 8897–8913. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, Q.; Du, B.; You, J.; Tao, D. Adaptive manifold regularized matrix factorization for data clustering. In Proceedings of the International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 3399–3405. [Google Scholar]
- Ansuini, A.; Laio, A.; Macke, J.H.; Zoccolan, D. Intrinsic dimension of data representations in deep neural networks. Adv. Neural Inf. Process. Syst. 2019, 33, 6111–6122. [Google Scholar]
- Gong, S.; Boddeti, V.N.; Jain, A.K. On the intrinsic dimensionality of image representations. In Proceedings of the 2019 IEEE CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3982–3991. [Google Scholar]
- Kohli, K.K.; Jobes, M.; Graur, I. Automated detection and classification of printing sub-resolution assist features using machine learning algorithms. In Optical Microlithography XXX, Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 26 February–2 March 2017; SPIE: Bellingham, WA, USA, 2017; Volume 10147, pp. 176–182. [Google Scholar]
- Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. In Proceedings of the International Conference on Machine Learning, Lile, France, 6–11 July 2015; PMLR: Westminster, UK, 2015; pp. 1180–1189. [Google Scholar]
- Vazquez, D.; Lopez, A.M.; Marin, J.; Ponsa, D.; Geronimo, D. Virtual and real world adaptation for pedestrian detection. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 797–809. [Google Scholar] [CrossRef] [PubMed]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Springer International Publishing: Cham, Switzerland, 2014; pp. 818–833. [Google Scholar]
- Bae, K.; Kim, T.; Lee, S.; Kim, B.; Jeong, S.; Tang, J.; Zhao, Q.; Zhao, Y.; Choi, C.-I.; Liang, J.; et al. Advanced Pattern Selection and Coverage Check for Computational Lithography. In Advances in Patterning Materials and Processes XLI, Proceedings of the SPIE Advanced Lithography + Patterning, San Jose, CA, USA, 25 February–1 March 2024; SPIE: Bellingham, WA, USA, 2024. [Google Scholar]
- Ding, D.; Wu, X.; Ghosh, J.; Pan, D.Z. Machine learning based lithographic hotspot detection with critical-feature extraction and classification. In Proceedings of the 2009 IEEE International Conference on IC Design and Technology, Austin, TX, USA, 18–20 May 2009; IEEE: New York, NY, USA, 2009; pp. 219–222. [Google Scholar]
- Yang, F.; Sinha, S.; Chiang, C.C.; Zeng, X.; Zhou, D. Improved tangent space-based distance metric for lithographic hotspot classification. IEEE Trans. Comput. -Aided Des. Integr. Circuits Syst. 2016, 36, 1545–1556. [Google Scholar] [CrossRef]
- Cavalcanti, G.D.; Soares, R.J. Ranking-based instance selection for pattern classification. Expert Syst. Appl. 2020, 150, 113269. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Divergence estimation for multidimensional densities via k-Nearest-Neighbor distances. IEEE Trans. Inf. Theory 2009, 55, 2392–2405. [Google Scholar] [CrossRef]
- Lombardi, D.; Pant, S. Nonparametric k-nearest-neighbor entropy estimator. Phys. Rev. E 2016, 93, 013310. [Google Scholar] [CrossRef] [PubMed]
- Socha, R.; Jhaveri, T.; Dusa, M.; Liu, X.; Chen, L.; Hsu, S.; Li, Z.; Strojwas, A.J. Design compliant source mask optimization (SMO). In Photomask and Next-Generation Lithography Mask Technology XVII, Proceedings of the Photomask and Ngl Mask Technology XVII, Yokohama, Japan, 13–15 April 2010; SPIE: Bellingham, WA, USA, 2010; Volume 7748, pp. 260–271. [Google Scholar]
- Socha, R. Freeform and SMO. In Optical Microlithography XXIV, Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 27 February–3 March 2011; SPIE: Bellingham, WA, USA, 2011; Volume 7973, pp. 19–35. [Google Scholar]
- He, X.; Deng, Y.; Zhou, S.; Li, R.; Wang, Y.; Guo, Y. Lithography hotspot detection with FFT-based feature extraction and imbalanced learning rate. ACM Trans. Des. Autom. Electron. Syst. 2019, 25, 1–21. [Google Scholar] [CrossRef]
- Choi, S.; Shim, S.; Shin, Y. Machine learning (ML)-guided OPC using basis functions of polar Fourier transform. In Optical Microlithography XXIX, Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 21–25 February 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9780, pp. 63–70. [Google Scholar]
- Zhang, Y.; Feng, M.; Liu, H.Y. A focus exposure matrix model for full chip lithography manufacturability check and optical proximity correction. In Photomask and Next-Generation Lithography Mask Technology XIII, Proceedings of thePhotomask and Next Generation Lithography Mask Technology XIII, Yokohama, Japan, 18–20 April 2006; SPIE: Bellingham, WA, USA, 2006; Volume 6283, pp. 220–232. [Google Scholar]
- Liu, P.; Zhang, Z.; Lan, S.; Zhao, Q.; Feng, M.; Liu, H.Y.; Vellanki, V.; Lu, Y.W. A full-chip 3D computational lithography framework. In Optical Microlithography XXV, Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 12–16 February 2012; SPIE: Bellingham, WA, USA, 2012; Volume 8326, pp. 84–101. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]


| Dataset | RMS (nm) | Error Range (nm) |
|---|---|---|
| Calibration | 1.62 | 7.94 |
| Verification | 3.04 | 37.06 |
| Verification excluding outliers | 2.09 | 15.35 |
| Dataset | RMS (nm) | Error Range (nm) |
|---|---|---|
| Calibration | 2.05 | 13.56 |
| Verification | 2.15 | 13.63 |
| Dimension | Training Loss (×103) | Verification Loss (×103) |
|---|---|---|
| 49 | 2.52 | 2.61 |
| 100 | 1.79 | 1.86 |
| 196 | 1.30 | 1.37 |
| 400 | 1.00 | 1.07 |
| 729 | 0.95 | 1.02 |
| Dimension | Training Loss (×104) | Verification Loss (×104) |
|---|---|---|
| 49 | 2.54 | 2.64 |
| 100 | 1.73 | 1.81 |
| 196 | 1.62 | 1.71 |
| 400 | 0.61 | 0.70 |
| 729 | 0.55 | 0.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Liu, J.; Jiang, H.; Liu, S. Feature Vector Effectiveness Evaluation for Pattern Selection in Computational Lithography. Photonics 2024, 11, 990. https://doi.org/10.3390/photonics11100990
Feng Y, Liu J, Jiang H, Liu S. Feature Vector Effectiveness Evaluation for Pattern Selection in Computational Lithography. Photonics. 2024; 11(10):990. https://doi.org/10.3390/photonics11100990
Chicago/Turabian StyleFeng, Yaobin, Jiamin Liu, Hao Jiang, and Shiyuan Liu. 2024. "Feature Vector Effectiveness Evaluation for Pattern Selection in Computational Lithography" Photonics 11, no. 10: 990. https://doi.org/10.3390/photonics11100990
APA StyleFeng, Y., Liu, J., Jiang, H., & Liu, S. (2024). Feature Vector Effectiveness Evaluation for Pattern Selection in Computational Lithography. Photonics, 11(10), 990. https://doi.org/10.3390/photonics11100990





