Quantitative Analysis of Acquisition Speed of High-Precision FLIM Technologies via Simulation and Modeling

Abstract

In practical applications such as cancer diagnosis and industrial detection, there is a critical demand for fast fluorescence lifetime imaging (Fast-FLIM). The Fast-FLIM systems suitable for complex environments are typically achieved by enhancing the hardware performance of time-correlated single-photon counting (TCSPC), with an acquisition speed of about a few frames per second (fps). However, due to the limitation of single-photon acquisition, the imaging speed is still far from the demand of practical application. The synchroscan streak camera (SC) maps signals from the temporal dimension to the spatial dimension, effectively overcoming the long acquisition time caused by single-photon acquisition. This paper constructs a method to calculate the acquisition time for the TCSPC-FLIM and SC-FLIM systems, and it quantitatively compares the speed. The research demonstrates that the main factors limiting the acquisition speed of the FLIM systems are the photon emission rate, the photon counting rate, the required SNR, the dwell time, and the number of parallel channels. In high-quality and large-scale lifetime imaging, the acquisition speed of the SC-FLIM is at least ${10}^4$ times faster than that of the TCSPC-FLIM. Therefore, the synchroscan streak camera has more significant potential to promote Fast-FLIM.

1. Introduction

FLIM technology provides detailed information about the microenvironment in which a molecule resides by measuring the time it takes for a fluorescent molecule to return from the excited state to the ground state [1]. Unlike conventional fluorescence intensity imaging, the fluorescence lifetime is independent of excitation intensity, fluorophore concentration, and photobleaching effects [2]. Consequently, multiple biochemical parameters in the microenvironment, such as oxygen content [3], viscosity [4], ionic concentration [5], and temperature [6], can be quantitatively measured via the fluorescence lifetime. In recent years, researchers have made significant progress by utilizing FLIM technology to conduct comprehensive investigations into cell metabolism [7], tumor microenvironment [8], material properties [9], and chemical reaction kinetics [10]. However, in practical applications such as biomedical clinical diagnosis [11,12] and large-scale industrial detection [13], there is a higher demand for the imaging speed of FLIM technology [14].

FLIM techniques are mainly divided into two categories: time-domain (TD) and frequency-domain (FD) methods. The common implementations in time-domain FLIM are based on time-gating (TG), TCSPC, and a synchroscan streak camera (SC).

Table 1. Comparison of performance metrics of four FLIM systems.

System Performance Metrics	FD [15]	TG [16]	TCSPC [17]	SC [18]
Temporal Resolution (ps)	100	200	3.5	15
Spatial Resolution ($\mathsf{\mu }$m)	5.6	16	0.2	0.2
Response Sensitivity	R 1 = 0.16 A/W @500 nm	R = 0.17 A/W @600 nm	SER 2 = 200 mV @490 nm	R = 250 A/W   @500 nm
Spectral Response Range (nm)	380–800	200–900	300–900	400–900
Data Acquisition Speed (fps)	22 (1008 × 1008)	50   (128 × 128)	2   (128 × 128)	0.3 (240 × 225)

¹ R is an abbreviation for “Responsivity”, which reflects the efficiency of a photodetector in converting incident light energy into electrical energy. ² SER is an abbreviation for “Single Photon Response”, which reflects the voltage (or current) output of the detector when it receives a single photon.

presents a comparative analysis of the temporal resolution, spatial resolution, response sensitivity, and data acquisition speed of these FLIM techniques.

Although FD-FLIM and TG-FLIM systems can achieve Fast-FLIM by using CCD or CMOS to construct multi-pixel (channel) parallel acquisition, the spatial resolution and sensitivity are unsatisfactory. In addition, FD-FLIM indirectly calculates the fluorescence lifetime by measuring the phase delay and modulation depth of fluorescence signals, and the measurement accuracy is limited due to the modulation frequency (${10}^8$ Hz) and sampling frequency (${10}^9$ Hz) [19]. Moreover, the process of measuring multi-exponential decay fluorescence is complex. TG-FLIM uses an electronic or optical shutter to turn the detector’s response on and off, and its temporal resolution depends on the width of the time gate (sub-nanoseconds) [2]. In contrast, TCSPC-FLIM and SC-FLIM use high-gain detection modules (Vgain = 1V [17]; gain = ${10}^3$ [18]) that can detect a single photon. A unique method of constructing fluorescence decay curves enables these two technologies to achieve a high temporal resolution [12]. Consequently, this paper focuses on TCSPC and SC methods.

The TCSPC method effectively overcomes the signal broadening caused by the instrument response function (IRF) through single-photon counting and statistical analysis, resulting in high measurement accuracy [20]. However, the excitation–detection process must be repeated tens of thousands of times to achieve the required accuracy and precision, leading to a slow acquisition speed and even photobleaching [21]. In order to improve the acquisition speed of TCSPC, researchers have proposed two schemes to reduce repetitive measurements: (1) reducing the dead time of a single channel and (2) using a parallel multi-channel. When KOENIG M et al. [22] used a combination of a hybrid photomultiplier tube (hybrid PMT) and a low dead-time (less than 1 ns) time-to-digital converter (TDC) to visualize fluorescent beads, the acquisition speed was 3 fps (128 × 128 pixels). BECKER W et al. [23] employed a multi-channel parallel strategy to construct a FLIM system comprising eight parallel TCSPC channels, which required approximately 5 s to acquire a set of 256 × 256 pixels FLIM. POLAND S et al. [24] developed a multi-channel parallel Fast-FLIM system using a single-photon avalanche diode (SPAD) line array. The system has a speed of up to 4 fps (516 × 516 pixels).

The synchroscan streak camera disperses photoelectrons that arrive at different moments to corresponding spatial positions, enabling high-resolution time measurements through spatio-temporal conversion [25]. Currently, the temporal resolution of the synchroscan streak camera is less than 1ps [26]. The streak camera method not only overcomes the slow speed problem caused by single-photon counting but also possesses a wide-field imaging capability [20]. These advantages make it a new choice for Fast-FLIM. At present, Liu et al. [27] have developed a high-speed SC-FLIM system by integrating a synchroscan streak camera with an ultra-high frame rate readout camera and a high-speed spatial scanning device.

The measurement principle of the synchroscan streak camera determines that it is an effective way to achieve Fast-FLIM. Therefore, this paper calculates the acquisition speed of the SC-FLIM system. We provide a detailed analysis of the factors that influence the acquisition speed in various processes of lifetime imaging, including fluorescence generation, fluorescence detection, spatial scanning, and data processing. Then, the acquisition time of TCSPC-FLIM and synchroscan SC-FLIM systems is calculated using a numerical simulation and a theoretical analysis. Finally, we quantitatively compare the data acquisition time of these FLIM systems by measuring the lifetime of a standard fluorescent dye, Erythrosin B, based on the developed acquisition time model.

This paper is organized as follows: In Section 2, the method of constructing acquisition time models for TCSPC-FLIM and synchroscan SC-FLIM is described. In Section 3, the simulated experimental conditions and the results are discussed, and a quantitative comparison of the speed of the FLIM system is presented. Conclusions are drawn in Section 4.

2. Theory

The FLIM technology, based on TCSPC or synchroscan streak camera, is regarded as a representative high-precision time-domain FLIM technology. As illustrated in Figure 1, the 2D time-domain FLIM technology can be divided into four processes sequentially: fluorescence generation, fluorescence detection, lifetime fitting, and spatial scanning. After the sample is excited to produce fluorescence, the measuring instrument captures the fluorescence intensity decay signal and transmits the signal to the data processing module. The scanner completes 2D data acquisition by continuously changing the laser position and repeating the above process.

2.1. Factors Influencing the Acquisition Speed in the Fluorescence Generation Process

The photon emission rate of the sample exerts a direct influence on the acquisition time during the fluorescence generation process. When the fluorescence signal is weak, the system must repeat the excitation–detection process to obtain a high signal-to-noise ratio (SNR) signal, and the number of repetitions increases with the decrease in the photon emission rate. Therefore, the acquisition speed is influenced by the photon emission rate. Especially in multi-photon detection systems, such as the SC-FLIM system, the photon emission rate is closely related to the acquisition time.

2.2. Factors Influencing the Acquisition Speed in the Fluorescence Detection Process

The primary factor influencing the acquisition speed during the fluorescence detection process is the photon detection rate of the detection system. To assess the influence of photon detection rate on acquisition speed, it is essential to first comprehend the operational principles of diverse FLIM systems.

The TCSPC-FLIM system generates a histogram of photon arrival times by measuring the time interval between excitation and emission, as illustrated in Figure 2. The laser beam is split into two signals, one of which is detected via the single-photon detection system to form a “start” signal, which is used to initiate the timing system. The other signal is employed to excite the sample, thereby producing a fluorescence signal. The fluorescence signal passes through the single-photon detection system to form a “stop” signal, which is used to terminate the timing system. The interval ($\Delta t$) between the “start” signal and the “stop” signal represents the delay time for fluorescent photon emission in the sample. The multi-channel analyzer records and accumulates the photon arrival time. This process is then repeated to form a histogram of the time distribution, as illustrated in Figure 2c.

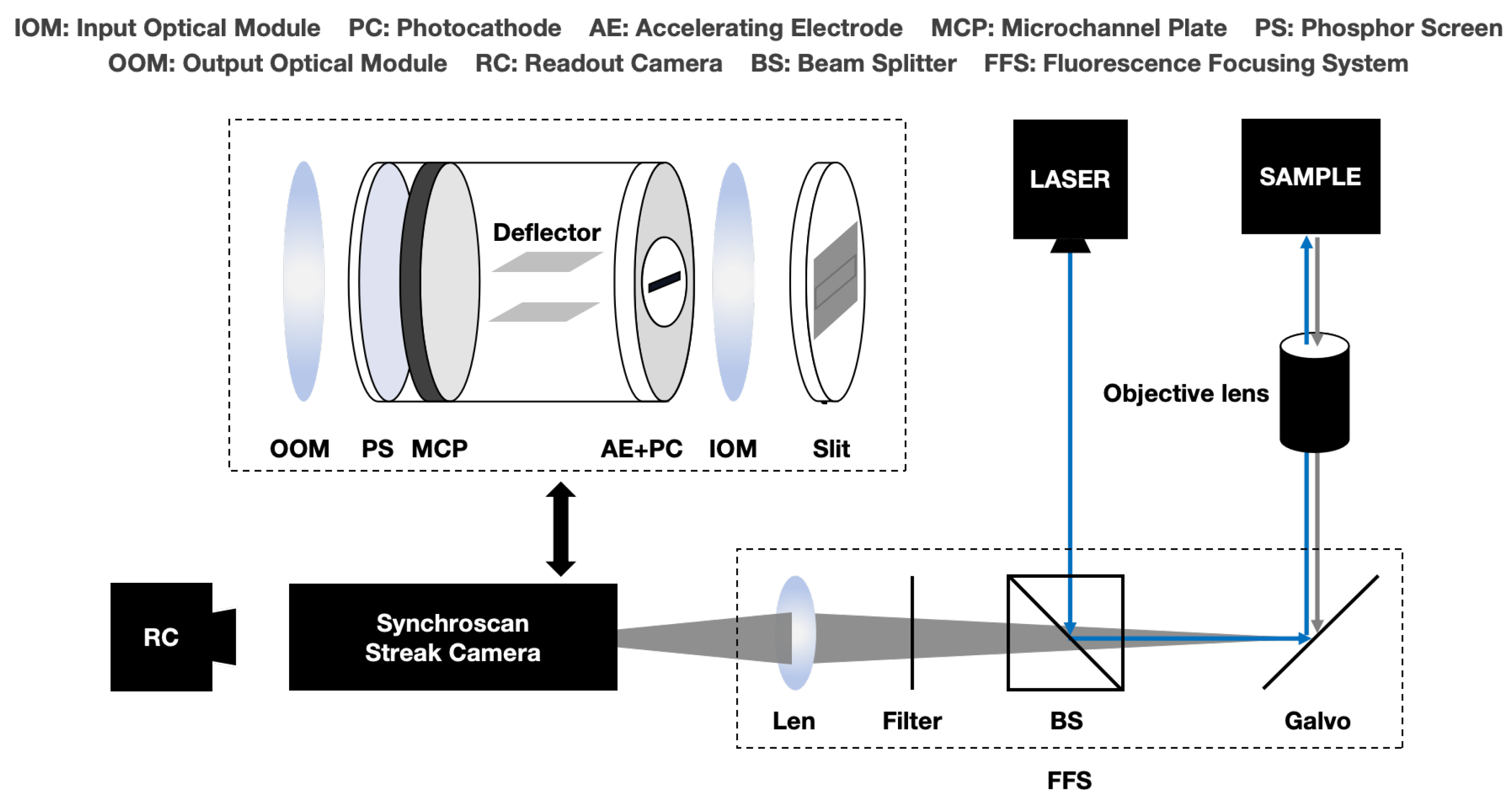
The synchroscan streak camera is capable of mapping temporal information onto the spatial axis, thereby facilitating the rapid and high-resolution measurement of temporal optical signals, as illustrated in Figure 3. The fluorescence decay signals are projected onto the slit-shaped photocathode (PC) through a relay lens (L1), and they are converted into electrons sequentially via the photocathode. The electrons are accelerated via the accelerating electrode and deflected via high-voltage sweep electrodes. During the sweep, the electrons are deflected at slightly different angles, depending on the arrival time at the electrodes. The electrons are then multiplied via a microchannel plate (MCP) and converted back into photons via a phosphor screen (PS) to form a streak image. A high-speed CCD camera is used to digitize and transfer the streak image to a processing module for lifetime processing [28].

In instances where the photon emission rate is high, the photon counting rate of the detection system assumes a primary role in influencing the acquisition speed, as it serves to determine the number of repetitions of the excitation–detection process. TCSPC-FLIM is a single-photon detection system that records at most one photon during a single excitation–detection process. Moreover, due to dead time in the detector, the photon detection rate is typically set to 20% of the laser frequency to minimize the waveform distortion of the recorded signal caused by the “pile-up” effect. The synchroscan streak camera realizes a multi-photon record in an excitation–detection process through a temporal-to-spatial mapping strategy with a high photon counting rate.

2.3. Factors Influencing the Acquisition Speed in the Lifetime Fitting Process

A fluorescence decay signal with a sufficient SNR is a prerequisite for accurately fitting fluorescence lifetimes. In the TCSPC-FLIM and SC-FLIM systems, the number of photons recorded in a time bin follows a Poisson distribution [29], so the noise mainly comes from the Poisson noise of the photon counts, and the standard deviation of the noise can be approximated as the square root of the number of photons in the corresponding time bin. Assume that the photon histogram has a total of M time bins, and the number of photons in the i-th time bin is $P_i$. The SNR can be expressed as follows:

$$SNR={\displaystyle \frac{{\sum }_{i=1}^M{P}_i}{\sqrt{{\sum }_{i=1}^M{P}_i}}}=\sqrt{\sum _{i=1}^M{P}_i}$$

(1)

The most straightforward method of enhancing the $SNR$ is to increase the number of photons. However, this often leads to extended acquisition times and photobleaching, especially in dynamic scenes where sample motion can cause blurred imaging [20]. Therefore, the most crucial step is determining the minimum $SNR$ before calculating the acquisition time.

2.4. Factors Influencing the Acquisition Speed in the Spatial Scanning Process

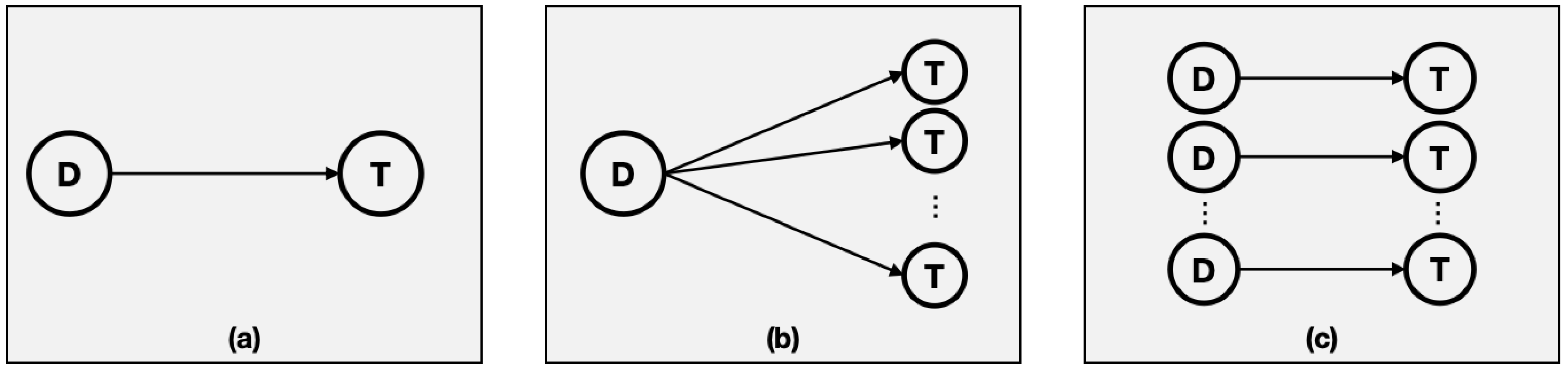
The most commonly utilized TCSPC-FLIM systems can be categorized into two principal types: laser scanning systems and wide-field imaging systems. The former can be further subdivided into single-channel and parallel multi-channel systems, as shown in Figure 4. Depending on the arrangement of the detectors, wide-field imaging systems can be divided into line-scanning and surface-scanning systems. The FLIM system based on a synchroscan streak camera is a line-scanning system.

In 2D-FLIM, the total acquisition time is influenced by the dwell time (DT) of the scanner and the number of parallel channels of the measuring instrument: (1) the dwell time is defined as the time during which the laser beam is fixed at a specific position before moving to the next position; (2) the number of parallel channels is defined as the number of independent detection channels capable of simultaneously acquiring fluorescence lifetime data from multi-pixels. The Polygon mirror (BFI Optilas, Lincoln Laser; Minimum(DT) = 0.07 $\mathsf{\mu }$s) and galvanometer (Superscan SC-30-Y-Dig2, Raylase; Minimum(DT) = 1.05 $\mathsf{\mu }$s) are generally selected as high-speed scanners [30].

Summary of the Factors Influencing the Acquisition Speed

Overall, in TCSPC-FLIM and synchroscan SC-FLIM systems, the factors influencing the acquisition speed include the photon emission rate, the photon counting rate, the required SNR, the dwell time, and the number of parallel channels.

Table 2. Factors and their definitions that determine the acquisition time.

Parameter	Definition
Photon Emission Rate (PER)	Number of photons emitted from the sample per unit time.
Photon Counting Rate (PCR)	Number of photons counted via a FLIM system per unit time.
Required SNR	Minimum SNR of the acquired signal when the fitting lifetime meets the fitting accuracy requirements.
Dwell Time (DT)	The time during which the laser beam is fixed at a specific position before moving to the next position.
Number of Parallel Channels (NPC)	The number of independent detection channels capable of simultaneously acquiring fluorescence lifetime data from multi-pixels.

presents these factors and their definitions.

3. Method

Calculating the acquisition time of 2D-FLIM can be divided into two steps: (1) Calculate the single-channel acquisition time ($T_{ch}$) of the FLIM system. (2) Calculate the total acquisition time ($T_{total}$) based on $T_{ch}$, the scanning speed, and the number of parallel channels. $T_{ch}$ is determined using the photon counting rate and required photons. In SC-FLIM, the photon emission rate of the sample and the photon transfer efficiency of the system constitute the photon counting rate. Therefore, when calculating the $T_{total}$ of TCSPC-FLIM and synchroscan SC-FLIM, the photon emission rate, the photon transfer efficiency, the photon counting rate, the required photons, and the number of parallel channels are calculated sequentially.

3.1. Calculation of the Photon Emission Rate

The photon emission rate (PER) is the product of the number of fluorescence photons ($P{h}_{fluorescence}$) produced in a single laser cycle and the laser frequency ($F_{laser}$):

$$PER=P{h}_{fluorescence}\times F_{laser}$$

(2)

where $F_{laser}\le 1/5\tau$ and $P{h}_{fluorescence}$ are represented as in Equations (3) and (4). A is defined as the absorption efficiency of the sample at the excitation wavelength. It is worth noting that the value of A is proportional to the number of chances for excitation; $\Phi$ is the fluorescence quantum yield, $P_{avg}$ and $P_{peak}$ are the average and peak power of the laser, respectively, and $\Delta t_{laser}$ is the pulse width.

$$P{h}_{fluorescence}=P{h}_{laser}\times (1-{10}^{-A})\times \Phi$$

(3)

$$P{h}_{laser}={\displaystyle \frac{P_{avg}/F_{laser}}{h·\nu }}={\displaystyle \frac{P_{peak}\times \Delta t_{laser}}{h·\nu }}$$

(4)

The most straightforward method for enhancing the photon emission rate is to increase the laser power. However, this approach may lead to photobleaching or even photodamage [31]. The use of multiphoton excitation effectively reduces the impact of laser light on sample stability. Single-photon excitation typically does not necessitate the use of high laser power, as the energy of a single photon is sufficient to prompt the molecule to transition directly to an excited state. In contrast, in multiphoton excitation, a fluorescent molecule enters the excited state by absorbing multiple low-energy photons simultaneously. This process necessitates the utilization of exceedingly high instantaneous laser power, with the objective of ensuring that effective nonlinear excitation occurs within the focal region of the laser. Single-photon excitation results in photon absorption across the entire laser path, affecting the sample in both the focal and non-focal regions. In contrast, the non-linear effect of multiphoton excitation occurs only in the focal region, significantly reducing photobleaching and photodamage in the non-focal region. In general, the laser requirements for multiphoton excitation are more demanding, necessitating the use of short-pulse, high-peak-power near-infrared lasers in conjunction with sophisticated optical focusing systems for the nonlinear imaging of deep biological samples [24].

In addition, increasing the fluorophore concentration to improve the photon emission rate is also limited by application scenarios. For example, the fluorophore concentration must be kept non-invasive in live FLIM. In industrial and materials science applications, samples are typically more stable and less sensitive to light damage than biological samples.

3.2. Calculation of the Photon Counting Rate

In the case of a high photon emission rate, the photon counting rate of the FLIM system becomes a significant factor influencing the acquisition time. In a TCSPC-FLIM system, the photon counting rate is dependent on the dead time of the detector and the timing circuit. However, in a multi-photon detection system such as synchroscan SC-FLIM, the photon count rate of the system is dependent on the photon transfer efficiency.

3.2.1. TCSPC-FLIM

For TCSPC at a high count rate and a high signal repetition rate, two instrumental effects have to be considered: (1) the counting loss, the loss of a photon detected within the signal processing time (“Dead time”) of a previous one, and (2) the pile-up effect, the loss of a photon detected in the same signal period with a previous one [17].

“Dead time” is the recovery time required for the photon detector after detecting a photon, during which the photon detector cannot detect new photons. In a time interval ${\Delta }_t$, the detector can detect ${\Delta }_t\times PDR$ photons without considering dead time. Due to the presence of the “Dead time”, the actual photon detection time of the detector in the time interval is ${\Delta }_t+N_{measured}\times t_d$, where $t_d$ is the dead time, $N_{measured}$ is the number of photons actually detected, and the $N_{measured}$ can be expressed in two ways:

$$N_{measured}=PDR\times {\Delta }_t$$

(5)

$$N_{measured}=PCR\times ({\Delta }_t+N_{measured}\times t_d)$$

(6)

where PCR is the photon counting rate, and PDR is the photon detection rate. Therefore, the photon count rate of the TCSPC system can be derived from Equations (5) and (6) as follows:

$$PC{R}_{TCSPC}={\displaystyle \frac{PDR}{(1+PDR\times t_d)}}$$

(7)

Unlike “Counting loss”, the “Pile-up” effect causes an error in the detected fluorescence lifetime:

$${\tau }_{mean}=\tau \times (1-{\displaystyle \frac{PDR/F_{laser}}{4}})$$

(8)

where $\tau$ is the fluorescence lifetime, $F_{laser}$ is the laser frequency, and ${\tau }_{mean}$ is the intensity-weighted lifetime of the measured decay profile. When the PDR is 20% of the excitation laser rate, the error is about 5%, which is small and acceptable in many applications [20].

3.2.2. Synchroscan SC-FLIM

Due to the isotropy of fluorescence and the loss of photons during transmission, the photon counting rate of the SC-FLIM system is determined according to the photon emission rate and the photon transfer efficiency (PTE). Calculating the PTE is a prerequisite for calculating the photon counting rate. In the synchroscan SC-FLIM, as shown in Figure 5, the PTE is composed of the fluorescence focusing system (FFS) and the synchroscan streak camera.

The numerical aperture (NA) determines the angular range over which the objective lens can collect photons. The photon transfer efficiency of an objective lens, ${\eta }_{objective}$, can be expressed in Equations (9) and (10), where $\Omega$ is the photon collection range, and n is the refractivity of the medium in which the objective lens is located.

$${\eta }_{objective}={\displaystyle \frac{\Omega }{4\pi }}={\displaystyle \frac{1-cos\left(\theta \right)}{2}}$$

(9)

$$\theta =si{n}^{-1}({\displaystyle \frac{NA}{n}})$$

(10)

Figure 5. Schematic diagram of synchroscan SC-FLIM system.

Figure 5. Schematic diagram of synchroscan SC-FLIM system.

The photon transfer efficiency of the fluorescence focusing system is denoted as ${\eta }_{FFS}$, which is jointly determined by the reflectivity of the galvanometer, the splitting ratio of the beam splitter, and the transmittance of the beam filter and focusing lens, which can be obtained from the instrument manual.

The photon transfer efficiency of the streak camera is also influenced by the slit size, the photon-electric conversion efficiency of the photocathode, and the electron penetration efficiency of the accelerating electrode. It is assumed that the imaging area of the fluorescence focusing system in the plane where the slit is located is S and that the width and height of the slit are $H_{silt}$ and $W_{silt}$, respectively; the photon transfer efficiency of the slit (${\eta }_{slit}$) is as follows:

$${\eta }_{slit}=\left\{\begin{array}{cc}& 1,S\le H_{slit}\times W_{slit}\\ & (H_{slit}\times W_{slit})/S,S>H_{slit}\times W_{slit}\end{array}\right.$$

(11)

The photon-electric conversion efficiency of the photocathode is ${\eta }_{photocathode}$, and the electron penetration efficiency of the accelerating electrode is ${\eta }_{accelerate}$, which also can be obtained from the instrument manual. The photon transfer efficiency of the whole FLIM system (${\eta }_{SC}$), can be expressed as follows:

$${\eta }_{SC}={\eta }_{objective}\times {\eta }_{FFS}\times {\eta }_{slit}\times {\eta }_{photocathode}\times {\eta }_{accelerate}$$

(12)

Synchroscan streak cameras employ a high-frequency sinusoidal scanning signal to convert a temporal signal into a spatial signal, rapidly accumulating it spatially to form a high-SNR spatial signal. Consequently, the photon counting rate of the streak camera is also dependent on the sinusoidal scanning signal frequency, $F_{sin}$:

$$PC{R}_{SC}={\displaystyle \frac{PER}{F_{laser}}}\times {\eta }_{SC}\times min(F_{laser},F_{sin})$$

(13)

The selection of the frequency of the sinusoidal signal must take into account the necessity of ensuring the accuracy of the signal accumulation. In most cases, the $F_{sin}$ is equal to the $F_{laser}$ or equal to the $F_{laser}/2K$, where $K\in [1,2,3...]$.

3.3. Calculation of the Required Photons

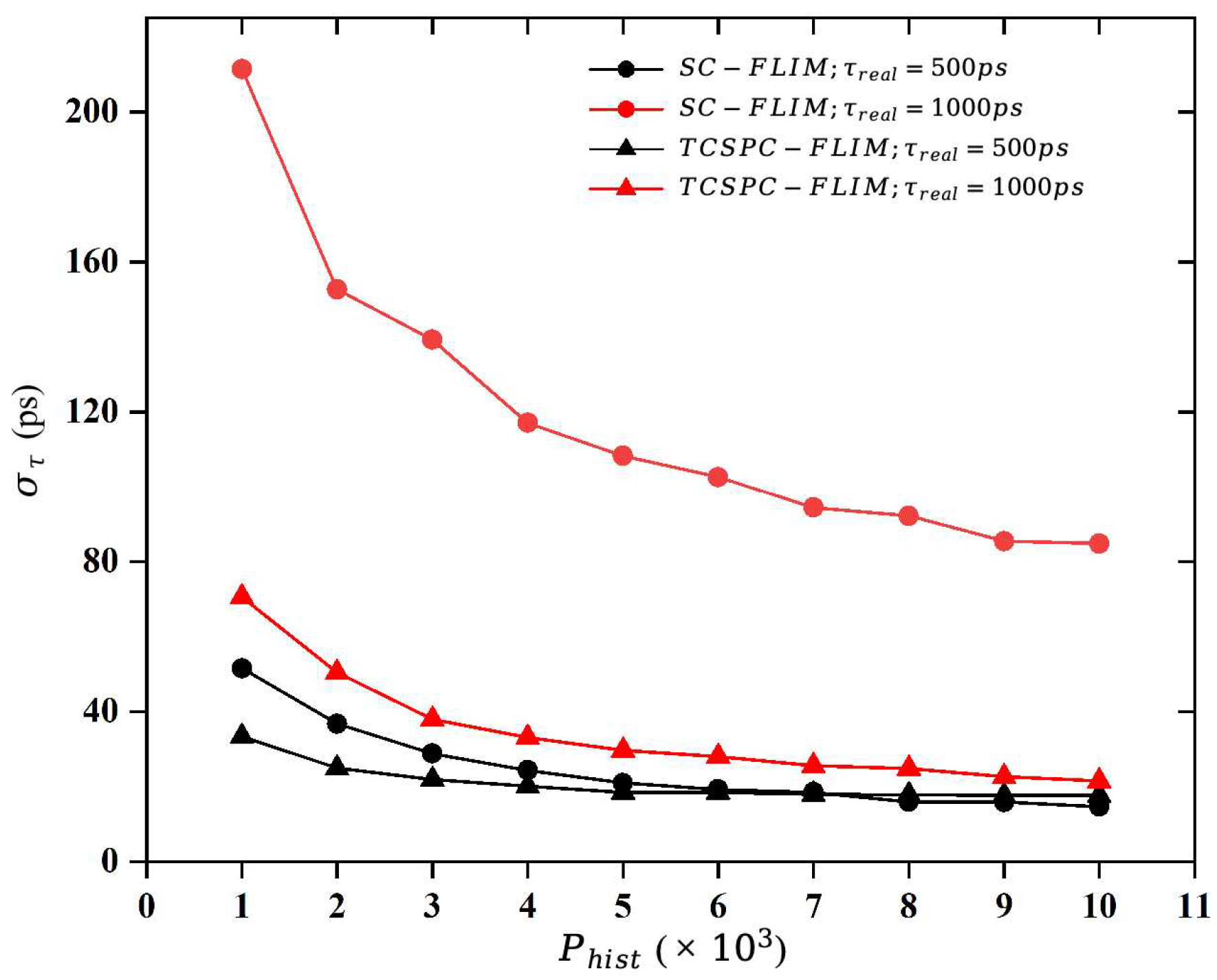
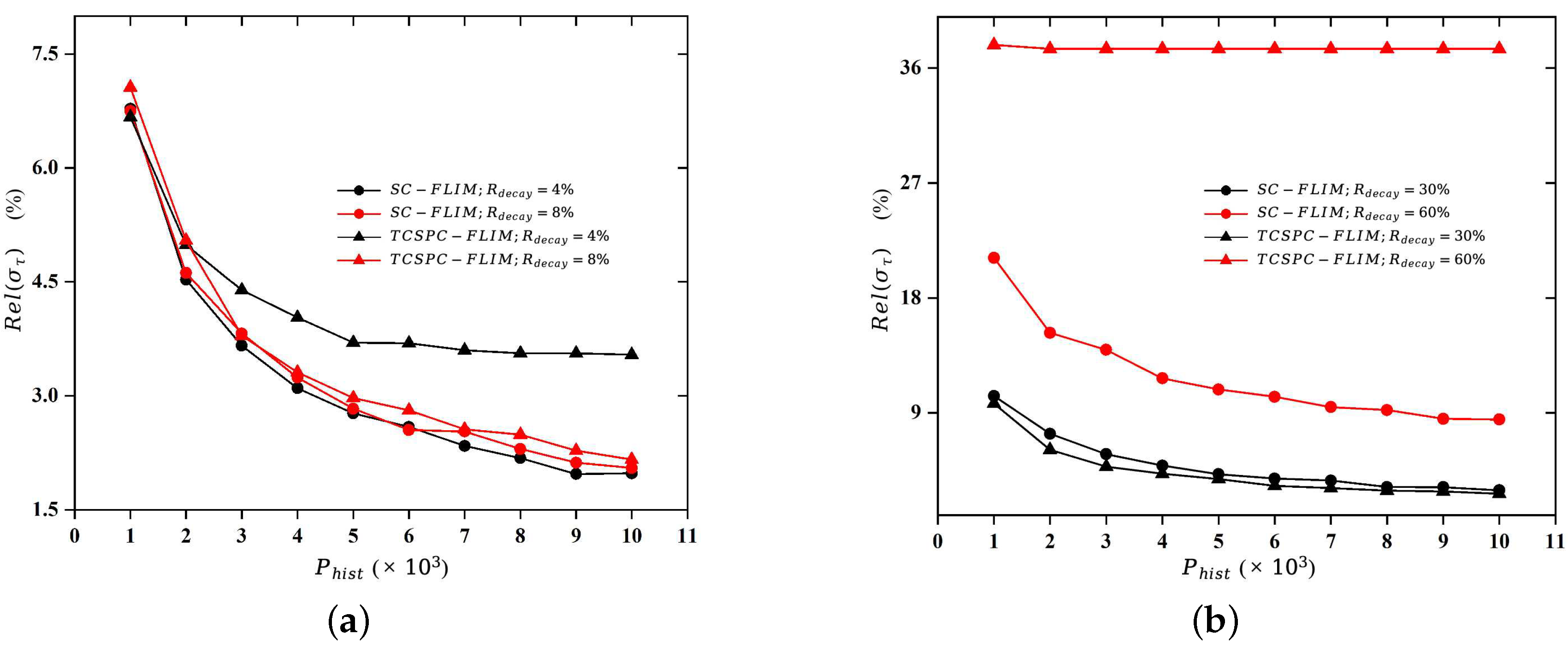
This paper uses numerical simulation methods to calculate the minimum number of photons required to form a fluorescence decay histogram when the fitting error is within a tolerable range, also known as the “Required Photons”. In the actual lifetime imaging process, the fitting error requirement, the systematic error, the fitting algorithm, and the decay model all affect the “Required Photons”.

This study firstly generated a histogram of photon distribution based on the mono-exponential decay model and reconstructed the lifetime using the least-squares fitting algorithm to explore the relationship between the photon number and the fitting accuracy. Then, the study calculated the “Required Photons” according to the fitting error requirement of a standard fluorescent dye, Erythrosin B.

The mono-exponential decay model of fluorescence signal can be expressed as follows:

$$I\left(t\right)=I_0{e}^{(-t/\tau )}$$

(14)

where $\tau$ is the lifetime, $I_0$ is the initial intensity, and $I\left(t\right)$ is the fluorescence intensity at time t. In the numerical simulation, the uniformly distributed random numbers $u\in [0,1]$ are initially converted into mono-exponentially distributed random numbers, t, based on the inverse transformation sampling method:

$$t=-\tau ln(1-u)$$

(15)

The number of mono-exponentially distributed random numbers, t, represents the number of photons, and the value of t represents the photon arrival time. Subsequently, a histogram of the photon arrival time distribution is generated through the mono-exponentially distributed random numbers, t, based on the number of time bins and the width of the time bin. The simulation parameters of the FLIM system are set as shown in

Table 3. Simulation parameter settings of the FLIM system.

	TCSPC-FLIM	Synchroscan SC-FLIM
Number of time bins	256	1600
Width of time bins	50 ps	1 ps

. After the photons are dispersed into different time bins, the fluorescence decay curve is a discrete curve that can be expressed as $I\left[t\right]$.

In a practical FLIM system, the laser pulse, the detector, and the electronics system all have their response times. In order to simulate the measurement signal more realistically, the instrument response function (IRF) is convolved with $I\left[t\right]$ to form the measurement signal $I_m\left[t\right]$ [32]:

$$I_m\left[t\right]=I\left[t\right]\ast IRF\left[t\right]+\epsilon +c$$

(16)

where $\epsilon$ is a system noise obeying a Gaussian distribution, and c is a low-frequency background noise. The IRF for two FLIM systems is defined in reference [33]:

$$IRF\left[t\right]=exp(-{(t-t_0)}^2\times {\displaystyle \frac{4\times ln2}{{\left(FWHM\right)}^2}})$$

(17)

Among them, $FWHM$ represents the full width at half the maximum of the IRF, $t_0$ follows a uniform distribution in the range of $[13\Delta t,15\Delta t]$, and $\Delta t$ is the temporal resolution of the system. Histograms of fluorescence decay with different $SNR$ values are generated by varying $P_{hist}$. Then, the lifetime is calculated using the least-squares fitting method.

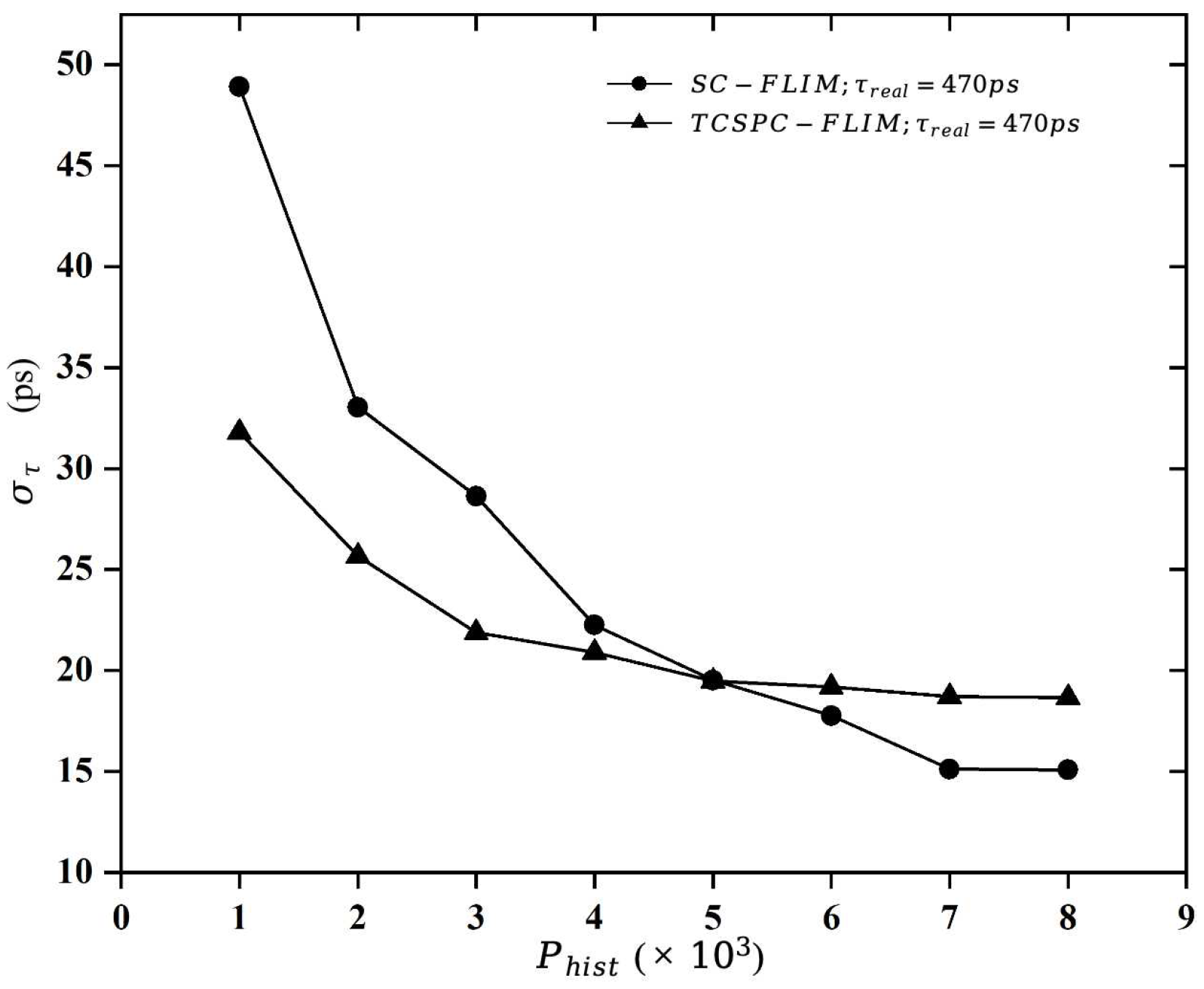
The ultimate goal of the numerical simulation experiment is to determine the “required photons”, which is the minimum number of photons required to form a fluorescence decay histogram ($P_{hist}$). Suppose that the real value of the lifetime is set to ${\tau }_{real}$ and the number of photons to $P_{hist}$ in each of the M simulation experiments. Then, the standard deviation of the measured lifetime ${\sigma }_{\tau }$ is expressed as follows:

$${\sigma }_{\tau }=\sqrt{{\displaystyle \frac{1}{M}}\sum _{k=1}^M{({\tau }_k-{\tau }_{real})}^2}$$

(18)

where ${\tau }_k$ is the fitting lifetime of the k-th experiment. When ${\sigma }_{\tau }$ satisfies the requirements of the experimental scenario, the minimum value of $P_{hist}$ is the “required photons”.

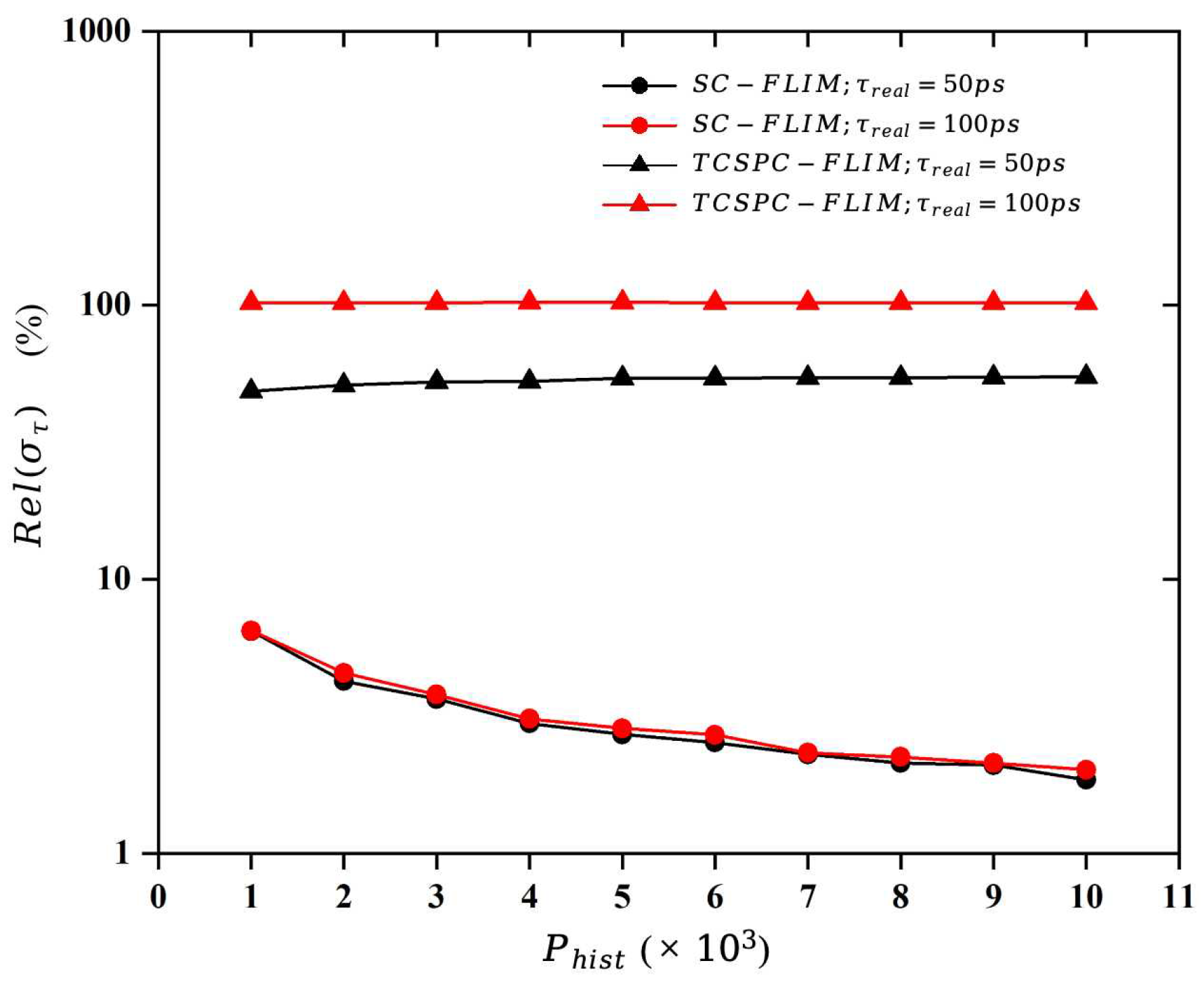
In the numerical simulation, the applicability of the two FLIM systems to the length of a lifetime is demonstrated by means of the relative standard deviation, which is defined as follows:

$$Rel\left({\sigma }_{\tau }\right)={\displaystyle \frac{{\sigma }_{\tau }}{{\tau }_{real}}}\times 100\%$$

(19)

3.4. Calculation of the Number of Parallel Channels

The conventional TCSPC-FLIM system employs a pixel-by-pixel scanning approach to achieve 2D-FLIM, whereas the wide field TCSPC-FLIM utilizes linear or planar array detectors, which no longer permit pixel-by-pixel scanning for 2D-FLIM. It can be observed that the number of parallel channels in a TCSPC-FLIM system is determined by the number of single-photon detectors. However, the synchroscan streak camera has a 1D-FLIM capability, and the number of parallel channels is related to the resolution of the readout camera (RC).

In a synchroscan streak camera, the number of parallel channels is less than or equal to the number of pixels in the x-direction ($P_X$) of the readout frame, as illustrated in Figure 6. This subsection needs to solve the problem of setting the spatial magnification of the fluorescence focusing system, the input optical module, the streak tube, and the output optical module so that the SC-FLIM system can maximize the number of parallel channels with a fixed sample spatial resolution ($C\times C$) and a fixed readout frame size ($P_X\times P_T$, and the pixel size is $A\times A$). The number of parallel channels is greatest when the fluorescence emitted from an area of $C\times C$ on the sample can be captured via a pixel sensor with a size of $A\times A$ on the readout camera.

The function of the slit is to perform a 1D sampling of spatial light signals. Consequently, the light passing through the slit only retains width information. The slit width is defined as $W_{slit}$, and when Equation (20) is satisfied, all light passing through the slit can be recorded via the readout camera.

$$W_{slit}={\displaystyle \frac{P_X\times A}{K_{ST}\times K_{OOM}}}$$

(20)

Among them, $K_{ST}$ and $K_{OOM}$ are the magnification factors of the streak tube and the output optical system, respectively. Typically, $K_{st}$ is fixed before the streak camera leaves the factory. $K_{oom}$ is affected by the area and distance of the effective detection area of the readout camera. Adjusting the $K_{OOM}$ enables the capture of all light signals passing through the slit with the readout camera. This maximizes the utilization of the effective imaging area of the readout camera.

The number of parallel channels is equal to $P_X$, the role of $K_{FFS}$ is to ensure that the system has the required sample spatial resolution (C × C), and C can be expressed as follows:

$$C={\displaystyle \frac{W_{slit}}{K_{FFS}\times NPC}}$$

(21)

Under the assumption that, in a FLIM experiment, the required spatial resolution is 10 $\mathsf{\mu }$m × 10 $\mathsf{\mu }$m (C = 10 $\mathsf{\mu }$m), the slit width is 5 cm ($W_{slit}=5$ cm), and the frame size is 1000 × 1000 ($P_X=P_T=1000$), then $K_{FFS}$ is as follows when NPC = 1000:

$$K_{FFS}={\displaystyle \frac{W_{slit}}{C\times NPC}}={\displaystyle \frac{5\times {10}^4}{10\times 1000}}=5$$

(22)

To ensure the one-dimensionality of the spatial signal, the slit height ($H_{slit}$) is typically a few microns to a dozen microns. However, during weak signal measurements, $H_{slit}$ can be increased appropriately, provided that the following requirements are met:

$$H_{slit}\le C\times K_{FFS}$$

(23)

3.5. Calculation of the Total Acquisition Time

In 2D-FLIM, the total acquisition time of a TCSPC-FLIM system is determined by the single-channel acquisition time ($T_{ch}$), the scanning speed (represented by the dwell time (DT) of the scanner), and the number of parallel channels (NPC). When a resolution of 2D-FLIM is assumed to be $N\times M$, the total acquisition time can be expressed as follows:

$$T_{total-TCSPC}=\lceil {\displaystyle \frac{M}{NPC}}\rceil \times N\times max(DT,T_{ch})$$

(24)

In the synchroscan SC-FLIM system, there is a mutual constraint between the speed of movement of the scanning device and the exposure time of the readout camera. Specifically, when the exposure time of the readout camera is long, the speed of the scanning device must be slowed down accordingly to ensure that, at each scanning position, the readout camera is able to fully complete the data acquisition and recording. Therefore, the total acquisition time for synchroscan SC-FLIM can be expressed as Equation (25), where $T_{exp}$ is the exposure time of the readout camera.

$$T_{total-SC}=\lceil {\displaystyle \frac{M}{NPC}}\rceil \times N\times max(DT,T_{ch},T_{exp})$$

(25)

4. Results

After analyzing the factors in TCSPC-FLIM and SC-FLIM systems, we quantitatively calculated the speed of different FLIM systems in measuring the standard fluorescent dye (Erythrosin B).

4.1. Details of Sample and Measuring Instrument

4.1.1. Standard Fluorescent Dye

Standard fluorescent dyes can be used to calibrate FLIM instruments. The recommended reference for the lifetime of standard fluorescent dyes is [34], a multinational collaborative project involving nine research institutions. We used Erythrosin B as an example. When the solvent is water, the average lifetime obtained via different research institutions is 89 ps with a standard deviation of 3 ps; when the solvent is methanol, the average lifetime is 470 ps with a standard deviation of 20 ps [35].

4.1.2. Parameter Settings in the Measuring Instrument

We quantitatively compared the acquisition time of TCSPC-FLIM and SC-FLIM through simulation experiments. Due to human factors such as the sample storage environment, device selection, and optical path design, the fluorescence photon emission rate and the photon transfer efficiency of SC-FLIM systems are affected. Therefore, this article quantitatively calculates the photon counting rate of the SC-FLIM system under two conditions:

• A high photon emission rate and high photon transfer efficiency: The photon counting rate of the SC-FLIM system is high enough to record the required photons without repeating the excitation-detection process.
• A low photon emission rate and low photon transfer efficiency: The photon counting rate of the SC-FLIM system is equal to the laser frequency, and the number of excitation–detection processes to be repeated is equal to the number of photons required.

Moreover, under the assumption that the laser pulse frequency is 100 MHz, the synchronous frequency of the synchroscan streak camera is 100 MHz, and the minimum dwell time of the galvanometer is 1.05 $\mathsf{\mu }$s.

4.2. Calculation Results of the Required Photons via Numerical Simulation

As the number of photons required to form a histogram ($P_{hist}$) increases, the measured lifetime gets closer to the real lifetime (${\tau }_{real}$), as shown in Figure 7.

When ${\tau }_{real}$ = 500 ps and $P_{hist}$ = 1000, the lifetime measured by the TCSPC method is more accurate because the TCSPC-FLIM system sacrifices some temporal resolution for acquiring a high-SNR signal. When ${\tau }_{real}$ = 1000 ps, the measurement accuracy of the SC-FLIM system is much lower than that of the TCSPC-FLIM system. This result is due to the difference between the FLIM systems in terms of temporal resolution and the number of time bins.

In order to normalize the difference between the FLIM systems in terms of the temporal resolution ($\Delta t$) and the number of time bins ($N_{bin}$), we defined a parameter to represent the ratio of the real lifetime to the total measurement time ($T_{total}=\Delta t\times N_{bin}$), called the $R_{decay}$:

$$R_{decay}={\displaystyle \frac{{\tau }_{real}}{T_{total}}}\ast 100\%$$

(26)

The relative standard deviation of the lifetime measurements of the two FLIM systems at different $R_{decay}$ values are shown in Figure 8.

Due to the low temporal resolution of the TCSPC-FLIM, this system is not able to achieve high-precision measurements for either short-lifetime signals ($R_{decay}$ = 4%) or signals with incomplete decay ($R_{decay}$ = 60%). Although the range of $R_{decay}$ applied to the TCSPC-FLIM system is narrower than the range of $R_{decay}$ applied to the SC-FLIM system, the TCSPC-FLIM system has a wide dynamic range of lifetime measurements because of the system’s long total measurement time ($T_{total}$). In the simulation experiment, four groups of $R_{decay}$ were set up, as shown in

Table 4. The lifetime of fluorescence signals collected via two FLIM systems under the same ${\mathrm{R}}_{decay}$ value.

${\mathbf{R}}_{\mathit{decay}}$	SC-FLIM $({\mathbf{\Delta }}_{\mathit{t}}=1\mathit{ps};{\mathit{N}}_{\mathit{bin}}=1600)$	TCSPC-FLIM $({\mathbf{\Delta }}_{\mathit{t}}=50\mathit{ps};{\mathit{N}}_{\mathit{bin}}=256)$
4%	64 ps	512 ps
8%	128 ps	1024 ps
30%	480 ps	3840 ps
60%	960 ps	7680 ps

.

To further illustrate the advantages of the high temporal resolution of the streak camera in short-lifetime signals’ measurement, we simulated the FLIM process for fluorescence signals with lifetimes of 50 ps and 100 ps, and the results are shown in Figure 9. This lifetime already exceeded the lower measurement limit of the TCSPC-FLIM system, while the SC-FLIM system can still realize high-precision FLIM.

Different application scenarios have different requirements for ${\sigma }_{\tau }$. In this numerical simulation, in order to quantitatively calculate the minimum $P_{hist}$, Erythrosine B, a standard fluorescent dye, was used as the simulation sample, and the requirement for ${\sigma }_{\tau }$ was less than 20 ps. As shown in Figure 10, when ${\sigma }_{\tau }$ satisfies the requirement, the minimum $P_{hist}$ is 5000. So, when the sample is Erythrosin B (the solvent is methanol), the “required Photons” of SC-FLIM system and TCSPC-FLIM system equal 5000.

Figure 9. Measurement accuracy of two FLIM systems for short-lifetime signals (${\tau }_{real}=50$ ps and ${\tau }_{real}=100$ ps).

Figure 9. Measurement accuracy of two FLIM systems for short-lifetime signals (${\tau }_{real}=50$ ps and ${\tau }_{real}=100$ ps).

Figure 10. Measurement accuracy of two FLIM systems for Erythrosine B (methanol as a solvent).

Figure 10. Measurement accuracy of two FLIM systems for Erythrosine B (methanol as a solvent).

4.3. Calculation of Acquisition Time

4.3.1. Acquisition Time of TCSPC-FLIMs

In practical scenarios, to minimize the occurrence of the “pile-up” effect, the photon detection rate (PDR) of classical TCSPC technology is usually set to one-tenth of the laser pulse frequency. In addition, in the classical TCSPC system, the dead time is usually in the range of 20 ns to 200 ns [20], and the minimum photon counting rate can be derived from Equation (7) to be 4 MHz. Therefore, the single-channel acquisition time ($T_{ch}$) of this system for a high-precision measurement of the fluorescence lifetime of Erythrosin B is at least 1.25 ms.

Hybrid PMTs can reduce the dead time of detectors to less than 1ns, and TDCs devices can reduce the dead time of counters to less than 1ns [32]. Therefore, the “Counting loss” due to dead time in the TCSPC-FLIM system is ignored, and the photon counting rate of the TCSPC system that combines PMT and TDC can be equivalent to one-twentieth of the laser pulse frequency. The $T_{ch}$ can be shortened to 0.25 ms. However, reducing the dead time is not a recommended approach to enhancing the photon counting rate because decreasing the detector’s dead time can lead to an increase in background noise caused via detector afterpulsing [17].

In these TCSPC-FLIM systems, the number of parallel channels is 1. When the resolution of the target lifetime image is $N\times M$, the data acquisition time for 2D-FLIM can be calculated according to Equation (24). Since the dwell time of the galvanometer is much lower than the single-channel acquisition time of the TCSPC system, the total acquisition time ($T_{N\times M}$) is determined via the single-channel acquisition time and the total number of pixels.

Table 5. Data acquisition time of the different TCSPC-FLIM systems.

TCSPC Technologies	Minimum PCR	${\mathbf{T}}_{\mathit{ch}}$	${\mathbf{T}}_{2048\times 2048}$	${\mathbf{T}}_{256\times 256}$
Classical TCSPC	4 MHz	1.25 ms	5242.88 s	81.92 s
Hybrid PMT	20 MHz	0.25 ms	1048.58 s	16.384 s
SPAD array (64 × 64)	13,516.8 MHz 1	1.25 ms 2	1.54 s 3	0.02 s 4

¹ The minimum global photon counting rate is equal to $3.3\times 64\times 64$ MHz. ² Each individual TCSPC-FLIM channel utilizes classical TCSPC technology. ³ For images with a size of 2048 × 2048, the 64 × 64 SPAD array requires 1024 repetitions of data acquisition. ⁴ For images with a size of 256 × 256, the 64 × 64 SPAD array requires 16 repetitions of data acquisition.

presents the single-channel acquisition time and 2D-FLIM acquisition time for various TCSPC systems.

In recent years, SPAD arrays with time measurement capabilities have promoted the rapid development and application of wide-field FLIM. The number of parallel channels of the TCSPC-FLIM system based on the SPAD array can reach up to 32 × 32, 64 × 64, and even 256 × 256 pixels [20].

4.3.2. Acquisition Time of Synchroscan SC-FLIMs

As previously stated in Section 4.1.2, we calculated the photon counting rate (PCR) of the synchroscan SC-FLIM system in two scenarios and calculated the acquisition time using PHANTOM’s T4040 as the readout camera (a frame rate of up to 13,510 fps at a resolution of 2048 × 1152 pixels) [36] and Raylase’s Superscan SC-30-Y-Dig2 as the scanning galvanometer (a dwell time as low as 1.05 $\mathsf{\mu }$s).

In the high photon emission rate and high photon transfer efficiency (High-PER and High-PTE) condition, when the SC-FLIM system measures the lifetime of Erythrosin B, the photon counting rate reaches up to ${10}^8$ MHz. The single-channel acquisition time ($T_{ch}$) is equal to the time of an excitation–detection process, which is the reciprocal of the laser frequency ($T_{ch}$ = 10 ns). However, the camera’s minimum exposure time is 74.02 $\mathsf{\mu }$s, which is much greater than 10 ns, so $T_{ch}$ = 74 $\mathsf{\mu }$s. In some special cases, the resolution of the camera can be reduced to increase the frame rate, such as when the fluorescence signal has a very short lifetime and the decay signal is only present on some of the line pixels of the readout image. At a resolution of 2560 × 256, the frame rate can be increased to 60,500 fps with a single-channel acquisition time of 16.53 $\mathsf{\mu }$s.

In the low photon emission rate and low photon transfer efficiency (Low-PER and Low-PTE) condition, when the SC-FLIM system measures the lifetime of Erythrosin B, the photon counting rate (PCR) is 100 MHz. The method for calculating the necessary exposure time of the readout camera at this time is as follows:

$$T_{exp}={\displaystyle \frac{Min\left(P_{hist}\right)}{PCR}}$$

(27)

When $Min\left(P_{hist}\right)$ = 5000, the necessary exposure time is 50 $\mathsf{\mu }$s. Since the lifetime of Erythrosin B is 470 ps, increasing the frame rate by reducing the resolution of the camera is not recommended, and the minimum exposure time of the camera remains at 74.02 $\mathsf{\mu }$s, so $T_{ch}$ = 74.02 $\mathsf{\mu }$s.

In 2D-FLIM, if the resolution of the readout camera is $N\times M$, the number of parallel channels is N. Since the dwell time of the galvanometer is smaller than the single-channel acquisition time of the SC-FLIM system, the total acquisition time ($T_{N\times M}$) is determined by the single-channel acquisition time, the total number of pixels, and the number of parallel channels. For a lifetime image of $2048\times 2048$ and $256\times 256$, the total acquisition time can be expressed as in

Table 6. Data acquisition time of the synchroscan SC-FLIM system in different conditions.

Simulated Conditions	Readout Camera	${\mathbf{T}}_{\mathit{ch}}$ vs. ${\mathbf{T}}_{\mathit{exp}}$ 1	${\mathbf{T}}_{2048\times 2048}$	${\mathbf{T}}_{256\times 256}$
High-PER and High-PTE	13,510 fps (2048 × 1152)	10 ns < 74.02 $\mathsf{\mu }$s	0.15 s	0.019 s
High-PER and High-PTE	60,500 fps (2560 × 256)	10 ns < 16.53 $\mathsf{\mu }$s	0.03 s	0.424 ms
Low-PER and Low-PTE	13,510 fps (2048 × 1152)	50 $\mathsf{\mu }$s < 74.02 $\mathsf{\mu }$s	0.15 s	0.019 s

¹$T_{ch}$ indicates the theoretical single-channel acquisition time, and the actual single-channel acquisition time is determined by the camera’s minimum exposure time and $T_{ch}$ together.

.

Although the speed of the wide-field TCSPC-FLIM system based on SPAD arrays can be close to that of the SC-FLIM system, it still cannot surpass the classical TCSPC-FLIM imaging in terms of spatial resolution and SNR. Moreover, as the number of channels increases in the wide-field TCSPC-FLIM system, the cost also doubles. Compared with high-precision TCSPC-FLIM, SC-FLIM has increased the imaging speed of FLIM systems by at least ${10}^4$ times.

5. Discussion

The acquisition time of FLIM systems is related to the photon emission rate, the photon counting rate, the number of “required photons”, the dwell time of the scanning device, and the number of parallel channels. Therefore, we provide a detailed analysis of these factors through numerical simulation and theoretical modeling, and we quantitatively compare the acquisition time of the TCSPC-FLIM and SC-FLIM systems when Erythromycin B is used as a sample. The results of this paper quantitatively illustrate that the synchroscan streak camera with a unique lifetime measurement approach has great potential for implementing Fast-FLIM, which has an acquisition speed about 14,000 times faster than the TCSPC-FLIM system.

Compared with TCSPC technology, the synchroscan streak camera is more suitable for the fluorescence lifetime imaging of samples with high fluorescence intensity and a short fluorescence lifetime. Although the acquisition speed of the TCSPC-FLIM system based on the SPAD array is similar to that of the SC-FLIM system (with a low photon detection rate), the TCSPC-FLIM system based on the SPAD array has a low spatial resolution and a low SNR for the acquired signal. As the readout camera frame rate increases, the acquisition speed of the SC-FLIM system will also be further improved. In addition, the synchroscan streak camera commonly has the single-photon detection mode of operation and a broader spectral response range, which can adapt to a more comprehensive range of application scenarios.

In the future, with the continuous development of streak camera technology, spatial scanning technology, and high frame rate camera technology, as well as the application of deep learning algorithms in lifetime fitting, synchroscan streak cameras will be able to be effectively applied to Fast-FLIM. This advancement will enable FLIM technology to play a crucial role in clinical diagnosis and industrial detection.