Enhancing the Cooling of a Rotating Mirror in a Laguerre–Gaussian Cavity Optorotational System via Nonlinear Cross-Kerr Interaction

Abstract

The cooling of a macroscopic mechanical oscillator to its quantum ground state is an important step for achieving coherent control over mechanical quantum states. Here, we theoretically study the cooling of a rotating mirror in a Laguerre–Gaussian (L-G) cavity optorotational system with a nonlinear cross-Kerr (CK) interaction. We discuss the effects of the nonlinear CK coupling strength, the cavity detuning, the power of the input Gaussian beam, the topological charge (TC) of the L-G cavity mode, the mass of the rotating mirror, and the cavity length on the cooling of the rotating mirror. We find that it is only possible to realize the improvement in the cooling of the rotating mirror by the nonlinear CK interaction when the cavity detuning is less than the mechanical frequency. Compared to the case without the nonlinear CK interaction, we find that the cooling of the rotating mirror can be improved by the nonlinear CK interaction at lower laser powers, smaller TCs of the L-G cavity mode, larger masses of a rotating mirror, and longer optorotational cavities. We show that the cooling of the rotating mirror can be enhanced by the nonlinear CK interaction by a factor of about 23.3 compared to that without the nonlinear CK interaction.

1. Introduction

In the last two decades, there has been a great surge of interest in optomechanical systems due to their potential applications in the exploration of the quantum–classical boundary of massive objects [1] and high-precision measurement [2]. The optomechanical systems are composed of optical modes coupled to micro- and nanomechanical oscillators by way of radiation pressure of light. Due to the coupling of the mechanical oscillator to the thermal environment, the inevitably thermal noise acting on the mechanical oscillator is the main obstacle towards observing quantum phenomena in the optomechanical system. Thus, cooling the mechanical oscillator down to its ground state is a necessary step to observe quantum phenomena in such a system. Up to now, many different methods have been employed to cool the mechanical oscillator. It has been reported that the mechanical oscillator can be cooled to near its quantum mechanical ground state with the aid of the measurement-based feedback loop [3,4,5] and the coherent feedback loop [6,7,8]. Moreover, it has been shown theoretically that a mechanical oscillator can be cooled down to near its quantum ground state in the resolved-sideband limit [9,10,11], which has been demonstrated experimentally [12,13,14]. It is noted that the method used in [9,10] is based on the steady-state of the system, whereas the method used in [11] is based on a dynamical process. In the experiments [12,13,14], the phonon number of the mechanical oscillator has been reduced to 0.34, 0.85, and 0.09 from 20 mK, 20 K, and 2 K, respectively. In addition, it has been shown that the ground state of the mechanical oscillator in the unresolved sideband regime can be approached by using a pulsed cooling scheme [15,16] and using electromagnetically induced transparency [17,18]. Additionally, it has been pointed out that the ground-state cooling of the mechanical oscillator can be reached by combining the optomechanical system with identical ground-state two-level atoms [19], an optical parametric amplifier [20,21], a second microwave (or optical) auxiliary resonator [22], a squeezed light [23], an incoherent thermal light [24], a three-level atomic ensemble [25], two controllable external optical driving fields [26], an auxiliary high-quality optical cavity [27], and two red-detuned driving lasers [28].

In 2007, Bhattacharya and Meystre proposed a Laguerre–Gaussian (L-G) cavity optorotational system, in which a L-G cavity mode is coupled to a macroscopic rotating mirror through radiation torque [29]. The L-G beam is characterized by a helical wavefront and a doughnut-shaped intensity distribution [30]. It carries an orbital angular momentum of $l\hslash$ per photon with l being the topological charge (TC) value [30]. Experimentally, there are many methods to generate the L-G beam, including spatial light modulators [31], spiral phase plate [32], and computer-generated holograms [33]. It has been pointed out that the phonon number of the rotating mirror can be reduced to less than 1 from 3 K due to the exchange of orbital angular momentum from a L-G cavity mode to the rotating mirror [29], which allows one to observe many physical phenomena in such systems. Feng et al. have shown the electromechanically induced transparency behavior in an L-G cavity optorotational system, and found that the TC carried by the L-G cavity mode can be detected via measuring the linewidth of the window of eletromechanically induced transparency [34]. Peng et al. have studied the double electromagnetically induced transparency in an L-G cavity optorotational system with two mechanical modes [35]. Abbas et al. have investigated the double electromechanically induced transparency behavior in the double optomechanical cavities, in which one cavity is the L-G cavity [36]. Xiong et al. have found that the L-G sum-sideband generation can be remarkable even at a lower input laser power under matching conditions [37]. Mahmoudi et al. have studied the influence of the coupling power and the cavity detuning on the second-order upper sideband generation in the L-G cavity optorotational system [38]. Bhattacharya et al. have shown that radiation torque can give rise to the entanglement between an L-G cavity mode and a rotating mirror [39]. Chen et al. have studied the stationary entanglement between the two rotating mirrors coupled to the same L-G cavity field [40]. Cheng et al. have shown that the genuine tripartite entanglement among the L-G cavity mode, the magnon mode, and the phonon mode in a hybrid rotating cavity optorotational system [41]. Lai et al. have studied that the cross-Kerr interaction can enhance the stationary entanglement between an L-G cavity mode and a rotating mirror [42]. Liu et al. have studied that a rotating mirror can be cooled close to its ground state in a double L-G cavity optorotational system with a two-level atomic ensemble [43].

The optical Kerr effect is the change in the refractive index of a nonlinear medium when a strong signal wave is applied [44], and the change in the refractive index is proportional to the intensity of the signal field. For two electric fields acting on a nonlinear medium simultaneously, the cross-Kerr (CK) effect is generated, and the variation in the refractive index of the nonlinear medium related to the propagation of one field is proportional to the intensity of the other [45]. During the past several decades, CK nonlinearity can complete many tasks in quantum information processing, such as constructing quantum phase gates [46], creating macroscopic quantum superposition states [47], completing quantum teleportation [48], and realizing entanglement purification [49]. Recent papers have shown that a CK type of coupling can appear between a micromechanical resonator and a microwave cavity field by using a Josephson junction qubit [50,51]. The reason is that there is a change in the photon Stark shift due to the phonon-driven qubit Stark shift, and it implies a term of the form $c^{†}c{a}^{†}a$, which is of the form of the CK effect between the microwave cavity mode c and the mechanical mode a [50]. The nonlinear CK coupling strength $g_{ck}$ depends on the radiation-pressure coupling strength $g_0$, the Josephson energies, the charging energy of a single electron, and so on [50], and it is estimated that $g_{ck}$ can be about $0.25g_0$ [50]. The CK coupling can also appear in a cold Rydberg gas [52] and a ferrimagnetic crystal [53]. In the past few years, the optomechanical systems with a nonlinear CK coupling are a subject of growing interest. For instance, it has been found that the CK coupling can affect the mechanical frequency shift, the optical damping rate, and the mechanical cooling [54], the stable behavior of the intracavity photon number [55,56], the optical nonreciprocity [57], the photon blockade effect [58], and the steady-state entanglement between the optical and mechanical modes [59,60].

In this paper, we study the cooling of the rotating end mirror in a L-G cavity optorotational system in the presence of the nonlinear CK interaction. We analyze how the nonlinear CK interaction strength, the cavity detuning, the power of the input Gaussian beam, the TC of the L-G cavity mode, the mass of the rotating mirror, and the cavity length affect the cooling of the rotating end mirror. In the presence of the nonlinear CK interaction, we find that it is possible to improve the cooling of the rotating end mirror only when the cavity detuning is less than the frequency of the rotating end mirror. With the nonlinear CK interaction, the cooling of the rotating end mirror can be substantially improved at lower input powers, smaller TCs of the L-G cavity mode, larger masses of the rotating mirror, and longer optical cavity.

The remainder of this paper is organized as follows. In Section 2, we introduce the theoretical model under study, give the Hamiltonian of the coupled system, and derive the time evolution equations, and calculate the steady-state solution to the time evolution equations. In Section 3, we calculate the variances of the angular displacement and the angular momentum of the rotating end mirror in the steady-state. In Section 4, we analyze the influence of the nonlinear CK interaction strength, the cavity detuning, the power of the input Gaussian beam, the TC of the L-G cavity mode, the mass of the rotating end mirror, and the cavity length on the cooling of the rotating end mirror. In Section 5, we summarize our results.

2. Model

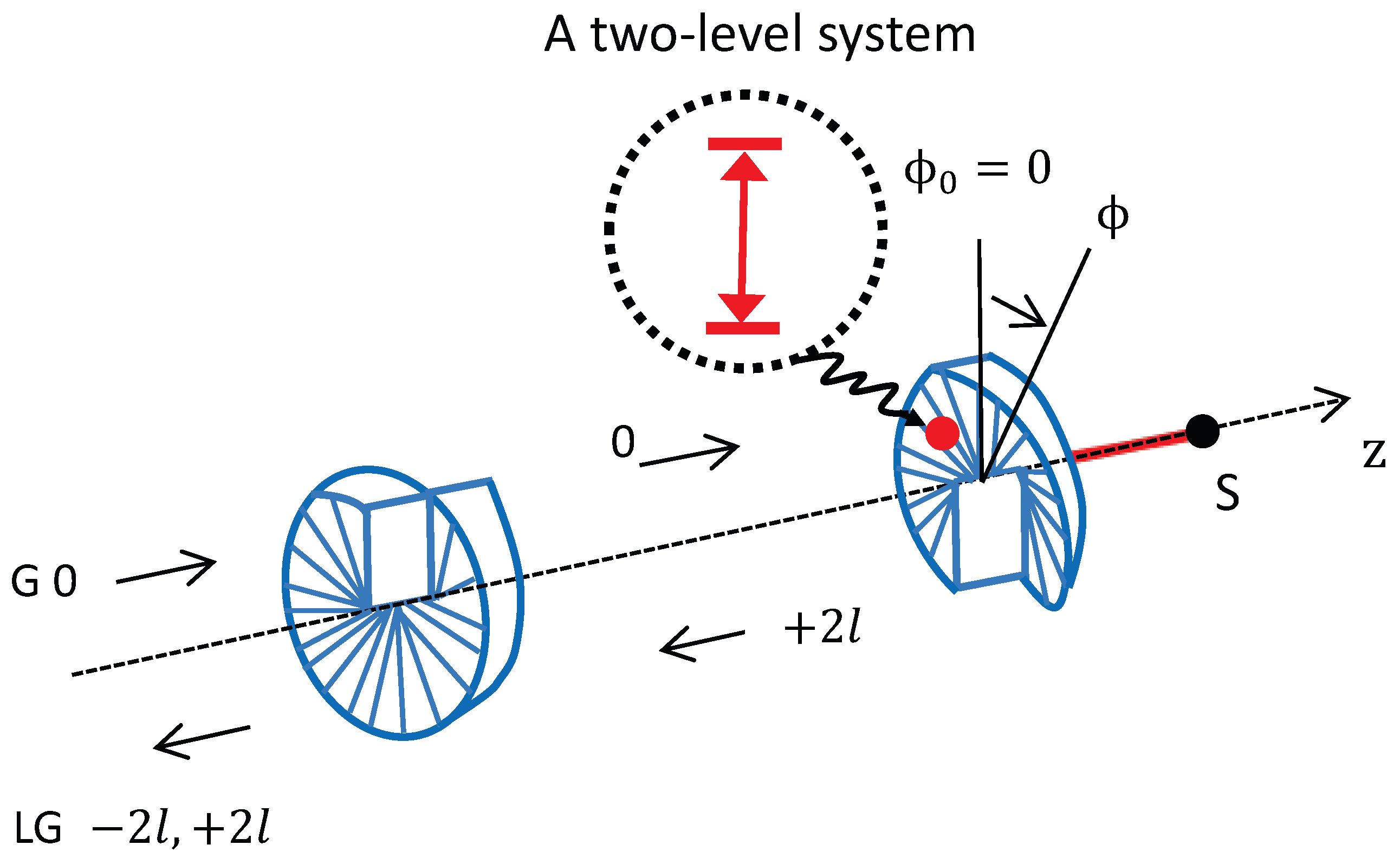
Our hybrid system consists of a one-dimensional L-G cavity optorotational system [29] with nonlinear CK interaction, as shown in Figure 1. The L-G cavity optorotational system is formed by two spiral phase elements separated by a distance of L. The left one is a fixed partially transmitting mirror, while the right one is a totally reflective mirror rotating about the z axis. Spiral phase elements are used to modify the TC of the light beams. The left mirror does not change the TC of the light beam transmitting through it, but reduces a TC $2l$ from the light beam upon reflection, while the right mirror adds a TC $2l$ to the light beam upon reflection. When a Gaussian light beam with TC zero is injected on the left mirror, an L-G cavity mode is built up in the cavity. The TCs of the light beams at different positions along the z axis are shown in Figure 1. When the photons in the cavity interact with the rotating end mirror, the angular momentum exchange between them leads to a radiation torque applied to the rotating end mirror, causing the rotating end mirror to oscillate about the z axis. During the time $2L/c$ taken by the photons in the cavity to travel each round trip, the angular momentum exchange between a photon in the cavity and the rotating end mirror is $2l\hslash$; thus, the optical torque exerted on the rotating end mirror is equal to the angular momentum exchange per unit time is $2l\hslash /(2L/c)=\hslash g_{\varphi }$, where $g_{\varphi }={\displaystyle \frac{cl}{L}}$ is the coupling parameter between a single intracavity photon and the rotating end mirror, c is the light speed in vacuum, and l is the TC of the cavity mode. The rotating end mirror is a thin disk with mass m, radius R, rotational frequency ${\omega }_m$, and damping rate ${\gamma }_m$. Thus, $I={\displaystyle \frac{1}{2}}m{R}^2$ is the moment of inertia of the rotating end mirror about the z axis passing through its center, and the rotating end mirror can be modeled as a damped harmonic oscillator. The angular displacement and conjugate angular momentum operators of the rotating end mirror are denoted by $\varphi$ and $L_z$, respectively. We define the annihilation (creation) operator b ($b^{†}$) of the rotating end mirror as $b={\displaystyle \frac{1}{\sqrt{2}}}(\varphi +i{L}_z)$ ($b^{†}={\displaystyle \frac{1}{\sqrt{2}}}(\varphi -i{L}_z)$), respectively. In the adiabatic limit, the frequency ${\omega }_m$ of the rotating end mirror satisfies ${\omega }_m\ll \pi c/L$, the mirror rotates so slowly that we can consider one cavity mode at frequency ${\omega }_c$ only, and the photons at other frequencies generated by the movement of the rotating end mirror can be neglected [61]. Under the adiabatic approximation, the photons produced by the Casimir effect [62] and the rotational Doppler effect [63] can be ignored. In addition, we assume that an additional CK coupling exists between the cavity field and the rotating end mirror [51].

The Hamiltonian of the entire optorotational system with the nonlinear CK interaction is given by

$$H_0=H_{opt}+H_{ck}.$$

(1)

In Equation (1), $H_{opt}$ is the Hamiltonian of the optorotational system without the nonlinear CK interaction, and is given by

$$H_{opt}=\hslash {\omega }_c{a}^{†}a+\hslash {\omega }_m{b}^{†}b-\hslash g{a}^{†}a(b+b^{†})+i\hslash \epsilon (a^{†}{e}^{-i{\omega }_{l}t}-a{e}^{i{\omega }_{l}t}),$$

(2)

where the first term is the energy of the cavity field, a and $a^{†}$ are the annihilation and creation photon operators in the cavity, satisfying the commutation relation $[a,a^{†}]=1$, the second term is the energy of the rotating end mirror, the third term describes the interaction between the cavity field and the rotating end mirror, and g characterizes the single-photon optorotational coupling rate and is related to the original coupling constant $g_{\varphi }$ by $g=g_{\varphi }\sqrt{{\displaystyle \frac{\hslash }{2I{\omega }_m}}}$, the final term denotes that the cavity field is driven by a Gaussian beam with amplitude $\epsilon =\sqrt{{\displaystyle \frac{2\kappa \wp }{\hslash {\omega }_l}}}$. It is noted that $\epsilon$ is proportional to the square root of the input laser power ℘ and the cavity decay rate $\kappa$. In Equation (1), $H_{ck}$ is the Hamiltonian corresponding to the nonlinear CK interaction, and is given by

$$H_{ck}=-\hslash g_{ck}{a}^{†}a{b}^{†}b.$$

(3)

where $a^{†}a$ denotes the photon number operator for the cavity field and $b^{†}b$ denotes the phonon number operator for the rotating end mirror. To transform the Hamiltonian of the system into the rotating frame, which rotates at the drive frequency ${\omega }_l$, we apply the unitary transformation $S=exp(-i{\omega }_l{a}^{†}at)$. Then, the total Hamiltonian for the coupled field-mirror system can be written as

$$\begin{array}{c}H=S{H}_0{S}^{†}+iS{\displaystyle \frac{\partial H_0}{\partial t}}{S}^{†},\hfill \\ =\hslash ({\omega }_c-{\omega }_l)a^{†}a+\hslash {\omega }_m{b}^{†}b-\hslash g{a}^{†}a(b+b^{†})-\hslash g_{ck}{a}^{†}a{b}^{†}b+i\hslash \epsilon (a^{†}-a),\hfill \end{array}$$

(4)

According to the Heisenberg equation of motion, the quantum dynamics of the considered system can be described by the following equations:

$$\begin{array}{c}\dot{a}=-[\kappa +i({\omega }_c-{\omega }_l)]a+iga(b+b^{†})+i{g}_{ck}a{b}^{†}b+\epsilon +\sqrt{2\kappa }{a}_{in},\hfill \\ \dot{b}=-({\displaystyle \frac{{\gamma }_m}{2}}+i{\omega }_m)b+ig{a}^{†}a+i{g}_{ck}{a}^{†}ab+\sqrt{{\gamma }_m}{b}_{in},\hfill \end{array}$$

(5)

where we have included the corresponding damping and noise terms, $a_{in}$ describes the vacuum noise entering the cavity through the fixed mirror, and $b_{in}$ describes the thermal noise acting on the rotating end mirror due to its contact with the thermal environment at temperature T. The expectation values of $a_{in}$ and $b_{in}$ vanish at all times, i.e., $\langle a_{in}\left(t\right)\rangle =\langle b_{in}\left(t\right)\rangle =0$. Under the Markov approximation, the time correlation functions for the input noise operators $a_{in}$ and $b_{in}$ are given by

$$\begin{array}{c}\langle a_{in}\left(t\right)a_{in}^{†}\left(t^{\prime }\right)\rangle =\delta (t-t^{\prime }),\hfill \\ \langle b_{in}^{†}\left(t\right)b_{in}\left(t^{\prime }\right)\rangle =n_{th}\delta (t-t^{\prime }),\hfill \\ \langle b_{in}\left(t\right)b_{in}^{†}\left(t^{\prime }\right)\rangle =(n_{th}+1)\delta (t-t^{\prime }),\hfill \end{array}$$

(6)

where $n_{th}={(e^{\hslash {\omega }_m/\left(k_{B}T\right)}-1)}^{-1}$ is the mean thermal phonon number of the rotating end mirror, and $k_B$ is the Boltzmann constant. When the system reaches the steady-state, the expectation values of the system operators are found to be

$$\begin{array}{c}{a}_s={\displaystyle \frac{\epsilon }{\kappa +i[{\Delta }_0-g(b_s+b_s^{*})-g_{ck}|b_s{|}^2]}},\hfill \\ b_s={\displaystyle \frac{ig{|a_s|}^2}{\frac{{\gamma }_m}{2}+i({\omega }_m-g_{ck}|a_s{|}^2)}},\hfill \end{array}$$

(7)

where ${\Delta }_0={\omega }_c-{\omega }_l$ is the cavity detuning with respect to the frequency ${\omega }_l$ of the input Gaussian beam, $a_s$ is the cavity amplitude at the steady-state, and $b_s$ is the mechanical amplitude at the steady-state. Notably, the stationary amplitudes $a_s$ and $b_s$ are dependent on the optorotational coupling rate g and the nonlinear CK interaction strength $g_{ck}$. In the absence of the optorotational coupling ($g=0$), the stationary mechanical amplitude is $b_s$ = 0, the stationary angular displacement is ${\varphi }_s=0$, and the stationary cavity amplitude is $a_s={\displaystyle \frac{\epsilon }{\kappa +i{\Delta }_0}}$, thus the cavity field and the rotating end mirror are decoupled.

3. Quantum Fluctuations

We are here concerned with the cooling of the rotating end mirror; thus, we need to calculate the small quadrature fluctuations of the rotating end mirror. We assume that an external strong Gaussian laser beam drives an L-G cavity mode. Thus, the operators a and b can be decomposed into the sum of the expectation values $o_s$ and the small fluctuations $\delta o$, i.e., $o=o_s+\delta o$ ($o=a,b$). Only taking into account the first order in the small fluctuations, we obtain the linearized equations for the fluctuations $\delta a$ and $\delta b$

$$\begin{array}{c}\delta \dot{a}=-(\kappa +i\Delta )\delta a+i{a}_s{G}^{*}\delta b+i{a}_{s}G\delta b^{†}+\sqrt{2\kappa }{a}_{in},\hfill \\ \delta \dot{b}=-({\displaystyle \frac{{\gamma }_m}{2}}+i{\overline{\omega }}_m)\delta b+i{a}_s^{*}G\delta a+i{a}_{s}G\delta a^{†}+\sqrt{{\gamma }_m}{b}_{in},\hfill \end{array}$$

(8)

where $\Delta ={\Delta }_0-g(b_s+b_s^{*})-g_{ck}{\left|b_s\right|}^2$, $G=g+g_{ck}{b}_s$, and ${\overline{\omega }}_m={\omega }_m-g_{ck}{\left|a_s\right|}^2$. In Equation (8), the dependence of $\delta \dot{a}$ ($\delta \dot{b}$) on $\delta b$ ($\delta a$) represents the beam-splitter interaction, which leads to the cooling of the rotating end mirror, and the dependence of $\delta \dot{a}$ ($\delta \dot{b}$) on $\delta b^{†}$ ($\delta a^{†}$) represents the two-mode squeezing interaction, which leads to the heating of the rotating end mirror [64].

The dimensionless quadrature fluctuations of the rotating end mirror are given by $\delta \varphi ={\displaystyle \frac{1}{\sqrt{2}}}(\delta b+\delta b^{†})$, $\delta L_z={\displaystyle \frac{1}{i\sqrt{2}}}(\delta b-\delta b^{†})$. The dimensionless quadrature fluctuations of the cavity field are given by $\delta x={\displaystyle \frac{1}{\sqrt{2}}}(\delta c+\delta c^{†})$ and $\delta y={\displaystyle \frac{1}{i\sqrt{2}}}(\delta c-\delta c^{†})$. The dimensionless quadrature fluctuations of the thermal noise of the rotating end mirror are given by ${\varphi }_{in}={\displaystyle \frac{1}{\sqrt{2}}}(b_{in}+b_{in}^{†})$, $L_{zin}={\displaystyle \frac{1}{i\sqrt{2}}}(b_{in}-b_{in}^{†})$. The dimensionless quadrature fluctuations of the input vacuum noise are given by $x_{in}={\displaystyle \frac{1}{\sqrt{2}}}(c_{in}+c_{in}^{†})$ and $y_{in}={\displaystyle \frac{1}{i\sqrt{2}}}(c_{in}-c_{in}^{†})$. Then, based on Equation (8), we obtain the equations of motion for the quadrature fluctuations of the mechanical and cavity modes

$$\dot{f}\left(t\right)=\Lambda f\left(t\right)+n\left(t\right),$$

(9)

where $f\left(t\right)$ is the column vector of the quadrature fluctuations of the mechanical and cavity modes, $n\left(t\right)$ is the column vector of the noises of the mechanical and cavity modes, their transposes are given by

$$\begin{array}{c}f{\left(t\right)}^T=(\delta \varphi ,\delta L_z,\delta x,\delta y),\hfill \\ n{\left(t\right)}^T=(\sqrt{{\gamma }_m}{\varphi }_{in},\sqrt{{\gamma }_m}{L}_{zin},\sqrt{2\kappa }{x}_{in},\sqrt{2\kappa }{y}_{in});\hfill \end{array}$$

(10)

and $\Lambda$ is a $4\times 4$ matrix given by

$$\Lambda =\left(\begin{array}{cccc}-{\displaystyle \frac{{\gamma }_m}{2}}& {\overline{\omega }}_m& -\alpha & -\beta \\ -{\overline{\omega }}_m& -{\displaystyle \frac{{\gamma }_m}{2}}& A& B\\ -B& -\beta & -\kappa & \Delta \\ A& \alpha & -\Delta & -\kappa \end{array}\right),$$

(11)

where $u={\displaystyle \frac{1}{\sqrt{2}}}(a_s+a_s^{*})$, $v={\displaystyle \frac{1}{i\sqrt{2}}}(a_s-a_s^{*})$, $\rho ={\displaystyle \frac{1}{\sqrt{2}}}(G+G^{*})$, $\sigma ={\displaystyle \frac{1}{i\sqrt{2}}}(G-G^{*})$, $\alpha =u\sigma$, $\beta =v\sigma$, $A=u\rho$, and $B=v\rho$. The stability of the coupled system is determined by the real parts of the eigenvalues of the matrix $\Lambda$. If all the real parts of the eigenvalues of the matrix $\Lambda$ are negative, the coupled system is stable. We apply the Routh–Hurwitz stability criterion [65] to derive the stability conditions for the system, which yields

$$\begin{array}{c}{s}_1=({\Delta }^2+{\kappa }^2)({\displaystyle \frac{{\gamma }^2}{4}}+{\overline{\omega }}_m^2)-(u^2+v^2)({\rho }^2+{\sigma }^2)\Delta {\overline{\omega }}_m>0,\hfill \\ s_2=w\{{\gamma }_m[{\Delta }^2+\kappa (\kappa +{\displaystyle \frac{{\gamma }_m}{2}})]+2\kappa {\overline{\omega }}_m^2\}-{(2\kappa +{\gamma }_m)}^2{s}_1>0,\hfill \end{array}$$

(12)

where $w=[2\kappa ({\kappa }^2+2\kappa {\gamma }_m+{\Delta }^2+{\displaystyle \frac{{\gamma }_m^2}{4}})]+{\gamma }_m({\displaystyle \frac{3}{2}}\kappa {\gamma }_m+{\displaystyle \frac{{\gamma }_m^2}{4}}+{\overline{\omega }}_m^2)$.

In Equation (9), we make a Fourier transform of the fluctuation and noise operators and solve it, and we find the fluctuations of angular displacement and angular momentum of the rotating end mirror in the frequency domain,

$$\begin{array}{c}\delta \varphi \left(\omega \right)=U_1\left(\omega \right)x_{in}\left(\omega \right)+U_2\left(\omega \right)y_{in}\left(\omega \right)+U_3\left(\omega \right){\varphi }_{in}\left(\omega \right)+U_4\left(\omega \right)L_{zin}\left(\omega \right),\hfill \\ \delta L_z\left(\omega \right)=V_1\left(\omega \right)x_{in}\left(\omega \right)+V_2\left(\omega \right)y_{in}\left(\omega \right)+V_3\left(\omega \right){\varphi }_{in}\left(\omega \right)+V_4\left(\omega \right)L_{zin}\left(\omega \right),\hfill \end{array}$$

(13)

where

$$\begin{array}{c}{U}_1\left(\omega \right)={\displaystyle \frac{1}{d\left(\omega \right)}}\{[{\overline{\omega }}_m-\alpha M_2\left(\omega \right)-\beta N_2\left(\omega \right)][A{M}_3\left(\omega \right)+B{N}_3\left(\omega \right)]\hfill \\ -R_2\left(\omega \right)[\alpha M_3\left(\omega \right)+\beta N_3\left(\omega \right)]\},\hfill \\ U_2\left(\omega \right)={\displaystyle \frac{1}{d\left(\omega \right)}}\{[{\overline{\omega }}_m-\alpha M_2\left(\omega \right)-\beta N_2\left(\omega \right)][A{M}_4\left(\omega \right)+B{N}_4\left(\omega \right)]\hfill \\ -R_2\left(\omega \right)[\alpha M_4\left(\omega \right)+\beta N_4\left(\omega \right)]\},\hfill \\ U_3\left(\omega \right)={\displaystyle \frac{\sqrt{{\gamma }_m}}{d\left(\omega \right)}}{R}_2\left(\omega \right),\hfill \\ U_4\left(\omega \right)={\displaystyle \frac{\sqrt{{\gamma }_m}}{d\left(\omega \right)}}[{\overline{\omega }}_m-\alpha M_2\left(\omega \right)-\beta N_2\left(\omega \right)],\hfill \end{array}$$

(14)

$$\begin{array}{c}{V}_1\left(\omega \right)={\displaystyle \frac{1}{d\left(\omega \right)}}\{[{\overline{\omega }}_m-A{M}_1\left(\omega \right)-B{N}_1\left(\omega \right)][\alpha M_3\left(\omega \right)+\beta N_3\left(\omega \right)]\hfill \\ +R_1\left(\omega \right)[A{M}_3\left(\omega \right)+B{N}_3\left(\omega \right)]\},\hfill \\ V_2\left(\omega \right)={\displaystyle \frac{1}{d\left(\omega \right)}}\{[{\overline{\omega }}_m-A{M}_1\left(\omega \right)-B{N}_1\left(\omega \right)][\alpha M_4\left(\omega \right)+\beta N_4\left(\omega \right)]\hfill \\ +R_1\left(\omega \right)[A{M}_4\left(\omega \right)+B{N}_4\left(\omega \right)]\},\hfill \\ V_3\left(\omega \right)={\displaystyle \frac{\sqrt{{\gamma }_m}}{d\left(\omega \right)}}[{\overline{\omega }}_m-A{M}_1\left(\omega \right)-B{N}_1\left(\omega \right)],\hfill \\ V_4\left(\omega \right)={\displaystyle \frac{\sqrt{{\gamma }_m}}{d\left(\omega \right)}}{R}_1\left(\omega \right),\hfill \end{array}$$

(15)

and $R_2\left(\omega \right)={\displaystyle \frac{{\gamma }_m}{2}}-i\omega -A{M}_2\left(\omega \right)-B{N}_2\left(\omega \right)$, $R_1\left(\omega \right)={\displaystyle \frac{{\gamma }_m}{2}}-i\omega +\alpha M_1\left(\omega \right)+\beta N_1\left(\omega \right)$, $\Gamma \left(\omega \right)={(\kappa -i\omega )}^2+{\Delta }^2$, $M_1\left(\omega \right)=[-B(\kappa -i\omega )+\Delta A]/\Gamma \left(\omega \right)$, $M_2\left(\omega \right)=[-\beta (\kappa -i\omega )+\Delta \alpha ]/\Gamma \left(\omega \right)$, $M_3\left(\omega \right)=\sqrt{2\kappa }(\kappa -i\omega )/\Gamma \left(\omega \right)$, $M_4\left(\omega \right)=\sqrt{2\kappa }\Delta /\Gamma \left(\omega \right)$, $N_1\left(\omega \right)=[A(\kappa -i\omega )+\Delta B]/\Gamma \left(\omega \right)$, $N_2\left(\omega \right)=[\alpha (\kappa -i\omega )+\Delta \beta ]/\Gamma \left(\omega \right)$, $N_3\left(\omega \right)=-\sqrt{2\kappa }\Delta /\Gamma \left(\omega \right)$, $N_4\left(\omega \right)=\sqrt{2\kappa }(\kappa -i\omega )/\Gamma \left(\omega \right)$, and $d\left(\omega \right)=R_1\left(\omega \right)R_2\left(\omega \right)+[{\overline{\omega }}_m-A{M}_1\left(\omega \right)-B{N}_1\left(\omega \right)][{\overline{\omega }}_m-\alpha M_2\left(\omega \right)-\beta N_2\left(\omega \right)]$. In Equation (13), the first two terms of $\delta \varphi \left(\omega \right)$ and $\delta L_z\left(\omega \right)$ are the contributions of the input vacuum noise, and the last two terms are the contributions of the thermal noise of the rotating end mirror. The spectra of fluctuations in angular displacement and angular momentum of the rotating end mirror can be calculated by

$$\begin{array}{c}{S}_{\varphi }\left(\omega \right)={\displaystyle \frac{1}{4\pi }}{\int }_{-\infty }^{+\infty }d\Omega e^{-i(\omega +\Omega )t}[\langle \delta \varphi \left(\omega \right)\delta \varphi (\Omega )\rangle +\langle \delta \varphi (\Omega )\delta \varphi \left(\omega \right)\rangle ],\hfill \\ S_{L_z}\left(\omega \right)={\displaystyle \frac{1}{4\pi }}{\int }_{-\infty }^{+\infty }d\Omega e^{-i(\omega +\Omega )t}[\langle \delta L_z\left(\omega \right)\delta L_z(\Omega )\rangle +\langle \delta L_z(\Omega )\delta L_z\left(\omega \right)\rangle ].\hfill \end{array}$$

(16)

With the aid of the correlation functions of the system noises in the frequency domain,

$$\begin{array}{c}\langle x_{in}\left(\omega \right)x_{in}(\Omega )\rangle =\langle y_{in}\left(\omega \right)y_{in}(\Omega )\rangle ={\displaystyle \frac{1}{2}}2\pi \delta (\omega +\Omega ),\hfill \\ \langle x_{in}\left(\omega \right)y_{in}(\Omega )\rangle =-\langle y_{in}\left(\omega \right)x_{in}(\Omega )\rangle ={\displaystyle \frac{i}{2}}2\pi \delta (\omega +\Omega ),\hfill \\ \langle {\varphi }_{in}\left(\omega \right){\varphi }_{in}(\Omega )\rangle =\langle L_{zin}\left(\omega \right)L_{zin}(\Omega )\rangle =(n_{th}+{\displaystyle \frac{1}{2}})2\pi \delta (\omega +\Omega ),\hfill \\ \langle {\varphi }_{in}\left(\omega \right)L_{zin}(\Omega )\rangle =-\langle L_{zin}\left(\omega \right){\varphi }_{in}(\Omega )\rangle ={\displaystyle \frac{i}{2}}2\pi \delta (\omega +\Omega ),\hfill \end{array}$$

(17)

we find that the spectra of fluctuations in the angular displacement and angular momentum of the rotating end mirror is as follows:

$$\begin{array}{c}{S}_{\varphi }\left(\omega \right)={\displaystyle \frac{1}{2}}[U_1\left(\omega \right)U_1(-\omega )+U_2\left(\omega \right)U_2(-\omega )]\hfill \\ +(n_{th}+{\displaystyle \frac{1}{2}})[U_3\left(\omega \right)U_3(-\omega )+U_4\left(\omega \right)U_4(-\omega )],\hfill \\ S_{L_z}\left(\omega \right)={\displaystyle \frac{1}{2}}[V_1\left(\omega \right)V_1(-\omega )+V_2\left(\omega \right)V_2(-\omega )]\hfill \\ +(n_{th}+{\displaystyle \frac{1}{2}})[V_3\left(\omega \right)V_3(-\omega )+V_4\left(\omega \right)V_4(-\omega )],\hfill \end{array}$$

(18)

where the first two terms of $S_{\varphi }\left(\omega \right)$ and $S_{L_z}\left(\omega \right)$ arise from the input vacuum noise, and the last two terms are from the thermal noise of the rotating end mirror. The variances of the angular displacement and angular momentum of the rotating end mirror are calculated as follows:

$$\begin{array}{c}\langle \delta {\varphi }^2\rangle ={\displaystyle \frac{1}{2\pi }}{\int }_{-\infty }^{+\infty }d\omega S_{\varphi }\left(\omega \right),\hfill \\ \langle {\delta \mathsf{Ł}}_z^2\rangle ={\displaystyle \frac{1}{2\pi }}{\int }_{-\infty }^{+\infty }d\omega S_{L_z}\left(\omega \right).\hfill \end{array}$$

(19)

Furthermore, from the mean energy of the rotating end mirror at the steady-state ${\displaystyle \frac{\hslash {\omega }_m}{2}}[\langle \delta {\varphi }^2\rangle +\langle {\delta \mathsf{Ł}}_z^2\rangle ]=\hslash {\omega }_m(n_{eff}+{\displaystyle \frac{1}{2}})$, we obtain the effective mean phonon number $n_{eff}$ of the rotating end mirror

$$n_{eff}={\displaystyle \frac{1}{2}}[\langle \delta {\varphi }^2\rangle +\langle {\delta \mathsf{Ł}}_z^2\rangle -1].$$

(20)

When $n_{eff}=0$, the rotating end mirror is in the quantum ground state. Moreover, we introduce the ratio of the variance of the angular displacement of the rotating end mirror to the variance of the angular momentum of the rotating end mirror $r={\displaystyle \frac{\langle \delta {\varphi }^2\rangle }{\langle {\delta \mathsf{Ł}}_z^2\rangle }}$ to show the relative importance of fluctuations in the angular displacement and angular momentum of the rotating end mirror.

4. The Cooling of the Rotating End Mirror in the Presence of the Nonlinear CK Interaction

In this section, we show how the cavity detuning ${\Delta }_0$, the nonlinear CK strength $g_{ck}$, the power ℘ of the input Gaussian beam, the value l of the TC of the L-G cavity mode, the mass m of the rotating end mirror, and the cavity length L affect the cooling of the rotating end mirror.

The parameters we use are close to those from Ref. [39]: the wavelength of the input Gaussian laser is $\lambda =810$ nm, the cavity decay rate is $\kappa =2\pi \times 1.5$ MHz, the radius, resonance frequency, and damping rate of the rotating end mirror are $R=10$ μm, ${\omega }_m=2\pi \times 10$ MHz, and ${\gamma }_m=2\pi \times 5$ Hz, respectively; thus, the quality factor of the rotating end mirror is $Q_m={\omega }_m/{\gamma }_m=2\times {10}^6$. The system is working in the resolved-sideband regime due to $\kappa /{\omega }_m=0.15\ll 1$. The temperature of the environment is $T=0.1$ K, the corresponding mean phonon number $n_{th}$ of the rotating end mirror is about 207.769.

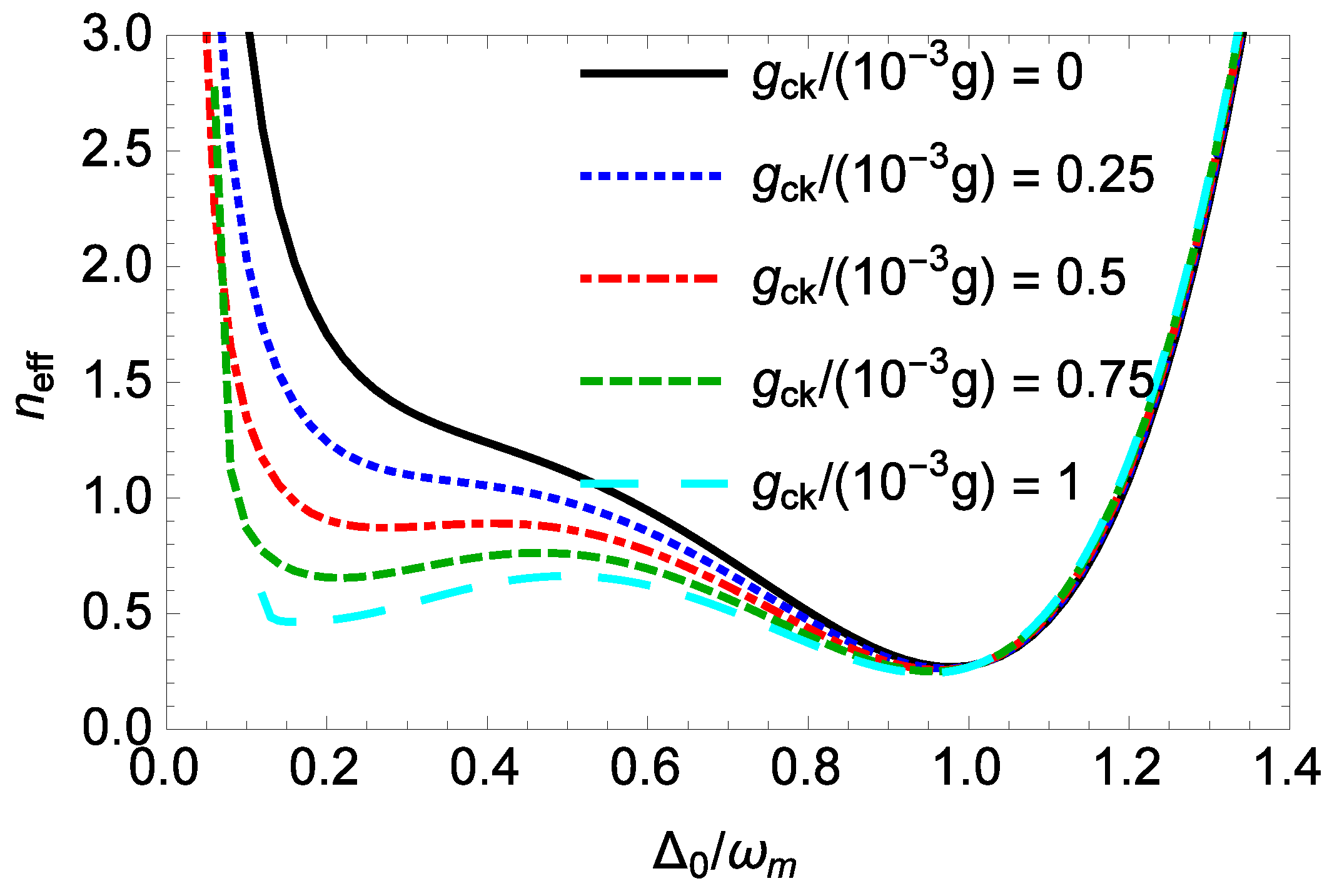
In Figure 2, we illustrate the effect of the normalized cavity detuning ${\Delta }_0/{\omega }_m$ on the effective mean phonon number $n_{eff}$ of the rotating end mirror for various values of the nonlinear CK strength $g_{ck}$ when $m=100$ ng, $L=1$ mm, $\wp =1$ mW, and $l=20$. Through calculations, we find $g/{\omega }_m\approx 1.24\times {10}^{-6}\ll 1$, thus the system is in the single-photon weak-coupling regime. For $g_{ck}/\left({10}^{-3}g\right)=0$, 0.25, 0.5, 0.75, 1, the stability conditions require that the cavity detuning ${\Delta }_0$ must be not less than $0.001 {\omega }_m$, $0.005 {\omega }_m$, $0.009 {\omega }_m$, $0.041 {\omega }_m$, and $0.116 {\omega }_m$, respectively. Thus, by increasing the nonlinear CK strength $g_{ck}$, the system becomes stable at a larger cavity detuning ${\Delta }_0$. For $g_{ck}/\left({10}^{-3}g\right)=0$, 0.25, 0.5, 0.75, 1, the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror is 0.269, 0.263, 0.256, 0.250, and 0.244 at ${\Delta }_0=0.98 {\omega }_m$, $0.97 {\omega }_m$, $0.964 {\omega }_m$, $0.956 {\omega }_m$, and $0.94 {\omega }_m$, respectively. Thus, by increasing the nonlinear CK strength $g_{ck}$, the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror decreases a little, and this also occurs at a smaller cavity detuning ${\Delta }_0$. Moreover, when the cavity detuning ${\Delta }_0$ is much less than the resonance frequency ${\omega }_m$ of the rotating end mirror, the improvement in the cooling of the rotating end mirror by the nonlinear CK interaction is more apparent. When ${\Delta }_0=0.35 {\omega }_m$, without the nonlinear CK interaction ($g_{ck}=0$), the effective mean phonon number $n_{eff}$ of the rotating end mirror is about 1.302, with the nonlinear CK interaction, the effective mean phonon number $n_{eff}$ of the rotating end mirror for $g_{ck}/\left({10}^{-3}g\right)=0.25,$ 0.5, 0.75, 1 are about 1.076, 0.884, 0.722, and 0.586, respectively—factors of about 1.2, 1.5, 1.8, and 2.2 lower than those without the nonlinear CK interaction. However, when the cavity detuning ${\Delta }_0$ is not less than the resonance frequency ${\omega }_m$ of the rotating end mirror, it is seen that the cooling of the rotating end mirror could not be improved by the nonlinear CK interaction.

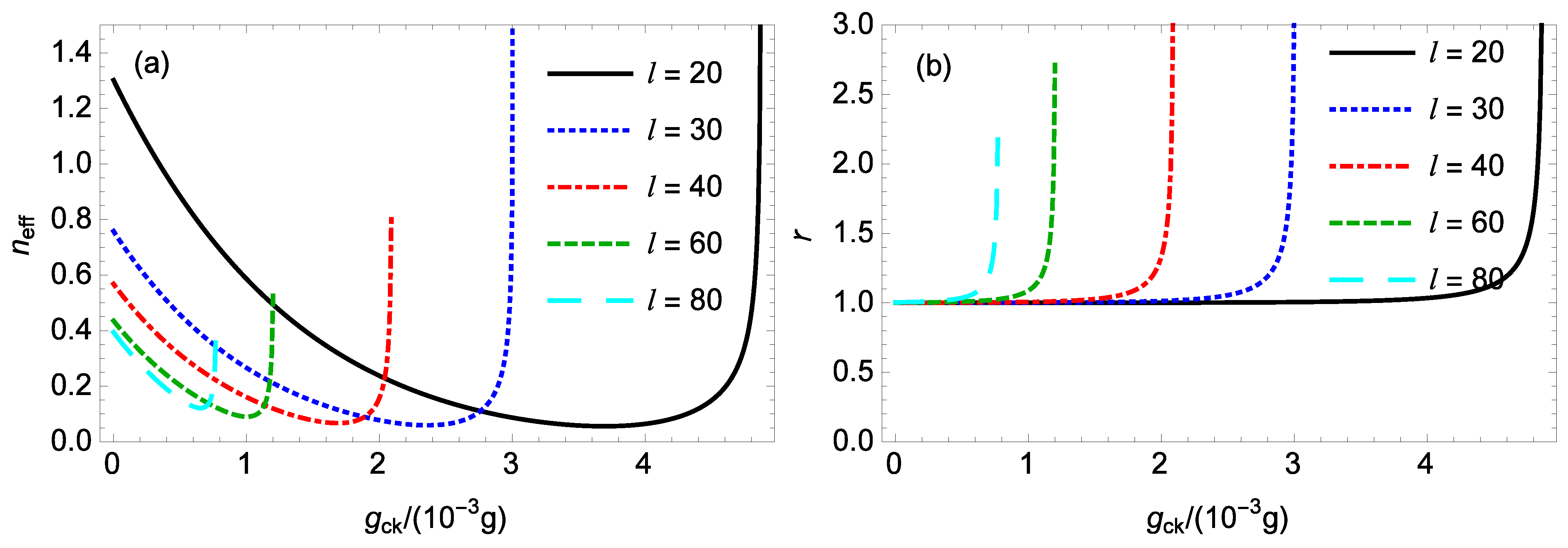
Figure 3a shows the effective mean phonon number $n_{eff}$ of the rotating end mirror against the normalized nonlinear CK strength $g_{ck}/\left({10}^{-3}g\right)$ for various values l of the TC of the L-G cavity mode when $m=100$ ng, $L=1$ mm, $\wp =1$ mW, and ${\Delta }_0=0.35{\omega }_m$. For $l=20,30,40,60$, and 80, the stability conditions require that the normalized nonlinear CK strength $g_{ck}/\left({10}^{-3}g\right)$ must not exceed 4.87, 3.01, 2.09, 1.2, and 0.77, respectively. Thus, increasing the value l of the TC of the L-G cavity mode makes the system unstable at a smaller value of $g_{ck}/\left({10}^{-3}g\right)$. For a fixed value l of the TC of the L-G cavity mode, with an increase in the nonlinear CK strength $g_{ck}$, the effective mean phonon number $n_{eff}$ of the rotating end mirror first decreases, and then increases before the unstable regime of the system. Thus, it is possible to improve the cooling of the rotating end mirror by increasing the nonlinear CK strength $g_{ck}$, which is the result of the competition between the two-mode squeezing interaction and the beam-splitter interaction shown in Equation (8). Without the nonlinear CK interaction ($g_{ck}=0$), the effective mean phonon number $n_{eff}$ of the rotating end mirror for $l=20$, 30, 40, 60, and 80 is about 1.302, 0.758, 0.568, 0.436, and 0.394, respectively. Thus, when the nonlinear CK interaction is absent ($g_{ck}=0$), increasing the value l of the TC of the L-G cavity mode can enhance the cooling of the rotating end mirror. This is due to the fact that a larger value l of the TC leads to a larger optorotational coupling strength g since $g\propto l$. With the nonlinear CK interaction, the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror for $l=20,30,40,60$, and 80 is 0.056, 0.059, 0.067, 0.090, and 0.121 at $g_{ck}/\left({10}^{-3}g\right)=3.7$, 2.36, 1.68, 1, and 0.65, respectively. Thus, with increasing the value l of the TC of the L-G cavity mode, the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror increases, and it takes place at a smaller value of $g_{ck}/\left({10}^{-3}g\right)$. For $l=20,30,40,60$, and 80, the cooling of the rotating end mirror can be maximally enhanced by the nonlinear CK interaction by a factor of about 23.3, 12.8, 8.5, 4.8, and 3.3, compared to that in the absence of the nonlinear CK interaction, respectively. 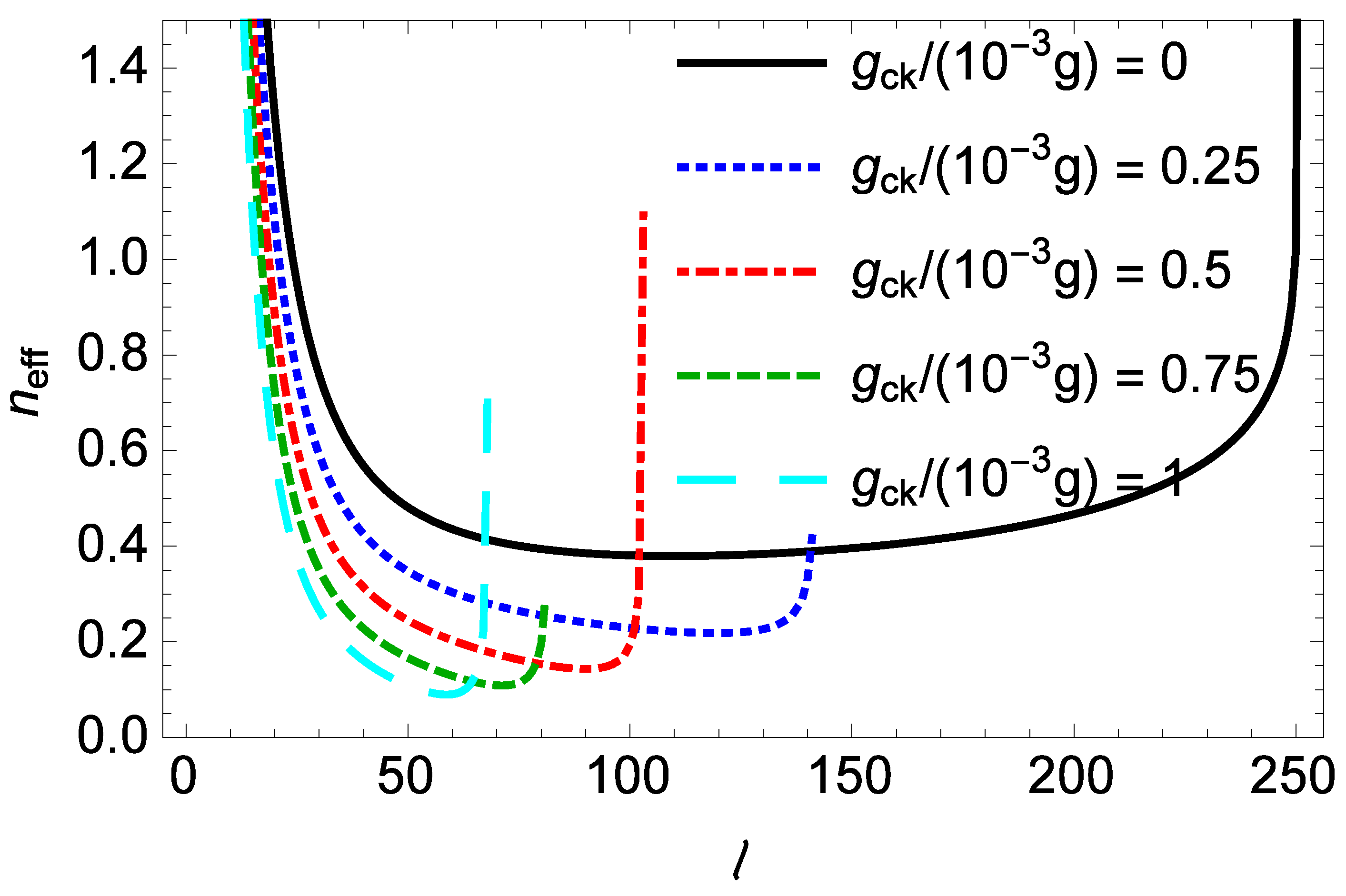Hence, the maximum improvement factor for the mirror cooling by the nonlinear CK interaction reduces with an increase in the value l of the TC of the L-G cavity mode. Figure 3b shows that the dependence of the ratio r on the normalized nonlinear CK strength $g_{ck}/\left({10}^{-3}g\right)$ for different values l of the TC of the L-G cavity mode when $m=100$ ng, $L=1$ mm, $\wp =1$ mW, and ${\Delta }_0=0.35 {\omega }_m$. Without the nonlinear CK interaction ($g_{ck}=0$), the ratio r is about equal to 1, which means that the angular displacement variance $\langle \delta {\varphi }^2\rangle$ of the rotating end mirror is almost equal to the angular momentum variance $\langle \delta L_z^2\rangle$ of the rotating end mirror. With the nonlinear CK interaction ($g_{ck}\ne 0$), it is seen that the ratio r is still almost equal to 1 with an increase in $g_{ck}/\left({10}^{-3}g\right)$, but when $g_{ck}/\left({10}^{-3}g\right)$ is close to the instability threshold, the ratio r increases nonlinearly with increasing $g_{ck}/\left({10}^{-3}g\right)$ and reaches the maximum value just before the unstable regime of the system. When the ratio r is larger than 1, the angular displacement variance $\langle \delta {\varphi }^2\rangle$ of the rotating end mirror is larger than the angular momentum variance $\langle \delta L_z^2\rangle$ of the rotating end mirror. This is different from the case by using the degenerate optical parametric amplifier to improve the stochastic feedback cooling of the moving mirror in an optomechanical system [66], in which the the ratio r is less than 1, and the displacement variance of the moving mirror is less than the momentum variance of the moving mirror.

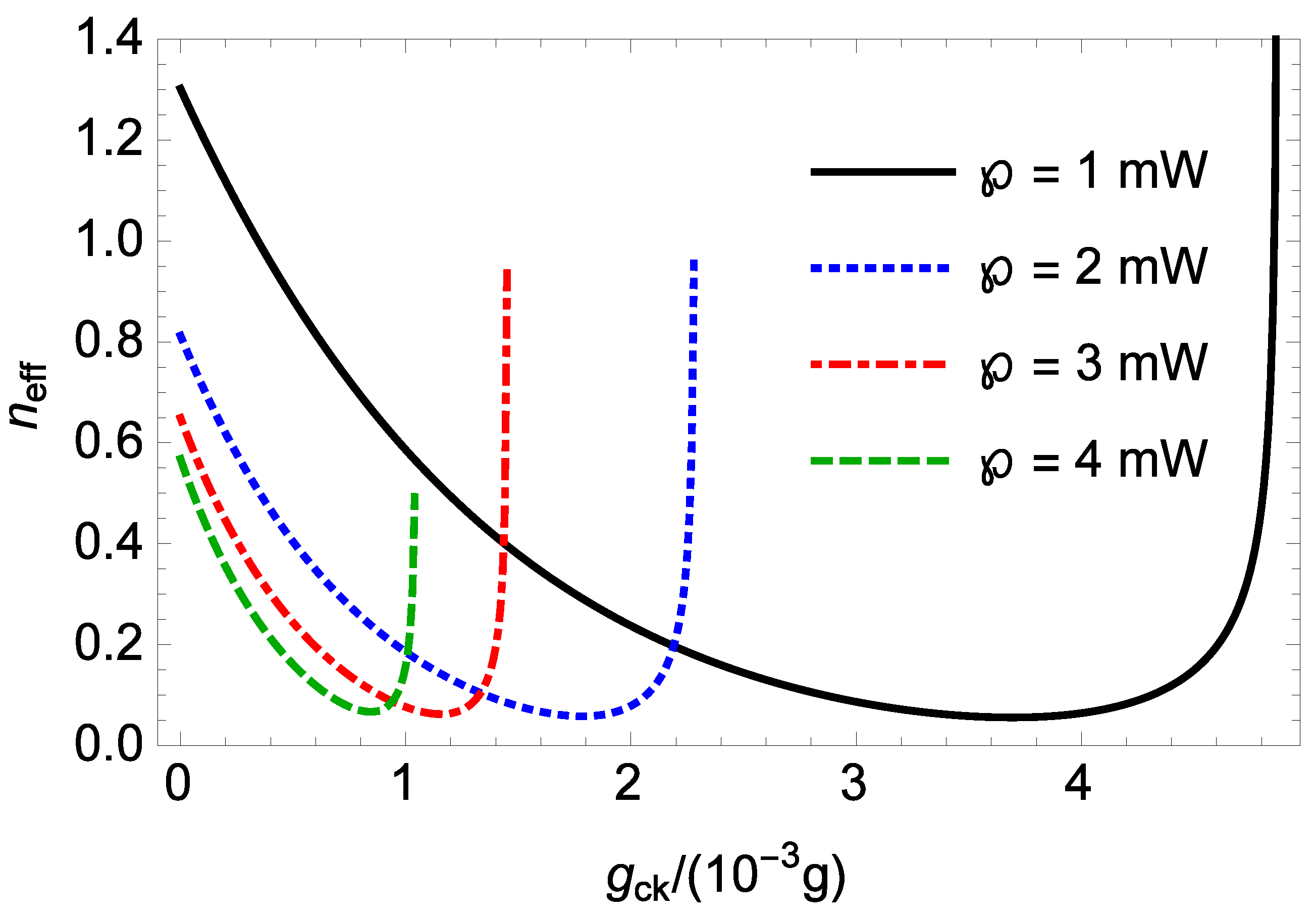
Figure 4a shows the effective mean phonon number $n_{eff}$ of the rotating end mirror against the normalized nonlinear CK strength $g_{ck}/\left({10}^{-3}g\right)$ for different powers ℘ of the input Gaussian beam when $m=100$ ng, $L=1$ mm, $l=20$, and ${\Delta }_0=0.35$${\omega }_m$. For $\wp =1,2,3$, and 4 mW, the stability conditions require that the normalized nonlinear CK strength $g_{ck}/\left({10}^{-3}g\right)$ must not exceed 4.87, 2.28, 1.45, and 1.04, respectively. Thus, for a higher input power ℘, the system becomes unstable at a smaller nonlinear CK strength $g_{ck}$. For a given power ℘ of the input laser, with an increase in the nonlinear CK strength $g_{ck}$, the effective mean phonon number $n_{eff}$ of the rotating end mirror first decreases, and then increases before the system goes into the unstable regime, which is similar to Figure 3a. Thus, it is possible to enhance the cooling of the rotating end mirror by increasing the nonlinear CK interaction strength $g_{ck}$. Without the nonlinear CK interaction ($g_{ck}=0$), the effective mean phonon number $n_{eff}$ of the rotating end mirror for $\wp =1,2,3$, and 4 mW is about 1.302, 0.812, 0.649, and 0.568, respectively. Thus, when the nonlinear CK interaction is absent ($g_{ck}=0$), increasing the power ℘ of the input laser is helpful for the improvement in the cooling of the rotating end mirror. This is because an increase in the input laser power ℘ increases the intracavity photon number $|a_s{|}^2$, thereby leading to a stronger optorotational coupling of the L-G cavity field to the rotating end mirror. With the nonlinear CK interaction, the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror for $\wp =1,2,3$, and 4 mW is about 0.056, 0.058, 0.063, and 0.067 at $g_{ck}/\left({10}^{-3}g\right)=3.7,1.78,1.16$, and 0.84, respectively. Thus, by increasing the power ℘ of the input laser, the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror rises, and it occurs at a smaller value of $g_{ck}/\left({10}^{-3}g\right)$. For $\wp =1,2,3$, and 4 mW, the cooling of the rotating end mirror can be maximally enhanced by the nonlinear CK interaction by a factor of about 23.3, 14.0, 10.3, and 8.5 compared to that without the nonlinear CK interaction, respectively. Hence, the maximum improvement factor for the mirror cooling by the nonlinear CK interaction decreases with an increase in the power ℘ of the input laser.

Figure 5 shows the effective mean phonon number $n_{eff}$ of the rotating end mirror against the power ℘ of the input Gaussian beam for various values of the nonlinear CK strengths $g_{ck}$ when $m=100$ ng, $L=1$ mm, $l=20$, and ${\Delta }_0=0.35$ ${\omega }_m$. We first see the case of ${\Delta }_0=0.35$ ${\omega }_m$, as shown in Figure 5a. Without the nonlinear CK interaction, the system is always stable when the power ℘ of the input laser is larger than 0 but less than 20 mW, and the effective mean phonon number $n_{eff}$ of the rotating end mirror decreases with increasing the power ℘ of the input laser. When $\wp =20$ mW, the effective mean phonon number $n_{eff}$ of the rotating end mirror takes a minimum value of about 0.386. With the nonlinear CK interaction, for $g_{ck}/\left({10}^{-3}g\right)=0.25,0.5,0.75,1$, the stability conditions impose the limitation $\wp \le$ 13.15, 7.5, 5.34, 4.15 mW, respectively. Thus, for a larger nonlinear CK strength $g_{ck}$, the system becomes unstable at a smaller input laser power, which implies that the nonlinear CK effect is harmful for the system stability. For a fixed value of the nonlinear CK strengths $g_{ck}$, when the power ℘ of the input laser increases, the effective mean phonon number $n_{eff}$ of the rotating end mirror first decreases, and then increases before the system passes into the unstable regime. Thus, it is possible to enhance the cooling of the rotating end mirror by increasing the power ℘ of the input laser. For $g_{ck}/\left({10}^{-3}g\right)=0.25,0.5,0.75,1$, the effective mean phonon number $n_{eff}$ of the rotating end mirror takes its minimum value of about 0.101, 0.078, 0.069, and 0.064 at 11.2, 6.3, 4.4, and 3.4 mW, respectively. Hence, increasing the nonlinear CK strengths $g_{ck}$ can lower the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror, and make it happen at a lower power ℘ of the input laser. For $g_{ck}/\left({10}^{-3}g\right)=0.25,0.5,0.75,1$, the cooling of the rotating end mirror can be maximally improved by a factor of about 3.8, 4.9, 5.6, and 6.0 compared to the case without the nonlinear CK interaction, respectively. Hence, the maximum improvement factor for the mirror cooling by the nonlinear CK interaction increases with the increase in the nonlinear CK strength $g_{ck}$. We next see the case of ${\Delta }_0={\omega }_m$, as shown in Figure 5b. According to the stability conditions, we find that the system is always stable in the input power range of 0–20 mW for $g_{ck}/\left({10}^{-3}g\right)=0,0.25,0.5,0.75,1$. From Figure 5b, as the nonlinear CK strength $g_{ck}$ increases, the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror increases, and happens at a lower input power ℘. Therefore, if the L-G cavity field is driven by a red-detuned Gaussian beam with ${\Delta }_0={\omega }_m$, the nonlinear CK interaction could not improve the cooling of the rotating end mirror. These results for the case of ${\Delta }_0={\omega }_m$ are consistent with those in Ref. [54], which focuses on the effect of nonlinear CK interaction on the cooling of a movable mirror in an optomechanical system.

Figure 6 shows the effective mean phonon number $n_{eff}$ of the rotating end mirror against the value l of the TC of the L-G cavity mode for various values of the nonlinear CK strengths $g_{ck}$ when $m=100$ ng, $L=1$ mm, $\wp =1$ mW, and ${\Delta }_0=0.35 {\omega }_m$. For $g_{ck}/\left({10}^{-3}g\right)=0,0.25,0.5,0.75,1$, the stability conditions impose the limitation $l \le$251, 141, 103, 81, 68, respectively. Thus, increasing the nonlinear CK strength $g_{ck}$ makes the system become unstable at a smaller value of the TC of the L-G cavity mode, which shows that the nonlinear CK effect has a negative effect on the system stability. For a given value of the nonlinear CK strength $g_{ck}$, as the value l of the TC of the L-G cavity mode increases, the effective mean phonon number $n_{eff}$ of the rotating end mirror first decreases, and then increases before the system enters the unstable regime. Thus, it is possible to enhance the cooling of the rotating end mirror by increasing the value l of the TC of the L-G cavity mode. For $g_{ck}/\left({10}^{-3}g\right)=0,0.25,0.5,0.75,1$, the effective mean phonon number $n_{eff}$ of the rotating end mirror takes minimum values of about 0.380, 0.218, 0.143, 0.109, and 0.090 at $l=$ 110, 119, 90, 71, and 59, respectively. By increasing the nonlinear CK strength $g_{ck}$, the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror is reduced. For a nonzero larger CK strength $g_{ck}$, the minimum effective mean phonon number $n_{eff}$ of the rotating end mirror appears at a smaller TC of the L-G cavity mode. For $g_{ck}/\left({10}^{-3}g\right)=0.25,0.5,0.75,1$, the cooling of the rotating end mirror can be maximally improved by the nonlinear CK interaction by factors of about 1.7, 2.7, 3.5, and 4.2 compared to the cases without the nonlinear CK interaction, respectively. Hence, when the nonlinear CK strength $g_{ck}$ is larger, the maximum improvement factor for the mirror cooling by the nonlinear CK interaction becomes larger.

Figure 7 shows the effective mean phonon number $n_{eff}$ of the rotating end mirror against the normalized nonlinear CK strength $g_{ck}/\left({10}^{-3}g\right)$ for different masses m of the rotating end mirror when $L=1$ mm, $\wp =1$ mW, $l=20$, and ${\Delta }_0=0.35 {\omega }_m$. For $m=50$, 100, 150 ng, the stability conditions require that the normalized nonlinear CK strength $g_{ck}/\left({10}^{-3}g\right)$ is less than 3.22, 4.86, and 6.14, respectively. Thus, for a heavier rotating end mirror, the system becomes unstable at a larger value of $g_{ck}/\left({10}^{-3}g\right)$. For a given mass m of the rotating end mirror, as the nonlinear CK strength $g_{ck}$ increases, the effective mean phonon number $n_{eff}$ of the rotating end mirror first decreases, and then increases before the system enters the unstable regime. Without the nonlinear CK interaction ($g_{ck}=0$), for $m=50$, 100, 150 ng, the effective mean phonon number $n_{eff}$ of the rotating end mirror is about 0.812, 1.302, and 1.789, respectively. Thus, when the nonlinear CK interaction is absent, increasing the mass m of the rotating end mirror makes the effective mean phonon number $n_{eff}$ of the rotating end mirror larger. This is because increasing the mass m of the rotating end mirror gives rise to a smaller optorotational coupling strength g due to $g\propto {\displaystyle \frac{1}{\sqrt{m}}}$. With the nonlinear CK interaction $(g_{ck}\ne 0)$, for $m=50$, 100, 150 ng, the effective mean phonon number $n_{eff}$ of the rotating end mirror has minimum values of about 0.058, 0.056, and 0.057 at $g_{ck}/\left({10}^{-3}g\right)=2.52$, 3.70, and 4.60, respectively. We find that $g_{ck}/\left({10}^{-3}g\right)=2.52$, 3.70, and 4.60 is equivalent to $g_{ck}\approx 0.277,0.287,0.292$ Hz, respectively. Thus, in order to cool a heavier rotating end mirror to almost the same minimum effective mean phonon number $n_{eff}$ as a lighter rotating end mirror, the nonlinear CK strength $g_{ck}$ has to be larger. 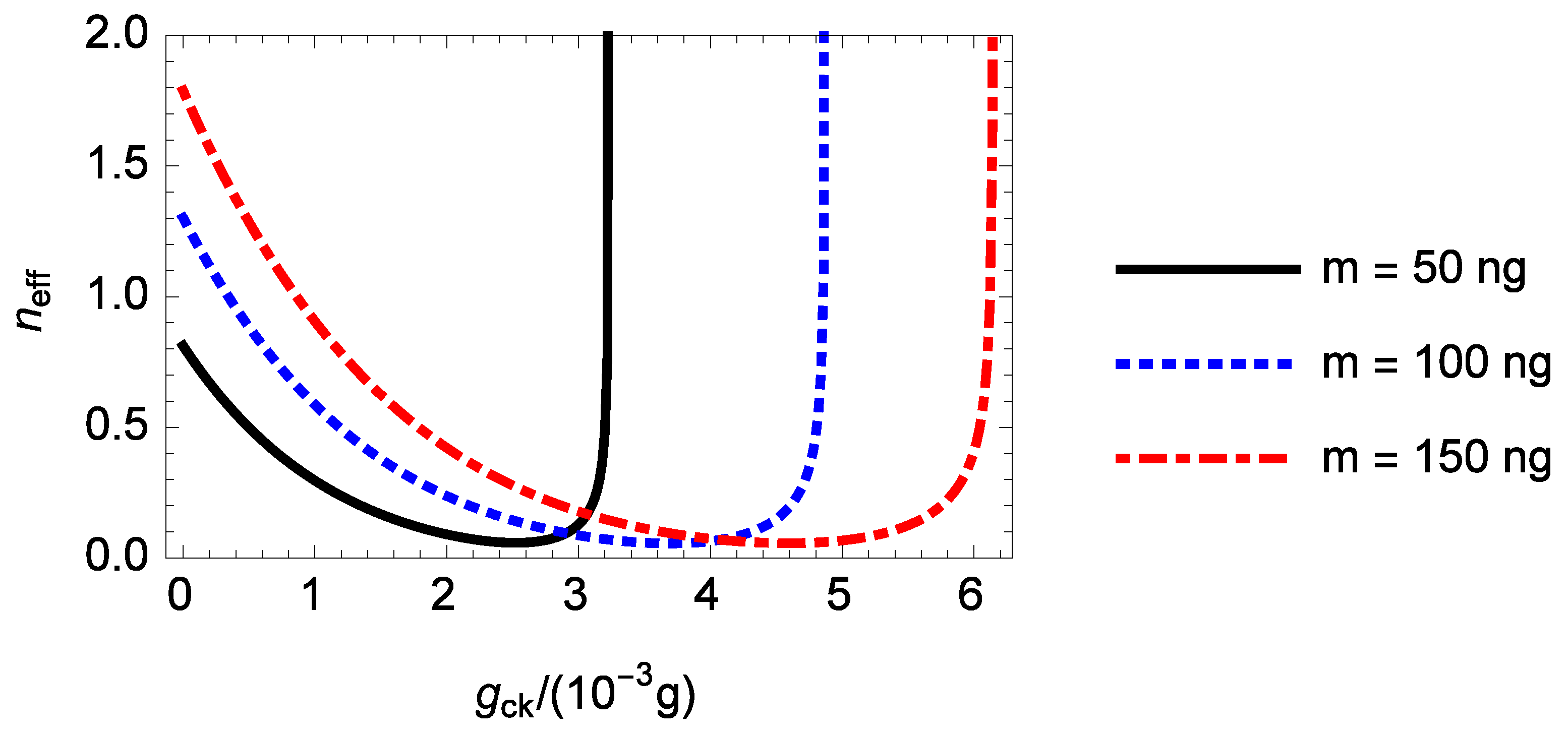For $m=50$, 100, 150 ng, it is found that the cooling of the rotating end mirror can be maximally improved by the nonlinear CK interaction by a factor of about 14.0, 23.3, and 31.4 compared to the case without the nonlinear CK interaction, respectively. Hence, for a heavier rotating mirror, the maximum improvement factor for the mirror cooling by the nonlinear CK interaction becomes larger.

Figure 8 shows the effective mean phonon number $n_{eff}$ of the rotating end mirror against the normalized nonlinear CK strength $g_{ck}/\left({10}^{-3}g\right)$ for different lengths L of the optical cavity when $m=100$ ng, $\wp =1$ mW, $l=20$, and ${\Delta }_0=0.35 {\omega }_m$. For $L=0.8$, 1, 1.2 mm, the stability conditions impose the limitation $g_{ck}/\left({10}^{-3}g\right)\le$ 3.75, 4.86, 6.00, respectively. Thus, for a larger length L of the cavity, the system becomes unstable at a larger value of $g_{ck}/\left({10}^{-3}g\right)$. For a given length L of the cavity, as the nonlinear CK strength $g_{ck}$ increases, the effective mean phonon number $n_{eff}$ of the rotating end mirror first decreases, and then increases before the system enters the unstable regime. Without the nonlinear CK interaction ($g_{ck}=0$), for $L=0.8$, 1, 1.2 mm, the effective mean phonon number $n_{eff}$ of the rotating end mirror is about 0.949, 1.302, and 1.731, respectively. Thus, when the nonlinear CK interaction is absent, increasing the length L of the cavity gives rise to the increase in the effective mean phonon number $n_{eff}$ of the rotating end mirror. The reason is that a larger length L of the cavity leads to a smaller optorotational coupling strength g due to $g\propto {\displaystyle \frac{1}{L}}$. With the nonlinear CK interaction $(g_{ck}\ne 0)$, for $L=0.8$, 1, 1.2 mm, the effective mean phonon number $n_{eff}$ of the rotating end mirror has its minimum value of about 0.057, 0.056, and 0.057 at $g_{ck}/\left({10}^{-3}g\right)=2.9$, 3.7, and 4.5, respectively. We find that $g_{ck}/\left({10}^{-3}g\right)=2.9$, 3.7, and 4.5 is equivalent to $g_{ck}\approx 0.281,0.287,0.291$ Hz, respectively. Thus, in order to cool a rotating end mirror in a longer cavity to almost the same minimum effective mean phonon number $n_{eff}$ as a rotating end mirror in a shorter cavity, the nonlinear CK strength $g_{ck}$ has to be larger. 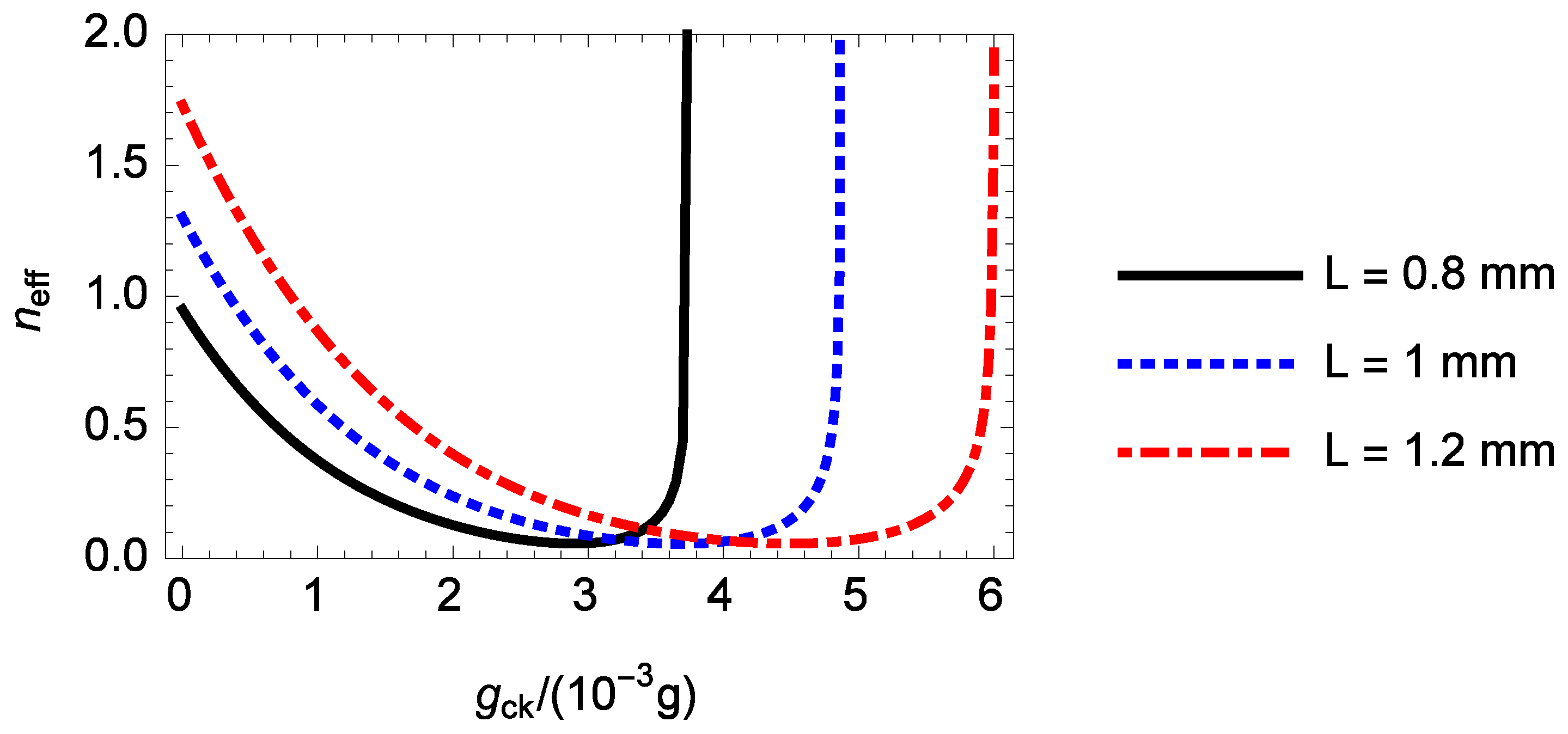For $L=0.8$, 1, 1.2 mm, it is found that the cooling of the rotating end mirror can be maximally improved by the nonlinear CK interaction by a factor of about 16.7, 23.3, and 30.4 compared to the case without the nonlinear CK interaction, respectively. Thus, for a longer cavity, the maximum improvement factor for the mirror cooling by the nonlinear CK interaction is larger.

Finally, we discuss the experimental feasibility of this proposal. Experimentally, an L-G laser beam with a TC of $l=1000$ can be achieved by using spiral-phase plates [67]. In addition, an experiment [68] has demonstrated the cooling of a micromechanical resonator with mass 25 ng, radius 15 μm, and mechanical quality factor $1.3\times {10}^5$. Moreover, it has shown experimentally that the torsional frequency of a mechanical oscillator can be in the range of 3-20 MHz [69]. Therefore, with the rapid development of the optomechanical devices, the rotating mirror with mass 100 ng, radius 10 μm, frequency $2\pi \times 10$ MHz and mechanical quality factor $2\times {10}^6$ in this work is within reach.

5. Conclusions

In conclusion, we have analyzed the cooling of the rotating end mirror in an L-G cavity optorotational system with the nonlinear CK interaction. We find that the presence of the nonlinear CK interaction can improve the cooling of the rotating end mirror only when the cavity detuning is less than the resonance frequency of the rotating end mirror. When the nonlinear CK interaction is present, it is possible to considerably improve the cooling of the rotating end mirror at lower input powers, smaller TCs of the L-G cavity mode, larger masses of the rotating end mirror, and longer optical cavity. The nonlinear CK interaction makes the system unstable at lower input powers and smaller TCs of the L-G cavity mode, which leads to the substantial enhancement of the cooling of the rotating end mirror near the instability threshold. The combination of the L-G cavity optorotational system with the nonlinear CK interaction provides an alternative method to enhance the cooling of the macroscopic rotating end mirror, which has possible applications in high-precision measurement [2].