A Multi-Objective Genetic Algorithm Approach for Silicon Photonics Design

Abstract

A multi-objective genetic algorithm approach is formulated to optimize the design of silicon-photonics complex circuits with contradicting performance metrics and no closed-form expression for the circuit performance. A case study is the interleaver/deinterleaver circuit which mixes/separates optical signals into/from different physical channels while preserving the wavelength-division-multiplexing specifications. These specifications are given as channel spacing of 50 GHz, channel 3-dB bandwidth of at least 20 GHz, channel free spectral range of 100 GHz, crosstalk of −23 dB or less, and signal dispersion less than 30 ps/nm. The essence of the proposed approach lies in the formulation of the fitness functions and the selection criteria to optimize the values of the three coupling coefficients, which govern the circuit performance, in order to accommodate the contradicting performance metrics of the circuit. The proposed approach achieves the optimal design in an incomparably short period of time when contrasted with the previous tedious design method based on employing Z-transform and visual inspection of the transmission poles and zeros.

1. Introduction

Integrated optics has witnessed profound progress in terms of material platforms [1,2,3,4,5,6,7,8,9] and fabrication technologies [10,11]. Consequently, several applications have evolved, with outstanding success achieved in the category of silicon photonics. This special platform offers one way out of the well-known bottleneck crisis which the traditional electronics industry is experiencing [12]. With silicon photonics, the well-established complementary metal-oxide-semiconductor (CMOS) fabrication facilities can be used with virtually no modifications to produce circuits that run optical waves instead of electrical current. Besides the inherited features of low cost and high fabrication density, the main additional advantage is the ultra-high speed of operation [13], since light possesses the ultimate speed known in nature.

In order to build complicated integrated optical circuits, efforts were focused first on developing the basic elements such as straight waveguides, Mach-Zehnder Interferometers (MZIs), multi-mode interferometers (MMIs), grating couplers, and ring resonators [12,14,15]. Complicated circuits grabbed more attention at a later stage. This includes optical crossing structures [16], spot size converters [17], vertical couplers [18], reflectors [19], polarization splitters [20], polarization rotators [21], filters [22,23,24], logic gates [25], modulators [26,27,28,29,30,31,32,33,34], sensors [35,36,37,38,39,40,41,42], light detection and ranging (LiDAR) devices [43], and gyroscopes [44]. A new trend in this field is enabling the silicon-photonics platform in the near-infrared (NIR) and the mid-infrared (MIR) ranges, despite material absorption losses [45,46,47].

In parallel, an evolution in the design approaches is taking place. For simple elements, basic physics and analytic models were sufficient [48]. However, for more complicated circuits, numerical electromagnetic simulators became essential [49]. Furthermore, optimization techniques, such as the genetic algorithm (GA), proved very useful as design tools [48,50,51,52].

In this work, we present a multi-objective GA design approach with a case study given by the interleaver/deinterleaver circuit [53,54,55]. This device can perform two opposite actions. In the interleave mode, the device combines two data streams, centered at two different carrier frequencies, from two different physical links into one. In the deinterleave mode, one data stream is split into two [53]. This device grabbed the attention of different designers [53,54,55]. However, with no closed-form expression for the circuit transmission characteristics, the design process is too complicated as it relies on a combination of extensive trial and error of the design parameters, as well as visual investigation of the device performance in the Z-domain, in order to determine the optimal design parameters that satisfy many constraints set by the standards of the wavelength-division-multiplexing (WDM) communications [53]. In the proposed GA approach, the optimal design parameters can be found in an impressively short time with no need for investigation of the Z-domain of the device transmission or lengthy trial and error attempts.

The rest of the paper is organized as follows. In Section 2, the GA in general is reviewed. In addition, the interleaver/deinterleaver circuit from [54] is briefly reviewed. In Section 3, the GA approach is formulated. In Section 4, the results of the algorithm are discussed before we draw the conclusions in Section 5.

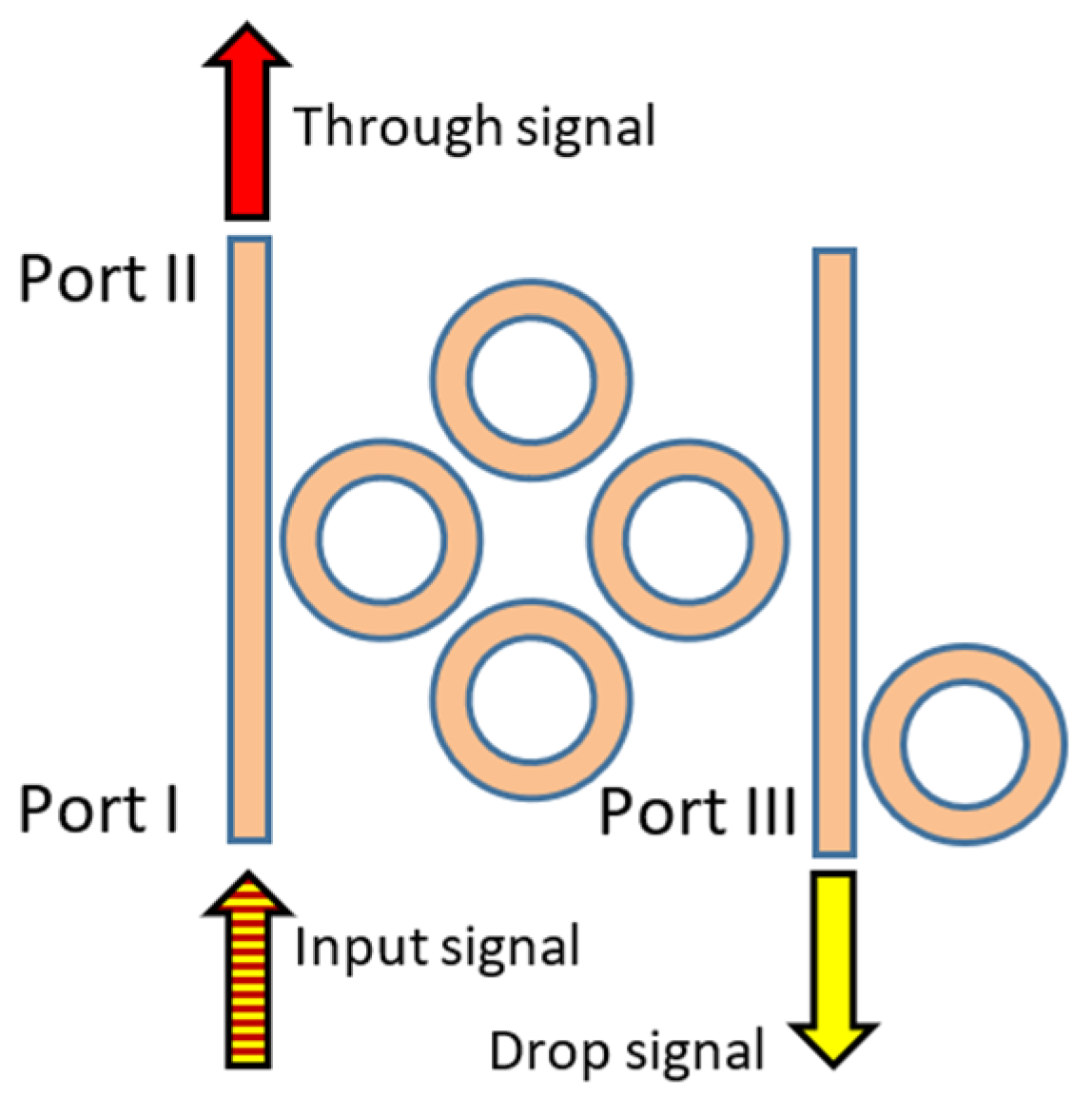
2. Review on the Genetic Algorithm and Interleaver/Deinterleaver Circuit

Genetic algorithms (GAs) are one of the oldest optimization algorithms [56,57]. In 1975, Holland J. [58] introduced the GA as an evolutionary algorithm inspired by the Darwinian theory; since then, the number of new GA variants and their applications has been increasing (as mentioned in [59] regarding the number of publications in the WoS database till 2018). What made the GA singular and powerful over other optimization algorithms such as gradient descent [60] and simulated annealing [61] is the population-based search techniques. In other words, the genetic algorithm starts with several solutions, instead of one, and tries to enhance throughout the iterations, thereby making the algorithm suitable for challenging optimization problems: non-convex optimization functions [62], parameters estimations [62,63], and systems identification [64].

In a traditional GA, an initial population that consists of several solutions has to be randomly created. The definition of a solution is related to the problem under consideration. Then, by performing evolutionary operators (selection, mutation, and cross over), a new generation of solutions is created. A well-tuned GA should generate new solutions that are better than the previous generation and that avoid, at the same time, the possibility of falling into a local optimum convergence. Several components compose a GA, as described in the pseudo-code indicated in the Supplementary Materials file (Algorithm S1). The main components of a GA are given in the Supplementary Materials file, where Figure S1 illustrates the cross-over and mutation genetic operators.

A schematic diagram of the case study circuit to optimize in this work is shown in Figure 1 [54]. The circuit is composed of four ring resonators, centered at the vertices of an imaginary 45°-rotated square. The four rings are squeezed between two straight buses. A fifth ring lies near the lower bus and away from the other four. The circuit works in the deinterleaver mode in this schematic where the signal, with two data streams, enters the circuit at port I and gets split into the through signal at port II and the drop signal at port III. The interleaver action is realized with the signal directions reversed. In this circuit, the coupling coefficient for the upper bus and the nearby ring is $k_o$ and it is the same for the lower bus and the nearest ring of the four. The coupling coefficient for the fifth ring and the lower bus is $k_{oa}$. For simplicity of design, the coupling coefficient, $k$, is the same for any pair of coupled rings of the four. The coupling coefficient represents the percentage of the electric field that hops from one element to a neighboring element and therefore its value has the bounds 0 and 1. The ratio of the through and drop electric fields to the input field is given by $\rho$ and $\tau$ respectively. The power ratio is then given by ${\left|\rho \right|}^2$ and ${\left|\tau \right|}^2$. A detailed analysis on how to calculate $\rho$ and $\tau$ is given in [54]. The through transmission is maximum when the rings are off resonance. This is given by the condition $\varphi =\pm \left(2n+1\right)\pi , n=0,1,2,\dots$, where $\varphi$ is the phase delay for one trip of light around the ring, also called the “normalized frequency”. The drop transmission is maximum at $\varphi =\pm 2n\pi , n=0,1,2,\dots$, i.e., when the rings are on resonance.

The requirements for this circuit for WDM communications are as follows [53]. The two channels are separated by $50 \mathrm{G}\mathrm{H}\mathrm{z}$. The free spectral range, $FSR$, for one channel is $FSR=100 \mathrm{G}\mathrm{H}\mathrm{z}$. This FSR corresponds to $\varphi =2\pi$. The $3-\mathrm{d}\mathrm{B}$ bandwidth, $BW$, for any channel should be at least $\pm 10 \mathrm{G}\mathrm{H}\mathrm{z}$. Within this bandwidth, the crosstalk, $CT$, should be $-23 \mathrm{d}\mathrm{B}$ or less and the absolute dispersion, $D$, should not exceed $30 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$. The insertion loss for any channel should be minimized. And finally, the shape factor, $SF$, defined as the ratio of the $-1 \mathrm{d}\mathrm{B}$ bandwidth to the $-10 \mathrm{d}\mathrm{B}$ bandwidth, should be greater than $0.6$. However, this factor is not a mandatory condition [53]. These specifications will be used then as the “performance parameters” for the design. More on how to calculate the coupling coefficients and the transmission characteristics is given in the Supplementary Materials file.

Thus, effectively, it is required to find the values for the three coupling coefficients, $k_o$, $k_{oa}$, and $k$, that will shape both $\rho$ and $\tau$ as required. Unfortunately, there is no direct analytical way to carry out this task. Instead, as shown in [54], the calculations are performed numerically through the multiplication of different matrices that represent the propagation loss and phase for the wave through each part of the circuit.

Such systems are very sensitive to the coupling coefficient values. Therefore, if each of the three coefficients is investigated with steps of $0.001$ between $0$ and $1$, there will be approximately one billion possible combinations to test. This is, of course, very time consuming. Therefore, the authors of both designs presented in [53,54] followed an alternative approach. The authors studied the performance of the device in the Z domain using the transform $z=e^{i\varphi }$. This way, the dynamics of the system poles and zeros can be followed as the coupling coefficients change values. This way, instead of randomly trying different combinations of values for the three coefficients, the designer can try some combinations of $\left[k_o,k_{oa},k\right]$, and visually study the dynamics of the system poles and zeros in the Z domain before trying a new set of combinations $\left[k_o,k_{oa},k\right]$, and so forth. While this approach is less time consuming, the visual investigation of the system poles and zeros is very tedious. Hence, in this work we propose a genetic algorithm-based approach. This approach reaches almost exactly the same solution found in [54] in a much faster and easier way.

3. Formulation of the Genetic Algorithm

The main steps of the proposed genetic algorithm are given in the next steps.

a.

Chromosome formation: In this approach, the three design parameters, i.e., the coupling coefficients, are arranged in the form of a $1\times 3$ array, $\left[k_o,k_{oa},k\right]$, called here a “chromosome”. A generation of $n$-chromosomes is then constructed as a matrix of $n$ rows, each with a combination of values for $\left[k_o,k_{oa},k\right]$. This means that a generation is given by a matrix of dimensions $n\times 3$. The initial population is created using random values of 3-decimal numbers between 0 and 1. The number of chromosomes attempted in our work was taken: $20, 40, 60, 80$, and $100$. The random initiation of the population is not needed afterwards since the next generations will be created using the crossover and mutation processes.

b.

Fitness functions: When the circuit performance is tested for a certain chromosome, or equivalently a $\left[k_o,k_{oa},k\right]$ combination, the corresponding performance parameters, i.e., the bandwidth ($BW$), the crosstalk ($CT$), the dispersion (D), the insertion loss ($IL$), and the shape factor ($SF$), are calculated for both channels. As stated in [53], the shape factor condition, $SF>0.6$, is not mandatory to satisfy. Also, the insertion loss cannot practically reach $0 \mathrm{dB}$; however, minimizing it is highly desirable. Therefore, the three conditions to focus on are $BW\ge \pm 10 \mathrm{G}\mathrm{H}\mathrm{z}$, i.e., $BW\ge 20 \mathrm{G}\mathrm{H}\mathrm{z}$ around the point of maximum transmission, $CT\le -23 \mathrm{d}\mathrm{B}$, and $D\le 30 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$. Recall that there are two channels and hence the six performance parameters must satisfy six conditions. This places the problem in the multi-objective optimization category [57]. In order to handle such a problem, we define a “performance metric”, for each performance parameter. This metric is calculated as the difference between the calculated performance parameter and the corresponding target value. The difference is calculated such that when the metric is zero or more, this indicates that the performance is acceptable. Then, the metric for the bandwidth, $V_{BW}$, is given by $V_{BW}=BW-20$, the metric for the crosstalk, $V_{CT}=-23-CT$, and the metric for the dispersion is given by $V_D=30-D$. Of course, there are two sets of these three metrics, one for each channel. For the through channel, we define $V_{B{W}_{\rho }}$, $V_{C{T}_{\rho }}$, and $V_{D_{\rho }}$. For the drop channel, we define $V_{B{W}_{\tau }}$, $V_{C{T}_{\tau }}$, and $V_{D_{\tau }}$. Then, in total, there are six metrics. Let us rename these metrics as $V_1, { V}_2$, and $V_3$ for the through channel, and $V_4, { V}_5$, and $V_6$ for the drop channel, respectively. We can then define a set for these metrics as follows:

$$V=\{V_i:1\le i\le 6, i\in N\}$$

(1)

For example, if the metric for the dispersion of one channel has the value of $2 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$, then the calculated dispersion parameter passed the required target by $2 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$. This means that the calculated dispersion is $28 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}<30 \mathrm{p}\mathrm{s}/\mathrm{n}\mathrm{m}$, which is an acceptable value.

A chromosome that hits a solution has all its metrics zero or positive. If all or some metrics are negative, then this chromosome does not provide a valid solution. However, in this case, the chromosome might be close to or far away from the target solution. Distinguishing between these two states is important so that the relatively better chromosomes are chosen to parent the next generation. So, the performance metrics are put in two subsets. The first subset, called $X$, includes the zero or positive metrics, i.e., those metrics that achieved the desired values, while the other subset, called $Y$, includes the negative metrics which fell short of achieving the desired WDM specifications. We can then define the subsets $X$ and Y as follows:

$$X=\{x:x=V_i if V_i\ge 0\}$$

(2)

$$Y=\{y:y=V_i if V_i<0\}$$

(3)

The average value for the first subset of metrics is fitness function $a$, while that for the second subset is fitness function $b$. Then,

$$a=\overline{X}$$

(4)

$$b=\overline{Y}$$

(5)

If $Y$ is an empty set, or equivalently $V_i\ge 0 \forall i$, then $b=0$ and a solution for the problem (good $\left[k_o,k_{oa},k\right]$ combination) is found. Then, these two functions, $a$ and $b$, are then used in the selection criterion, as explained in the next step.

c.

Selection criterion: A selection criterion is used to pick the best chromosomes that will parent the next generation. Intuitively, one would think that the chromosomes to select for the next stage of the process, the crossover, are those with maximum $a$ and minimum $\left|b\right|$. However, after some attempts, we found that maximizing $a$ does not necessarily lead to an acceptable solution that satisfies all conditions. For example, pushing the bandwidth way above the required minimum of $20 \mathrm{G}\mathrm{H}\mathrm{z}$ leads automatically to worse crosstalk, lower than the required $-23 \mathrm{d}\mathrm{B}$. This is a clear result of the physics of the problem since a wider bandwidth means more overlap between adjacent channels and therefore worse crosstalk; a positive bandwidth metric, $V_{BW}$, and a negative crosstalk metric, $V_{CT}$. Hence, $V_{BW}$ contributes to the calculation of $a$, while $V_{CT}$ belongs to the calculation of $b$. So, $a$ can grow because of the positive metric for the bandwidth but at the same time $b$ gets more negative, due to the bad crosstalk, and thereby no acceptable solution is found. This contradiction of the performance metrics is not unexpected for multi-objective problems [65]; however, the issue now is how to find a design with all design parameters satisfied, i.e., $b=0$.

Therefore, we changed the approach to favor the chromosomes with minimum $a$ and minimum $\left|b\right|$. In other words, instead of choosing the champions of each generation to parent the next, we choose the middling individuals [66]. This goes as follows: the original chromosomes are ordered ascendingly according to the $a$-values. Then, we pick the first $n/4$ chromosomes. Again, the original chromosomes, including those picked in the previous step, are ordered ascendingly according to the $\left|b\right|$-values. Again, we pick the first $n/4$ chromosomes. Now, the chromosomes picked in the two steps are used to create a group of $n/2$ chromosomes, which will be subject to the crossover step and creating the next generation with new $n$-chromosomes.

If, for any chromosome, $b=0$, this means that there are no negative metrics and hence a valid solution is found. Of course, such a chromosome qualifies for the next stage, the crossover. However, the algorithm does not stop once such a solution is found, and the program keeps running until the complete number of generations, selected here as $g=100$ generations, is attempted, giving a chance to find a different solution. Based on that, we decided to select the best half of the population of one generation for the crossover process that produces the next generation.

d.

Crossover: Each coupling coefficient value, in the favored chromosomes, is converted to an equivalent 10-digit binary number. This binary number is split at a position called the “crossing site”, designated by $S$, into two parts. For example, if $S=3$, then the binary number is split into two parts, the leftmost 3 bits and the rightmost 7 bits. The crossover is accomplished by randomly exchanging the right parts of the crossing site between the favored chromosomes. Note that the selected chromosomes in our design represent only 50% of a generation and will be responsible for creating the next generation. This means that one chromosome might have the opportunity to mate more than once. In our work, we attempted $S=$ $1, 2, 3, 4$, and $5$. Note that each coupling coefficient is treated independently from the other. Meaning that the mating takes place between two binary numbers that belong to the same coupling coefficient, $k_o$, $k_{oa}$, or $k$.

e.

Mutation: After the crossover, the new coupling coefficients are converted back from binary to decimal. Mutation is applied. If the maximum mutation allowed is $M_{max}$, then a random value $M$ is added to the values of the coupling coefficients where, $-M_{max}<M<M_{max}$. In our work, we tried $M_{max}=0.02, 0.04, 0.06, 0.08$, and $0.1$. We found out that mutation is necessary to avoid the saturation in the values of the chromosomes, away from a solution. Also, after hitting a solution, mutation is necessary to push the calculations away in the hope of finding a different solution. Finally, the new generation is ready, and the process starts over.

4. Results and Discussions

Recall that the parameters of the genetic algorithm take different values in our calculations as follows. The number of chromosomes takes values $n=20,40,60,80$, and $100$. The crossing site takes values $S=1,2,3,4$, and $5$. And finally, the maximum mutation takes values $M_{max}=0.02,0.04,0.06,0.08,$ and $0.1$. This makes $125$ different combinations of parameters $[n,M_{max},S]$. The number of generations was fixed at $g=100$ generations. Also, recall that the program completes the calculations for all $100$ generations even if a valid solution is hit on the way. For each combination $[n,M_{max},S]$, the program was executed $10$ times. The reason for this is to check the probability of finding a solution corresponding to this combination, since, for some combinations, there could be no solutions after some complete runs.

In Figure 2, a visualization of the probability of finding a solution is shown for different split positions, $S$. This probability is found as the ratio of the number of runs where a solution is found to the total number of runs for this combination $[n,M_{max},S]$. Clearly, the probability of finding a solution is higher for a larger number of chromosomes and a smaller mutation. While it is intuitive to understand why more chromosomes give a higher probability of finding a solution, the effect of mutation can be explained based on the way it was used in our algorithm. In order to avoid saturation either away from or nearby a solution, we applied mutation repeatedly. Mutation was injected at each generation as long as there is no solution hit yet, and also for two generations immediately after finding a solution in order to push the calculations away in the hope of finding a different solution. After these two generations, mutation is not applied for ten generations, but gets applied again if there is no solution and until one is found. Given that this problem proved it has one solution, i.e., one valid $\left[k_o,k_{oa},k\right]$ combination, apparently with strong mutation, $M_{max}=0.1$, there are strong deviations from the target solution and catching a solution is not as easy as with light mutation such as $M_{max}=0.02$. For example, in Figure 3, the generation number with first solution is illustrated for each $[n,M_{max},S]$ combination. Clearly, this shows the same trend as in Figure 2. The combinations with high solution probability also have much earlier generations with solutions.

Regarding the effect of the crossing site, $S$, in general, $S=1$ shows better probability of finding a solution for a given number of chromosomes, $n$, and for lower mutations. However, as $M_{max}$ increases, the effect of $S$ decreases for the same $n$. This might be attributed to the fact that with $S=1$, a bigger change of the chromosome values takes place since nine bits are exchanged, which means that up to $50\mathrm{\%}$ of the value of a coupling coefficient is subject to change. As $S$ increases, the exchanged part is of much less value and therefore there is no significant progress in the crossover stage. But in any case, the effect of the crossing site, $S$, does not seem very decisive. The strongest effects in this study turn out to be that of $n$ and $M_{max}$.

In

Table 1. The $[n,M_{max},S]$ combinations with $100\%$ probability of finding a solution. The first row shows the solution reported in [54].

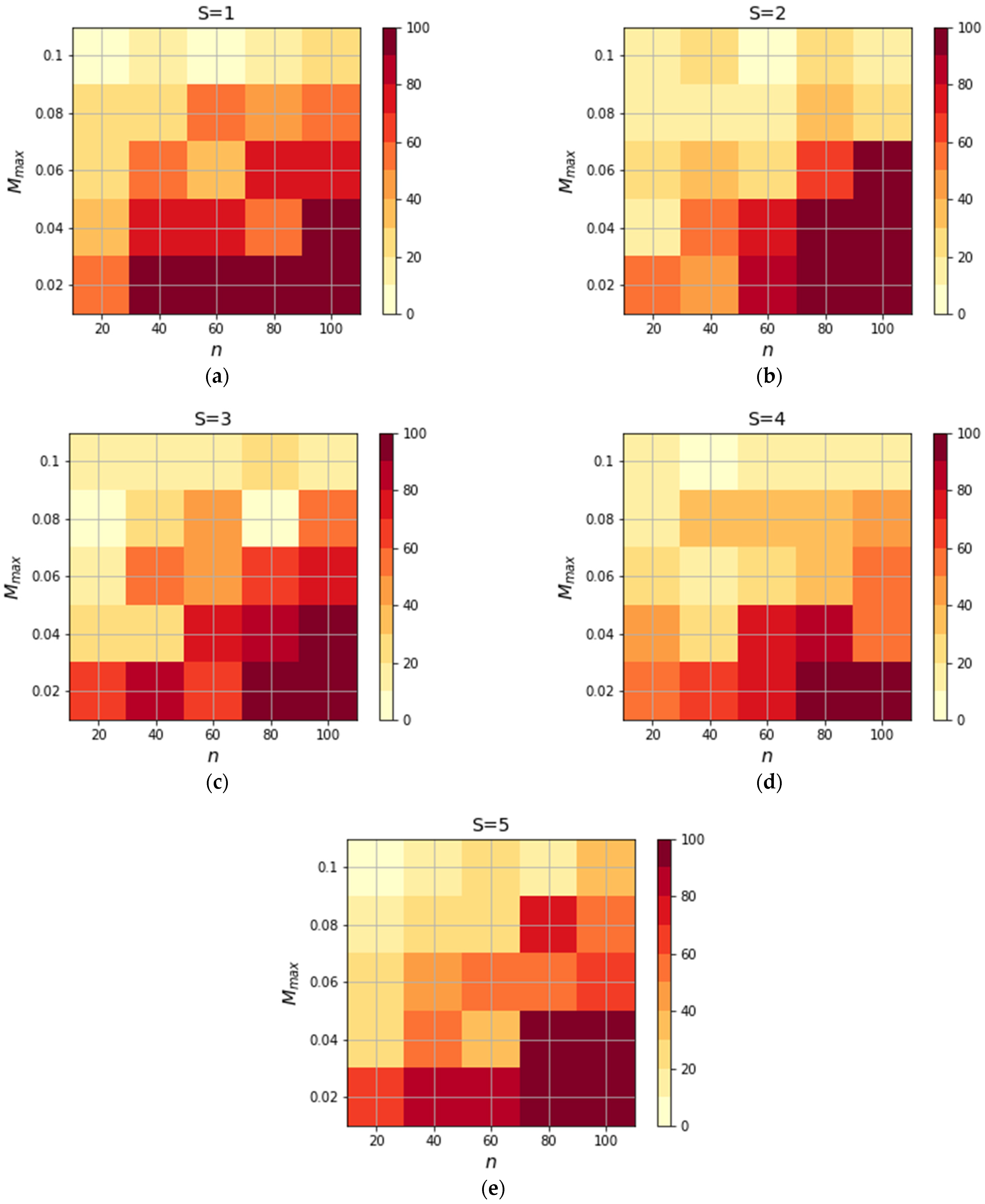
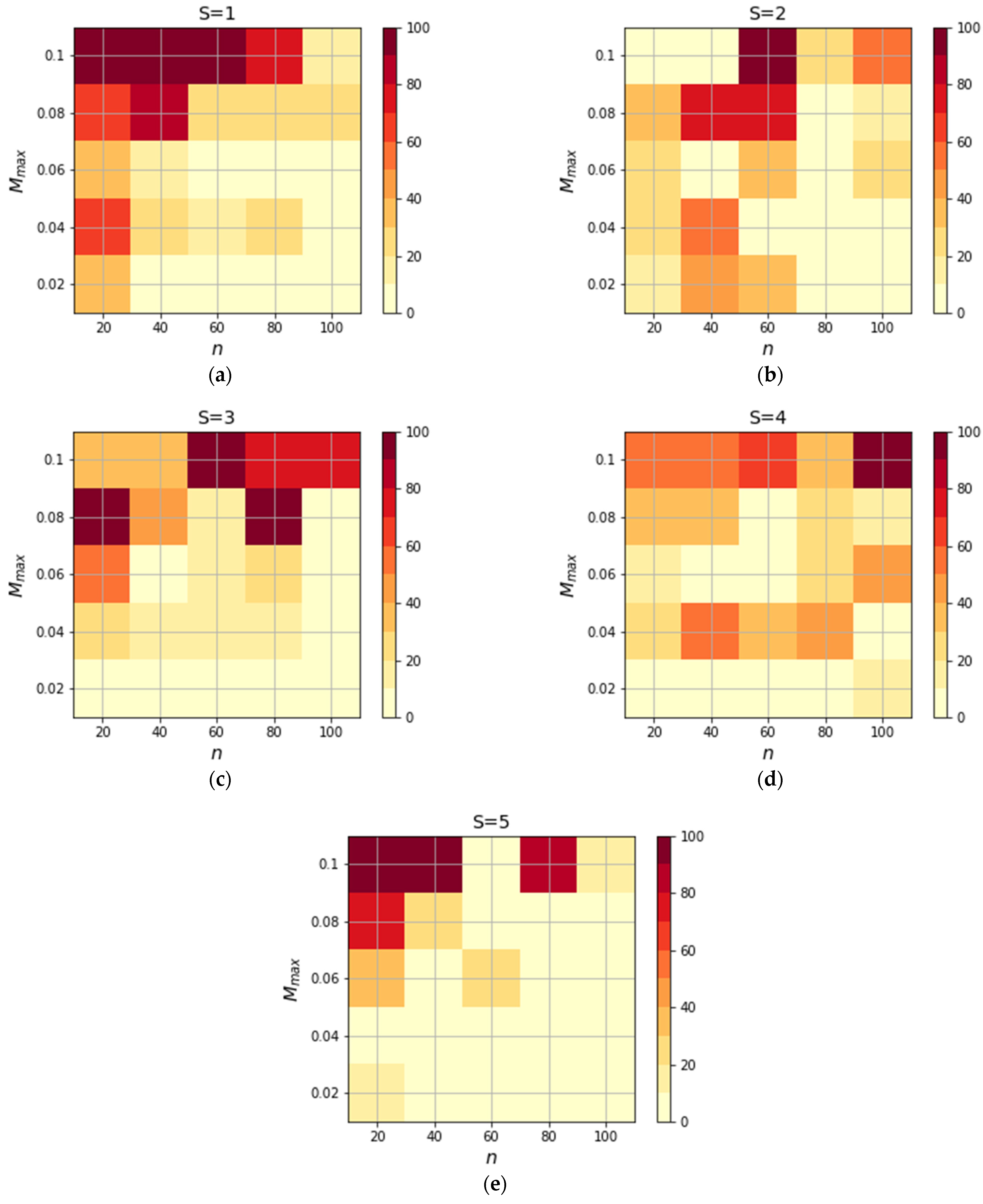
$\mathit{n}$	$\mathit{S}$	${\mathit{M}}_{\mathit{m}\mathit{a}\mathit{x}}$	First Generation with a Solution	Solution Chromosome	${\mathit{k}}_{\mathit{o}}$	${\mathit{k}}_{\mathit{o}\mathit{a}}$	$\mathit{k}$
$-$	$-$	$-$	$-$	$-$	$0.935$ [54]	$0.952$ [54]	$0.525$ [54]
40	1	0.02	11	$9$	$0.935$	$0.951$	$0.535$
60	1	0.02	11	$49$	$0.938$	$0.951$	$0.534$
80	1	0.02	7	$53$	$0.935$	$0.946$	$0.531$
80	2	0.02	9	$62$	$0.934$	$0.951$	$0.541$
80	3	0.02	12	$2$	$0.934$	$0.950$	$0.540$
80	4	0.02	5	$53$	$0.932$	$0.950$	$0.541$
80	5	0.04	7	$25$	$0.934$	$0.948$	$0.534$
100	1	0.02	9	$46$	$0.937$	$0.949$	$0.536$
100	2	0.02	10	$62$	$0.936$	$0.952$	$0.538$
100	2	0.04	11	$22$	0.933	0.948	0.535
100	3	0.02	9	$58$	$0.939$	$0.950$	$0.533$
100	3	0.04	12	$26$	$0.939$	$0.948$	$0.535$
100	4	0.02	11	$67$	$0.936$	$0.950$	$0.535$
100	5	0.04	8	$25$	$0.936$	$0.945$	$0.529$

, the $[n,M_{max},S]$ combinations with $100\%$ probability of finding a solution are shown, with the corresponding solutions $[k_o,k_{oa},k]$. Also, the solution reported in [54] is shown in the first row of this table. Clearly, there is a strong matching between the solutions found using the algorithm suggested in this work and those in [54].

Obviously, $n=20$ does not guarantee finding a solution and at least $n=40$ chromosomes are needed. With $M_{max}>0.04$, the probability of finding a solution is less than $100\%$, regardless of the values of $n$ or $S$. For fastest guaranteed solutions, $n=40$, $M_{max}=0.02$, and $S=1$ can be employed. This means that more extensive calculations with $n=60, 80$, and $100$ are not necessary for this problem.

Regarding the simulation time, for one run with 100 generations, if the number of chromosomes is $n$, the time needed is $0.1n$ min using a laptop with an Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz processor and $12 \mathrm{G}\mathrm{B}$ of RAM. This means that a solution can be found for this complex problem within only four minutes using $\left[n,M_{max},S\right]=\left[\mathrm{40,0.02,1}\right]$ if the whole 100 generations are attempted. If the program is set to stop at the first acceptable solution, the required time can be less than $0.5$ min.

The evolution of $b$, for the best chromosome in a generation, throughout the $100$-generation with $\left[n,M_{max},S\right]=\left[\mathrm{40,0.02,1}\right]$, is illustrated in Figure 4. Recall that $b$ represents the average of the negative metrics. When $b$ hits zero, this means that all of the metrics are zero or positive and a valid solution is found. At the first generation, the error is so big because this generation has completely random values. Note that the first solution is found at the ${11}^{\mathrm{t}\mathrm{h}}$ generation. Then, the solution deviates, thanks to the mutation, before it hits a solution again at the ${43}^{rd}$ generation and again at the ${100}^{th}$ solution.

Genetic algorithm grabbed attention for its use in solving different integrated optics design problems. For example, the work in [67] addresses the design of beam shaping using photonic crystals. Luckily, for that design, an analytical expression is available to optimize the design parameters. This makes the problem much easier than the one tackled in the current work, which has no closed form solution. The work in [68] shows the design of a polarization beam splitter. The work relies on using a ready tool from Lumerical that is integrated into its 3D FDTD tool. This method proves to be time consuming. The same applies for the polarization rotator design presented in [69]. A delay line is designed in [70], with the number of rings in the study up to seven. The authors used a ready tool in MATLAB and required 1000 generations with 400 individuals each to reach the optimal results. Our approach clearly requires a one order of magnitude smaller number of generations and one order of magnitude smaller number of individuals. Finally, a classic genetic algorithm is adopted in [71] to optimize the design of a photonic crystal structure with no advancement in terms of the genetic algorithm approach.

5. Conclusions

In this work, a genetic algorithm approach is proposed to optimize the performance of silicon photonics circuits. In this approach, the design parameters, or the inputs to the algorithm, are grouped in one chromosome which is written in the form of a matrix with one row and as many columns as the design parameters. A generation is then written as a matrix of multiple rows, each with one different chromosome. For each chromosome in one generation, after evaluating the circuit transmission, the performance metrics are calculated. A performance metric, or an output of the algorithm, is calculated as the difference between the calculated performance parameter and the corresponding target value. If the metric is zero or positive, then it satisfies the corresponding standard. After testing any chromosome, the corresponding metrics are separated into two groups, one group with the metrics that fulfilled the required specifications and the other with the poor performing metrics. The average of the values of the second group metrics is the main fitness function that is pursued as a lead during the quest for a solution. During the evolutionary process, when this average reaches zero, then a solution is found. The main issue is then how to choose the chromosomes that will parent the next generation. The multi-objective nature of such problems leads to contradicting trends of the performance metrics. So, a chromosome with very good performance in one aspect shows a corresponding very poor performance in another. Following such chromosomes in the evolutionary process leads to unsatisfactory end results where the photonic circuit performs according to, or even exceeding, the standards in some but not all of the target performance specifications. Therefore, we chose to use the middling individuals from one generation to parent the next. This means eliminating the chromosomes with extremely good metrics, which are typically associated with other extremely bad metrics. The process is repeated until all performance conditions are met.

A case study is the interleaver/deinterleaver circuit which was designed previously using a tedious mix of visual investigation of the Z-domain of the transmission alongside with trial and error of the design parameters, here the coupling coefficients. The circuit has no closed-form expression to calculate its transmission, but instead is studied numerically through multiplication of matrices representing the coupling and the propagation phase and losses. The circuit performance parameters must obey the constraints set by WDM telecommunications standards. Therefore, for each chromosome, six different performance metrics are defined for the bandwidth, crosstalk, and dispersion of the circuit two channels. With the proposed approach, mutation less than $0.02$ of the coupling coefficient value, $40$ chromosomes per generation, and a maximum of $100$ generations are required to find the best design in less than four minutes using an Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz processor.

For such multi-objective design problems, choosing the middling points, instead of only the best performing chromosomes, proves effective to alleviate the natural contradiction between performance metrics, and facilitates finding the optimal solution in a very short period of time.