Design of a Spaceborne, Compact, Off-Axis, Multi-Mirror Optical System Based on Freeform Surfaces
Abstract
1. Introduction
2. Methods
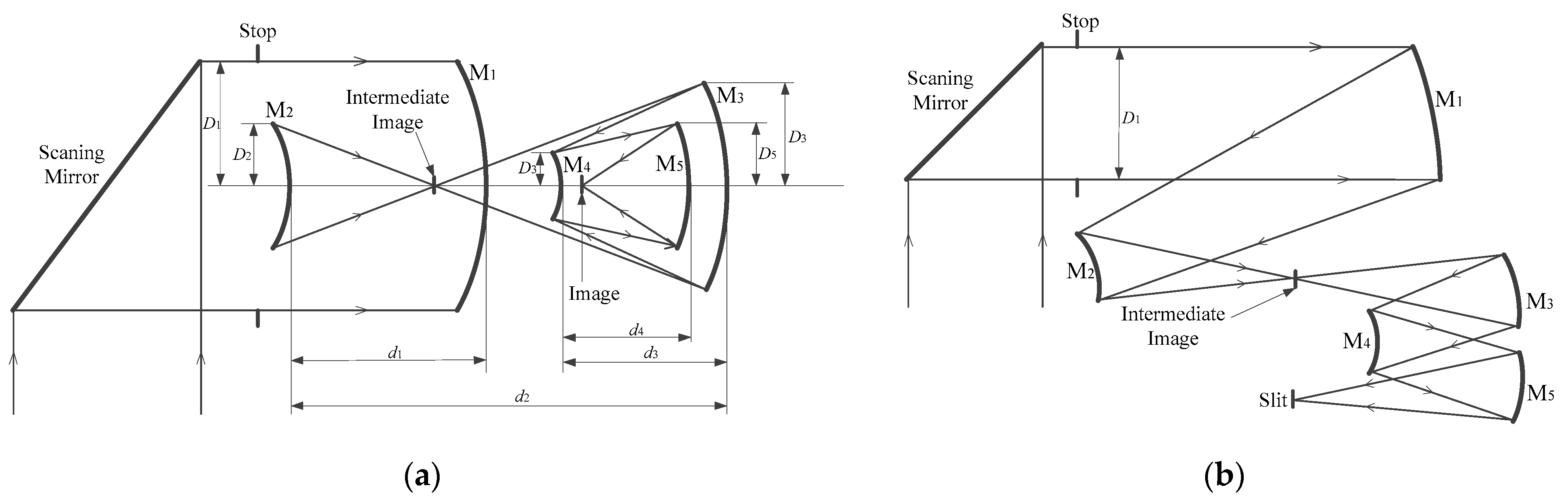
2.1. The Off-Axis Multi-Mirror Telescope System (MMTS)
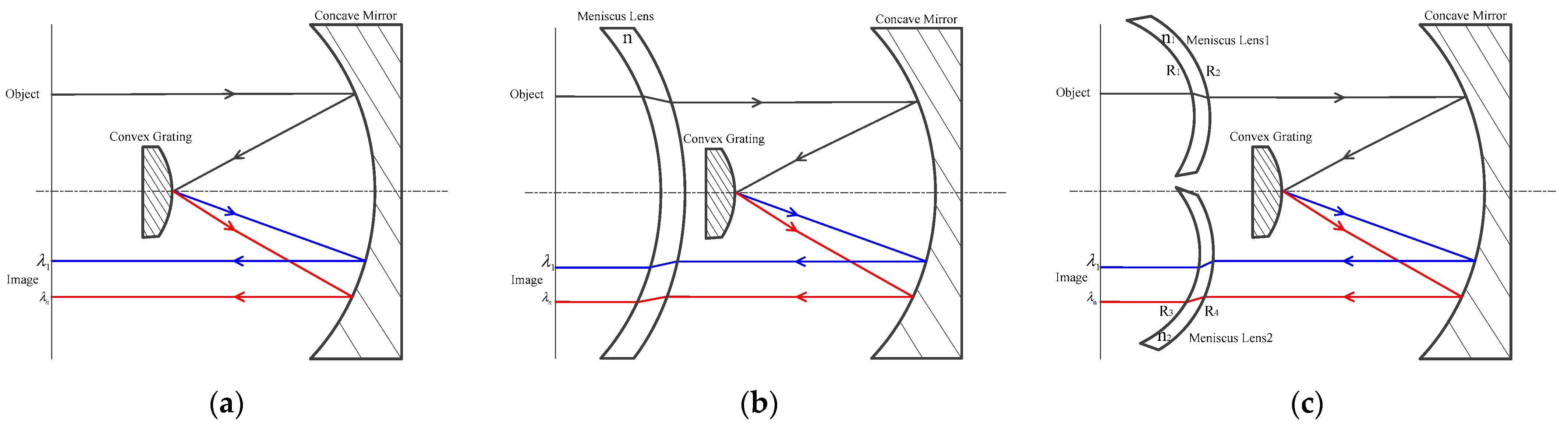
2.2. The Off-Axis Lens-Compensated Offner Spectral Imaging System
2.3. Freeform Surface Aberration Correction Method
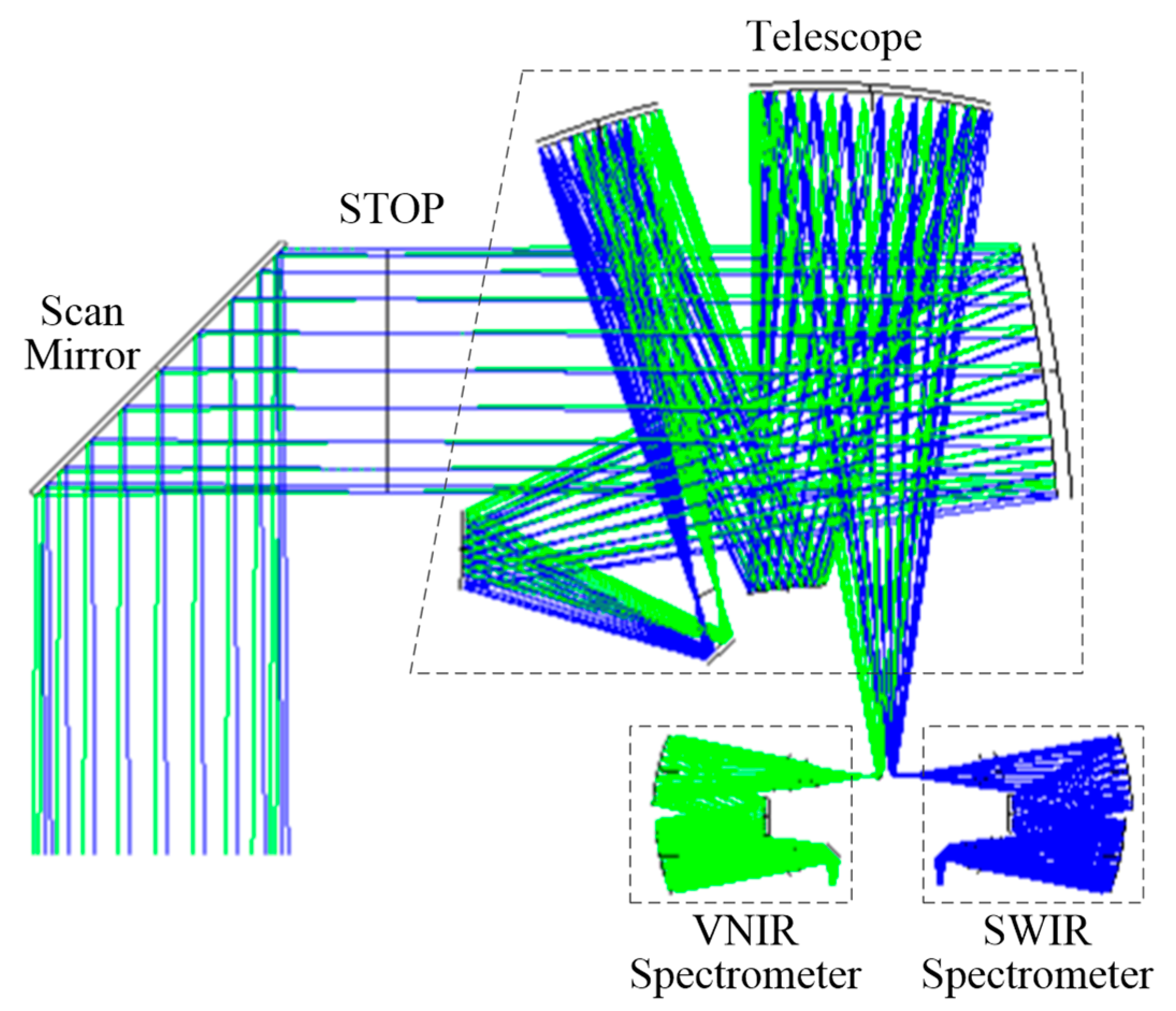
3. System Design and Analysis
3.1. Telescope System Design and Analysis
3.2. Spectral Imaging System Design and Analysis
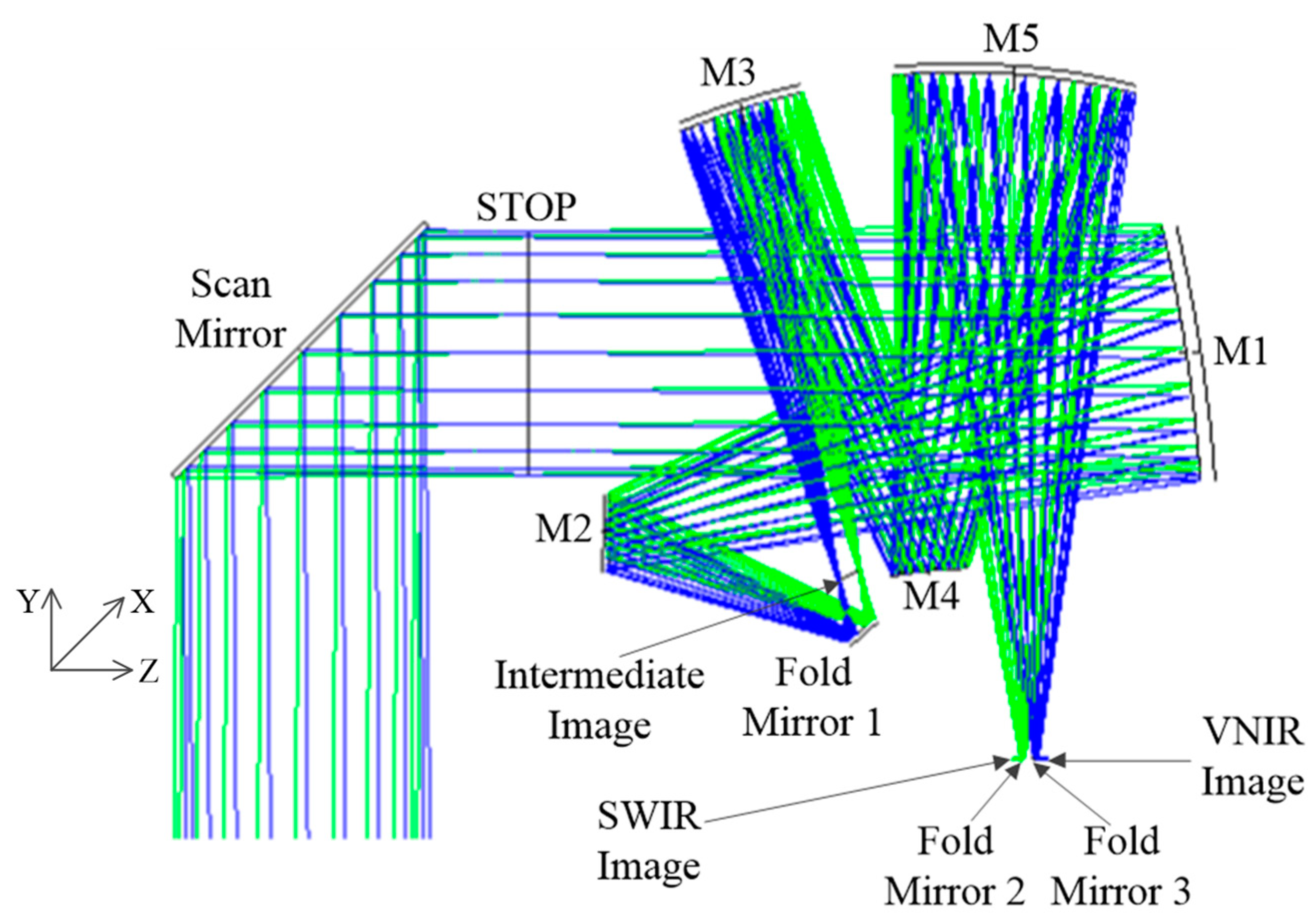
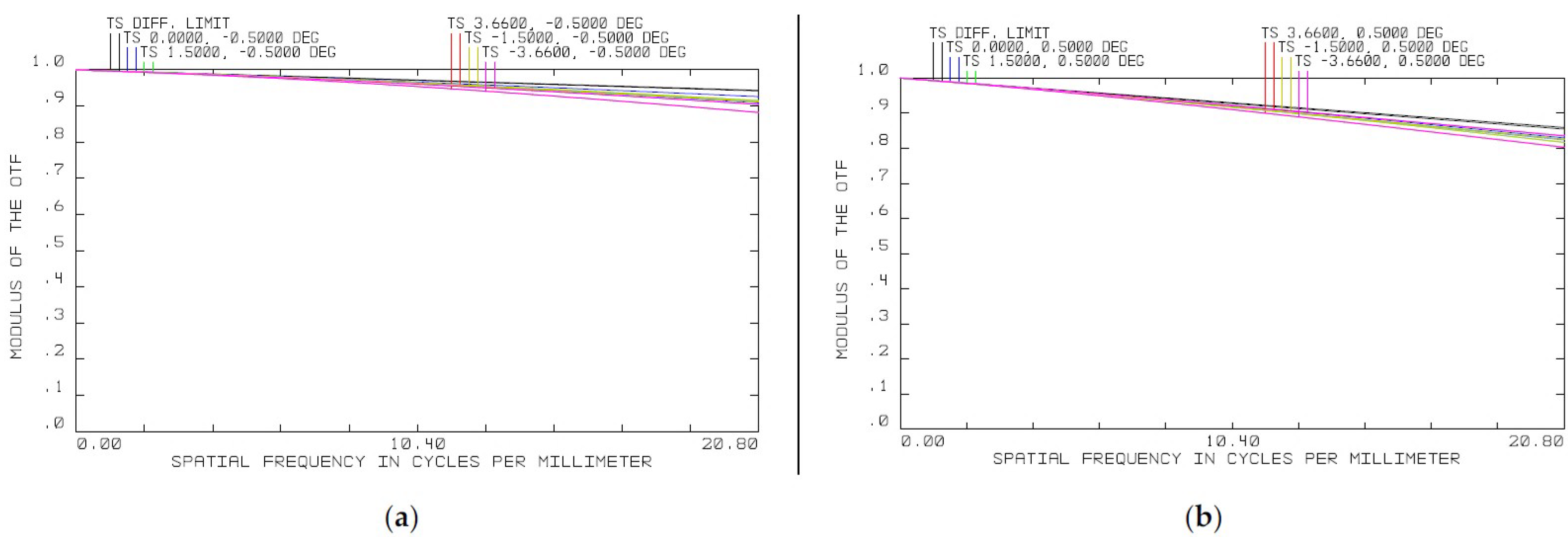
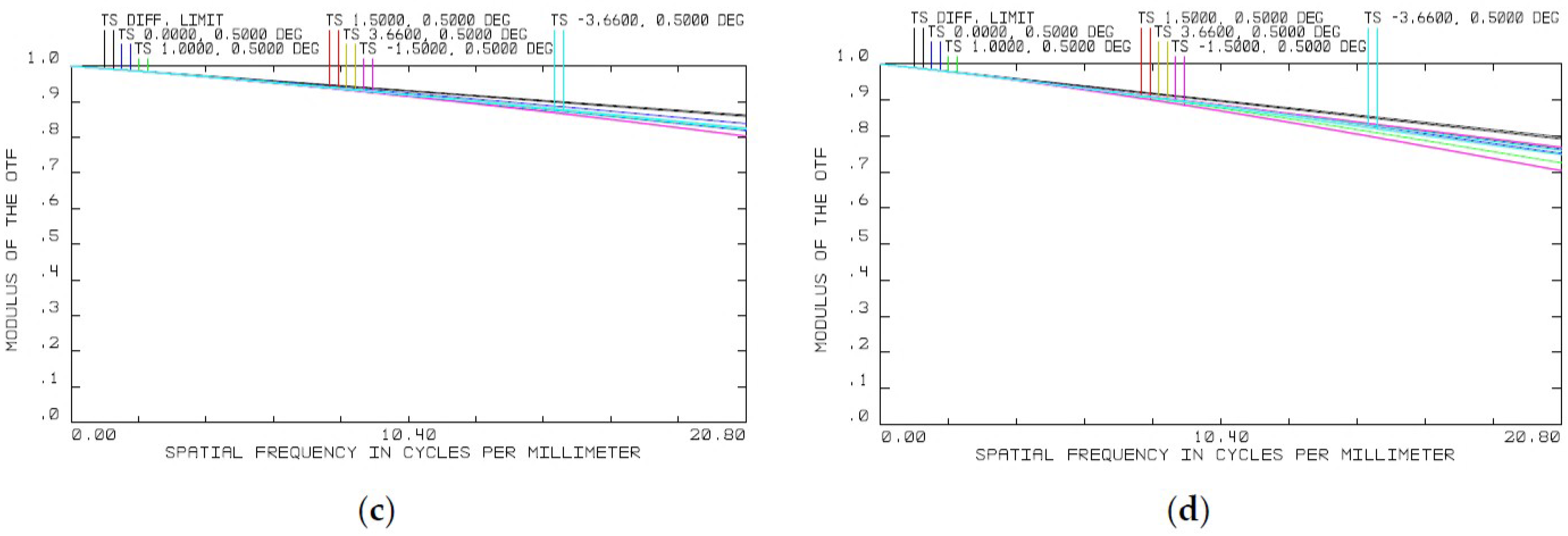
3.3. The Complete Optical System Design and Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hank, T.B.; Berger, K.; Bach, H. Spaceborne imaging spectroscopy for sustainable agriculture: Contributions and challenges. Surv. Geophys. 2019, 40, 515–551. [Google Scholar] [CrossRef]
- Roth, K.L.; Roberts, D.A.; Dennison, P.E. The impact of spatial resolution on the classification of plant species and functional types within imaging spectrometer data. Remote Sens. Environ. 2015, 171, 45–57. [Google Scholar] [CrossRef]
- Meyer, J.M.; Kokaly, R.F.; Holley, E. Hyperspectral remote sensing of white mica: A review of imaging and point-based spectrometer studies for mineral resources, with spectrometer design considerations. Remote Sens. Environ. 2022, 275, 113000. [Google Scholar] [CrossRef]
- Liu, Y.M.; Ma, X.; Men, C.G. A hyperspectral remote sensing image classification method based on multi-spatial information. Chin. Space Sci. Technol. 2019, 2, 73–81. [Google Scholar]
- Gao, B.C.; Li, R.R.; Lucke, R.L. Vicarious calibrations of HICO data acquired from the International Space Station. Appl. Opt. 2012, 14, 2559–2567. [Google Scholar] [CrossRef] [PubMed]
- Mahalingam, S.; Srinivas, P.; Devi, P.K. Reflectance based vicarious calibration of HySIS sensors and spectral stability study over pseudo-invariant sites. In Proceedings of the 2019 IEEE Recent Advances in Geoscience and Remote Sensing: Technologies, Standards and Applications (TENGARSS), Kochi, India, 17–20 October 2019; pp. 132–139. [Google Scholar]
- Matsunag, T.; Iwasaki, A.; Tachikawa, T. The status of hyperspectral imager suite (HISUI): One year after launch. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Belgium, The Netherlands, 11–16 July 2021; pp. 1384–1385. [Google Scholar]
- Cogliati, S.; Sarti, F.; Chiarantini, L. The PRISMA imaging spectroscopy mission: Overview and first performance analysis. Remote Sens. Environ. 2021, 262, 112499. [Google Scholar] [CrossRef]
- Alonso, K.; Bachmann, M.; Burch, K. Data products, quality and validation of the DLR earth sensing imaging spectrometer (DESIS). Sensors 2019, 20, 4471. [Google Scholar] [CrossRef] [PubMed]
- Guanter, L.; Kaufmann, H.; Segl, K. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Lee, C.M.; Cable, M.L.; Hook, S.J. An introduction to the NASA Hyperspectral InfraRed Imager (HyspIRI) mission and preparatory activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Borguet, B.; Moreau, V.; Santandrea, S. The challenges of broadband performances within a compact imaging spectrometer: The ELOIS solution. Proc. SPIE 2021, 11852, 572–582. [Google Scholar]
- Borguet, B.; Moreau, V.; Renotte, E. The dual-blazed diffraction grating of the CHIME hyperspectral instrument: Design, modelling & breadboarding. Proc. SPIE 2023, 12777, 1041–1056. [Google Scholar]
- Pastena, M.; Domínguez, B.C.; Mathieu, P.P. ESA Earth observation directorate NewSpace initiatives. In Proceedings of the AIAA/USU Conference on Small Satellites, Logan, UT, USA, 3–8 August 2019. SSC19-V-05, 1-4. [Google Scholar]
- Hu, X.; Liao, Q.; Huang, A. High SNR eSWIR Image Sensor Applied in Advanced Hyperspectral Imager (AHSI) aboard China’s GaoFen-5 Satellite and ZY-1 Satellite. IEEE Sens. J. 2023. [Google Scholar] [CrossRef]
- Niu, C.; Tan, K.; Wang, X. Radiometric cross-calibration of the ZY1-02D hyperspectral imager using the GF-5 AHSI imager. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Wang, B.H.; Li, K.; Tang, S.F. Optical system design of a spaceborne imaging spectrometer with high resolution and super swatch. Spacecr. Recovery Remote Sens. 2021, 1, 92–99. [Google Scholar]
- Kwo, D.; Lawrence, G.; Chrisp, M. Design of a grating spectrometer from a 1:1 Offner mirror system. Proc. SPIE 1987, 818, 275–281. [Google Scholar]
- Lobb, D.R. Theory of concentric designs for grating spectrometers. Appl. Opt. 1994, 13, 2648. [Google Scholar] [CrossRef] [PubMed]
- Prieto-Blanco, X.; Fuente, R. Compact Offner–Wynne imaging spectrometers. Opt. Commun. 2014, 328, 143–150. [Google Scholar] [CrossRef]
- Stuffler, T.; Förster, K.; Hofer, S. Hyperspectral imaging—An advanced instrument concept for the EnMAP mission (Environmental Mapping and Analysis Programme). Acta Astronaut. 2009, 7–8, 1107–1112. [Google Scholar] [CrossRef]
- Holly, A.; Bender, P.M.; Ronald, J. Wide-field imaging spectrometer for the hyperspectral infrared imager (HyspIRI) mission. In Proceedings of the SPIE 9222, Imaging Spectrometry XIX, 92220E, San Diego, CA, USA, 15 September 2014; Volume 9222, pp. 113–120. [Google Scholar]
- Thompson, K.P. Description of the third-order optical aberrations of near-circular pupil optical systems without symmetry. JOSA A 2005, 7, 1389–1401. [Google Scholar] [CrossRef]
- Fuerschbach, K.; Rolland, J.P.; Thompson, K.P. Theory of aberration fields for general optical systems with freeform surfaces. Opt. Express 2014, 22, 26585–26606. [Google Scholar] [CrossRef]
- Shi, H.; Jiang, H.; Zhang, X. Analysis of nodal aberration properties in off-axis freeform system design. Appl. Opt. 2016, 24, 6782–6790. [Google Scholar] [CrossRef]
- Jia, B.; Li, Y.; Lv, Q. Design of a Large Field of View and Low-Distortion Off-Axis Optical System Based on a Freeform Surface. Photonics 2023, 5, 506. [Google Scholar] [CrossRef]
- Ye, J.; Chen, L.; Li, X. Review of optical freeform surface representation technique and its application. Opt. Eng. 2017, 11, 110901. [Google Scholar] [CrossRef]
- Shi, Y.; Zheng, Y.; Lin, C. Design Method of Freeform Anamorphic Telescopes with an Ultrawide Field of View. Photonics 2022, 11, 836. [Google Scholar] [CrossRef]
- Tan, Y.; Zhu, J. Spatial three-mirror off-axis freeform optical system without any symmetry. Photonics 2022, 9, 326. [Google Scholar] [CrossRef]
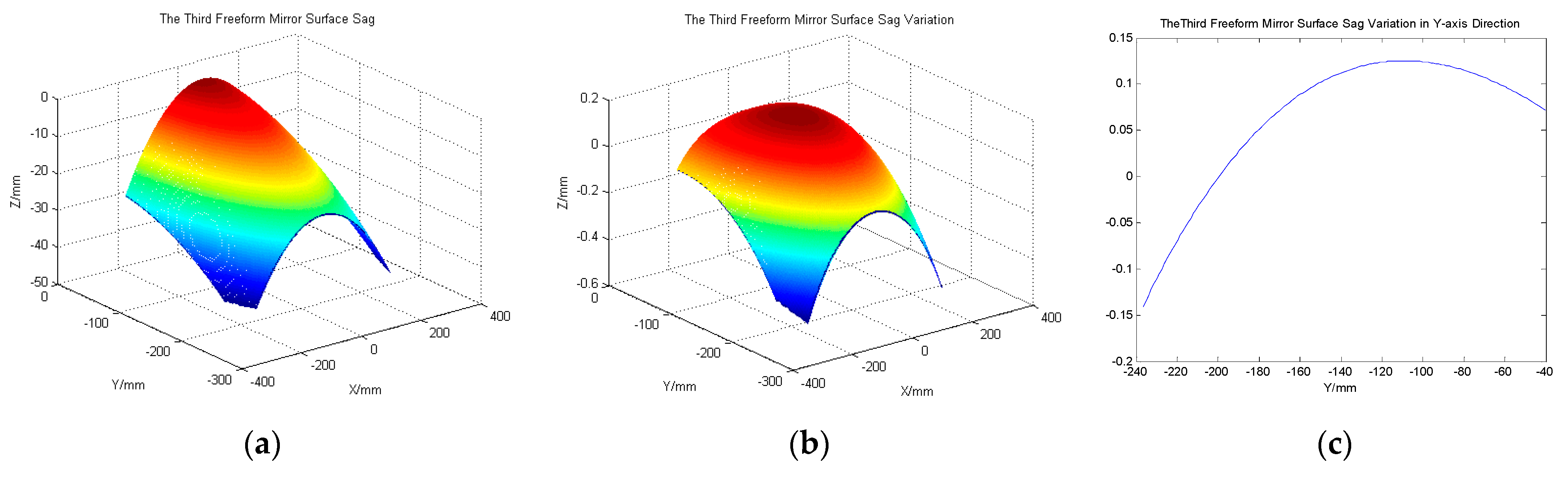
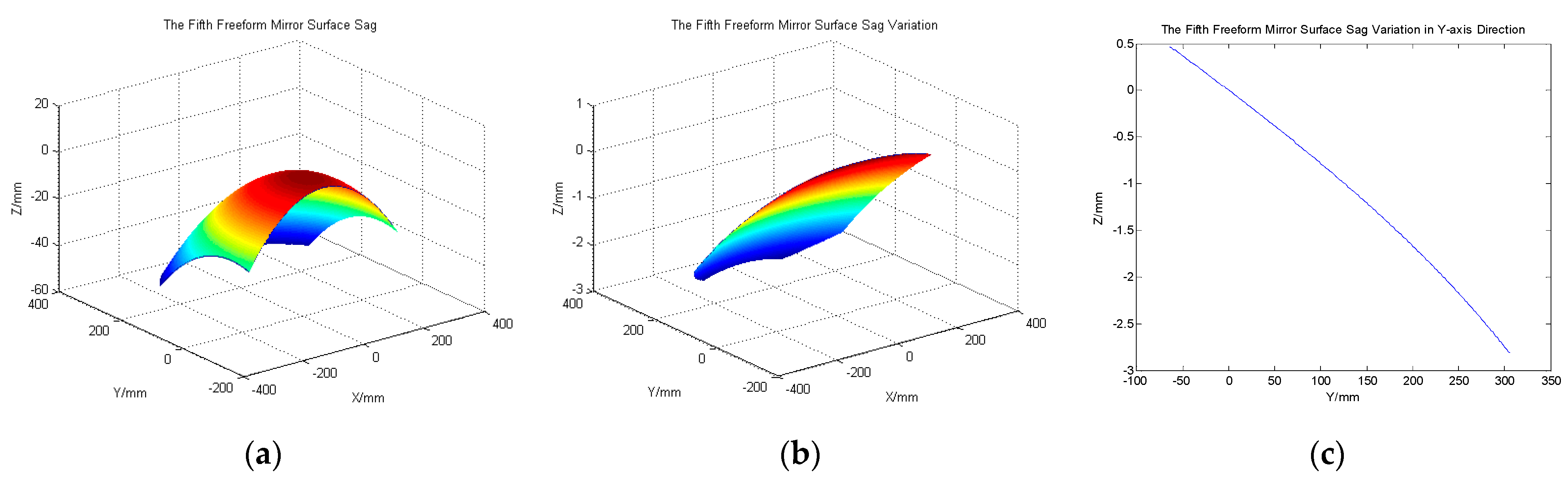

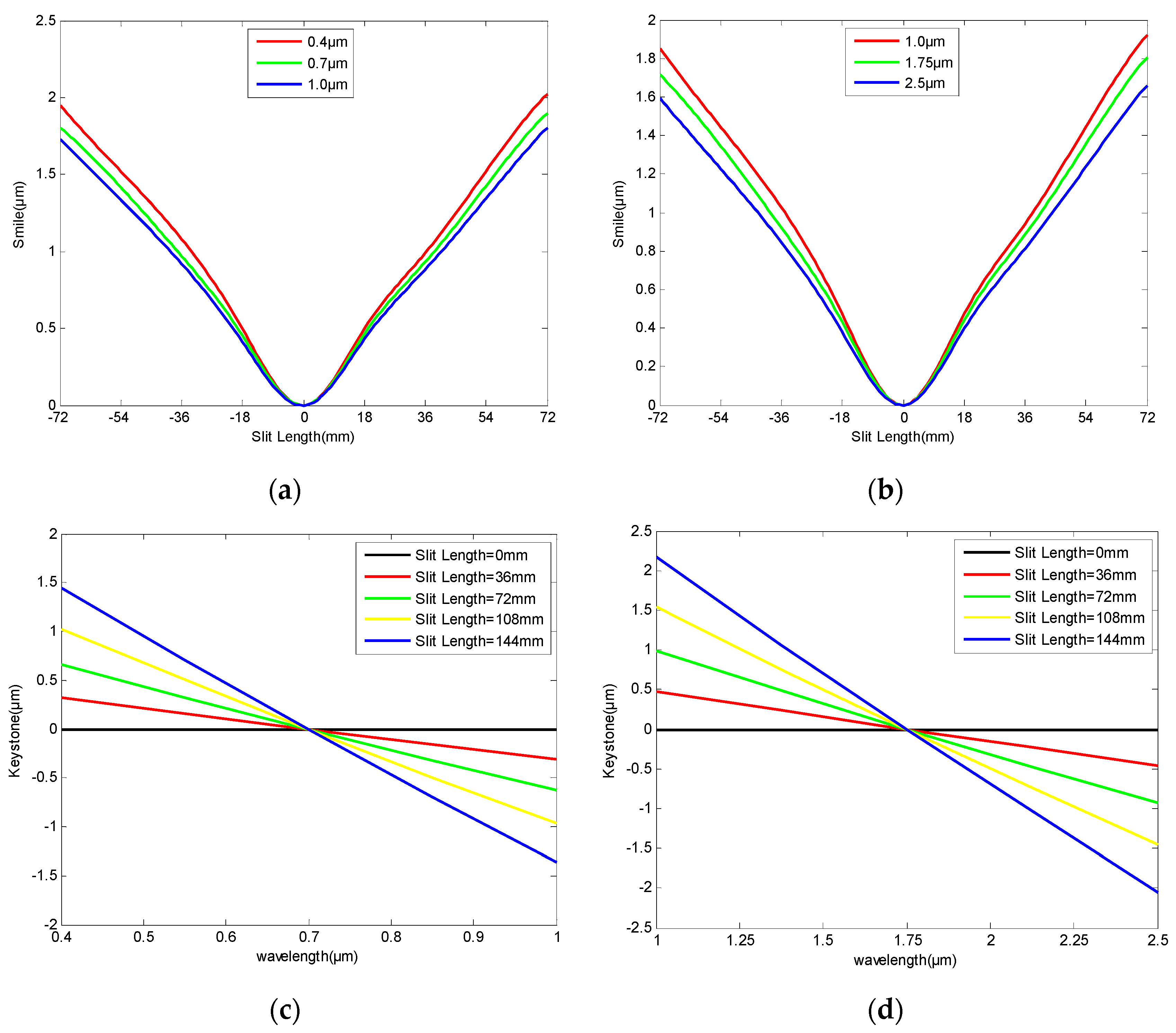
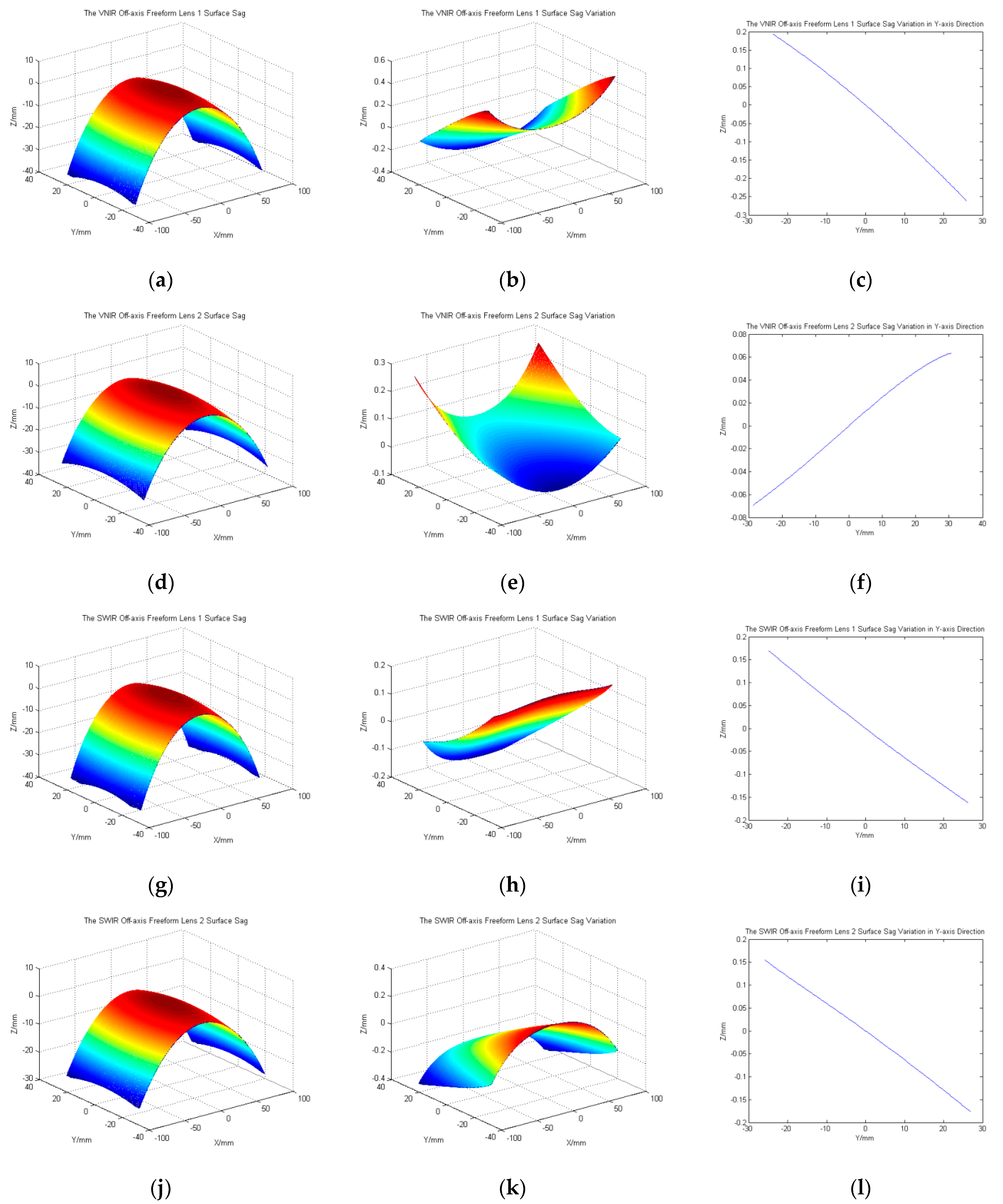

| Parameters | Specifications |
|---|---|
| Spectral Range | 0.4~2.5 μm |
| Spectral Resolution | 5 nm (0.4~1.0 μm) |
| 10 nm (1.0~2.5 μm) | |
| FOV | 7.32° |
| Focal Length | 1128 mm |
| Aperture | 376 mm |
| F-number | 3 |
| Slit Length | 144 mm |
| Scanning Angle | ±7.32° |
| Smile | ≤±2.4 μm |
| Keystone | ≤±2.4 μm |
| Aberration | Radial Coordinate | Cartesian Coordinate | X-Y Polynomial Combinations |
|---|---|---|---|
| Spherical | |||
| Coma | |||
| Astigmatism | |||
| Field Curve | |||
| Distortion |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Wang, X.; Jiang, H.; Wang, Y.; Yang, C.; Meng, Y. Design of a Spaceborne, Compact, Off-Axis, Multi-Mirror Optical System Based on Freeform Surfaces. Photonics 2024, 11, 51. https://doi.org/10.3390/photonics11010051
Wang B, Wang X, Jiang H, Wang Y, Yang C, Meng Y. Design of a Spaceborne, Compact, Off-Axis, Multi-Mirror Optical System Based on Freeform Surfaces. Photonics. 2024; 11(1):51. https://doi.org/10.3390/photonics11010051
Chicago/Turabian StyleWang, Baohua, Xiaoyong Wang, Huilin Jiang, Yuanyuan Wang, Chao Yang, and Yao Meng. 2024. "Design of a Spaceborne, Compact, Off-Axis, Multi-Mirror Optical System Based on Freeform Surfaces" Photonics 11, no. 1: 51. https://doi.org/10.3390/photonics11010051
APA StyleWang, B., Wang, X., Jiang, H., Wang, Y., Yang, C., & Meng, Y. (2024). Design of a Spaceborne, Compact, Off-Axis, Multi-Mirror Optical System Based on Freeform Surfaces. Photonics, 11(1), 51. https://doi.org/10.3390/photonics11010051




