Attitude Determination of Photovoltaic Device by Means of Differential Absorption Imaging
Abstract
:1. Introduction
2. Attitude Estimation of the GaAs Target
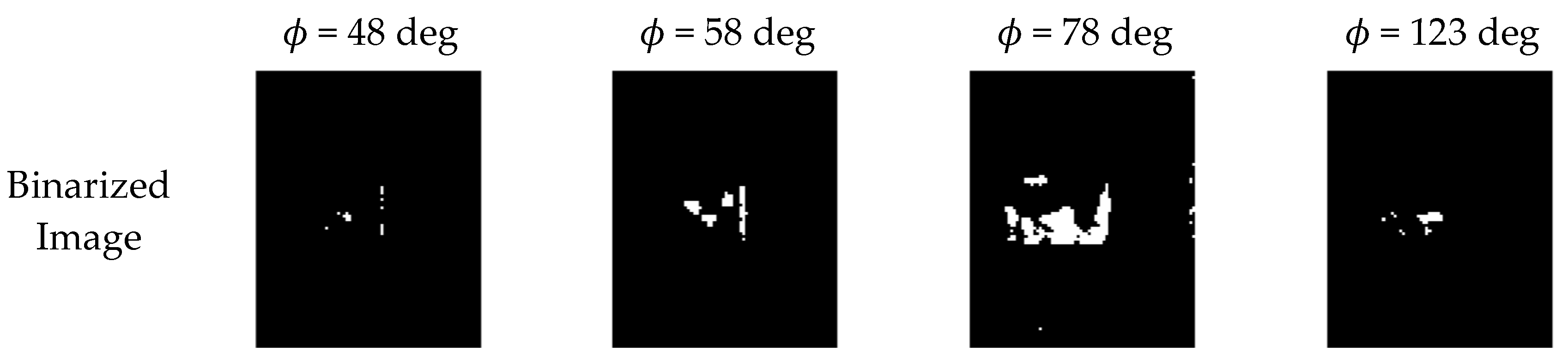
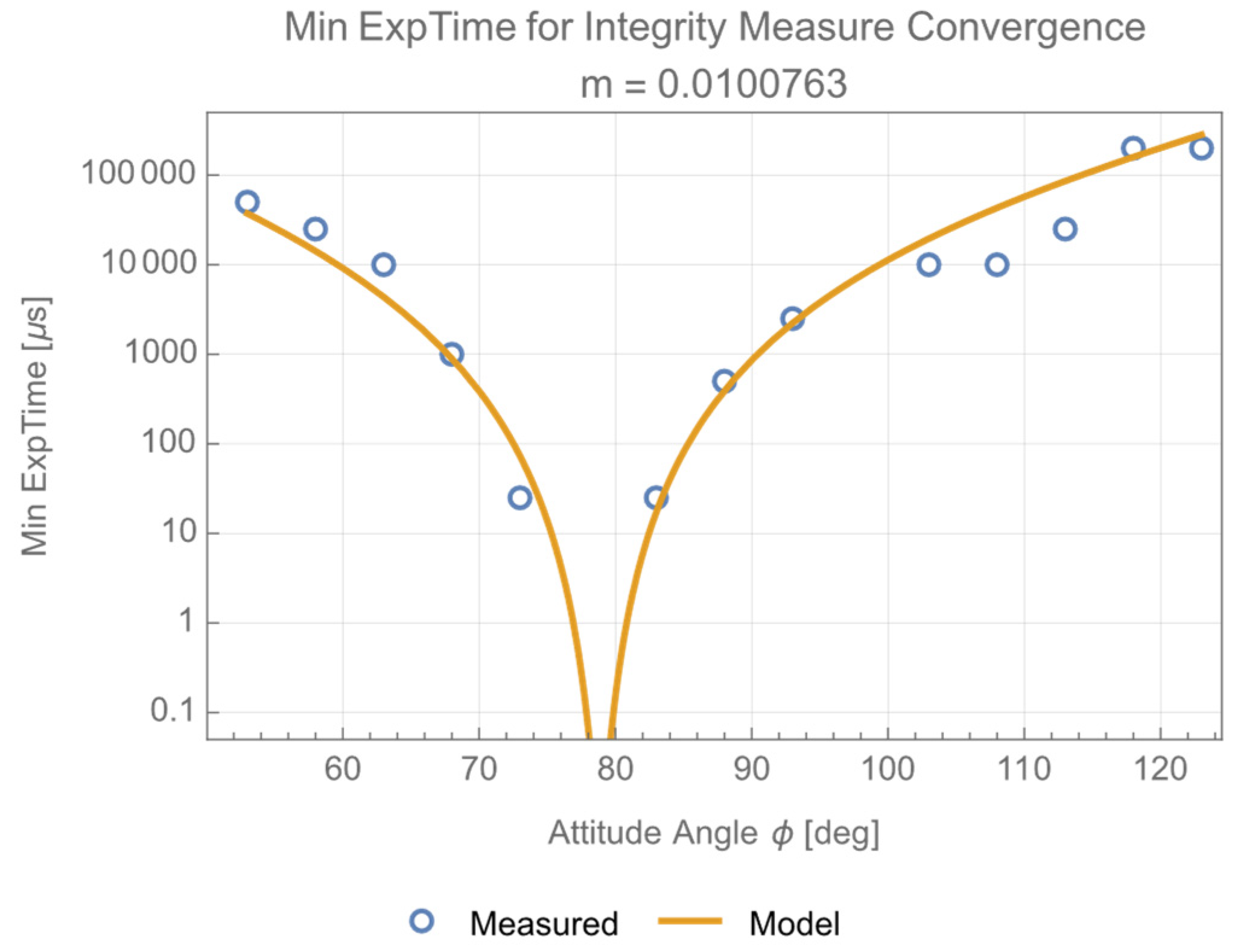
2.1. Review of Integrity Measure and Its Experiments
2.2. Preliminary Target Attitude Estimation Experiments
3. The Physical Model of the Integrity Measure’s Minimum Exposure Time and Attitude Estimation
3.1. Derivation of the Integrity Measure’s Minimum Exposure Time
- The attitude angle of the target (), the irradiation (incident) angle of the beam (), and the view angle from the camera () are extended to include non-zero values.
- The reflection characteristics of the target are extended to include a non-diffuse one.
- The profile of the irradiation beam is extended to Gaussian.
3.2. Reflectance Model of the PV
4. Discussion
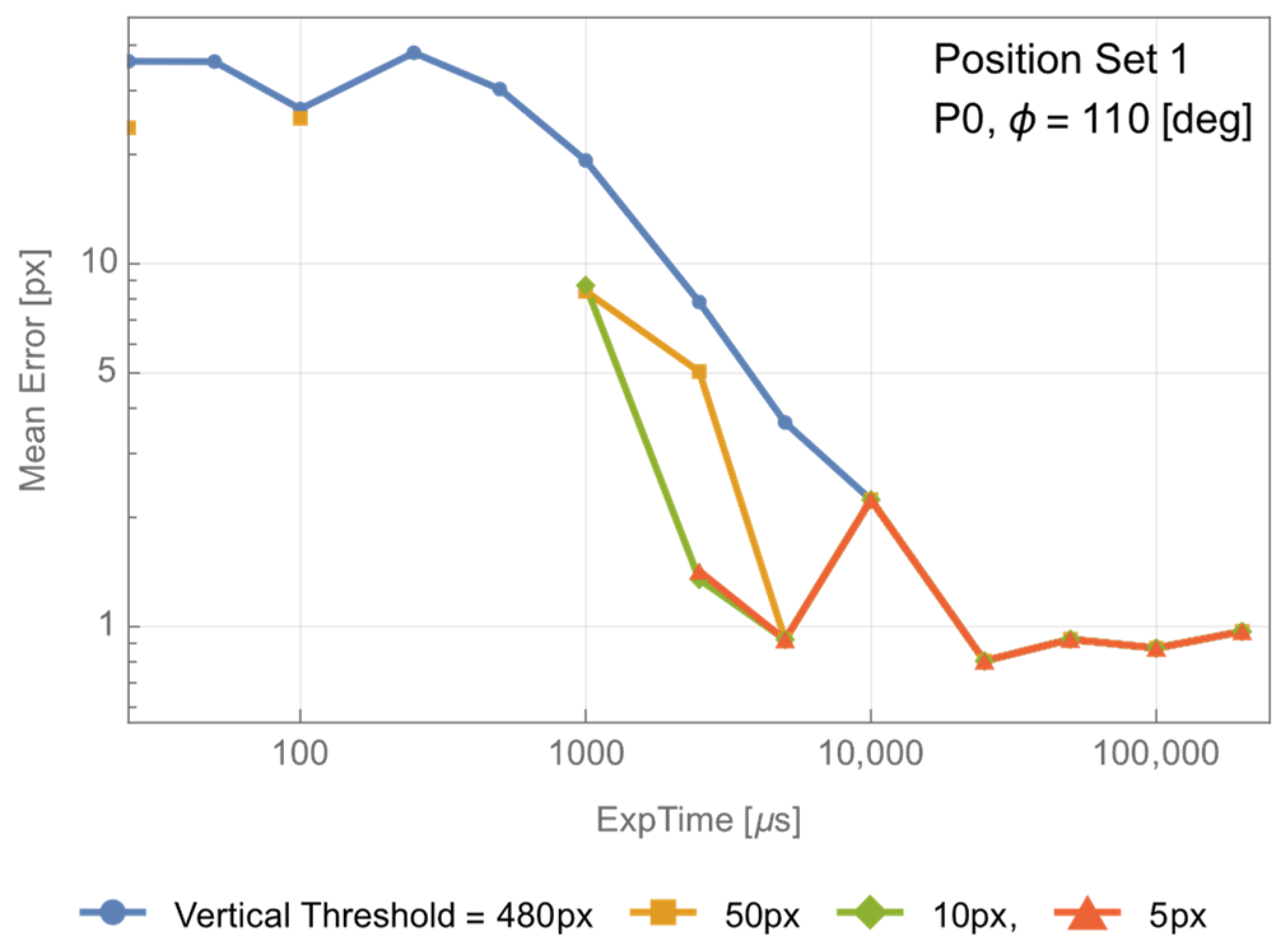
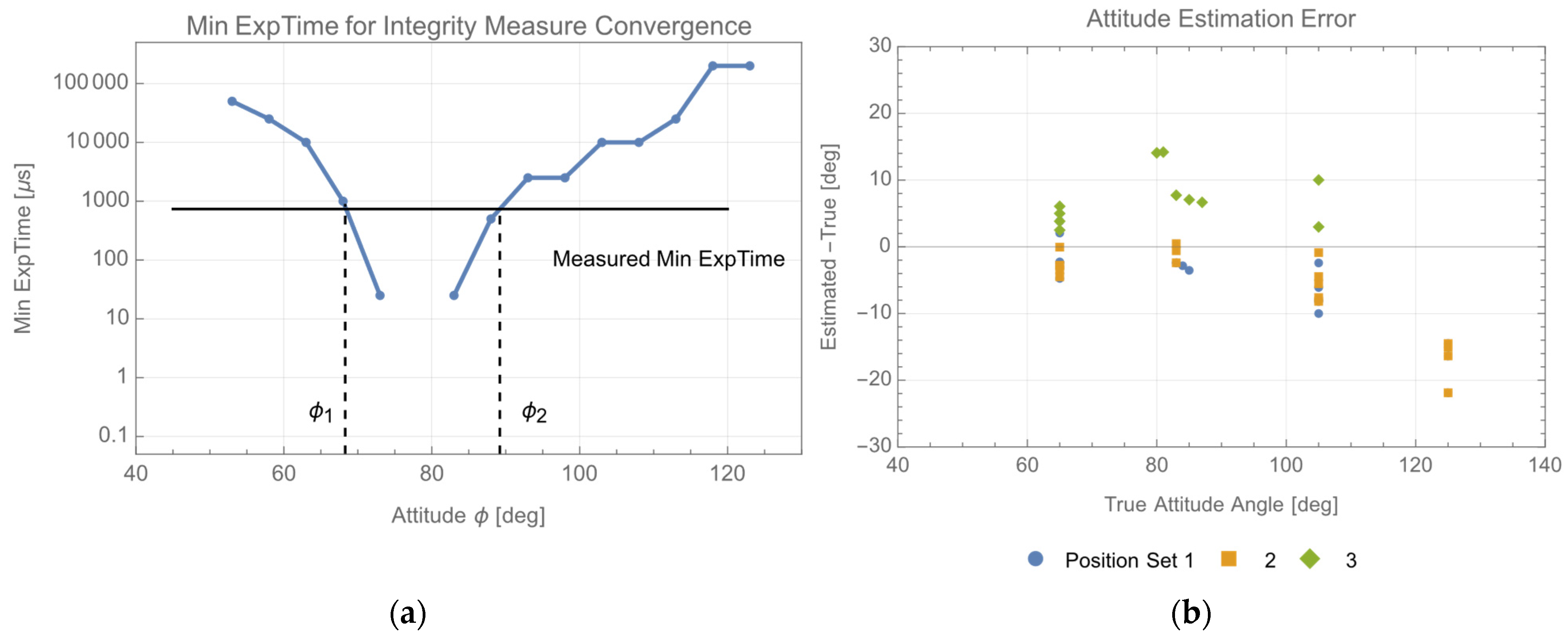
4.1. Error Model of the Minimum Exposure Time Method
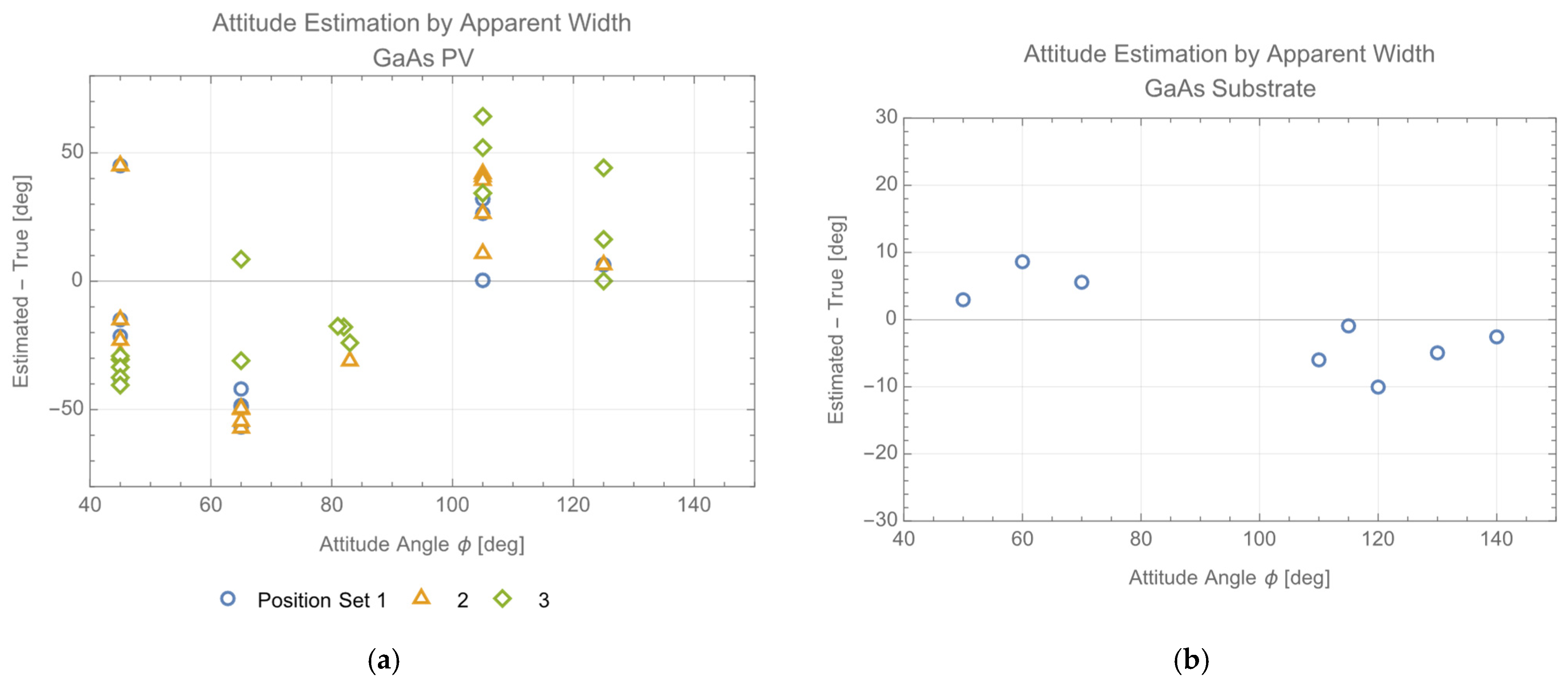
4.2. Attitude Estimation by the Apparent Size of the Target
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Frolova, E.; Dobroskok, N.; Morozov, A. Critical Review of Wireless Electromagnetic Power Transmission Methods; Atlantis Press International B.V.: Saint-Petersburg, Russia, 2022. [Google Scholar]
- Hajimiri, A. Wireless Power Transfer at Distance. In Proceedings of the 2023 IEEE Custom Integrated Circuits Conference (CICC), San Antonio, TX, USA, 23–26 April 2023; pp. 1–4. [Google Scholar]
- Armenta, J.M.R.; Bazmohammadi, N.; Saha, D.; Vasquez, J.C.; Guerrero, J.M. Optimal Multi-Site Selection for a PV-Based Lunar Settlement Based on A Novel Method to Estimate Sun Illumination Profiles. Adv. Space Res. 2023, 71, 2059–2074. [Google Scholar] [CrossRef]
- Mishra, R.K.; Mishra, A.K. Space Based Solar Power: Feasibility Microwave Based Wireless Power System. J. Mar. Sci. Res. 2023, 2. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.H. Dynamic Optical Wireless Power Transfer for Electric Vehicles. IEEE Access 2023, 11, 2787–2795. [Google Scholar] [CrossRef]
- Marko, I.P.; Duffy, D.A.; Misra, R.; Dattani, K.; Sweeney, S.J. Optical Wireless Power Transfer for Terrestrial and Space-Based Applications (Conference Presentation). In Proceedings of the Physics, Simulation, and Photonic Engineering of Photovoltaic Devices XII, SPIE OPTO, San Francisco, CA, USA, 30 January–1 February 2023; p. PC1241608. [Google Scholar]
- Liu, Q.; Xiong, M.; Liu, M.; Jiang, Q.; Fang, W.; Bai, Y. Charging A Smartphone Over the Air: The Resonant Beam Charging Method. IEEE Internet Things J. 2022, 9, 13876–13885. [Google Scholar] [CrossRef]
- Lahmeri, M.-A.; Kishk, M.A.; Alouini, M.-S. Charging Techniques for UAV-Assisted Data Collection: Is Laser Power Beaming the Answer? IEEE Commun. Mag. 2022, 60, 50–56. [Google Scholar] [CrossRef]
- Asaba, K.; Miyamoto, T. System Level Requirement Analysis of Beam Alignment and Shaping for Optical Wireless Power Transmission System by Semi–Empirical Simulation. Photonics 2022, 9, 452. [Google Scholar] [CrossRef]
- Setiawan Putra, A.W.; Kato, H.; Maruyama, T. Infrared LED Marker for Target Recognition in Indoor and Outdoor Applications of Optical Wireless Power Transmission System. Jpn. J. Appl. Phys. 2020, 59, SOOD06. [Google Scholar] [CrossRef]
- Imai, H.; Watanabe, N.; Chujo, K.; Hayashi, H.; Yamauchi, A. Beam-Tracking Technology Developed for Free-Space Optical Communication and Its Application to Optical Wireless Power Transfer. In Proceedings of the 4th Optical Wireless and Fiber Power Transmission Conference (OWPT2022), Yokohama, Japan, 18–21 April 2022; p. OWPT-5-01. [Google Scholar]
- Asaba, K.; Moriyama, K.; Miyamoto, T. Preliminary Characterization of Robust Detection Method of Solar Cell Array for Optical Wireless Power Transmission with Differential Absorption Image Sensing. Photonics 2022, 9, 861. [Google Scholar] [CrossRef]
- Asaba, K.; Miyamoto, T. Solar Cell Detection and Position, Attitude Determination by Differential Absorption Imaging in Optical Wireless Power Transmission. Photonics 2023, 10, 553. [Google Scholar] [CrossRef]
- Asaba, K.; Miyamoto, T. Positioning of a Photovoltaic Device on a Real Two-Dimensional Plane in Optical Wireless Power Transmission by Means of Infrared Differential Absorption Imaging. Photonics 2023, 10, 1111. [Google Scholar] [CrossRef]
- Asaba, K.; Miyamoto, T. Solar Cell Position, Attitude Determination by Differential Absorption Imaging in Optical Wireless Power Transmission. In Proceedings of the Physics, Simulation, and Photonic Engineering of Photovoltaic Devices XIII, SPIE OPTO, San Francisco, CA, USA, 29–30 January 2024; p. 12881-33. [Google Scholar]
- OS13CA5111A. Available online: https://www.optosupply.com/uppic/20211028118028.pdf (accessed on 29 December 2022).
- OSI5FU511C-40. Available online: https://akizukidenshi.com/download/OSI5FU5111C-40.pdf (accessed on 29 December 2022).
- Depth Camera D435. Available online: https://www.intelrealsense.com/depth-camera-d435/ (accessed on 15 May 2023).
- ATI—Advanced Technology Institute, Inc.—BioInformatics/Mathematical Information Engineering. Available online: http://www.advanced-tech-inst.co.jp/ (accessed on 14 February 2023).
- Cook, R.L.; Torrance, K.E. A Reflectance Model for Computer Graphics. ACM Trans. Graph. 1982, 1, 7–24. [Google Scholar] [CrossRef]
- Gregory, J. Ward Measuring and Modeling Anisotropic Reflection. Comput. Graph. 1992, 26, 8. [Google Scholar]
- Schlick, C. An Inexpensive BRDF Model for Physically-Based Rendering. In Computer Graphics Forum; Blackwell Science Ltd.: Edinburgh, UK, 1994; Volume 13, pp. 233–246. [Google Scholar]
- Walter, B.; Marschner, S.R.; Li, H.; Torrance, K.E. Microfacet Models for Refraction through Rough Surfaces. In Proceedings of the 18th Eurographics Conference on Rendering Techniques, Eurographics Association, Aire-la-Ville, Switzerland, 25–27 June 2007; pp. 195–206. [Google Scholar]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Wave from Rough Surfaces; Pergamon Press: New York, NY, USA, 1963. [Google Scholar]
- Trowbridge, T.S.; Reitz, K.P. Average Irregularity Representation of a Rough Surface for Ray Reflection. J. Opt. Soc. Am. 1975, 65, 531. [Google Scholar] [CrossRef]
- N- and p-Type GaAs|AXT Inc. Available online: http://www.axt.com/site/index.php?q=node/37 (accessed on 14 February 2023).
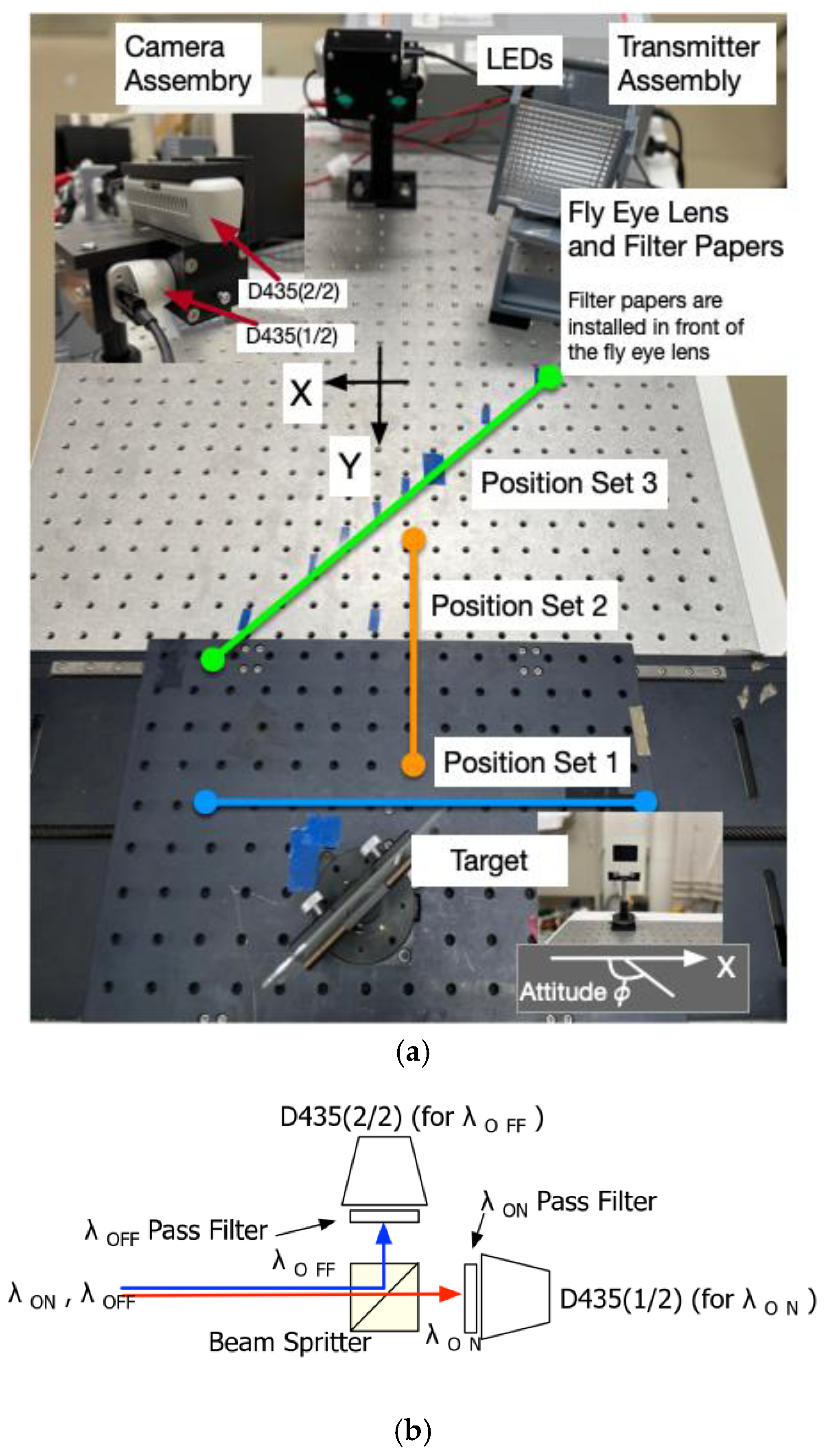





| Transmitter Assembly | |
| LED power | 4 mW (2 mW × 2) for both = 850 nm and 940 nm |
| Beam divergence | 85 deg (full angle) |
| Filter paper transmittance | 50%/paper(typical) |
| Target Assembly | |
| GaAs substrate | 2-inch diameter |
| GaAs PV | 6 cm × 4 cm |
| Distance from the camera assembly | 660 mm(typical) |
| Attitude angle | 43~123 deg (typical) |
| Camera Assembly | |
| Camera | Intel D435TM × 2 |
| Exposure time | 25, 50, 100, 250, 500, 1000, 2500, 5000, 10,000, 25,000, 50,000, 100,000 and 200,000 |
| Image size | 640 × 480 px |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asaba, K.; Miyamoto, T. Attitude Determination of Photovoltaic Device by Means of Differential Absorption Imaging. Photonics 2024, 11, 32. https://doi.org/10.3390/photonics11010032
Asaba K, Miyamoto T. Attitude Determination of Photovoltaic Device by Means of Differential Absorption Imaging. Photonics. 2024; 11(1):32. https://doi.org/10.3390/photonics11010032
Chicago/Turabian StyleAsaba, Kaoru, and Tomoyuki Miyamoto. 2024. "Attitude Determination of Photovoltaic Device by Means of Differential Absorption Imaging" Photonics 11, no. 1: 32. https://doi.org/10.3390/photonics11010032
APA StyleAsaba, K., & Miyamoto, T. (2024). Attitude Determination of Photovoltaic Device by Means of Differential Absorption Imaging. Photonics, 11(1), 32. https://doi.org/10.3390/photonics11010032





