Unified Performance Analysis of Direct Air-to-Underwater RF/UWOC Systems

Abstract

In general, wireless relays are used for connecting wireless communication links, but relays can bring security and deployment issues. This paper investigates the performance of air-to-water communication systems without relay nodes. The probability density function (PDF) of the RF link is obtained by unifying $\alpha -\mu$, the extended generalized -$\mathcal{K}$ (EGK) and Fisher Snedecor ($ℱ$) distributions of atmospheric turbulence. We obtained the joint PDF of the RF/UWOC system for atmospheric turbulence and ocean turbulence with nonzero mean single-sided pointing error as well as air–water interface under foggy conditions. Based on statistical results, exact expressions for outage probability (OP), bit error rate (BER), and channel capacity (CC) were derived. Finally, we validated the analytical expression using Monte Carlo simulation. The simulation results show that the fading parameters of the channel have a significant impact on the performance of a without-relay-assisted RF/UWOC system.

1. Introduction

Underwater wireless optical communication [1,2,3,4] has become a suitable and efficient transmission solution with high security, high data rate, low energy consumption, low cost, and short delay. In recent years, hybrid RF/UWOC systems have been widely used due to their ability to meet various requirements for high-speed underwater data transmission [5,6,7]. Collaborative RF/UWOC communication systems generally use amplification forwarding (AF) or decoding forwarding (DF) to establish connections between underwater vehicles and ground base stations within the ocean. Specifically, the source node sends signals to relay buoys with communication, sensing, and processing capabilities through FSO/RF links. Subsequently, the relay converts the electrical signal into an optical signal and sends the signal to the terminal through the UWOC link. Asymmetric Cloned Short-Term Memory (LSTM)–Depth Determined Policy Gradient (DDPG) algorithm is used to solve traversal and rate optimization problems in satellite–air–ground integrated network systems [8]. A dual-hop system module based on single hop and a space–air–ground integrated network (SAGIN) was proposed for uplink satellite communication with hybrid FSO/RF links [9]. The power-adaptive strategy based on truncated channel reversal for hybrid FSO/RF systems using an adaptive combination is adopted [10]. A wireless backhaul hybrid transmission [11] system used an opportunistic selection combination (OSC) and a maximum-ratio combination (MRC) with decoding and forward (DF) protocols. An adoption $\alpha -\mu$ communication of distributed and AF protocols is considered [12]. The fading RF link is mixed with a pointing error, while the FSO link adopts the performance of a dual-hop hybrid RF/FSO system with Nakagami-m fading [13]. This paper analyzes the channel capacity of the Space-to-Ground (SAG)–FSO transmission/Hybrid Single-Hop (SH)–FSO/Radio Frequency (RF) transmission (SAG–FSO/SH–FSO/RF) communication system [14]. It proves that direct detection intensity modulation has more advantages than heterodyne detection technology.

The pointing error caused by the beam drift significantly impacts the performance of communication systems, and there are many types of pointing errors in free space. Considering the influence of the pointing error in free space on strong atmospheric turbulence under nonzero line of sight [15], V.K. Chaubey et al. used the pointing error of the generalized nonzero positive distance model to analyze the precise performance of $ℱ$ distribution in atmospheric turbulence through assisting AF relay [16]. In addition, we also analyzed the effects of atmospheric turbulence and pointing errors on optical communication systems under foggy conditions. The system outage probability performance was analyzed under fog and pointing error conditions [17]. An RF/UWOC system with a fixed-gain amplification relay has been studied, and new closed-form expressions for CDF and PDF with end-to-end signal-to-noise ratios have been derived [18]. The UWOC chain uses spatial diversity, and the precise and upper bound error rate (BER) expressions for optimal and equal-gain combinations are obtained [19]. In atmospheric turbulence, different distribution functions represent different levels of turbulence intensity. Several distribution functions were unified, and the statistical results of atmospheric turbulence channels with pointing errors under random fog conditions were derived and expressed in the form of multidimensional Fox-H functions [20]. Recently, the mixture exponential generalized gamma (EGG) distribution model [21] was proposed to describe UWOC links. The author applied the moment generating function (MGF)-based method [22] to analyze the performance of Alamouti codes based on mixed exponential generalized gamma distribution. The performance of multi-input multi-output (MIMO) systems was analyzed using the EGG channel model combined with the PDF-based [23] method. The effective rate of multi-input single-output (MISO) systems under independent and incomplete (i.n.i.d) distributions in EGK fading channels has been studied [24]. Traditionally, relay buoys connect land and underwater vehicles, but relay deployment brings many cost and safety problems. Therefore, it is a promising solution to study the performance of a direct communication system without relay nodes from land to underwater. The author studied pulse response models of water–air channels under different turbulent water surface conditions [25]. Two scenarios are proposed for the uplink and downlink transmissions between the Autonomous Underwater Vehicle (AUV) and the Unmanned Aerial Vehicle (UAV), subject to water-to-air and air-to-water interface impacts direct transmission scenario (DTS) and retro-reflection scenario (RRS) [26]. The outage probability and statistical characteristics of direct air-to-water wireless optical communication without relay are studied by considering the effects of turbulence and fog [27]. The author studied the propagation of Gaussian coherent beams from underwater laser emitters to outdoor receivers in the presence of gravity-generated water waves in the deep-sea plane through direct wireless communication of beams from underwater to airborne platforms [28]. The author statistically models the fading coefficient of direct air-to-water optical wireless communication channels and the statistical photon counting behavior of Single-Photon Avalanche Diode (SPAD) and then evaluates the performance of the communication link by obtaining the analysis relationship of bit error rates [29].

The author derived the outage probability of the without-relay hybrid system with fog conditions in [27]. However, ref. [27] only considered one distribution function of the FSO system and did not consider pointing errors to improve system reliability. This paper considers various distribution functions of atmospheric turbulence and takes into account pointing errors in hybrid systems. In this paper, the major contributions of the proposed work are summarized as follows:

(1)

We analyzed the performance of atmospheric turbulence systems with nonzero boresight pointing errors as well as random path loss in foggy conditions with underwater turbulence.

(2)

We derived PDF and CDF by unifying EGK, $ℱ$, and $\alpha -\mu$ distributions for atmospheric turbulence with nonzero boresight pointing errors as well as random path loss in foggy conditions with the oceanic and the Birnbaum–Saunders (BS) distribution to model the aquatic waves at the air–water interface. It should be mentioned that papers usually use zero boresight pointing errors, and this paper considers nonzero mean single-sided pointing errors in the system. To the best of the author’s knowledge, a direct air-to-underwater hybrid system with nonzero mean single-sided pointing error under foggy conditions has been studied for the first time.

(3)

We used the statistical results to analyze system performance and derived the outage probability, bit error rate, and channel capacity of the system.

(4)

We validated the derived analytical results using Monte Carlo simulations, demonstrating the effectiveness of direct air-to-underwater systems under various atmospheric turbulence, pointing errors, ocean turbulence, and weather conditions.

2. System and Channel Models

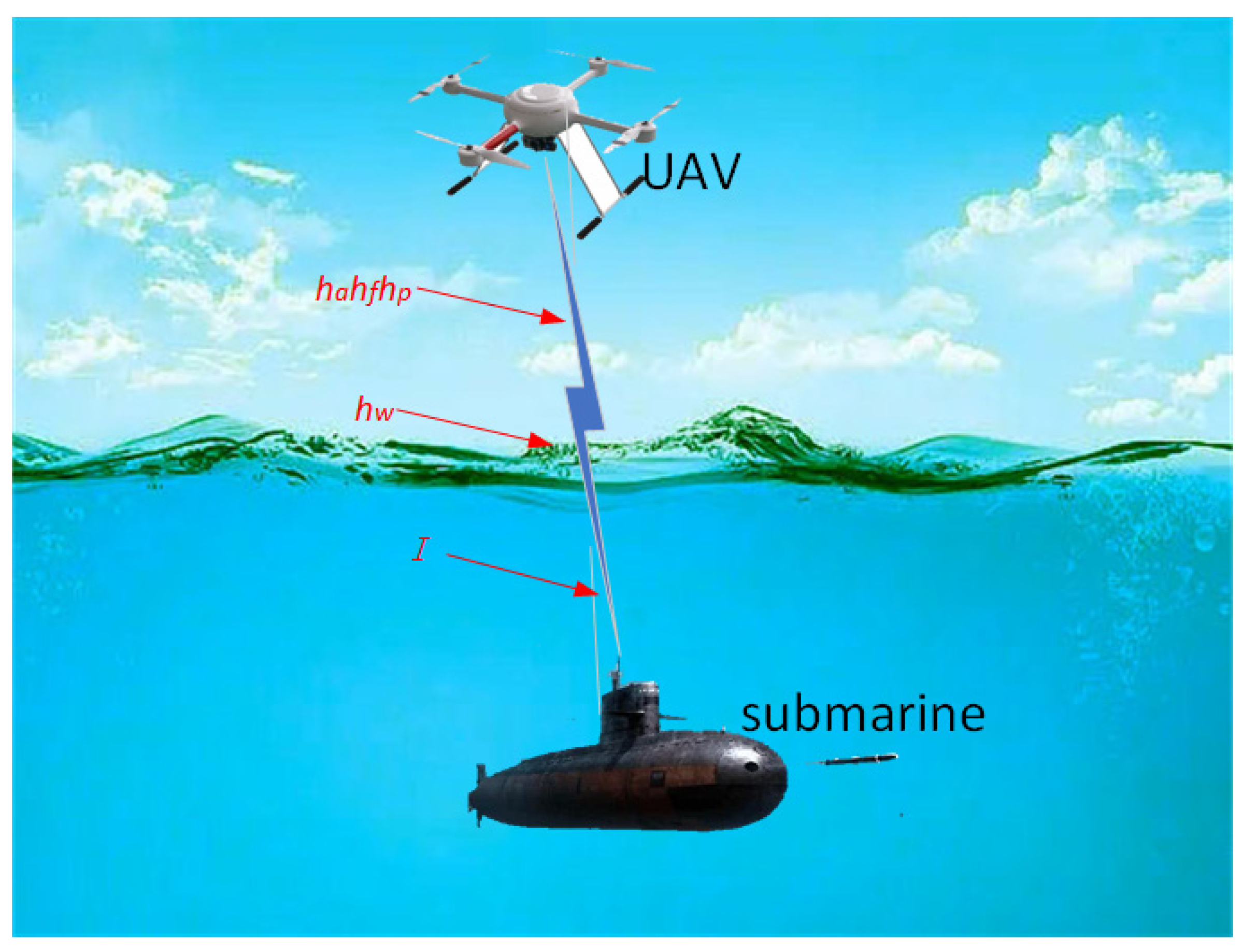
As shown in Figure 1, we considered an RF/UWOC system in which airborne unmanned aerial vehicles (UAVs) communicate directly with underwater submarines without a relay connection. Under foggy conditions, signals emitted by UAVs experiencing atmospheric turbulence and pointing errors can lead to channel fading. When passing through the air–water interface, assuming only the influence of water waves is considered and there is no bubble effect on the transmission interface, the signal is directly transmitted to the underwater submarine for communication through the air–water interface. The signal received by the underwater detector is

$$s(t)=h_a{h}_f{h}_p{h}_{w}It+n$$

(1)

where t is the transmission signal, h₁ is the channel coefficient of atmospheric turbulence, and the randomness of the path gain of the h₂ model due to fog conditions. h_p represents the channel gain of the pointing error. h_w simulates the scattering and reflection of water waves at the air–water interface and their effects on the signal. I represents the path loss of ocean turbulence. n represents noise with detector ${\sigma }^2$.

We have considered providing a unified PDF for the signal-to-noise ratio r under atmospheric turbulence effects [30].

$$f_r(r)=k_0{H}_{p,q}^{m,n}\left[\lambda r|{}_{{\left(b_i,B_i\right)}_{i=1}^q}^{{\left(a_i,A_i\right)}_{i=1}^p}\right]$$

(2)

The parameters in Equation (2) define a specific atmospheric turbulence model, as shown in

Table 1. The parameters of a unified PDF.

	$(m,n,p,q)$	${(a_i,A_i)}_{i=1}^p$	${({\mathrm{b}}_i,B_i)}_{i=1}^q$	$k_0$	$\lambda$
$\alpha -\mu$	$(1,0,0,1)$	$-$	$(\mu -1/\alpha )$	${\mu }^{1/\alpha }/\Omega \Gamma (\mu )$	${\mu }^{1/\alpha }/\Gamma (\mu )$
$F$	$(1,0,0,1)$	$-$	$\begin{array}{l}(m_i,m_{si}),\\ (2{\beta }_i,2{\beta }_{mi})\end{array}$	$\frac{1}{\Gamma (m_0)\Gamma (m_{s0})r}$	$\frac{b_i{b}_{si}r}{\overline{r}}$
$EGK$	$(1,1,1,1)$	$(-m_s,1)$	$(m,1)$	$\frac{m/m_s}{\Gamma (m)\Gamma (m_s)\overline{r}}$	$\frac{mr}{m_s\overline{r}}$

.

The relationship between the signal-to-noise ratio and the channel gain can be defined as

$$r=\overline{r}{h}^2$$

(3)

where $\overline{r}$ represents the average signal-to-noise ratio, and $h$ represents the product of $h_a{h}_f{h}_p{h}_{w}I$.

The PDF of the channel gain under atmospheric turbulence can be expressed as

$$f_{h_a}(h_a)=2\overline{r}{h}_a{H}_{p,q}^{m,n}\left[\lambda \overline{r}{h}_a^2|{}_{{\left(b_i,B_i\right)}_{i=1}^q}^{{\left(a_i,A_i\right)}_{i=1}^p}\right]$$

(4)

The PDF of the channel gain of h_f under foggy conditions [20] is shown below:

$$f_{h_f}(h_f)=\frac{v^k}{\Gamma \left(k\right)}{\left[\ln \left(\frac{1}{h_f}\right)\right]}^{k-1}{h}_f{}^{v-1}$$

(5)

where k is the shape parameter 0 < k < 1, v = 4.343/dβ^fog, β^fog are the scale parameter.

If k and v are parameters of the fog channel, let $h_3=h_a{h}_f$; afterward, Equations (4) and (5) are taken into Equation (6), and the joint PDF under the influence of atmospheric turbulence combined with fog conditions can be expressed as

$$f_{h_3}(h_3)={\displaystyle {\int }_{h_3}^{\infty }\frac{1}{h_a}{f}_{h_a}\left(h_a\right)f_{h_f}\left(\frac{h_3}{h_a}\right)d_{h_a}}$$

(6)

And expand the H-fox function to obtain the result.

$$f_{h_3}(h_3)=2\overline{r}{v}^k{h}_3{H}_{p+k,q+k}^{m+k,n}\left[\lambda \overline{r}{h}_3^2|{}_{{\left(b_i,B_i\right)}_{i=1}^q;{\left(v-2,2\right)}_{i=1}^k}^{{\left(a_i,A_i\right)}_{i=1}^p;{\left(v-1,2\right)}_{i=1}^k}\right]$$

(7)

The expression for PDF with a pointing error of nonzero mean single-sided is as follows [31].

$$\begin{array}{ll}f(h_p)=& \frac{{\epsilon }^2}{A_0^{{\epsilon }^2}}{h}_p^{{\epsilon }^2-1}\sqrt{\frac{2\mu }{w_{zq}\sqrt{2\ln \frac{A_0}{h_p}}}}\exp (-\frac{2u^2{\epsilon }^2}{w_{zq}^2})\\ & \times {\mathrm{I}}_{-\frac{1}{2}}(\frac{{2\mathrm{u}\mathsf{\epsilon }}^2}{{\mathrm{w}}_{\mathrm{zq}}}\sqrt{2\ln \frac{{\mathrm{A}}_0}{{\mathrm{h}}_p}})\end{array}$$

(8)

After a series of simplifications, the following results can be obtained.

$$\begin{array}{ll}f(H)=& B{\displaystyle \sum _{i=0}^1{\displaystyle \sum _{k=0}^{\infty }\frac{H{(-1)}^{ik}{u}^k\Gamma (\frac{k+1}{2})}{k!(k+1)}}}\\ & \times H_{p+k+1,q+k+1}^{m+k+1,n}[\frac{\lambda \overline{r}{H}^2}{A_0^2}|{}_{{\beta }_i,({\epsilon }^2-2,1)}^{{\chi }_i,({\epsilon }^2-1,1)}]\end{array}$$

(9)

where $B=2\sqrt{\frac{1}{\pi w_{eq}}}\frac{\overline{r}{k}_0{v}^k}{A_0^{2-{\epsilon }^2}\Gamma (k)}\frac{{\epsilon }^2}{A_0^{{\epsilon }^2}}\exp (-\frac{2u^2{\epsilon }^2}{w_{eq}^2})$.

Theory 1.

Under the influence of atmospheric turbulence, fog conditions, and a pointing error of nonzero mean single-sided, the PDF expression of the new channel gain under the combined channel fading effect was obtained. The PDF expression for the channel gain of the RF link can be represented by Equation (9).

Proof:

See Appendix A. □

To analyze the air-to-water interface, we rely on the BS distribution. The BS distribution has been applied in various works, including environmental, health indicators, and neural spikes. Applying mathematical concepts to different fields is a meaningful approach. The probability density function of the BS distribution can be expressed as follows [27]:

$$\begin{array}{l}{f}_{h_{\mathrm{w}}}(h_w)=\frac{1}{2\sqrt{2\pi }{\alpha }_0\beta }{{\displaystyle \sum _{i=0}^1(\frac{\beta }{h_w})}}^{\frac{1}{2}+i}\\ \exp (\frac{1}{{\alpha }_0^2})\exp (\frac{-h_w}{2{\alpha }_0^3\beta })\exp (\frac{-\beta }{2{\alpha }_0^2{h}_w})\end{array}$$

(10)

The parameters ${\alpha }_0=\frac{{\sigma }_0}{\sqrt{L_{th}{\mu }_0}}>0$ and $\beta =\frac{L_{th}}{{\mu }_0}>0$ are used to describe the BS distribution. L_th is the attenuation of signals caused by aquatic waves, with the mean and variance being u₀. The shape parameter ${\alpha }_0$ determines the skewness of the distribution, while the proportion parameter $\beta$ determines the variability of the distribution.

Let $I_0=h_{w}H$. After derivation and simplification, we can obtain the PDF of I₀ as

$$\begin{array}{cc}{f}_{I_0}(I_0)=& \frac{B}{2\sqrt{2\pi }{\alpha }_0^2\beta }{\displaystyle \sum _{i=0}^1{(\frac{\beta }{I_0})}^{i+1/2}}\exp (\frac{1}{{\alpha }_0^2})\hfill \\ & {\displaystyle {\int }_0^{\infty }{H}^{i+1/2}}\exp (-\frac{I_0}{2{\alpha }_0^2\beta H})\times \exp (-\frac{\beta H}{2{\alpha }_0^2{I}_0})\hfill \\ & H_{p+k+1,q+k+1}^{m+k+1,n}[\frac{\lambda \overline{r}{H}^2}{A_0^2}{|}_{{\beta }_i,({\epsilon }^2-2,1)}^{{\chi }_i,({\epsilon }^2-1,1)}]dH\hfill \end{array}$$

(11)

After the simplification calculation, the result Equation (12) can be obtained and is shown below.

$$\begin{array}{ll}{f}_{I_0}(I_0)=& \frac{B{I}_0}{2\sqrt{2\pi }{\alpha }_0^2{\beta }^2}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+1,q+k+1}^{0,1;0,1;m+k+1,n}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2{I}_0)}^2\overline{r}}{\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,({\epsilon }^2-2,1)}^{{\chi }_i,({\epsilon }^2-1,1)}]\end{array}$$

(12)

Recently, the newly proposed mixed EGG distribution caused by bubbles and temperature gradients is a highly effective model for ocean turbulence analysis [32]:

$$f_I(I)=\frac{1}{\lambda }\exp (-\frac{I}{\lambda })+\frac{(1-w)c}{\Gamma (a)b^{ac}}{I}^{ac-1}\exp (-{(\frac{I}{b})}^c)$$

(13)

where a and b are parameters. We assume parameter c is a positive number and let ${\mathrm{h}}_4=I_{0}I$.

Theory 2.

The PDF of the joint signal-to-noise ratio $r$ of system atmospheric turbulence, model random fog, air–water interface, and ocean turbulence models is represented by the sum of Equations (14) and (15).

$$\begin{array}{ll}{f}_1{}_{h_4}(h_4)=& \frac{wB{h}_4}{2\sqrt{2\pi }{\alpha }_0{\beta }^2{\lambda }^2}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+1,q+k+2}^{0,1;0,1;m+k+2,n}[\frac{1}{4{\alpha }_0^2},\frac{{(2{\alpha }_0^2{h}_4)}^2\overline{r}}{\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,({\epsilon }^2-2,1),(-1,2)}^{{\chi }_i,({\epsilon }^2-1,1)}]\end{array}$$

(14)

$$\begin{array}{l}{f}_{2h_4}(h_4)=\frac{(1-w)cB{h}_4}{2\sqrt{2\pi }{\alpha }_0{\beta }^2\Gamma (a)b^{ac}}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ \times H_{1,0;1,0;p+k+1,q+k+2}^{0,1;0,1;m+k+2,n}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2{h}_4)}^2\overline{r}}{\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,({\epsilon }^2-2,1),(a-\frac{2}{c},\frac{2}{c})}^{{\chi }_i,({\epsilon }^2-1,1)}]\end{array}$$

(15)

Proof:

See Appendix B. □

We assume that all average signal-to-noise ratios $\overline{r}$ are equal. The PDF of the signal-to-noise ratio can be obtained based on the relationship between the signal-to-noise ratio and the channel gain, $\overline{r}{h}_4^2=r_4$. The signal-to-noise ratio of the combined channel is represented by the sum of Equations (16) and (17).

$$\begin{array}{ll}{f}_1{}_{r_4}(r_4)=& \frac{wB}{2\sqrt{2\pi }{\alpha }_0{\beta }^2\overline{r}{\lambda }^2}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+1,q+k+2}^{0,1;0,1;m+k+2,n}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2)}^2{r}_4}{\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,({\epsilon }^2-2,1),(-1,2)}^{{\chi }_i,({\epsilon }^2-1,1)}]\end{array}$$

(16)

$$\begin{array}{ll}{f}_{2r_4}(r_4)=& \frac{(1-w)cB}{2\sqrt{2\pi }{\alpha }_0{\beta }^2\Gamma (a)\overline{r}{b}^{ac}}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+1,q+k+2}^{0,1;0,1;m+k+2,n}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2)}^2{r}_4}{\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,({\epsilon }^2-2,1),(a-\frac{2}{c},\frac{2}{c})}^{{\chi }_i,({\epsilon }^2-1,1)}]\end{array}$$

(17)

3. Performance Analysis

3.1. Outage Probability

The outage probability is an indicator that measures whether a communication system can successfully transmit data. It represents the probability of receiving the communication system and helps to evaluate the performance and reliability of the system by optimizing system design parameters to improve system efficiency and reduce outage probability [29].

$$p_{out}={\displaystyle {\int }_0^{rth}{f}_r(r)}dr=F_{1r_4}(r_{th})+F_{2r_4}(r_{th})$$

(18)

Subsequently, by substituting Equations (16) and (17) into Equation (18), their CDF expressions can be obtained. This CDF is represented as the sum of Equations (19) and (20).

$$\begin{array}{ll}{F}_{1r_4}(r_4)=& \frac{wB{r}_4}{2\sqrt{2\pi }{\alpha }_0{\beta }^2{\lambda }^2}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+1,q+k+3}^{0,1;0,1;m+k+3,n}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2)}^2{r}_4}{\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,({\epsilon }^2-2,1),(-1,2),(-2,2)}^{{\chi }_i,({\epsilon }^2-1,1)}]\end{array}$$

(19)

$$\begin{array}{ll}{F}_{2r_4}(r_4)=& \frac{(1-w)B{r}_4}{2\sqrt{2\pi }{\alpha }_0{\beta }^2\Gamma (a)b^{ac}}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0{}^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+1,q+k+2}^{0,1;0,1;m+k+2,n}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2)}^2{r}_4}{\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,({\epsilon }^2-2,1),(a-\frac{2}{c},\frac{2}{c}),(-2,,2)}^{{\chi }_i,({\epsilon }^2-1,1)}]\end{array}$$

(20)

3.2. Bit Error Rate

Bit error rate refers to the frequency of errors that occur during digital data transmission. It is typically expressed as a percentage or a ratio of the number of erroneous bits to the total number of transmitted bits. The higher the BER, the higher the transmission error rate and the greater the probability of data damage or loss. Therefore, it is important to minimize the BER in order to ensure reliable communication between devices [20].

$$p_e=\frac{q^p}{2\Gamma (p)}{\displaystyle {\int }_0^{\infty }{r}^{p-1}}{e}^{-qr}F(r)dr=be{r}_1+be{r}_2$$

(21)

By introducing Equations (16) and (17) into Equation (21), the expression for BER can be obtained as the sum of Equations (22) and (23).

$$\begin{array}{ll}be{r}_1=& \frac{wB}{4\sqrt{2\pi }{\alpha }_0{\beta }^2\overline{r}{\lambda }^2{q}^p}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+2,q+k+1}^{0,1;0,1;m+k+1,n+1}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2)}^2}{q\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,({\epsilon }^2-2,1)}^{{\chi }_i,({\epsilon }^2-1,1),(1-p,1)}]\end{array}$$

(22)

$$\begin{array}{ll}be{r}_2=& \frac{(1-w)B}{2\sqrt{2\pi }{\alpha }_0{\beta }^2\Gamma (a)b^2\overline{r}{q}^p}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0{}^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+1,q+k+2}^{0,1;0,1;m+k+2,n}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2{h}_4)}^2\overline{r}}{\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,({\epsilon }^2-2,1)}^{{\chi }_i,({\epsilon }^2-1,1),(1-p,1)}]\end{array}$$

(23)

3.3. The Channel Capacity

Channel capacity refers to the maximum amount of information transmitted on the communication channel. Channel capacity is affected by various factors, such as the bandwidth and signal-to-noise ratio. We optimize channel capacity to achieve higher data rate and more reliable transmission. The mathematical expression of channel capacity is as follows [27]:

$$c={\displaystyle {\int }_0^{\infty }\log (u_{1}r+1)}f(r)dr=c_1+c_2$$

(24)

where the value of parameter u₁ determines whether HD technology or MI/DD technology is used. When u₁ = 1, HD technology is used, and when u₁ = 2, MI/DD technology is used. The multidimensional H-fox function of BER is represented at the bottom of Equations (25) and (26). The expression for channel capacity can be obtained as the sum of Equations (25) and (26).

$$\begin{array}{cc}{c}_1=& \frac{wB{u}_1}{2\sqrt{2\pi }{\alpha }_0{\beta }^2\overline{r}{\lambda }^2}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+2,q+k+2}^{0,1;0,1;m+k+2,n+1}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2)}^2{u}_1}{\lambda {\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,(-1,1),({\epsilon }^2-2,1)}^{{\chi }_i,(-1,1),({\epsilon }^2-1,1),(0,1)}]\end{array}$$

(25)

$$\begin{array}{cc}{\mathrm{c}}_2=& \frac{(1-w)B{u}_1}{2\sqrt{2\pi }{\alpha }_0{\beta }^2\Gamma (a)b^{ac}}{\displaystyle \sum _{i=0}^1{(\frac{1}{2{\alpha }_0^2})}^{-i-3/2}}\exp (\frac{1}{{\alpha }_0^2})\\ & \times H_{1,0;1,0;p+k+1,q+k+2}^{0,1;0,1;m+k+2,n}[\frac{1}{4{\alpha }_0^4},\frac{{(2{\alpha }_0^2)}^2\lambda u_1}{b^2{\beta }^2{A}_0^2}{|}_{{}_{\begin{array}{cc}& \end{array}}-}^{(-1/2-j;1,2)}{|}_{{}_{} -}^{(1,1)}{|}_{{\beta }_i,(-1,1),({\epsilon }^2-2,1)}^{{\chi }_i,()-1,1,({\epsilon }^2-1,1),(0,1)}]\end{array}$$

(26)

4. Simulation Analysis

In this section, we select the results based on the average number of channels, fog concentration, and other parameters selected to validate our analysis results. We validated the results using the Monte Carlo method. We calculated the analytical expressions given in the previous sections under different turbulent RF channel conditions, fog conditions, and pointing errors. In the following figure, the numerical results and simulation results are presented, respectively. 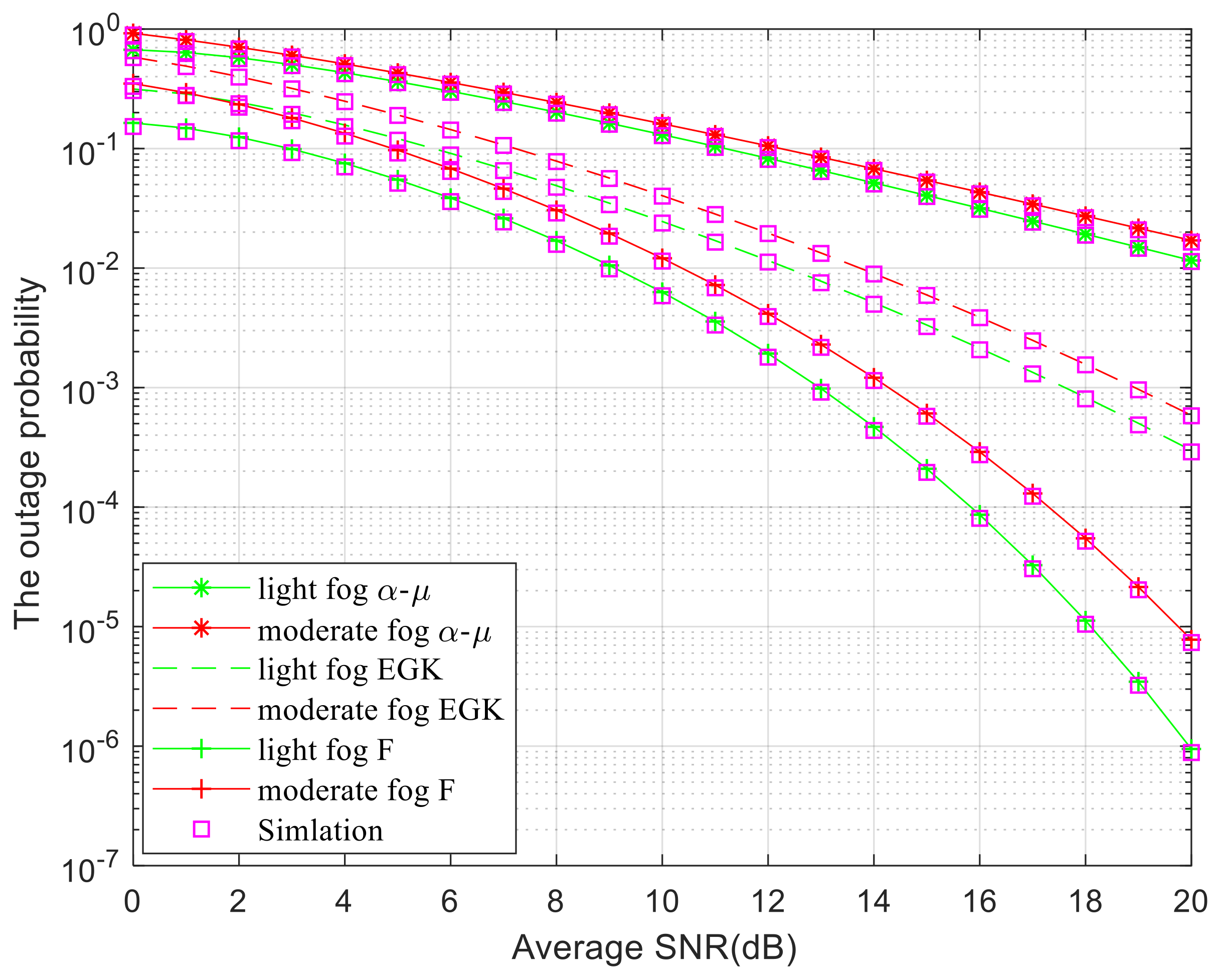Figure 2 and Figure 3 describe the effects of the number of selected channels, fog conditions, and different turbulent channels on OP, as well as the effects of parameters of the air–water interface and ocean turbulence intensity on OP.

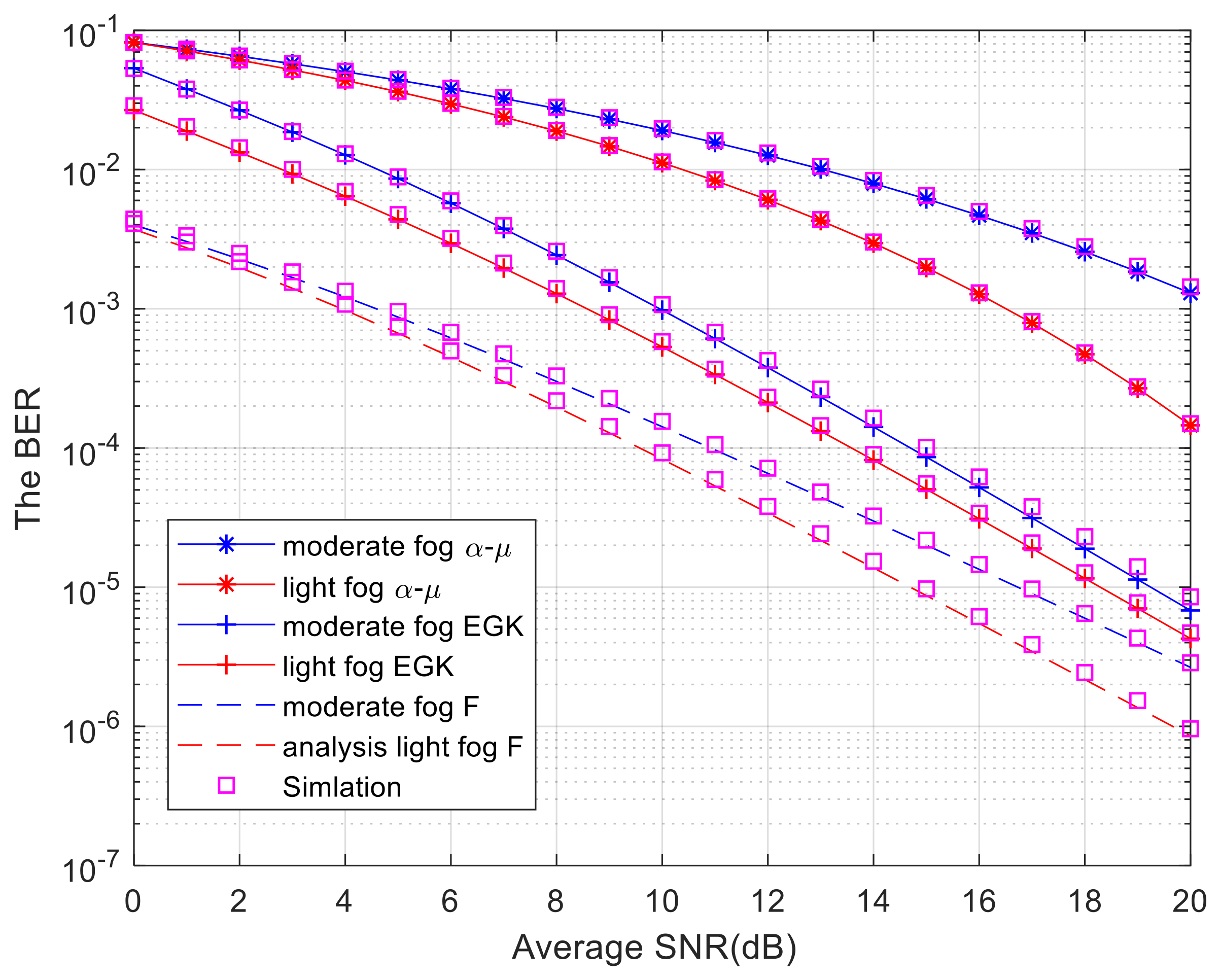
The higher the concentration of fog, the greater the absorption and scattering effect of the signal, which weakens the strength of the signal and reduces the performance of the system. We assume that all average signal-to-noise ratios are equal $\overline{r_1}=\overline{r_2}=\overline{r}$ and that the parameter c of EGG is a positive integer. Figure 2 compares the outage probability of the system under light and moderate fog conditions, $w=0.098$. Set the value for moderate fog to 6.37 and for mild fog to 4.70. When the signal-to-noise ratio is 20 dB and under light fog conditions, the outage probability of the $ℱ$ distribution is 10⁻⁶, the outage probability of the EGK distribution is 10⁻⁴, the outage probability of the $\alpha -\mu$ distribution is 10⁻², and $ℱ$ < EGK < $\alpha -\mu$. It can be seen from the figure that light fog has a better performance compared to moderate fog. From the graph, it can also be seen that the higher the turbulence intensity, the greater the OP. Compared to moderate fog, light fog has a lower concentration of substances in the air, which reduces the probability of signal absorption and scattering, resulting in higher reliability and stability of signal arrival at the receiving end. Therefore, the performance of the outage probability under light fog conditions is superior. From the results of numerical analysis and Monte Carlo analysis, it can be seen that the two curves have good agreement, indicating that the correctness of the numerical simulation results is verified through Monte Carlo simulation.

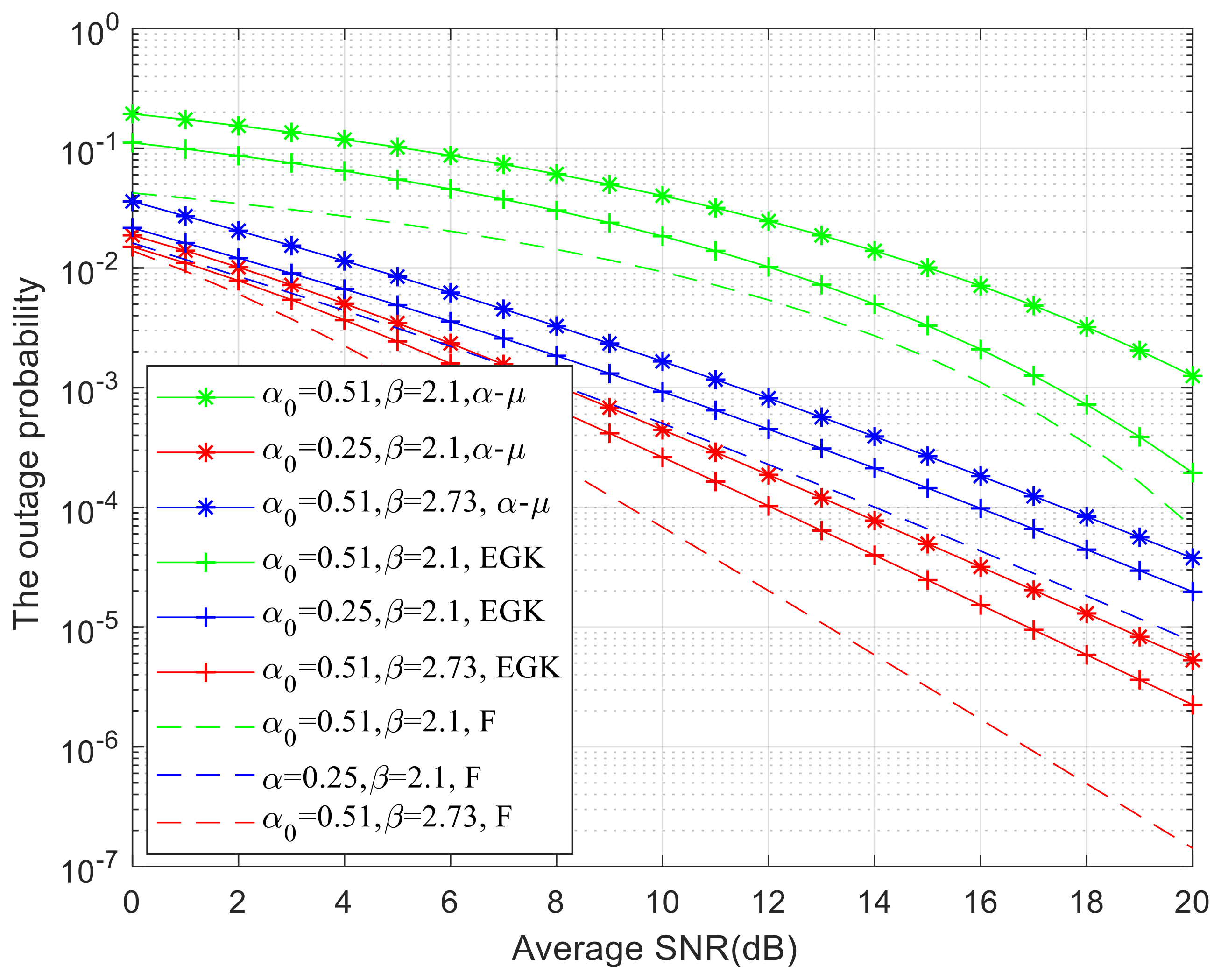
In order to study the influence of parameters in the distribution of base stations on the outage probability of system, Figure 3 analyzes the relationship between different parameter values and outage probability when using BS distribution. From the figure, it can be seen that when the parameters of the distribution α₀ = 0.51, β = 2.73, the probability of power outage can reach 10⁻⁷, which can be said to be very small. When α₀ = 0.25, β = 2.1, the outage probability can reach 10⁻⁵. When α₀ = 0.51, β = 2.1, the outage probability can reach 10⁻⁴. From the figure, it can be seen that as the parameter increases, the outage probability value increases. As the parameter value b increases, the outage probability decreases. This is because as the parameters change, the water surface fluctuates, leading to changes in signal stability.

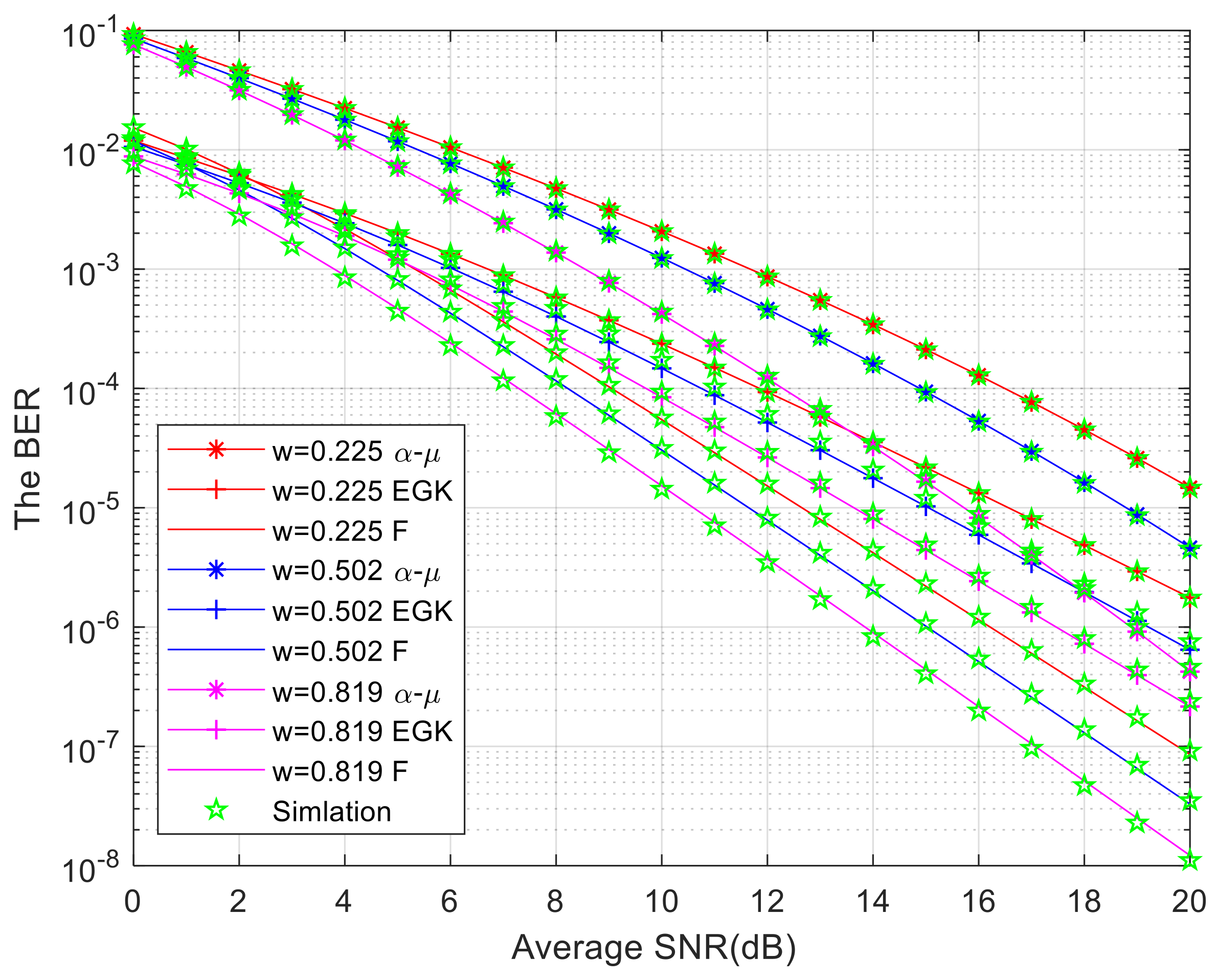
The parameter w of the EGG distribution determines which of the exponential and gamma distributions dominates the EGG distribution. Figure 4 shows the effect of the parameter w of the EGG distribution on the BER of the system, which decreases as the parameter w increases. In addition, it can be seen that different turbulence intensities can cause significant changes in BER, and turbulence channels also have a significant impact on the performance of the system. When the average signal-to-noise ratio of $\alpha -\mu$ distribution is 20 dB and w = 0.225, the probability of power outage can reach 10⁻⁴. When w = 0.502, the outage probability can reach 10⁻⁵, and when w = 0.819, the outage probability can reach 10⁻⁶. This is because the parameters of w change, resulting in a change in the role of exponential and gamma distributions in the EGG distribution.

To investigate the impact of fog conditions on the system BER, Figure 5 shows the effect of fog conditions on the BER of the system. From the figure, it can be seen that as the concentration of fog increases, the BER of the system increases. It is obvious that higher fog concentrations will increase the absorption and scattering of light, leading to weaker optical signals and thus affecting the BER. In addition, we can also conclude that $ℱ$ distribution is more suitable for the RF link. When the signal-to-noise ratio is 20 dB, the value of moderate fog is 6.37, and the value of light fog is 4.70. At this time, under moderate fog conditions, the BER value of the $ℱ$ distribution exceeds 10⁻⁵, while the error rate value of the $ℱ$ distribution under mild fog is close to 10⁻⁴. Light fog has a lower concentration of moderate fog compared to moderate fog, resulting in less absorption and scattering of signals, better signal reliability and stability, and better system performance. Comparing the Monte Carlo simulation with the numerical results, the simulated photon number is 10⁴. From the figure, it can be seen that the simulation results are in good agreement with the numerical results.

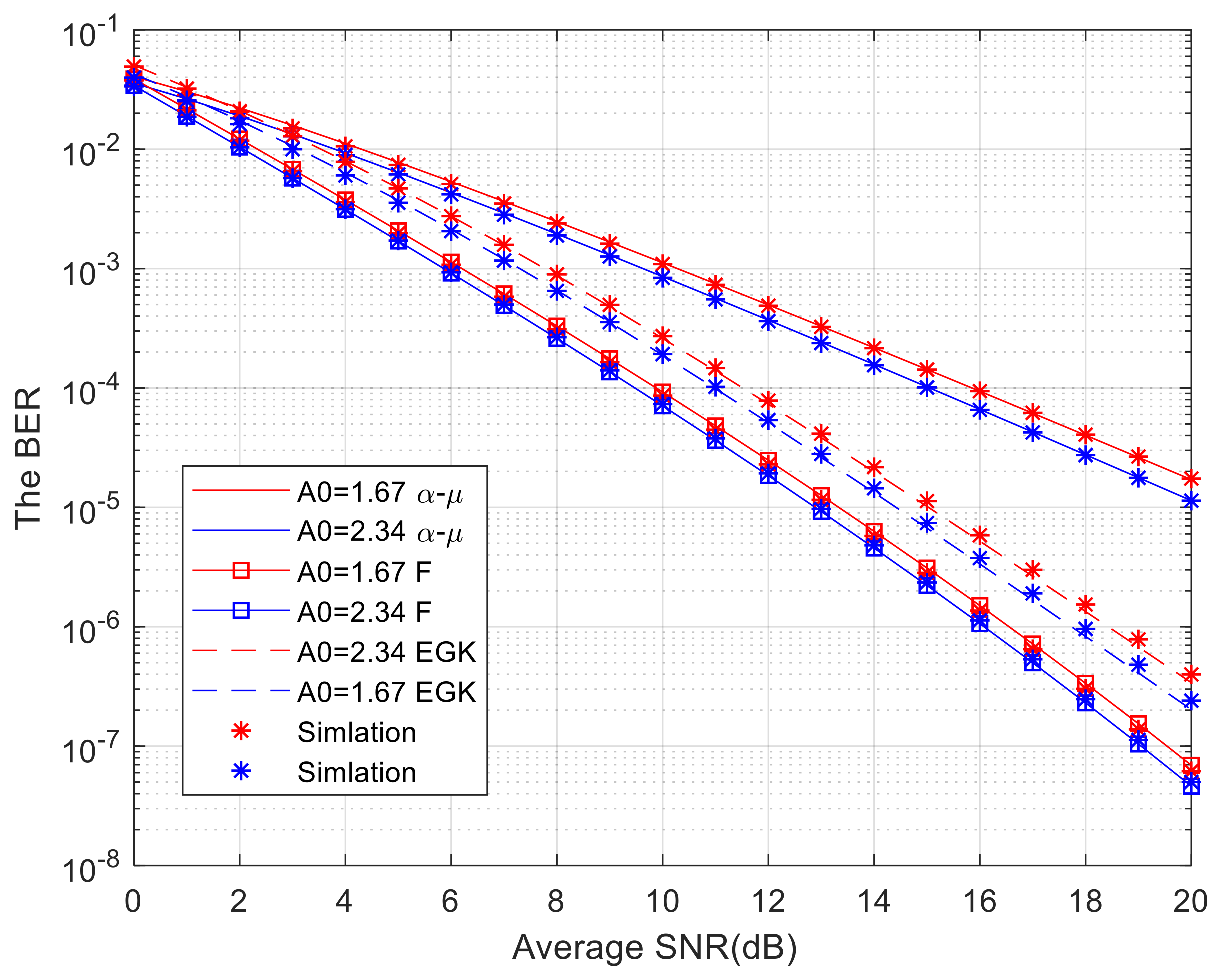
Figure 6 shows the effect of parameter A₀ of the pointing error on the system BER. Assuming that all average signal-to-noise ratios are equal and parameter c is a positive integer, it can be observed from the graph that as A₀ increases, the error rate shows a decreasing trend. At this point, for convenience, c = 1, w = 0.0035, A₀ = 1.67, and A₀ = 2.34. From the figure, it can be seen that when the distribution function of the atmospheric turbulence channel is $ℱ$ distribution, under the condition of A₀ = 1.67 and a signal-to-noise ratio of 10 dB, the BER of the system can reach about 10⁻⁴. Under the condition of A₀ = 2.34 and a signal-to-noise ratio of 10 dB, the BER of the system can reach about 9 × 10⁻⁵. It can be seen that as the parameter A₀ of the pointing error increases, the error rate decreases. The simulation results are in good agreement with the numerical simulation curve, indicating that the derived results are correct.

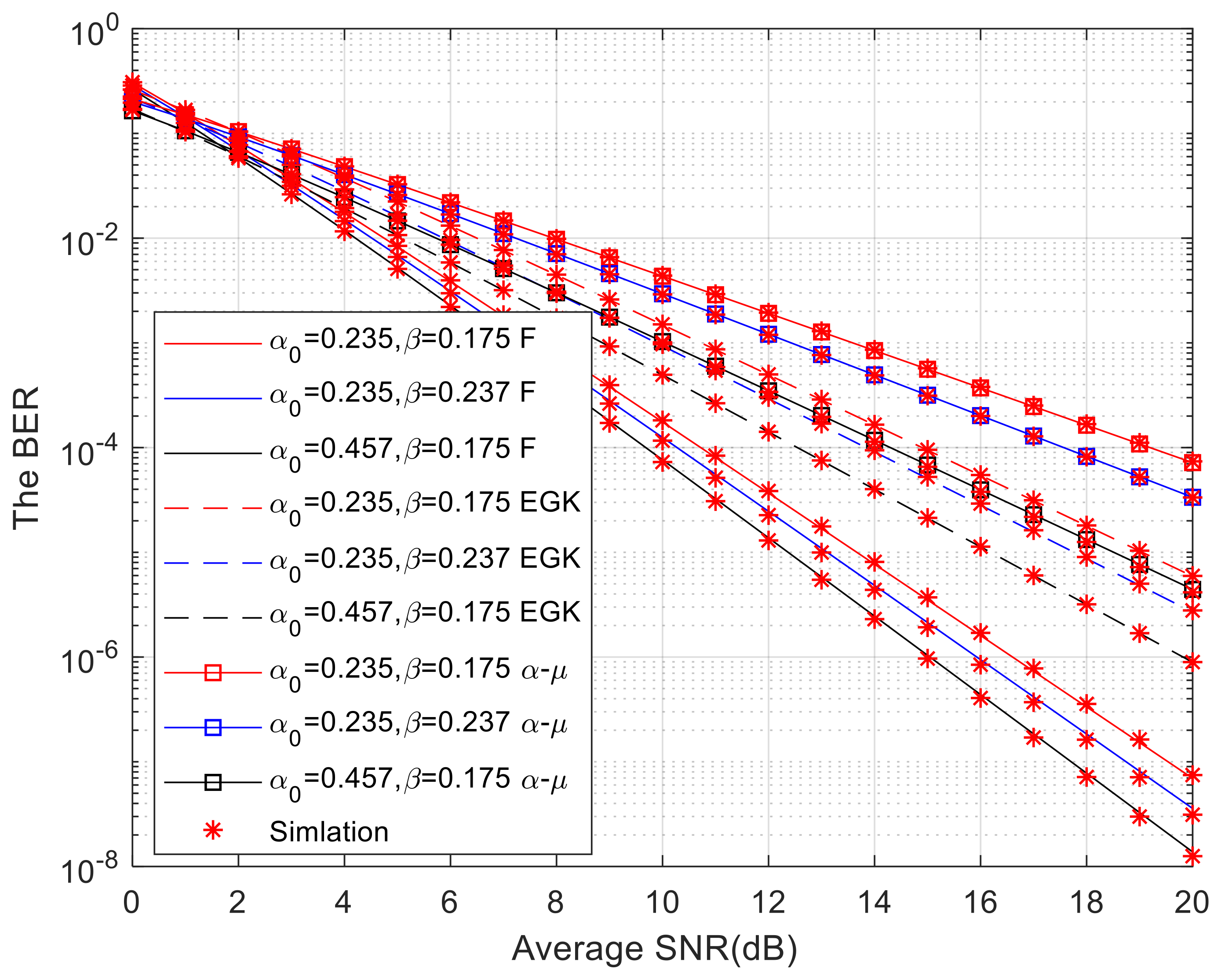
To investigate the impact of EGG parameters a and b on the system BER, Figure 7 shows the impact of EGG parameters ${\alpha }_0$ and $\beta$ on the BER. We assume that all average signal-to-noise ratios are equal and that parameter c is a positive integer. It can be observed from the graph that as a increases, the error rate decreases, while as b increases, the error rate increases. At this point, for convenience, we assume c = 1. From the figure, it can be seen that when the distribution function of the atmospheric turbulence channel is $ℱ$ distribution, ${\alpha }_0$ = 0.457 and $\beta$ = 0.175, and the signal-to-noise ratio is 20 dB, the BER of the system is close to 10⁻⁸. When the signal-to-noise ratio of EGK and $\alpha -\mu$ is 20 dB, the BER is 10⁻⁶ and 10⁻⁴, respectively. The BER obtained by using EGK distribution and $\alpha -\mu$ distribution in the RF link is higher than that of the $ℱ$ distribution. The lower the BER, the better the system performance. The simulation results are in good agreement with the numerical simulation curve, indicating that the derived results are correct.

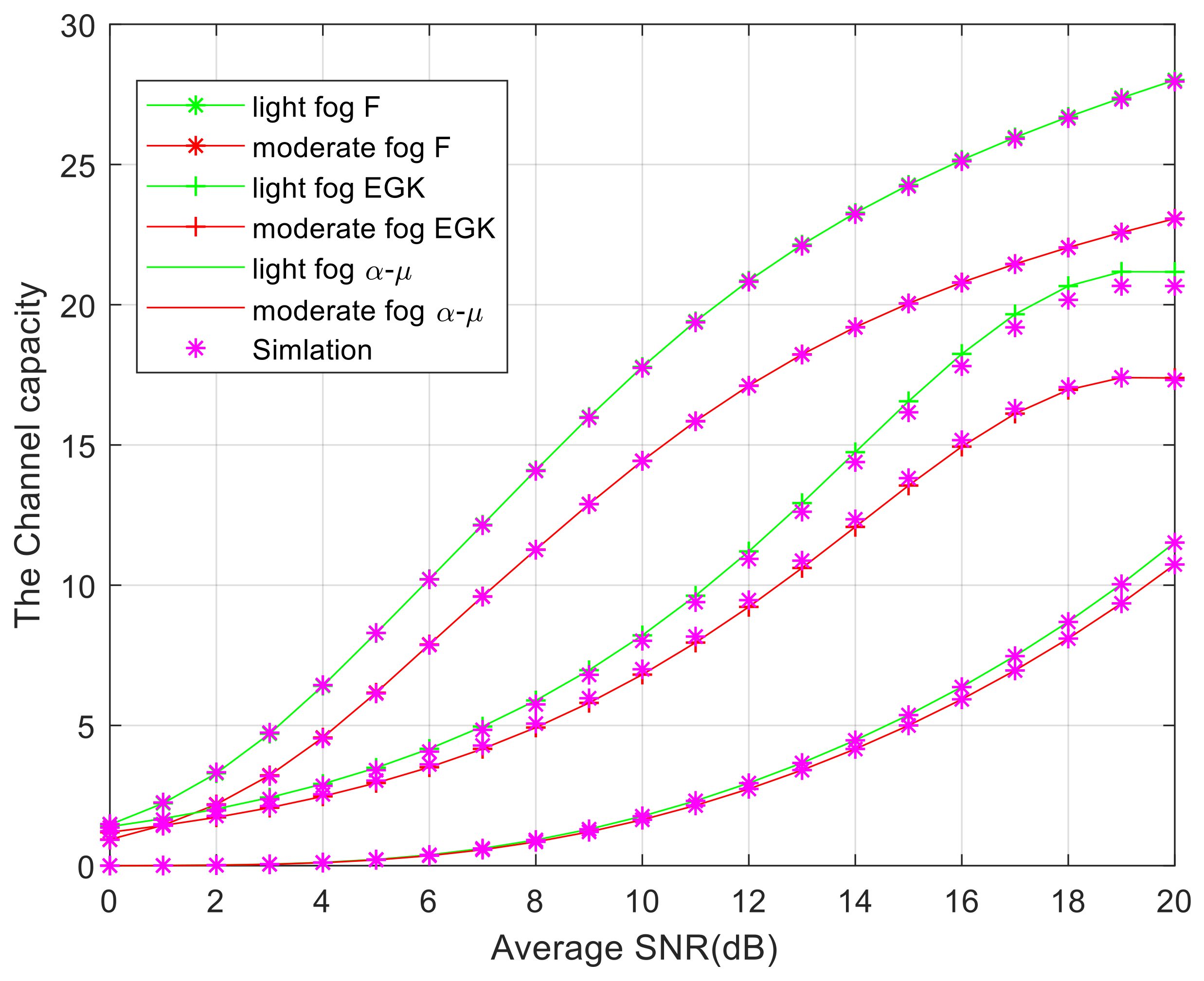
The channel capacity determines the transmission rate of a system. To investigate the impact of fog conditions on system channel capacity, Figure 8 shows the effect of fog concentration on the system channel capacity. We assume that all average signal-to-noise ratios are equal and that parameter c is a positive integer. It can be observed from the graph that as the concentration increases, the transmission rate of the channel weakens. At this point, the parameter u₁ of the channel capacity is set to 1 for convenience, with a moderate fog value of 6.37 and a light fog value of 4.70. From the figure, it can be seen that when the distribution function of atmospheric turbulence channels is distributed, and under light fog conditions, when the signal-to-noise ratio is 20 dB, the channel capacity of the system can reach about 27. When the RF link adopts EGK and $\alpha -\mu$ distribution, the channel capacity is 5 and 15 lower than when the RF link adopts $ℱ$ distribution, respectively. As the fog concentration increases, the signal is absorbed and scattered. This leads to a decrease in signal reliability and thus affects transmission rate. The simulation results show good agreement with the numerical simulation curve, indicating that the derivation results are correct.

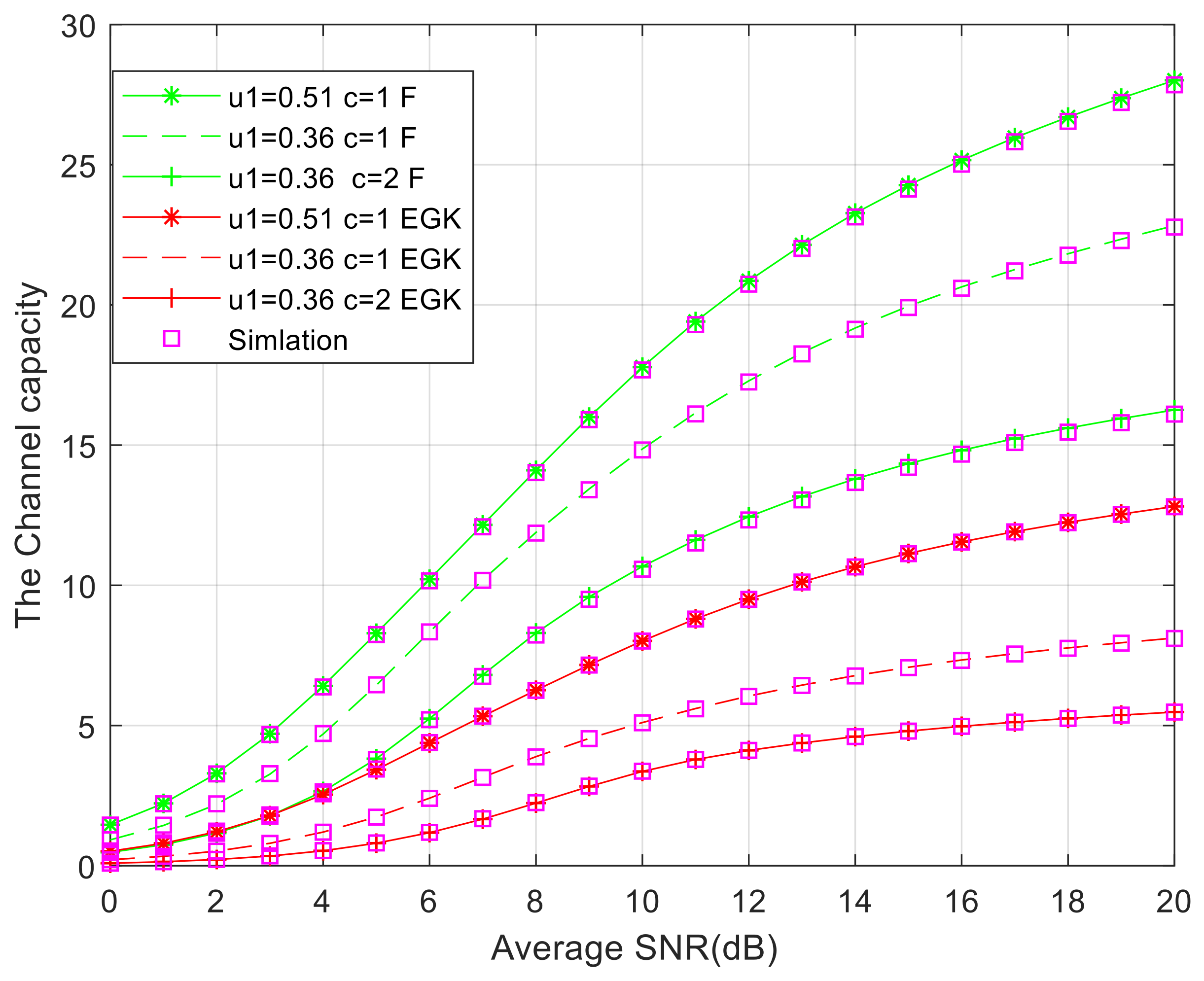
In the UWOC link, the parameters of the EGG distribution also have a significant impact on the system performance. Figure 9 shows the impact of parameters on the system channel capacity. We assume that all average signal-to-noise ratios are equal and that parameter c is a positive integer. It can be observed from the graph that as the parameter $u_1$ increases, the stability and transmission rate of the channel $c$ increase, while as the parameter increases, the transmission rate of the channel decreases. Similarly, taking the $ℱ$ distribution as an example, when u₁ = 0.51, c = 1, and the signal-to-noise ratio is 16 dB, the channel capacity of the system reaches 15. When the signal-to-noise ratio is 20 dB, the channel capacity can reach 26. The simulation results match well with the numerical simulation curve.

5. Conclusions

This paper studies the performance of air-to-water communication systems without relay nodes. We analyze the PDF of RF/UWOC systems by unifying $\alpha -\mu$, the extended generalized-$\mathcal{K}$ (EGK) and Fisher-Snedecor ($ℱ$) distributions for atmospheric turbulence with nonzero mean single-sided pointing error as well as random path loss in foggy conditions with air-to-water interface and ocean turbulence. Based on statistical analysis, the accurate expressions of performance are derived. The fading parameters of the channel have a significant impact on the performance of relay-assisted RF/UWOC systems.