The Topological Origin of Boundary Charges at Edges of One-Dimensional Crystals without Inversion Symmetry
Abstract
:1. Introduction
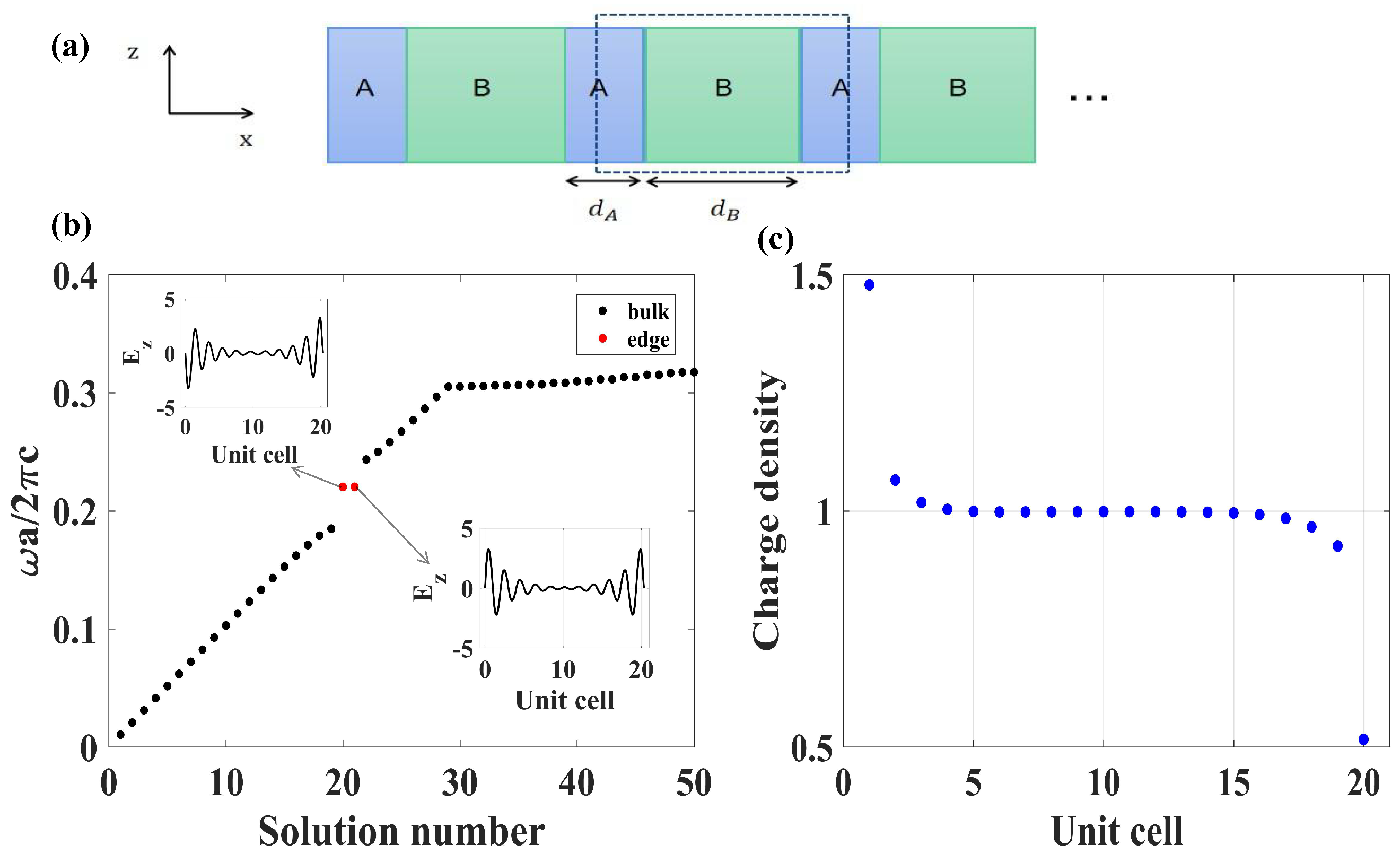
2. Models
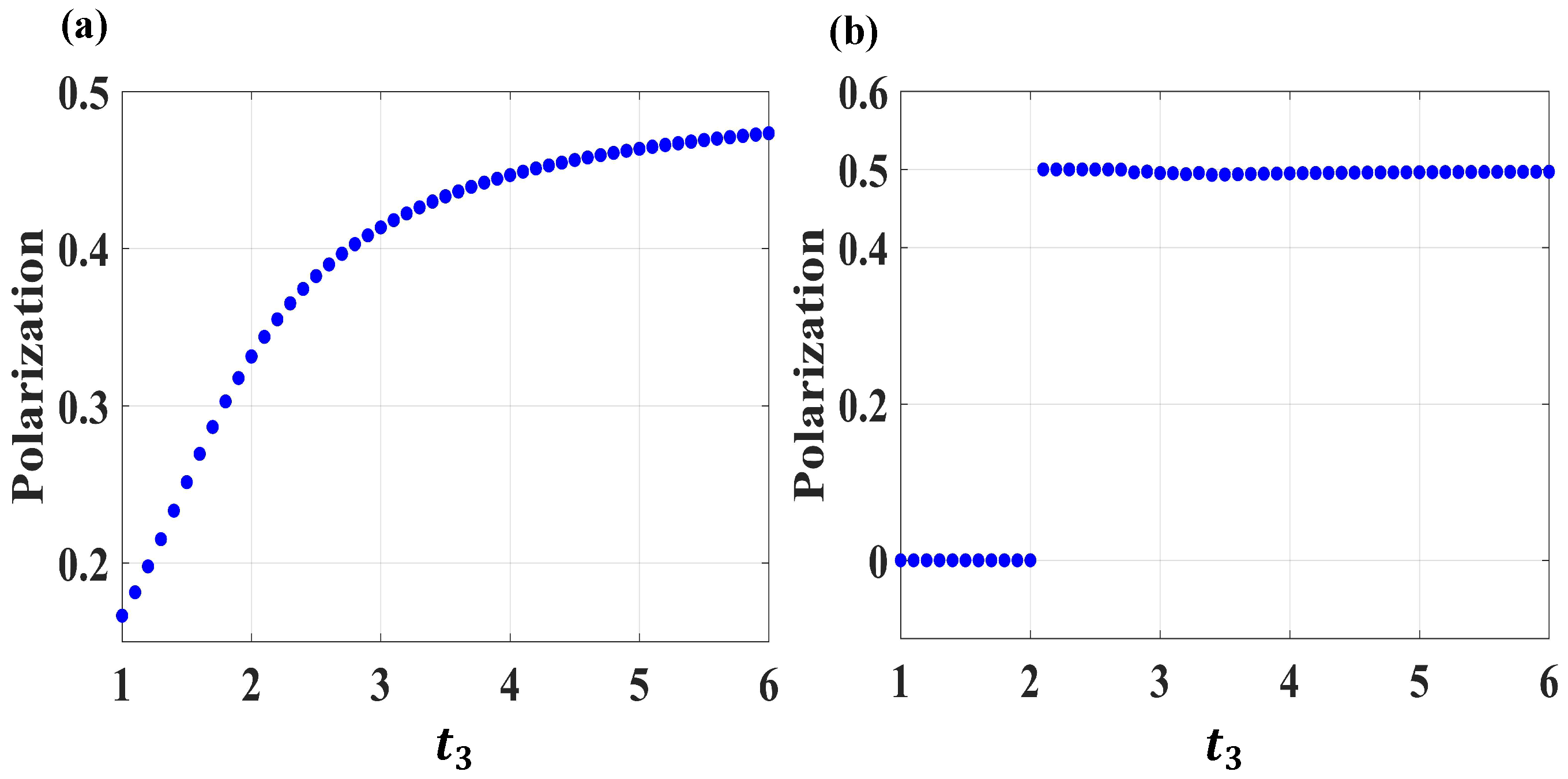
2.1. The Boundary Charges with Inversion Symmetry
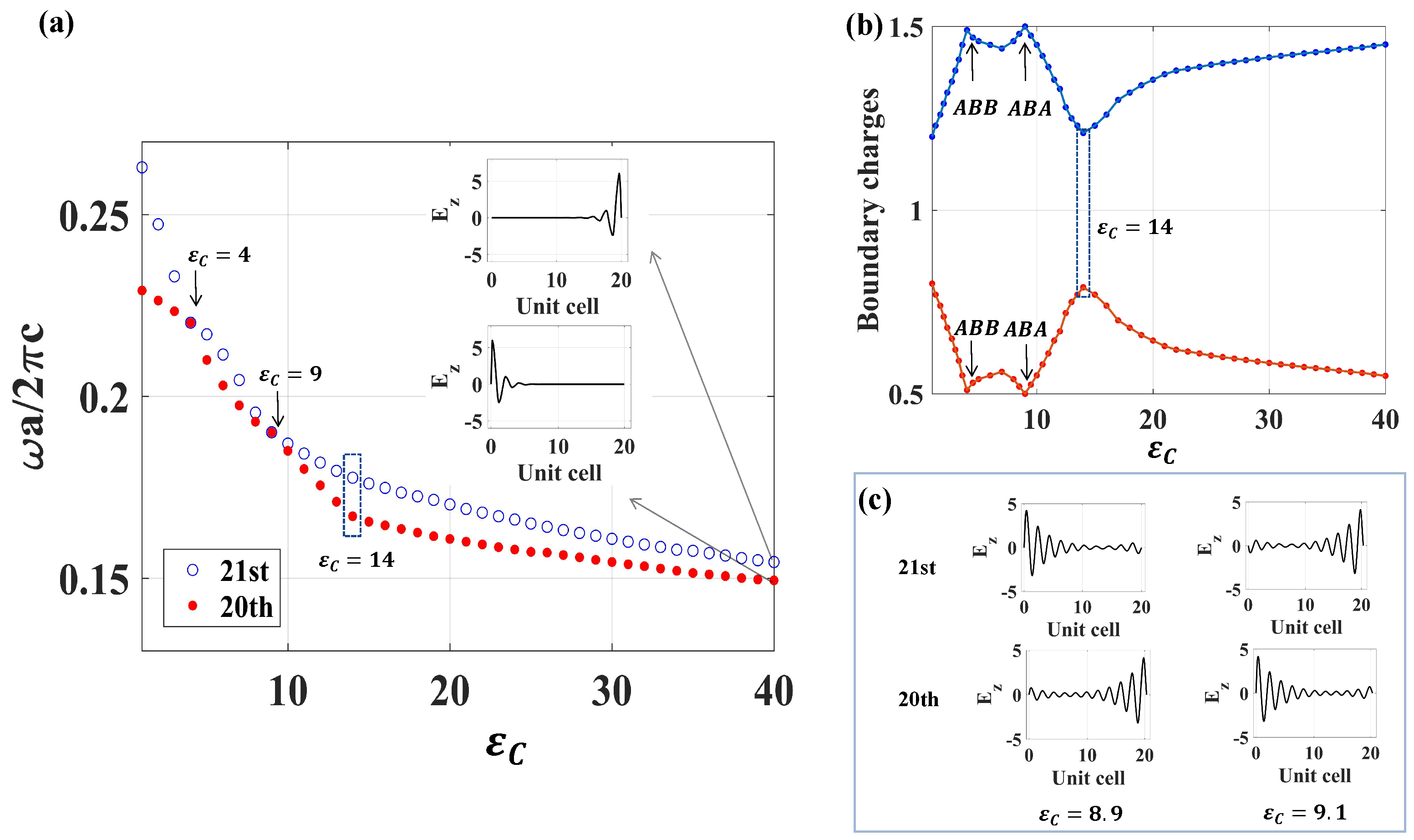
2.2. The Boundary Charges without Inversion Symmetry
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Tight-Binding Model without Inversion Symmetry

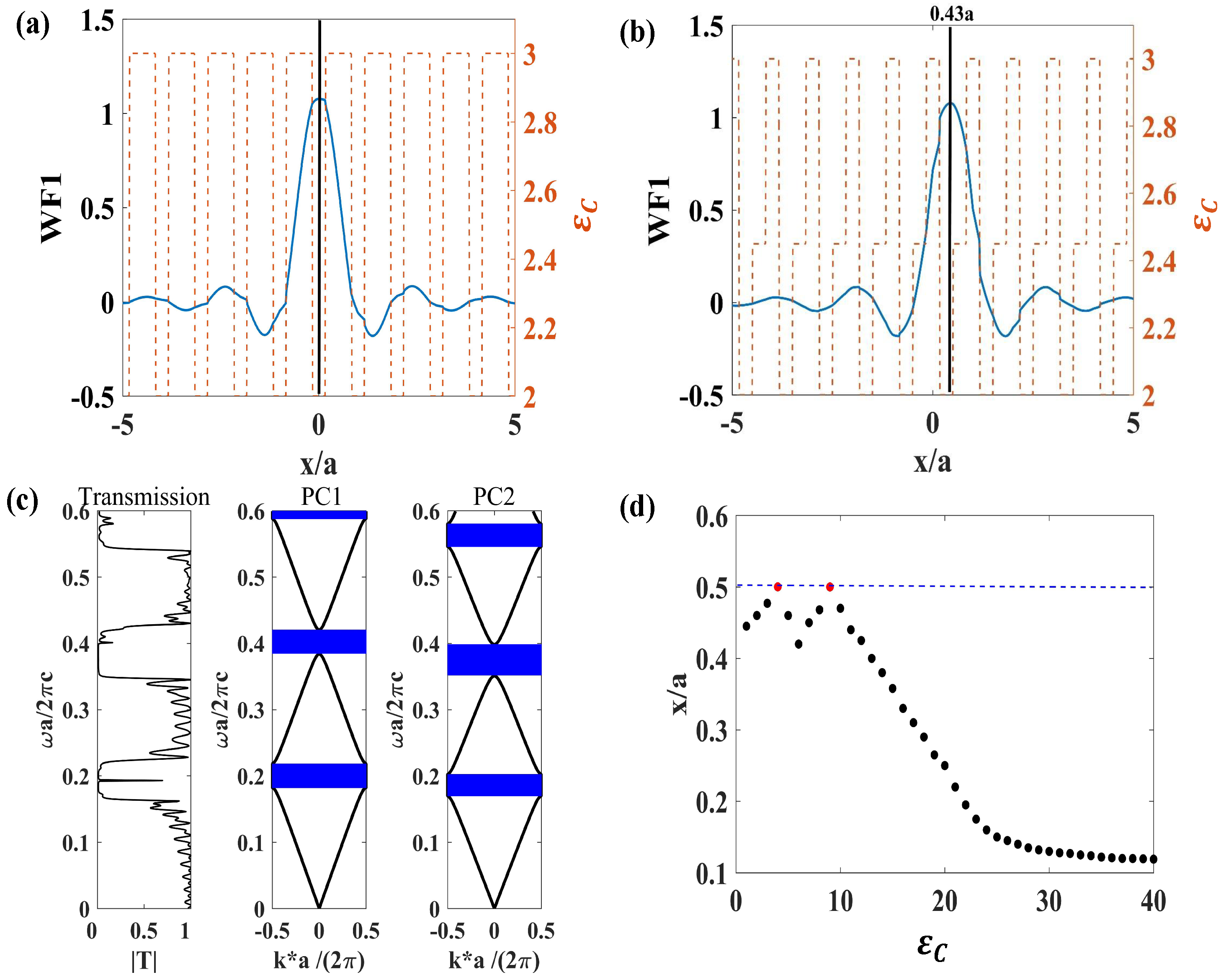
Appendix B. Calculation Method of MLWF
Appendix C. The Effect of the Number of Cells on Boundary Charges

References
- Lu, L.; Joannopoulos, J.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef]
- Bansil, A.; Lin, H.; Das, T. Colloquium: Topological band theory. Rev. Mod. Phys. 2016, 88, 021004. [Google Scholar] [CrossRef]
- Shen, S. Topological Insulators: Dirac Equation in Condensed Matter, 2nd ed.; Springer: Singapore, 2018; pp. 51–90. [Google Scholar]
- Wang, H.; Gupta, S.K.; Xie, B.; Lu, M. Topological photonic crystals: A review. Front. Optoelectron. 2020, 13, 50–72. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys 2019, 91, 015006. [Google Scholar] [CrossRef]
- Chiu, C.-K.; Teo, J.C.Y.; Schnyder, A.P.; Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 2016, 88, 035005. [Google Scholar] [CrossRef]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef] [PubMed]
- Xiao, M.; Zhang, Z.Q.; Chan, C.T. Surface impedance and bulk band geometric phases in one-dimensional systems. Phys. Rev. X 2014, 4, 021017. [Google Scholar] [CrossRef]
- Gao, W.S.; Xiao, M.; Chan, C.T. Determination of zak phase by reflflection phase in 1d photonic crystals. Opt. Lett. 2015, 40, 5259–5262. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 2017, 96, 245115. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Li, T.; Hughes, T.L. Quantization of fractional corner charge in Cn-symmetric higher-order topological crystalline insulators. Phys. Rev. B 2017, 99, 245151. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Quantized electric multipole insulators. Science 2017, 357, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xiong, L.; Zhang, M.; Jiang, X. Fractal topological band-gap structure induced by singularities in the one-dimensional Thue–Morse system. Photonics Res. 2021, 9, 622–629. [Google Scholar] [CrossRef]
- Wheeler, W.A.; Wagner, L.K.; Hughes, T.L. Many-body electric multipole operators in extended systems. Phys. Rev. B 2019, 100, 245135. [Google Scholar] [CrossRef]
- Delplace, P.; Ullmo, D.; Montambaux, G. Zak phase and the existence of edge states in graphene. Phys. Rev. B 2011, 84, 195452. [Google Scholar] [CrossRef]
- Xie, B.; Wang, H.X.; Zhang, X.; Zhan, P.; Jiang, J.H.; Lu, M.; Chen, Y. Higher-order band topology. Nat. Rev. Phys. 2021, 3, 520–532. [Google Scholar] [CrossRef]
- Liu, Y.; Leung, S.; Li, F.F.; Lin, Z.K.; Tao, X.; Poo, Y.; Jiang, J.H. Bulk–disclination correspondence in topological crystalline insulators. Nature 2021, 589, 381–385. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, Y.; Zhang, Y.; Zhen, Y.; Jiang, X. Topological properties of two-dimensional photonic square lattice without C4 and Mx(y) symmetries. ACS Photonics 2022, 9, 2448–2454. [Google Scholar] [CrossRef]
- Liu, Y.; Xiong, L.; Jiang, X. The evolution of topological singularities between real- and complex-frequency domains and the engineering of photonic bands for Hermitian and non-Hermitian photonic crystals. New J. Phys. 2022, 24, 123042. [Google Scholar] [CrossRef]
- Xiong, L.; Zhang, Y.; Jiang, X. Resonance and topological singularity near and beyond zero frequency for waves: Model, theory, and effects. Photonics Res. 2021, 9, 2024–2036. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y.; Jiang, X. Two classes of singularities and novel topology in a specially designed synthetic photonic crystals. Opt. Express 2019, 27, 4956–4975. [Google Scholar] [CrossRef]
- Li, Q.; Jiang, X. Singularity induced topological transition of different dimensions in one synthetic photonic system. Opt. Commun. 2019, 440, 32–40. [Google Scholar] [CrossRef]
- King-Smith, R.D.; Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 1993, 47, 1651. [Google Scholar] [CrossRef]
- Vanderbilt, D.; King-Smith, R.D. Electric polarization as a bulk quantity and its relation to surface charge. Phys. Rev. B 1993, 48, 4442. [Google Scholar] [CrossRef]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 1997, 56, 12847–12865. [Google Scholar] [CrossRef]
- Kivelson, S. Wannier functions in one-dimensional disordered systems:Application to fractionally charged solitons. Phys. Rev. B 1982, 26, 4269–4277. [Google Scholar] [CrossRef]
- Tanaue, H.B.; Bruno-Alfonso, A. Wannier-function expansion of localized modes in 1D photonic crystals without inversion symmetry. J. Opt. Soc. Am. B 2020, 37, 3698–3706. [Google Scholar] [CrossRef]
- Alvarez, V.M.M.; Coutinho-Filho, M.D. Edge states in trimer lattices. Phys. Rev. A 2019, 99, 013833. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S. Kaleidoscope of symmetry-protected topological phases in one-dimensional periodically modulated lattices. Phys. Rev. B 2015, 91, 041402. [Google Scholar] [CrossRef]
- Cooper, N.R.; Dalibard, J.; Spielman, I.B. Topological bands for ultracold atoms. Rev. Mod. Phys. 2019, 91, 015005. [Google Scholar] [CrossRef]
- Asbóth, J.K.; Oroszlány, L.; Pályi, A. A Short Course on Topological Insulators, 1st ed.; Springer: Cham, Switzerland, 2016; pp. 45–53. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, P.; Qi, X.; Liu, Y.; Wang, X.; Xiong, L.; Jiang, X. The Topological Origin of Boundary Charges at Edges of One-Dimensional Crystals without Inversion Symmetry. Photonics 2023, 10, 992. https://doi.org/10.3390/photonics10090992
Shi P, Qi X, Liu Y, Wang X, Xiong L, Jiang X. The Topological Origin of Boundary Charges at Edges of One-Dimensional Crystals without Inversion Symmetry. Photonics. 2023; 10(9):992. https://doi.org/10.3390/photonics10090992
Chicago/Turabian StyleShi, Pengdong, Xingchao Qi, Yufu Liu, Xianjun Wang, Langlang Xiong, and Xunya Jiang. 2023. "The Topological Origin of Boundary Charges at Edges of One-Dimensional Crystals without Inversion Symmetry" Photonics 10, no. 9: 992. https://doi.org/10.3390/photonics10090992
APA StyleShi, P., Qi, X., Liu, Y., Wang, X., Xiong, L., & Jiang, X. (2023). The Topological Origin of Boundary Charges at Edges of One-Dimensional Crystals without Inversion Symmetry. Photonics, 10(9), 992. https://doi.org/10.3390/photonics10090992




