Study of Field Enhancement in the Subnanometer Gap of Plasmonic Dimers Accounting for the Surface Quantum Effect

Abstract

We investigate the influence of the surface quantum effect on the optical characteristics of a plasmonic dimer consisting of two identical gold nanoparticles with a tiny gap. To account for the corresponding surface quantum effect, an electromagnetic theory based on mesoscopic boundary conditions and surface response functions is used. It is shown that the quantum surface effect leads to a blue shift and damping of the corresponding plasmon resonance. This effect becomes more substantial when the constituent particles are elongated, and the gap size shrinks to subnanometer values. In this case, the difference in the results obtained using the surface response functions and the local response approximation can be up to four times and is accompanied by a spectral blue shift of 10 nm.

1. Introduction

Nanoplasmonics is an emerging field of nanophotonics, where electrons oscillate coherently and collectively inside nanostructures as surface plasmons. The effects arising from the interaction of light with metal plasmonic nanostructures are of great interest since they can be used to obtain strong localized electromagnetic fields. The reason for such behavior of fields in nanostructures is the localized surface plasmon resonance (PR), which occurs in the metal components of nanostructures during collective oscillations of free electrons under the impact of light radiation. Plasmon resonance leads to a substantial increase in the field intensity by several orders of magnitude at a certain frequency of external excitation. In this case, not only does a huge amplification of the field near the structure occur, but also its concentration in tiny volumes increases, allowing manipulation of the field far beyond the Rayleigh limit. These properties of plasmonic materials are widely used in numerous practical applications [1,2,3].

In several important applications of spectroscopy, metal structures are used, consisting of elements with a small gap between them. The idea is based on the results related to plasmon-based Surface-Enhanced Raman Scattering (SERS) of light by single molecules [4]. The maximum level of sensitivity in such structures is achieved precisely due to localized surface PR arising due to the presence of a nanogap, inside which the electric field intensity can be enhanced by several orders of magnitude [5,6]. An example of the application of such a plasmonic structure can be paired particles (dimers) made of noble metals [7,8], which are arranged in such a way that the gap between them is minimal. It should be noted that advanced synthesis technologies enable the obtainment of a subnanometer gap of the order of 1 nm [9,10]. Structures with nanogaps are used, for example, to decipher the spectra of individual molecules and develop biosensors of various types [11,12,13,14].

With a decrease in the size of particles consisting of noble metals, quantum effects appear in them, such as bulk nonlocality and the escape of free electrons beyond the particle surface [15,16,17]. In paired particles, quantum effects also depend on the size of the gap between them. There are three main types of gaps depending on their size δ [18]:

• $\delta >$ 2 nm: the classical Maxwell’s theory gives almost the same results as the approach that takes into account quantum effects;
• 0.5 nm $<\delta \le$ 2 nm: quantum effects at such gaps become noticeable, and local and quantum descriptions predict approximately the same qualitative behavior of optical characteristics, but there are significant quantitative differences both in the PR amplitude and in its position in the frequency domain;
• $\delta \le$ 0.5 nm: the main role is played by such quantum effects as electron escape from the metal and electron tunneling between nanoparticles [19,20] and it is required to use an appropriate method to analyze the behavior of optical characteristics.

The description of the emerging effects using purely quantum methods, such as time-dependent density functional theory TDDFT [21], seems to be very cumbersome, especially when considering paired particles, due to the significant volume of the nanostructure and, as a result, the enormous consumption of computing resources and time [22]. That is why, in this case, quasi-classical approaches seem to be preferable, such as, for example, the hydrodynamic Drude model and its generalization, the generalized non-local optical response theory (GNOR) [23,24]. GNOR makes it possible to consider volume quantum effects, i.e., the appearance of longitudinal fields inside plasmonic nanoparticles and Landau damping. Good agreement was established between the results obtained using GNOR and other theories, as well as with experimental data [25]. At the same time, GNOR does not account for the effect of electron spill-out beyond the surface, which can be crucial in the analysis of fields in the subnanometer gap between nanoparticles [26,27,28].

To consider the surface quantum effect, use of the Surface Response Functions (SRF)—the Feibelman d-parameters—was recently suggested [29]. This approach allows one to describe the effect of electron spill-out when electrons leave the metal surface. The spill-out (or spill-in) scale is characterized by the Feibelman d-parameters, the values of which are usually several angstroms [30]. Such a small length scale makes the spill-out effect noticeable only in a nanometer-sized metal particle [31] or a subnanometer gap [32].

In recent years, the theory of d-parameters has rapidly developed and become more sophisticated in considering the surface quantum effects. A general theoretical framework for nanooptics was developed [33], which was indicated to be effective for describing nonclassical effects associated with the surface, including the effect of nonlocality and Landau damping. The so-called “mesoscopic” boundary conditions were proposed, which incorporate Feibelman’s parameters and represent a generalization of the classical transmission conditions for fields at the interfaces between media with different characteristics, accounting for the occurrence of induced surface charges and currents. In this case, the field inside the structures is described by the classical Maxwell equations. This approach is considered as the missing link connecting the purely quantum description of the observed effects with the semiclassical ones [16,17].

In this paper, we consider the influence of surface quantum effects associated with the scattering of polarized light by a dimer consisting of two homogeneous gold nanoparticles separated by a subnanometer gap. We investigate both the extinction cross section and the field enhancement factor inside the gap. In our research, we use the Discrete Sources Method (DSM) [34]. The DSM is a rigorous semi-analytical surface-based method which does not require a mesh generation or an integration procedure. It provides near and far fields directly in clear analytic form without any additional effort. The DSM provides an opportunity to solve the scattering problem for all sets of excitations and polarizations at once. Moreover, the DSM scheme allows the estimation of the errors of the fields obtained via surface residual computation tracking the real results’ convergence [34,35].

The paper is organized as follows. Section 2 formulates the mathematical statement of the scattering problem of a polarized plane wave by a dimer consisting of two identical axially symmetric homogeneous metal nanoparticles. Section 3 is devoted to the description of the modified scheme of the DSM that will be used for our investigation. Section 4 presents the results of computer simulations. Section 5 discusses in detail the features of the DSM in solving nanoplasmonics problems and provides a comparative analysis of the results of this research and other studies. Finally, in Section 6, the main results of the research are formulated.

2. Problem Statement

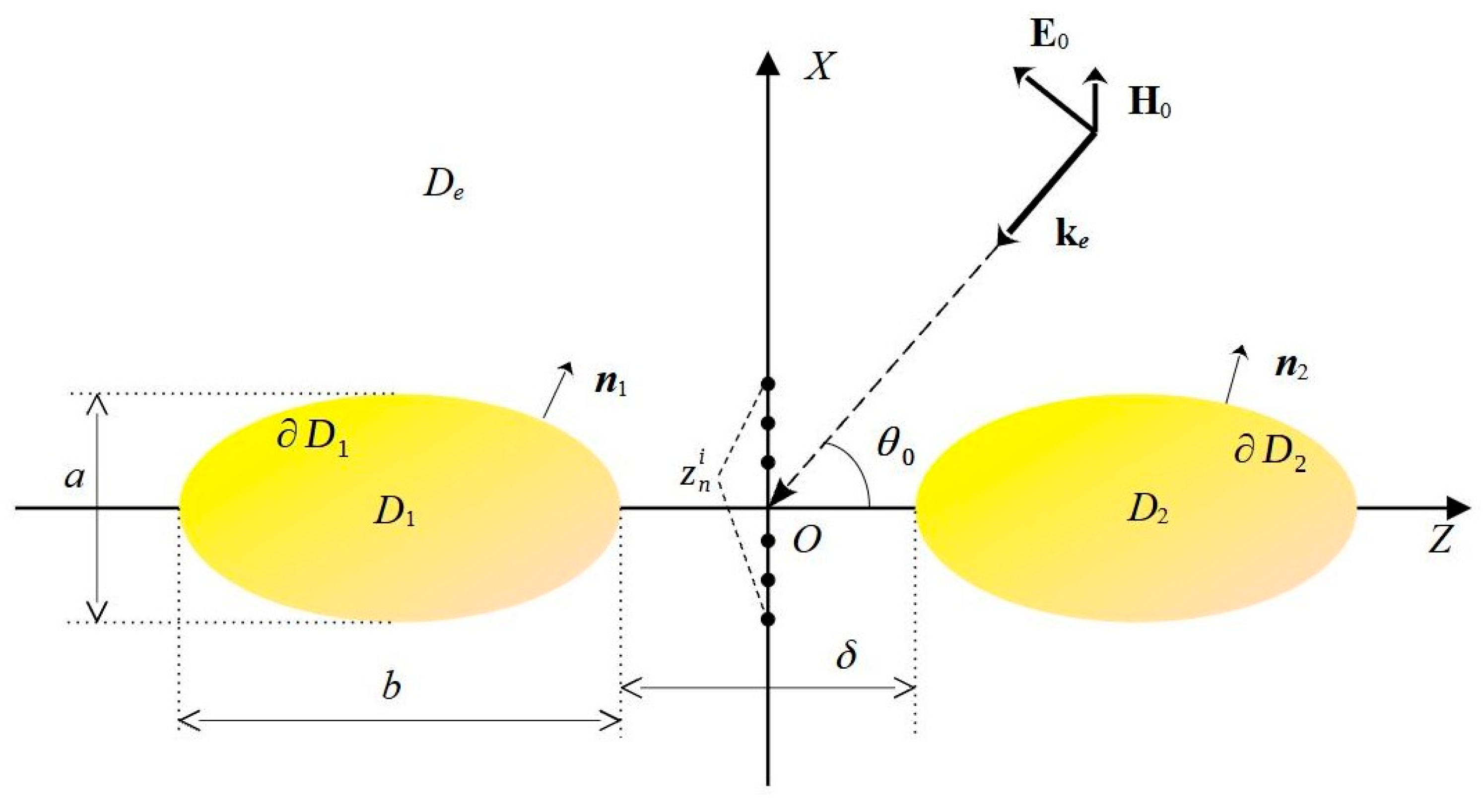
We consider scattering of a linearly polarized electromagnetic plane wave $\left\{{\mathit{E}}_{0,}{\mathit{H}}_0\right\}$ by a dimer consisting of two identical axisymmetric homogeneous particles placed in an isotropic homogeneous medium, as shown in Figure 1. Particles occupy the domain $D_i$ with smooth boundary ${𝜕D}_i{\in C}^{(2,\tau )}$, where $i=\mathrm{1,2}$ and the external region is denoted as $D_e$. By assumption, the particles have a common axis of symmetry Oz.

Let the wave vector ${\mathit{k}}_e$ of the electromagnetic plane wave belong to the Oxz plane and enclose the angle $\pi -{\theta }_0$ with the Oz axis:

$${\mathit{E}}_0={\mathit{e}}_0\mathit{exp}\left(-j{\mathit{k}}_e·\mathit{r}\right),$$

(1)

where ${\mathit{e}}_0$—field polarization vector. We will assume that all media are non-magnetic and the time dependence has the form $exp\left(j\omega t\right)$.

The corresponding P/S polarized plane wave fields $\left\{{\mathit{E}}_0^{P,S},{\mathit{H}}_0^{P,S}\right\}$ can be written as

$${\mathit{E}}_0^P=\left({\mathit{e}}_{x}cos{\theta }_0+{\mathit{e}}_{z}sin{\theta }_0\right)·\chi \left(x,z\right),{\mathit{H}}_0^P=-\sqrt{{\epsilon }_e}{\mathit{e}}_y·\chi \left(x,z\right),$$

(2)

$${\mathit{E}}_0^S=\sqrt{{\epsilon }_e}{\mathit{e}}_y·\chi \left(x,z\right),{\mathit{H}}_0^S=\left({\mathit{e}}_{x}cos{\theta }_0+{\mathit{e}}_{z}sin{\theta }_0\right)·\chi \left(x,z\right),$$

(3)

where $\chi \left(x,z\right)=exp\left\{-j{k}_e\left(xsin{\theta }_0-zcos{\theta }_0\right)\right\},k_e=k\sqrt{{\epsilon }_e},$ $k=\frac{\omega }{c}$ and $\left({\mathit{e}}_x,{\mathit{e}}_y,{\mathit{e}}_z\right)$ is a Cartesian basis.

Let us proceed to the description of the SRF theory and consider the mathematical formulation of the scattering problem with mesoscopic boundary conditions.

In the external domain, the scattered field $\left\{{\mathit{E}}_e,{\mathit{H}}_e\right\}$ satisfies the system of Maxwell equations of the form

$$rot{\mathit{H}}_e=ik{\epsilon }_e{\mathit{E}}_e;rot{\mathit{E}}_e=-ik{\mathit{H}}_e; \mathrm{in} D_e.$$

(4)

Inside the particles, the total internal fields $\left\{{\mathit{E}}_i,{\mathit{H}}_i\right\}$ satisfy the classical system of Maxwell equations

$$rot{\mathit{H}}_i=jk{\epsilon }_i{\mathit{E}}_i;rot{\mathit{E}}_i=-jk{\mathit{H}}_i; \mathrm{inside} D_i .$$

(5)

The following boundary conditions are enforced on the particle surface ${𝜕D}_i$

$$\begin{gathered} {\mathit{n}}_i\times \left({\mathit{E}}_i\left(P\right)-{\mathit{E}}_{\mathrm{e}}\left(P\right)-{\mathit{E}}_0\left(P\right)\right)=-d_{\perp }{\mathit{n}}_i\times \nabla \left\{{\mathit{n}}_i·\left({\mathit{E}}_i\left(P\right)-{\mathit{E}}_{\mathrm{e}}\left(P\right)-{\mathit{E}}_0\left(P\right)\right)\right\}, \\ {\mathit{n}}_i\times \left({\mathit{H}}_i\left(P\right)-{\mathit{H}}_{\mathrm{e}}\left(P\right)-{\mathit{H}}_0\left(P\right)\right){={-j\omega d_{\parallel }\{\mathit{n}}_i\times [\mathit{D}}_{\mathrm{i}}\left(P\right)-{\mathit{D}}_{\mathrm{e}}\left(P\right)-{\mathit{D}}_0\left(P\right)\left]\right\}\times {\mathit{n}}_i, \\ P\in 𝜕D_i \end{gathered}$$

(6)

At infinity, the scattered field satisfies the Silver–Muller radiation conditions [36]

$$\underset{r\to \mathrm{\infty }}{\mathit{lim}}r·\left(\sqrt{{\epsilon }_e}{\mathit{E}}_{\mathrm{e}}\times \frac{\mathit{r}}{r}-{\mathit{H}}_e\right)=0;r=\left|M\right|.$$

(7)

Here, ${\epsilon }_{e,i}$ are the dielectric permittivities of the media in the corresponding domains, ${\mathit{n}}_i$ are the unit external normals to the surfaces ${𝜕D}_i$, respectively, $Im{\epsilon }_e$= 0, $Im{\epsilon }_{\mathrm{i}}\le$0, $k=\frac{\omega }{c}$ and $\mathit{D}$ is the displacement of the electric field.

The Feibelman parameters $d_{\perp },d_{\parallel }$ for a plane interface (y = 0) are formally defined as follows [16]

$$d_{\perp }\left(\omega \right)=\frac{\int \rho (x,\omega )xdx}{\int \rho (x,\omega )dx},d_{\parallel }\left(\omega \right)=\frac{\int {𝜕}_x{J}_y(x,\omega )xdx}{\int {𝜕}_x{J}_y(x,\omega )dx}$$

(8)

where $\rho (x,\omega )$ is the density of the surface charges induced by an external field and $J(x,\omega )$—surface current. It is believed that at the metal–dielectric interface, the normal component of the induced current vanishes, hence $d_{\parallel }\left(\omega \right)=0$ [17]. The value $d_{\perp }\left(\omega \right)$ is complex: the real part corresponds to the center of mass of the electron cloud of the induced charges and the imaginary part describes the Landau damping [37]. The $d_{\perp }\left(\omega \right)$ parameter, usually obtained for a planar metal–vacuum interface, has been widely used to determine the optical response of arbitrary-shaped metallic nanostructures [38,39]. The current implementation of the $d_{\perp }\left(\omega \right)$ parameter neglects the nonlocality of the metal response in the direction parallel to the surface (long wavelength limit). This is a reasonable approximation when the radius of curvature of the nanostructure is much larger than the Fermi wavelength (for Au~0.5 nm). We assume that the boundary value scattering problem (4)–(7) is uniquely solvable. In the case of a single homogeneous sphere, this was proven in [40].

3. The Discrete Sources Method

In this section, we show how the DSM numerical scheme can be adjusted to simulate the scattering of polarized light by coupled plasmonic nanoparticles separated by a subnanometer gap, taking into account the mesoscopic boundary conditions (6). Recall that in the framework of the DSM the electromagnetic fields are constructed as finite linear combinations of the fields generated by the lowest order multipoles distributed along the axis of rotation [34]. Thus, the approximate solution satisfies both the Maxwell equations inside and outside the obstacle and the radiation conditions analytically. The unknown amplitudes of the discrete sources (DSs) are to be determined from the boundary conditions enforced at the obstacle surface [35].

For an axisymmetric dimer, the P- and S-polarized excitations are treated separately. To account for axial symmetry, we expand each polarized plane wave in a Fourier series in terms of the azimuthal angle φ using the following expansion

$$exp\left\{\pm jxcos\phi \right\}={\sum }_{m=0}^{\mathrm{\infty }}(2-{\delta }_{0m}){(\pm j)}^m{J}_m\left(x\right)cos\left(m\phi \right),$$

(9)

where $J_m$ are cylindrical Bessel functions and ${\delta }_{0m}$ is the Kronecker delta symbol. Due to the axial symmetry of the dimer, the scattering problem is split over the azimuthal modes m and a separate solution for each mode can be obtained.

The DSs are distributed along the axis of rotation Oz, and, in this regard, we denote by ${\left\{z_n^e\right\}}_{n=1}^{N_e^m}$ the positions of DSs for the scattered field representation, by ${\left\{z_n^i\right\}}_{n=1}^{N_i^m}$ the positions of the DSs for representing the total field inside each particle. Note that the numbers of discrete sources $N_e^m$ and $N_i^m$ may depend on the azimuthal mode index m.

We will construct fields in the regions $D_{\beta },\beta =\mathrm{1,2},e$ based on the following vector potentials, which can be written as [35]

$$\begin{gathered} {\mathit{A}}_{mn}^{1,\alpha }=Y_m^{\alpha }\left(\zeta ,z_n^{\alpha }\right)\left\{{\mathit{e}}_{\rho }cos\left[\left(m+1\right)\phi \right]-{\mathit{e}}_{\phi }sin\left[\left(m+1\right)\phi \right]\right\};\alpha =1,2,e; \\ {\mathit{A}}_{mn}^{2,\alpha }=Y_m^{\alpha }\left(\zeta ,z_n^{\alpha }\right)\left\{{\mathit{e}}_{\rho }sin\left[\left(m+1\right)\phi \right]+{\mathit{e}}_{\phi }cos\left[\left(m+1\right)\phi \right]\right\}; \\ {\mathit{A}}_n^{3,\alpha }=Y_0^{\alpha }\left(\zeta ,z_n^{\alpha }\right){\mathit{e}}_z. \end{gathered}$$

(10)

Here the corresponding functions are

$$Y_m^{\mathrm{i}}\left(\zeta ,z_n^{\mathrm{i}}\right)=h_m^{\left(1\right)}\left(k_{\mathrm{i}}{R}_{z_n^{\mathrm{i}}}\right){\left(\frac{\rho }{R_{z_n^{\mathrm{i}}}}\right)}^m,Y_m^e\left(\zeta ,z_n^e\right)=h_m^{\left(2\right)}\left(k_e{R}_{z_n^e}\right){\left(\frac{\rho }{R_{z_n^e}}\right)}^m,$$

(11)

where $h_m^{\left(\mathrm{1,2}\right)}$ are the spherical Hankel functions, $k_{i,e}=k\sqrt{{\epsilon }_{i,e}}$, $\zeta =\left(\rho ,z\right)$, ${\rho }^2=x^2+y^2$, $R_{z_n}^2={\rho }^2+{\left(z-z_n\right)}^2$, ${\left\{z_n^{\alpha }\right\}}_{n=1}^{N_{\alpha }^m}$ are the DS coordinates and $\left({\mathit{e}}_{\rho },{\mathit{e}}_{\phi },{\mathit{e}}_z\right)$ represents the basis of the cylindrical coordinate system. We emphasize that Cartesian components of (10) satisfy the Helmholtz equation.

A feature of the DSM application for the case of a dimer with a subnanometric gap is the representation of the approximate solution for internal fields $\left\{{\mathit{E}}_i,{\mathit{H}}_i\right\}$. As a rule, in the classical DSM scheme, internal fields are represented through spherical Bessel functions [35] and $z_n^i$ are deposited inside the domains $D_i$. But in our case, Hankel functions $h_m^{\left(1\right)}$ are used instead. The corresponding DSs are located outside $D_i$, in the complex plane W [34] passing through the origin of the Cartesian system and perpendicular to the axis of rotation Oz. Its imaginary axis coincides with the Oy axis of the real space. That is, the coordinates $z_n^i$ are complex valued and ${Rez}_n^i=0$, but ${Imz}_n^i$ are located symmetrically with respect to the Oz axis [34], taking both positive and negative values (see Figure 1). In contrast, the DSs for the scattered fields $z_n^e$ are deposited on the axis of rotation inside $D_i$.

The field representations in the case of P-polarization can be written as

$$\begin{array}{c}{\mathit{E}}_{\alpha }^N={\displaystyle \sum _{m=0}^{\mathrm{M}}}{\displaystyle \sum _{n=1}^{N_{\alpha }^m}}\left\{p_{mn}^{\alpha }\frac{j}{k{\epsilon }_{\alpha }}rotrot{\mathit{A}}_{mn}^{1,\alpha }+q_{mn}^{\alpha }\frac{1}{{\epsilon }_{\alpha }}rot{\mathit{A}}_{mn}^{2,\alpha }\right\}+\\ +{\displaystyle \sum _{n=1}^{N_{\alpha }^0}}{r}_n^{\alpha }\frac{j}{k{\epsilon }_{\alpha }}rotrot{\mathit{A}}_n^{3,\alpha };\hspace{1em}{\mathit{H}}_{\alpha }^N=\frac{j}{k}rot{\mathit{E}}_{\alpha }^N,\alpha =i,e\end{array}$$

(12)

and for S-polarization as

$$\begin{array}{c}{\mathit{E}}_{\alpha }^N={\displaystyle \sum _{m=0}^{\mathrm{M}}}{\displaystyle \sum _{n=1}^{N_{\alpha }^m}}\left\{p_{mn}^{\alpha }\frac{j}{k{\epsilon }_{\alpha }}rotrot{\mathit{A}}_{mn}^{2,\alpha }+q_{mn}^{\alpha }\frac{1}{{\epsilon }_{\alpha }}rot{\mathit{A}}_{mn}^{1,\alpha }\right\}+\\ +{\displaystyle \sum _{n=1}^{N_{\alpha }^0}}{r}_n^{\alpha }\frac{1}{{\epsilon }_{\alpha }}rot{\mathit{A}}_n^{3,\alpha };\hspace{1em}{\mathit{H}}_{\alpha }^N=\frac{j}{k}rot{\mathit{E}}_{\alpha }^N,\alpha =i,e.\end{array}$$

(13)

It is easy to verify that the constructed fields (12)–(13) satisfy all the conditions of the boundary value scattering problem (4)–(7) except for the transmission conditions (6). The unknown DS amplitudes ${\mathit{p}}_m^N=\left\{p_{mn}^{\mathsf{\alpha }},q_{mn}^{\mathsf{\alpha }},r_n^{\mathsf{\alpha }}\right\},\alpha =i,e$ are determined from fitting these conditions. The fields ${\{\mathit{E}}_{\alpha }^N,{\mathit{H}}_{\alpha }^N\}$ (12)–(13) are finite linear combinations of Fourier harmonics in the φ angle. Therefore, fitting the transmission conditions leads to separation of the fields in the azimuthal modes m and each mode can be treated separately.

Let us briefly describe the DSM numerical scheme. It consists of several steps:

• Evaluation of the number M which equals the amount of Fourier harmonics in the plane wave representation (9), assuming that the relative error in the plane wave approximation is less than 0.05%.
• Estimation of the matching points (MPs) amount L. MPs are distributed along the meridian of the particle for a given value of the excitation wavelength. For a spheroidal particle, the MP distribution along the meridian is performed as follows:

  $$z_l=cos{ \theta }_l, {\rho }_l=sin {\theta }_l, { \theta }_l=\frac{\pi }{L-1}(l-1), l=\mathrm{1,2},\dots L.$$

  (14)
• For external fields, the DSs $\left\{z_n^e\right\}$ are located on the axis of symmetry in between the spheroid focuses and for internal fields the corresponding points $\left\{z_n^i\right\}$ are deposited in the complex plane, as shown in Figure 1. The number of DSs might be different for internal ($N_i$) and external ($N_e$) fields; their values are as a rule are between L/4 and L/2.
• Then, Fourier harmonics of the internal and external fields are matched to the corresponding harmonics of the exciting field following the mesoscopic transmission conditions in the given MP set. The resulting matrix is overdetermined [41].
• Matrix factorization is performed using the Givens algorithm [42] and the DS amplitudes are calculated as a pseudosolution of the corresponding linear system.
• The DS amplitudes are determined for all the angles of incidence and both polarizations at once.
• To control the convergence of the results, the surface residual is evaluated if necessary.

After determining the amplitudes of the DSs, the scattered field can be calculated using representations (12)–(13). An important characteristic describing the response of an obstacle to external excitation is the Far Field Pattern of the scattered field $\mathit{F}\left(\theta ,\phi \right)$ [36]. This is defined on a unite sphere as

$${\mathit{E}}_{\mathit{e}}\left(M\right)/\left|{\mathit{E}}^0\left(M\right)\right|=\frac{exp\left(-j{k}_{e}r\right)}{r}\mathit{F}\left(\theta ,\phi \right)+O\left(r^{-2}\right),\hspace{1em}r\to \mathrm{\infty }.$$

(15)

Following the asymptotics of the scattered field (12)–(13), the $\theta ,\phi$ components of $\mathit{F}\left(\theta ,\phi \right)$ for P-polarization accepts the following form

$$\begin{gathered} \begin{array}{c}{F}_{\theta }^P\left(\theta ,\phi \right)=j{\displaystyle \sum _{m=0}^M}{\left(jsin\theta \right)}^m\mathit{cos}\left(m+1\right)\phi {\displaystyle \sum _{n=1}^{N_e^m}}\left\{p_{mn}^{e}cos\theta +q_{mn}^e\right\}exp\left\{j{k}_e{z}_n^{e}cos\theta \right\}\\ -jsin\theta {\displaystyle \sum _{n=1}^{N_e^0}}{r}_n^{e}exp\left\{j{k}_e{z}_n^{e}cos\theta \right\},\end{array} \\ {F}_{\phi }^P\left(\theta ,\phi \right)=-j{\displaystyle \sum _{m=0}^M}{\left(jsin\theta \right)}^m\mathit{sin}\left(m+1\right)\phi \sum _{n=1}^{N_e^m}\left\{p_{mn}^e+q_{mn}^{e}cos\theta \right\}exp\left\{j{k}_e{z}_n^{e}cos\theta \right\}. \end{gathered}$$

(16)

In the case of the S-polarized wave, the $\theta ,\phi$ components are written as

$$\begin{gathered} F_{\theta }^S\left(\theta ,\phi \right)=j{\displaystyle \sum _{m=0}^M}{\left(jsin\theta \right)}^m\mathit{sin}\left(m+1\right)\phi {\displaystyle \sum _{n=1}^{N_e^m}}\left\{p_{mn}^{e}cos\theta -q_{mn}^e\right\}exp\left\{j{k}_e{z}_n^{e}cos\theta \right\}, \\ \begin{array}{c}{F}_{\phi }^S\left(\theta ,\phi \right)=j{\displaystyle \sum _{m=0}^M}{\left(jsin\theta \right)}^m\mathit{cos}\left(m+1\right)\phi {\displaystyle \sum _{n=1}^{N_e^m}}\left\{p_{mn}^e-q_{mn}^{e}cos\theta \right\}exp\left\{j{k}_e{z}_n^{e}cos\theta \right\}\\ +jsin\theta \sum _{n=1}^{N_e^0}{r}_n^{e}exp\left\{j{k}_e{z}_n^{e}cos\theta \right\}.\end{array} \end{gathered}$$

(17)

We will compute the extinction cross section, which shows how much energy the obstacle takes to absorb and scatter from the plane wave energy. Note that the extinction cross section exceeds the scattering cross section by several orders of magnitude. For the scattering problem under consideration, the extinction cross section will be determined by the following relations

$${\sigma }_{ext}^P\left({\theta }_0\right)=-\frac{4\pi }{k_e}Im{F}_{\theta }^P\left(\pi -{\theta }_0,\pi \right),{\sigma }_{ext}^S\left({\theta }_0\right)=\frac{4\pi }{k_e}Im{F}_{\phi }^S\left(\pi -{\theta }_0,\pi \right).$$

(18)

The dimension of the extinction cross section is nm². Our main goal is to analyze the behavior of the intensity Enhancement Factor (EF) in the gap between particles in the wavelengths range λ

$$F\left(\lambda \right)={\left|{\mathit{E}}_e^N+{\mathit{E}}^0\right|}^2/{\left|{\mathit{E}}^0\right|}^2,$$

(19)

which is dimensionless.

4. Numerical Results

In this section, we analyze the polarized plane wave scattering by a plasmonic dimer composed of two identical gold nanospheres or elongated nanospheroids. Each spheroid has an equivolume diameter D = 14 nm. The corresponding frequency-dependent refractive index for gold is taken from [43] and the Feibelman d-parameters from [44].

In [35], it was found that the maximum enhancement is achieved at the angle ${\theta }_0={90}^0$ and P-polarization of the incident plane wave. In this case, the vector ${\mathit{E}}_0$ is parallel to the Oz axis (the axis of symmetry of the prolate spheroids). So, we consider only this particular case. Rhodamine 6G R6G was chosen as an environment; its refractive index is $n_{\mathrm{e}}=1.326$.

In Figure 2a, we plot the enhancement factor (19) computed by means of local response approximation (LRA) and SRF theories for a dimer consisting of gold spheres with a diameter of D = 14 nm at different gap sizes $\mathsf{\delta }=5,2,1 \mathrm{n}\mathrm{m}$. The results indicate that narrowing the gap leads to an increase in the enhancement factor and demonstrates a substantial difference between the LRA and SRF results. Similar results can be seen in Figure 2b for prolate spheroids with equivolume diameter D = 14 nm and aspect ratio r = 3. In this case, the semiaxes of the spheroids are a = 9.8 nm and b = 29.4 nm, and the gap sizes are $\mathsf{\delta }=5,2,1 \mathrm{n}\mathrm{m}$. It can be seen that EF for spheroids exceeds EF for spheres by almost two orders of magnitude. The accompanying blue shift of the PR for the case of the surface quantum effect varies from 5 to 10 nm.

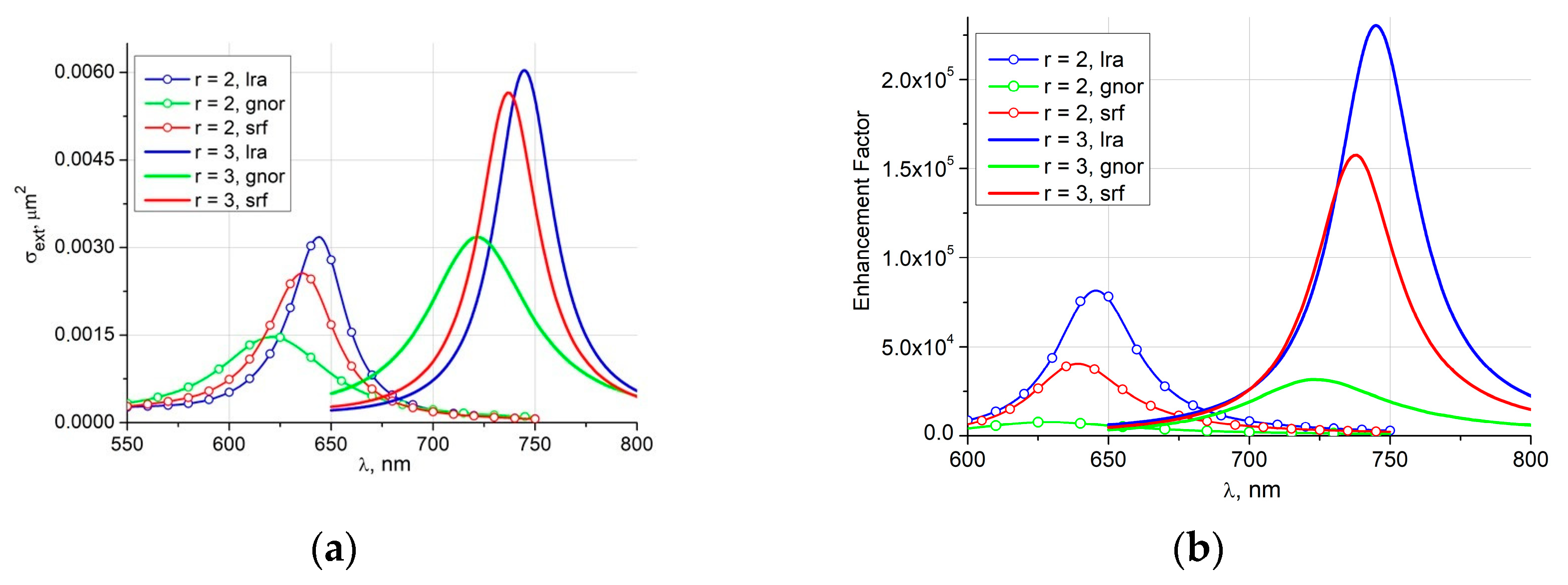
In Figure 3, one can observe the results corresponding to prolate spheroids with an equivolume diameter D = 14 nm and a gap $\mathsf{\delta }=1 \mathrm{n}\mathrm{m}$ for different aspect ratios r = 1, 2, 3. Case r = 1 corresponds to a sphere. Figure 3a,b demonstrate, respectively, the extinction cross section (18) and the enhancement factor (19), obtained with the LRA and SRF theories. It can be noticed that an increase in the aspect ratio leads to a spectral shift of the PR by almost 100 nm for each ratio value and is accompanied by an increase in its amplitude. Again, accounting for the surface quantum effect leads to PR damping and a blue shift of 5 to 10 nm.

We would like to emphasize that the elongation of the constituting particles (Figure 3) demonstrates the ability to manage the position of the PR in the frequency domain, which seems to be important in cases when it is required to obtain a shift to the longer wavelength with the same volume of gold.

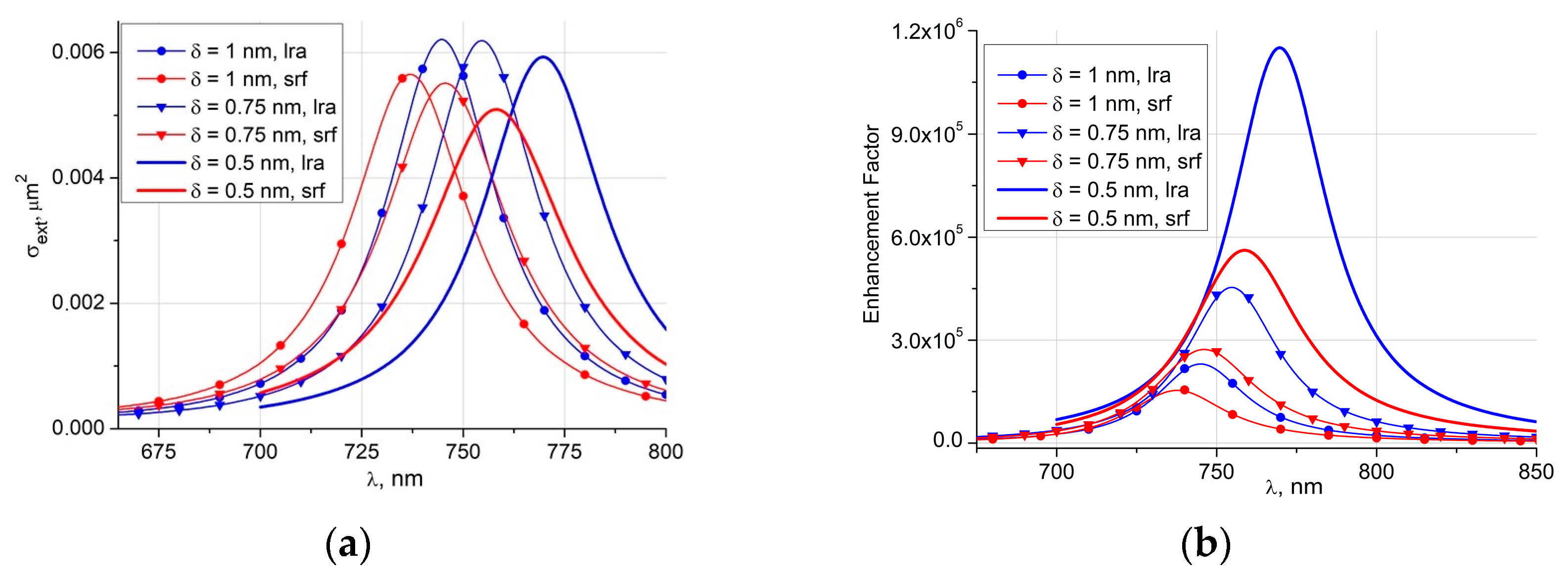
Figure 4 shows the extinction cross section and the enhancement factor for spheroids with an aspect ratio r = 3 when the spheroids approach each other, and the gap size reaches subnanometer values δ = 1, 0.75, 0.5 nm. It is clear that the extinction cross section decreases as δ shrinks, in contrast to the enhancement factor, which increases monotonically. In the case of SRF, the damping of the plasmon resonance can reach 50%, which is accompanied by a blue shift of 10 nm. Thus, in the case of the enhancement factor, the quantum surface effect leads to a significant decrease in the intensity at the hot spot inside the gap.

It worth emphasizing that both spheroid elongation and gap shrinking lead to hot spot intensity enhancement and plasmon resonance shift to the longer wavelength region.

Figure 5a presents the enhancement factor for a dimer with a gap of $\mathsf{\delta }=0.5 \mathrm{n}\mathrm{m}$ for spherical particles with diameters D = 14, 15, 16 nm. The SRF plots indicate a damping of the plasmon resonance by almost a factor of four, accompanied by a slight spectral blue shift of 10 nm. Similar results can be seen in Figure 5b, which demonstrates graphs corresponding to prolate spheroids with the aspect ratio r = 3 and gap size δ = 0.5 nm. Obviously, the field enhancement for the spheroids is almost an order of magnitude greater than the spheres. Accounting for the quantum effect results in enhancement factor damping by almost 50%, accompanied by a blue shift of about 10 nm.

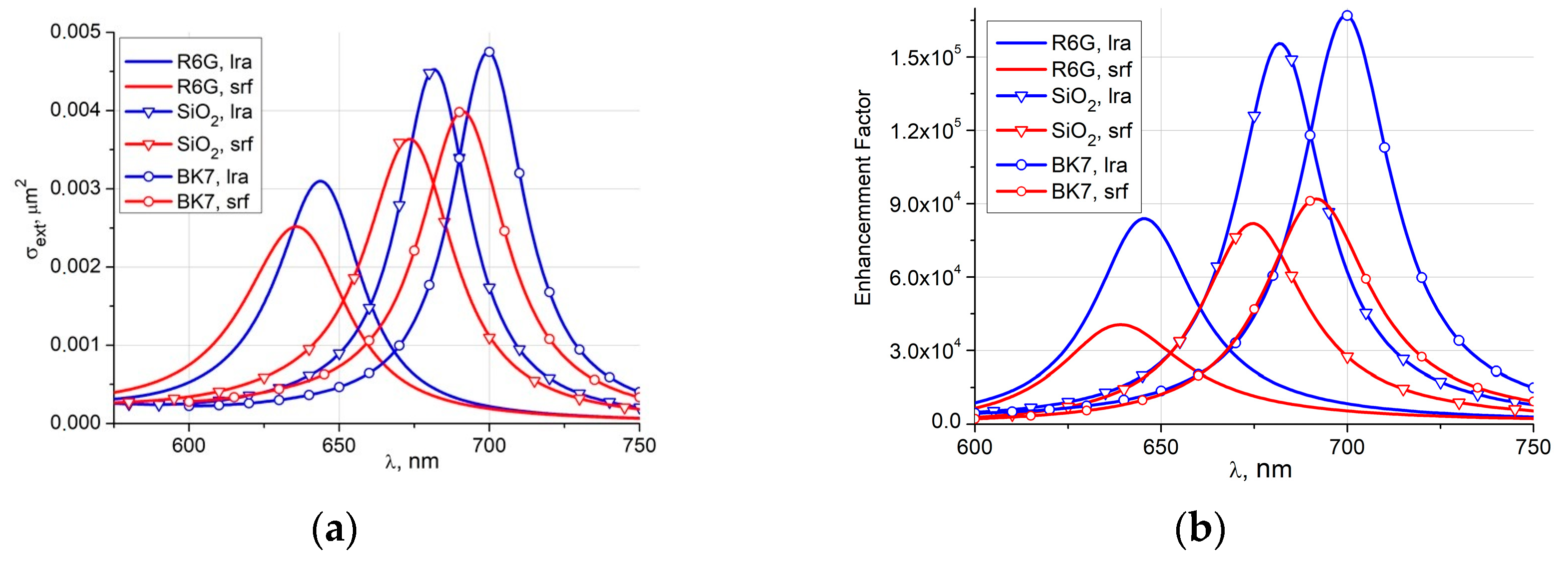
The results presented in Figure 2, Figure 3, Figure 4 and Figure 5 were obtained for the R6G medium with a refractive index n_e = 1.326. Let us consider how the extinction cross section and the enhancement factor change if a dimer with the axis ratio r = 2 and the gap δ = 1 nm is placed in a denser medium. Let us choose, for example, SiO₂ and BK7 glasses with the refractive indices n_e = 1.46 and n_e = 1.52, respectively. The corresponding results can be seen in Figure 6. An increase in the environment refractive index leads to an increase in the ratio of particle size to the excitation wavelength. This circumstance yields a shift of the PR to the long wavelength region and growth of its amplitude.

Figure 7 shows a comparison of the GNOR and SRF approaches describing, respectively, the volume quantum effect associated with the appearance of a longitudinal field inside the metal, and the surface quantum effect, which deals only with a transverse electromagnetic field. For convenience, classical LRA results are also presented. The plots correspond to a dimer with equivolume diameter D = 14 nm and gap δ = 1 nm, deposited in R6G medium. When compared with the classical case, the SRF theory predicts a much smaller damping in PR amplitude and slightly smaller blue shift than the GNOR model.

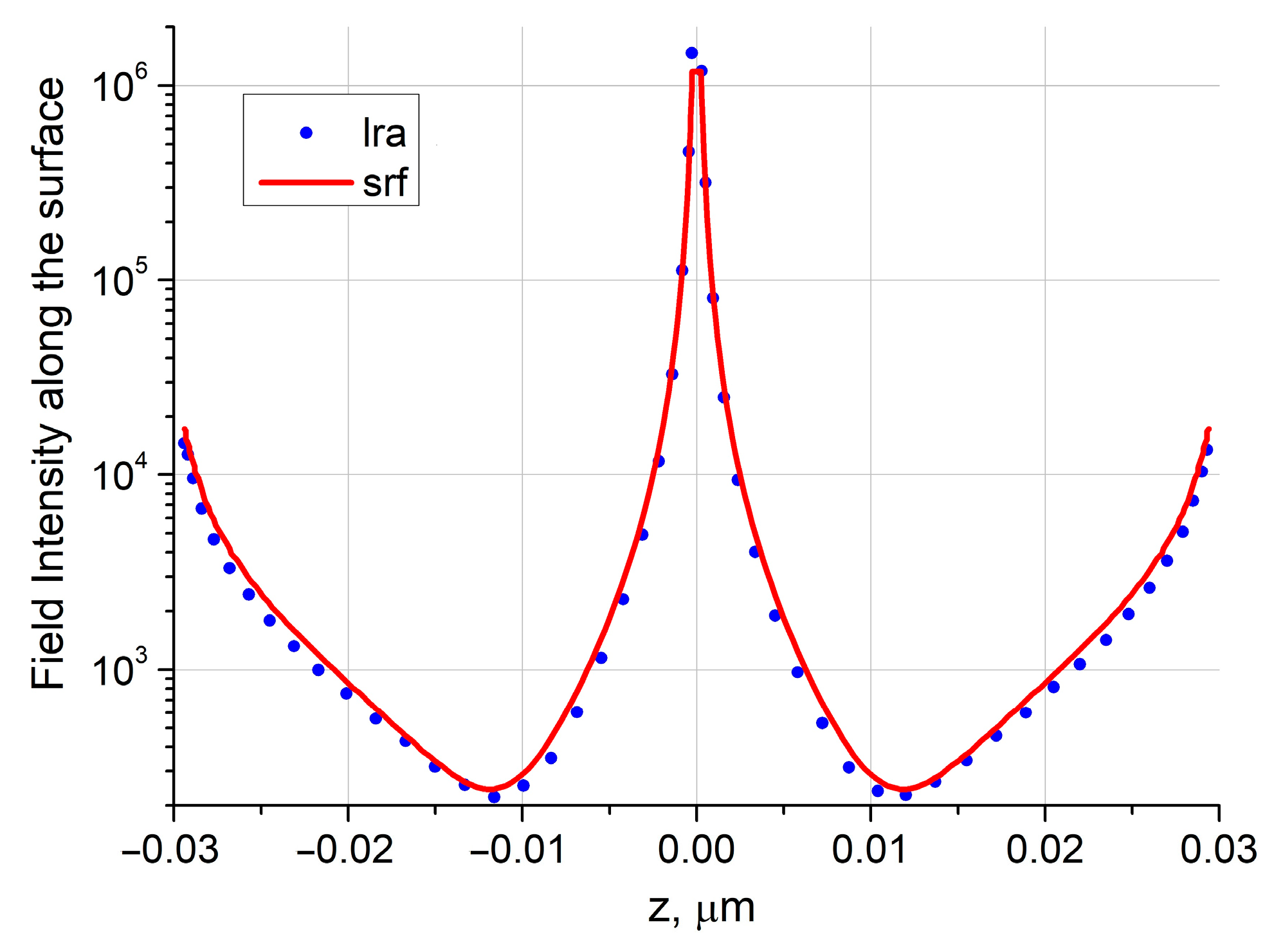
In the last part of our study, we considered the field in a subnanometric gap between particles. Since the size of the gap is extremely small compared to the excitation wavelength (~1/500), the field inside the gap is almost constant. The value of this constant can be estimated from the magnitude of the EF, if we take into account that the main contribution comes from the z-component of the electric field.

Figure 8 demonstrates the distribution of the relative electric field intensity along the meridians of the particles, including the gap. Calculations were performed for dimer parameters D = 14 nm, r = 3, δ = 0.5 nm, λ = 770 nm and R6G environment. As can be seen from the graphs, the maximum intensity value is in the center of the gap (z = 0), and the intensity also has large values on the opposite sides of the particles.

5. Discussion

The Discrete Source Method has a long history of use in solving the scattering problems of nanoplasmonics. Using DSM for the analysis of scattering by plasmonic dimers in the frame of LRA emerged as early as 10 years ago [45]. Particular interest was paid to the investigation of the phenomenon of intensity enhancement in the gap between the particles constituting the dimer, the so-called hot spot. This enhancement is associated with a decrease in the gap between the particles. However, the latter circumstance leads to a strong interaction between particles, which creates some problems in ensuring sufficient accuracy of the results when using numerical methods.

In [45], a modification of the DSM was proposed, which provides stable numerical results for near fields inside the gap. This modification is related to the representation of the fields inside particles through discrete sources located in the complex plane [34]. Usually, the fields inside each particle are represented separately, with their own sources [41]. In our case, a unitary set of discrete sources deposited in the complex plane with a unitary set of amplitudes (12) is employed for the internal field representation. Thus, the interaction of particles occurs not only through scattered fields, but also through internal ones. This circumstance made it possible to increase the accuracy of the results in the hot spot by an order of magnitude.

Based on the modified DSM scheme, a numerical analysis of the total field intensity behavior in the gap between two noble metal elongated spheroids was performed [45]. It was found that P-polarized light and incidence at angle ${\theta }_0={90}^0$ play a key role in the scattering behavior and intensity enhancement inside the gap. In particular, it was demonstrated that it is possible to achieve PR at any desired exciting wavelength by using an appropriate geometrical configuration of the dimer (scale, elongation, gap size) and material of the coupled spheroids.

With a decrease in the size of the particles that compose the dimer, quantum effects appear, such as a bulk nonlocality and the leaving of electrons from the surface of the particle. In [35], the influence of nonlocality on the absorption and scattering cross sections was studied. Spatial nonlocality was considered within the framework of the GNOR theory. In this regard, the DSM was substantially modified to account for the longitudinal fields inside the particles and additional boundary conditions on the surfaces.

The extinction and scattering cross sections of a plasmonic dimer consisting of two identical metallic prolate spheroids have been computed in the frequency domain for different spheroid aspect ratios and gap sizes [35]. Comparing the results obtained by the DSM combining with the GNOR theory and calculated with the local response approximation demonstrated a blue shift, a PR damping and a PR broadening in the optical cross sections. These effects become more significant with a decrease in the gap and deformation of the constituent spheroids when the aspect ratio increases.

In this paper, the DSM numerical scheme was extended for the analysis of the influence of the surface quantum effect on the optical properties of a plasmonic dimer consisting of nonspherical gold nanoparticles. There are only a few publications that study the influence of surface quantum effects using the mesoscopic boundary conditions with the Feibelman d-parameters [27,46,47].

In [46], it was shown how to include mesoscopic boundary conditions in the boundary integral equation approach based on the Galerkin scheme with Raviart–Thomas shape elements. The extinction cross section for coupled gold nanospheres with a diameter of 20 nm and a gap size of 2, 4, and 8 nm has been studied. It has been found that mesoscopic boundary conditions result in a blue shift and damping of the PR compared to the LRA.

The main differences between the studies [46] and our case are:

• The research [46] used a Drude dielectric function for gold ${\hslash \omega }_p=3.3 \mathrm{e}\mathrm{V}$ but we employed the experimental data for gold [43];
• The following Feibelman d-parameter formula was applied in [46]: $d_{\perp }\left(\omega \right)=-\frac{\mathsf{\beta }}{\sqrt{{\omega }_p^2-{\omega }^2}},$ $d_{\parallel }\left(\omega \right)=0$, in the range $0.8 \mathrm{e}\mathrm{V}\le \hslash \omega \le 2.2 \mathrm{e}\mathrm{V}$. But in this region of the spectrum, the Feibelman d-parameter takes purely real values. Thus, the Landau damping effect is not accounted for there;
• In addition, the formula for the Feibelman d-parameter used in [46] indicates a monotonic decrease in the d-parameter as the wavelength changes from 300 to 900 nm. At the same time, the experimental data that we use have a distinct dip in this region [44]. This is the main difference between the approach [46] and our study.

In [47], a self-consistent quasi-normal mode theory of nanometer-scale electromagnetism was considered, in which possible nonlocal quantum effects are determined through quantum surface responses. To describe quantum surface responses with frequency-dependent Feibelman d-parameters, Maxwell’s source-free equations were transformed into a generalized linear eigenvalue problem to determine quasi-normal modes.

Gold and sodium dimers with spheres 60 nm in diameter were considered. Feibelman d-parameters for metal–air interfaces were obtained using high-level theories (TDDFT for sodium and specular reflection model for gold). The first 12 eigenfrequencies of the quasi-normal modes were studied for various gap sizes and calculated using quantum surface responses and within the framework of the LRA theory. In particular, for spherical gold particles with a diameter of D = 60 nm, gap sizes of 1, 3, 5 nm were considered. It was found that the deviation of the quasi-normal LRA modes from the surface quantum responses increases as the gap shrinks.

Let us emphasize that quasi-normal mode approach does not give a direct estimate of how much the real optical characteristics of the dimer change. It gives only a qualitative description of the possible changes.

In [27], the influence of quantum phenomena on the electromagnetic interaction between a point quantum emitter and a classical dimer consisting of two identical spherical nanoparticles is studied. A semiclassical model is considered, which includes surface quantum-response corrections incorporating the Feibelman d-parameters. The overall good agreement between TDDFT and the semiclassical model for the dimer confirms that surface Landau damping and spill-out of the induced electron density occur for jellium nanoparticles. These quantum effects lead to a red shift and a broadening of plasmon resonances, which are absent in classical theories attributed to the local response of metals.

In our research, it was established that the gold nanoparticles are responsible for the blue shift and spill-in, which is typical for noble metals.

At the end of this section, we would like to note that there are publications discussing experimental results on dimers or optical antennas [17,19,32,48]. However, most of the experimental results are devoted to nanodimers with sizes exceeding 10–20 nm, where the contribution of quantum effects can be insignificant. In addition, most publications consider the dimers located on a substrate, but the existing implementation of the discrete source method is not intended for studying nanostructures located near the substrate. Therefore, unfortunately, comparison of the results presented in this study with experimental data was not possible.

6. Conclusions and Findings

The influence of the surface quantum effect on the optical characteristics in the problem of a plane electromagnetic wave scattering by a dimer composed of two identical gold nanoparticles with a subnanometric gap has been investigated. The extinction cross section and field enhancement factor inside the gap of a plasmonic dimer are calculated in the frequency domain for various particle elongations and gap sizes. To account for the corresponding surface quantum effect, a semiclassical theory based on mesoscopic boundary conditions and surface response functions was used. A strong influence of surface quantum effects on optical characteristics has been demonstrated.

It is shown that the quantum surface effect becomes more substantial when the constituent particles are elongated and the gap size shrinks to subnanometric values. Under these conditions, the results obtained using the surface response functions can deviate from the predictions of the local response approximation by up to four times, with a blue spectral shift of 10 nm. This phenomenon is a consequence of an electron cloud spill-in by the surface of particles which is typical for noble metals. As a result of the spill-in effect, the particle size reduces and the gap size increases, which causes a decrease in the amplitude of the plasmon resonance and a shift of its maximum to the short wavelength region.

The main novelties of our research are:

• The DSM was adjusted to analyze the scattering of polarized light by coupled plasmonic nanoparticles separated by a subnanometer gap;
• We considered a dimer consisting of non-spherical particles. The elongation of the constituting particle demonstrates an ability to control the position of the PR in the frequency domain, which seems to be important in cases when obtaining a shift to the longer wavelength with the same volume of gold is required. This method is more effective than increasing the diameter of the constituent nanoparticles;
• It has been demonstrated that surface quantum effects can reduce the enhancement factor inside the gap by a factor of four, which is accompanied by a blue spectral shift of 10 nm.