Automated Segmentation and Morphometry of Zebrafish Anterior Chamber OCT Scans
Abstract
1. Introduction
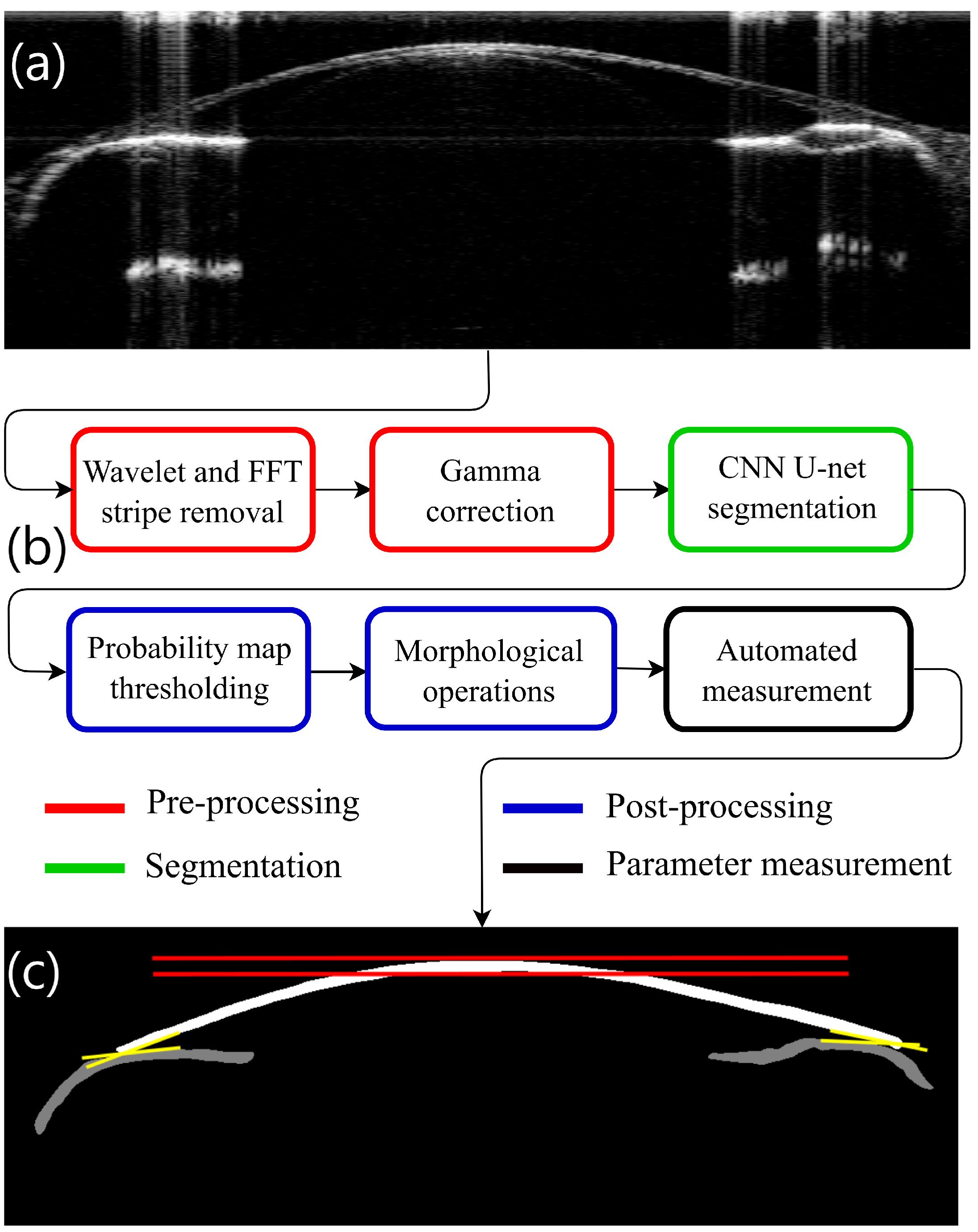
2. Methods
2.1. Imaging System Setup
2.2. Zebrafish Image Acquisition Protocol
2.3. Image Preprocessing
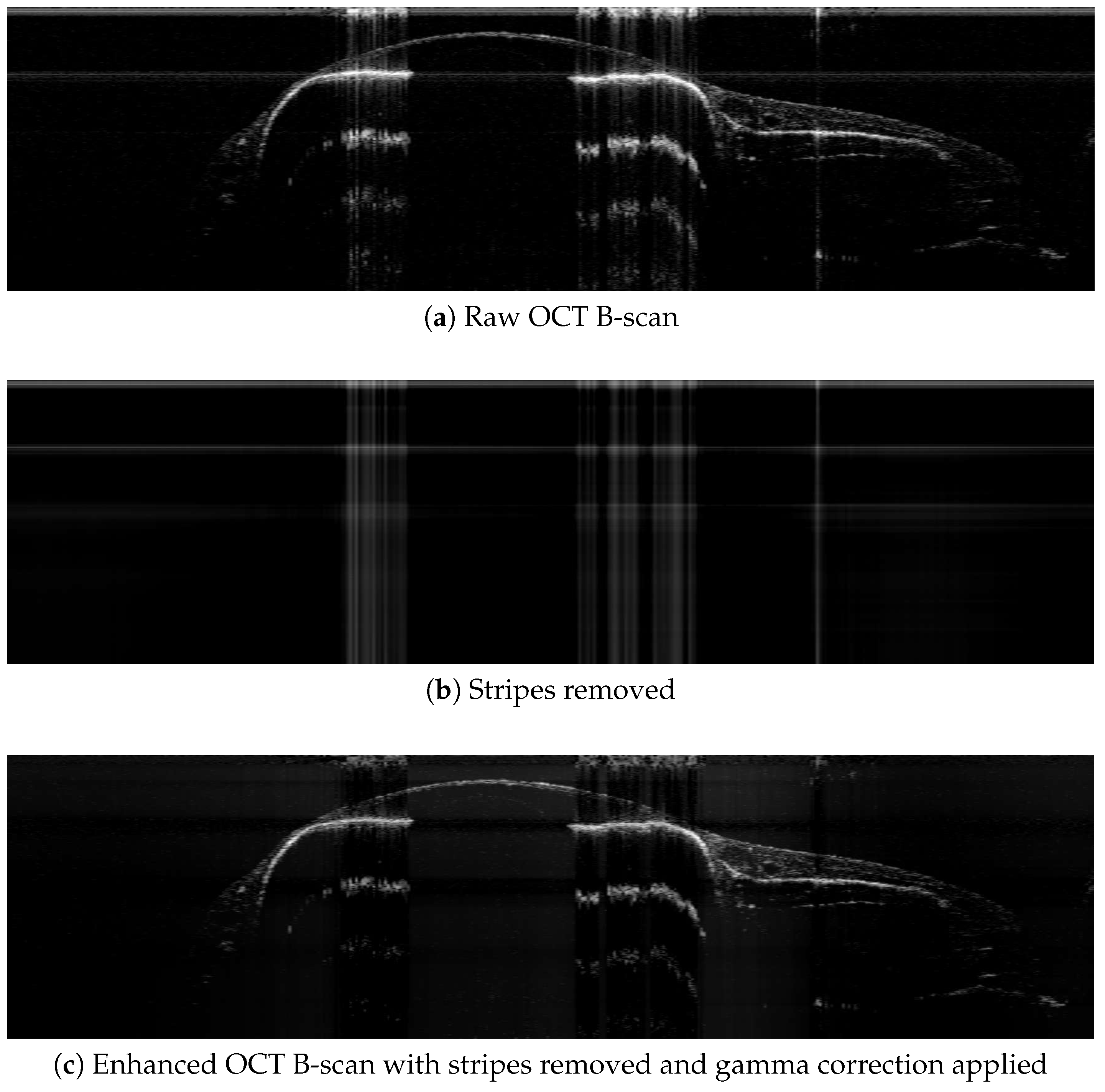
2.3.1. Wavelet + Fourier Transforms for Stripe Removal
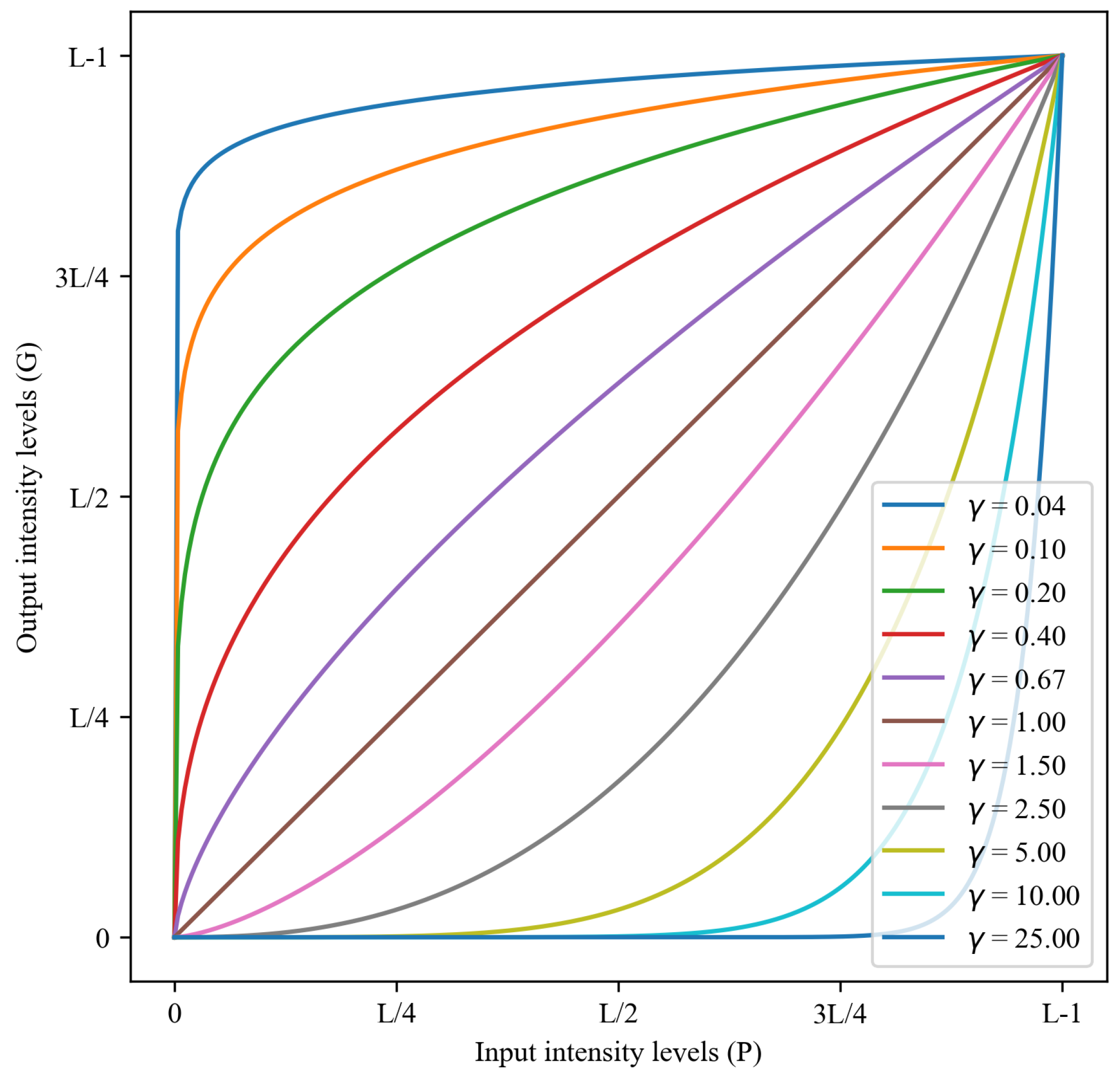
2.3.2. Gamma Correction
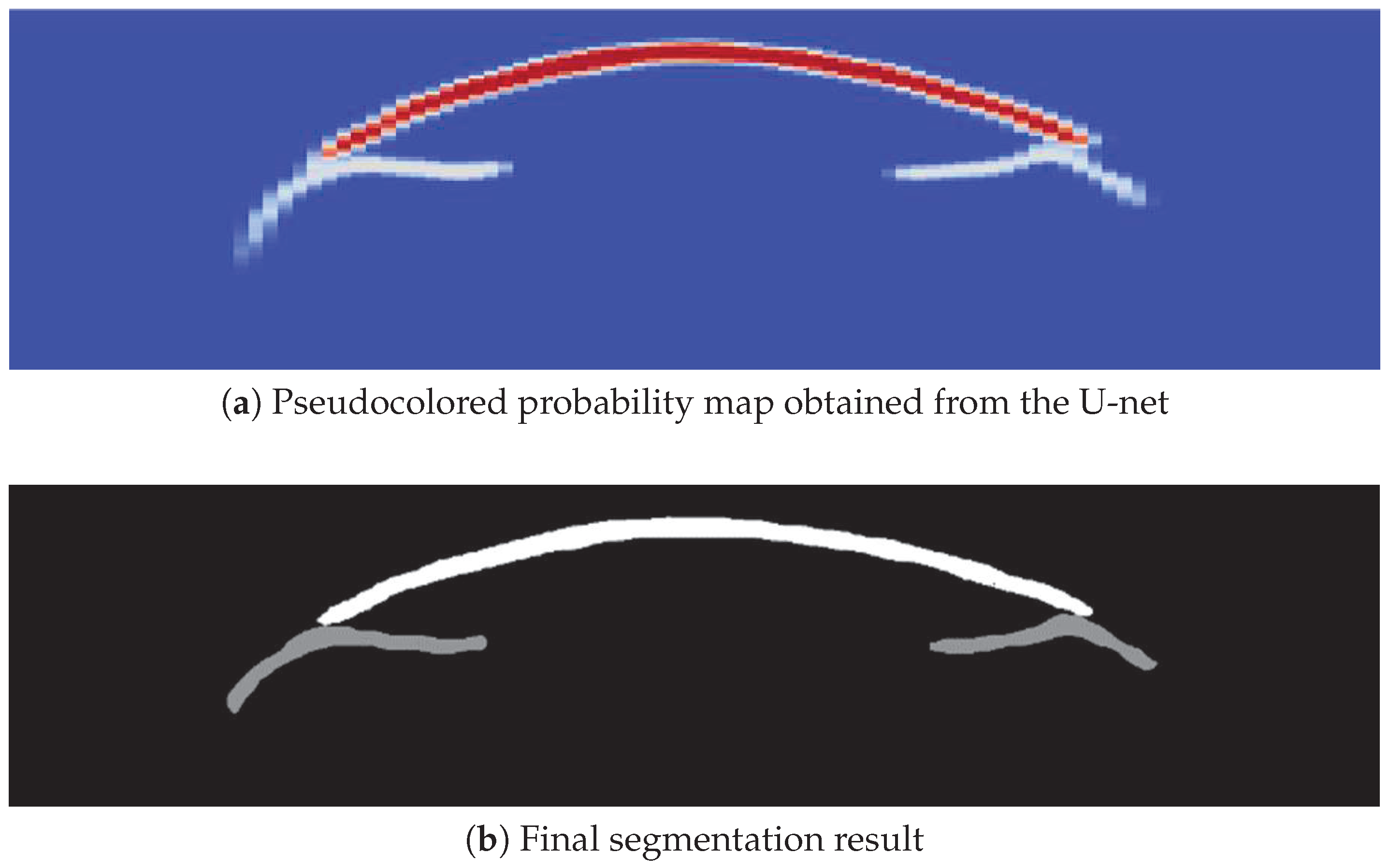
2.4. Segmentation Process
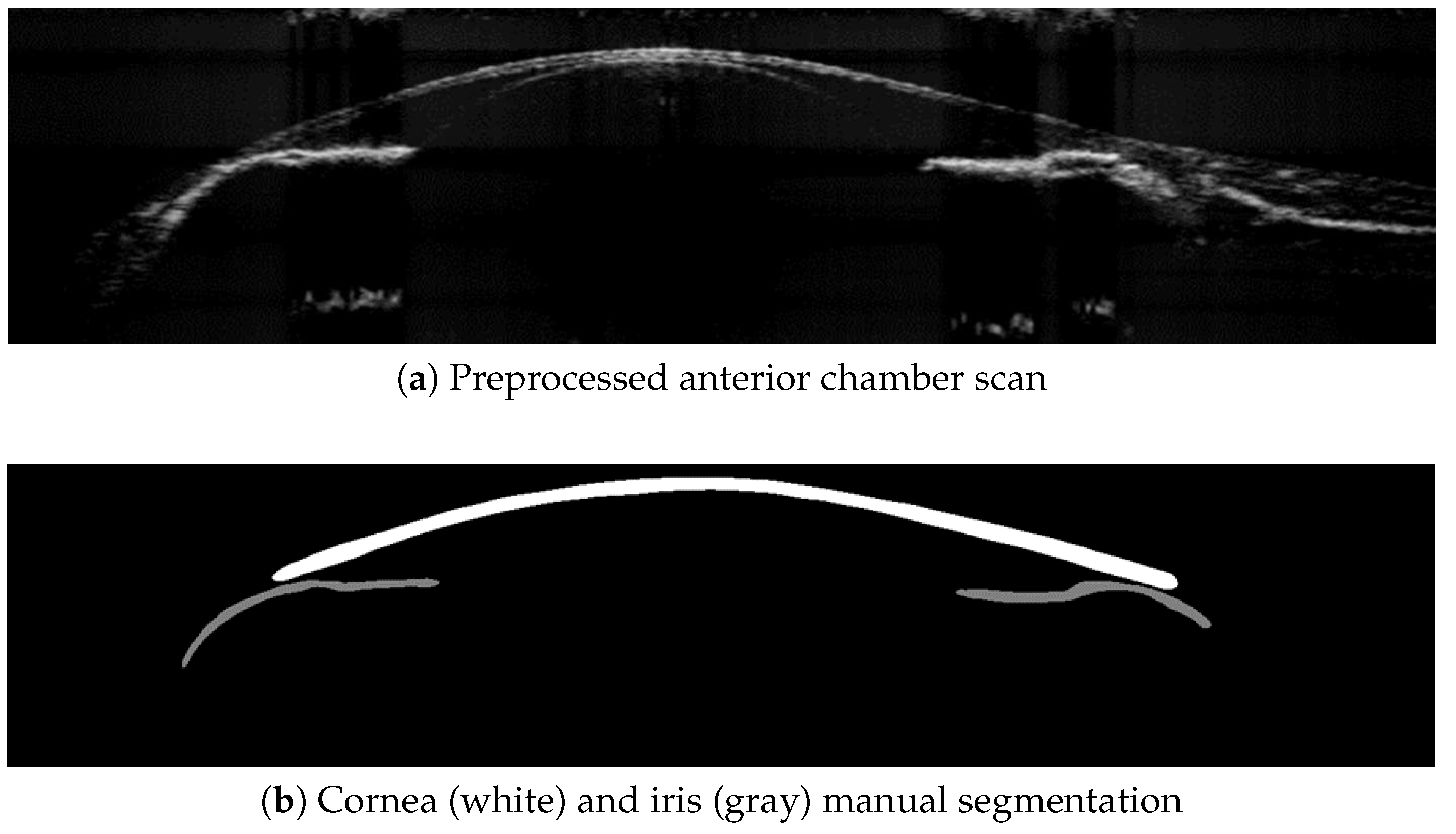
2.4.1. Manual Multilabel Segmentation and Data Labeling
2.4.2. CNN-Based Cornea and Iris Segmentation
2.5. Postprocessing
2.6. Automated Measurements
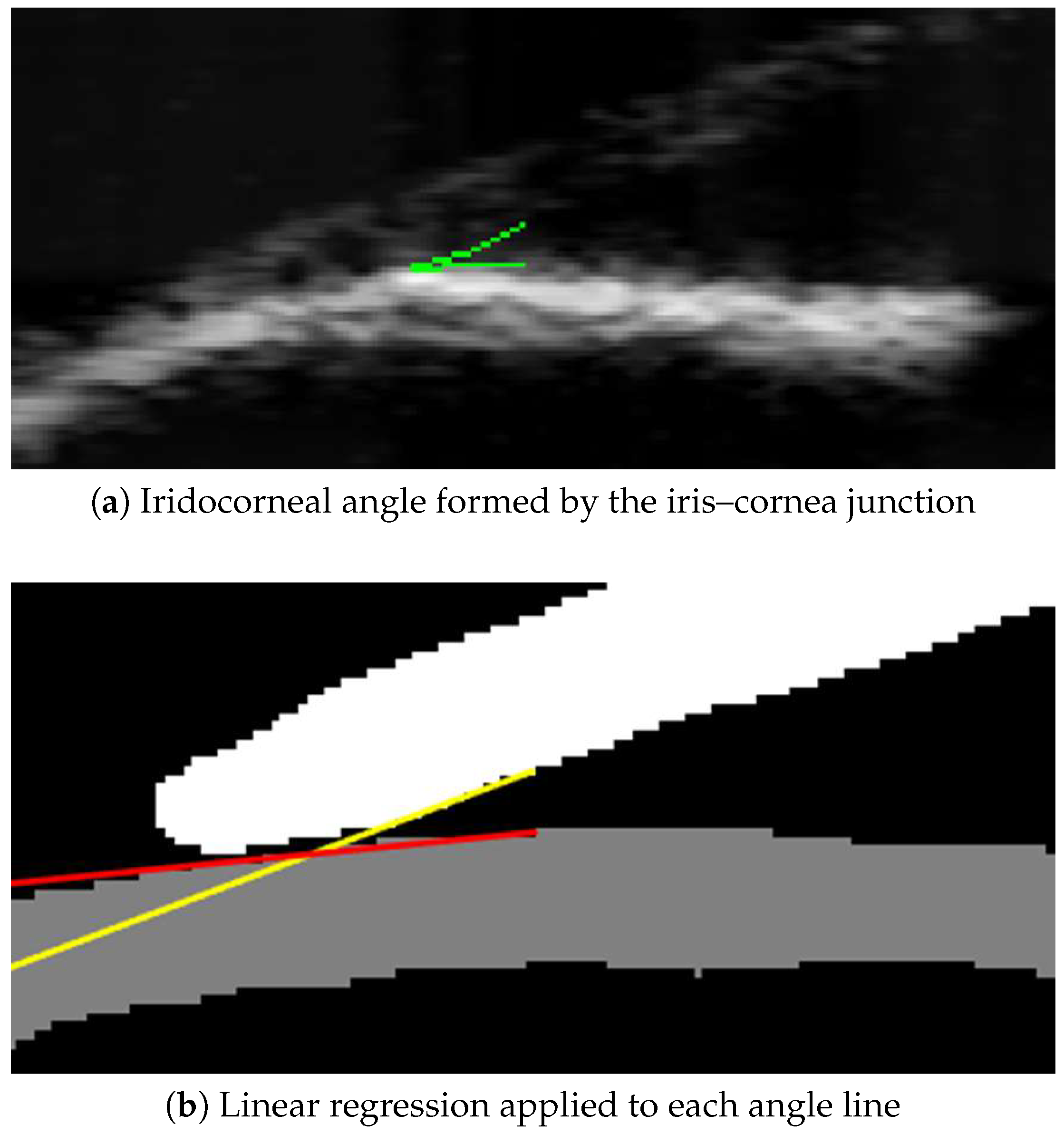
2.6.1. Anterior Chamber Angle (ACA)
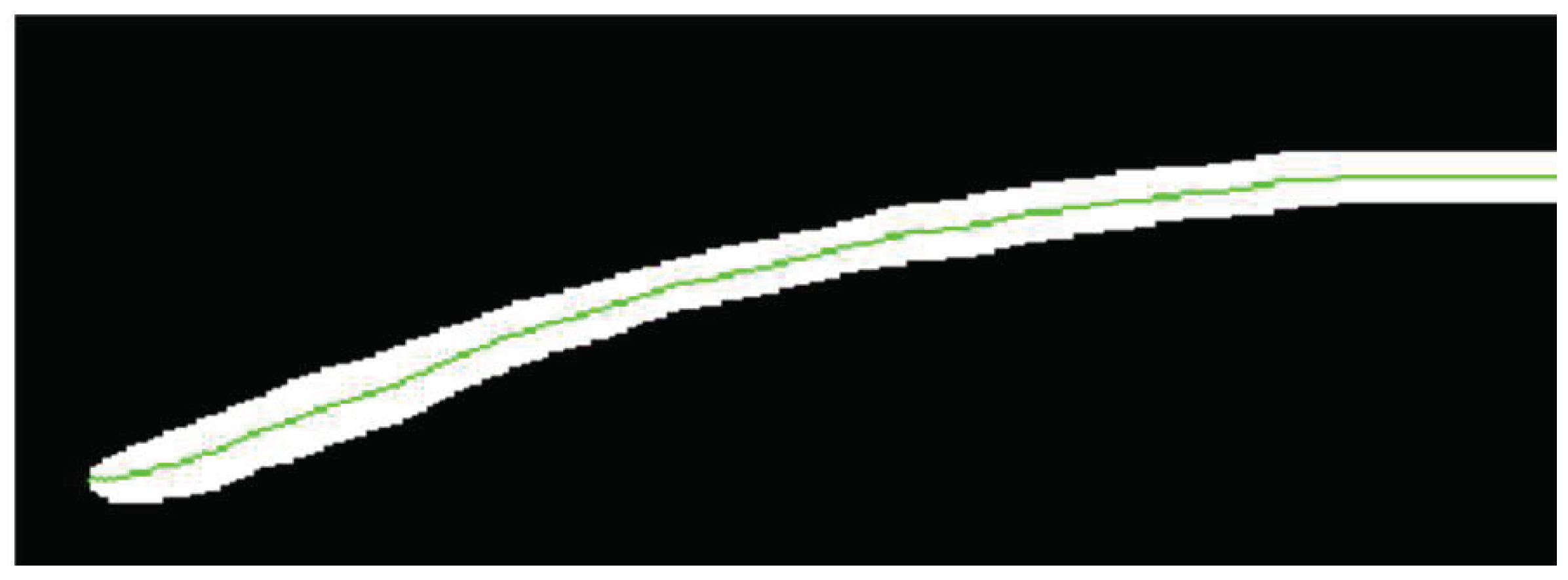
2.6.2. Central Corneal Thickness (CCT)
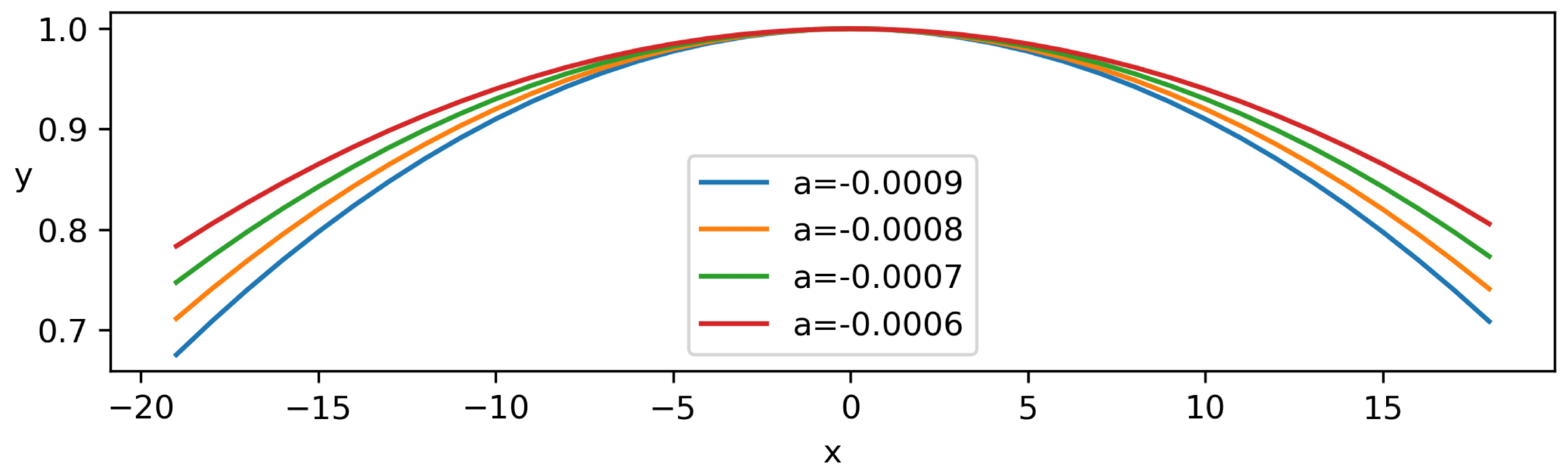
2.6.3. Corneal Curvature (CC)
3. Results
4. Conclusions and Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goel, M.; Picciani, R.G.; Lee, R.K.; Bhattacharya, S.K. Aqueous humor dynamics: A review. Open Ophthalmol. J. 2010, 4, 52. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, U.R.; Madden, B.J.; Charlesworth, M.C.; Fautsch, M.P. Proteome analysis of human aqueous humor. Investig. Ophthalmol. Vis. Sci. 2010, 51, 4921–4931. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.Y.; Nongpiur, M.; He, M.G.; Sakata, L.; Friedman, D.; Chan, Y.H.; Lavanya, R.; Aung, T. Association of narrow angles with anterior chamber area and volume measured with anterior-segment optical coherence tomography. Arch. Ophthalmol. 2011, 129, 569–574. [Google Scholar] [CrossRef] [PubMed]
- Chong, R.S.; Sakata, L.; Narayanaswamy, A.; Nongpiur, M.; He, M.G.; Chan, Y.H.; Friedman, D.; Lavanya, R.; Wong, T.Y.; Aung, T. Relationship between intraocular pressure and angle configuration: An anterior segment OCT study. Investig. Ophthalmol. Vis. Sci. 2013, 54, 1650–1655. [Google Scholar] [CrossRef] [PubMed]
- Leydolt, C.; Findl, O.; Drexler, W. Effects of change in intraocular pressure on axial eye length and lens position. Eye 2008, 22, 657–661. [Google Scholar] [CrossRef]
- Rabsilber, T.M.; Khoramnia, R.; Auffarth, G.U. Anterior chamber measurements using Pentacam rotating Scheimpflug camera. J. Cataract Refract. Surg. 2006, 32, 456–459. [Google Scholar] [CrossRef]
- Jain, N.; Zia, R. The prevalence and break down of narrow anterior chamber angle pathology presenting to a general ophthalmology clinic. Medicine 2021, 100, e26195. [Google Scholar] [CrossRef]
- Rabsilber, T.M.; Becker, K.A.; Frisch, I.B.; Auffarth, G.U. Anterior chamber depth in relation to refractive status measured with the Orbscan II Topography System. J. Cataract Refract. Surg. 2003, 29, 2115–2121. [Google Scholar] [CrossRef]
- Howe, K.; Clark, M.D.; Torroja, C.F.; Torrance, J.; Berthelot, C.; Muffato, M.; Collins, J.E.; Humphray, S.; McLaren, K.; Matthews, L.; et al. The zebrafish reference genome sequence and its relationship to the human genome. Nature 2013, 496, 498–503. [Google Scholar] [CrossRef]
- Nasiadka, A.; Clark, M.D. Zebrafish breeding in the laboratory environment. ILAR J. 2012, 53, 161–168. [Google Scholar] [CrossRef]
- Zhao, X.C.; Yee, R.W.; Norcom, E.; Burgess, H.; Avanesov, A.S.; Barrish, J.P.; Malicki, J. The zebrafish cornea: Structure and development. Investig. Ophthalmol. Vis. Sci. 2006, 47, 4341–4348. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Heur, M.; Jiao, S.; Schindler, S.; Crump, J.G. Regenerative potential of the zebrafish corneal endothelium. Exp. Eye Res. 2013, 106, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.Y.; Chiang, M.; Pardeshi, A.A.; Moghimi, S.; Varma, R. Deep neural network for scleral spur detection in anterior segment OCT images: The Chinese American eye study. Transl. Vis. Sci. Technol. 2020, 9, 18. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.H.; Devalla, S.K.; Ang, A.; Soh, Z.D.; Thiery, A.H.; Boote, C.; Cheng, C.Y.; Girard, M.J.A.; Koh, V. Deep learning algorithms to isolate and quantify the structures of the anterior segment in optical coherence tomography images. Br. J. Ophthalmol. 2021, 105, 1231–1237. [Google Scholar] [CrossRef] [PubMed]
- Richardson, R.; Tracey-White, D.; Webster, A.; Moosajee, M. The zebrafish eye—A paradigm for investigating human ocular genetics. Eye 2017, 31, 68–86. [Google Scholar] [CrossRef]
- Chhetri, J.; Jacobson, G.; Gueven, N. Zebrafish—On the move towards ophthalmological research. Eye 2014, 28, 367–380. [Google Scholar] [CrossRef]
- Link, B.A.; Gray, M.P.; Smith, R.S.; John, S.W. Intraocular pressure in zebrafish: Comparison of inbred strains and identification of a reduced melanin mutant with raised IOP. Investig. Ophthalmol. Vis. Sci. 2004, 45, 4415–4422. [Google Scholar] [CrossRef]
- Belovay, G.W.; Goldberg, I. The thick and thin of the central corneal thickness in glaucoma. Eye 2018, 32, 915–923. [Google Scholar] [CrossRef]
- Bajwa, A.; Burstein, E.; Grainger, R.M.; Netland, P.A. Anterior chamber angle in aniridia with and without glaucoma. Clin. Ophthalmol. 2019, 13, 1469. [Google Scholar] [CrossRef]
- Gestri, G.; Link, B.A.; Neuhauss, S.C. The visual system of zebrafish and its use to model human ocular diseases. Dev. Neurobiol. 2012, 72, 302–327. [Google Scholar] [CrossRef]
- Özcura, F.; Aydin, S.; Dayanir, V. Central corneal thickness and corneal curvature in pseudoexfoliation syndrome with and without glaucoma. J. Glaucoma 2011, 20, 410–413. [Google Scholar] [CrossRef] [PubMed]
- Chong, S.P.; Merkle, C.W.; Leahy, C.; Radhakrishnan, H.; Srinivasan, V.J. Quantitative microvascular hemoglobin mapping using visible light spectroscopic Optical Coherence Tomography. Biomed. Opt. Express 2015, 6, 1429–1450. [Google Scholar] [CrossRef] [PubMed]
- Collymore, C.; Tolwani, A.; Lieggi, C.; Rasmussen, S. Efficacy and safety of 5 anesthetics in adult zebrafish (Danio rerio). J. Am. Assoc. Lab. Anim. Sci. 2014, 53, 198–203. [Google Scholar] [PubMed]
- Gaertner, M.; Weber, A.; Cimalla, P.; Köttig, F.; Brand, M.; Koch, E. Towards a comprehensive eye model for zebrafish retinal imaging using full range spectral domain optical coherence tomography. In Proceedings of the Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XVIII, San Francisco, CA, USA, 3–5 February 2014; International Society for Optics and Photonics: Bellingham, DC, USA, 2014; Volume 8934, p. 89342. [Google Scholar]
- Turani, Z.; Fatemizadeh, E.; Xu, Q.; Daveluy, S.; Mehregan, D.; Avanaki, M.R.N. Refractive index correction in optical coherence tomography images of multilayer tissues. J. Biomed. Opt. 2018, 23, 070501. [Google Scholar] [CrossRef]
- Huang, Y.; Kang, J.U. Real-time reference A-line subtraction and saturation artifact removal using graphics processing unit for high-frame-rate Fourier-domain optical coherence tomography video imaging. Opt. Eng. 2012, 51, 073203. [Google Scholar] [CrossRef]
- Ramos-Soto, O.; Rodríguez-Esparza, E.; Pérez-Cisneros, M.; Balderas-Mata, S.E. Inner limiting membrane segmentation and surface visualization method on retinal OCT images. In Proceedings of the Medical Imaging 2021: Biomedical Applications in Molecular, Structural, and Functional Imaging, Online, 15–19 February 2021; International Society for Optics and Photonics: Bellingham, DC, USA, 2021; Volume 11600, p. 1160016. [Google Scholar]
- Reif, R.; Baran, U.; Wang, R.K. Motion artifact and background noise suppression on optical microangiography frames using a naïve Bayes mask. Appl. Opt. 2014, 53, 4164–4171. [Google Scholar] [CrossRef]
- Münch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and ring artifact removal with combined wavelet—Fourier filtering. Opt. Express 2009, 17, 8567–8591. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Wintz, P. Digital Image Processing; Number 13 in Applied Mathematics and Computation; Addison-Wesley Publishing Co., Inc.: Reading, MA, USA, 1977; p. 451. [Google Scholar]
- Farid, H. Blind inverse gamma correction. IEEE Trans. Image Process. 2001, 10, 1428–1433. [Google Scholar] [CrossRef]
- Iqbal, S.; Naqvi, S.S.; Khan, H.A.; Saadat, A.; Khan, T.M. G-Net Light: A Lightweight Modified Google Net for Retinal Vessel Segmentation. Photonics 2022, 9, 923. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, Z.; Li, Y. A Novel Intraretinal Layer Semantic Segmentation Method of Fundus OCT Images Based on the TransUNet Network Model. Photonics 2023, 10, 438. [Google Scholar] [CrossRef]
- Calderon-Auza, G.; Carrillo-Gomez, C.; Nakano, M.; Toscano-Medina, K.; Perez-Meana, H.; Gonzalez-H. Leon, A.; Quiroz-Mercado, H. A teleophthalmology support system based on the visibility of retinal elements using the CNNs. Sensors 2020, 20, 2838. [Google Scholar] [CrossRef] [PubMed]
- Elsawy, A.; Abdel-Mottaleb, M. PIPE-Net: A pyramidal-input-parallel-encoding network for the segmentation of corneal layer interfaces in OCT images. Comput. Biol. Med. 2022, 147, 105595. [Google Scholar] [CrossRef] [PubMed]
- He, F.; Chun, R.K.M.; Qiu, Z.; Yu, S.; Shi, Y.; To, C.H.; Chen, X. Choroid Segmentation of Retinal OCT Images Based on CNN Classifier and l2-lq Fitter. Comput. Math. Methods Med. 2021, 2021, 8882801. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the Computer Vision–ECCV 2022 Workshops, Tel Aviv, Israel, 23–27 October 2022; Part III. Springer: Berlin/Heidelberg, Germany, 2023; pp. 205–218. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Dev, S.; Manandhar, S.; Lee, Y.H.; Winkler, S. Multi-label cloud segmentation using a deep network. In Proceedings of the 2019 USNC-URSI Radio Science Meeting (Joint with AP-S Symposium), Atlanta, GA, USA, 7–12 July 2019; pp. 113–114. [Google Scholar]
- Li, J.; Wang, H.; Zhang, A.; Liu, Y. Semantic Segmentation of Hyperspectral Remote Sensing Images Based on PSE-UNet Model. Sensors 2022, 22, 9678. [Google Scholar] [CrossRef]
- Bilal, A.; Sun, G.; Mazhar, S.; Imran, A.; Latif, J. A Transfer Learning and U-Net-based automatic detection of diabetic retinopathy from fundus images. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2022, 10, 663–674. [Google Scholar] [CrossRef]
- Kashyap, R.; Nair, R.; Gangadharan, S.M.P.; Botto-Tobar, M.; Farooq, S.; Rizwan, A. Glaucoma Detection and Classification Using Improved U-Net Deep Learning Model. Healthcare 2022, 10, 2497. [Google Scholar] [CrossRef]
- Subramaniam, S.; Jayanthi, K.; Rajasekaran, C.; Kuchelar, R. Deep learning architectures for medical image segmentation. In Proceedings of the 2020 IEEE 33rd International Symposium on Computer-Based Medical Systems (CBMS), Rochester, MN, USA, 28–30 July 2020; pp. 579–584. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Chawla, B.; Swain, W.; Williams, A.L.; Bohnsack, B.L. Retinoic Acid Maintains Function of Neural Crest–Derived Ocular and Craniofacial Structures in Adult Zebrafish. Investig. Ophthalmol. Vis. Sci. 2018, 59, 1924–1935. [Google Scholar] [CrossRef]
- Kim, M.; Park, K.H.; Kim, T.W.; Kim, D.M. Changes in anterior chamber configuration after cataract surgery as measured by anterior segment optical coherence tomography. Korean J. Ophthalmol. 2011, 25, 77–83. [Google Scholar] [CrossRef]
- Pavlin, C.; Ritch, R.; Foster, F. Ultrasound biomicroscopy in plateau iris syndrome. Am. J. Ophthalmol. 1992, 113, 390–395. [Google Scholar] [CrossRef]
- Riva, I.; Micheletti, E.; Oddone, F.; Bruttini, C.; Montescani, S.; De Angelis, G.; Rovati, L.; Weinreb, R.N.; Quaranta, L. Anterior chamber angle assessment techniques: A review. J. Clin. Med. 2020, 9, 3814. [Google Scholar] [CrossRef] [PubMed]
- Goldsmith, J.A.; Li, Y.; Chalita, M.R.; Westphal, V.; Patil, C.A.; Rollins, A.M.; Izatt, J.A.; Huang, D. Anterior chamber width measurement by high-speed optical coherence tomography. Ophthalmology 2005, 112, 238–244. [Google Scholar] [CrossRef] [PubMed]
- Weisberg, S. Applied Linear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]

| Zebrafish Number Set | Manual ACW (mm) | Manual CCT (m) | Automated CCT (m) | Automated CC (Coefficient) |
|---|---|---|---|---|
| 1 | 1.25 | 34.51 | 39.27 | −0.0009 |
| 2 | 1.28 | 35.70 | 41.65 | −0.0009 |
| 3 | 1.46 | 36.89 | 42.84 | −0.0007 |
| 4 | 1.46 | 32.12 | 39.27 | −0.0007 |
| 5 | 1.29 | 36.89 | 42.84 | −0.0008 |
| 6 | 1.41 | 29.75 | 30.94 | −0.0007 |
| 7 | 1.34 | 27.37 | 32.13 | −0.0007 |
| 8 | 1.46 | 28.56 | 33.32 | −0.0008 |
| 9 | 1.35 | 28.56 | 34.51 | −0.0008 |
| 10 | 1.58 | 27.37 | 36.89 | −0.0006 |
| Mean ± SD | 1.38 ± 0.10 | 31.77 ± 3.92 | 37.36 ± 4.45 | −0.00076 ± 0.000096 |
| Zebrafish | Manual ACA () | Automated ACA () | ||
|---|---|---|---|---|
| Number Set | Left Side | Right Side | Left Side | Right Side |
| 1 | 22.95 | 24.33 | 22.45 | 23.01 |
| 2 | 23.04 | 24.38 | 21.77 | 22.62 |
| 3 | 14.27 | 21.96 | 13.20 | 20.56 |
| 4 | 13.57 | 22.44 | 12.60 | 19.47 |
| 5 | 23.25 | 22.51 | 21.13 | 21.02 |
| 6 | 14.26 | 21.86 | 16.98 | 20.16 |
| 7 | 18.67 | 22.58 | 20.10 | 21.20 |
| 8 | 15.85 | 20.83 | 18.37 | 19.02 |
| 9 | 17.93 | 24.68 | 15.34 | 21.45 |
| 10 | 20.71 | 22.46 | 19.45 | 20.12 |
| Mean ± SD | 18.45 ± 3.87 | 22.80 ± 1.25 | 18.14 ± 3.50 | 20.86 ± 1.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Soto, O.; Jo, H.C.; Zawadzki, R.J.; Kim, D.Y.; Balderas-Mata, S.E. Automated Segmentation and Morphometry of Zebrafish Anterior Chamber OCT Scans. Photonics 2023, 10, 957. https://doi.org/10.3390/photonics10090957
Ramos-Soto O, Jo HC, Zawadzki RJ, Kim DY, Balderas-Mata SE. Automated Segmentation and Morphometry of Zebrafish Anterior Chamber OCT Scans. Photonics. 2023; 10(9):957. https://doi.org/10.3390/photonics10090957
Chicago/Turabian StyleRamos-Soto, Oscar, Hang Chan Jo, Robert J. Zawadzki, Dae Yu Kim, and Sandra E. Balderas-Mata. 2023. "Automated Segmentation and Morphometry of Zebrafish Anterior Chamber OCT Scans" Photonics 10, no. 9: 957. https://doi.org/10.3390/photonics10090957
APA StyleRamos-Soto, O., Jo, H. C., Zawadzki, R. J., Kim, D. Y., & Balderas-Mata, S. E. (2023). Automated Segmentation and Morphometry of Zebrafish Anterior Chamber OCT Scans. Photonics, 10(9), 957. https://doi.org/10.3390/photonics10090957






