Prediction of Shock Wave Velocity Induced by a Combined Millisecond and Nanosecond Laser Based on Convolution Neural Network
Abstract
1. Introduction
2. Material and Method
2.1. Experiment
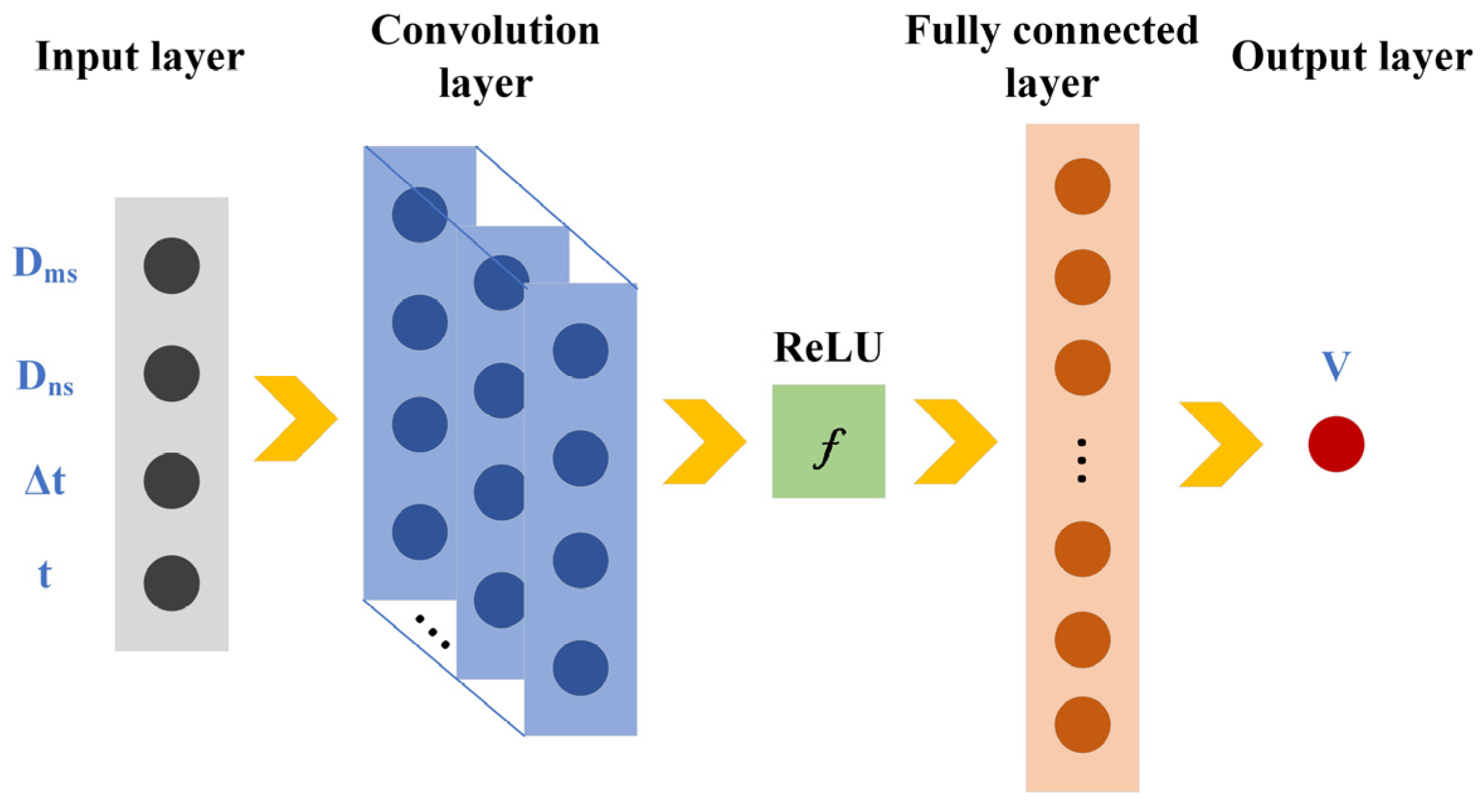
2.2. CNN Model
3. Results and Discussion
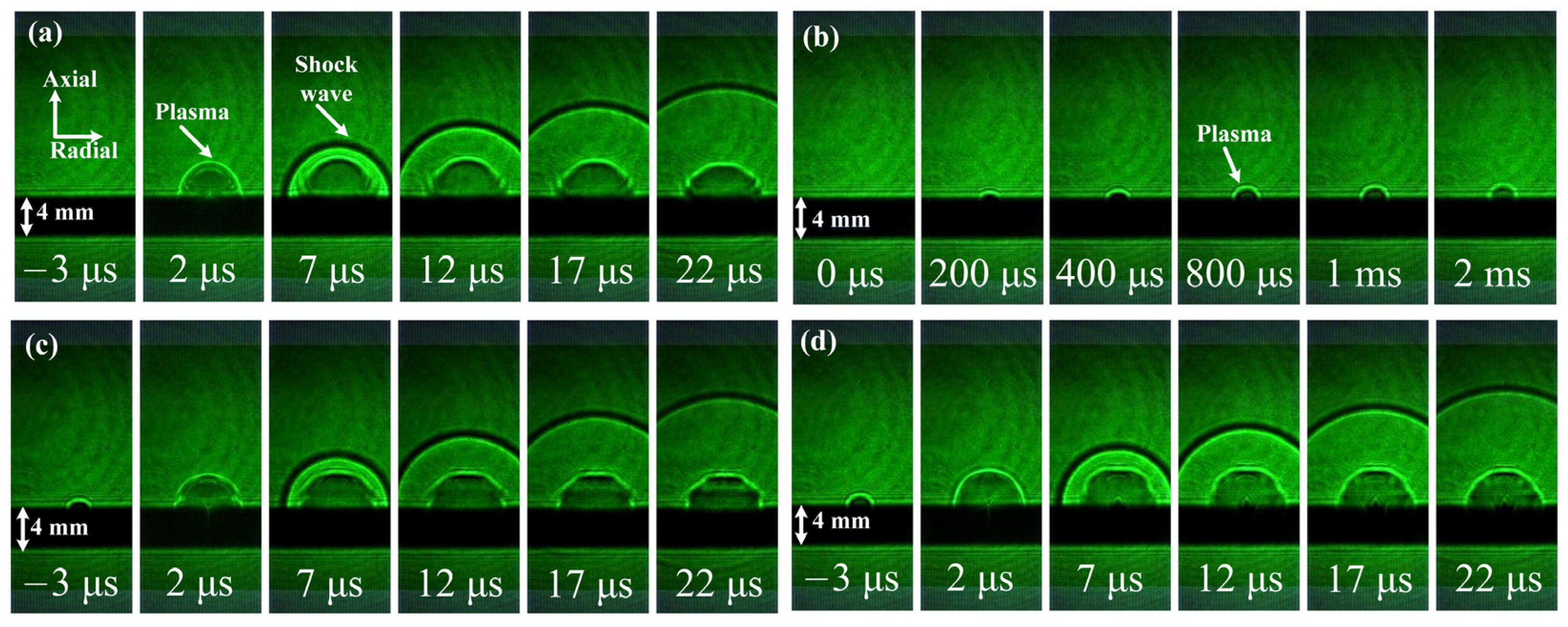
3.1. Experimental Shock-Wave Velocity
3.2. CNN Prediction for Shock-Wave Velocity
4. Conclusions
- (1)
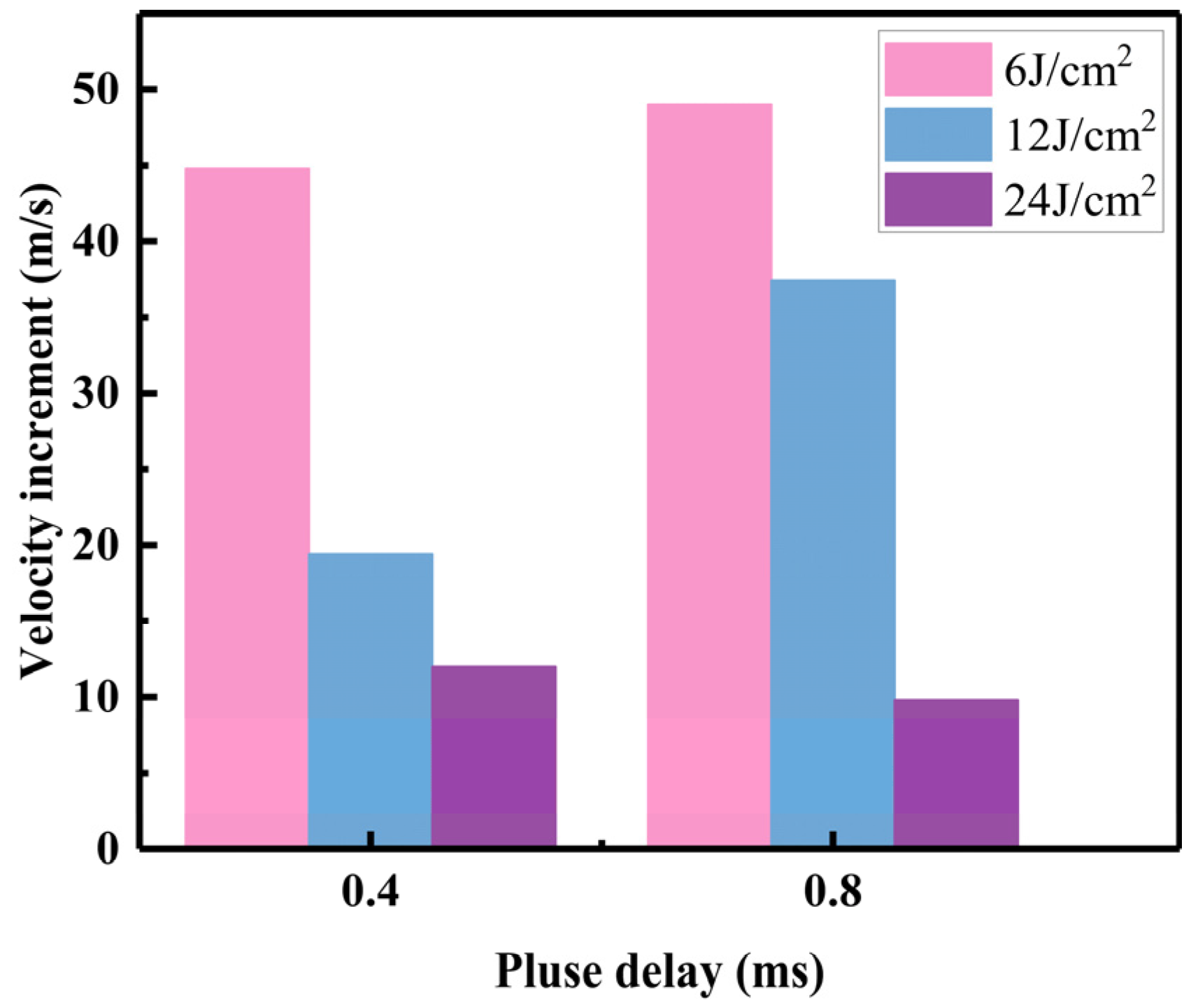
- Compared with the single ns laser, the CPL can induce shock-wave acceleration. Furthermore, the CPL-induced shock-wave velocity increment is inversely proportional to the energy density of the ns laser.
- (2)
- The predicted shock-wave velocity obtained by the CNN model fits well with the experimental value. The R2, RMSE and MAE of the CNN model on the test data set are 0.9865, 3.54 and 3.01, respectively. It is indicated that the CNN model has a high reliability for predicting the shock-wave velocity.
- (3)
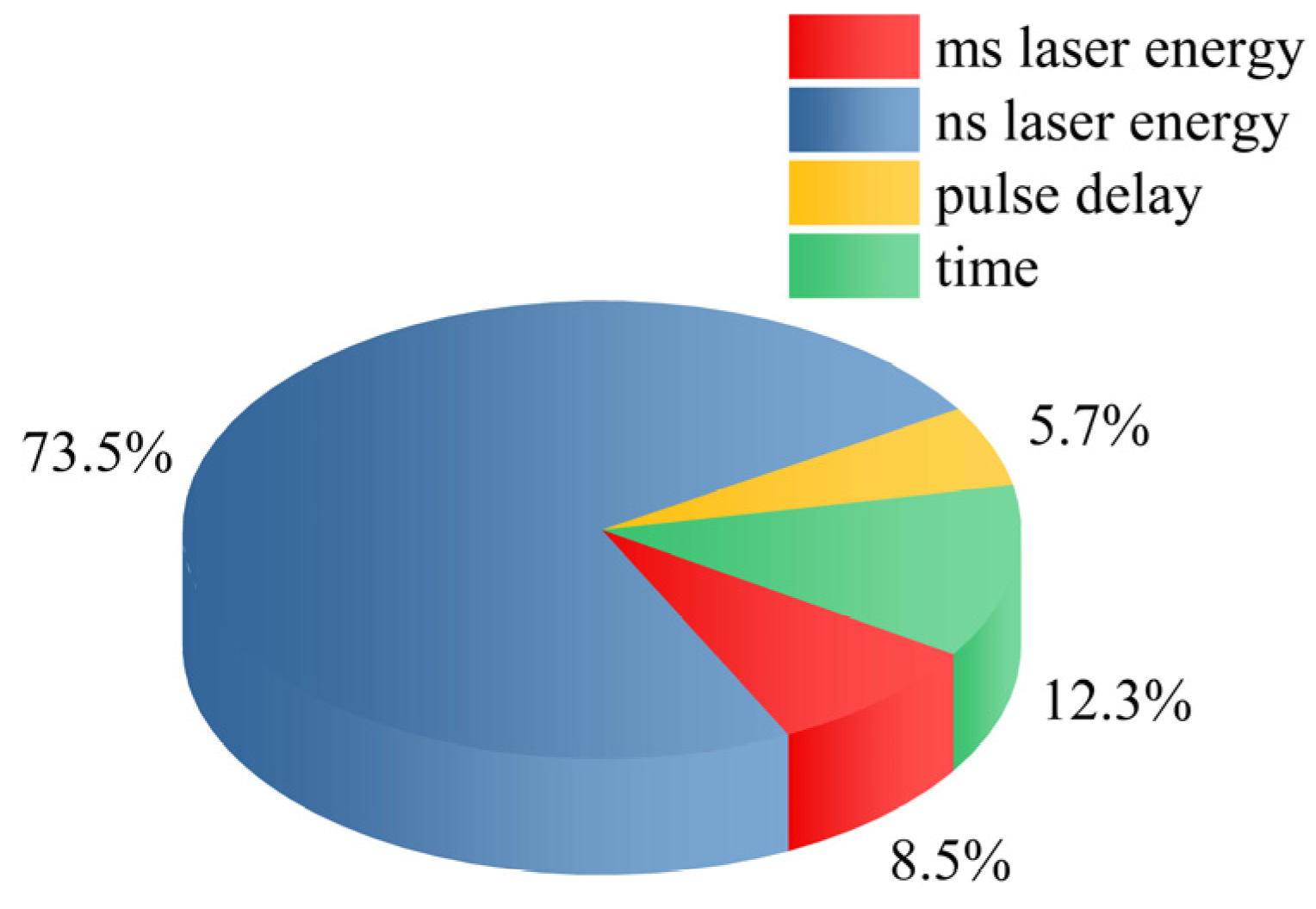
- In order to obtain a higher shock-wave velocity, the ranking importance of the input parameters’ effect on the shock-wave velocity is: ns laser energy > ms laser energy > pulse delay. This provides a theoretical basis when setting ms-ns CPL parameters with a higher shock-wave velocity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phipps, C.R.; Baker, K.L.; Libby, S.B.; Liedahl, D.A.; Olivier, S.S.; Pleasance, L.D.; Rubenchik, A.; Trebes, J.E.; George, E.V.; Marcovici, B.; et al. Removing orbital debris with lasers. Adv. Space Res. 2012, 49, 1283–1300. [Google Scholar] [CrossRef]
- Shen, S.; Jin, X.; Hao, C. Cleaning space debris with a space-based laser system. Chin. J. Aeronaut. 2014, 27, 805–811. [Google Scholar] [CrossRef]
- Nishida, S.I.; Kawamoto, S.; Okawa, Y.; Terui, F.; Kitamura, S. Space debris removal system using a small satellite. Acta Astronaut. 2009, 65, 95–102. [Google Scholar] [CrossRef]
- Pasley, J.; Bush, I.A.; Robinson, A.P.; Rajeev, P.P.; Mondal, S.; Lad, A.D.; Ahmed, S.; Narayanan, V.; Kumar, G.R.; Kingham, R.J. Generation of shock waves in dense plasmas by high-intensity laser pulses. Nukleonika 2015, 60, 193–198. [Google Scholar] [CrossRef][Green Version]
- Garbaruk, A.V.; Gritskevich, M.S.; Kalmykov, S.G.; Sasin, M.E. Computational simulation of laser plasma emission with shock-wave-affected density distribution in the gas-jet target. Technol. Phys. Lett. 2016, 42, 993–996. [Google Scholar] [CrossRef]
- Ukai, T.; Kontis, K.; Yang, L. Flow structure generated by laser-induced blast wave propagation through the boundary layer of a flat plate. Aerosp. Sci. Technol. 2018, 78, 569–573. [Google Scholar] [CrossRef]
- Yoh, J.J.; Lee, H.; Choi, J.; Lee, K.; Kim, K. Ablation-induced explosion of metal using a high-power Nd: YAG laser. J. Appl. Phys. 2008, 103, 043511. [Google Scholar] [CrossRef]
- Gregorčič, P.; Možina, J. High-speed two-frame shadowgraphy for velocity measurements of laser-induced plasma and shockwave evolution. Opt. Lett. 2011, 36, 2782. [Google Scholar] [CrossRef]
- Cao, S.; Su, M.; Min, Q.; Sun, D.; Ma, P.; Wang, K.; Jiao, Z.; Dong, C. Dynamics and density distribution of laser-produced Al plasmas using optical interferometry and optical emission spectroscopy. J. Quant. Spectrosc. Radiat. Transf. 2019, 225, 69–75. [Google Scholar] [CrossRef]
- Kraft, S.; Schille, J.; Mauersberger, S.; Schneider, L.; Loeschner, U. Pump-probe imaging for process control and optimization in high-speed laser micro machining. In Proceedings of the Laser-based Micro- and Nanoprocessing XIV, San Francisco, CA, USA, 12 March 2020. [Google Scholar]
- Radziejewska, J.; Strzelec, M.; Ostrowski, R.; Sarzyński, A. Experimental investigation of shock wave pressure induced by a ns laser pulse under varying confined regimes. Opt. Laser. Eng. 2020, 126, 105913. [Google Scholar] [CrossRef]
- Frster, D.J.; Faas, S.; Weber, R.; Thomas, G. Thrust enhancement and propellant conservation for laser propulsion using ultra-short double pulses. Appl. Surf. Sci. 2020, 510, 145391. [Google Scholar] [CrossRef]
- Guthikonda, N.; Manikanta, E.; Chelikani, L.; Shiva, S.S.; Harsha, S.S.; Ikkurthi, V.R.; Kiran, P.P. Interaction of two counterpropagating laser induced plasmas and shock waves in air. Phy. Plasma. 2020, 27, 023107. [Google Scholar] [CrossRef]
- Cao, S.; Su, M.; Ma, P.; Wang, K.; Dong, C. Expansion dynamics and emission characteristics of nanosecond–picosecond collinear double pulse laser-induced Al plasma in air. J. Quant. Spectrosc. Radiat. Transf. 2019, 242, 106773. [Google Scholar] [CrossRef]
- Cao, S.; Su, M.; Liu, J.; Min, Q.; Dong, C. Expansion dynamics and compression layer in collinear double-pulse laser produced plasmas in a vacuum. Phys. Plasmas 2020, 27, 052101. [Google Scholar] [CrossRef]
- Smijesh, N.; Rao, K.H.; Chetty, D.; Litvinyuk, I.V.; Sang, R.T. Plasma plumes produced by laser ablation of Al with single and double pulse schemes. Opt. Lett. 2017, 43, 6081–6084. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Qi, H.; Zeng, X.; Chen, A.; Gao, X.; Jin, M. Time-resolved spectroscopy of collinear femtosecond and nanosecond dual-pulse laser-induced Cu plasmas. Plasma Sci. Technol. 2021, 23, 121–127. [Google Scholar] [CrossRef]
- Jia, X.; Chen, Y.; Zhu, G.; Wang, H.; Zhu, X. Experimental study on the optimum matching of CW-nanosecond combined pulse laser drilling. Appl. Opt. 2019, 58, 9105. [Google Scholar] [CrossRef]
- Pan, Y.; Lv, X.; Zhang, H.; Chen, J.; Han, B.; Shen, Z.; Lu, J.; Ni, X. Millisecond laser machining of transparent materials assisted by a nanosecond laser with different delays. Opt. Lett. 2016, 41, 2807–2810. [Google Scholar] [CrossRef]
- Yuan, B.; Zhang, Y.; Zhang, W.; Dong, Y.; Jin, G. The Effect of Spot Size Combination Mode on Ablation Morphology of Aluminum Alloy by Millisecond-Nanosecond Combined-Pulse Laser. Materials 2018, 11, 1419. [Google Scholar] [CrossRef]
- Yuan, B.S.; Wang, D.; Dong, Y.; Zhang, W.; Jin, G.Y. Experimental study of the morphological evolution of the millisecond–nanosecond combined-pulse laser ablation of aluminum alloy. Appl. Opt. 2018, 57, 5743–5748. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Zhou, Y.; Yuan, B.; Cai, J.; Jin, G. The acceleration mechanism of shock wave induced by millisecond-nanosecond combined-pulse laser on silicon. Plasma Sci. Technol. 2021, 23, 055507. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Li, Y.; Jin, G. The Acceleration Phenomenon of Shock Wave Induced by Nanosecond Laser Irradiating Silicon Assisted by Millisecond Laser. Photonics 2023, 10, 260. [Google Scholar] [CrossRef]
- Wu, J.; Li, Y.; Jibin, Z.; Qiao, H.; Yang, Y. Prediction of residual stress induced by laser shock processing based on artificial neural networks for FGH4095 superalloy. Mater. Lett. 2021, 286, 129269. [Google Scholar] [CrossRef]
- Wu, J.; Xu, Z.; Qiao, H.; Zhao, J.; Huang, Z. Mechanical properties prediction of superalloy FGH4095 treated by laser shock processing based on machine learning. Mater. Lett. 2021, 297, 129970. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Z.; Qiao, H.; Zhao, Y.; Li, J.; Zhao, J. Artificial neural network approach for mechanical properties prediction of TC4 titanium alloy treated by laser shock processing. Opt. Laser Technol. 2021, 143, 107385. [Google Scholar] [CrossRef]
- Matsui, K.; Shimano, T.; Ofosu, J.A.; Komurasaki, K.; Schoenherr, T.; Koizumi, H. Accurate propagation velocity measurement of laser supported detonation waves. Vacuum 2016, 136, 171–176. [Google Scholar] [CrossRef]
- András, F.; György, C.; András, H. A Convolutional Neural Network with a Wave-Based Convolver. Electronics 2023, 12, 1126. [Google Scholar]
- Xing, J.; Xu, J. An Improved Convolutional Neural Network for Recognition of Incipient Faults. IEEE Sens. J. 2022, 22, 16314–16322. [Google Scholar] [CrossRef]



| Laser Parameters | Value |
|---|---|
| Laser wavelength | 1064 nm |
| Pulse width for ms laser | 1 ms |
| Pulse width for ns laser | 10 ns |
| Spot diameter for ms laser | 1.3 mm |
| Spot diameter for ns laser | 1 mm |
| Energy density of ms laser | 226.13 J/cm2 |
| Energy density of ns laser | 6, 12 and 24 J/cm2 |
| Repetition rate | 1 Hz |
| Condition Number | ns Laser Energy Density Dns (J/cm2) | ms Laser Energy Density Dms (J/cm2) | Pulse Delay Δt (ms) |
|---|---|---|---|
| 1 | 6 | 0 | 0 |
| 2 | 6 | 226.13 | 0.4 |
| 3 | 6 | 226.13 | 0.8 |
| 4 | 12 | 0 | 0 |
| 5 | 12 | 226.13 | 0.4 |
| 6 | 12 | 226.13 | 0.8 |
| 7 | 24 | 0 | 0 |
| 8 | 24 | 226.13 | 0.4 |
| 9 | 24 | 226.13 | 0.8 |
| Training Data | Test Data | ||||
|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE |
| 0.9912 | 4.18 | 3.27 | 0.9865 | 3.54 | 3.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhang, W.; Li, Y.; Jin, G. Prediction of Shock Wave Velocity Induced by a Combined Millisecond and Nanosecond Laser Based on Convolution Neural Network. Photonics 2023, 10, 1034. https://doi.org/10.3390/photonics10091034
Li J, Zhang W, Li Y, Jin G. Prediction of Shock Wave Velocity Induced by a Combined Millisecond and Nanosecond Laser Based on Convolution Neural Network. Photonics. 2023; 10(9):1034. https://doi.org/10.3390/photonics10091034
Chicago/Turabian StyleLi, Jingyi, Wei Zhang, Ye Li, and Guangyong Jin. 2023. "Prediction of Shock Wave Velocity Induced by a Combined Millisecond and Nanosecond Laser Based on Convolution Neural Network" Photonics 10, no. 9: 1034. https://doi.org/10.3390/photonics10091034
APA StyleLi, J., Zhang, W., Li, Y., & Jin, G. (2023). Prediction of Shock Wave Velocity Induced by a Combined Millisecond and Nanosecond Laser Based on Convolution Neural Network. Photonics, 10(9), 1034. https://doi.org/10.3390/photonics10091034




