Nonlocal Soft Plasmonics in Planar Homogeneous Multilayers
Abstract
:1. Introduction
2. Methodology
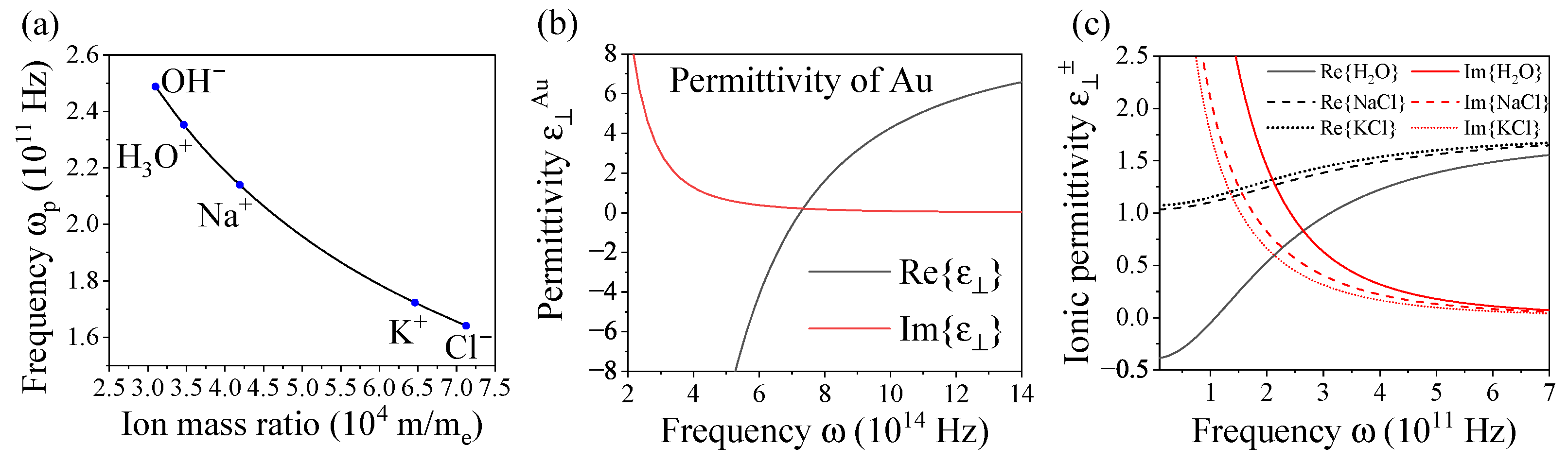
2.1. Classical Soft Plasmonics—General Characteristics of Ionic Systems
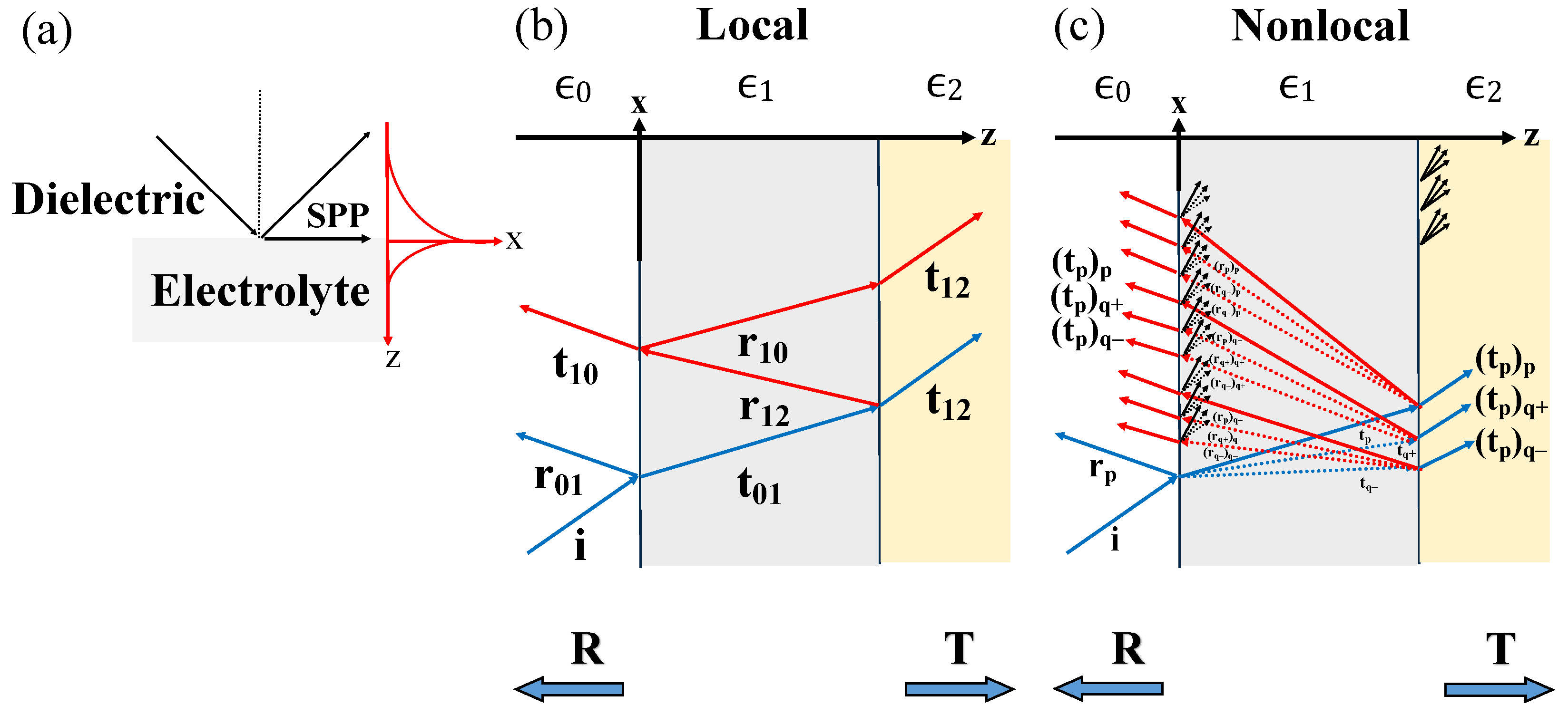
2.2. Nonlocal Interactions in Dielectric-Electrolyte Multilayered Systems
3. Results and Discussion
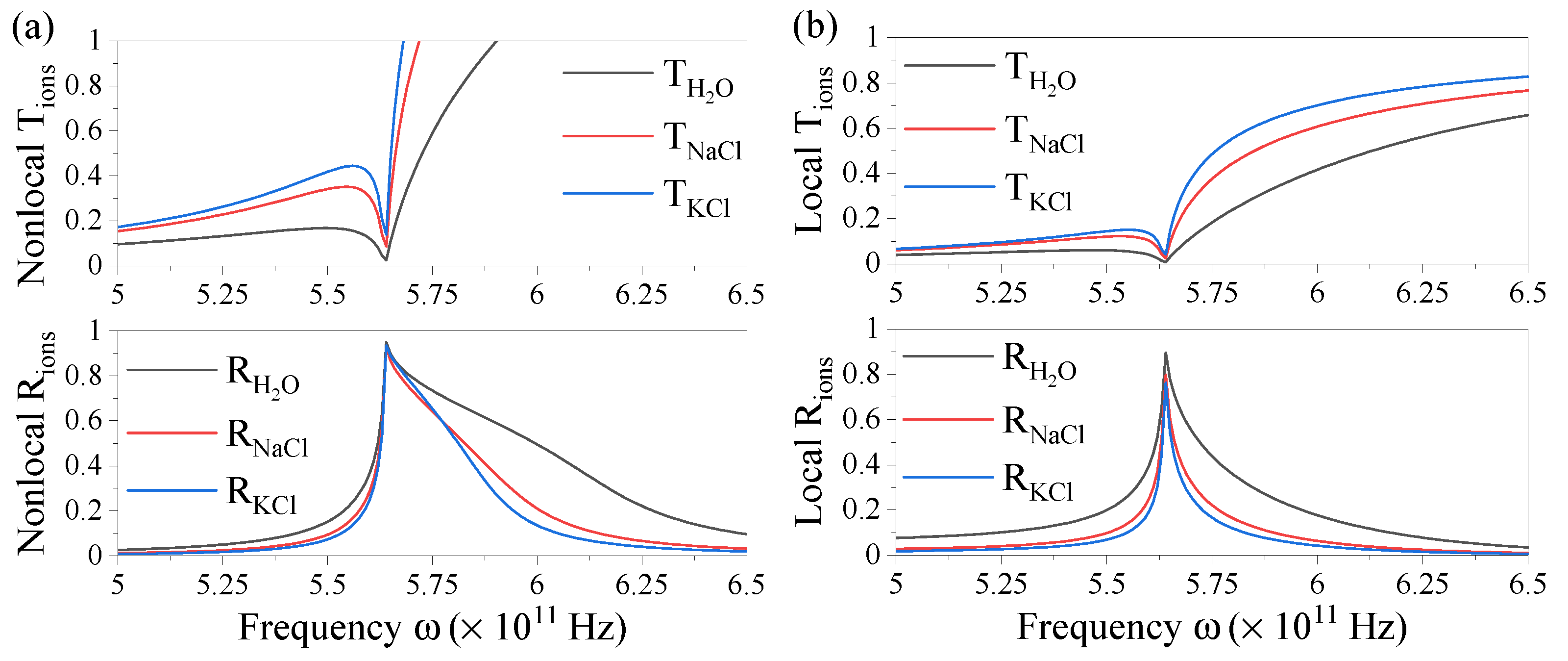
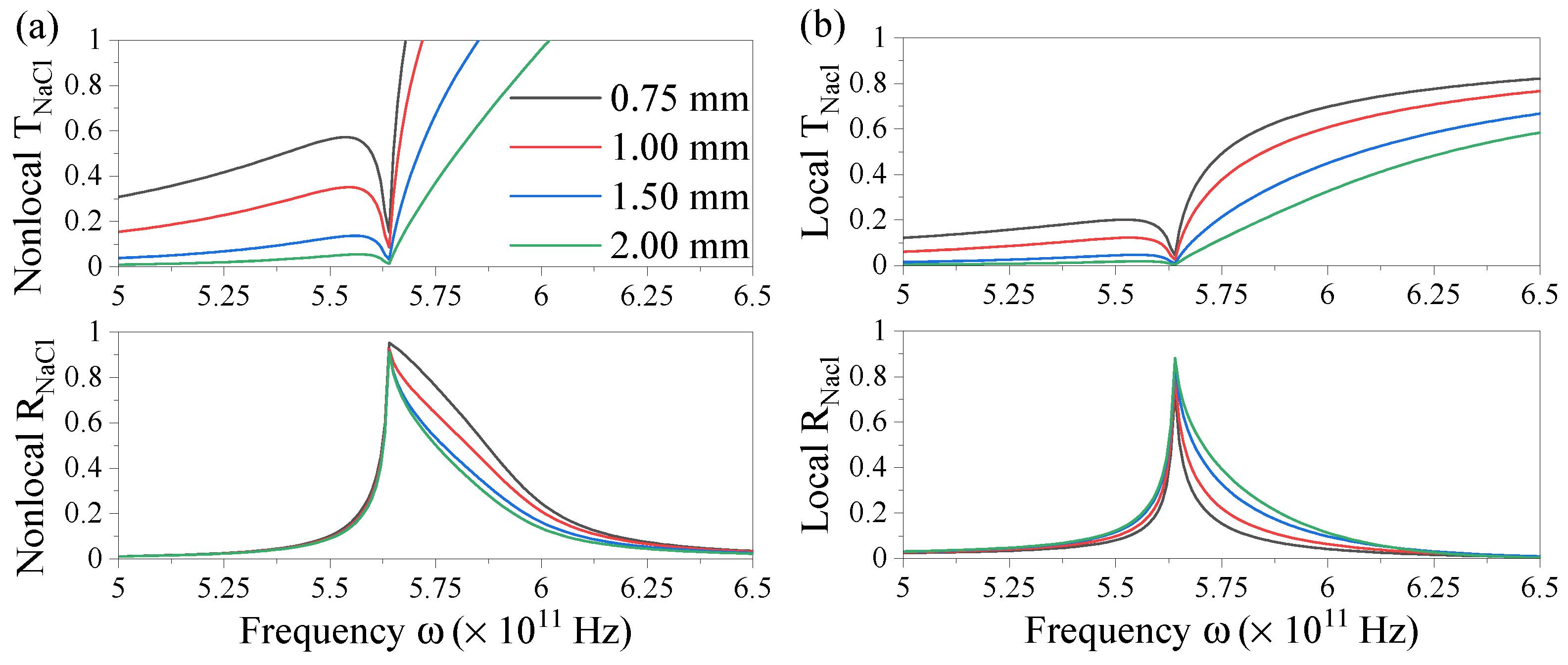
3.1. Nonlocal Optical Coefficients for Finite Multilayers
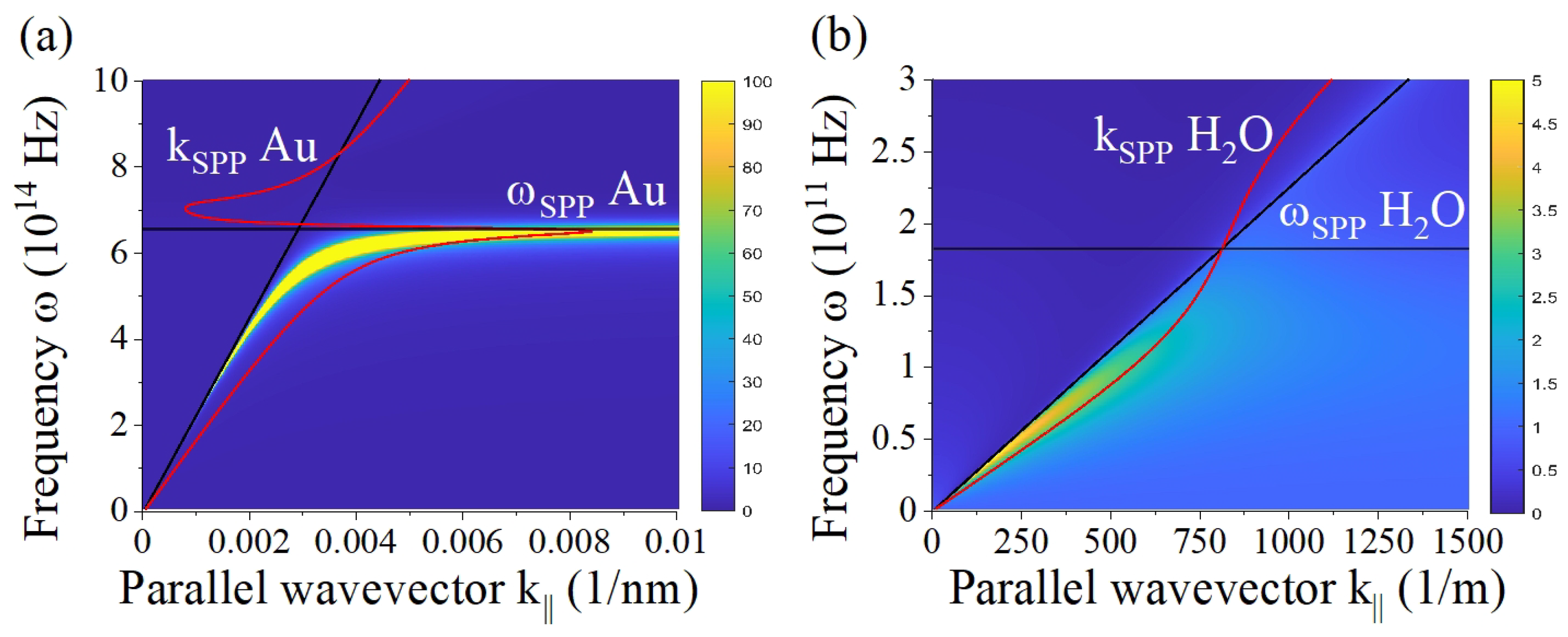
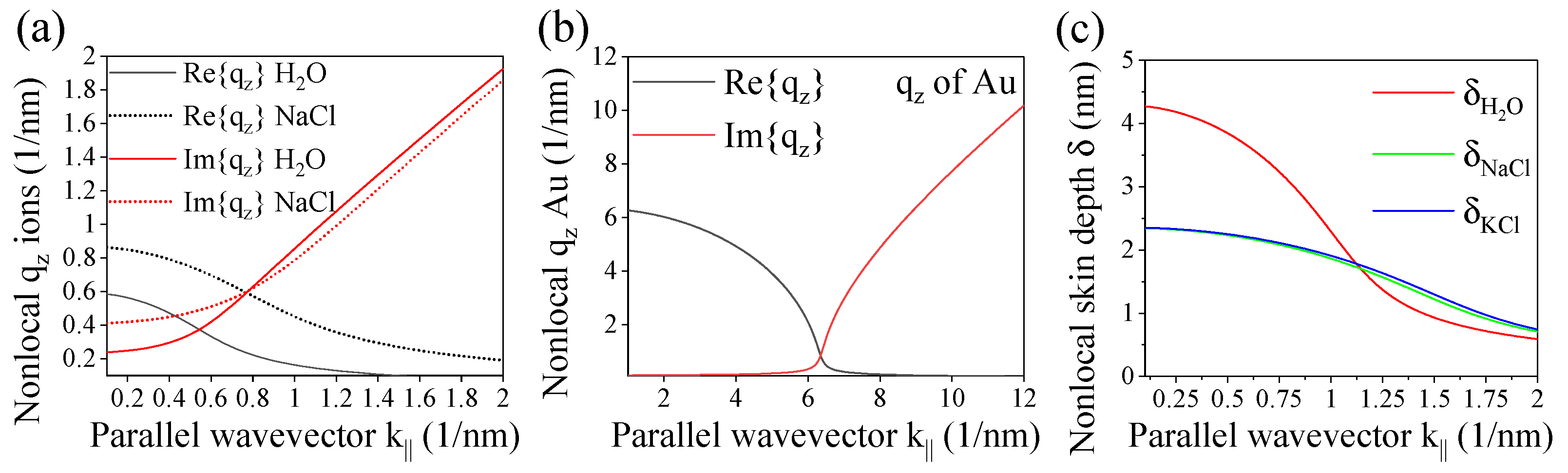
3.2. Evaluating Three-Layer Systems
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Nonlocal Function Fl±
Appendix B. Nonlocal Transmission and Reflection Coefficients
References
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Tang, B.; Guo, Z.; Jin, G. Polarization-controlled and symmetry-dependent multiple plasmon-induced transparency in graphene-based metasurfaces. Opt. Express 2022, 30, 35554–35566. [Google Scholar] [CrossRef] [PubMed]
- Lai, R.; Shi, P.; Yi, Z.; Li, H.; Yi, Y. Triple-Band Surface Plasmon Resonance Metamaterial Absorber Based on Open-Ended Prohibited Sign Type Monolayer Graphene. Micromachines 2023, 14, 953. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; Wu, P.; Wang, H.; Jiang, S.; Huang, M.; Lei, D.; Wu, F. Multimode tunable terahertz absorber based on a quarter graphene disk structure. Results Phys. 2023, 48, 106420. [Google Scholar] [CrossRef]
- Chen, Z.; Cai, P.; Wen, Q.; Chen, H.; Tang, Y.; Yi, Z.; Wei, K.; Li, G.; Tang, B.; Yi, Y. Graphene Multi-Frequency Broadband and Ultra-Broadband Terahertz Absorber Based on Surface Plasmon Resonance. Electronics 2023, 12, 2655. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Chamanzar, M.; Adibi, A. Compact on-chip plasmonic light concentration based on a hybrid photonic-plasmonic structure. Opt. Express 2013, 21, 1898. [Google Scholar] [CrossRef] [PubMed]
- Kauranen, M.; Zayats, A.V. Nonlinear plasmonics. Nat. Photonics 2012, 6, 737–748. [Google Scholar] [CrossRef]
- Krasavin Alexey, V.; Pavel, G.; Zayats Anatoly, V. Free-electron Optical Nonlinearities in Plasmonic Nanostructures: A Review of the Hydrodynamic Description. Laser Photonics Rev. 2018, 12, 1700082. [Google Scholar] [CrossRef]
- Mesch, M.; Metzger, B.; Hentschel, M.; Giessen, H. Nonlinear Plasmonic Sensing. Nano Lett. 2016, 16, 3155–3159. [Google Scholar] [CrossRef] [PubMed]
- Beer, S.; Gour, J.; Alberucci, A.; David, C.; Nolte, S.; Zeitner, U.D. Second harmonic generation under doubly resonant lattice plasmon excitation. Opt. Express 2022, 30, 40884. [Google Scholar] [CrossRef]
- Daryakar, N.; David, C. Thin Films of Nonlinear Metallic Amorphous Composites. Nanomaterials 2022, 12, 3359. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, M.; Zhou, X.; Mi, X.; Chen, H.; Zhang, B.; Fu, Z.; Zhang, Z.; Zheng, H. Plasmon-Assisted Self-Encrypted All-Optical Memory. Adv. Funct. Mater. 2022, 33, 2208561. [Google Scholar] [CrossRef]
- Taylor, A.B.; Michaux, P.; Mohsin, A.S.M.; Chon, J.W.M. Electron-beam lithography of plasmonic nanorod arrays for multilayered optical storage. Opt. Express 2014, 22, 13234. [Google Scholar] [CrossRef]
- Green, M.A.; Pillai, S. Harnessing plasmonics for solar cells. Nat. Photonics 2012, 6, 130–132. [Google Scholar] [CrossRef]
- Enrichi, F.; Quandt, A.; Righini, G. Plasmonic enhanced solar cells: Summary of possible strategies and recent results. Renew. Sustain. Energy Rev. 2018, 82, 2433–2439. [Google Scholar] [CrossRef]
- David, C.; Koduvelikulathu, L.J.; Kopecek, R. Comparative Simulations of Conductive Nitrides as Alternative Plasmonic Nanostructures for Solar Cells. Energies 2021, 14, 4236. [Google Scholar] [CrossRef]
- Fusco, Z.; Catchpole, K.; Beck, F.J. Investigation of the mechanisms of plasmon-mediated photocatalysis: Synergistic contribution of near-field and charge transfer effects. J. Mater. Chem. C 2022, 10, 7511–7524. [Google Scholar] [CrossRef]
- Taylor, A.B.; Zijlstra, P. Single-Molecule Plasmon Sensing: Current Status and Future Prospects. ACS Sens. 2017, 2, 1103–1122. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.L.; Yang, Y.; Wang, S.; Liu, X.W. Surface Plasmon Resonance Microscopy: From Single-Molecule Sensing to Single-Cell Imaging. Angew. Chem. Int. Ed. 2020, 59, 1776–1785. [Google Scholar] [CrossRef] [PubMed]
- Sharma, B.; Frontiera, R.R.; Henry, A.I.; Ringe, E.; Duyne, R.P.V. SERS: Materials, applications, and the future. Mater. Today 2012, 15, 16–25. [Google Scholar] [CrossRef]
- Schlücker, S. Surface-Enhanced Raman Spectroscopy: Concepts and Chemical Applications. Angew. Chem. Int. Ed. 2014, 53, 4756–4795. [Google Scholar] [CrossRef]
- Stockman, M.I.; Kneipp, K.; Bozhevolnyi, S.I.; Saha, S.; Dutta, A.; Ndukaife, J.; Kinsey, N.; Reddy, H.; Guler, U.; Shalaev, V.M.; et al. Roadmap on plasmonics. J. Opt. 2018, 20, 043001. [Google Scholar] [CrossRef]
- Rezaei, S.D.; Dong, Z.; Chan, J.Y.E.; Trisno, J.; Ng, R.J.H.; Ruan, Q.; Qiu, C.W.; Mortensen, N.A.; Yang, J.K. Nanophotonic Structural Colors. ACS Photonics 2020, 8, 18–33. [Google Scholar] [CrossRef]
- García de Abajo, F.J. Nonlocal Effects in the Plasmons of Strongly Interacting Nanoparticles, Dimers, and Waveguides. J. Phys. Chem. C 2008, 112, 17983–17987. [Google Scholar] [CrossRef]
- Scholl, J.A.; Koh, A.L.; Dionne, J.A. Quantum plasmon resonances of individual metallic nanoparticles. Nature 2012, 483, 421–427. [Google Scholar] [CrossRef] [PubMed]
- David, C.; García de Abajo, F.J. Spatial Nonlocality in the Optical Response of Metal Nanoparticles. J. Phys. Chem. C 2011, 115, 19470–19475. [Google Scholar] [CrossRef]
- Raza, S.; Stenger, N.; Kadkhodazadeh, S.; Fischer, S.V.; Kostesha, N.; Jauho, A.P.; Burrows, A.; Wubs, M.; Mortensen, N.A. Blueshift of the surface plasmon resonance in silver nanoparticles studied with EELS. Nanophotonics 2013, 2, 131. [Google Scholar] [CrossRef]
- Raza, S.; Bozhevolnyi, S.I.; Wubs, M.; Mortensen, N.A. Nonlocal optical response in metallic nanostructures. J. Phys. Cond. Matter. 2015, 27, 183204. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Domínguez, A.I.; Wiener, A.; García-Vidal, F.J.; Maier, S.A.; Pendry, J.B. Transformation-Optics Description of Nonlocal Effects in Plasmonic Nanostructures. Phys. Rev. Lett. 2012, 108, 106802. [Google Scholar] [CrossRef] [PubMed]
- Zuloaga, J.; Prodan, E.; Nordlander, P. Quantum Description of the Plasmon Resonances of a Nanoparticle Dimer. Nano Lett. 2009, 9, 887–891. [Google Scholar] [CrossRef] [PubMed]
- Ciracì, C.; Hill, R.T.; Mock, J.J.; Urzhumov, Y.; Fernández-Domínguez, A.I.; Maier, S.A.; Pendry, J.B.; Chilkoti, A.; Smith, D.R. Probing the Ultimate Limits of Plasmonic Enhancement. Science 2012, 337, 1072–1074. [Google Scholar] [CrossRef] [PubMed]
- Toscano, G.; Straubel, J.; Kwiatkowski, A.; Rockstuhl, C.; Evers, F.; Xu, H.; Mortensen, N.A.; Wubs, M. Resonance shifts and spill-out effects in self-consistent hydrodynamic nanoplasmonics. Nat. Commun. 2015, 6, 7132. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Esteban, R.; Borisov, A.G.; Baumberg, J.J.; Nordlander, P.; Lezec, H.J.; Aizpurua, J.; Crozier, K.B. Quantum mechanical effects in plasmonic structures with subnanometre gaps. Nat. Commun. 2016, 7, 11495. [Google Scholar] [CrossRef] [PubMed]
- Wiener, A.; Fernández-Domínguez, A.I.; Horsfield, A.P.; Pendry, J.B.; Maier, S.A. Nonlocal Effects in the Nanofocusing Performance of Plasmonic Tips. Nano Lett. 2012, 12, 3308–3314. [Google Scholar] [CrossRef]
- David, C.; Christensen, J.; Mortensen, N.A. Spatial dispersion in two-dimensional plasmonic crystals: Large blueshifts promoted by diffraction anomalies. Phys. Rev. B 2016, 94, 165410. [Google Scholar] [CrossRef]
- Mortensen, N.A.; Raza, S.; Wubs, M.; Søndergaard, T.; Bozhevolnyi, S.I. A generalized non-local optical response theory for plasmonic nanostructures. Nat. Commun. 2014, 5, 3809. [Google Scholar] [CrossRef] [PubMed]
- Raza, S.; Wubs, M.; Bozhevolnyi, S.I.; Mortensen, N.A. Nonlocal study of ultimate plasmon hybridization. Opt. Lett. 2015, 40, 839–842. [Google Scholar] [CrossRef] [PubMed]
- Mortensen, N.A. Mesoscopic electrodynamics at metal surfaces. Nanophotonics 2021, 10, 2563–2616. [Google Scholar] [CrossRef]
- Kolle, M.; Lee, S. Progress and Opportunities in Soft Photonics and Biologically Inspired Optics. Adv. Mater. 2017, 30, 1702669. [Google Scholar] [CrossRef]
- van der Gucht, J. Grand Challenges in Soft Matter Physics. Front. Phys. 2018, 6, 87. [Google Scholar] [CrossRef]
- Jacak, J.; Jacak, W. Plasmons and Plasmon–Polaritons in Finite Ionic Systems: Toward Soft-Plasmonics of Confined Electrolyte Structures. Appl. Sci. 2019, 9, 1159. [Google Scholar] [CrossRef]
- Jacak, W.A. Plasmons in finite spherical electrolyte systems: RPA effective jellium model for ionic plasma excitations. Plasmonics 2016, 11, 637–651. [Google Scholar] [CrossRef] [PubMed]
- David, C. Two-fluid, hydrodynamic model for spherical electrolyte systems. Sci. Rep. 2018, 8, 7544. [Google Scholar] [CrossRef] [PubMed]
- Maack, J.R.; Mortensen, N.A.; Wubs, M. Size-dependent nonlocal effects in plasmonic semiconductor particles. EPL (Europhys. Lett.) 2017, 119, 17003. [Google Scholar] [CrossRef]
- Maack, J.R.; Mortensen, N.A.; Wubs, M. Two-fluid hydrodynamic model for semiconductors. Phys. Rev. B 2018, 97, 115415. [Google Scholar] [CrossRef]
- Dong, T.; Yin, K.; Gao, X.; Ma, X. Generalized local analogue model for nonlocal plasmonic nanostructures based on multiple-fluid hydrodynamic framework. J. Phys. Appl. Phys. 2020, 53, 295105. [Google Scholar] [CrossRef]
- Jacak, J.E.; Jacak, W.A. New wave-type mechanism of saltatory conduction in myelinated axons and micro-saltatory conduction in C fibres. Eur. Biophys. J. 2020, 49, 343–360. [Google Scholar] [CrossRef] [PubMed]
- Jacak, J.E.; Jacak, W.A. Explanation of saltatory conduction in myelinated axons and of micro-saltatory conduction in C fibers of pain sensation by a wave-type ion plasmonic mechanism of stimulus kinetics. bioRxiv 2023. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Kluczyk, K.; Jacak, L.; Jacak, W.; David, C. Microscopic Electron Dynamics in Metal Nanoparticles for Photovoltaic Systems. Materials 2018, 11, 1077. [Google Scholar] [CrossRef]
- Toscano, G.; Raza, S.; Jauho, A.P.; Mortensen, N.A.; Wubs, M. Modified field enhancement and extinction by plasmonic nanowire dimers due to nonlocal response. Opt. Express 2012, 20, 4176–4188. [Google Scholar] [CrossRef] [PubMed]
- David, C.; García de Abajo, F.J. Surface Plasmon Dependence on the Electron Density Profile at Metal Surfaces. ACS Nano 2014, 8, 9558–9566. [Google Scholar] [CrossRef] [PubMed]
| Ion | Mass () | Velocity (m/s) | Frequency ( Hz) | Damping ( Hz) |
|---|---|---|---|---|
| OH | ||||
| HO | ||||
| Na | ||||
| K | ||||
| Cl |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramesh Narayan, P.; David, C. Nonlocal Soft Plasmonics in Planar Homogeneous Multilayers. Photonics 2023, 10, 1021. https://doi.org/10.3390/photonics10091021
Ramesh Narayan P, David C. Nonlocal Soft Plasmonics in Planar Homogeneous Multilayers. Photonics. 2023; 10(9):1021. https://doi.org/10.3390/photonics10091021
Chicago/Turabian StyleRamesh Narayan, Preethi, and Christin David. 2023. "Nonlocal Soft Plasmonics in Planar Homogeneous Multilayers" Photonics 10, no. 9: 1021. https://doi.org/10.3390/photonics10091021
APA StyleRamesh Narayan, P., & David, C. (2023). Nonlocal Soft Plasmonics in Planar Homogeneous Multilayers. Photonics, 10(9), 1021. https://doi.org/10.3390/photonics10091021






