Experimental Direct Measurement of the Relative Entropy of Coherence
Abstract
1. Introduction
2. Theoretical Method
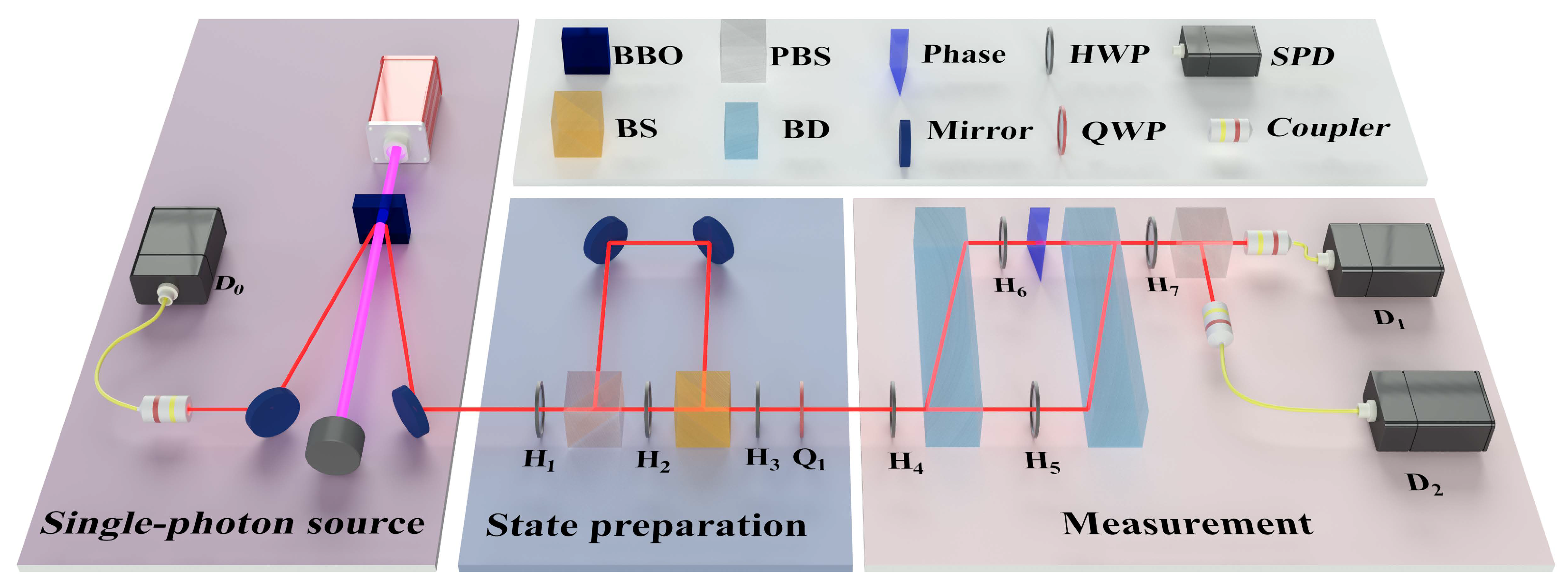
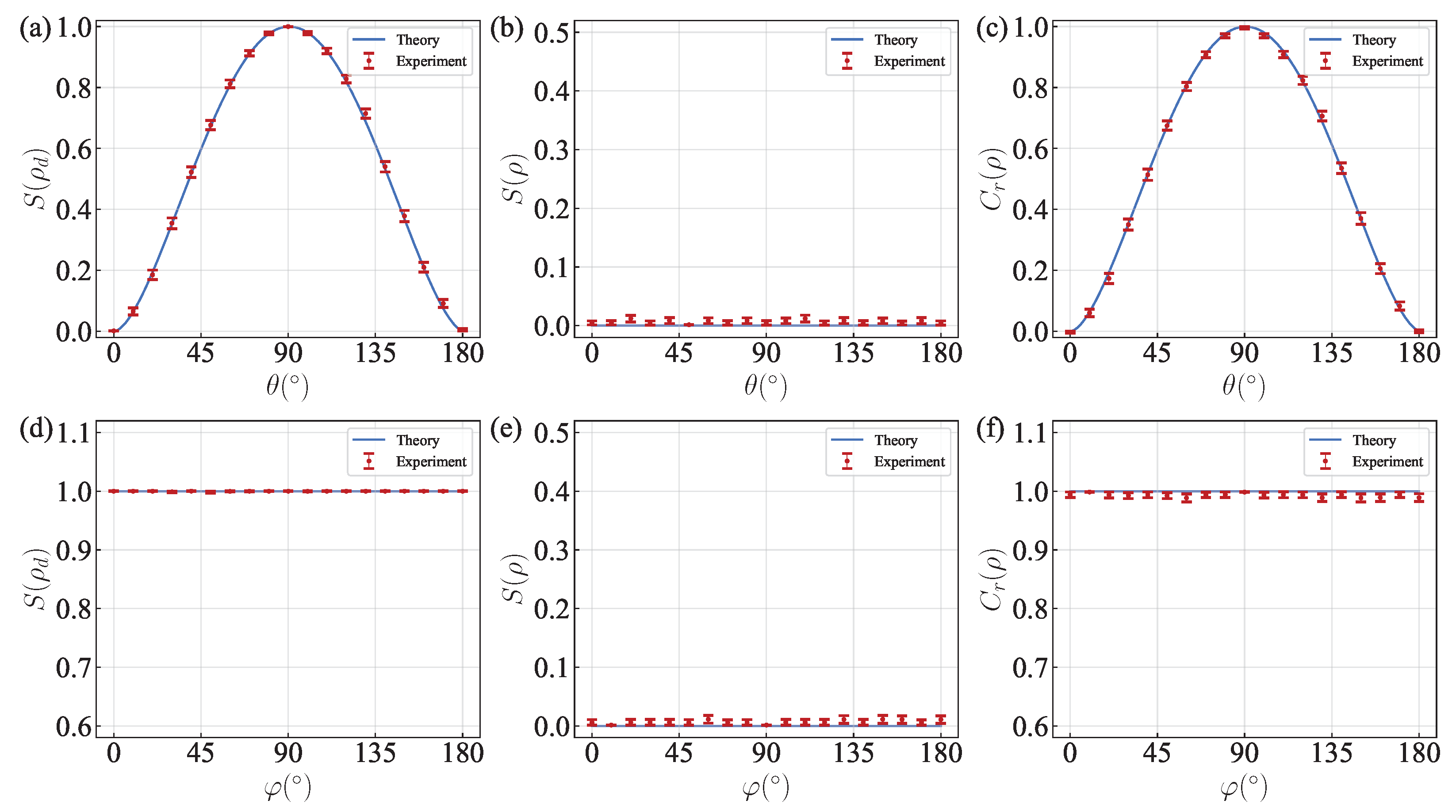
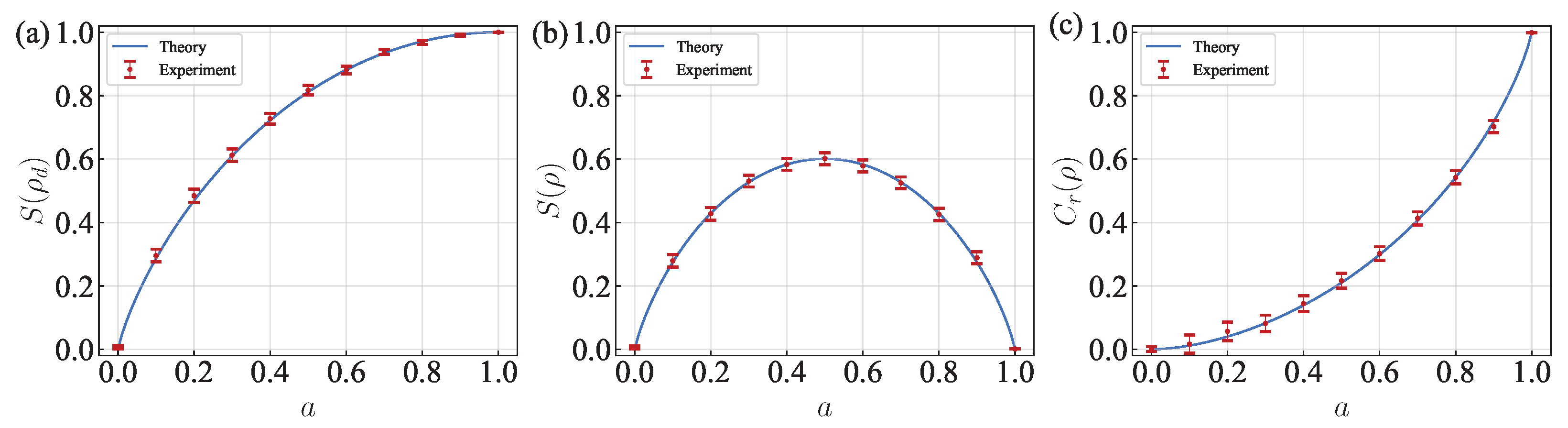
3. Experimental Implementation
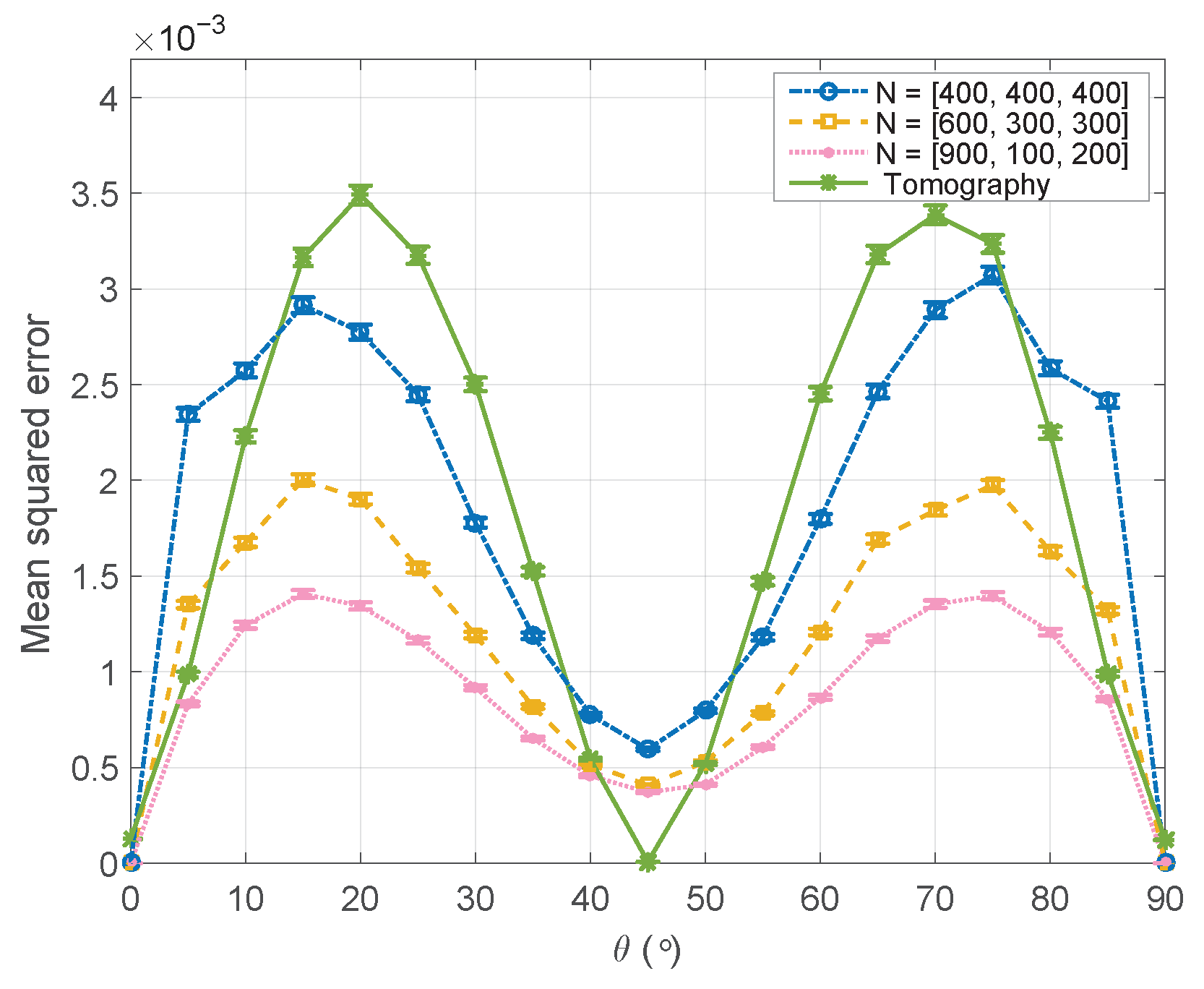
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Narasimhachar, V.; Gour, G. Low-temperature thermodynamics with quantum coherence. Nat. Commun. 2015, 6, 7689. [Google Scholar] [CrossRef] [PubMed]
- Lostaglio, M.; Jennings, D.; Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 2015, 6, 6383. [Google Scholar] [CrossRef] [PubMed]
- Korzekwa, K.; Lostaglio, M.; Oppenheim, J.; Jennings, D. The extraction of work from quantum coherence. New J. Phys. 2016, 18, 023045. [Google Scholar] [CrossRef]
- Gour, G. Role of quantum coherence in thermodynamics. PRX Quantum 2022, 3, 040323. [Google Scholar] [CrossRef]
- Santos, J.P.; Céleri, L.C.; Landi, G.T.; Paternostro, M. The role of quantum coherence in non-equilibrium entropy production. npj Quantum Inf. 2019, 5, 23. [Google Scholar] [CrossRef]
- Karlström, O.; Linke, H.; Karlström, G.; Wacker, A. Increasing thermoelectric performance using coherent transport. Phys. Rev. B 2011, 84, 113415. [Google Scholar] [CrossRef]
- Herranen, M.; Kainulainen, K.; Rahkila, P.M. Kinetic transport theory with quantum coherence. Nucl. Phys. A 2009, 820, 203c–206c. [Google Scholar] [CrossRef][Green Version]
- Lambert, N.; Chen, Y.N.; Cheng, Y.C.; Li, C.M.; Chen, G.Y.; Nori, F. Quantum biology. Nat. Phys. 2013, 9, 10–18. [Google Scholar] [CrossRef]
- Romero, E.; Augulis, R.; Novoderezhkin, V.I.; Ferretti, M.; Thieme, J.; Zigmantas, D.; Van Grondelle, R. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 2014, 10, 676–682. [Google Scholar] [CrossRef]
- Huelga, S.F.; Plenio, M.B. A vibrant environment. Nat. Phys. 2014, 10, 621–622. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [PubMed]
- Levi, F.; Mintert, F. A quantitative theory of coherent delocalization. New J. Phys. 2014, 16, 033007. [Google Scholar] [CrossRef]
- Winter, A.; Yang, D. Operational resource theory of coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef] [PubMed]
- Yadin, B.; Ma, J.; Girolami, D.; Gu, M.; Vedral, V. Quantum processes which do not use coherence. Phys. Rev. X 2016, 6, 041028. [Google Scholar] [CrossRef]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- Hu, M.L.; Hu, X.; Wang, J.; Peng, Y.; Zhang, Y.R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 762, 1–100. [Google Scholar] [CrossRef]
- Matera, J.M.; Egloff, D.; Killoran, N.; Plenio, M.B. Coherent control of quantum systems as a resource theory. Quantum Sci. Technol. 2016, 1, 01LT01. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, Y.; Yuan, X.; Ma, X. Operational interpretation of coherence in quantum key distribution. Phys. Rev. A 2019, 99, 062325. [Google Scholar] [CrossRef]
- Yin, H.L.; Fu, Y.; Li, C.L.; Weng, C.X.; Li, B.H.; Gu, J.; Lu, Y.S.; Huang, S.; Chen, Z.B. Experimental quantum secure network with digital signatures and encryption. Natl. Sci. Rev. 2023, 10, nwac228. [Google Scholar] [CrossRef]
- Gu, J.; Cao, X.Y.; Fu, Y.; He, Z.W.; Yin, Z.J.; Yin, H.L.; Chen, Z.B. Experimental measurement-device-independent type quantum key distribution with flawed and correlated sources. Sci. Bull. 2022, 67, 2167–2175. [Google Scholar] [CrossRef]
- Li, L.; Wang, Q.W.; Shen, S.Q.; Li, M. Quantum coherence measures based on Fisher information with applications. Phys. Rev. A 2021, 103, 012401. [Google Scholar] [CrossRef]
- Hillery, M. Coherence as a resource in decision problems: The Deutsch-Jozsa algorithm and a variation. Phys. Rev. A 2016, 93, 012111. [Google Scholar] [CrossRef]
- Shi, H.L.; Liu, S.Y.; Wang, X.H.; Yang, W.L.; Yang, Z.Y.; Fan, H. Coherence depletion in the Grover quantum search algorithm. Phys. Rev. A 2017, 95, 032307. [Google Scholar] [CrossRef]
- Sun, Y.; Luo, S. Coherence as uncertainty. Phys. Rev. A 2021, 103, 042423. [Google Scholar] [CrossRef]
- Piani, M.; Cianciaruso, M.; Bromley, T.R.; Napoli, C.; Johnston, N.; Adesso, G. Robustness of asymmetry and coherence of quantum states. Phys. Rev. A 2016, 93, 042107. [Google Scholar] [CrossRef]
- Napoli, C.; Bromley, T.R.; Cianciaruso, M.; Piani, M.; Johnston, N.; Adesso, G. Robustness of coherence: An operational and observable measure of quantum coherence. Phys. Rev. Lett. 2016, 116, 150502. [Google Scholar] [CrossRef]
- Marvian, I.; Spekkens, R.W. How to quantify coherence: Distinguishing speakable and unspeakable notions. Phys. Rev. A 2016, 94, 052324. [Google Scholar] [CrossRef]
- Streltsov, A.; Singh, U.; Dhar, H.S.; Bera, M.N.; Adesso, G. Measuring quantum coherence with entanglement. Phys. Rev. Lett. 2015, 115, 020403. [Google Scholar] [CrossRef]
- Chitambar, E.; Hsieh, M.H. Relating the resource theories of entanglement and quantum coherence. Phys. Rev. Lett. 2016, 117, 020402. [Google Scholar] [CrossRef]
- Theurer, T.; Satyajit, S.; Plenio, M.B. Quantifying dynamical coherence with dynamical entanglement. Phys. Rev. Lett. 2020, 125, 130401. [Google Scholar] [CrossRef]
- He, R.D.; Wu, K.D.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Experimental quantification of dynamical coherence via entangling two qubits. Opt. Express 2022, 30, 10346–10353. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.C.; Kwon, H.; Park, C.Y.; Jeong, H. Unified view of quantum correlations and quantum coherence. Phys. Rev. A 2016, 94, 022329. [Google Scholar] [CrossRef]
- Regula, B.; Fang, K.; Wang, X.; Adesso, G. One-shot coherence distillation. Phys. Rev. Lett. 2018, 121, 010401. [Google Scholar] [CrossRef] [PubMed]
- Regula, B.; Lami, L.; Streltsov, A. Nonasymptotic assisted distillation of quantum coherence. Phys. Rev. A 2018, 98, 052329. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Yuan, X.; Chitambar, E.; Winter, A. One-shot coherence distillation: Towards completing the picture. IEEE Trans. Inf. Theory 2019, 65, 6441–6453. [Google Scholar] [CrossRef]
- Xiong, S.J.; Sun, Z.; Su, Q.P.; Xi, Z.J.; Yu, L.; Jin, J.S.; Liu, J.M.; Nori, F.; Yang, C.P. Experimental demonstration of one-shot coherence distillation: Realizing N-dimensional strictly incoherent operations. Optica 2021, 8, 1003–1008. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Yuan, X.; Chitambar, E.; Ma, X. One-shot coherence dilution. Phys. Rev. Lett. 2018, 120, 070403. [Google Scholar] [CrossRef]
- Ma, J.; Yadin, B.; Girolami, D.; Vedral, V.; Gu, M. Converting coherence to quantum correlations. Phys. Rev. Lett. 2016, 116, 160407. [Google Scholar] [CrossRef]
- Chitambar, E.; Streltsov, A.; Rana, S.; Bera, M.; Adesso, G.; Lewenstein, M. Assisted distillation of quantum coherence. Phys. Rev. Lett. 2016, 116, 070402. [Google Scholar] [CrossRef]
- Streltsov, A.; Rana, S.; Bera, M.N.; Lewenstein, M. Towards resource theory of coherence in distributed scenarios. Phys. Rev. X 2017, 7, 011024. [Google Scholar] [CrossRef]
- Streltsov, A.; Chitambar, E.; Rana, S.; Bera, M.N.; Winter, A.; Lewenstein, M. Entanglement and coherence in quantum state merging. Phys. Rev. Lett. 2016, 116, 240405. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.D.; Hou, Z.; Zhong, H.S.; Yuan, Y.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Experimentally obtaining maximal coherence via assisted distillation process. Optica 2017, 4, 454–459. [Google Scholar] [CrossRef]
- Wu, K.D.; Hou, Z.; Zhao, Y.Y.; Xiang, G.Y.; Li, C.F.; Guo, G.C.; Ma, J.; He, Q.Y.; Thompson, J.; Gu, M. Experimental cyclic interconversion between coherence and quantum correlations. Phys. Rev. Lett. 2018, 121, 050401. [Google Scholar] [CrossRef] [PubMed]
- Vedral, V. The role of relative entropy in quantum information theory. Rev. Mod. Phys. 2002, 74, 197. [Google Scholar] [CrossRef]
- Bagan, E.; Bergou, J.A.; Cottrell, S.S.; Hillery, M. Relations between coherence and path information. Phys. Rev. Lett. 2016, 116, 160406. [Google Scholar] [CrossRef]
- Yuan, Y.; Hou, Z.; Zhao, Y.Y.; Zhong, H.S.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Experimental demonstration of wave-particle duality relation based on coherence measure. Opt. Express 2018, 26, 4470–4478. [Google Scholar] [CrossRef]
- Zhu, H.; Hayashi, M.; Chen, L. Coherence and entanglement measures based on Rényi relative entropies. J. Phys. A-math. Theor. 2017, 50, 475303. [Google Scholar] [CrossRef]
- Bu, K.; Singh, U.; Fei, S.M.; Pati, A.K.; Wu, J. Maximum relative entropy of coherence: An operational coherence measure. Phys. Rev. Lett. 2017, 119, 150405. [Google Scholar] [CrossRef]
- Smith, G.; Smolin, J.A.; Yuan, X.; Zhao, Q.; Girolami, D.; Ma, X. Quantifying coherence and entanglement via simple measurements. arXiv 2017, arXiv:1707.09928. [Google Scholar] [CrossRef]
- Horová, N.; Stárek, R.; Mičuda, M.; Kolář, M.; Fiurášek, J.; Filip, R. Deterministic controlled enhancement of local quantum coherence. Sci. Rep. 2022, 12, 22455. [Google Scholar] [CrossRef]
- Horová, N.; Stárek, R.; Mičuda, M.; Fiurášek, J.; Kolář, M.; Filip, R. Experimental mutual coherence from separable coherent qubits. Phys. Rev. A 2022, 106, 012440. [Google Scholar] [CrossRef]
- Wang, Y.T.; Tang, J.S.; Wei, Z.Y.; Yu, S.; Ke, Z.J.; Xu, X.Y.; Li, C.F.; Guo, G.C. Directly measuring the degree of quantum coherence using interference fringes. Phys. Rev. Lett. 2017, 118, 020403. [Google Scholar] [CrossRef]
- Zhang, D.J.; Liu, C.; Yu, X.D.; Tong, D. Estimating coherence measures from limited experimental data available. Phys. Rev. Lett. 2018, 120, 170501. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.D.; Gühne, O. Detecting coherence via spectrum estimation. Phys. Rev. A 2019, 99, 062310. [Google Scholar] [CrossRef]
- Yuan, Y.; Hou, Z.; Tang, J.F.; Streltsov, A.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Direct estimation of quantum coherence by collective measurements. npj Quantum Inf. 2020, 6, 46. [Google Scholar] [CrossRef]
- de Lima Bernardo, B. Proposal for a direct measurement of the von Neumann entropy and the relative entropy of coherence. Phys. Scr. 2020, 95, 045104. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Z.; Dai, Y.; Dong, Y.; Chengjie, Z. Detecting and estimating coherence based on coherence witnesses. Phys. Rev. A 2021, 103, 012409. [Google Scholar] [CrossRef]
- Dai, Y.; Dong, Y.; Xu, Z.; You, W.; Zhang, C.; Gühne, O. Experimentally accessible lower bounds for genuine multipartite entanglement and coherence measures. Phys. Rev. Appl. 2020, 13, 054022. [Google Scholar] [CrossRef]
- Sun, L.L.; Yu, S. Universal method to estimate quantum coherence. Phys. Rev. A 2022, 106, 042428. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Yuan, Y.; Niu, Y.; Gong, S. Experimental Direct Measurement of the Relative Entropy of Coherence. Photonics 2023, 10, 1004. https://doi.org/10.3390/photonics10091004
Huang X, Yuan Y, Niu Y, Gong S. Experimental Direct Measurement of the Relative Entropy of Coherence. Photonics. 2023; 10(9):1004. https://doi.org/10.3390/photonics10091004
Chicago/Turabian StyleHuang, Xufeng, Yuan Yuan, Yueping Niu, and Shangqing Gong. 2023. "Experimental Direct Measurement of the Relative Entropy of Coherence" Photonics 10, no. 9: 1004. https://doi.org/10.3390/photonics10091004
APA StyleHuang, X., Yuan, Y., Niu, Y., & Gong, S. (2023). Experimental Direct Measurement of the Relative Entropy of Coherence. Photonics, 10(9), 1004. https://doi.org/10.3390/photonics10091004




