Advantages of Using Hard X-ray Photons for Ultrafast Diffraction Measurements
Abstract
:1. Introduction
2. Computational Approach
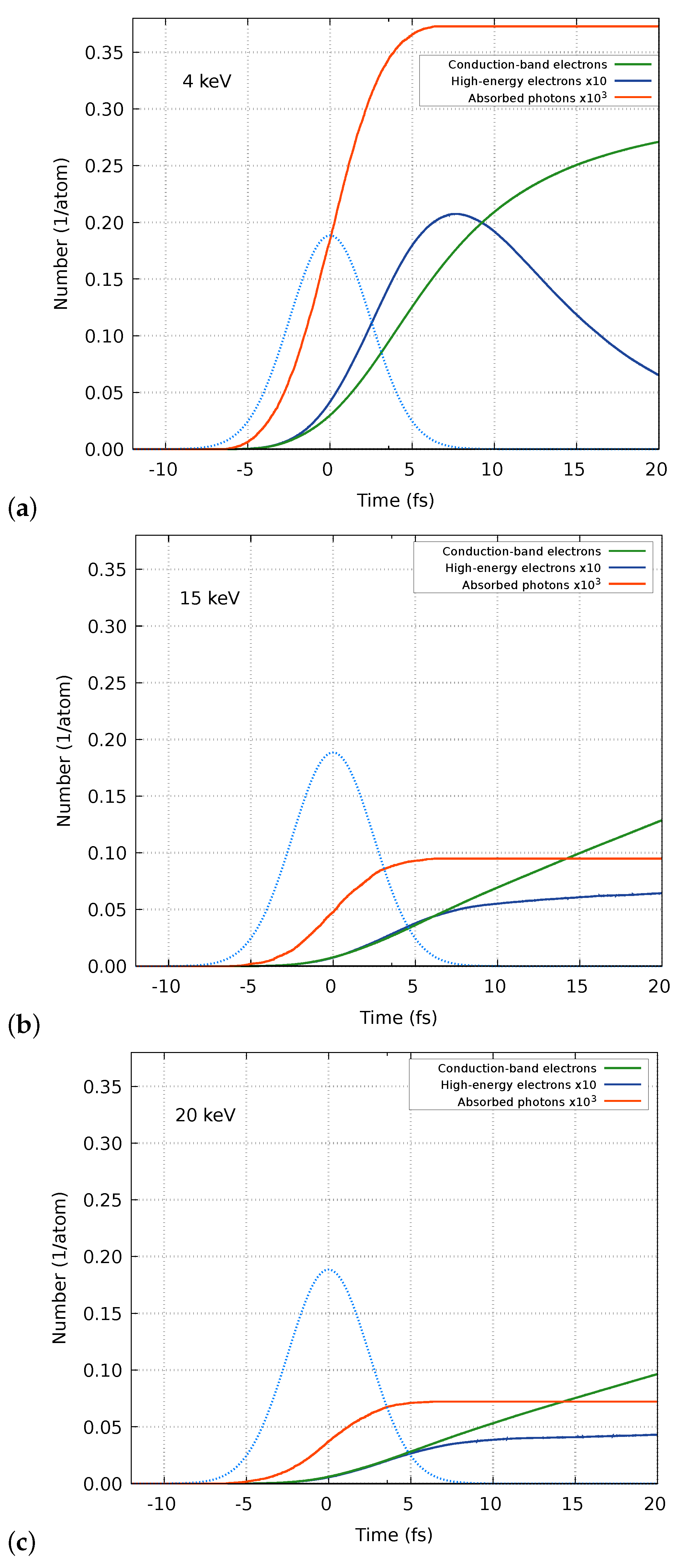
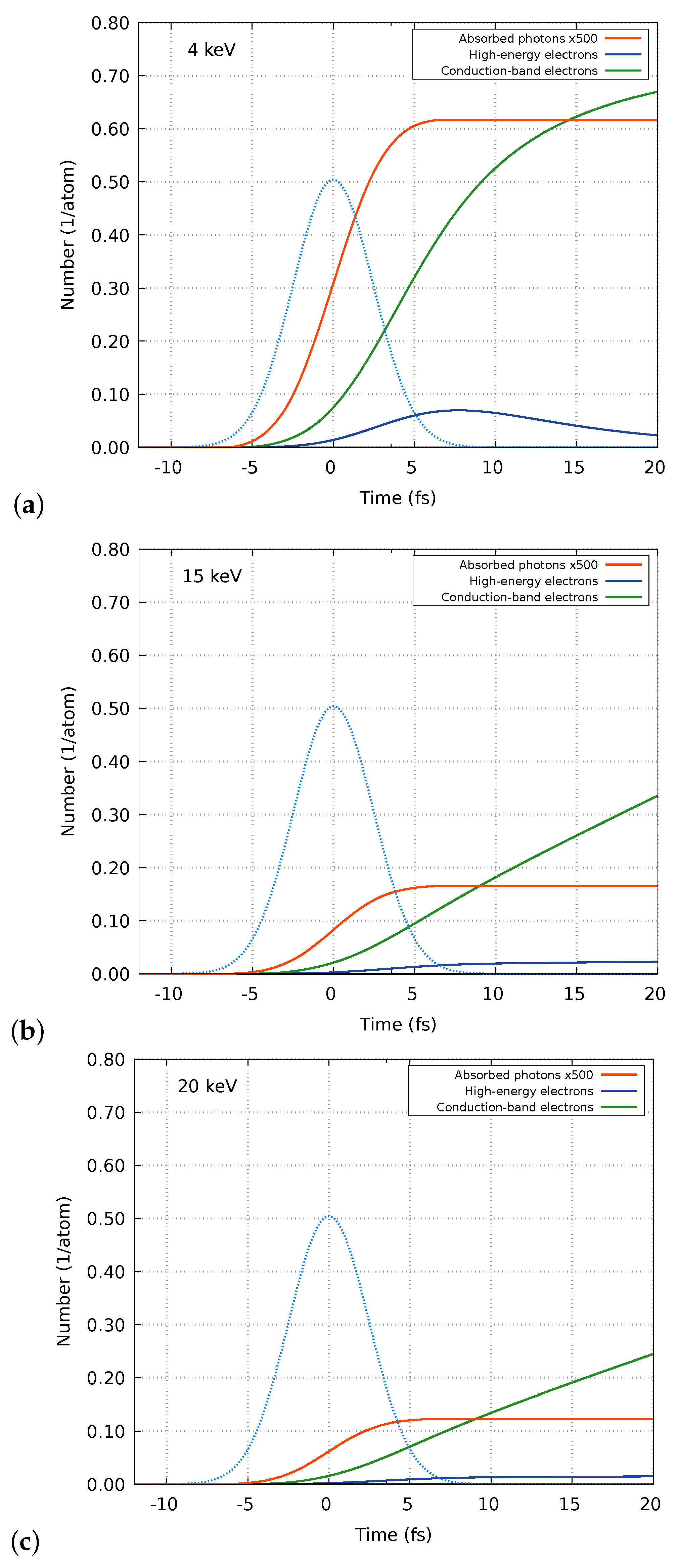
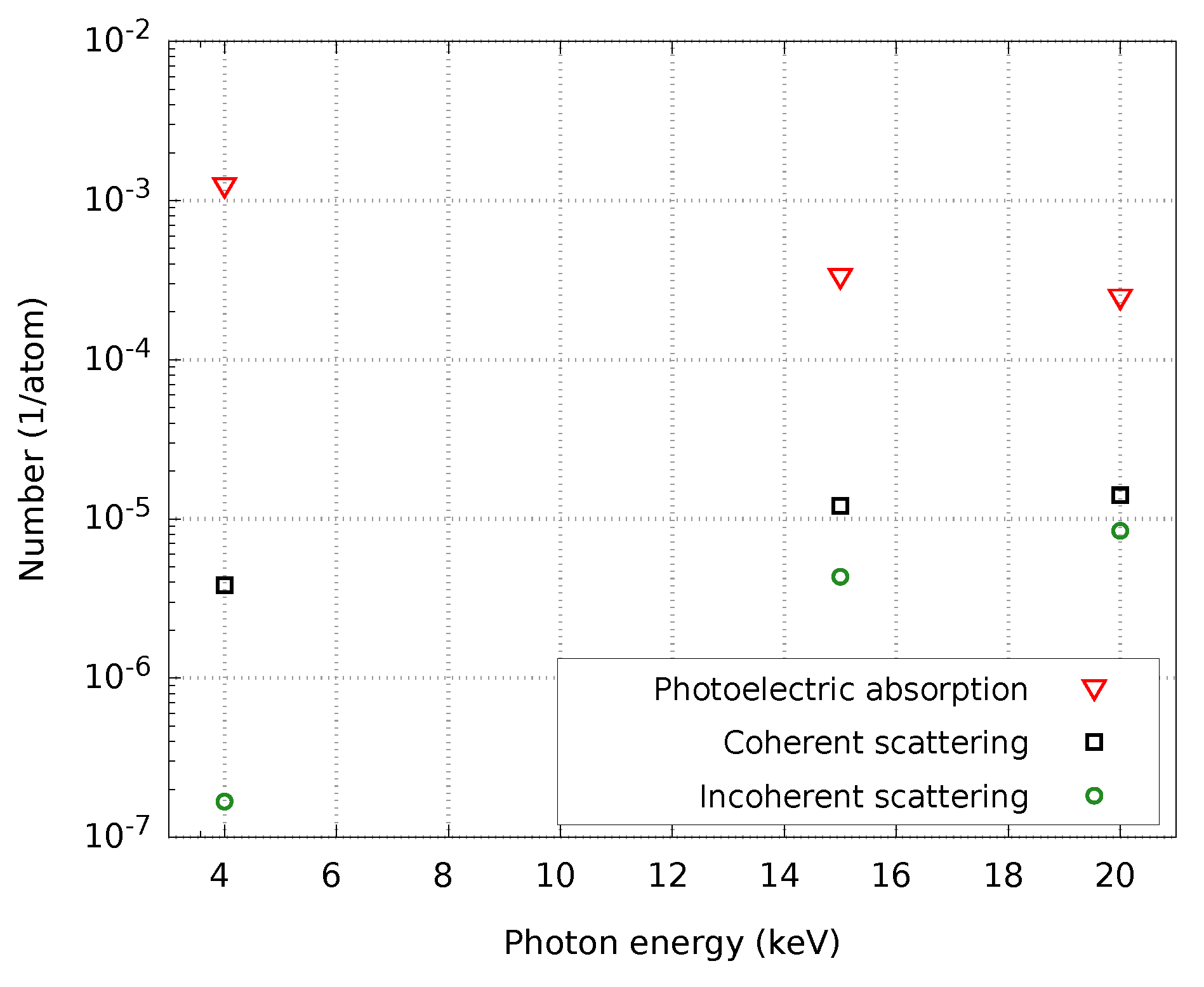
3. Results
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| XFEL | X-ray free-electron laser |
| MC | Monte Carlo |
| TB | Tight Binding |
| MD | Molecular Dynamics |
References
- Yabashi, M.; Tanaka, H. The next ten years of X-ray science. Nat. Photonics 2017, 11, 12–14. [Google Scholar] [CrossRef]
- McNeil, B.W.; Thompson, N.R. X-ray free-electron lasers. Nat. Photonics 2010, 4, 814–821. [Google Scholar] [CrossRef]
- Pellegrini, C.; Marinelli, A.; Reiche, S. The physics of X-ray free-electron lasers. Rev. Mod. Phys. 2016, 88, 015006. [Google Scholar] [CrossRef]
- Neutze, R.; Wouts, R.; Van der Spoel, D.; Weckert, E.; Hajdu, J. Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 2000, 406, 752–757. [Google Scholar] [CrossRef] [PubMed]
- Gaffney, K.; Chapman, H.N. Imaging atomic structure and dynamics with ultrafast X-ray scattering. Science 2007, 316, 1444–1448. [Google Scholar] [CrossRef]
- Boutet, S.; Lomb, L.; Williams, G.J.; Barends, T.R.; Aquila, A.; Doak, R.B.; Weierstall, U.; DePonte, D.P.; Steinbrener, J.; Shoeman, R.L.; et al. High-resolution protein structure determination by serial femtosecond crystallography. Science 2012, 337, 362–364. [Google Scholar] [CrossRef] [PubMed]
- Chapman, H.N.; Caleman, C.; Timneanu, N. Diffraction before destruction. Philos. Trans. R. Soc. B 2014, 369, 20130313. [Google Scholar] [CrossRef]
- Ziaja, B.; Jurek, Z.; Medvedev, N.; Saxena, V.; Son, S.K.; Santra, R. Towards Realistic Simulations of Macromolecules Irradiated under the Conditions of Coherent Diffraction Imaging with an X-ray Free-Electron Laser. Photonics 2015, 2, 256–269. [Google Scholar] [CrossRef]
- Inoue, I.; Deguchi, Y.; Ziaja, B.; Osaka, T.; Abdullah, M.M.; Jurek, Z.; Medvedev, N.; Tkachenko, V.; Inubushi, Y.; Kasai, H.; et al. Atomic-scale visualization of ultrafast bond breaking in X-ray-excited diamond. Phys. Rev. Lett. 2021, 126, 117403. [Google Scholar] [CrossRef]
- Inoue, I.; Tkachenko, V.; Kapcia, K.J.; Lipp, V.; Ziaja, B.; Inubushi, Y.; Hara, T.; Yabashi, M.; Nishibori, E. Delayed Onset and Directionality of X-Ray-Induced Atomic Displacements Observed on Subatomic Length Scales. Phys. Rev. Lett. 2022, 128, 223203. [Google Scholar] [CrossRef]
- Schlichting, I. Serial femtosecond crystallography: The first five years. IUCrJ 2015, 2, 246–255. [Google Scholar] [CrossRef] [PubMed]
- Barends, T.R.; Stauch, B.; Cherezov, V.; Schlichting, I. Serial femtosecond crystallography. Nat. Rev. Methods Prim. 2022, 2, 59. [Google Scholar] [CrossRef] [PubMed]
- Coppens, P. X-ray Charge Densities and Chemical Bonding; International Union of Crystallography: Chester, UK, 1997; Volume 4. [Google Scholar]
- Medvedev, N.; Jeschke, H.O.; Ziaja, B. Nonthermal phase transitions in semiconductors induced by a femtosecond extreme ultraviolet laser pulse. New J. Phys. 2013, 15, 015016. [Google Scholar] [CrossRef]
- Medvedev, N.; Tkachenko, V.; Lipp, V.; Li, Z.; Ziaja, B. Various damage mechanisms in carbon and silicon materials under femtosecond X-ray irradiation. 4Open 2018, 1, 3. [Google Scholar] [CrossRef]
- Yumoto, H.; Mimura, H.; Koyama, T.; Matsuyama, S.; Tono, K.; Togashi, T.; Inubushi, Y.; Sato, T.; Tanaka, T.; Kimura, T.; et al. Focusing of X-ray free-electron laser pulses with reflective optics. Nat. Photonics 2013, 7, 43–47. [Google Scholar] [CrossRef]
- Schriber, E.A.; Paley, D.W.; Bolotovsky, R.; Rosenberg, D.J.; Sierra, R.G.; Aquila, A.; Mendez, D.; Poitevin, F.; Blaschke, J.P.; Bhowmick, A.; et al. Chemical crystallography by serial femtosecond X-ray diffraction. Nature 2022, 601, 360–365. [Google Scholar] [CrossRef] [PubMed]
- Støckler, L.J.; Krause, L.; Svane, B.; Tolborg, K.; Richter, B.; Takahashi, S.; Fujita, T.; Kasai, H.; Sugahara, M.; Inoue, I.; et al. Towards pump–probe single-crystal XFEL refinements for small-unit-cell systems. IUCrJ 2023, 10, 103. [Google Scholar] [CrossRef] [PubMed]
- Takaba, K.; Maki-Yonekura, S.; Inoue, I.; Tono, K.; Hamaguchi, T.; Kawakami, K.; Naitow, H.; Ishikawa, T.; Yabashi, M.; Yonekura, K. Structural resolution of a small organic molecule by serial X-ray free-electron laser and electron crystallography. Nat. Chem. 2023, 15, 491–497. [Google Scholar] [CrossRef]
- Cullen, D.E.; Hubbell, J.H.; Kissel, L. EPDL97: The Evaluated Photon Data Library; 97 Version; Technical Report; Lawrence Livermore National Lab. (LLNL): Livermore, CA, USA, 1997. [Google Scholar]
- Perkins, S.; Cullen, D.; Chen, M.; Rathkopf, J.; Scofield, J.; Hubbell, J. Tables and Graphs of Atomic Subshell and Relaxation Data Derived from the LLNL Evaluated Atomic Data Library (EADL). Z = 1–100; Technical Report; Lawrence Livermore National Lab.: Livermore, CA, USA, 1991. [Google Scholar]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1985. [Google Scholar]
- Medvedev, N.; Li, Z.; Ziaja, B. Thermal and nonthermal melting of silicon under femtosecond x-ray irradiation. Phys. Rev. B 2015, 91, 054113. [Google Scholar] [CrossRef]
- Inoue, I.; Hara, T.; Inubushi, Y.; Tono, K.; Inagaki, T.; Katayama, T.; Amemiya, Y.; Tanaka, H.; Yabashi, M. X-ray Hanbury Brown-Twiss interferometry for determination of ultrashort electron-bunch duration. Phys. Rev. Accel. Beams 2018, 21, 080704. [Google Scholar] [CrossRef]
- Henke, B.; Gullikson, E.; Davis, J. X-ray interactions: Photoabsorption, scattering, transmission, and reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Follath, R.; Koyama, T.; Lipp, V.; Medvedev, N.; Tono, K.; Ohashi, H.; Patthey, L.; Yabashi, M.; Ziaja, B. X-ray induced damage of B4C-coated bilayer materials under various irradiation conditions. Sci. Rep. 2019, 9, 2029. [Google Scholar] [CrossRef]
- Koritsanszky, T.S.; Coppens, P. Chemical applications of X-ray charge-density analysis. Chem. Rev. 2001, 101, 1583–1628. [Google Scholar] [CrossRef]
- Berger, M.J.; Hubbell, J.H.; Seltzer, S.M.; Chang, J.; Coursey, J.S.; Sukumar, R.; Zucker, D.S.; Olsen, K. XCOM: Photon Cross Sections Database. NIST, PML, Radiation Physics Division. 2010. Available online: https://dx.doi.org/10.18434/T48G6X (accessed on 17 August 2023).
- White, T.A.; Kirian, R.A.; Martin, A.V.; Aquila, A.; Nass, K.; Barty, A.; Chapman, H.N. CrystFEL: A software suite for snapshot serial crystallography. J. Appl. Crystallogr. 2012, 45, 335–341. [Google Scholar] [CrossRef]
- Tkachenko, V.; Abdullah, M.M.; Jurek, Z.; Medvedev, N.; Lipp, V.; Makita, M.; Ziaja, B. Limitations of Structural Insight into Ultrafast Melting of Solid Materials with X-ray Diffraction Imaging. Appl. Sci. 2021, 11, 5157. [Google Scholar] [CrossRef]
- Inubushi, Y.; Tono, K.; Togashi, T.; Sato, T.; Hatsui, T.; Kameshima, T.; Togawa, K.; Hara, T.; Tanaka, T.; Tanaka, H.; et al. Determination of the Pulse Duration of an X-Ray Free Electron Laser Using Highly Resolved Single-Shot Spectra. Phys. Rev. Lett. 2012, 109, 144801. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lipp, V.; Inoue, I.; Ziaja, B. Advantages of Using Hard X-ray Photons for Ultrafast Diffraction Measurements. Photonics 2023, 10, 948. https://doi.org/10.3390/photonics10080948
Lipp V, Inoue I, Ziaja B. Advantages of Using Hard X-ray Photons for Ultrafast Diffraction Measurements. Photonics. 2023; 10(8):948. https://doi.org/10.3390/photonics10080948
Chicago/Turabian StyleLipp, Vladimir, Ichiro Inoue, and Beata Ziaja. 2023. "Advantages of Using Hard X-ray Photons for Ultrafast Diffraction Measurements" Photonics 10, no. 8: 948. https://doi.org/10.3390/photonics10080948
APA StyleLipp, V., Inoue, I., & Ziaja, B. (2023). Advantages of Using Hard X-ray Photons for Ultrafast Diffraction Measurements. Photonics, 10(8), 948. https://doi.org/10.3390/photonics10080948




