Second-Harmonic Generation of the Vortex Beams with Integer and Fractional Topological Charges
Abstract
1. Introduction
2. Theoretical Analysis
3. Experimental Setup
4. Results and Discussion
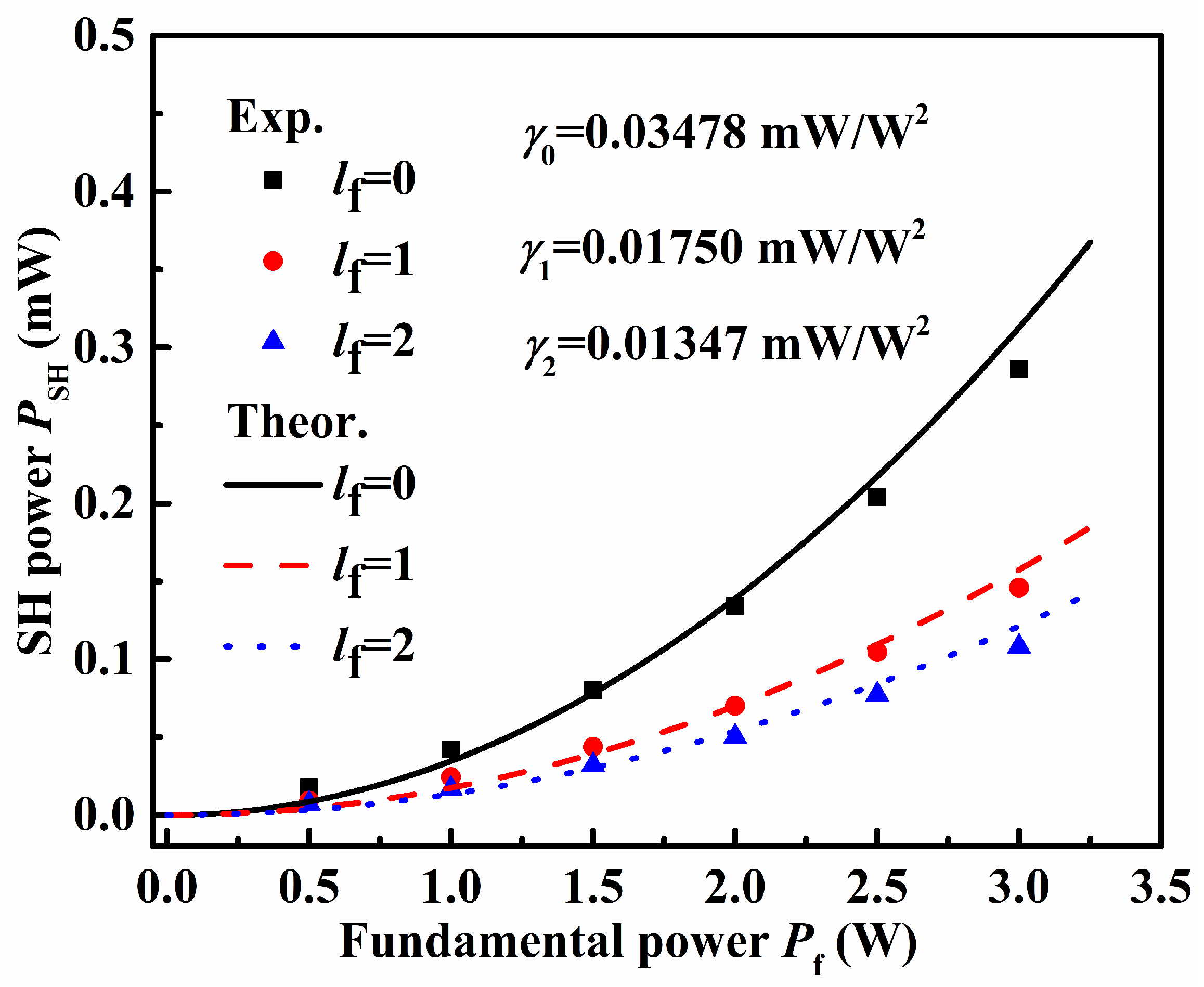
4.1. The Single-Pass SHG Characteristics of LG0,l Vortex Beams with Different Vortex Orders
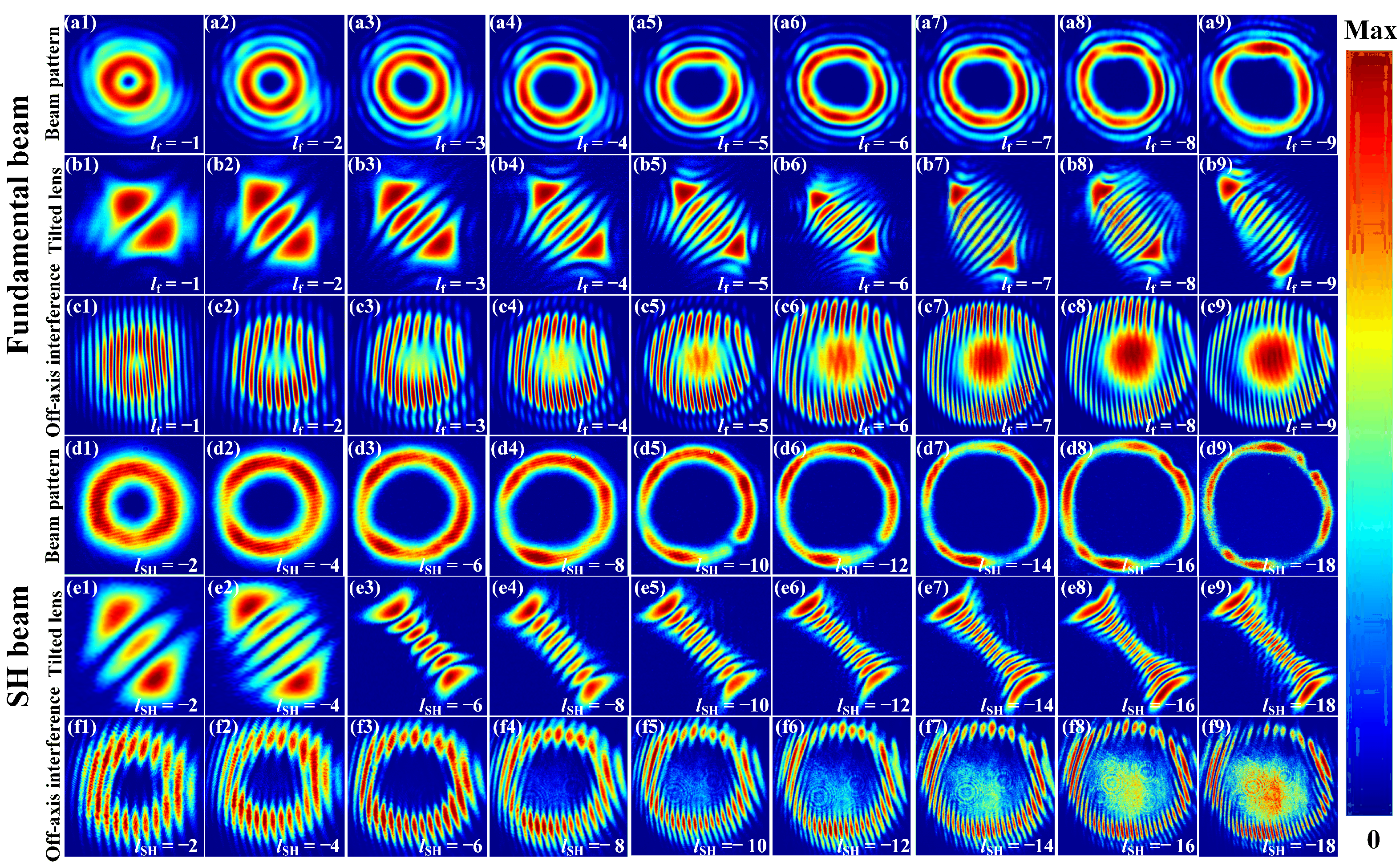
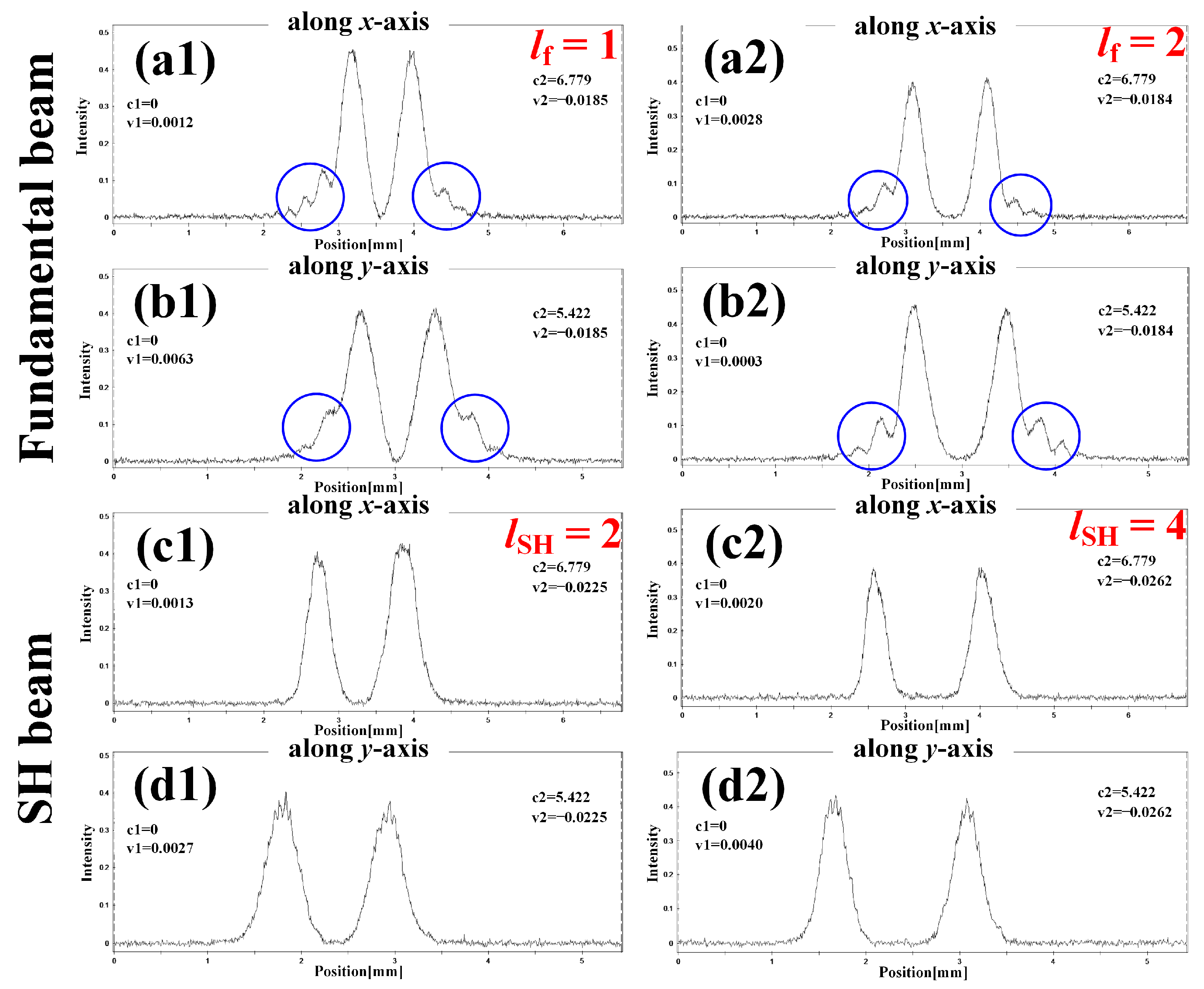
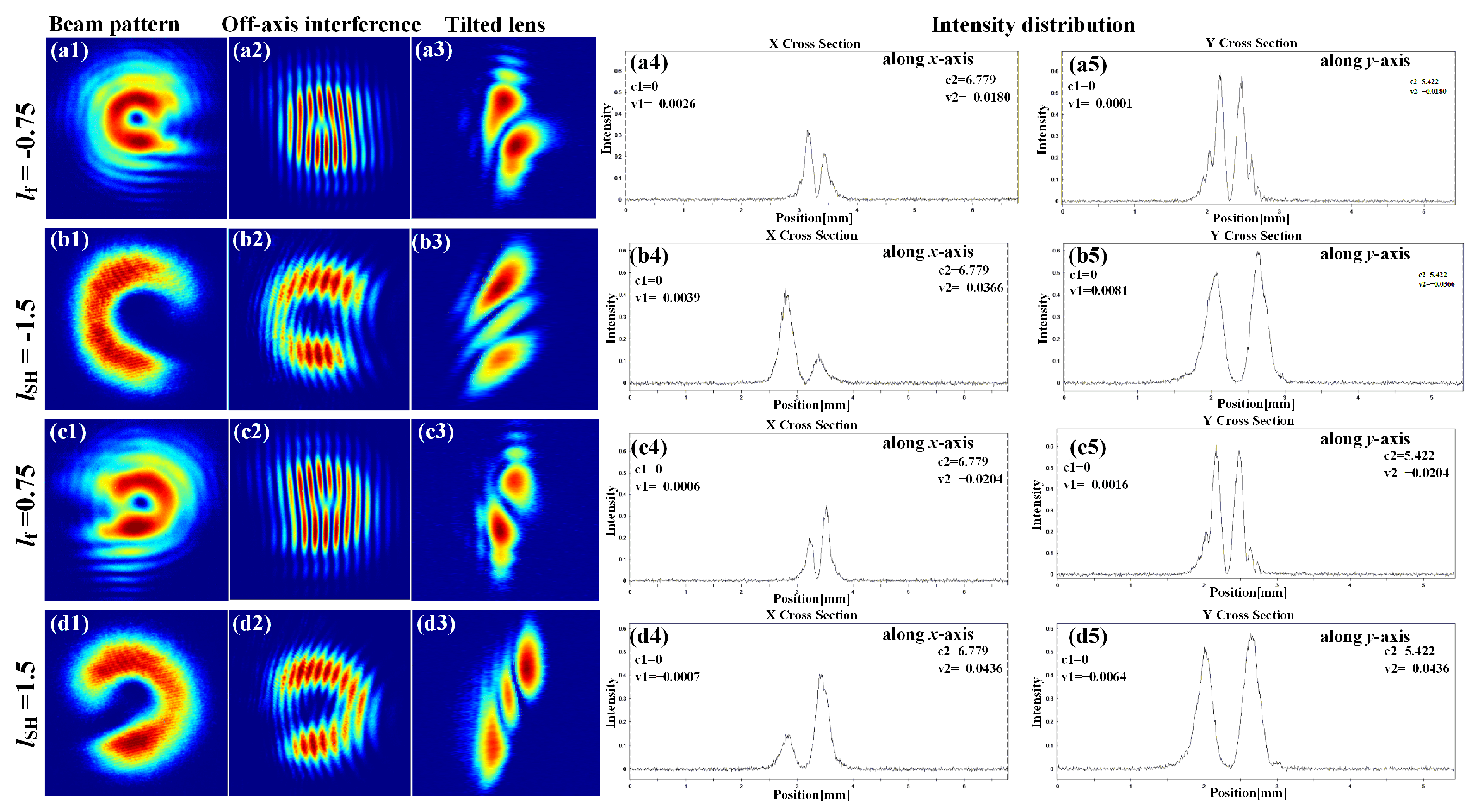
4.2. Beam Patterns and TCs of the Fundamental/SH Vortex Beams
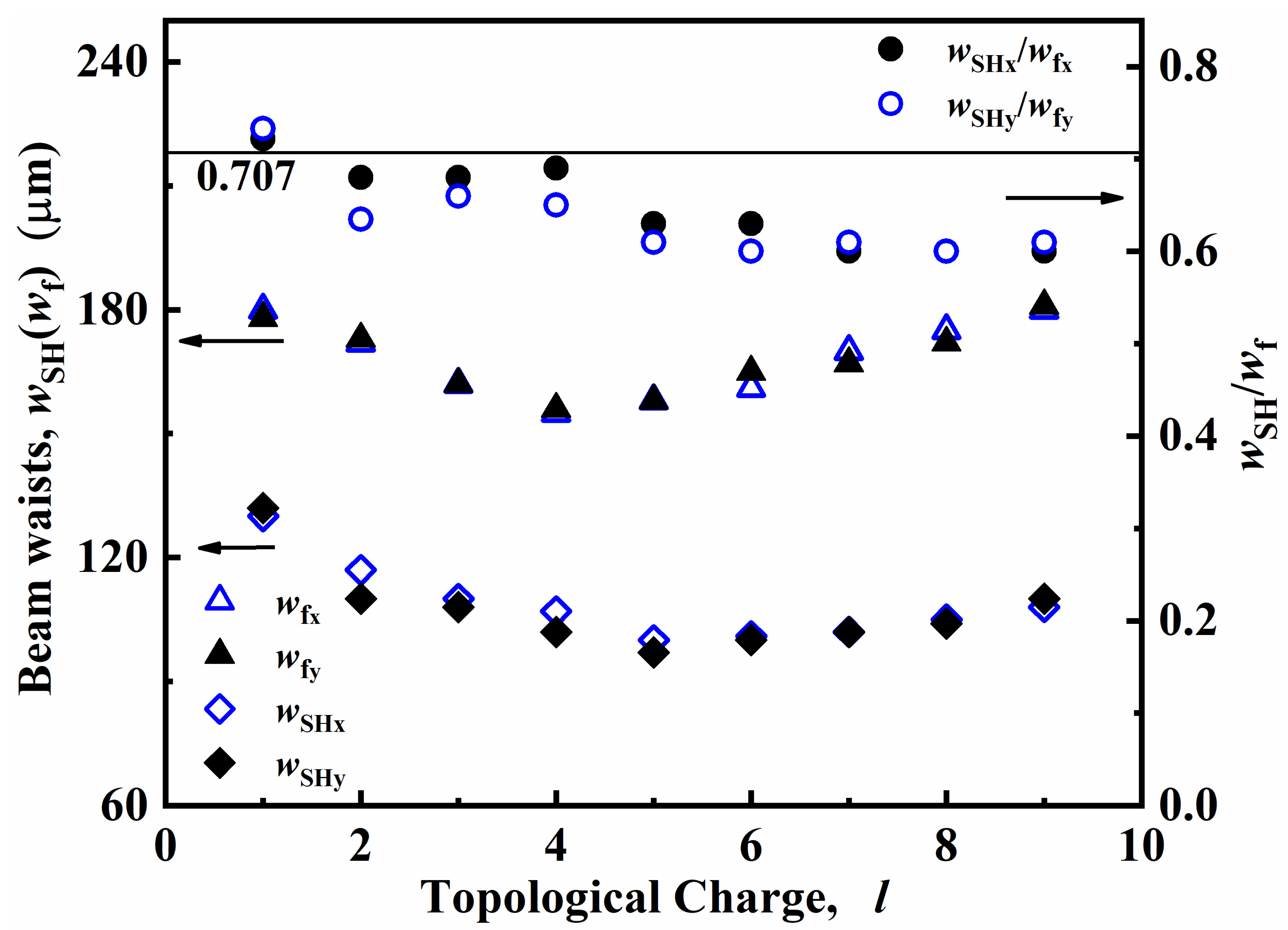
4.3. Beam Waists of Fundamental/SH Vortex Beams in KTP Measured Using 4f System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Sueda, K.; Miyaji, G.; Miyanaga, N.; Nakatsuka, M. Laguerre-Gaussian beam generated with a multilevel spiral phase plate for high intensity laser pulses. Opt. Expr. 2004, 12, 3548–3553. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.H.; Lv, H.R.; Fu, X.; Yang, Y.J. Vortex beam: Generation and detection of orbital angular momentum. Chin. Opt. Lett. 2022, 20, 012601. [Google Scholar] [CrossRef]
- Yu, T.; Xia, H.; Xie, W.K.; Xiao, G.Z.; Li, H.J. The generation and verification of Bessel-Gaussian beam based on coherent beam combining. Results Phys. 2020, 16, 102872. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K. Generation of high-order Bessel beams by use of an axicon. Opt. Commun. 2000, 177, 297–301. [Google Scholar] [CrossRef]
- Chen, M.S.; Huang, S.J.; Shao, W.; Liu, X.P. Experimental study on the propagation characteristics of ring Airy Gaussian vortex beams. Appl. Phys. B 2017, 123, 215. [Google Scholar] [CrossRef]
- Yang, Y.J.; Dong, Y.; Zhao, C.L.; Cai, Y.J. Generation and propagation of an anomalous vortex beam. Opt. Lett. 2013, 38, 5418–5421. [Google Scholar] [CrossRef]
- Li, X.Z.; Ma, H.X.; Yin, C.L.; Tang, J.; Li, H.H.; Tang, M.M.; Wang, J.G.; Tai, Y.P.; Li, X.F.; Wang, Y.S. Controllable mode transformation in perfect optical vortices. Opt. Expr. 2018, 26, 651–662. [Google Scholar] [CrossRef]
- Yuan, W.M.; Xu, Y.; Zheng, K.P.; Fu, S.N.; Wang, Y.C.; Qin, Y.W. Experimental generation of perfect optical vortices through strongly scattering media. Opt. Lett. 2021, 46, 4156–4159. [Google Scholar] [CrossRef] [PubMed]
- Xue, M.; Yan, X.S.; Wu, J.W.; Ge, R.; Yuan, T.G.; Chen, Y.P.; Chen, X.F. On-chip ultraviolet second-harmonic generation in lithium-tantalate thin film microdisk. Chin. Opt. Lett. 2023, 21, 061902. [Google Scholar] [CrossRef]
- Shen, Y.N.; Weitz, D.A.; Forde, N.R.; Shayegan, M. Line optical tweezers as controllable micromachines: Techniques and emerging trends. Soft Matter 2022, 18, 5359–5365. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.H.; Tang, M.M.; Li, H.H.; Tai, Y.P.; Li, X.Z. Optical vortex lattice: An exploitation of orbital angular momentum. Nanophotonics 2021, 10, 2487–2496. [Google Scholar] [CrossRef]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Berning, S.; Willig, K.I.; Steffens, H.; Dibaj, P.; Hell, S.W. Nanoscopy in a living mouse brain. Science 2012, 335, 551. [Google Scholar] [CrossRef]
- Yasir, P.A.A.; Hegde, A.S.; Chandrashekar, C.M. Optical realization of one-dimensional generalized split-step quantum walks. Opt. Commun. 2023, 2, 90–99. [Google Scholar] [CrossRef]
- Shen, Y.J.; Nape, I.; Yang, X.L.; Fu, X.; Gong, M.; Naidoo, D.; Forbes, A. Creation and control of high-dimensional multi-partite classically entangled light. Light-Sci. Appl. 2021, 10, 50. [Google Scholar] [CrossRef] [PubMed]
- Kysela, J.; Erhard, M.; Hochrainer, A.; Krenn, M.; Zeilinger, A. Path identity as a source of high-dimensional entanglement. Proc. Natl. Acad. Sci. USA 2020, 117, 26118–26122. [Google Scholar] [CrossRef]
- Qiao, Z.; Wan, Z.Y.; Xie, G.Q.; Wang, J.; Qian, L.J.; Fan, D.Y. Multi-vortex laser enabling spatial and temporal encoding. PhotoniX 2020, 1, 13. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J. A review of multiple optical vortices generation: Methods and applications. Front. Optoelectron. 2019, 12, 52–68. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Zhang, S.R.; Duan, Y.H.; Guo, M.H.; Li, P. Theoretical Analysis of continuous-wave mid-infrared optical vortex source generated by singly resonant optical parametric oscillator. Photonics 2022, 9, 1002. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Wang, C. Generation and expansion of Laguerre–Gaussian beams. J. Opt. 2022, 51, 910–926. [Google Scholar] [CrossRef]
- Dholakia, K.; Simpson, N.B.; Padgett, M.J.; Allen, L. Second-harmonic generation and the orbital angular momentum of light. Phys. Rev. A 1996, 54, R3742. [Google Scholar] [CrossRef] [PubMed]
- Courtial, J.; Dholakia, K.; Allen, L.; Padgett, M.J. Second-harmonic generation and the conservation of orbital angular momentum with high-order Laguerre-Gaussian modes. Phys. Rev. A 1997, 56, 4193. [Google Scholar] [CrossRef]
- Chen, S.Y.; Ding, P.F.; Pu, J.X. Second harmonic generation of off axial vortex beam in the case of walk-off effect. Opt. Commun. 2016, 370, 267–275. [Google Scholar] [CrossRef]
- Hu, X.P.; Xu, P.; Zhu, S.N. Engineered quasi-phase-matching for laser techniques. Photonics. Res. 2013, 1, 171–185. [Google Scholar] [CrossRef]
- Shao, G.H.; Wu, Z.J.; Chen, J.H.; Xu, F.; Lu, Y.Q. Nonlinear frequency conversion of fields with orbital angular momentum using quasi-phase-matching. Phys. Rev. A 2013, 88, 063827. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Li, Y.; Ding, D.S.; Zhang, W.; Shi, S.; Shi, B.S.; Guo, G.C. Highly efficient second harmonic generation of a light carrying orbital angular momentum in an external cavity. Opt. Expr. 2014, 22, 23673–23678. [Google Scholar] [CrossRef][Green Version]
- Heinze, J.; Vahlbruch, H.; Willke, B. Numerical analysis of LG3,3 second harmonic generation in comparison to the LG0,0 case. Opt. Expr. 2020, 28, 35816–35832. [Google Scholar] [CrossRef]
- Heinze, J.; Vahlbruch, H.; Willke, B. Frequency-doubling of continuous laser light in the Laguerre–Gaussian modes LG0,0 and LG3,3. Opt. Lett. 2020, 45, 5262–5265. [Google Scholar] [CrossRef]
- Li, S.M.; Kong, L.J.; Ren, Z.C.; Li, Y.N.; Tu, C.H.; Wang, H.T. Managing orbital angular momentum in second-harmonic generation. Phys. Rev. A 2013, 88, 035801. [Google Scholar] [CrossRef]
- Pereira, L.J.; Buono, W.T.; Tasca, D.S.; Dechoum, K.; Khoury, A.Z. Orbital-angular-momentum mixing in type-II second-harmonic generation. Phys. Rev. A 2017, 96, 053856. [Google Scholar] [CrossRef]
- Jarutis, V.; Matijosius, A.; Piskarskas, S.A.; Smilgevièius, V.; Stabinis, A. Second harmonic generation of hollow Bessel beams. In ICONO 2001: Nonlinear Optical Phenomena and Nonlinear Dynamics of Optical Systems; SPIE: Bellingham, WA, USA, 2002; Volume 4751, pp. 77–86. [Google Scholar]
- Dai, K.J.; Li, W.Z.; Morgan, K.S.; Li, Y.; Miller, J.K.; Watkins, R.J.; Johnson, E.G. Second-harmonic generation of asymmetric Bessel-Gaussian beams carrying orbital angular momentum. Opt. Expr. 2020, 28, 2536–2546. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, A.; Jangir, N.; Kad, P.; Walia, K.; Singh, A. Second harmonic generation of zeroth-order Bessel-Gaussian laser beam in collisionless plasma. Optik 2022, 269, 169867. [Google Scholar] [CrossRef]
- Piskarskas, A.; Smilgevičius, V.; Stabinis, A.; Jarutis, V. Noncollinear second-harmonic generation in periodically poled KTiOPO4 excited by the Bessel beam. Opt. Lett. 1999, 24, 1053–1055. [Google Scholar] [CrossRef] [PubMed]
- Jarutis, V.; Matijošius, A.; Smilgevičius, V.; Stabinis, A. Second harmonic generation of higher-order Bessel beams. Opt. Commun. 2000, 185, 159–169. [Google Scholar] [CrossRef]
- Saltiel, S.M.; Neshev, D.N.; Fischer, R.; Krolikowski, W.; Arie, A.; Kivshar, Y.S. Generation of second-harmonic bessel beams by transverse phase-matching in annular periodically poled structures. Jpn. J. Appl. Phys. 2008, 47, 6777. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Ding, D.S.; Jiang, Y.K.; Li, Y.; Shi, S.; Wang, X.S.; Shi, B.S. Orbital angular momentum light frequency conversion and interference with quasi-phase matching crystals. Opt. Expr. 2014, 22, 20298–20310. [Google Scholar] [CrossRef]
- Liu, J.; Duan, Y.M.; Li, Z.H.; Zhang, G.; Zhu, H.Y. Recent Progress in Nonlinear Frequency Conversion of Optical Vortex Lasers. Front. Phys. 2022, 10, 865029. [Google Scholar] [CrossRef]
- Dai, K.; Miller, J.K.; Li, W.; Watkins, R.J.; Johnson, E.G. Fractional orbital angular momentum conversion in second-harmonic generation with an asymmetric perfect vortex beam. Opt. Lett. 2021, 46, 3332–3335. [Google Scholar] [CrossRef]
- Han, J.X.; Tang, X.Y.; Yin, Z.M.; Wang, K.; Fu, Y.; Wang, B.Y.; Chen, Y.B.; Zhang, C.; Jin, C. Role of fractional high harmonics with non-integer OAM on the generation of a helical attosecond pulse train. Opt. Expr. 2022, 30, 47942–47956. [Google Scholar] [CrossRef]
- Ni, R.; Niu, Y.F.; Du, L.; Hu, X.P.; Zhang, Y.; Zhu, S.N. Topological charge transfer in frequency doubling of fractional orbital angular momentum state. Appl. Phys. Lett. 2016, 109, 151103. [Google Scholar] [CrossRef]
- Stanislovaitis, P.; Matijosius, A.; Ivanov, M.; Smilgevicius, V. Topological charge transformation of beams with embedded fractional phase step in the process of second harmonic generation. J. Opt. 2017, 19, 105603. [Google Scholar]
- Liu, Z.F.; Ren, Z.C.; Lou, Y.C.; Cheng, Z.M.; Yang, Y.X.; Li, Y.N.; Ding, J.P.; Wang, X.L.; Wang, H.T. Control of harmonic orbital angular momentum in second-harmonic generation of perfect vortices. Phys. Rev. A 2022, 105, 063518. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Li, P.; Ma, J.B.; Zhang, S.R.; Gu, Y.Z. Generation and Detection of Optical Vortices with Multiple Cascaded Spiral Phase Plates. Photonics 2022, 9, 354. [Google Scholar] [CrossRef]
- Wu, Y.J.; Liu, H.G.; Chen, X.F. Highly efficient detection of near-infrared optical vortex modes with frequency upconversion. Opt. Lett. 2022, 47, 2474–2477. [Google Scholar] [CrossRef] [PubMed]
- Venkataraman, V.; Ghosh, J. Impact of focusing and polarization inhomogeneity on SHG in type-II PPKTP. J. Opt. 2023, 25, 055501. [Google Scholar]
- Assanto, G.; Wang, Z.; Hagan, D.J.; VanStryland, E.W. All-optical modulation via nonlinear cascading in type II second-harmonic generation. Appl. Phys. Lett. 1995, 67, 2120–2122. [Google Scholar] [CrossRef]
- Ma, J.B.; Li, P.; Zhou, Z.H.; Gu, Y.Z. Characteristics of fork-shaped fringes formed by off-axis interference of two vortex beams. J. Opt. Soc. Am. A 2021, 38, 115–123. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.Y.; Liu, S.L.; Liu, S.K.; Yang, C.; Xu, Z.H.; Li, Y.H.; Shi, B.S. Frequency doubling of twisted light independent of the integer topological charge. OSA Continuum. 2019, 2, 470–477. [Google Scholar] [CrossRef]
- Oemrawsingh, S.S.R.; Van Houwelingen, J.A.W.; Eliel, E.R.; Woerdman, J.P.; Verstegen, E.J.K.; Kloosterboer, J.G.; Hooft, G.W. Production and characterization of spiral phase plates for optical wavelengths. Appl. Opt. 2004, 43, 688–694. [Google Scholar] [CrossRef]
- Wu, L.X.; Feng, X.K.; Lin, Z.Z.; Wen, Y.H.; Chen, H.J.; Chen, Y.J.; Yu, S.Y. Spiral fractional vortex beams. Opt. Expr. 2023, 31, 7813–7824. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.X.; Yusufu, T.; Ma, Y.Y.; Omatsu, T. Generation of tunable, non-integer OAM states from an optical parametric oscillator. Appl. Phys. Lett. 2023, 122, 121106. [Google Scholar] [CrossRef]



| lf | 0 | 1 | 2 | 3 | 4 |
| 1 | |||||
| lf | 5 | 6 | 7 | 8 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Hou, W.; Tao, X.; Guo, M.; Li, Y.; Li, P. Second-Harmonic Generation of the Vortex Beams with Integer and Fractional Topological Charges. Photonics 2023, 10, 867. https://doi.org/10.3390/photonics10080867
Zhang S, Hou W, Tao X, Guo M, Li Y, Li P. Second-Harmonic Generation of the Vortex Beams with Integer and Fractional Topological Charges. Photonics. 2023; 10(8):867. https://doi.org/10.3390/photonics10080867
Chicago/Turabian StyleZhang, Shirui, Weizhou Hou, Xin Tao, Minghao Guo, Yueqing Li, and Peng Li. 2023. "Second-Harmonic Generation of the Vortex Beams with Integer and Fractional Topological Charges" Photonics 10, no. 8: 867. https://doi.org/10.3390/photonics10080867
APA StyleZhang, S., Hou, W., Tao, X., Guo, M., Li, Y., & Li, P. (2023). Second-Harmonic Generation of the Vortex Beams with Integer and Fractional Topological Charges. Photonics, 10(8), 867. https://doi.org/10.3390/photonics10080867





