Modification of the Emission Spectrum of a Quantum Emitter in the Vicinity of Bismuth Chalcogenide Microparticles
Abstract
1. Introduction
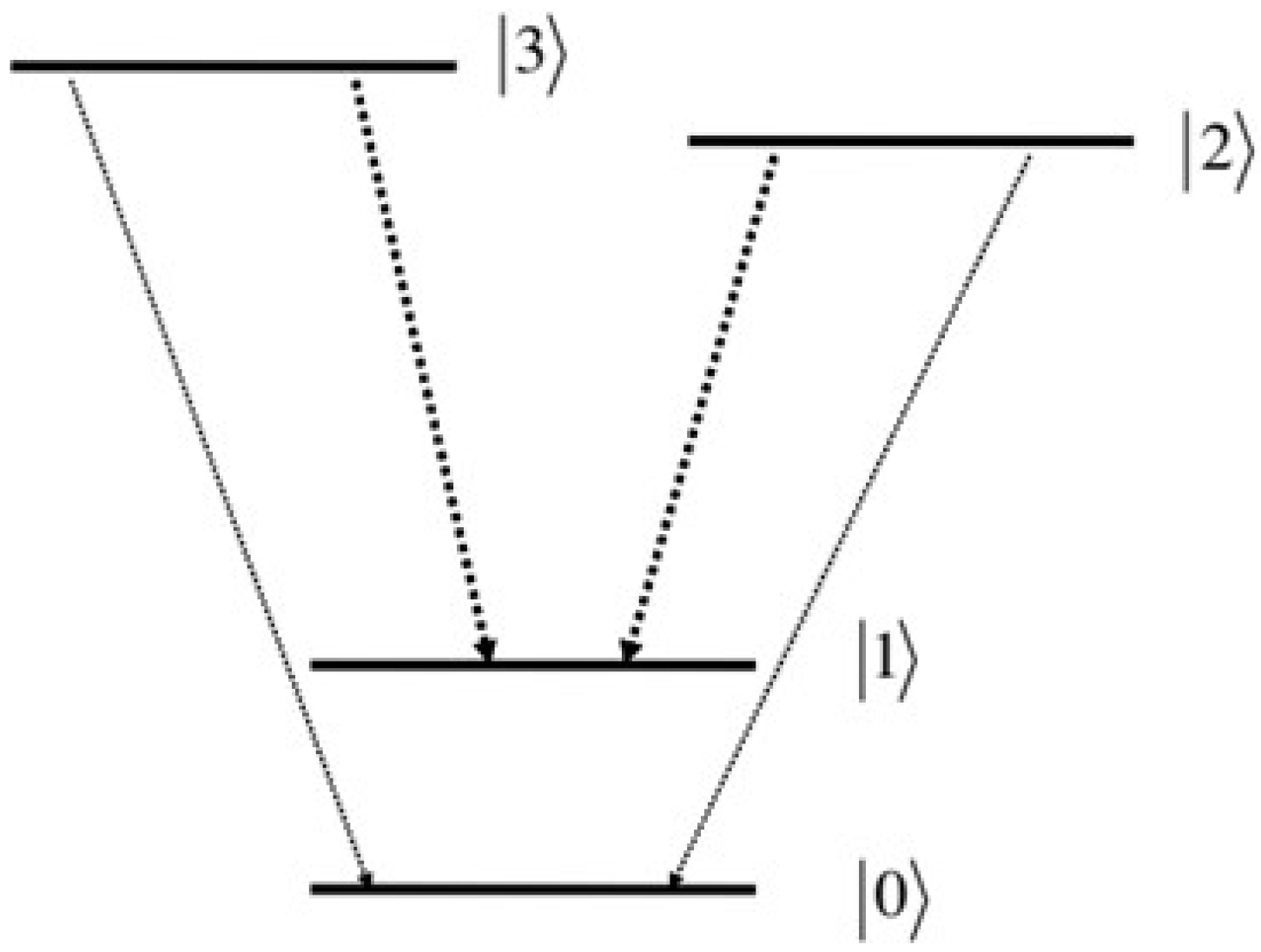
2. Quantum Interference in a Double-V-Type Quantum Emitter
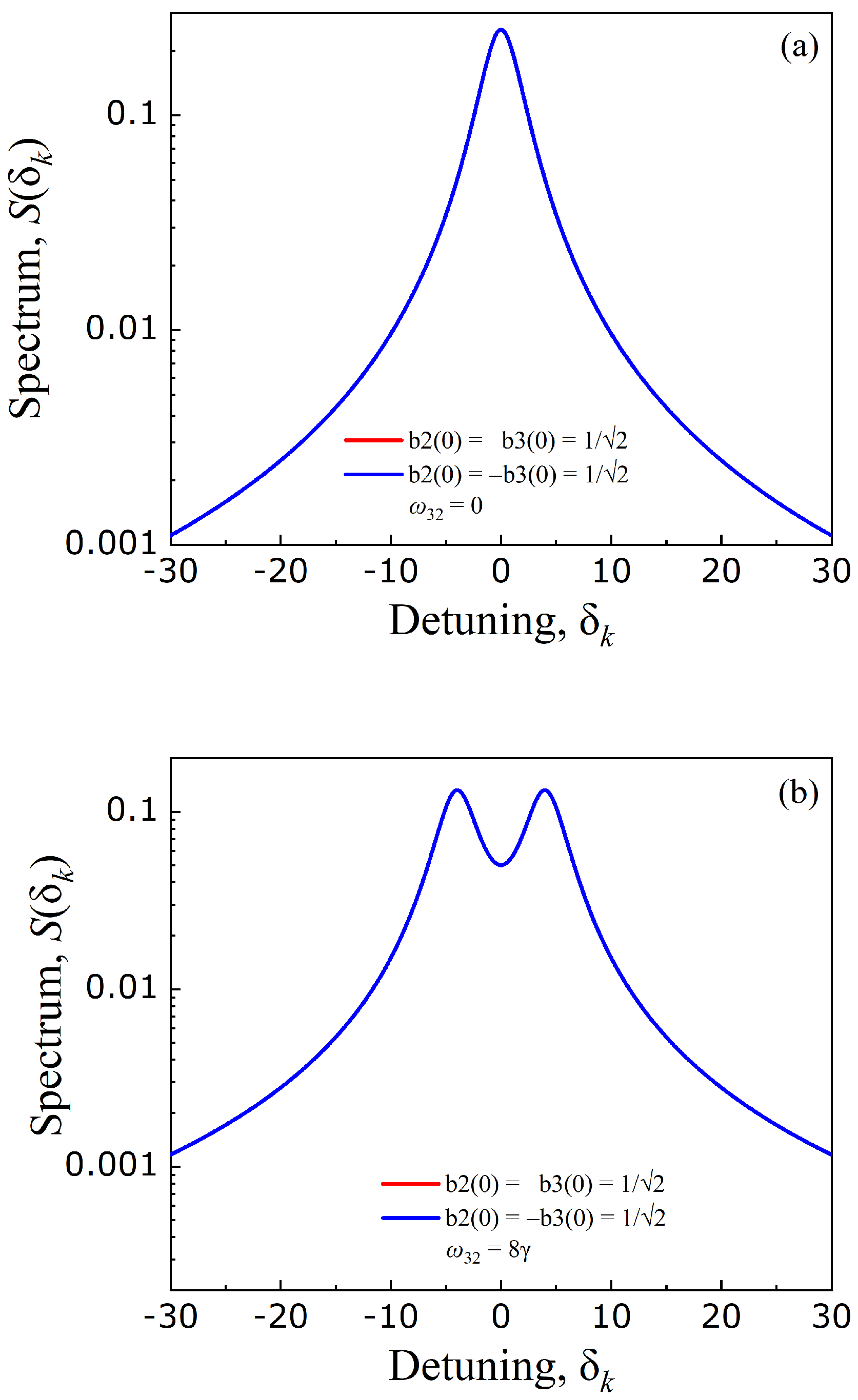
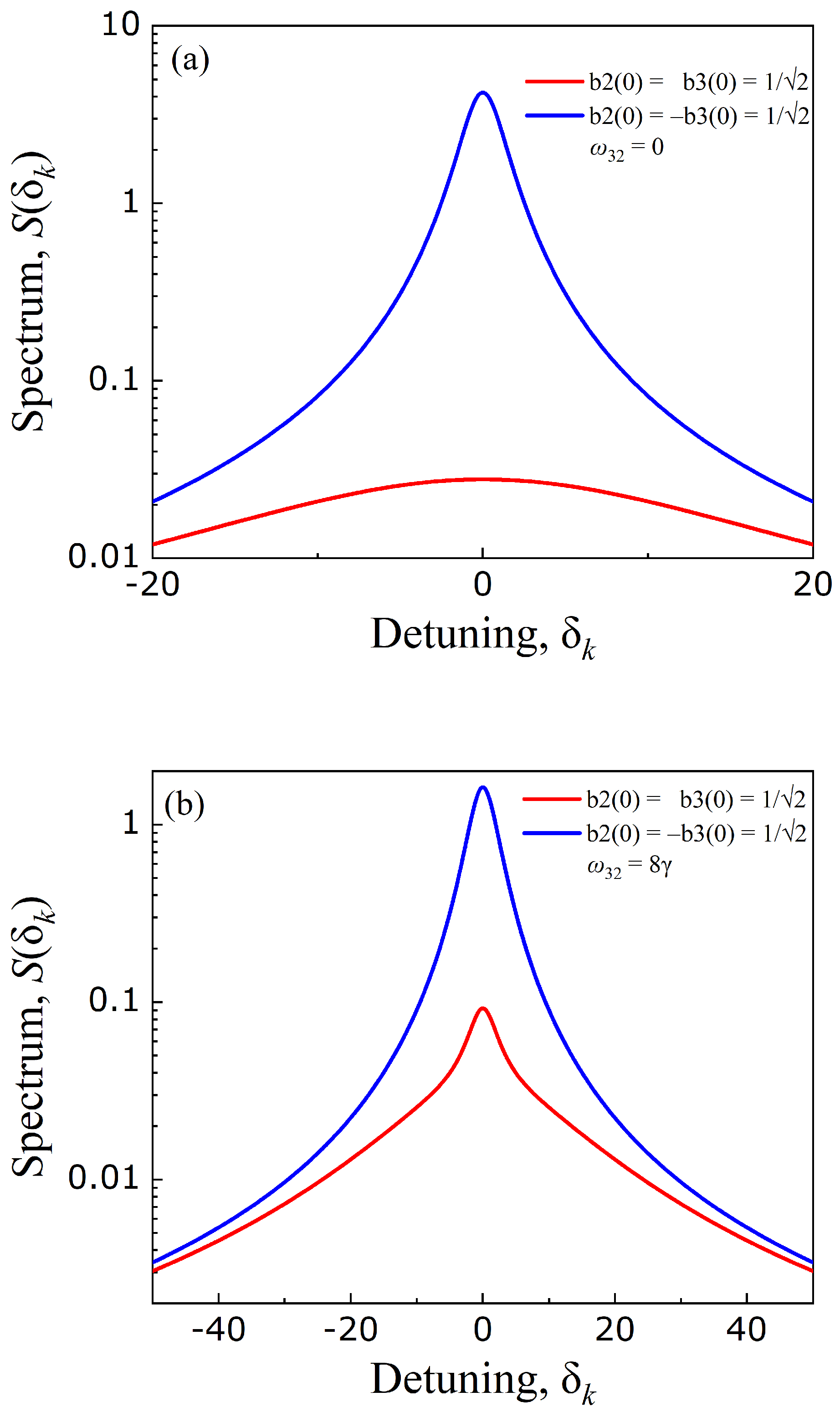
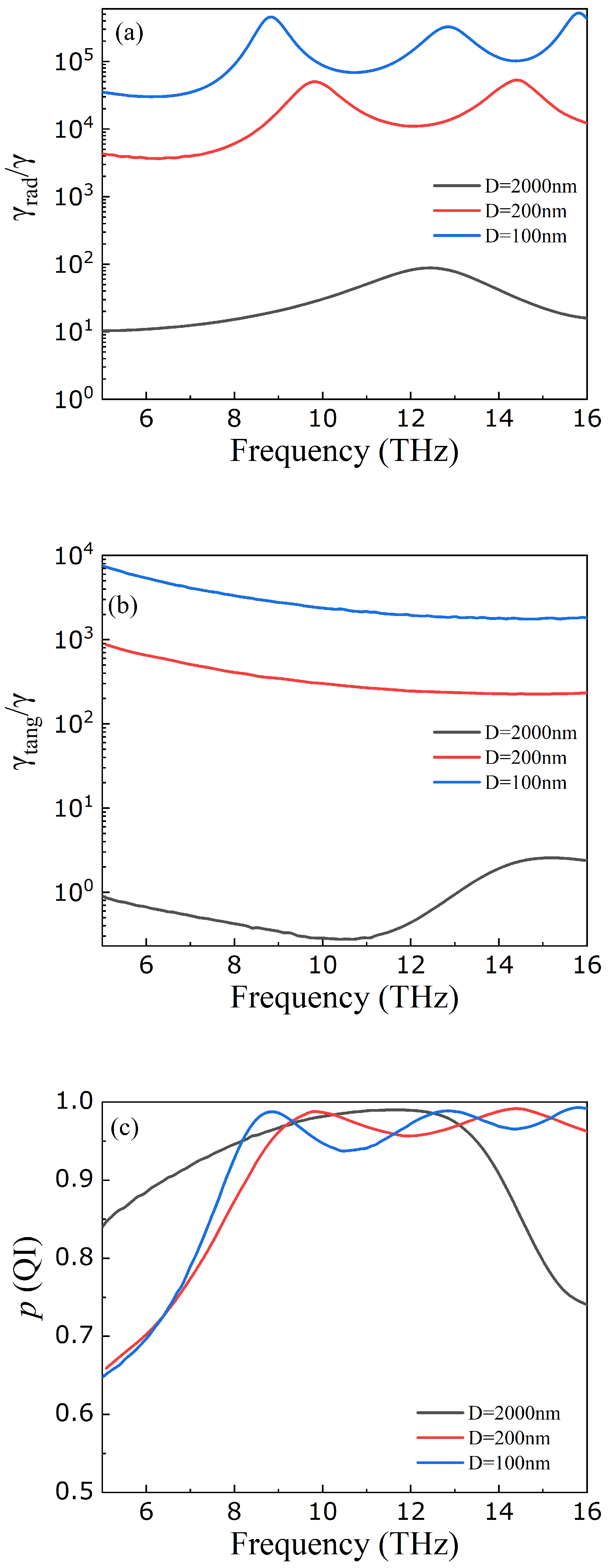
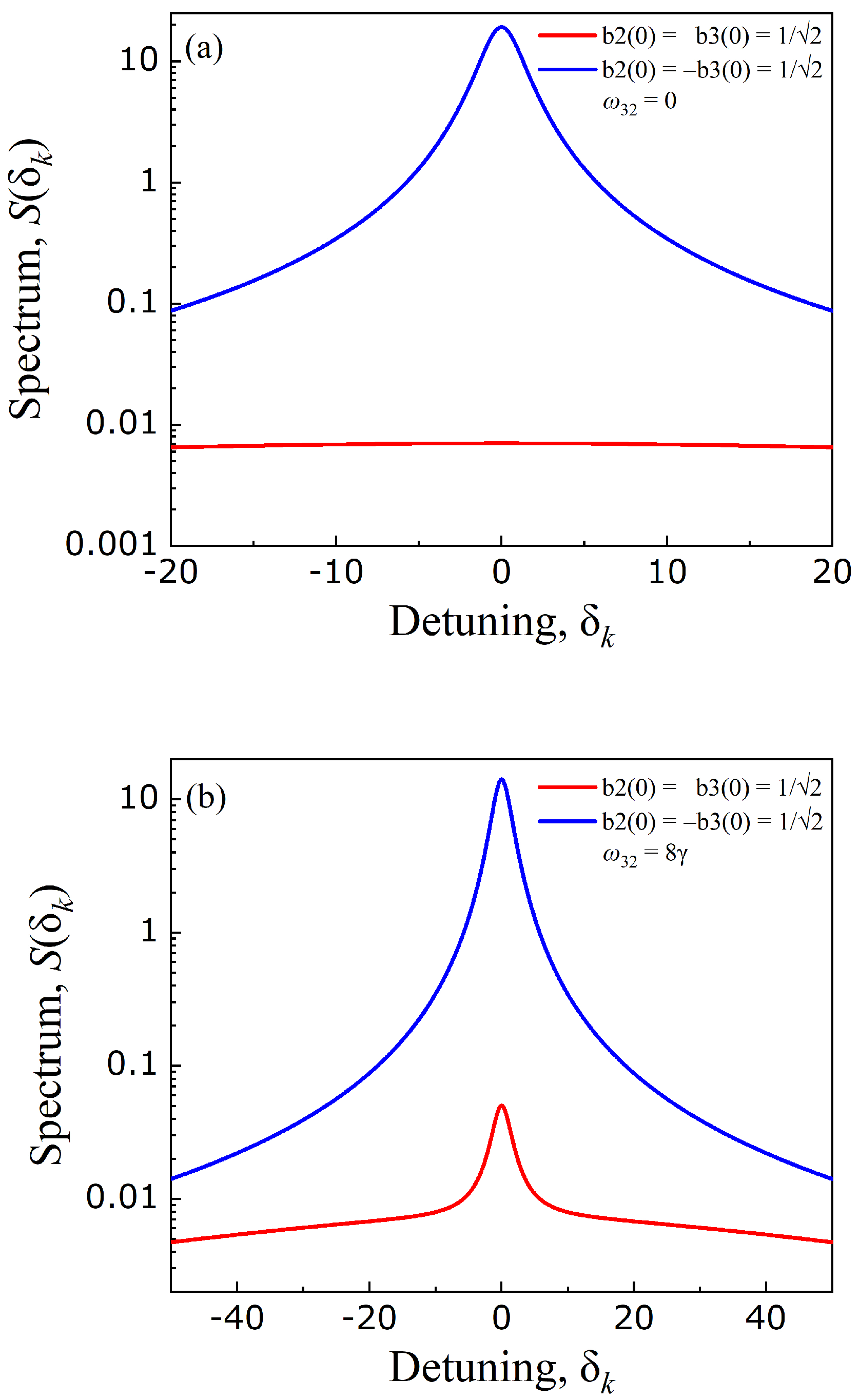
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tame, M.; McEnery, K.; Özdemir, Ş.; Lee, J.; Maier, S.A.; Kim, M.S. Quantum plasmonics. Nat. Phys. 2013, 9, 329. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347. [Google Scholar] [CrossRef]
- Hohenester, U. Nano and Quantum Optics: An Introduction to Basic Principles and Theory; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Tserkezis, C.; Fernandez-Dominguez, A.I.; Dias Gonçalves, P.A.; Todisco, F.; Cox, J.D.; Busch, K.; Stenger, N.; Bozhevolnyi, S.I.; Mortensen, N.A.; Wolff, C. On the applicability of quantum-optical concepts in strong-coupling nanophotonics. Rep. Prog. Phys. 2020, 83, 082401. [Google Scholar] [CrossRef] [PubMed]
- Schuller, J.; Barnard, E.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193. [Google Scholar] [CrossRef] [PubMed]
- Baranov, D.G.; Wersäll, M.; Cuadra, J.; Antosiewicz, T.J.; Shegai, T. Novel Nanostructures and Materials for Strong Light–Matter Interactions. ACS Photonics 2018, 5, 24. [Google Scholar] [CrossRef]
- Purcell, E.M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 1946, 69, 681. [Google Scholar]
- Drexhage, K.H. Influence of a dielectric interface on fluorescence decay time. J. Luminesc. 1970, 1, 693–701. [Google Scholar] [CrossRef]
- Drexhage, K.H. Interaction of light with monomolecular dye lasers. Prog. Opt. 1974, 12, 163–232. [Google Scholar]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photon. Rev. 2010, 4, 795. [Google Scholar] [CrossRef]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative plasmonic materials: Beyond gold and silver. Adv. Mater. 2013, 25, 3264. [Google Scholar] [CrossRef]
- Kinsey, N.; Ferrera, M.; Shalaev, V.M.; Boltasseva, A. Examining nanophotonics for integrated hybrid systems: A review of plasmonic interconnects and modulators using traditional and alternative materials. J. Opt. Soc. Am. B Opt. Phys. 2015, 32, 121. [Google Scholar] [CrossRef]
- Xia, C.; Li, J. Recent advances in optoelectronic properties and applications of two-dimensional metal chalcogenides. J. Semicond. 2016, 37, 051001. [Google Scholar] [CrossRef]
- You, J.W.; Bongu, S.R.; Bao, Q.; Panoiu, N.C. Nonlinear optical properties and applications of 2D materials: Theoretical and experimental aspects. Nanophotonics 2018, 8, 63. [Google Scholar] [CrossRef]
- Mandal, A.; Cui, Y.; McRae, L.; Gholipour, B. Reconfigurable chalcogenide phase change metamaterials: A material, device, and fabrication perspective. J. Phys. Photonics 2021, 3, 022005. [Google Scholar] [CrossRef]
- Dubroka, A.; Caha, O.; Hroncek, M.; Friš, P.; Orlita, M.; Holý, V.; Steiner, H.; Bauer, G.; Springholz, G.; Humlicek, J. Interband absorption edge in the topological Bi(Te1−xSex)3. Phys. Rev. B 2017, 96, 235202. [Google Scholar] [CrossRef]
- Siroki, G.; Lee, D.; Haynes, P. Single-electron induced surface plasmons on a topological nanoparticle. Nat. Commun. 2016, 7, 12375. [Google Scholar] [CrossRef]
- Rider, M.S.; Sokolikova, M.; Hanham, S.M.; Navarro-Cia, M.; Haynes, P.D.; Lee, D.K.K.; Daniele, M.; Guidi, M.C.; Mattevi, C.; Lupi, S.; et al. Experimental signature of a topological quantum dot. Nanoscale 2020, 12, 22817–22825. [Google Scholar] [CrossRef]
- Kianinia, M.; Xu, Z.-Q.; Toth, M.; Aharonovich, I. Quantum emitters in 2D materials: Emitter engineering, photophysics, and integration in photonic nanostructures. Appl. Phys. Rev. 2022, 9, 011306. [Google Scholar] [CrossRef]
- Colas des Francs, G.; Barthes, J.; Bouhelier, A.; Weeber, J.C.; Dereux, A.; Cuche, A.; Girard, C. Plasmonic Purcell factor and coupling efficiency to surface plasmons. Implications for addressing and controlling optical nanosources. J. Opt. 2016, 18, 094005. [Google Scholar] [CrossRef]
- Chatzidakis, G.D.; Yannopapas, V. Strong electromagnetic coupling in dimers of topological-insulator nanoparticles and quantum emitters. Phys. Rev. B 2020, 101, 165410. [Google Scholar] [CrossRef]
- Karaoulanis, D.; Paspalakis, E.; Yannopapas, V. Quantum interference near bismuth-chalcogenide microstructures. J. Opt. Soc. Am. B 2021, 38, 3301–3308. [Google Scholar] [CrossRef]
- Kyvelos, N.; Tsigaridas, G.; Paspalakis, E.; Yannopapas, V. Quantum Interference in Spontaneous Decay of a Quantum Emitter Placed in a Dimer of Bismuth-Chalcogenide Microparticles. Photonics 2022, 9, 596. [Google Scholar] [CrossRef]
- Vladimirova, Y.V.; Zadkov, V.N. Quantum Optics in Nanostructures. Nanomaterials 2021, 11, 1919. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, G.S. Anisotropic Vacuum-Induced Interference in Decay Channels. Phys. Rev. Lett. 2000, 84, 5500–5503. [Google Scholar] [CrossRef]
- Paspalakis, E.; Keitel, C.H.; Knight, P.L. Fluorescence control through multiple interference mechanisms. Phys. Rev. A 1998, 58, 4868. [Google Scholar] [CrossRef]
- Ficek, Z.; Swain, S. Simulating quantum interference in a three-level system with perpendicular transition dipole moments. Phys. Rev. A 2004, 69, 023401. [Google Scholar] [CrossRef]
- Zhu, S.-Y.; Scully, M.O. Spectral line elimination and spontaneous emission cancellation via quantum interference. Phys. Rev. Lett. 1996, 76, 388–391. [Google Scholar] [CrossRef]
- Menon, S.; Agarwal, G.S. Gain components in the Autler-Townes doublet from quantum interferences in decay channels. Phys. Rev. A 1999, 61, 013807. [Google Scholar] [CrossRef]
- Evangelou, S.; Yannopapas, V.; Paspalakis, E. Simulating quantum interference in spontaneous decay near plasmonic nanostructures: Population dynamics. Phys. Rev. A 2011, 83, 055805. [Google Scholar] [CrossRef]
- Hughes, S.; Agarwal, G.S. Anisotropy-Induced Quantum Interference and Population Trapping between Orthogonal Quantum Dot Exciton States in Semiconductor Cavity Systems. Phys. Rev. Lett. 2017, 118, 063601. [Google Scholar] [CrossRef]
- Karanikolas, V.; Paspalakis, E. Plasmon-induced quantum interference near carbon nanostructures. J. Phys. Chem. C 2018, 122, 1478. [Google Scholar] [CrossRef]
- Das, S.; Agarwal, G.S. Protecting bipartite entanglement by quantum interferences. Phys. Rev. A 2010, 81, 052341. [Google Scholar] [CrossRef]
- Iliopoulos, N.; Terzis, A.F.; Yannopapas, V.; Paspalakis, E. Prolonging entanglement dynamics near periodic plasmonic nanostructures. Phys. Rev. B 2017, 96, 075405. [Google Scholar] [CrossRef]
- Sangshekan, B.; Sahrai, M.; Asadpour, S.H. Controllable atom-photon entanglement via quantum interference near plasmonic nanostructure. Sci. Rep. 2022, 12, 677. [Google Scholar] [CrossRef]
- Zhou, P.; Swain, S. Quantum interference in probe absorption: Narrow resonances, transparency, and gain without population inversion. Phys. Rev. Lett. 1997, 78, 832–835. [Google Scholar] [CrossRef]
- Paspalakis, E.; Gong, S.-Q.; Knight, P.L. Spontaneous emission induced coherent effects in absorption and dispersion of a V-type three-level atom. Opt. Commun. 1998, 152, 293–298. [Google Scholar] [CrossRef]
- Zhou, P.; Swain, S. Ultranarrow spectral lines via quantum interference. Phys. Rev. Lett. 1996, 77, 3995. [Google Scholar] [CrossRef]
- Wang, C.-L.; Kang, Z.-H.; Tian, S.-C.; Jiang, Y.; Gao, J.-Y. Effect of spontaneously generated coherence on absorption in a V-type system: Investigation in dressed states. Phys. Rev. A 2009, 79, 043810. [Google Scholar] [CrossRef]
- Kosionis, S.G.; Yannopapas, V.; Thanopulos, I.; Paspalakis, E. Controlling resonance fluorescence spectra and photon statistics in a driven V-Type quantum emitter—metal nanoparticle coupled structure. Photonics 2022, 9, 629. [Google Scholar] [CrossRef]
- Evangelou, S.; Yannopapas, V.; Paspalakis, E. Transparency and slow light in a four-level quantum system near a plasmonic nanostructure. Phys. Rev. A 2012, 86, 053811. [Google Scholar] [CrossRef]
- Evangelou, S.; Yannopapas, V.; Paspalakis, E. Modifying free-space spontaneous emission near a plasmonic nanostructure. Phys. Rev. A 2011, 83, 023819. [Google Scholar] [CrossRef]
- Chen, H.; Ren, J.; Gu, Y.; Zhao, D.-X.; Zhang, J.; Gong, Q. Nanoscale Kerr Nonlinearity Enhancement Using Spontaneously Generated Coherence in Plasmonic Nanocavity. Sci. Rep. 2015, 5, 18315. [Google Scholar] [CrossRef] [PubMed]
- Paspalakis, E.; Kylstra, N.J.; Knight, P.L. Transparency induced via decay interference. Phys. Rev. Lett. 1999, 82, 2079. [Google Scholar] [CrossRef]
- Bortman-Arbiv, D.; Wilson-Gordon, A.D.; Friedmann, H. Phase control of group velocity: From subluminal to superluminal light propagation. Phys. Rev. A 2001, 63, 043818. [Google Scholar] [CrossRef]
- Gurudev Dutt, M.V.; Cheng, J.; Li, B.; Xu, X.; Li, X.; Berman, P.R.; Steel, D.G.; Bracker, A.S.; Gammon, D.; Economou, S.E.; et al. Stimulated and spontaneous optical generation of electron spin coherence in charged GaAs quantum dots. Phys. Rev. Lett. 2005, 94, 227403. [Google Scholar] [CrossRef] [PubMed]
- Niu, Y.-P.; Gong, S.-Q. Enhancing Kerr nonlinearity via spontaneously generated coherence. Phys. Rev. A 2006, 73, 053811. [Google Scholar] [CrossRef]
- Asadpour, S.H.; Sahrai, M.; Soltani, A.; Hamedi, H.R. Enhanced Kerr nonlinearity via quantum interference from spontaneous emission. Phys. Lett. A 2012, 376, 147–152. [Google Scholar] [CrossRef]
- Thanopulos, I.; Yannopapas, V.; Paspalakis, E. Non-Markovian dynamics in plasmon-induced spontaneous emission interference. Phys. Rev. B 2017, 95, 075412. [Google Scholar] [CrossRef]
- Barnett, S.M.; Radmore, P.M. Methods in Theoretical Quantum Optics; Chapter 7; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Xu, J.-P.; Wang, L.-G.; Yang, Y.-P.; Lin, Q.; Zhu, S.-Y. Quantum interference between two orthogonal transitions of an atom in one-dimensional photonic crystals. Opt. Lett. 2008, 33, 2005. [Google Scholar] [CrossRef]
- Yannopapas, V.; Paspalakis, E.; Vitanov, N.V. Plasmon-induced enhancement of quantum interference near metallic nanostructures. Phys. Rev. Lett. 2009, 103, 063602. [Google Scholar] [CrossRef]
- Xu, J.-P.; Yang, Y.-P. Quantum interference of V-type three-level atom in structures made of left-handed materials and mirrors. Phys. Rev. A 2010, 81, 013816. [Google Scholar] [CrossRef]
- Li, G.X.; Li, F.L.; Zhu, S.-Y. Quantum interference between decay channels of a three-level atom in a multilayer dielectric medium. Phys. Rev. A 2001, 64, 013819. [Google Scholar] [CrossRef]
- Yang, Y.-P.; Xu, J.-P.; Chen, H.; Zhu, S.-Y. Quantum Interference Enhancement with Left-Handed Materials. Phys. Rev. Lett. 2008, 100, 043601. [Google Scholar] [CrossRef]
- Li, G.-X.; Evers, J.; Keitel, C.H. Spontaneous emission interference in negative-refractive-index waveguides. Phys. Rev. B 2009, 80, 045102. [Google Scholar] [CrossRef]
- Pelton, M. Modified spontaneous emission in nanophotonic structures. Nat. Photon. 2015, 9, 427–435. [Google Scholar] [CrossRef]
- Yannopapas, V.; Vitanov, N.V. Spontaneous emission of two-level atoms placed within clusters of metallic nanoparticles. J. Phys. Cond. Matter 2007, 19, 096210. [Google Scholar] [CrossRef]
- Yannopapas, V.; Vitanov, N.V. Electromagnetic Green’s tensor and local density of states calculations for collections of spherical scatterers. Phys. Rev. B 2007, 75, 115124. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadaki, M.-G.; Kyvelos, N.; Paspalakis, E.; Yannopapas, V. Modification of the Emission Spectrum of a Quantum Emitter in the Vicinity of Bismuth Chalcogenide Microparticles. Photonics 2023, 10, 658. https://doi.org/10.3390/photonics10060658
Papadaki M-G, Kyvelos N, Paspalakis E, Yannopapas V. Modification of the Emission Spectrum of a Quantum Emitter in the Vicinity of Bismuth Chalcogenide Microparticles. Photonics. 2023; 10(6):658. https://doi.org/10.3390/photonics10060658
Chicago/Turabian StylePapadaki, Margarita-Georgia, Nikolaos Kyvelos, Emmanuel Paspalakis, and Vassilios Yannopapas. 2023. "Modification of the Emission Spectrum of a Quantum Emitter in the Vicinity of Bismuth Chalcogenide Microparticles" Photonics 10, no. 6: 658. https://doi.org/10.3390/photonics10060658
APA StylePapadaki, M.-G., Kyvelos, N., Paspalakis, E., & Yannopapas, V. (2023). Modification of the Emission Spectrum of a Quantum Emitter in the Vicinity of Bismuth Chalcogenide Microparticles. Photonics, 10(6), 658. https://doi.org/10.3390/photonics10060658






