Survey on Applications of Machine Learning in Low-Cost Non-Coherent Optical Systems: Potentials, Challenges, and Perspective

Abstract

Direct Detection (DD) optical performance monitoring (OPM), Modulation Format Identification (MFI), and Baud Rate Identification (BRI) are envisioned as crucial components of future-generation optical networks. They bring to optical nodes and receivers a form of adaptability and intelligent control that are not available in legacy networks. Both are critical to managing the increasing data demands and data diversity in modern and future communication networks (e.g., 5G and 6G), for which optical networks are the backbone. Machine learning (ML) has been playing a growing role in enabling the sought-after adaptability and intelligent control, and thus, many OPM, MFI, and BRI solutions are being developed with ML algorithms at their core. This paper presents a comprehensive survey of the available ML-based solutions for OPM, MFI, and BFI in non-coherent optical networks. The survey is conducted from a machine learning perspective with an eye on the following aspects: (i) what machine learning paradigms have been followed; (ii) what learning algorithms are used to develop DD solutions; and (iii) what types of DD monitoring tasks have been commonly defined and addressed. The paper surveys the most widely used features and ML-based solutions that have been considered in DD optical communication systems. This results in a few observations, insights, and lessons. It highlights some issues regarding the ML development procedure, the dataset construction and training process, and the solution benchmarking dataset. Based on those observations, the paper shares a few insights and lessons that could help guide future research.

1. Introduction

Mobile broadband could be viewed as a prominent means to get people and machines connected. The International Telecommunication Union (ITU) estimates the number of worldwide mobile broadband subscribers in 2021 to be in the neighborhood of 6.9 billion [1]. This number represents a 24% growth in subscriptions since 2019 (an additional of roughly 1.2 billion subscribers), and it is approximately 5 times the number of fixed broadband subscribers in 2022. Such numbers indicate how reliant the world is on wireless connectivity.

Technologies such as 4th and 5th generation (4G and 5G) cellular networks represent major contributors to the data traffic generated by mobile broadband subscribers. The backbone of such technologies is optical fiber; it represents the main medium for backhaul connections, which link cellular networks together and to the Internet. Communication through a network of optical fibers (henceforth referred to as an optical network) has to meet the growing demands for mobile traffic (the amount of data transferred through wireless links) as well as the growing demand for high data-rates (i.e., increasing per-link wireless throughput).

Optical networks need to evolve in order to shoulder the burden of increasing traffic. Current optical networks are static, where the physical channel path from the transmitter to the receiver is fixed. This network architecture reduces the complexity and requirements of the network nodes and terminals, yet it lacks the elasticity and reconfigurability that allow it to meet traffic demands. Future optical networks, such as cognitive networks, are expected to be dynamic [2], spectrum grid-free, and modulation format-free [3,4]. A transition towards elastic and reconfigurable networks, however, comes at a price. Impairments experienced by the network become time-variant because of the constantly changing network routes (i.e., light paths). Those impairments result in fluctuations in the network performance, which degrade the spectrum efficiency. It is, hence, crucial for the network to be able to track and anticipate performance fluctuations along different optical links in real-time [2,5,6].

Future optical networks need to be capable of self-diagnosing and self-optimizing. This means that the network can detect anomalies along specific paths and optimize its operation. For instance, it could adjust its traffic routing, adapt the modulation format of signals based on link and traffic conditions, and predict future network demands or failures along different paths. Achieving such levels of adaptability and control mandates the acquisition of data through the monitoring of some key network parameters. The monitoring involves measuring and estimating different physical parameters of transmitted signals and components in the network, whether at the receiver or at an intermediate node [7]. Common physical parameters include chromatic dispersion (CD), polarization mode dispersion (PMD), differential group delay (DGD), optical signal to noise ratio (OSNR), Q-factor, polarization dependent loss (PDL), and fiber nonlinearities. Conventional performance monitoring techniques require a complete recovery of the transmitted signal to measure and estimate the parameters. In addition, signal parameters need to be known at various distributed points along the network to allow for mitigation of signal degradation. This adds significant complexity and cost to the monitoring system, and to the whole network.

1.1. The Challenge

Coherent receivers and digital signal processing are typical methods for recovering signal information at the optical system’s end node [8]. However, it would be too expensive to use them in the optical system’s intermediate nodes. The demand for low-cost and high-speed optical networks has become more and more prominent in recent years [9]. Compared with its coherent detection counterpart, direct detection (DD) is widely adopted for short-reach links such as data center interconnects and intermediate nodes due to its simple structure and low cost.

The DD optical communication system comprises three main segments: (1) optical transmitter, where electrical-to-optical signal conversion and laser modulation are achieved. Different types of modulation formats can be generated to improve the spectral efficiency of optical systems. (2) Optical channel, where optical signals are transmitted and impaired with various channel impairments, depending on the optical channel type. The wire channel introduces linear impairments such as fiber chromatic dispersion (CD), polarization mode dispersion (PMD), mode-coupling (MC), etc., and non-linear impairments such as self-phase modulation (SPM), cross-phase modulation (XPM), and four-wave mixing. Whereas wireless optical channels are characterized by different impairment types such as weather turbulence and pointing error. (3) Optical receiver, where optical-to-electrical conversion is accomplished as well as signal demodulation and decoding. A simple and low-cost photodetector is employed to recover the transmitted electrical signals. At this stage, ML algorithms can be used to identify the different modulation formats and/or monitor optical signal performance.

The reduction of hardware requirements and costs in direct detection does not come without challenges. It inevitably brings about many detrimental linear and/or nonlinear effects on the DD systems, which could lead to severe degradation in system performance. Therefore, it is crucial to develop algorithms to monitor these introduced effects (impairments). The proposed OPM techniques themselves must adhere to the low-cost requirement to which direct detection adheres. This is because their implementation on a large number of intermediate nodes will entail high deployment costs. Further, the proposed algorithms should be able to monitor multiple parameters simultaneously and be transparent to signals with different baud rates and modulation formats to satisfy the demands of intelligent network management [10,11,12]. As stated earlier, conventional OPM methods are unable to meet these requirements because they are either too expensive or sophisticated, and most of them can only monitor a single type of parameter [13].

1.2. Motivation

Machine learning (ML) has emerged as a promising contender for monitoring and optimization in optical networks. It avoids the strict need to recover the original signal, such as conventional monitoring and optimization techniques do. ML algorithms are developed to learn the network conditions from propagating signals at different points, and they are able to predict those conditions proactively. Such ability is valuable for an array of reasons. Following is a brief discussion of some of the most important ones [7,14].

• Fault detection and reconfigurability: OPM and MFI with machine learning enable an optical network to identify failures proactively. This is an important feature, for it allows the network to reconfigure its parameters and mitigate the consequences of incoming failures [15,16].
• Network security: OPM and MFI provide a means to secure optical networks; an attack on the network usually results in disruptions to the network parameters. Detecting the disruption may aid in the discovery of attacks and, maybe, in preventing them. This could be enabled by OPM and MFI using machine learning [17].
• Boosting network efficiency: Implementing OPM and MFI with machine learning helps the optical network improve its utilization of resources. Proactively anticipating certain events, such as failures and traffic bursts, provides valuable information for the network to adjust its resource utilization in the best way possible [15].

1.3. Related Survey Articles

Recently, a number of review papers have appeared addressing the utilization of ML for various optical applications such as fiber non-linearity compensation [18,19,20], nonlinear phase noise (PN) compensation [21], optical biosensors [22], photonics modeling [23], and nonlinear equalizers design [19]. Common to all that work is the utilization of machine learning to build models that mitigate the channel or impairment effect, especially in cases where theoretical analysis is not feasible [2,19]. Moreover, the authors in ref. [22] discuss the challenges in various research fields and how machine learning and soft computing have improved efficiency in different applications. Soft computing is inspired by natural systems, mainly the human brain, and incorporates uncertainty and imprecision that are inherent to the real world. Machine learning is related to the ability of machines to infer approximate solutions from past data or to discover patterns and rules from unknown data. The article also highlights the opportunities for optical biosensors based on nonlinear optics for the detection of the SARS-CoV-2 virus and how nonlinear optical applications assisted by ML have increased their efficiency and speed, making them a potential tool for sensing performance.

Recently, ML has been proposed in the literature for performing optical performance monitoring (OPM) and modulation format identification (MFI) [24], which enables the use of adaptive modulation formats according to the transmission conditions [25].

Existing and future OPM methods for both direct and coherent detection systems are reviewed in ref. [7], but it presents a broad range of techniques with no focus on ML techniques. A detailed review of the different ML techniques is given in ref. [15,20,26,27], which highlights their use in optical communications and networking functions such as OPM, fault detection, non-linearity compensation, and software-defined networking. The paper in ref. [15] introduces artificial neural networks and support vector machines, followed by other popular ML techniques such as K-means clustering, expectation-maximization (EM) algorithms, principal component analysis (PCA), and independent component analysis (ICA). It also investigates the more recent deep learning (DL) approaches such as deep neural networks (DNNs), convolutional neural networks (CNNs), and recurrent neural networks (RNNs). The analytical derivations presented in ref. [15] are slightly different from those in standard introductory ML material to better align with the fields of communications and signal processing. The paper further discussed the applications of ML techniques in various aspects of optical communications and networking. The work in ref. [26] gives an overview of the application of ML to both areas of optical communication and optical networking to potentially stimulate new cross-layer research directions. However, the review has limited coverage of OPM and MFI. A detailed survey on OPM and MFI has been done in ref. [24], in terms of standards, monitoring parameters, availability of commercial products, and their limitations. The survey considers the ML techniques, proposed during the last two decades for MFI, OPM, and joint MFI/OPM for direct and coherent optical networks. It further evaluates and compares the different proposed techniques in a tabular manner according to different algorithmic aspects. The authors in ref. [20] focus on the implementation of fully learnable ANN transceivers, or auto-encoders. Specifically, they discuss the design of a deep learning-based receiver for conventional pulse amplitude modulation (PAM) transmission. The work in ref. [28] proposed a method for mitigating the performance penalty caused by correlated noise in IM/DD systems. The method involves using an iterative back-propagation cascaded convolution neural network (CNN) decoder to identify and mitigate the noise correlation. The proposed method was tested in a 50-Gb/s 4-ary pulse amplitude modulation (PAM-4) IM/DD system and was found to achieve a BER performance improvement that is robust to transmission distance and launch optical power. Authors in ref. [29] discuss the use of machine learning techniques to build self-adaptive and self-awareness-free space optic (FSO) networks. The goal is to create autonomous networks that can learn and adapt to the dynamic environment by classifying the modulation format/baud rate and predicting the number of channel impairments. The study considers four modulation formats and four baud rates applicable in current commercial FSO systems, as well as two main channel impairments. The results show that the proposed ML algorithm is capable of achieving 100% classification accuracy for the considered modulation formats/baud rates even under harsh channel conditions. Moreover, the algorithm can predict channel impairments with an accuracy ranging from 71% to 100%, depending on the predicted parameter type and channel conditions. Finally, the work in ref. [30] considers a detailed description of ML techniques and reviews work pertaining to their applications in the optical communications space. In conclusion, the review papers have emphasized the advantages of using ML in OPM and MFI, which may be listed as: (1) Real-time adaptability using online learning procedures, (2) Flexibility and reconfigurability, (3) Improved network security (4) Low implementation cost, (5) Higher network efficiency.

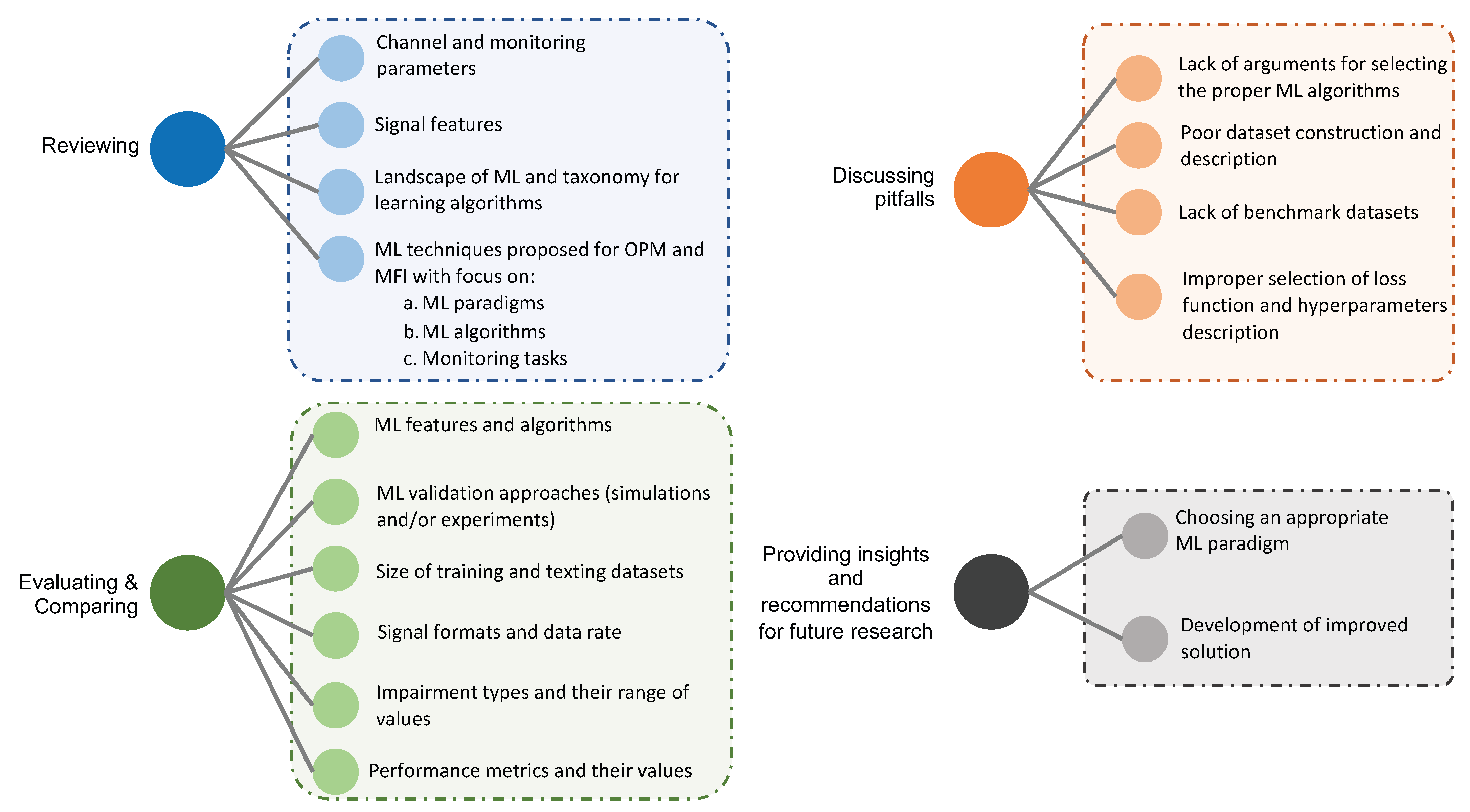
1.4. Paper Contributions

This paper aims to update the current literature and survey the existing works where machine learning has been applied to aid monitoring non-coherent optical systems. It analyzes and evaluates the current approaches to OPM/MFI from a new perspective, one that focuses on how the machine learning algorithms are selected and developed for different OPM/MFI task. This exact perspective is what differentiates this survey paper from the rest of the literature. It proposes a novel taxonomy of the literature that sees OPM/MFI solutions categorized based on the type of machine learning algorithm used. This taxonomy exposes some issues in how machine learning is applied to tackle different OPM/MFI tasks. This is one of the main added values this paper presents to the literature; the exposed issues give rise to important discussions on pinpointing the most prominent challenges and how to address them, which is expected to foster more practical machine-learning-based solutions in future research papers. More to the point, the contributions of this paper are summarized as follows:

• Reviews the current situation of OPM and MFI for direct detection systems in terms of channel impairments and monitoring parameters, and discusses the most widely used features that have been considered for ML algorithms in direct detection optical communication systems.
• Reviews the proposed ML solutions for OPM and MFI with a keen eye on what machine learning paradigms have been followed, what learning algorithms are used to develop monitoring solutions, and what type of monitoring tasks have been defined and addressed. This is preceded by a brief overview of the landscape of machine learning.
• Evaluates and analyzes the proposed machine learning solutions. It discusses, from a machine learning perspective, some pitfalls in the development of those solutions, such as the lack of clear arguments for some algorithm choices and the misinterpretation of some core machine learning assumptions. It also emphasizes important issues with the current literature such as the poor dataset construction and description as well as the lack of benchmarking datasets.
• Discuss recommendations for the potential implementation of machine-learning-based monitoring solutions in non-coherent optical systems. In particular, this paper provides observations on the developed ML methods, presents insights into how to solve the observed pitfalls, and highlights some lessons to help guide future research.

Figure 1 summarizes the main contributions of present work in a compact and easy to follow form.

We systematically searched for relevant papers using keywords and phrases related to our research topic which is “ML methods and algorithms used for OPM and MFI in low-cost direct detection optical communication systems” in academic databases such as Scopus, Web of Science, and Google Scholar. We also searched conference proceedings and reference lists of relevant papers to identify additional sources. Our search was limited to papers published from 2010 to 2023. We screened the papers based on their quality and relevance to our research question and inclusion criteria. After a careful screening process, we included a total of 113 papers in our review.

1.5. Paper Organization

The rest of this paper is organized as follows. Section 2 presents the features commonly used in OPM and MFI. These features include eye diagram, asynchronous Delay tap plot (ADTP), asynchronous amplitude histogram (AAH), asynchronous single channel sampling (ASCS), and constellation diagram. Section 3, discusses the different machine learning paradigms in the context of optical performance monitoring which includes shallow learning and deep learning techniques. Section 4 surveys the proposed ML-based solutions for OPM of non-coherent optical systems. Section 5 discusses certain issues pertaining to ML implementation. Section 6 presents the lessons learnt and recommendations for future research. Section 7 provides concluding remarks.

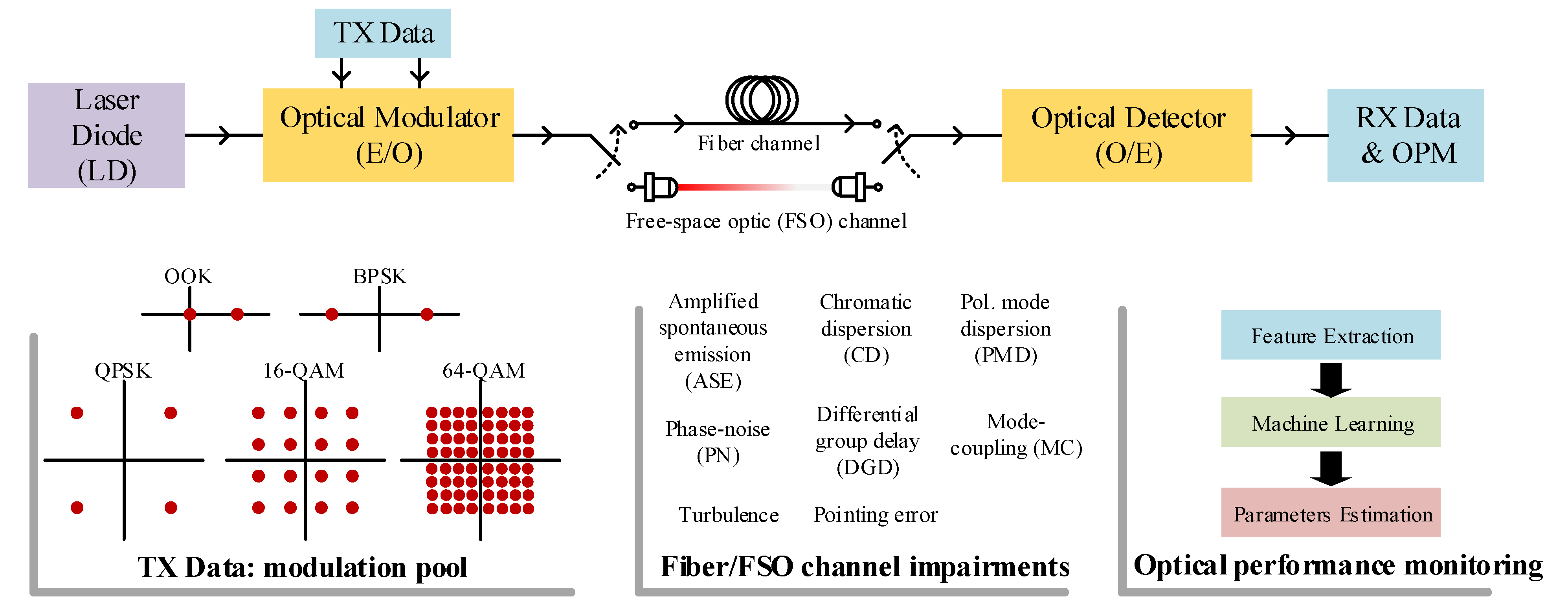
2. Feature Selection for OPM

This paper presents a comprehensive survey about ML methods and algorithms used for OPM and MFI in low-cost direct detection (DD) optical communication systems which have a generic block diagram shown in Figure 2.

The DD optical communication system comprises three main segments:

• Optical transmitter, where electrical-to-optical (E/O) signal conversion and laser modulation are achieved. Different types of modulation formats can be generated to improve the spectral efficiency (SE) of optical systems. These vary from low-order modulations (i.e., less number of bits per symbol-such as On-Off keying (OOK) and binary phase-shift keying (BPSK) formats) up to high-order formats (i.e., high number of bits per symbol-such as M-ary quadrature amplitude modulation (M-QAM), M = 4, 16, 64, and 128), as shown in the inset of Figure 2, and very recently the optimized modulation schemes, known as geometric and probabilistic modulation formats.
• Optical channel, where optical signals are transmitted and impaired with various channel impairments, as shown in the inset of Figure 2. Through optical channel, the optical modulated signals suffer from various optical impairments depending on the optical channel type (i.e., wired or wireless optical channels). For instance, wire channel, known as standard single-mode fiber (SMF) or few-mode fiber (FMF), introduces linear impairments-such as fiber chromatic dispersion (CD), polarization mode dispersion (PMD), mode-coupling (MC), etc., and non-linear impairments-such as self-phase modulation (SPM), cross-phase modulation (XPM), and four-wave mixing. Whereas, wireless optical channel (known as free-space optics (FSO) channel) is characterized by different impairments types such as weather turbulence and pointing error [31].
• Optical receiver, where optical-to-electrical (O/E) conversion is accomplished as well as signal demodulation and decoding. At the receiver side of the DD system, a simple photodetector is employed to recover the transmitted electrical signals. At this stage ML algorithms can take place to identify the different modulation formats (i.e., MFI) and/or monitor optical signal performance (i.e., OPM). It is noteworthy to mention that before applying different ML methods, a feature extraction step is implemented to extract the most useful information from the received signals to ease the task of the ML algorithm, as shown in the inset of Figure 2.

In this section, we reviewed the widely used signal features that have been considered in literature for DD optical communication systems. Typically, the input to the ML classifier or regressor algorithm is the signal features which have relationships formed by the ML algorithm to classify the signal type or predict the amount of signal impairment. The signal features can be obtained from the signal’s time, frequency, or polarization domain [7]. For instance, synchronous and asynchronous sampling methods were utilized to produce distinct features from signal’s time-domain representation. These features exploit the statistical characteristics of the signal’s time-domain representation. In DD systems, the input features are directly obtained from the output of the O/E device using cost-effective electronic digital signal processing (DSP). These include asynchronous eye diagrams, asynchronous amplitude histograms (AAHs), asynchronous delay tap plots (ADTPs), and asynchronous single channel sampling (ASCS). In the following, we explain the main characteristics of each type.

Table 1. Summary of features and monitored impairments in DD optical systems.

Feature Source	OSNR	PMD	CD	Non-Linearity	Crosstalk
Eye diagram	[32,33,34]	[32,34,35]	[33,35]	[33]	[35]
AAH	[10,11,25,36]
ADTP and ASCS (phase portrait)	[37,38,39,40,41,42,43]	[37,38,39,40,41,43,44]	[37,38,39,40,41,43,44]	–	[45,46]
PAED	[47]	[47]	[47]	–	–
ASSA	[48]	[48]	[48]	–	–
OPS	[49,50]	–	–	–	–

summaries the monitored impairments in DD optical systems for different feature types used in literature.

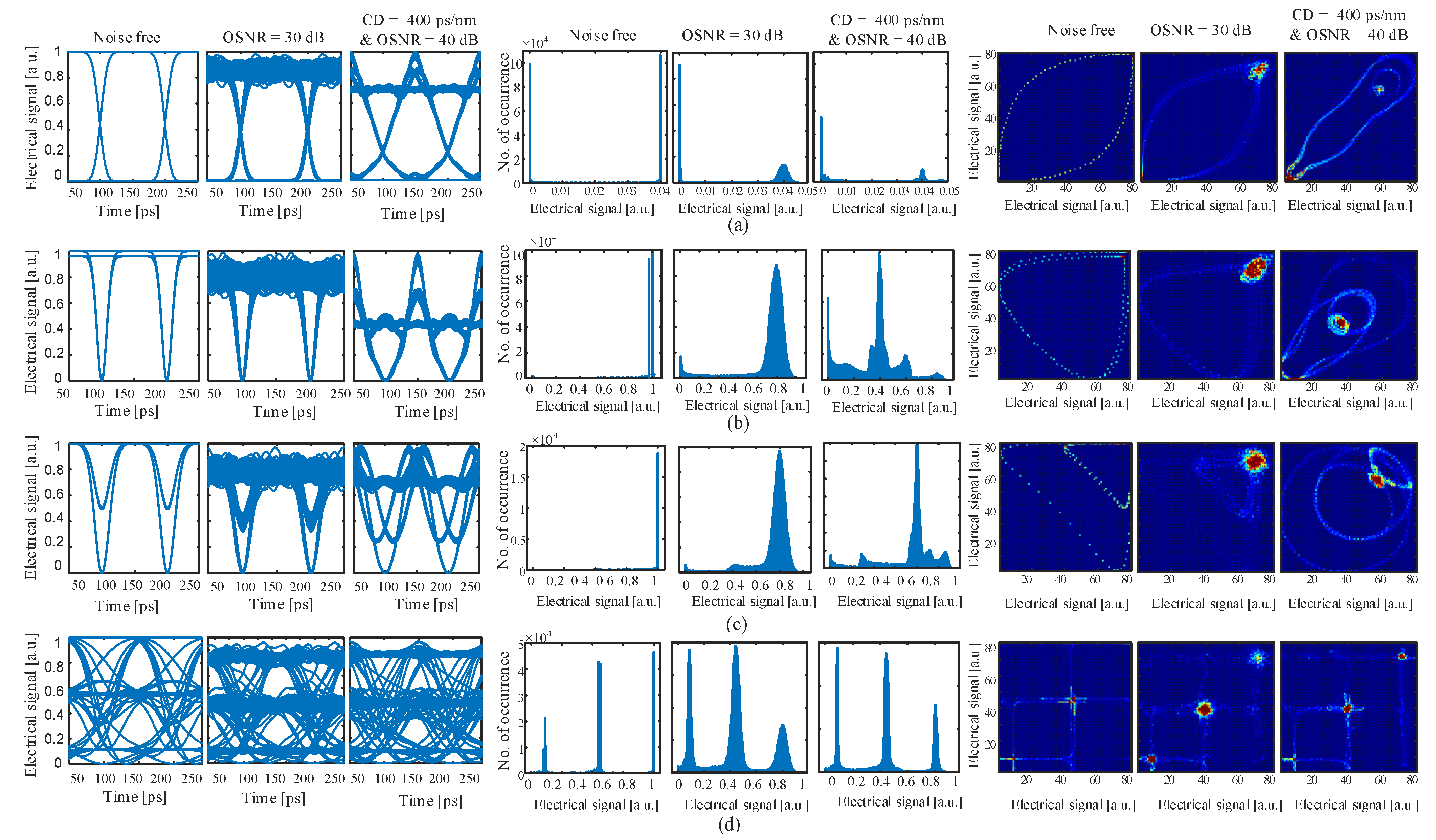
2.1. Eye Diagrams

Eye diagram is a synchronous-based sampling feature that is obtained by overlapping the amplitude of received signal symbols in a time window of one or more bit periods. This produces a graphical representation of the data signals which can be used as input features to ML algorithms. This feature characterizes unique graphical representations for each optical modulation formats. In addition, the eye-opening is affected differently by the various optical impairments and their levels, which facilitates the monitoring process. Figure 3 compares the eye diagrams of 10Gbps OOK, BPSK, QPSK, and 16-QAM signals for noise-free, 30-dB OSNR, and 40-dB OSNR, and 400 ps/nm CD impairments. It is evident that there is a distinct graphical shape for each modulation and impairment type. This can be exploited by applying image processing techniques, as in [35], by defining statistical features (i.e., mean and variance) from the sampled amplitudes at specific points on the eye diagram [33], or by calculating the widely used parameters of the eye diagrams [32,34]. It is worth mentioning that constructing eye diagrams depends on the modulation format and requires timing synchronization, hence clock recovery is needed which increases system cost.

2.2. Asynchronous Amplitude Histograms (AAHs)

The second commonly used feature in DD optical systems is the AAH, which is generated by the random asynchronous sampling of the data signal within the bit period. This generates a distinct amplitude distribution for each modulation format [51]. The frequency of signal levels is utilized to create a histogram vector, known as AAH, from the binned amplitude samples that correspond to some specifically defined quantization levels. AAH is different from the synchronous AH. The latter considers samples within a specific window (for example, 10% [46]) of the bit period around the center of the eye diagram at the optimal decision time. The samples around the eye’s greatest and minimum values correspond to the peaks in the AAH, and the samples in between correspond to the crossings of the waveform’s rising and falling edges.

The simplicity of AAH and its transparency to signal modulation format and bit rate make it a unique feature for DD optical systems; nonetheless, the contribution of each specific impairment cannot be separated out on its own. As a result, AAHs lose favor with multiple impairment monitoring. Figure 3 shows the AAHs of 10 Gbps OOK, BPSK, QPSK, and 16-QAM signals for noise-free, 30-dB OSNR, and 40-dB OSNR, and 400 ps/nm CD impairments. It has been shown that the AAH monitoring accuracy is dependent on the number of samples [7,10,11]. It is important to point out here that quantization level frequency is not the only measure used to construct the AAH vector. The variance of amplitude samples within each bin is also used instead of the frequency to construct an AAH vector [36].

2.3. Asynchronous Delay Tap Plots (ADTP’s)

ADTP is another asynchronous-based sampling feature extracted from the time-domain signal amplitude. In contrast to the one-dimensional (1D) AAH feature, ADTP’s are two-dimensional (2D) histograms known as phase portraits. In DD optical systems, the ADTP’s are obtained by splitting the signal waveform into two parts, where one part is a delayed version of the signal by a certain amount $\tau$. The signal and its delayed version are then asynchronously sampled simultaneously, where pairs of values $(x,y)$ are obtained to plot a 2D histogram [45,46]. Figure 3 shows the phase portrait feature of 10Gbps OOK, BPSK, QPSK, and 16-QAM signals for noise-free, 30-dB OSNR, 40-dB OSNR, and 400 ps/nm CD impairments. As can be seen, the generated phase portraits are dependent on each modulation format and impairment type, which reflects the richness of this feature type. These portraits can be treated as images and exploited using pattern recognition methods [38,44,52]. Furthermore, image processing algorithms were used to extract specific statistical characteristics. For instance, the work in [37] used statistical means and standard deviations of the $(x,y)$ pairs and radial coordinates to achieve OPM using ML approaches. Phase portraits also depend on the tap delay, which is typically a multiple of the symbol rate. As a result, it must be precisely adjusted for various data rates to enable proper monitoring [53]. The ADTP features have been used for multiple impairment monitoring methods such as OSNR, CD, and PMD, as in [37,38,39,40]. In [41,42,43], the authors proposed the asynchronous single channel sampling (ASCS) feature method, which is more cost-effective than ADTP. In this method, the signal $s\left(t\right)$ is sampled asynchronously using one tap, after which the samples are shifted by k samples and utilized to build the sample pairs $s\left[i\right]$ and $s[i+k]$ phase portrait. The generated phase portraits can be used as input images to ML algorithms, as in [41,43].

2.4. Other Methods

Due to the nature of asynchronous sampling, some signal’s information could be lost. Therefore, it may be challenging in some situations to distinguish the effects of various impairments from the overall received signal in the event that they produce similar changes in the plots [45]. Additionally, the distribution of signal amplitudes exhibits overlap, which makes it more difficult in practice to isolate individual distributions from AAH [53]. Parametric asynchronous eye diagram (PAED) was proposed in [47] as a transparent method for modulation formats and data rates. In addition, the authors in [53] proposed asynchronously sampled signal amplitude (ASSA) as a solution for eliminating the requirement of continuously adjusting the tap delay for multiple bit rates and for better CD monitoring; prior techniques demonstrated that changes in OSNR and differential group delay (DGD) had a significant negative impact on CD monitoring. Furthermore, optical power spectrum (OPS) data from an optical spectrum analyzer (OSA) was proposed in [49,50] to monitor the OSNR parameter.

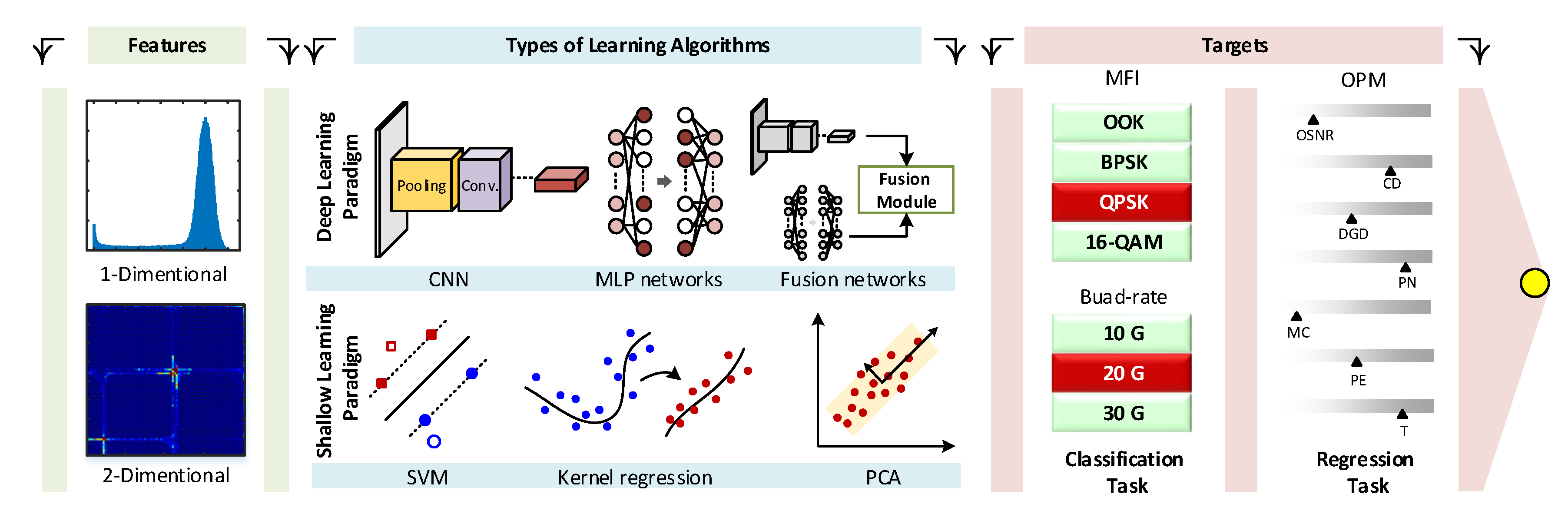
3. Overview of Machine Learning Paradigms

Tackling difficult problems with machine learning has become the go-to approach in many areas of optical communications, and Direct-Detection Optical Performance Monitoring (DD-OPM) and Modulation Format Identification (MFI) are no exception. Many solutions based on machine learning have been proposed for DD-OPM and MFI. They cover a wide spectrum of learning algorithms. With the objective of this paper being a survey of their literature with a keen eye for what learning algorithms are used and how solutions are developed, it is imperative to have a brief overview of the landscape of machine learning and establish a taxonomy for learning algorithms.

A modern view of machine learning could be anchored in how algorithms represent data to perform their tasks. Such a view results in a popular classification of learning paradigms as either deep or shallow. The two terms refer to how many layers of feature representation an algorithm has, and they are not necessarily a reflection of how well the algorithm understands its data or performs its task [54]. Shallow learning defines a paradigm where an algorithm extracts features from t he raw data and directly performs a task, e.g., classify, cluster, estimate, … etc. Deep learning, in contrast, defines a paradigm where the focus is on extracting a hierarchy of features before performing a task [55]. The two paradigms are the foundation of the survey in this paper, and they are further discussed in the subsections below.

3.1. Shallow Learning

Shallow learning is the classical approach to developing machine learning algorithms. It encompasses two typical stages: (i) feature extraction and (ii) prediction [55,56,57]. The first stage aims to extract useful features from raw data. This could be formally viewed as a transformation between vector spaces; every data point in the raw data, represented as a vector, is transformed into another vector called the feature vector in a new space referred to as the feature space. The transformation commonly takes vectors from a low-dimensional space to a high-dimensional one. These feature vectors are then passed to the prediction stage, where the algorithm produces the output, or, in other words, makes a prediction. The type of prediction is determined by the task the algorithm is designed to perform. For instance, it could be required to assign a data point to a category (i.e., classification) or estimate a desired response associated with a data point (i.e., regression).

The design of feature extraction is the most crucial step for shallow learning algorithms for two reasons. The first is rooted in the raw data, while the second is rooted in the task. It is common for raw data to contain irrelevant information, such as in the case of an image showing a person in a park. The main object is the person, but the image depicts other information, such as trees, benches, … etc. It is also common for raw data to have redundant information, such as in the case of a video sequence showing a person walking down a street. Consecutive frames could have the person in relatively same position (People typically walk in at a slower pace compared with the number of frames a camera captures per second.) which makes them redundant. Therefore, feature extraction is expected to remove such irrelevance and redundancy and transform the raw data into a form suitable for the task the algorithm needs to perform.

Feature extraction in many shallow learning algorithms is designed to uphold a certain assumption about the task itself. The assumption is called the smoothness prior [58]. It basically means that for any two N-dimensional feature vectors ${\mathbf{x}}_1,{\mathbf{x}}_2\in {\mathbb{R}}^N$, if they are similar under some similarity measure $d({\mathbf{x}}_1,{\mathbf{x}}_2)\in \mathbb{R}$, then their corresponding outputs should also be similar [55,57,58]. The interest in such an assumption is motivated by: (i) the need to design learning algorithms that generalize well, and (ii) the use of simple predictors (e.g., linear predictors). Smoothness prior has resulted in a large body of manually designed features, commonly referred to as hand-crafted or hand-engineered features. Examples are Scale-Invariant Feature Transform (SIFT) [59], Histograms of Oriented Gradients (HOG) [60], and Gaussian kernels [61], among others. Those features make up most of the popular shallow learning algorithms known today, e.g., Support Vector Machine (SVM) with Gaussian kernel [61] and HOG-based person detector [60].

3.2. Deep Learning

Deep learning algorithms represent the most recent and most successful learning paradigm [54,62]; they have driven many of the advances in various fields such as computer vision, natural language processing, and, more recently, wireless communications. It differs from shallow learning in two principle aspects: (i) how features are extracted and (ii) the number of feature extraction stages [56]. Deep learning algorithms comprise multiple stages of feature extraction as opposed to one stage, or sometimes two, in shallow learning, and they have a single prediction stage [57,58]. Feature extraction happens in a layered manner, and most importantly, it is not manually engineered. It is a data-driven process; each layer of feature extraction learns a representation of the raw data and passes it on to the next layer [62]. These representations arguably grow in abstraction from detecting simple patterns, such as edges and corners in an image, to recognizing abstract concepts, such as a person or a dog [58,63].

Deep learning is a paradigm encompassing any algorithm that can learn layers of representations; however, Artificial Neural Networks (ANN) are the driving force behind all of its modern advances [54]. In ANNs, the notation “ANN(n,m)” refers to a feedforward neural network with n input neurons and m hidden neurons (also known as nodes or units). The number of neurons in the input layer is determined by the number of input features, while the number of neurons in the hidden layer is determined by the complexity of the problem being solved and the desired level of accuracy. The output layer of the ANN is typically determined by the number of classes or regression values being predicted. They are intrinsically layered and capable of learning a hierarchy of representations. ANNs in general could be designed to be shallow (two-layer) or deep (multiple layers), yet shallow ANNs have not been quite as successful as their deep counterparts [57]. They comprise a wide variety of network architectures. Such architectures are fashioned out of one or multiple basic network types, which are Multilayer Perceptron (MLP) networks, Convolutional Neural Networks (CNNs), and Recurrent Neural Networks (RNN). Some good examples of Deep Neural Networks (DNNs) are Residual Network (ResNet) [64], Transformer [65], and EfficientDet [66].

4. Survey of Proposed Solutions for DD-OPM

Machine learning has a proliferating impact on DD-OPM that has resulted in a rich literature. Geared toward the overview in Section 3, this section will survey that literature with an eye on the following: (i) what machine learning paradigms have been followed; (ii) what learning algorithms are used to develop monitoring solutions; and (iii) what types of monitoring tasks have been commonly defined and addressed. The discussion will start with an overview subsection of the literature. It provides a general idea of how machine learning is utilized to address DD-OPM problems. Then, a detailed survey of the proposed monitoring solutions is presented in two subsections following the overview. These subsections survey the proposed solutions from a machine learning perspective. More to the point, they cluster the solutions based on the learning paradigm to which their algorithms belong, i.e., either shallow or deep learning, see Section 3 for more details of the two learning paradigms.

4.1. Bird-Eye View

A good starting point is a view of the landscape of DD-OPM that is summarized visually in Figure 4. This landscape is composed of three main components: (i) types of observed variables, (ii) types of learning algorithms, and (iii) types of targets. The three components represent the basic building blocks for any monitoring solution based on machine learning; the observed variables (first component) are the data vessels from which a learning algorithm (second component) extracts information relevant to the learning task defined by the prediction targets of the algorithm (third component). Each of the three components has its own elements, and Figure 4 depicts those elements that are prevalent in DD-OPM.

Types of observed variables could be divided into two categories based on how they are structured: one- and two-dimensional (1-/2-D) structures. The former has the variables organized into a vector, while the latter has them organized into a matrix. AAH and ADTP are good examples of, respectively, 1-D and 2-D structured variables. The structure of observed variables is crucial; it conveys information on the relationship between the variables, which subsequently influences the choice of the learning algorithm. To understand this, consider an ADTP matrix. Each element expresses the frequency of a pair of values occurring in a waveform and its delayed version. The matrix is usually sparse, and only small neighborhoods of elements are non-zero, showing some form of local relation (also referred to as local dependency). Such local relations suggest that a convolutional neural network (CNN) [55] is a good choice for a learning algorithm when the observed variables form an ADTP matrix.

A variety of learning algorithms have been explored for DD-OPM. The famous categorization of learning algorithms as deep or shallow could also be applied here. This is illustrated in the middle column of Figure 4. What is not reflected in the figure is how much attention has been paid to each category. Only a handful of papers have utilized shallow learning algorithms. Deep learning algorithms, on the other hand, have received the lion’s share of attention. This is not quite surprising, and it is, in fact, in line with current advances in the fields of machine learning and AI; deep learning has proven to be quite effective in handling complex learning problems [54,55], and it has defined the state-of-the-art across many applications, including object detection [67,68] and speech recognition [69,70], to name two examples.

The final component of the landscape defines the performance-monitoring objectives. Defining the type of targets for a machine learning algorithm basically defines the optical network parameters that need to be monitored. Various monitoring objectives have been identified for direct detection in the literature, ranging from OSNR, CD, and DGD all the way to modulation format identification (MFI). They are illustrated in the third column of Figure 4. From a machine learning perspective, the choice of objectives determines whether the learning task is posed as regression, classification, or a hybrid of the two. Monitoring OSNR, CD, DGD, visibility range, and pointing error are commonly posed as a regression tasks, while MFI and baud-rate identification are posed as a classification tasks.

Remark: Moving forward, the phrase observed variables will be used interchangeably with the word “features” when discussing DD-OPM solutions based on shallow learning algorithms. This is because shallow learning typically requires feature engineering (as discussed in Section 3.1), a step that is omitted in deep learning [55]. Therefore, what is fed to a shallow learning algorithm is commonly referred to as features, while it is referred to as simply inputs (or more formally observed variables) when it is fed to a deep learning algorithm.

4.2. Shallow Learning Algorithms

Applying shallow machine learning to DD-OPM has a relatively long yet sparse literature. Early work could be roughly traced back to the mid-2000s (e.g., [35]). They generally take advantage of two important values of shallow machine learning. The first is the explainable nature of those algorithms; both the features and the predictor (see Section 3.1) are meticulously designed by the developers, which makes them explainable. The second value is that shallow algorithms commonly have manageable computational demands, which makes their implementation possible in variety of practical situations. That literature on shallow learning for DD-OPM, however, is composed of merely a handful of papers. This is not quite surprising, for the dawn of the deep learning era starts roughly in 2006 with the seminal work in [71,72]. This subsection will survey DD-OPM, MFI, and BRI solutions that are developed around shallow learning algorithms, and it is organized based on the type of learning algorithm adopted by the proposed solution.

Table 2. Summary of available shallow learning solutions for direct detection OPM, MFI, and BRI.

ML Algorithm	Feature	SIM/EXP	Train:Test	Signal Format	Rate (Gb/s)	Impairment (Range) ${}^1$	Performance (Acc/CORR)	Year	Ref
SVM	Eye diagram (23 zernike moments)	Both	164:17	-	-	CD (-) PMD (-) DGD (-) XT (-)	ACC = 95% (SIM) ACC = 60% (EXP)	2006	[35]
SVM	176,000 AAHs	SIM	70%:30%	NRZ-OOK	10	OSNR (5:25) PE, $\xi$ (0.3:3.3) V (500:1000 m)	ACC $>0.98$ @PE&V ACC $=0.86$ @OSNR	2021	[73]
SVR	Stokes Space 420,175 sim	EXP	–	NRZ PDM-QPSK	112	OSNR (11:35) CD (0:700)	ACC = 0.9821	2019	[74]
Multiclass SVM	multi-dim ADTPE	SIM	70%:30%	RZ-OOK NRZ-DPSK DUO RZ-DQPSK PM RZ-QPSK PM-NRZ-16QAM	10 40 40 40 100 200	OSNR (10:30) CD (0:4000) ps/nm DGD (0:10 ps)	Overall ACC = 99.05% Recog. time $=332$ ms	2016	[12]
SVM & CNN	AAH & ADTP	SIM	70%:30%	NRZ-OOK NRZ-DPSK RZ-DPSK	10 40	OSNR (10:25) CD (0:700)	ACC = 98.46% Error $=1$ @OSNR	2021	[31]
PCA	26,208 ADTP’s	SIM	70:30 60:40 50:50	RZ-OOK PDM-RZ-QPSK PDM-NRZ-16QAM	10/20 40/100 100/200	OSNR (14:28) CD (−500:500) DGD (0:10)	ME = 1.0 @OSNR ME = 4.0 @CD ME = 1.6 @DGD	2014	[38]
PCA	26,208 ADTP’s	SIM	70:30 60:40 50:50	RZ-OOK PDM-RZ-QPSK PDM-NRZ-16QAM	10/20 40/100 100/200	OSNR (14:28) CD (−500:500) DGD (0:10) Non-linearity	ME = 1.2 @OSNR ME = 12 @CD ME = 2.1 @DGD	2014	[38]
PCA	ASCS 432 scatter plot	EXP	70%:30%	NRZ-OOK NRZ-DPSK RZ-DPSK	10	OSNR (10:25) CD (0:700)	ACC = 98.46% Error $=1$ @OSNR	2015	[75]
Kernel ridge regression	ADTP (Phase portrait-900 features each)	SIM	1200:500	NRZ-DPSK	40	OSNR (13–26) CD (0–700) DGD (0–20)	RMSE = ± 11 @CD RMSE = ± 0.75 @DGD	2009	[44]
Kernel ridge regression	ADTP (Phase portrait-900 features each)	EXP	1500:500	NRZ-DPSK	40	OSNR (15–25) CD (−400:400) DGD (0–22.5)	RMSE = ± 11 @CD RMSE = ± 1.9 @DGD	2009	[44]

¹ OSNR in dB, CD in ps/nm, DGD in ps, XT in dB, and PMD in ps.

provides a summary of what will be discussed below.

4.2.1. Solutions Based on Support Vector Machine (SVM)

SVM is one of the popular shallow algorithms that are used to develop OPM solutions. Chromatic dispersion (CD), cross-talk, and polarization mode dispersion (PMD) are all monitored in [35] using hand-crafted features and a kernel-based SVM classifier. In particular, the authors propose to extract features from eye diagrams using Zernike moments and train an SVM classifier on those features to predict the type of impairment affecting the optical signal. Their classifier follows a one-to-one approach, where for each pair of classes, one SVM classifier is trained to separate them. This means the solution requires $\frac{n(n-1)}{2}$ classifiers where n is the number of impairments being monitored plus one ($n=4$ in [35]). In a similar spirit, but ten years later, ref. [12] proposes modulation format identification using SVM. Different from [35], the solution engineers feature vectors using various types of entropies calculated from an ADTP, and it uses them to train a one-to-one SVM classifier. They go further to optimize their classifier for real-time implementation.

The above papers propose solutions for DD-OPM in optical-fiber networks. This can be extended to free-space optics (FSO) as [31,73] do to monitor channel impairments. Both papers propose SVM-based solutions to monitor impairments such as pointing error, OSNR, visibility range, amplified spontaneous emission (ASE) noise, and turbulence. In [73], the proposed solution uses AAH as the extracted feature from the optical signal and trains an SVM regressor to predict pointing error, OSNR, and visibility range. The author develops one regressor per target (impairment type) and benchmarks the performance with monitoring techniques that do not use machine learning. On the other hand, ref. [31] addresses a similar problem to that of [73]; along with pointing error, it defines ASE noise and turbulence as new targets. What sets this paper apart from ref. [73] are the comparisons it makes. First, it compares AAH and ADTS as the observed variables for the SVM algorithm and reports a slight edge for the latter. Furthermore, it presents a comparison between SVM and Convolutional Neural Networks (CNNs) as candidates for learning algorithms for the monitoring solution. The paper shows that in the worse case scenario, CNNs perform as well as an SVM.

4.2.2. Solutions Based on Principle Component Analysis (PCA)

A different set of solutions takes advantage of unsupervised machine learning to reduce the dimensionality of extracted feature vectors before applying simple classifiers for OPM. Good examples are the solutions proposed in [38,75]. They are similar in how they apply PCA and predict targets, but they differ in the type of observed variables and how the prediction function is optimized.

In [38], simulated ADTP features and their corresponding targets (i.e., bit-rate, modulation format, OSNR, DGD, and CD) are collected to construct a development dataset (training and validation sets). PCA is applied to vectorized versions of ADTP features in the training set to reduce their dimensionality and construct what they call a “reference database”. This database has each reduced feature associated with its targets. To predict impairments, modulation format, and bit-rate, a new feature vector (e.g., one from the validation set) has to first be reduced in dimensions. Furthermore, a nearest neighbor algorithm with Euclidean distance is applied using the reference database to make the prediction.

A similar solution to that in [38] is proposed in ref. [75], but with some minor differences. The solution relies on ACSC features instead of ADTP and constructs a development dataset (i.e., training and validation sets of features and their targets) from experimental data, not simulated data. PCA is applied to vectorized ACSC features in the training set, and a reference database is constructed, much like that in ref. [38]. The prediction process is exactly the same as that of [38], but the authors here provide an empirical justification for the choice of distance metric used with the nearest neighbor algorithm; they test four different distance measures and show experimentally that the Euclidean distance is the best choice.

4.2.3. Solutions Based on Kernel Regression

A possible alternative to an SVM regressor that is easier to train and implement is a kernel-based linear regressor. Such a regressor is the core of the proposed solution in [44]. The authors identify phase portraits (i.e., ADTPs) as the observed variables in their solution, and they train multiple kernel regressors to predict CD and DGD. The development dataset (training and validation sets) is made up of synthetic data samples obtained from a computer simulator.

4.3. Deep Learning Algorithms

A great deal of the literature on ML for DD-OPM, MFI, and BRI is focused on solutions based on deep learning algorithms. This is influenced by Deep Neural Networks (DNNs) having become the driver of many state-of-the-art intelligent solutions for challenging problems such as object detection, language translation, face recognition, and so on [54,55,69,76]. Such success is anchored in two important values that deep learning, as a paradigm, promotes. The first is that representative features are better learned from large datasets instead of being handcrafted by engineers or developers. The second value is the hierarchical nature of learning, which has empirically been proven to result in better generalizing algorithms than shallow ones. Various DNN architectures have been explored for DD-OPM purposes, ranging from Multi-Layer Perceptron (MLP) networks to Convolutional Neural Networks (CNNs) and transfer learning. Below is a survey of proposed monitoring solutions that are developed around DNNs, and it is summarized in

Table 3. Summary of available deep learning solutions developed with ANNs for direct detection OPM, MFI, and BRI.

ML Algorithm	Feature	SIM/EXP	Train:Test	Signal Format	Rate (Gb/s)	Impairment (Range) ${}^1$	Performance (Acc/CORR)	Year	Ref
ANN(1;12)	Eye diagram (4 inputs)	SIM	-	NRZ-OOK RZ-DPSK	10 40	OSNR (16–32) CD (0–800) DGD (0–40)	CORR = 0.91 (@10G) CORR = 0.96 (@40G)	2009	[32]
ANN(1;28)	ADTP (7 statistics)	SIM	125:64	NRZ-OOK	10	OSNR (16–32) CD (0–60) DGD (0–10)	CORR = 0.97	2009	[37]
ANN(1;28)	Constellation (7 statistics)	SIM	216:125	RZ-QPSK	40	OSNR (12–32) CD (0–200) DGD (0–20)	CORR = 0.987 RMSE = 0.77 @OSNR RMSE = 18.71@CD RMSE = 1.17 @DGD	2010	[77]
ANN(1;12)	Eye diagram (4 inputs)	SIM	125:64	RZ-OOK RZ-DPSK	40	OSNR (16–32) CD (0–60) PMD (1.25–8.78)	CORR = 0.97, 0.96 RMSE = 0.57, 0.77 @OSNR RMSE = 4.68, 4.47 @CD RMSE = 1.53, 0.92 @PMD	2009	[34]
ANN(1;12)	Eye diagram (4 inputs)	EXP	20:12	RZ-OOK RZ-DPSK	40	OSNR (16–32) CD (0–60)	CORR = 0.99, 0.99 RMSE = 0.58, 1.85 @OSNR RMSE = 2.53, 3.18 @CD	2009	[34]
ANN(1;12)	Eye diagram (4 inputs)	SIM	135:32	RZ-DPSK (3ch WDM)	40	Opt Power (−5:3) OSNR (20–36) CD (0–40) PMD (0–8)	CORR = 0.97 RMSE = 0.46 @Power RMSE = 1.45 @OSNR RMSE = 3.98 @CD RMSE = 0.65 @PMD	2009	[34]
ANN(1;42)	3627 groups of moments per BR & MF	SIM	–	RZ-DQPSK RZ-DQPSK RZ-DPSK	40 56 40	OSNR (10:26) CD (−500:500) DGD (0:14)	RMSE = 0.1, 0.1, 0.1 @OSNR RMSE = 27.3, 29, 17 @CD RMSE = 0.94, 1.3, 1 @DGD	2012	[48]
ANN(1;3)	Eye diagram (1 feature)	EXP	1664:832	PDM-64QAM	32	OSNR (4:30)	RMSE = 0.2 @OSNR (4–17)	2016	[33]
ANN(1;12)	ADPT (7 features)	SIM/ EXP	180:144	QPSK with: -Balanced detection -Single-ended detection	100	OSNR (14:32) CD (0:50) DGD (0:10)	CORR = 0.995, 0.996 RMSE = 0.45, 1.62 @OSNR RMSE = 3.67, 8.75 @CD RMSE = 0.8, 7.02 @DGD	2010	[39]
ANN(1;40)	Eye diagram (PAED- 24 features)	SIM	–	QPSK	40	OSNR (10:30) CD (0:200) PMD (0:25)	ME = 1.5:2 @OSNR ME = $<20$ @CD ME = $<1.3$ @PMD	2012	[47]
ANN(5;40)	5 features AHs	SIM	–	4QAM, 16QAM 32QAM, 64QAM, 128QAM	-	OSNR (15:20)	Error $<1.1$ @OSNR	2018	[78]
ANN-AE	AAH & ADTH	SIM	70%:30%	DP-QPSK	10	OSNR (8:20) CD (160:1120) MC	RMSE = 0.0015 @OSNR RMSE = 0.28 @CD RMSE = $7.88\times {10}^{-6}$ @MC	2022	[79]
ANN	Eye diagram	SIM	70%:30%	NRZ-OOK	10	OSNR (15:30) CD (0:2.5) DGD (0.1-0.5)	MSE = 4.6071 @OSNR MSE = 0.0417 @CD MSE = 1.6 @DGD	2021	[80]
MTL-ANN (1,100,2,50)	AHs	SIM/ EXP	9072:1008 4320:480	NRZ-OOK PAM4 PAM8	28	OSNR (10:25) OSNR (15:30) OSNR (20:35)	ME = 0.12 @SIM ME = 0.11 @EXP @CD (−100:100)	2019	[11]
MT-DNN-TL (4,100,50,30,2)	AHs	EXP	440:243	PDM-16QAM PDM-64QAM	10	OSNR (14:24) OSNR (23:34)	RMSE = 1.9 @OSNR	2020	[10]
MTL-ANN (64 neurons/layer)	5 Feature per OSNR	EXP	70:30	NRZ-QPSK PDM-16QAM	10 32	OSNR (1:30) in WDM systems	RMSE = 0.48 MAE = 0.28	2020	[49]
MTL-DNN	AADTPs & AAHs 36,000 samples	SIM/ EXP	70%:30%	QPSK 16QAM	14/28	OSNR (15:29) CD (0, 858.5, 1507.9)	ACC = 99.92% @MFI ACC = 99.11% @BRI ACC = 99.94% @CDI MAE $=0.5944$ @OSNR	2020	[81]
MTL-DNN	AAH	SIM/ EXP	–	PDM-QPSK PDM-8QAM PDM-16QAM	2.9/9.8	OSNR (10:22) OSNR (14:24) OSNR (17:26) CD (0:1600)	ACC = 97.25% @MFI ACC = 100% @BRI RMSE = 0.58% @OSNR RMSE = 0.97% @CD	2019	[82]

¹ OSNR in dB, CD in ps/nm, DGD in ps, and PMD in ps.

and

Table 4. Summary of available deep learning solutions developed with CNNs for direct detection OPM, MFI, and BRI.

ML Algorithm	Number of Layers	Feature	SIM/EXP	Train:Test	Signal Format	Rate (Gb/s)	Impairment (Range) ${}^1$	Performance (Acc/CORR)	Year	Ref
MTL-CNN	5	Eye diagram 2500 diagrams	SIM/ EXP	75%:25%	NRZ-OOK RZ-OOK PAM4	10	OSNR (5:12) OSNR (7:12) OSNR (15:23)	RMSE $<0.6$ @OSNR MFI ACC = 100%	2021	[83]
CNN	–	ADTS 62,000 images	SIM	90%:10%	NRZ-OOK DPSK	10	OSNR (10:30) CD (400:1600)	ACC = 99.9% @CD ACC = 95.6% @OSNR ACC = 99.3% @Crosstalk	2021	[84]
CNN	6	AAH	SIM/ EXP	70%:30%	PM-QPSK PM-16QAM PM-64QAM	16	OSNR (2:13) CD (0:16,000)	ACC = 100%	2020	[85]
CNN	6	ADTP 12,985 sample	EXP	–	16QAM 32QAM 64QAM	28	OSNR (15:30) OSNR (25:40)	ACC = 97.81% ACC = 96.56%	2019	[86]
CNN	–	ADTS 10,000 images	SIM	90%:10%	NRZ-OOK	10	OSNR (10:40) CD (0:2000)	ACC = < $\pm 2\%$ @CD ACC = < $\pm 0.5\%$ @OSNR	2018	[87]
CNN	5	Eye diagram	EXP	70%:30%	RZ-OOK NRZ-OOK RZ-DPSK 4PAM	-	OSNR (10:25)	ACC = 100% @OSNR ACC = 100% @MFI	2017	[88]
MTL-CNN	8	6600 ADTP’s	EXP	5940:660	RZ-QPSK NRZ-OOK NRZ-DPSK	10/20	OSNR (10:28) CD (0:450) DGD (0:10)	RMSE = 0.73 @OSNR RMSE = 1.34 @CD RMSE = 0.47 @DGD	2018	[40]
MTL-CNN	10	6600 ASCS	SIM	—	QPSK 16QAM 64QAM	60/100	OSNR (10:28) CD (0:450) DGD (0:10)	RMSE = 0.81 @OSNR RMSE = 1.52 @CD RMSE = 0.32 @GDG	2019	[41]
MTL-DNN	9	36,000 AADTPs & AAH’s each	EXP	90%:10%	QPSK 16QAM	14/28	OSNR (10:24) OSNR (15:29) CDI (0, 858.5, 1508)	MAE = 0.2867 @OSNR MAE = 0.2867 @OSNR ACC = 99.83% @CD	2021	[9]

¹ OSNR in dB, CD in ps/nm, DGD in ps, and PMD in ps.

. Similar to Section 4.2, this survey is presented in a few subsections, each of which revolves around a type of deep neural network.

4.3.1. Solutions Based on MLP Networks

MLP networks are among the most widely utilized DNN types in the literature of DD-OPM with machine learning; a swath of solutions have been developed with MLP networks at their core. Those solutions could be divided into two categories: (i) early solutions and (ii) recent solutions. Both are discussed below.

Early solutions [32,34,37,39,47,48,77] appear roughly between the years of 2009 and 2013. They share a common interest in three important targets for OPM, which are OSNR, CD, and PMD, and they do that using MLP networks. The learning task for all three targets is posed as regression task. Most of the novelty in those early solutions comes from the types of observed variables from which the MLP network is learning. Ref. [32] and its extension [34] propose deriving a 4-dimensional feature vector from an eye diagram to be the vector of observed variables, while refs. [37,39] instead derive a 7-dimensional vector of observed variables from the three quarters of ADTPs, namely quarters 1, 2, and 3. Another 7-dimensional vector of observed variables has been proposed in [77], but different from that in [37,39]; it is derived from quarters 1 and 3 of an asynchronous constellation diagram instead of ADTP. Ref. [47] proposes parametric asynchronous eye diagrams (PAED), from which it derives a 24-dimensional vector of observed variables. Finally, ref. [48] turns attention to Asynchronously Sampled Signal Amplitudes (ASSA) to derive a vector of ten empirical moments and use them as the observed-variables vector.

More recent work on DD-OPM with MLP networks has shown increasing interest in addressing Modulation Format and Baud Rate Identification (MFI/BRI) along with other targets (e.g., OSNR, CD, DGD, … etc). Such interest has surfaced roughly around 2012 with the work in ref. [89], yet it has only become mainstream for the past four to five years, as evident in refs. [11,49,78,82,90]. That being said, it is important to point out that not all recent work considers modulation or baud rate identification. Solutions such as those in refs. [79,80] have targets similar to those of the early work, i.e., OSNR and CD.

When MFI surfaced as a target of interest, solutions were developed to predict modulation format in isolation from other targets. For instance, the solution in ref. [89]—which paved the way for MFI—predicts modulation format from AAH vectors using a simple three-layer MLP network. That solution is tweaked a little bit in ref. [78] to perform OSNR prediction in addition to MFI. The authors develop a two-stage solution where the first stage solely focuses on MFI and the second performs OSNR prediction based on the first stage’s outcome. More specifically, the first stage has a single MLP network trained on AAH vectors for MFI, while the second stage has multiple parallel networks, one per modulation format. The first stage prediction identifies the modulation format and acts as a selector for the second stage network that predicts the OSNR from an AAH vector.

Following in the footsteps of refs. [11,78,82,89] have both proposed solutions for modulation format identification along with other OPM targets by utilizing the framework of Multi-Task Learning (MTL). In particular, ref. [11] proposes a MLP network that learns from AAH vectors how to predict modulation format and OSNR simultaneously. The network has common layers that feed into two separate prediction layers, one for MFI and the other for OSNR estimation. It is trained for both tasks at the same time using a loss comprising a term for MFI and another for OSNR prediction. In ref. [82], on the other hand, follows the same MTL framework, but it adds BRI to the targets. It improves on the proposed solution in ref. [11] by forming a truely multi-task loss function; the function has two cross-entropies terms for MFI and BRI predictions and a regression term for OSNR predictions. The solution in ref. [49] also utilizes the MTL framework, but it focuses on BRI along with OSNR and launch power. It does so using a different form of observed-variables vector than AAH, which is a vector of sampled powers from different optical wavelengths.

In a change of pace, the authors of [79,90] consider MFI and OPM, respectively, in few-mode fiber networks instead of the prevalent single-mode fiber networks. Ref. [90] proposes a MLP network capable of predicting modulation formats. The network is trained on the in-phase/quadrature histograms of the optical signal instead of the most commonly used AAHs and ADTPs. The MFI is posed as classification task with a cross-entropy loss function. Deviating from MFI and BRI, the proposed solution in ref. [79] tackles the problem of CD, OSNR, and Mode Coupling (MC) prediction from AAH or vectorized Asynchronous delay-tap sampling (ADTH) observed variables using MLP networks. It does that in a different way than other solutions; it first trains an autoencoder to perform dimensionality reduction for the vector of observed variables. Then, a regressor is trained on the reduced-dimensionality features to predict the targets.

4.3.2. Solutions Based on CNNs

Many features for direct detection have a 2D structure: ADTP, ASCS, and eye diagrams, to name three examples. This fact has triggered strong interest in developing CNN algorithms to perform OPM and MFI/BRI [31,40,41,84,85,86,87,88,91]. Overall, this wealth of literature could be viewed from the perspective of target type, for it derives the choice of learning settings (regression, classification, multi-task, … etc). Some of the proposed solutions focus on performance monitoring targets such as OSNR, CD, DGD, pointing error, and so forth, while others incorporate modulation format and/or baud rate identification along with performance monitoring targets.

Addressing problems that involve MFI/BRI and performance monitoring could be done with multi-task learning. Ref. [40] utilizes multi-task learning to develop a CNN that predicts OSNR, BRI, and MFI from phase portraits. The network has base layers that learn task-agnostic features, which are fed into task-specific layers to produce predictions. MFI and BRI are posed as classification tasks, while OSNR is posed as a regression task. That CNN architecture is tweaked in ref. [41] to perform MFI and BRI; it is equipped with parallel projection layers such that task-agnostic features from different layers of the CNN are projected onto the same feature space. Furthermore, they are concatenated and fed to the task-specific layers to produce the MFI and BRI predictions. Again, both MFI and BRI are posed as classification tasks.

Single-task learning is another dominant choice to develop CNN models for performance monitoring and MFI/BRI. Ref. [88] proposes a CNN that learns to predict OSNR and modulation format from eye-diagrams. The proposed solution assumes both targets have a categorical form, where they take values from finite and discrete sets. The CNN is trained in a regression setting with mean square error (MSE) loss using binary ground truth vectors. Ref. [85] makes a similar algorithm choice to that of [88], but it chooses AAH as observed variable and focuses on MFI alone. Another solution proposed in ref. [86] transforms ADTP to an RGB image and trains a CNN to learn OSNR estimation and modulation format identification separately. The authors in ref. [91] tackle the MFI problem in new optical network settings, specifically super-channel settings. They propose a simple CNN trained to predict modulation format from Inphase-Quadrature Histograms (IQHs).

CNNs are also developed for performance monitoring alone. Good examples are refs. [31,84,87]. Refs. [84,87] both propose CNNs that learn from ADTS how to predict different performance parameters, i.e., targets. The CNN in ref. [87] learns to predict OSNR and CD, while the other adds cross-talk to the OSNR and CD targets. Both proposed solutions are trained separately for each parameter in a regression setting. Performance monitoring with CNNs is not only restricted to optical networks; it could also be applied to FSO, and this is exactly what [31] has done. It proposes a solution to predict ASE, turbulence, and pointing errors using a CNN from ADTS. It compares the CNN to the SVM trained for the same target but on ADTS and AAH separately. The comparison establishes the superiority of CNNs, for the SVM performance is empirically shown to be mostly inferior to that of the CNN.

4.3.3. Solutions Based on Fusion Networks

Very recent solutions, such as refs. [9,81], have followed a different approach to developing a deep learning algorithm for OPM, MFI, and BRI. In both papers, the MTL framework is combined with two-type observed variables to develop a DNN for OSNR, CD, MFI, and BRI. The proposed network architecture learns from AAH and Adaptive Asynchronous Delay Tap Plot (AADTP) together. This is done by designing a network with two branches. One is a CNN designed to extract features from AADTP, while the other is a MLP layer designed to extract features from AAH. Both features are then concatenated and fed to four task-specific mini MLP networks, each of which learns to predict one target. The approach shows a slight improvement over the performance of MTL for one type of observed variable (either AAH or AADTS).

5. Survey Observations

One of the conclusions one could draw from the survey in Section 4 is that machine learning has an immense potential for optical networks. Developing intelligent algorithms for DD-OPM could advance how optical networks operate and push them closer to being dynamic and scalable. However, for that potential to be fully realized, there are a few knots to be untied. More specifically, three main issues are observed in the survey and need to be addressed, namely under-developed arguments, unclear datasets and preprocessing, and a lack of benchmark datasets. All three are discussed below.

5.1. Under-Developed Arguments for Algorithm Design

A typical foundation of a good engineering solution should be a clear and well-rounded underlying argument. The argument clarifies why a certain approach or perspective is taken to tackle the problem of interest. It also lays the groundwork for why the proposed solution is, to some extent, the optimal or best possible one. The literature on ML for DD-OPM seems to struggle in that regard; many of the proposed solutions lack the support of good arguments. This is discussed in the following few subsections, where each one is devoted to a specific missing argument.

5.1.1. Arguments Supporting Shallow Learning

Picking a shallow learning algorithm commonly needs to be supported with a clear argument, especially in the deep learning era. Shallow algorithms are commonly prone to overfitting, and they lack the ability to generalize well [55,58]. Therefore, when a shallow learning algorithm is chosen to tackle a learning task, a good argument for why it is favored over deep learning or other shallow learning algorithms needs to be presented.

Solutions such as those in refs. [12,35,38,44,73,75] all lack good arguments. The details of that are as follows:

• Although it was proposed prior to the deep learning era, ref. [35] proposed an SVM algorithm for OPM, yet it does not compare it with any competing shallow learning algorithms. This makes the choice of SVM seem a bit arbitrary, which could raise some questions on the worthiness of the reported results.
• Both refs. [12,73] utilize SVM to perform OPM tasks, and both have been proposed in the heydays of deep learning. Nonetheless, none has provided a convincing argument—whether theoretical or empirical—for why SVM is favored over deep learning algorithms. Ref. [73] claims superiority for SVM over artificial neural networks and K-nearest neighbors (K-NNs), and it also claims scalability for SVM. However, these two claims need to be reconsidered; kernel-based SVM is a shallow learning algorithm, and it suffers the same drawbacks other kernel machines suffer; see refs. [58,92] for more information. Deep learning algorithms have been proposed as a solution for those drawbacks [55,58], which invalidates those claims.
• The solutions in refs. [38,75] are developed around PCA, which is an unsupervised learning algorithm for dimensionality reduction. It does not, per se, help tackle a regression of classification tasks, and this is why both solutions apply a K-nearest neighbor (K-NN) on top of PCA to perform the classification and regression tasks of interest. Neither paper presents a clear argument for why PCA is needed in the first place and why it is followed by K-NN and not other shallow learning algorithms—especially given the fact that K-NN typically requires more memory and processing at inference time than the likes of SVM [61] require. Furthermore, no comparison with deep learning algorithms is presented, considering deep learning was state-of-the-art at the time of publishing both solutions.
• No clear reasoning for the choice of kernel-based regression is presented in [44]. The solution requires careful selection of the kernel, which is not discussed in the paper. In addition, the paper does not have proper reasoning for why kernel-based regression is chosen over competing algorithms such as kernel SVM. This casts some doubt on the reported results, i.e., whether they are, at their time, the best one could hope for or not.

5.1.2. Argument for DNN Development

DNNs define state-of-the-art algorithms for many learning tasks in various fields [62], e.g., computer vision [64,68], machine translation [65,93], wireless communications [94,95], etc. Nonetheless, they do not hold the magical answer to every problem; DNNs are powerful learning algorithms, yet throwing them at problems without a sense of why they are used and how they are developed may lead to deceiving results. This basically means that behind any developed DNN must be a well-rounded argument, something that could be considered missing in the literature on DD-OPM with deep learning.

Many proposed DNN-based solutions for DD-OPM are riddled with underdeveloped arguments. The following list attempts to highlight and discuss the most prominent of them.

• Early proposed solutions with neural networks lack proper arguments for the choice of architecture. Neither of the papers [32,34,37,39,77] discuss how the architecture is developed. They, in general, provide a brief description of artificial neural networks and provide simple reasoning of why MLP networks are chosen. That is all well and good, but it does not explain how an architecture (i.e., the number of hidden layers and the breadths of each hidden layer) is developed.
• MLP networks have long been established as universal function approximators [96]. That means they theoretically have enough representational power to express the relation between any observed variables and targets. This is not fully utilized in [78]. The paper develops multiple networks to predict modulation format and OSNR, which could be done with one network, as the work in refs. [11,82] has shown.
• Multi-task learning is proposed in [11,49,82] as a way to develop more effective and computationally efficient solutions for MFI and OPM. They all try to motivate MLT from the perspective of the empirical evidence reported in [97], yet all arguments fall short of being well-rounded; the development process of the DNNs in all papers is not clearly described, especially the reasoning behind the choices of breadth, depth, and activation functions. Such a description could define the boundary line for whether the reported results of MTL are convincing or not compared with single-task learning. Furthermore, refs. [49,82] go beyond the inadequate development of their proposed DNN; they only rely on [97] to motivate MTL and present no comparison to single-task learning at all.
• Developing CNNs for MFI and OPM problems needs to be well motivated, for convolution could be considered a form of regularization [55], which typically restricts the representational capability of an algorithm (It is well established that regularization is a way to constrain the hypothesis space of a learning algorithm, which means it can represent a smaller number of functions. See refs. [55,61] for more information.). Some papers, such as [40,41,86,88] resort to insufficient or incomplete arguments to motivate the choice of CNNs. All argue that the 2-dimensional observed variables call for convolution. This is not entirely wrong, but it is insufficient; the underlying principle of CNNs is capturing and utilizing local structure in 2-dimensional signals [55], which is not clearly mentioned in those papers. Furthermore, some of the papers provide incomplete or mis-presented arguments for using CNNs. Some examples of that are:
  • Machine learning algorithms such as artificial neural networks are claimed to have limited feature-extraction ability in ref. [88]. This is in contrary to the fact that MLP networks, a form of artificial neural networks, are proven to be universal approximators [96], and recent deep learning literature has shown them to be powerful in learning complex functions [54,55].
  • In [41], the blurriness of deep feature maps (commonly called high-level features) is claimed to be a clue to their ability to represent abstract concepts. This is not wrong, but it is also not quite correct. Blurriness in itself is a byproduct of systematic downsampling in CNNs (i.e., pooling operations). It may indicate an increased level of abstraction, but such an observation has been brought forward in the context of computer vision, where the observed variables are image pixels. There is nothing to suggest that blurriness carries the same meaning for other applications as it does for computer vision.
  • Finally, CNNs in ref. [86] are claimed to be the only type of neural networks capable of “automatic feature extraction”. However, this claim needs to be reconsidered, as all DNNs are capable of automatic feature extraction because they are developed around the idea of data-driven feature learning [55]. This is a competing idea to feature engineering that is intrinsic to classical machine learning.

5.2. Unclear Dataset Description and Training Procedure

Proposing a machine learning algorithm to perform a task does not only mean picking and designing a certain type of algorithm or model, but it also entails the construction of a proper development dataset and the development of an effective training procedure. A dataset should be representative of the system where the proposed algorithm is deployed, henceforth referred to as the target system. It must have data points (i.e., samples of observed variables) and their corresponding ground truth responses that represent various states of the target system. This is necessary for any algorithm to achieve generalization, which is the ability to perform well on unseen data and beyond the experienced data points in the training dataset [55].

Effective algorithm training is as instrumental as the design of the learning algorithm itself and the construction of the development dataset [55]. It determines how the algorithm learns and assesses its performance. A good training experience typically encompasses the choice of a training optimizer, the design of a loss function, and the fine-tuning of training hyper-parameters. The optimizer is the core of the training process, for it is responsible for navigating the algorithm parameter space (also referred to as the hypothesis space). The search of the parameter space is mainly guided by the loss function. Carefully designed functions result in effective training, which, consequently, leads to a better performing algorithm. Controlling the optimizer while it searches for the parameters minimizing the loss function is a set of training hyper-parameters, e.g., learning rate, regularization, and mini-batch size, to name three examples. Such hyper-parameters require careful fine-tuning as they dictate how the optimizer behaves and how the algorithm parameter space is navigated.

The literature on ML for DD-OPM seems to under-estimate the role datasets and training play in the development of effective learning algorithms. Some publications are riddled with improper description of the dataset and training procedure while others rely on unsuitable datasets or loss functions. Both issues are discussed in the next couple of subsections.

5.2.1. Poor Dataset Construction and Description

A major shortcoming for many proposed DD-OPM solutions is how the development dataset is constructed and used. Commonly, the relation between the observed variables and targets is modeled probabilistically, and the distribution governing that relation (typically referred to as the data-generating distribution) is typically unknown [55]. Hence, a dataset needs to be sampled randomly and carefully from that distribution to be expressive and useful, yet this is not the widespread case in the DD-OPM literature. The main shortcoming could be summarized as follows

• Uniform and coarse sampling of a continuous space generates biased datasets. This is the problem with several papers, especially when considering continuous variables (whether observed variables or targets) such as OSNR or CD. Many DD-OPM solutions attempt to predict OSNR, yet they do not provide a proper dataset; the OSNR space is typically sampled uniformly with a relatively large step. The datasets in refs. [9,40,41,73,84,87] all are good examples of that problem. They consider a wide OSNR space, from ∼10 to ∼30 dB, and sample it uniformly with a relatively large step, 1 or 2 dB. Such sampling results in a discrete set of OSNR values. This is misleading, as OSNR is a real-valued parameter, not discrete.
• Proposing a machine-learning-based solution requires a careful and clear description of the development dataset. Many publications do not distinguish between four important elements, namely experimental setup, data collection, dataset construction, and data pre-processing. Typically, experimental setup and data collection are described together—see ref. [94,98]—for they describe how the optical system is set up and how the data samples are collected. Dataset construction focus on the details of the development dataset—constructing pairs of observed variables and their target responses—such as how the raw data are processed, how the dataset is structured, and what the total number of data points is. Papers such as refs. [9,31,40,49,73,87] fail to provide such a clear distinction, and, hence, basic details such as the number of data points are missing.

5.2.2. Improper Loss Function and Missing Training Hyper-Parameters

The choice of loss function and the selection of training hyper-parameters are two important aspects of machine learning development that are missing in many papers in the literature of DD-OPM. Those two issues are further discussed below.

• Monitoring the training and validation losses is instrumental to developing a machine learning algorithm. Some papers do not provide information on those two losses. This casts some doubt on the validity of the results and elicits questions about how well the algorithm learns from the dataset and how suitable the training hyper-parameters are to the task in hand. Papers such as refs. [11,47,80,84] all lack information on training and validation losses.
• Picking the right loss function must reflect how the monitoring or identification tasks are posed, from a machine learning perspective, of course. For instance, picking an MSE loss function encodes two facts about the machine learning task. The first one is explicit; the domain of the targets has a continuous nature, see ref. [61]. This simply means the vector of targets could live in a sub-space of any dimensionality. The other fact is implicit and rooted in the modeling of the relation between the observed variables and the targets; the conditional probability of the targets given the observed variables follows a Gaussian distribution—see [61] for more details. Keeping those two facts in mind, a classification task should not be addressed with an MSE loss function; the targets are discrete in nature, and, as a consequence, the conditional probability governing the relation between the targets and the observed variables cannot be Gaussian. Such an observation, i.e., using MSE loss for classification, has appeared a few times in the DD-OPM literature, ref. [78,88,89] to name three examples.

5.3. Lack of Benchmark Dataset and Evaluation Metrics

This is the last, but most important, issue of the three. The whole literature on DD-OPM is lacking a benchmark datasets and clear protocols for performance comparison. None of the proposed solutions could be compared with others. This is not due to novelty in the task being tackled or the optical communication setup. Rather, it is a consequence of the unavailability of benchmark datasets or performance evaluation protocols.

5.3.1. Lack of Benchmark Datasets

Although there are various choices of targets and observed variables in DD-OPM, one could argue that many proposed solutions have a degree of overlap in terms of the tasks they address. For instance, [11,78,82] all address problems with MFI among other targets, and [32,34,36] all focus on OSNR, CD, and PMD monitoring—other examples could also be found in the literature. They generally differ in terms of what algorithms they use, how they address the learning task (e.g., single-task or multi-task learning), and what observed variables to consider. However, none of those proposed solutions could be compared with each other or benchmarked. This casts serious doubts on the validity or merit of the proposed solutions, for their generalization cannot be quantified when the datasets used vary in terms of size, diversity, and source. Some datasets could be designed to fit certain solutions, which makes them unrepresentative of real direct detection optical systems. Others could be too small to draw any conclusions about the effectiveness of the proposed solution.

5.3.2. Lack of Common Performance Monitoring Metrics

All problems addressed in the DD-OPM literature are either tackled as regression or classification tasks. Using metrics such as MSE, RMSE, accuracy, and confusion matrix makes sense from a machine learning perspective, for they are common measures of performance. However, when one factors in the fact that those solutions are developed for a specific engineering system, there is a need for a more context-relevant performance metric, something to relate the performance of a proposed solution to the performance of the system. For instance, an ML algorithm developed for a wireless communication system is better evaluated in terms of achievable rate [94,99] or latency [100]. The same thing should be applied to solutions developed for DD-OPM; they should have their own system-specific evaluation metrics. Such metrics are important because they allow comparison between proposed ML-based solutions, especially when benchmark datasets are available.

6. Lessons Learned and Recommendation for Future Research

With Section 4 and Section 5, respectively, surveying the literature of DD-OPM and MFI and discussing the main issues with proposed solutions, a few lessons could be highlighted to help guide future ML research work in optical networks. They revolve around the choice of learning paradigm, the choice of an algorithm, and how it is developed into a solution.

6.1. Carefully Choosing a Paradigm

Picking the right learning paradigm could be argued to be the first step towards developing good ML algorithms for any problem. Deep learning has been pushing the boundaries of AI for the past decade. State-of-the-art performance on many intelligence tasks, such as object detection, machine translation, and image generation, among others, has been achieved with deep learning algorithms. Despite its success, understanding the limits of deep learning capabilities is not fully formed [55]; the efforts are still ongoing to unravel the mysteries of deep learning, i.e., address questions such as what its limits are, how to design a neural network architecture, what each layer of a deep learning algorithm learns, and many others [101,102,103,104]. In contrast, shallow learning is well-understood as it involves heavy engineering, yet shallow algorithms, collectively, do not rise to the challenge posed by complex problems as their deep learning counterparts do.

If deep learning is not well understood and shallow learning is but does not rise to the challenge, how could one pick between the two? In spite of the glaring imbalance in paradigm understanding, the choice between deep and shallow learning could be made by contemplating the following two criteria: (i) size of the development dataset (development dataset is composed of three sets of data points, namely training, validation, and testing.), and (ii) available computing resources. The following discusses the two.

• Dataset size: this is a crucial and practical point to consider when choosing a paradigm. Deep learning algorithms tend to have an extremely large number of parameters [55], in the order of millions. Therefore, a considerably large dataset is needed to train deep algorithms. How big the dataset should be is still an open-ended question in the field of deep learning and the realm of machine learning in general. What is known for sure at this point in time is that the size is problem- and algorithm-dependent. Nevertheless, given the empirical evidence observed in the fields of computer vision and natural language processing, it could be said that dataset sizes should be in the order of hundreds of thousands to millions of data points, see refs. [105,106], for instance. Typically, the larger the dataset is, the more reliable the results of a deep algorithm are [54]. Therefore, One might consider this the first criteria to choose between the two paradigms; the availability of a large number of data points makes deep learning a favorable choice.
• Computing resources: this is another crucial and practical point; when the number of parameters as well as the dataset size are large, special computing resources are needed, ones with enough memory and processing units. This is the usual requirement for deep algorithms [107], for they have a large number of parameters and require large datasets. A solution that needs to be implemented with limited resources is better developed with a shallow learning algorithm than with a deep one, for shallow algorithms tend to have a smaller number of parameters compared with deep algorithms.

6.2. Improved Solution Development

Picking a learning paradigm is not the end of the road for solution development, for each paradigm has a large number of candidate algorithms. As mentioned earlier in Section 5, the literature on using machine learning for DD-OPM lacks well-developed arguments for algorithm choice, clear dataset descriptions and training procedures, and, finally, benchmark datasets and protocols. All three together lead to what is called here “inadequate solution development.” It is suggested that they are addressed as follows:

• Algorithm choice: picking a learning algorithm should first be justified by the requirements of the DD-OPM problem itself, the type of observed variables, and type of targets. A common consequence of that step is that a few learning algorithms could be found suitable, so those algorithms should be pitted against each other using the same development dataset. This provides enough empirical evidence to favor one algorithm over the others, and it helps build a clear reasoning for how the proposed solution comes together.
• Clear development methodology: it is crucial to clearly describe how an algorithm is trained and tested on a dataset. Many algorithms are developed based on a heuristic design approach, such as in the case of neural networks [55], and some algorithms assume a certain relation between the observed variables and targets, such as the conditional Gaussian distribution used in regression problems [61]. In all cases, clearly specifying the hyper-parameters and how the algorithm is trained helps others verify the results and test the developed solution on different problems.
• Benchmark datasets: this suggestion is the most important lesson in this paper; solutions that depend on machine learning are data-driven and developed empirically. Hence, having large, diverse, and open-source datasets available to the community makes the published results trustworthy for three reasons: (i) they are obtained from well-designed datasets representing specific optical communication setups; (ii) comparison of DD-OPM and MFI solutions can be conducted across research groups; and (iii) verification of published results is possible. Benchmark datasets are common practice in all research fields adopting machine learning, e.g., ImageNet in computer vision [105], ViWi in wireless communications [108], and GLEU in natural Language Understanding (NLU) [109], and it should be adopted by the optical communications community.

7. Conclusions

The literature on developing DD-OPM, MFI, and BRI solutions with machine learning is surveyed with a keen eye on three aspects: (i) what monitoring tasks are commonly addressed, (ii) which learning paradigm is followed, and (iii) what type of algorithms are used to develop the solutions. The first outcome of the survey is a novel taxonomy of the proposed machine-learning-based solutions. The taxonomy sees the literature partitioned into two broad categories pertaining to the two major learning paradigms, namely deep learning and shallow learning. Within each category, the solutions are further grouped into relatively homogeneous clusters based on the type of proposed algorithms. The taxonomy reveals some interesting observations on all survey aspects, which, when analyzed, give rise to important insights and lessons. The observations and their relevant insights and lessons are summarized in Figure 5 in a way that shows their underlying connections.