Focusing and Wavefront Splitting of an Extreme Ultraviolet Laser with a Tubular Optical Element
Abstract
1. Introduction
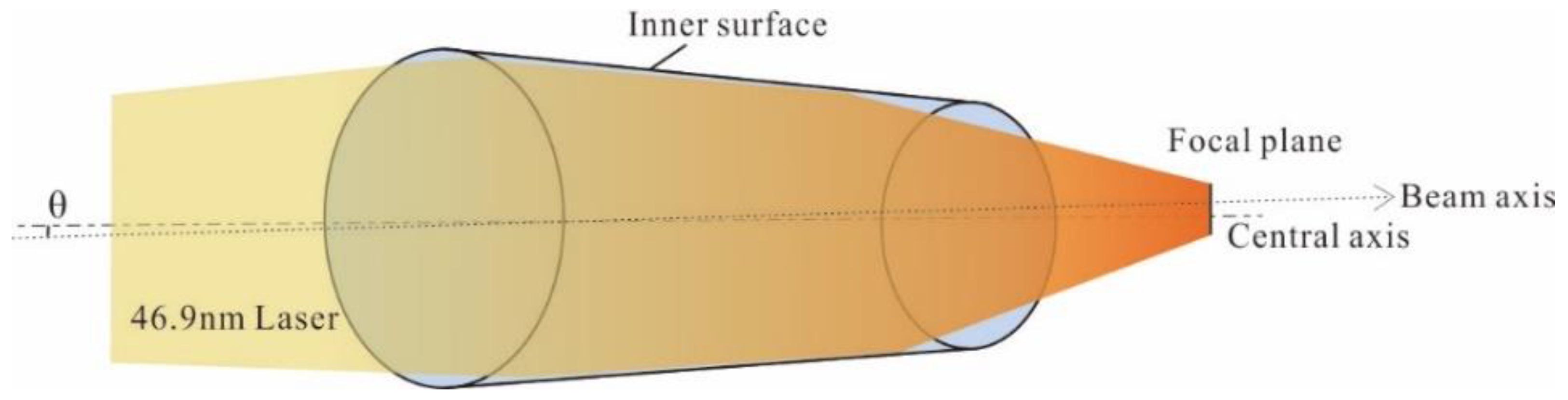
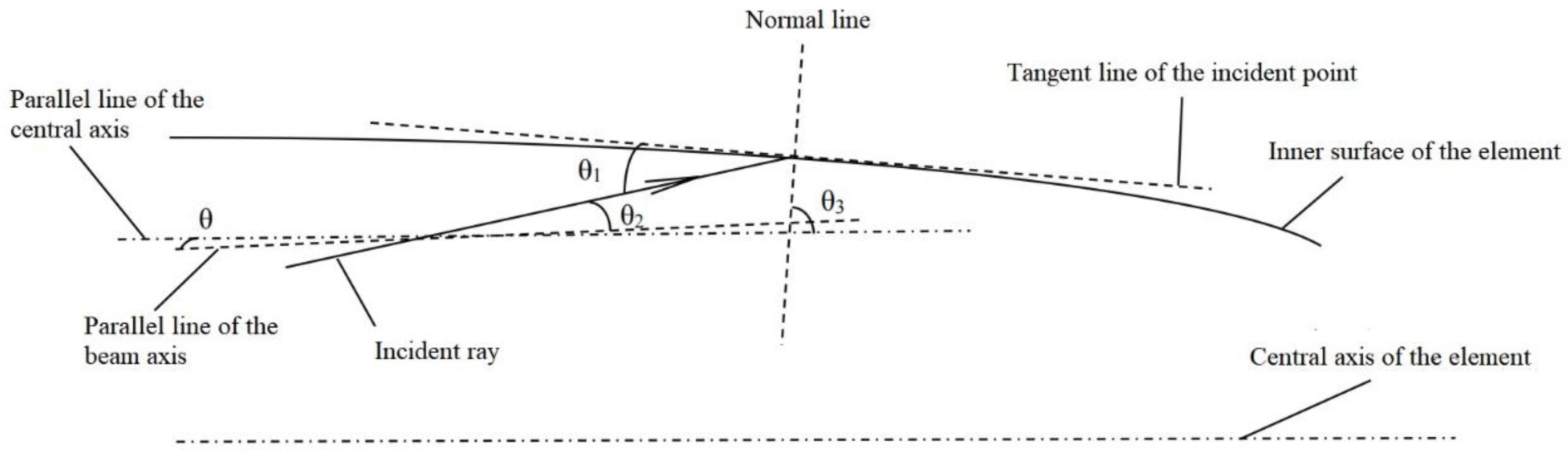
2. Materials and Methods
3. Results
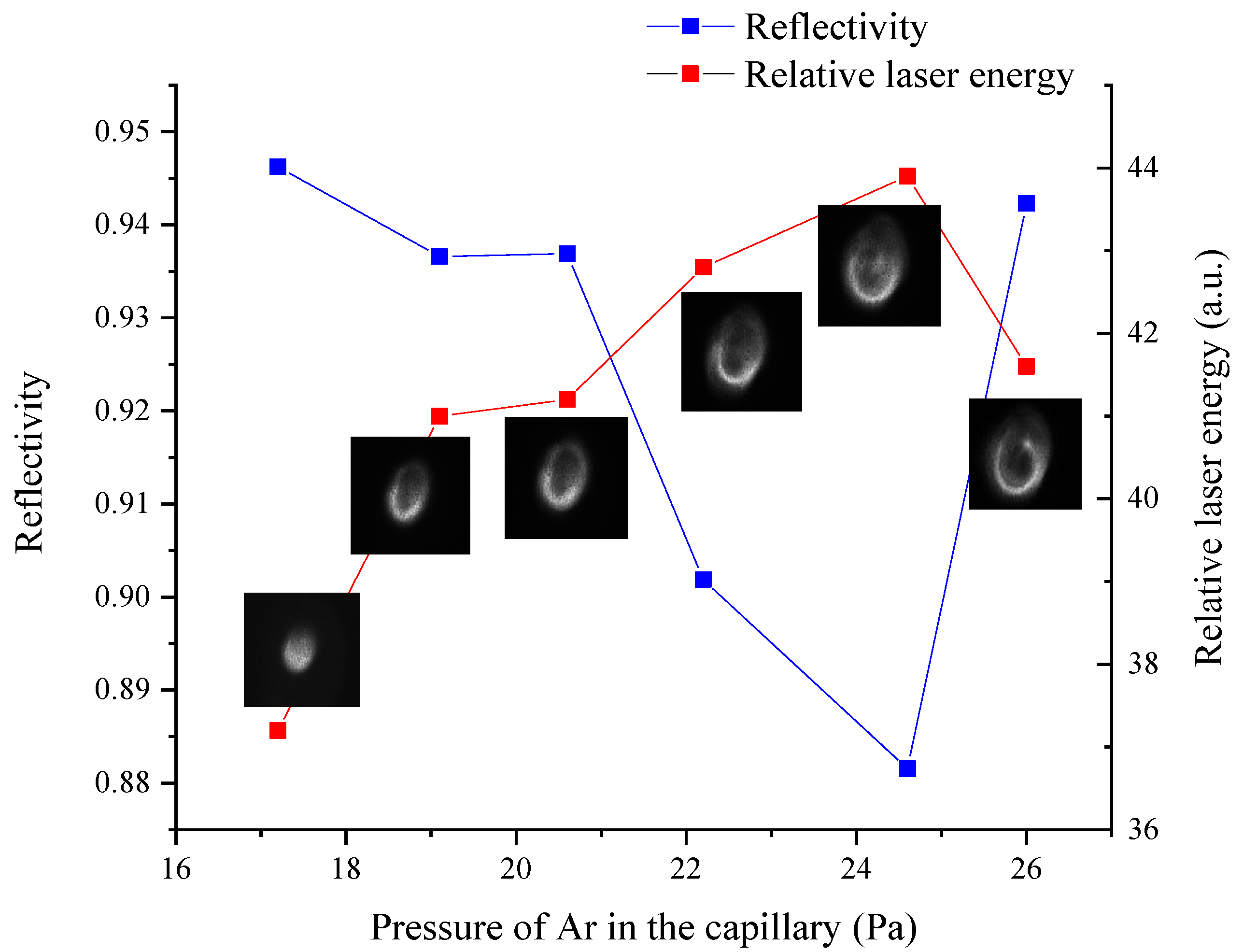
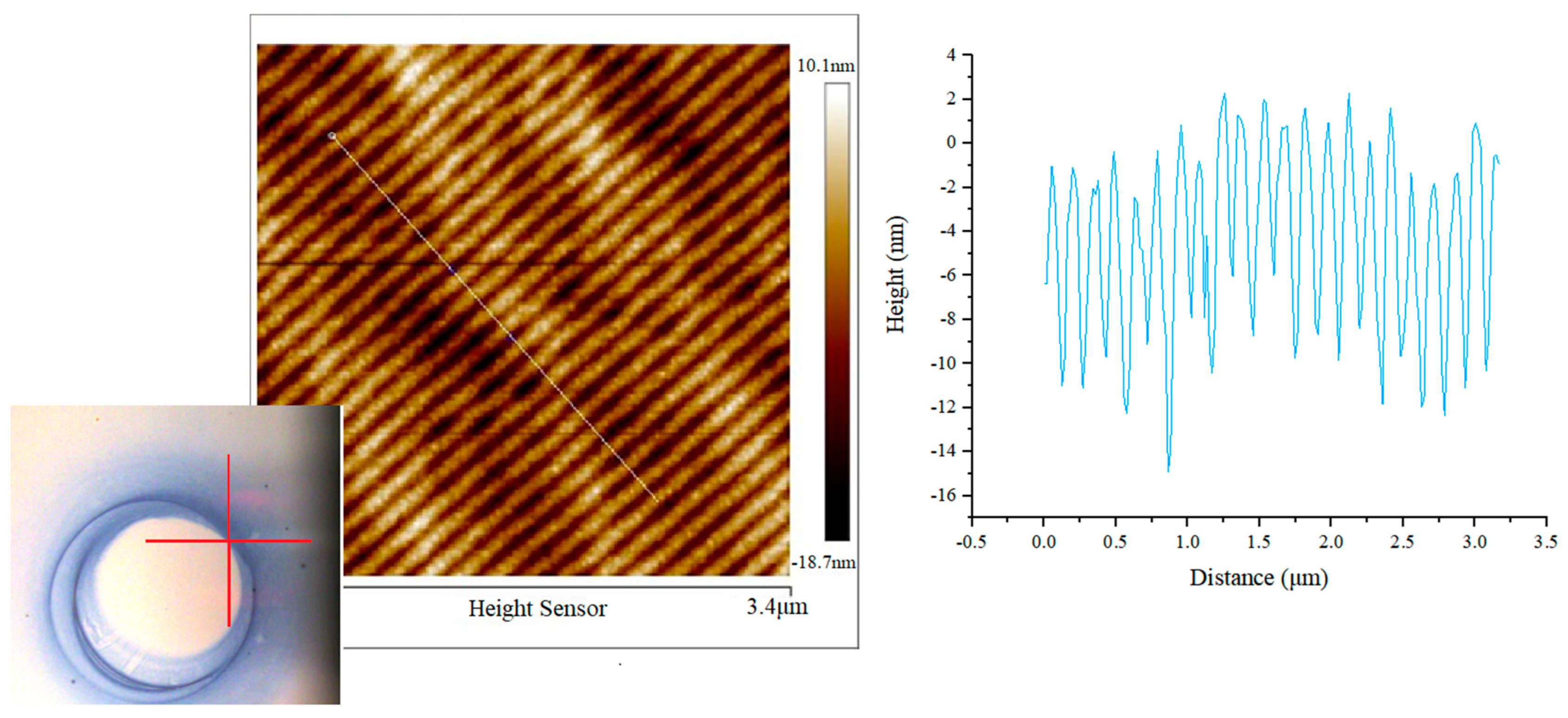
3.1. The Reflectivity Measurement
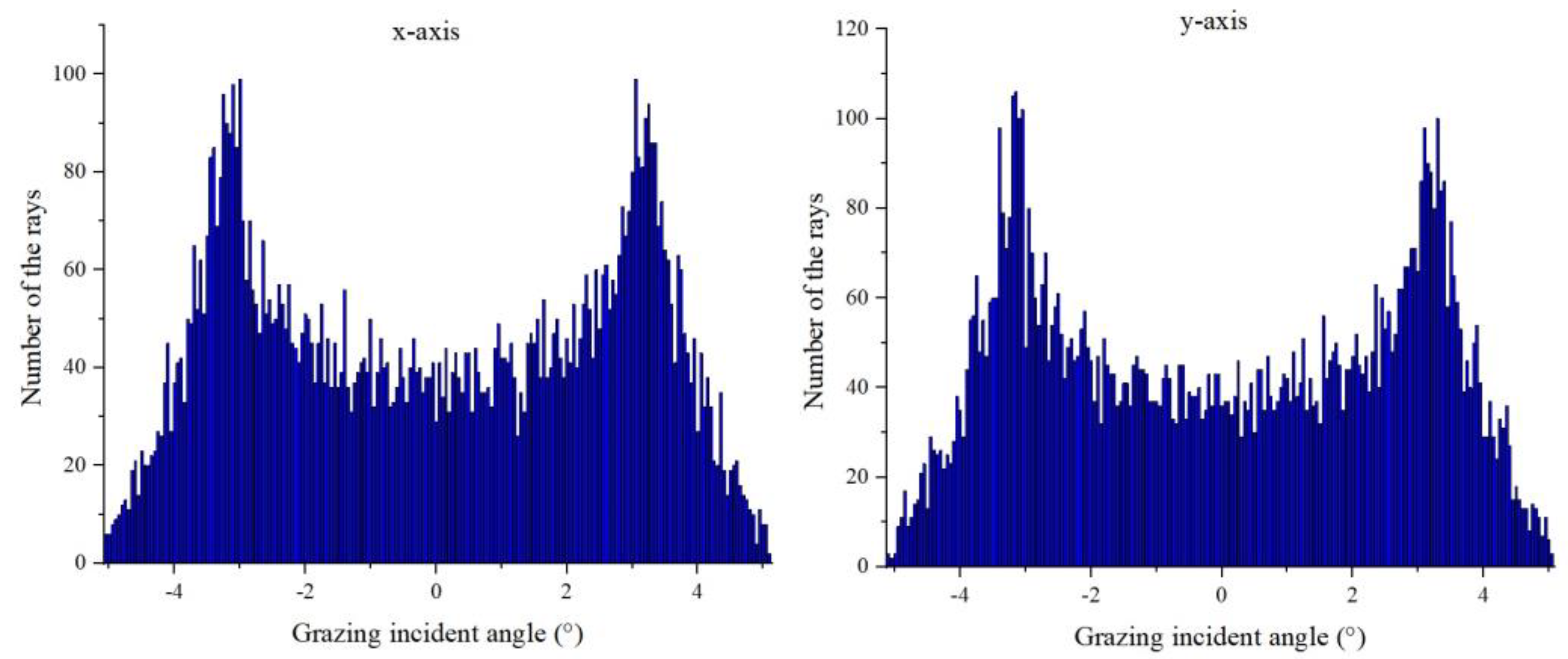
3.2. The Focusing and Interfering of 46.9 nm Laser
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rocca, J.J.; Hammarsten, E.C.; Jankowska, E.; Filevich, J.; Marconi, M.C.; Moon, S.; Shlyaptsev, V.N. Application of Extremely Compact Capillary Discharge Soft X-ray Lasers to Dense Plasma Diagnostics. Phys. Plasmas 2003, 10, 2031–2038. [Google Scholar] [CrossRef]
- Kuznetsov, I.; Filevich, J.; Dong, F.; Woolston, M.; Chao, W.; Anderson, E.H.; Bernstein, E.R.; Crick, D.C.; Rocca, J.J.; Menoni, C.S. Three-Dimensional Nanoscale Molecular Imaging by Extreme Ultraviolet Laser Ablation Mass Spectrometry. Nat. Commun. 2015, 6, 6944. [Google Scholar] [CrossRef] [PubMed]
- Vaschenko, G.; Etxarri, A.; Menoni, C.; Rocca, J.; Hemberg, O.; Bloom, S.; Chao, W.; Anderson, E.; Attwood, D.; Lu, Y.; et al. Nanometer-Scale Ablation with a Table-Top Soft X-ray Laser. Opt. Lett. 2006, 31, 3615–3617. [Google Scholar] [CrossRef] [PubMed]
- Green, T.; Kuznetsov, I.; Willingham, D.; Naes, B.E.; Eiden, G.C.; Zhu, Z.; Chao, W.; Rocca, J.J.; Menoni, C.S.; Duffin, A.M. Characterization of Extreme Ultraviolet Laser Ablation Mass Spectrometry for Actinide Trace Analysis and Nanoscale Isotopic Imaging. J. Anal. At. Spectrom. 2017, 32, 1092–1100. [Google Scholar] [CrossRef]
- Attwood, D. Wave propagation and refractive index at X-ray and EUV wavelengths. In X-rays and Extreme Ultraviolet Radiation: Principles and Applications, 2nd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2016; pp. 61–65. [Google Scholar]
- Zhang, Z.; Li, W.; Huang, Q.; Zhang, Z.; Yi, S.; Pan, L.; Xie, C.; Wachulak, P.; Fiedorowicz, H.; Wang, Z. A Table-Top EUV Focusing Optical System with High Energy Density Using a Modified Schwarzschild Objective and a Laser-Plasma Light Source. Rev. Sci. Instrum. 2018, 89, 103109. [Google Scholar] [CrossRef] [PubMed]
- Benware, B.; Ozols, A.; Rocca, J.; Artioukov, I.; Kondratenko, V.; Vinogradov, A. Focusing of a Tabletop Soft-X-ray Laser Beam and Laser Ablation. Opt. Lett. 1999, 24, 1714–1716. [Google Scholar] [CrossRef] [PubMed]
- Rossall, A.K.; Aslanyan, V.; Tallents, G.J.; Kuznetsov, I.; Rocca, J.J.; Menoni, C.S. Ablation of Submicrometer Holes Using an Extreme-Ultraviolet Laser. Phys. Rev. Appl. 2015, 3, 064013. [Google Scholar] [CrossRef]
- Korobenko, A.; Rashid, S.; Heide, C.; Naumov, A.; Reis, D.; Berini, P.; Corkum, P.; Vampa, G. In-Situ Nanoscale Focusing of Extreme Ultraviolet Solid-State High Harmonics. Phys. Rev. X 2022, 12, 041036. [Google Scholar] [CrossRef]
- Capeluto, M.G.; Vaschenko, G.; Grisham, M.; Marconi, M.C.; Luduena, S.; Pietrasanta, L.; Lu, Y.; Parkinson, B.; Menoni, C.S.; Rocca, J.J. Nanopatterning with Interferometric Lithography Using a Compact/Spl Lambda/=46.9-Nm Laser. IEEE Trans. Nanotechnol. 2006, 5, 3–7. [Google Scholar] [CrossRef]
- Wachulak, P.; Capeluto, M.; Marconi, M.; Patel, D.; Menoni, C.; Rocca, J. Nanoscale Patterning in High Resolution HSQ Photoresist by Interferometric Lithography with Tabletop Extreme Ultraviolet Lasers. J. Vac. Sci. Technol. B 2007, 25, 2094–2097. [Google Scholar] [CrossRef]
- Wachulak, P.; Grisham, M.; Heinbuch, S.; Martz, D.; Rockward, W.; Hill, D.; Rocca, J.; Menoni, C.; Anderson, E.; Marconi, M. Interferometric Lithography with an Amplitude Division Interferometer and a Desktop Extreme Ultraviolet Laser. J. Opt. Soc. Am. B-Opt. Phys. 2008, 25, B104–B107. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, H.; Zhang, W.; Li, W.; Jiang, S.; Li, L. Si and Cu Ablation with a 46.9-Nm Laser Focused by a Toroidal Mirror. Opt. Express 2015, 23, 14126–14134. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.; Zhao, Y.; Khan, M.; Zhao, D.; Fan, Z. Study of Thermal Effect in the Interaction of Nanosecond Capillary Discharge Extreme Ultraviolet Laser with Copper. Appl. Sci. 2020, 10, 214. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, D.; Yu, Q.; Khan, M.; Lu, H.; Li, J.; Cui, H. Influence of He Mixture on He Pulse Amplitude and Spatial Distribution of an Ne-like Ar 46.9 Nm Laser under Gain Saturation. J. Opt. Soc. Am. B-Opt. Phys. 2020, 37, 2271–2277. [Google Scholar] [CrossRef]
- Li, J.; Cui, H.; Zhao, D.; An, B.; Zhao, Y. Influence of Ar-He Mixture Gas Pressure on Output Characteristics of Ne-like Ar 46.9 Nm Laser. Acta Opt. Sin. 2022, 42, 1134022. [Google Scholar]
- Wang, Z.; Zhang, J.; Li, G.; Xu, Z.; Zhang, H.; Zhang, J.; Hartmaier, A.; Fang, F.; Yan, Y.; Sun, T. Anisotropy-related machining characteristics in ultra-precision diamond cutting of crystalline copper. Nanomanuf. Metrol. 2020, 3, 123–132. [Google Scholar] [CrossRef]
- Spielman, R.B.; Anthes, J.P. A study of bare X-ray diode saturation due to a high fluence X-ray pulse. AIP Conf. Proc. 1981, 75, 278–279. [Google Scholar]
- Pershyn, Y.; Zubarev, E.; Voronov, D.; Sevryukova, V.; Kondratenko, V.; Vaschenko, G.; Grisham, M.; Menoni, C.; Rocca, J.; Artioukov, I.; et al. Mechanisms of Radiation Damage to Sc/Si Multilayer Mirrors under EUV Laser Irradiation. J. Phys. D-Appl. Phys. 2009, 42, 125407. [Google Scholar] [CrossRef]
- Bravo, H.; Szapiro, B.; Wachulak, P.; Marconi, M.; Chao, W.; Anderson, E.; Menoni, C.; Rocca, J. Demonstration of Nanomachining With Focused Extreme Ultraviolet Laser Beams. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 443–448. [Google Scholar] [CrossRef]
- Ritucci, A.; Tomassetti, G.; Reale, A.; Arrizza, L.; Zuppella, P.; Reale, L.; Palladino, L.; Flora, F.; Bonfigli, E.; Faenov, A.; et al. Damage and Ablation of Large Bandgap Dielectrics Induced by a 46.9 Nm Laser Beam. Opt. Lett. 2006, 31, 68–70. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Wang, Z.; Wu, S.; An, H.; Wang, J.; Zhao, Y. Focusing and Wavefront Splitting of an Extreme Ultraviolet Laser with a Tubular Optical Element. Photonics 2023, 10, 629. https://doi.org/10.3390/photonics10060629
Cui H, Wang Z, Wu S, An H, Wang J, Zhao Y. Focusing and Wavefront Splitting of an Extreme Ultraviolet Laser with a Tubular Optical Element. Photonics. 2023; 10(6):629. https://doi.org/10.3390/photonics10060629
Chicago/Turabian StyleCui, Huaiyu, Zhiyuan Wang, Shan Wu, Haojie An, Jinshi Wang, and Yongpeng Zhao. 2023. "Focusing and Wavefront Splitting of an Extreme Ultraviolet Laser with a Tubular Optical Element" Photonics 10, no. 6: 629. https://doi.org/10.3390/photonics10060629
APA StyleCui, H., Wang, Z., Wu, S., An, H., Wang, J., & Zhao, Y. (2023). Focusing and Wavefront Splitting of an Extreme Ultraviolet Laser with a Tubular Optical Element. Photonics, 10(6), 629. https://doi.org/10.3390/photonics10060629




