Periodic Artifacts Generation and Suppression in X-ray Ptychography
Abstract
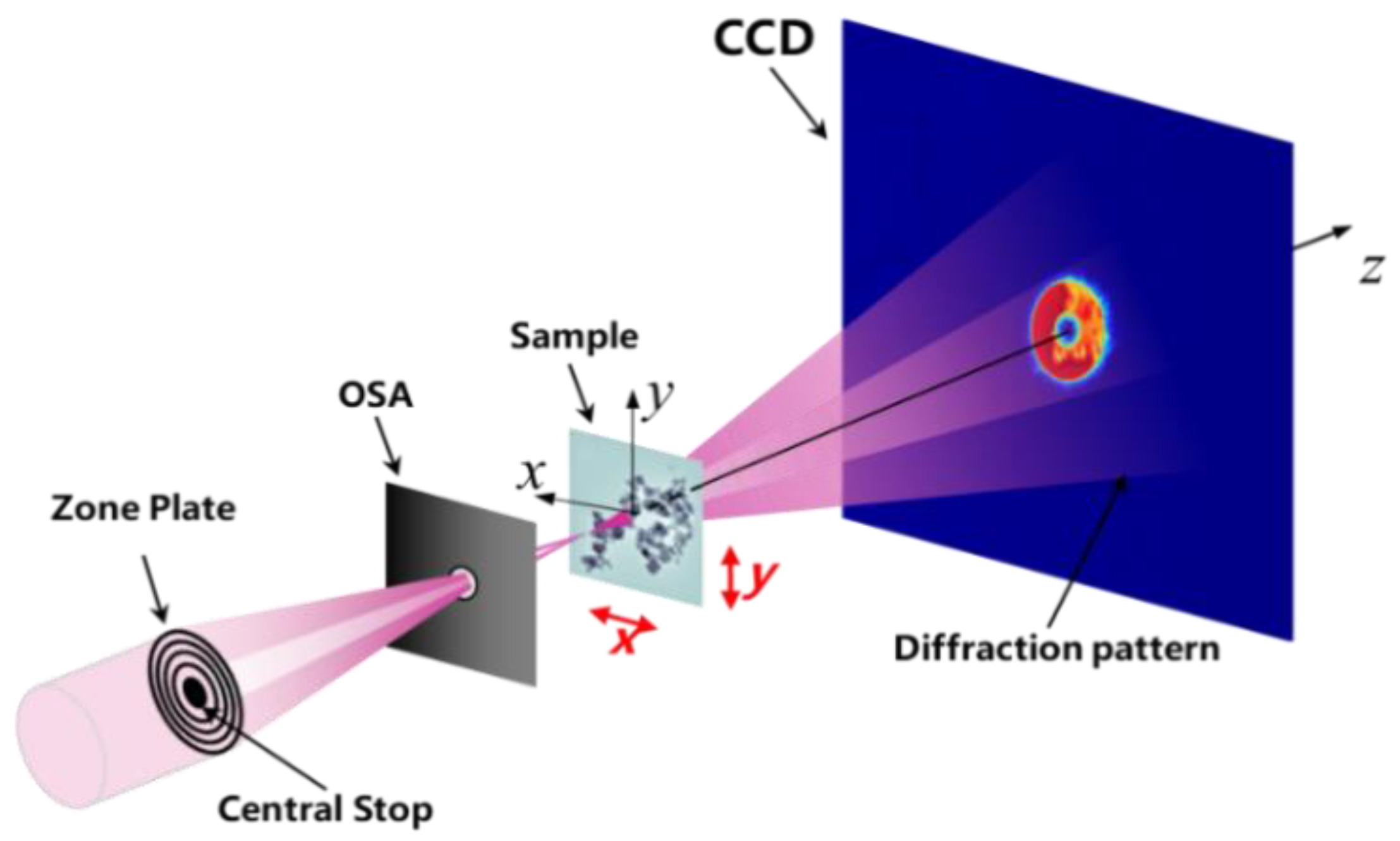
1. Introduction
- (1)
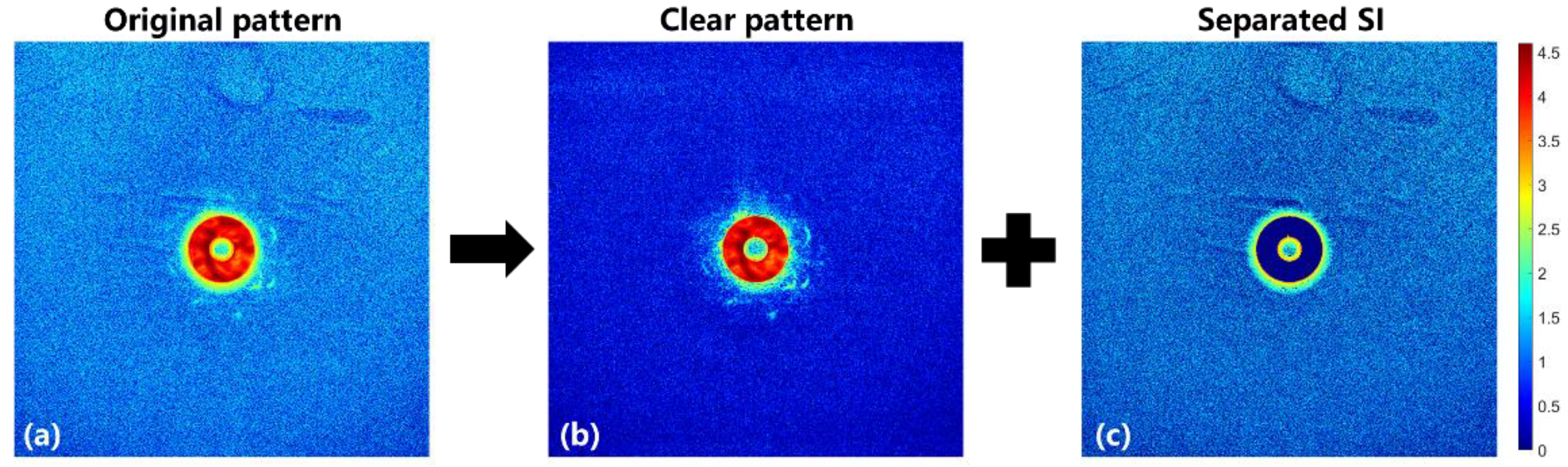
- No interaction with objects: The SI comes from the light or noise factors that do not interact with the object in the illuminated area, and it is incoherently added with the diffracted signals from the object and probe beam on the CCD plane.
- (2)
- Time invariability: The SI does not vary with time (scanning process), i.e., it is the static part in the recorded dataset and does not change with the scanned position of the object.
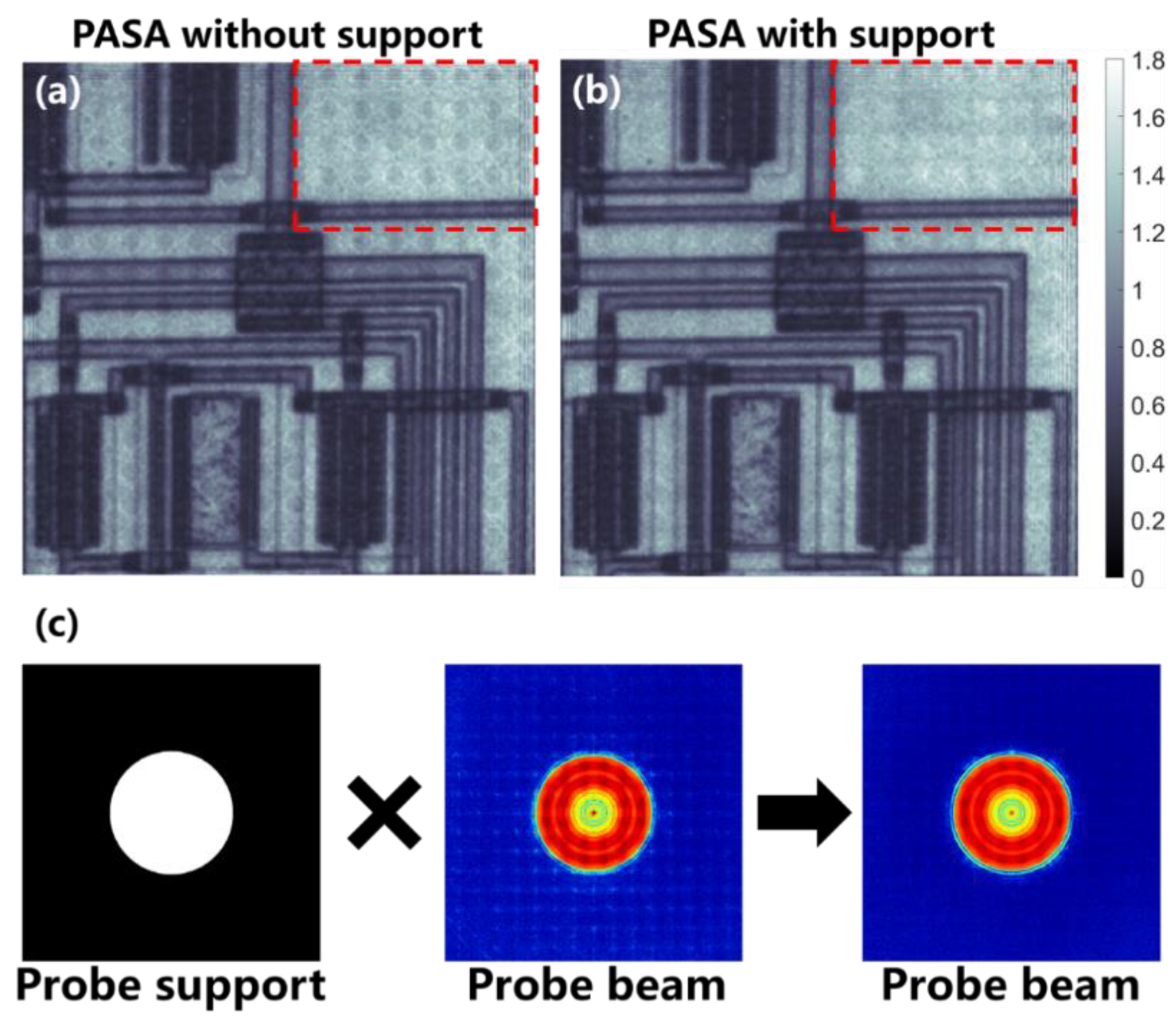
2. Periodic-Artifact Suppressing Algorithm (PASA)
3. Results
3.1. Parameter Settings
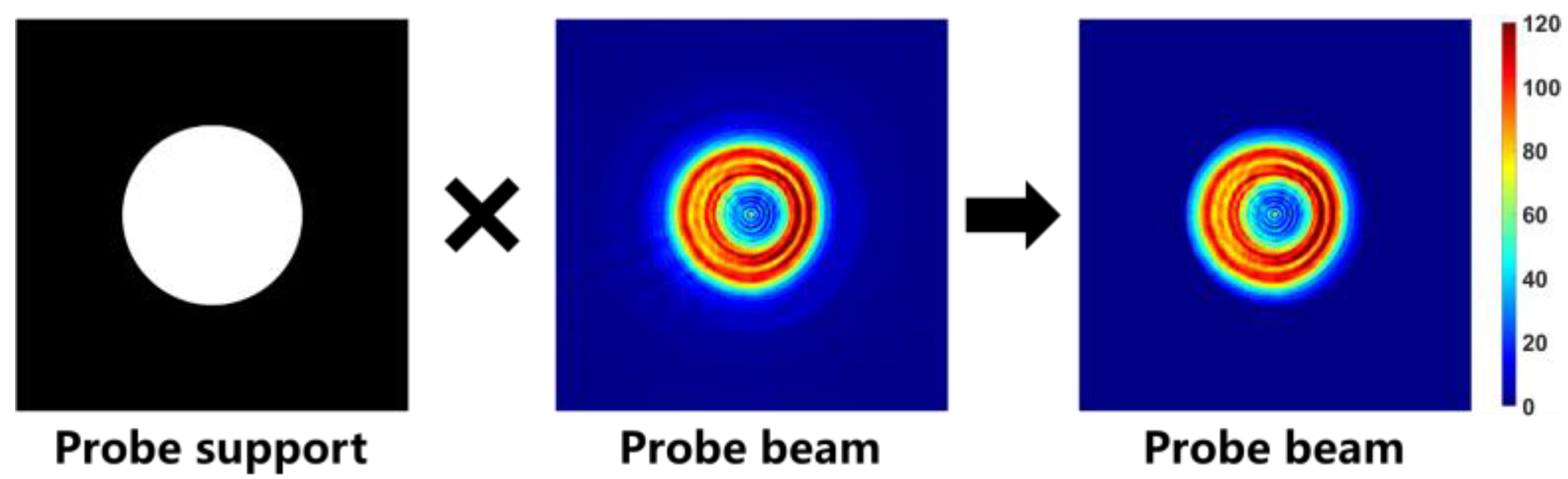
3.2. Simulation and Raster-Grid Pathology Cause Analysis
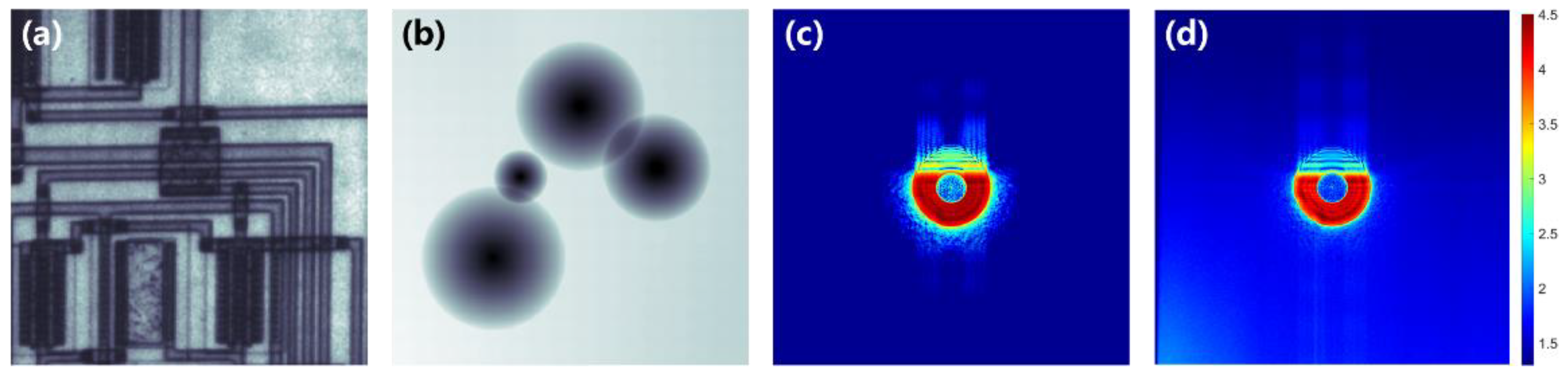
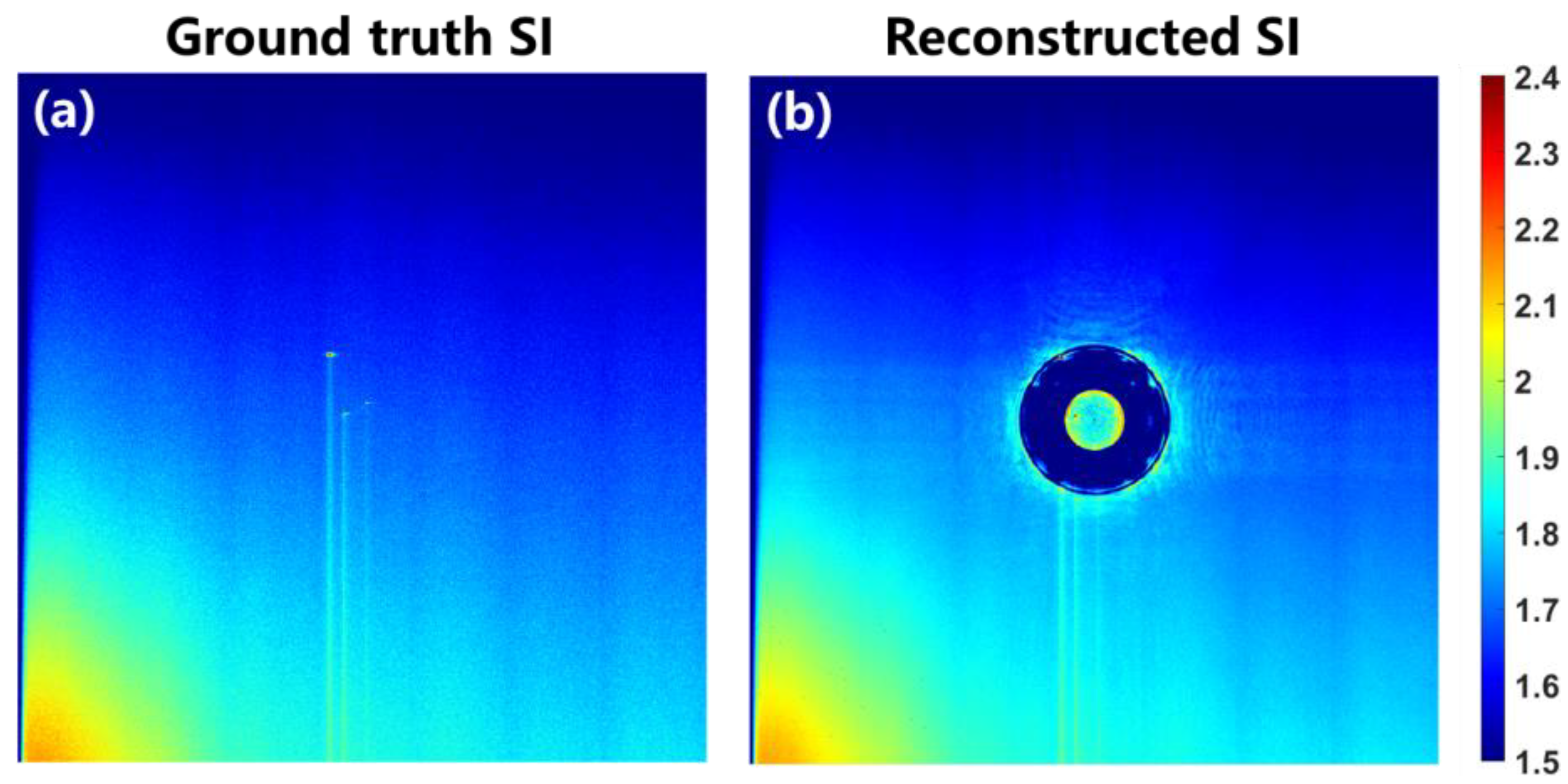
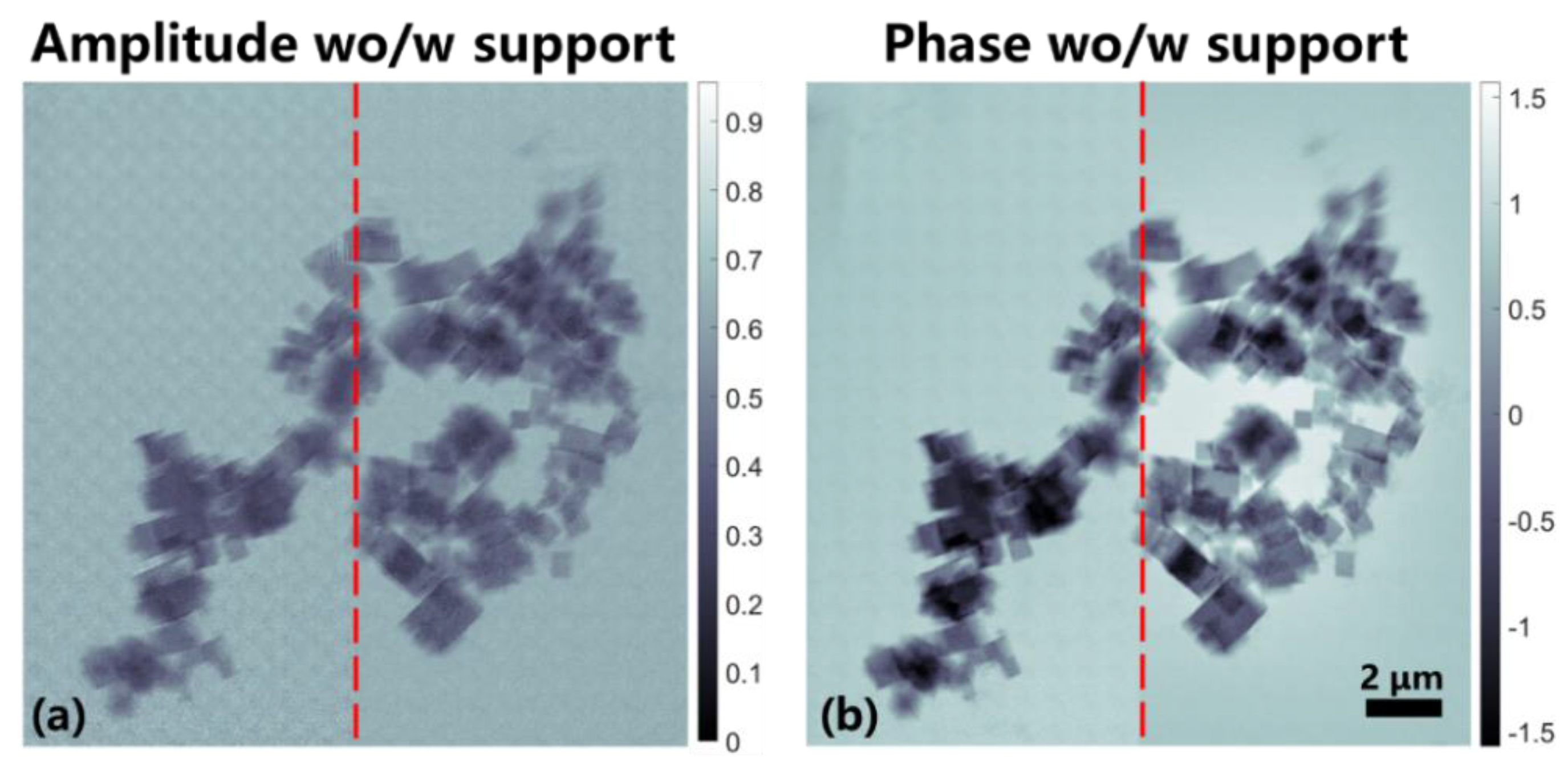
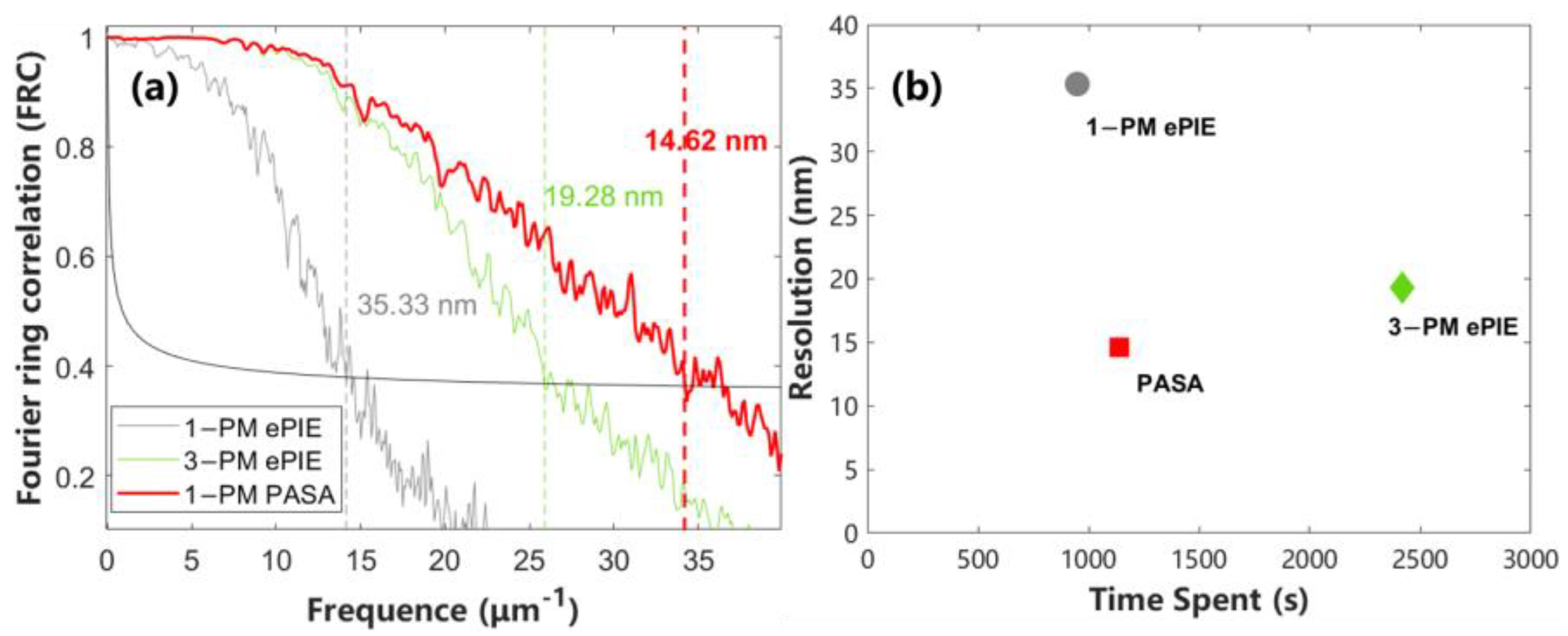
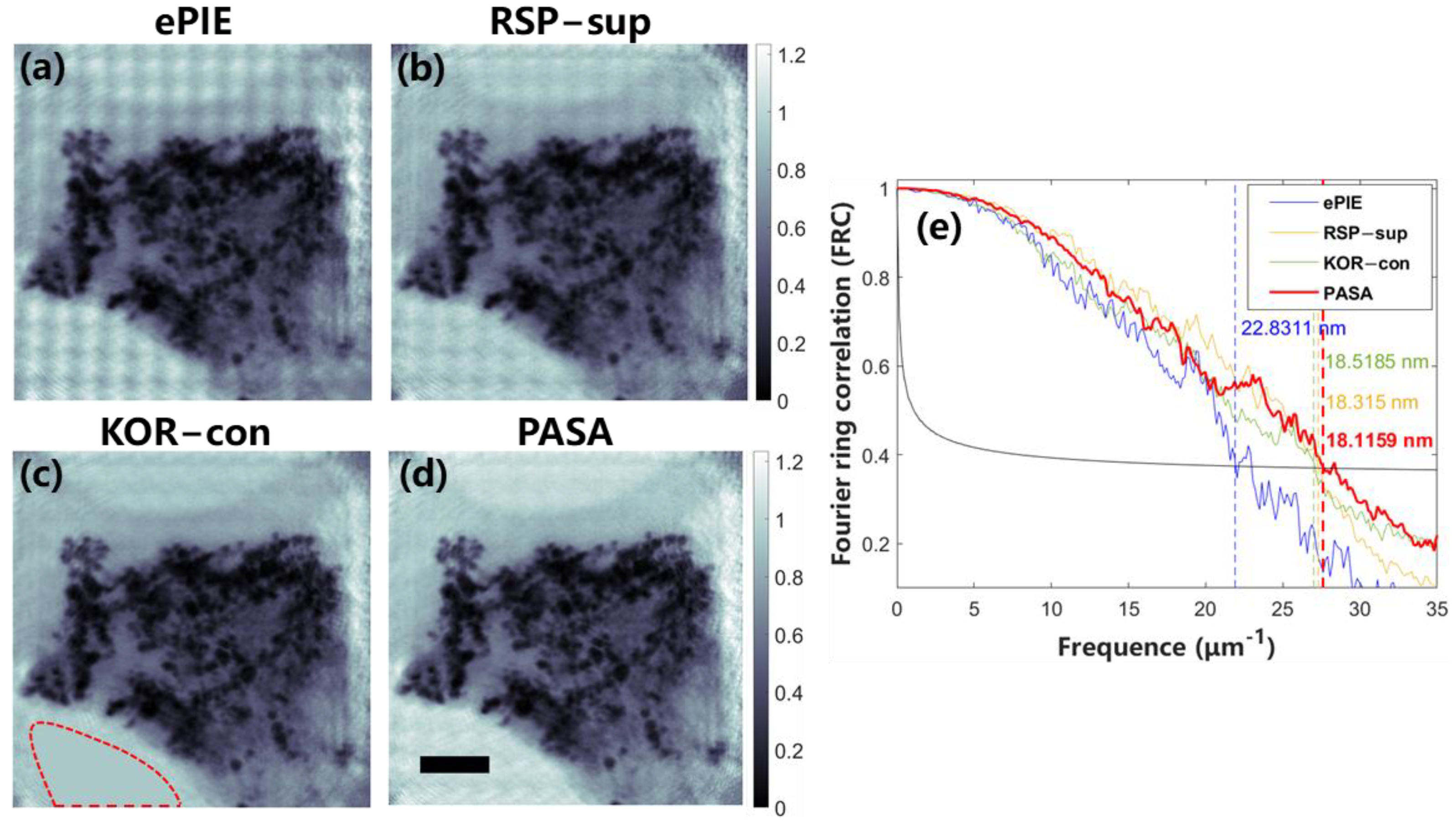
3.3. Experiment
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miao, J.; Charalambous, P.; Kirz, J.; Sayre, D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Jiang, Y.; Deng, J.; Yao, Y.; Klug, J.A.; Mashrafi, S.; Roehrig, C.; Preissner, C.; Marin, F.S.; Cai, Z.; Lai, B. Achieving high spatial resolution in a large field-of-view using lensless X-ray imaging. Appl. Phys. Lett. 2021, 119, 124101. [Google Scholar] [CrossRef]
- Chang, H.; Enfedaque, P.; Zhang, J.; Reinhardt, J.; Enders, B.; Yu, Y.-S.; Shapiro, D.; Schroer, C.G.; Zeng, T.; Marchesini, S. Advanced denoising for X-ray ptychography. Opt. Express 2019, 27, 10395–10418. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, Y.; Suzuki, A.; Zettsu, N.; Kohmura, Y.; Senba, Y.; Ohashi, H.; Yamauchi, K.; Ishikawa, T. Towards high-resolution ptychographic X-ray diffraction microscopy. Phys. Rev. B 2011, 83, 214109. [Google Scholar] [CrossRef]
- Maiden, A.; Humphry, M.; Sarahan, M.; Kraus, B.; Rodenburg, J. An annealing algorithm to correct positioning errors in ptychography. Ultramicroscopy 2012, 120, 64–72. [Google Scholar] [CrossRef] [PubMed]
- Edo, T.; Batey, D.; Maiden, A.; Rau, C.; Wagner, U.; Pešić, Z.; Waigh, T.; Rodenburg, J. Sampling in X-ray ptychography. Phys. Rev. A 2013, 87, 053850. [Google Scholar] [CrossRef]
- Beckers, M.; Senkbeil, T.; Gorniak, T.; Giewekemeyer, K.; Salditt, T.; Rosenhahn, A. Drift correction in ptychographic diffractive imaging. Ultramicroscopy 2013, 126, 44–47. [Google Scholar] [CrossRef]
- Pelz, P.M.; Guizar-Sicairos, M.; Thibault, P.; Johnson, I.; Holler, M.; Menzel, A. On-the-fly scans for X-ray ptychography. Appl. Phys. Lett. 2014, 105, 251101. [Google Scholar] [CrossRef]
- Nashed, Y.S.; Peterka, T.; Deng, J.; Jacobsen, C. Distributed automatic differentiation for ptychography. Procedia Comput. Sci. 2017, 108, 404–414. [Google Scholar] [CrossRef]
- Moxham, T.E.; Parsons, A.; Zhou, T.; Alianelli, L.; Wang, H.; Laundy, D.; Dhamgaye, V.; Fox, O.J.; Sawhney, K.; Korsunsky, A.M. Hard X-ray ptychography for optics characterization using a partially coherent synchrotron source. J. Synchrotron Radiat. 2020, 27, 1688–1695. [Google Scholar] [CrossRef]
- Thibault, P.; Menzel, A. Reconstructing state mixtures from diffraction measurements. Nature 2013, 494, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Peterson, I.; Vila-Comamala, J.; Diaz, A.; Berenguer, F.; Bean, R.; Chen, B.; Menzel, A.; Robinson, I.K.; Rodenburg, J.M. Translation position determination in ptychographic coherent diffraction imaging. Opt. Express 2013, 21, 13592–13606. [Google Scholar] [CrossRef] [PubMed]
- Batey, D.; Edo, T.; Rau, C.; Wagner, U.; Pešić, Z.; Waigh, T.; Rodenburg, J. Reciprocal-space up-sampling from real-space oversampling in X-ray ptychography. Phys. Rev. A 2014, 89, 043812. [Google Scholar] [CrossRef]
- Marchesini, S.; Schirotzek, A.; Yang, C.; Wu, H.T.; Maia, F. Augmented projections for ptychographic imaging. Inverse Probl. 2013, 29, 115009. [Google Scholar] [CrossRef]
- Kupyn, O.; Budzan, V.; Mykhailych, M.; Mishkin, D.; Matas, J. Deblurgan: Blind motion deblurring using conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8183–8192. [Google Scholar]
- Kim, J.W.; Messerschmidt, M.; Graves, W.S. Enhancement of Partially Coherent Diffractive Images Using Generative Adversarial Network. AI 2022, 3, 274–284. [Google Scholar] [CrossRef]
- Wang, B.; Brooks, N.J.; Johnsen, P.C.; Jenkins, N.W.; Esashi, Y.; Binnie, I.; Tanksalvala, M.; Kapteyn, H.C.; Murnane, M.M. High-fidelity ptychographic imaging of highly periodic structures enabled by vortex high harmonic beams. arXiv 2023, arXiv:2301.05563. [Google Scholar]
- Brooks, N.J.; Wang, B.; Binnie, I.; Tanksalvala, M.; Esashi, Y.; Knobloch, J.L.; Nguyen, Q.L.; McBennett, B.; Jenkins, N.W.; Gui, G. Temporal and spectral multiplexing for EUV multibeam ptychography with a high harmonic light source. Opt. Express 2022, 30, 30331–30346. [Google Scholar] [CrossRef]
- Eschen, W.; Loetgering, L.; Schuster, V.; Klas, R.; Kirsche, A.; Berthold, L.; Steinert, M.; Pertsch, T.; Gross, H.; Krause, M. Material-specific high-resolution table-top extreme ultraviolet microscopy. Light Sci. Appl. 2022, 11, 117. [Google Scholar] [CrossRef]
- Tanksalvala, M.; Porter, C.L.; Esashi, Y.; Wang, B.; Jenkins, N.W.; Zhang, Z.; Miley, G.P.; Knobloch, J.L.; McBennett, B.; Horiguchi, N. Nondestructive, high-resolution, chemically specific 3D nanostructure characterization using phase-sensitive EUV imaging reflectometry. Sci. Adv. 2021, 7, eabd9667. [Google Scholar] [CrossRef]
- Baksh, P.D.; Ostrčil, M.; Miszczak, M.; Pooley, C.; Chapman, R.T.; Wyatt, A.S.; Springate, E.; Chad, J.E.; Deinhardt, K.; Frey, J.G. Quantitative and correlative extreme ultraviolet coherent imaging of mouse hippocampal neurons at high resolution. Sci. Adv. 2020, 6, eaaz3025. [Google Scholar] [CrossRef]
- Mochi, I.; Fernandez, S.; Nebling, R.; Locans, U.; Rajeev, R.; Dejkameh, A.; Kazazis, D.; Tseng, L.-T.; Danylyuk, S.; Juschkin, L. Quantitative characterization of absorber and phase defects on EUV reticles using coherent diffraction imaging. J. Micro/Nanolithogr. MEMS MOEMS 2020, 19, 014002. [Google Scholar] [CrossRef]
- Thibault, P.; Dierolf, M.; Bunk, O.; Menzel, A.; Pfeiffer, F. Probe retrieval in ptychographic coherent diffractive imaging. Ultramicroscopy 2009, 109, 338–343. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, Y.; Suzuki, A.; Furutaku, S.; Yamauchi, K.; Kohmura, Y.; Ishikawa, T. High-resolution and high-sensitivity phase-contrast imaging by focused hard X-ray ptychography with a spatial filter. Appl. Phys. Lett. 2013, 102, 094102. [Google Scholar] [CrossRef]
- Pfeiffer, F. X-ray ptychography. Nat. Photonics 2018, 12, 9–17. [Google Scholar] [CrossRef]
- Huang, X.; Yan, H.; Ge, M.; Öztürk, H.; Nazaretski, E.; Robinson, I.K.; Chu, Y.S. Artifact mitigation of ptychography integrated with on-the-fly scanning probe microscopy. Appl. Phys. Lett. 2017, 111, 023103. [Google Scholar] [CrossRef]
- Giewekemeyer, K.; Beckers, M.; Gorniak, T.; Grunze, M.; Salditt, T.; Rosenhahn, A. Ptychographic coherent X-ray diffractive imaging in the water window. Opt. Express 2011, 19, 1037–1050. [Google Scholar] [CrossRef]
- Dierolf, M.; Thibault, P.; Menzel, A.; Kewish, C.M.; Jefimovs, K.; Schlichting, I.; Von Koenig, K.; Bunk, O.; Pfeiffer, F. Ptychographic coherent diffractive imaging of weakly scattering specimens. New J. Phys. 2010, 12, 035017. [Google Scholar] [CrossRef]
- Yun, W.-B.; Kirz, J.; Sayre, D. Observation of the soft X-ray diffraction pattern of a single diatom. Acta Crystallogr. Sect. A Found. Crystallogr. 1987, 43, 131–133. [Google Scholar] [CrossRef]
- Shapiro, D.A.; Yu, Y.-S.; Tyliszczak, T.; Cabana, J.; Celestre, R.; Chao, W.; Kaznatcheev, K.; Kilcoyne, A.; Maia, F.; Marchesini, S. Chemical composition mapping with nanometre resolution by soft X-ray microscopy. Nat. Photonics 2014, 8, 765–769. [Google Scholar] [CrossRef]
- Zhang, J.; Fan, J.; Sun, Z.; Yao, S.; Tong, Y.; Tai, R.; Jiang, H. Enhancement of phase retrieval capability in ptychography by using strongly scattering property of the probe-generating device. Opt. Express 2018, 26, 30128–30145. [Google Scholar] [CrossRef]
- Maiden, A.M.; Rodenburg, J.M. An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy 2009, 109, 1256–1262. [Google Scholar] [CrossRef]
- Curry, H.B. The method of steepest descent for non-linear minimization problems. Q. Appl. Math. 1944, 2, 258–261. [Google Scholar] [CrossRef]
- Saxton, W.; Baumeister, W. The correlation averaging of a regularly arranged bacterial cell envelope protein. J. Microsc. 1982, 127, 127–138. [Google Scholar] [CrossRef]
- Van Heel, M.; Schatz, M. Fourier shell correlation threshold criteria. J. Struct. Biol. 2005, 151, 250–262. [Google Scholar] [CrossRef]
- Attwood, D. Soft X-rays and Extreme Ultraviolet Radiation: Principles and Applications; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Shimomura, K.; Hirose, M.; Higashino, T.; Takahashi, Y. Three-dimensional iterative multislice reconstruction for ptychographic X-ray computed tomography. Opt. Express 2018, 26, 31199–31208. [Google Scholar] [CrossRef]
- Xing, Z.; Xu, Z.; Zhang, X.; Chen, B.; Guo, Z.; Wang, J.; Wang, Y.; Tai, R. Virtual depth-scan multi-slice ptychography for improved three-dimensional imaging. Opt. Express 2021, 29, 16214–16227. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Xu, Z.; Zhang, X.; Chen, B.; Wang, Y.; Tai, R. Position-guided ptychography for vibration suppression with the aid of a laser interferometer. Opt. Lasers Eng. 2023, 160, 107297. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Energy | 703 eV |
| Probe size | 3 μm |
| Step size | 600 nm |
| ZP diameter | 240 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Xu, Z.; Xing, Z.; Zhang, X.; Li, R.; Qin, Z.; Wang, Y.; Tai, R. Periodic Artifacts Generation and Suppression in X-ray Ptychography. Photonics 2023, 10, 532. https://doi.org/10.3390/photonics10050532
Liu S, Xu Z, Xing Z, Zhang X, Li R, Qin Z, Wang Y, Tai R. Periodic Artifacts Generation and Suppression in X-ray Ptychography. Photonics. 2023; 10(5):532. https://doi.org/10.3390/photonics10050532
Chicago/Turabian StyleLiu, Shilei, Zijian Xu, Zhenjiang Xing, Xiangzhi Zhang, Ruoru Li, Zeping Qin, Yong Wang, and Renzhong Tai. 2023. "Periodic Artifacts Generation and Suppression in X-ray Ptychography" Photonics 10, no. 5: 532. https://doi.org/10.3390/photonics10050532
APA StyleLiu, S., Xu, Z., Xing, Z., Zhang, X., Li, R., Qin, Z., Wang, Y., & Tai, R. (2023). Periodic Artifacts Generation and Suppression in X-ray Ptychography. Photonics, 10(5), 532. https://doi.org/10.3390/photonics10050532





