Maximum Pump Power Coupled in Raman Resonator for Maximum Power Delivered at 1115 and 1175 nm

Abstract

In this report, we present our analysis of the relationship between critical power and stimulated Raman scattering in Raman fiber lasers. Through our research, we have established a connection between the R.G. Smith constant at critical power and the necessary pump power required to reach the maximum power delivered by the first Stokes just prior to the generation of the second Stokes. In our experiments, two setups were successful in reaching the second Stokes generation, one utilizing a glass–air interface as the output coupler without HR mirrors and the other using HR-FBGs for both Stokes in conjunction with a glass–air interface. We found that the 1 Km 1060-XP fiber has an R.G. Smith constant of ~4.94 at critical power, which when multiplied by 2 gives ~9.88, a value close to the R.G. Smith constant (9.75) for maximum Stokes corresponding to a pump power of 5.5 W, with an approximation of ~98.6%. Our results demonstrate the importance of knowing the R.G. Smith constant at critical power in estimating the necessary pump power to achieve maximum power delivery in any Stokes component.

1. Introduction

Raman fiber lasers and Raman amplifiers are active areas of research, particularly in the spectral range spanning from 1.1 to 1.7 μm, with broad applications in diverse fields such as industry, telecommunications systems, medical procedures such as ophthalmology and dermatology, and laser guide star technologies, among others [1,2,3,4]. Various architectures for Raman fiber lasers have been proposed, ranging from conventional designs utilizing cascaded Raman resonators [3] to more innovative approaches such as random distributed feedback fiber lasers (DFB-FL) [4]. These architectures have been investigated extensively to improve output powers, energy conversion efficiency, and wavelength/frequency conversion scalability. Recent reports have provided comprehensive analyses of the current state of the art in these types of fiber lasers [5]. Optimization studies of output power characteristics have been conducted for random DFB-FLs using fibers such as TrueWave XL Fiber [6] and phospho-silicate fiber [7]. Precise knowledge of the pump powers required for achieving complete signal generation in the first, second, and N-Stokes is crucial for estimating the pump power levels necessary for a specific Raman laser architecture. In this context, several reports have documented experimental investigations and numerical simulations of the parameters involved in stimulated Raman scattering, as well as the generation of Stokes lines [8,9]. Additionally, Raman gain coefficients scaling with wavelength and fiber loss for numerical simulations have been reported in previous studies [10,11].

In general, when analyzing the propagation of pumping power and Stokes signals along the z-direction, particular attention is given to critical powers and the maximum power delivered by the Stokes lines. These parameters are of significant interest as they provide crucial information about the behavior of the system. The governing equations for the propagation of pump and Stokes signals have been previously solved, resulting in an analytical equation that enables estimation of the power required to reach the critical power and the maximum power of the first Stokes signal [12]. Traditionally, these estimations have been based on a commonly used R.G. Smith constant of approximately 16 [8].

In the current study, our investigation revolves around the typical structures of Raman fiber lasers in telecom optical fibers. Our primary objective is to calculate the pump powers at which the critical powers occur, and the maximum powers are reached by each subsequent Stokes line before generating the next one. We have specifically focused on obtaining wavelengths close to 1175 nm, as these wavelengths are crucial for generating laser emissions through frequency doubling in the yellow spectral region. Such emissions find applications in various medical procedures and astronomical telescopes calibrations through “artificial star” projections on the sky [13,14,15]. In particular, we propose the use of general expressions that allows us to estimate the maximum pumping power required for any Stokes line to reach its maximum power level.

2. Theory

Let us briefly analyze the propagation along z of a continuous wave (CW) pump beam and stimulated Raman scattering in an optical fiber. These are described by the following set of coupled differential equations [12,16]:

$${\mathrm{dP}}_{\mathrm{P}}/\mathrm{dz}=-{\mathsf{\alpha }}_{\mathrm{P}}{\mathrm{P}}_{\mathrm{P}}-({\mathsf{\upsilon }}_{\mathrm{P}}/{\mathsf{\nu }}_{\mathrm{S}})({\mathrm{g}}_{\mathrm{r}}/{\mathrm{A}}_{\mathrm{eff}}){\mathrm{P}}_{\mathrm{P}}{\mathrm{P}}_{\mathrm{F}}$$

(1)

$${\mathrm{dP}}_{\mathrm{F}}/\mathrm{dz}=-{\mathsf{\alpha }}_{\mathrm{S}}{\mathrm{P}}_{\mathrm{F}}+({\mathrm{g}}_{\mathrm{r}}/{\mathrm{A}}_{\mathrm{eff}}){\mathrm{P}}_{\mathrm{P}}{\mathrm{P}}_{\mathrm{F}}$$

(2)

where P_P and P_F, ν_P and ν_S, and α_P and α_S correspond, respectively, to pump powers, frequencies, and losses coefficients of pump and Stokes signals; A_eff is the effective area of the TEM00 spatial mode, and g_r is the Raman gain coefficient of the Stokes signal.

Assuming that α = α_P = α_S, because the attenuation curve of the silica fiber is approximately constant in the transparency window, an analytical solution for the set of equations can be given by [11]:

$$\ln \left(({\mathrm{P}}_{\mathrm{F}}{\mathrm{P}}_{\mathrm{P}0})/({\mathrm{P}}_{\mathrm{p}}{\mathrm{P}}_{\mathrm{F}0})\right)={\mathrm{g}}_{\mathrm{r}}/{\mathrm{A}}_{\mathrm{eff}}{\mathrm{P}}_{\mathrm{P}0}{\mathrm{L}}_{\mathrm{eff}}$$

(3)

where L_eff = [(1 − exp(−αL))/α] represents the interaction length of the pump and the Stokes signal; L is the fiber length; P_P0 is the coupled pump power; and P_F0 is the Stokes power generated at the fiber input. At critical power, just when P_F = P_P, Equation (3) becomes the R.G. Smith constant, $({\mathrm{g}}_{\mathrm{r}}/{\mathrm{A}}_{\mathrm{eff}}){\mathrm{P}}_{\mathrm{cr}}{\mathrm{L}}_{\mathrm{eff}}~16$; in this sense, $\ln \left({\mathrm{P}}_{\mathrm{P}0}/{\mathrm{P}}_{\mathrm{Fo}}\right)=16$. Such a value, as we will see later on, is different for optical fibers used in telecom systems [8], where P_P0 is called the critical power (P_cr). In Equation (3), the argument of the natural logarithm is a relation of powers that can be replaced by the dimensionless number $\ln \left(\mathsf{\epsilon }\right)$, and it is useful to calculate the critical power in free running or cascaded Raman fiber laser configurations. Hence, it is necessary to estimate the value of the Stokes P_P0 signal at the fiber input. This constant can be obtained at any point.

In this work, we focus our attention on the pump power, P_P0, necessary for the N-th Stokes to reach its maximum power, before starting the generation of the next Stokes.

3. Experiment and Results

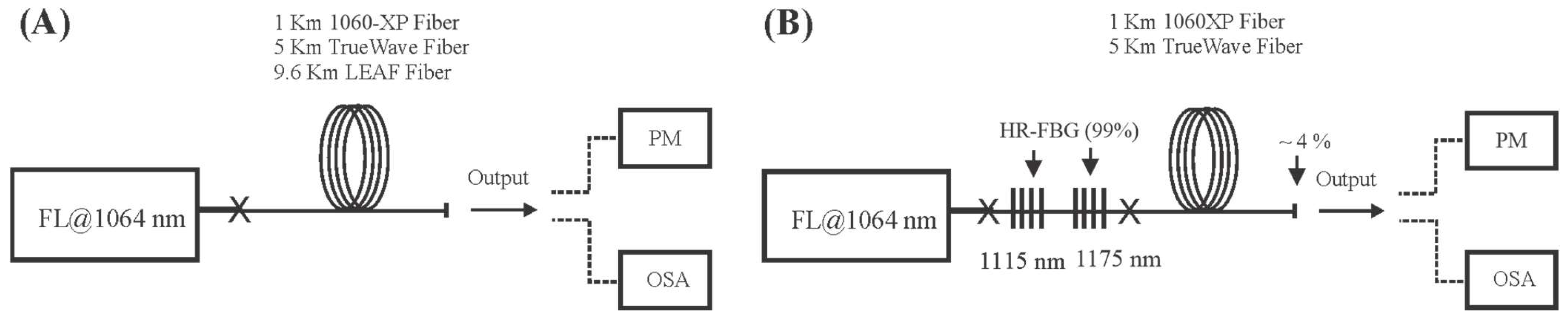
We have based our studies on two experimental configurations: Figure 1A free running and Figure 1B using high reflectivity fiber Bragg gratins (HR-FBGs). The HR-FBGs operating for first and second Stokes (1115 and 1175 nm), with ~99% reflectivity, were patterned on Flexcore-1060 SM fiber (almost identical to 1060-XP) with a core diameter of ~6 μm (5.3 μm MFD of 6.2 μm at 1064) and linewidth of ~0.8 nm. The pump source is a CW Yb fiber laser (FL) model YLR-10-1064-LP fabricated by IPG Photonics, delivering up to 10 W at 1064 nm in a linearly polarized beam in TME00 output mode, emission linewidth 0.5 nm, with output fiber type PM SM Panda 1060 that was already spliced to a 1060-XP fiber.

In Figure 1A, the delivery fiber of the pump source was spliced to the test fibers—1 Km of 1060-XP, 5 Km of TrueWave, and 9.6 Km of LEAF fiber; the splice loss was negligible for the 1060-XP, and it is estimated to be ~0.41 dB when spliced to the TrueWave and LEAF fibers; the same loss estimation is valid when connecting through the HR-FBGs as in Figure 1B. In both configurations, an optical spectrum analyzer (OSA) and a power meter (PM), were placed at the output end of the fiber.

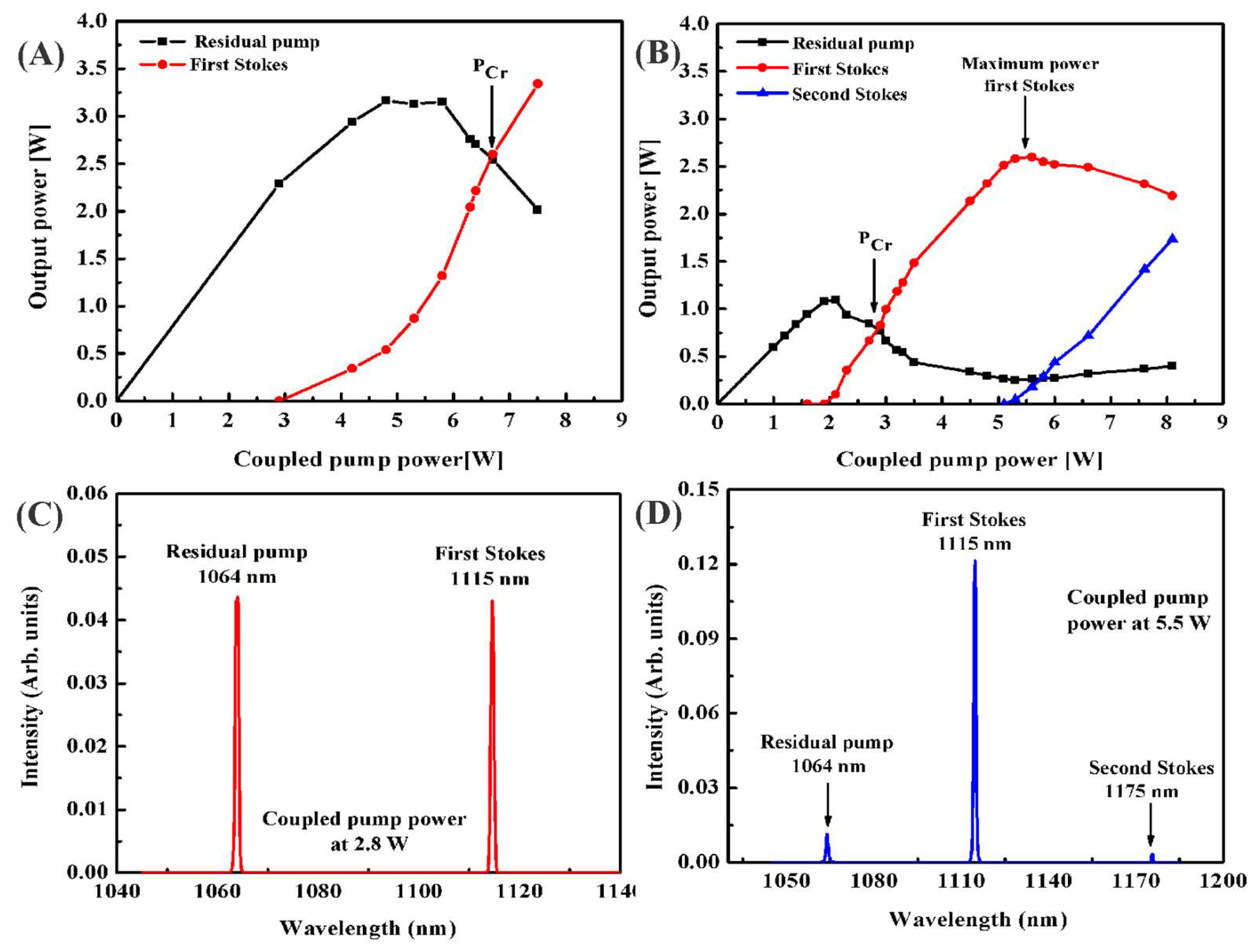
With these experimental configurations, we obtained the measurements of the spectra for each pump power up to 10 W. The spectra were obtained on a linear scale with a resolution of 0.1 nm; see Figure 2C,D. For each spectrum, the power at the output end of the fiber was measured. The areas of the residual power, the first and the second Stokes, were taken into account to calculate the values of the respective output powers.

We start with the splicing of the 1 Km 1060-XP fiber to the FL@1064 nm. The critical power (P_cr) was 6.693 W in the free configuration (see Figure 2A), while using HR-FBGs, the critical power was 2.8 W (see Figure 2B). On the other hand, with the free running configuration, it was not possible to obtain the first stokes with its maximum power level ($P_F^{Max}$). However, using HR-FBGs, the first Stokes reached its maximum value $P_F^{Max}$ = 2.5 W at a maximum coupled pump power ($P_{Max}^{1st}$) of ~5.5 W.

From this $P_F^{Max}$ power, the first Stokes reached a saturation level, and the residual pump ceased to convert to the first Stokes. It is important to mention that this residual pump power is also not used for transfer to the second Stokes.

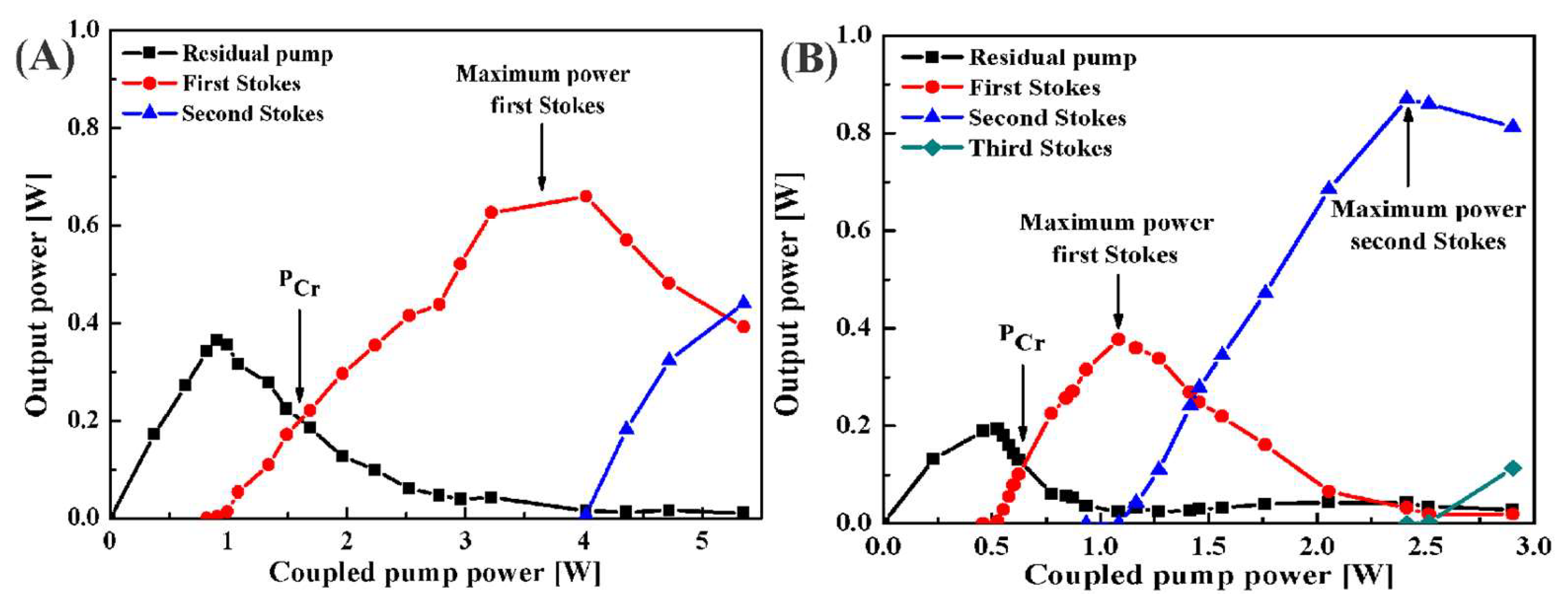
For the 5 Km TrueWave fiber, in the free running configuration, the critical power occurred at 1.6 W and at 3.5 W of coupled pump power, and the first Stokes reached its maximum power level, whereas for the configuration using HR-FBGs, the critical power occured at ~0.63 W, and the first Stokes reached its maximum power level at ~1.12 W of coupled pump power (see Figure 3A,B, respectively).

Although the TrueWave and LEAF fibers are multimode (quasi-single-mode) within the region of study, when spliced-excited by the 1060-XP single mode fiber, although bigger in diameter, only the TEM00 mode becomes excited; then, practically all of the system operates as single-mode.

It is important to mention that for the free running configuration, specifically between 3 and 4 W of coupled pump power, the spectra presented fluctuations between the residual power and the first Stokes, which caused uncertainty in the measurements; hence, those measurements were not accurately considered.

Finally, 9.6 Km of LEAF fiber was pumped and characterized up to 6 W of coupled pump power in a free running configuration. The critical power occurred at 1.3 W, and the first Stokes reached its maximum power at 2.4 W.

Note that the residual pump has been totally depleted at 4 W of coupled pump power, just as the second Stokes reached its maximum energy level. This occurred mainly because the residual pump power was being totally consumed by the first Stokes. At 6 W of coupled power, the third Stokes had already been formed, and the residual power of the second Stokes tended to be extinguished. This same process of energy transfer is observed in Figure 3A for the 5 Km true wave fiber. If more Stokes were to be generated, the residual pumps would have tended to be completely depleted.

The energy transfer process is very different in experimental setups that use a resonant cavity formed by HR-FBGs; see Figure 1B. The HR-FBGs select a spectral portion of spontaneous Raman scattering, which occurs naturally in silica optical fibers, to be amplified at the first and second Stokes wavelengths corresponding to 1115 and 1175 nm. The first Stokes amplification has the following characteristics: it occurs at low pump power; stability in the Stokes wavelength; and saturation of the maximum power reached by the first Stokes is below the free running configuration.

At 1064 nm pump wavelength, 1 Km 1060-XP, 5 Km TrueWave, and 9.6 Km LEAF fiber were estimated to have attenuations of ~1.5, ~1, and ~0.96-dB/Km, and effective fiber lengths (L_eff) of ~0.8455, ~2.97 and ~3.98 Km, respectively. Likewise, the Raman gain coefficients (g_R = g_r/A_eff) were estimated to be 2.19 ± 0.05, 2.55 ± 0.10, and 2.31 ± 0.10-W⁻¹ Km⁻¹, respectively. On the other hand, at 1115 nm wavelength, the 5 Km TrueWave fiber had an estimated attenuation of 0.73-dB/Km, the effective fiber length of L_eff1 = 3.3820-m, and the Raman gain coefficient of $g_{R1}$~1.86-W⁻¹ Km⁻¹ [17].

In

Table 1. Summary of results of the three fibers under test in the free running configuration.

Fiber Span	Pcr [W]	$P_{Max}^{\mathbf{1}st}\left[\mathbf{W}\right]$	$P_{Max}^{2nd}\left[\mathbf{W}\right]$	gRLeffPcr	${\mathbf{g}}_{\mathbf{R}}{\mathbf{L}}_{\mathbf{eff}}{P}_{Max}^{1st}$	$\mathbf{g}{\mathbf{R}}_1{\mathbf{L}}_{\mathbf{eff}}{P}_{Max}^{2nd}$
1 Km 1060-XP	6.693	-------	------	~11.90	------	-------
5 Km TrueWave	1.600	3.50	------	~12.11	~26.50	-------
9.6 Km LEAF	1.300	2.40	4.00	~11.95	~23.00	~36.77

, the 9.6 Km LEAF fiber has an R.G. Smith constant (g_RL_effP_cr) of ~11.95. By simple inspection, if we multiply this value by 2, we obtain ~23.9, which corresponds to a coupled pumping power of 2.6 W, which is close to the value obtained experimentally of 2.40 W. Then, if we multiply by 3, we obtain an R.G. Smith constant of ~35.85, which corresponds to a pump power of ~3.9 W, which is close to the experimental value of 4 W; the experimental results are similar to those shown in reference [12]. Although this analysis is not conclusive, they do prove the mathematical expression in the first instance, which predicts the maximum pump power needed for the Stokes spectrum to reach its maximum power level [12], where the R.G. Smith constant ~16 must be replaced by ~11.95.

In

Table 2. Summary of results of the two fibers under test using HR-FBGs.

Fiber Span	Pcr [W]	$P_{Max}^{1st}\left[\mathbf{W}\right]$	$P_{Max}^{2nd}\left[\mathbf{W}\right]$	gRLeffPcr	${\mathbf{g}}_{\mathbf{R}}{\mathbf{L}}_{\mathbf{eff}}{P}_{Max}^{1st}$	$\mathbf{g}{\mathbf{R}}_1\mathbf{L}{\mathbf{eff}}_1{P}_{Max}^{2nd}$
1 Km 1060-XP	2.8	5.50	-------	~4.94	~9.75	-------
5 Km TrueWave	0.63	1.12	2.5	~4.77	~9.65	~15.72

, for the 1060-XP fiber, the R.G. Smith constant for the critical power is ~4.94, and if we multiply by 2, we obtain ~9.88, which corresponds to a pump power of 5.33 W, which is close to the experimentally obtained value of 5.50 W; see Figure 2B. On the other hand, for 5 Km TrueWave fiber, the R.G. Smith constant is ~4.77 W, and by multiplying by 2, ~9.54 W is obtained, which corresponds to a coupled pumping power of 1.26 W, which is very close to the experimental value of 1.12 W. In this same sense, multiplying by 3, we have ~14.31, which corresponds to a pumping power of 2.27 W, a value very close to the 2.5 W reached experimentally by the second Stokes; see Figure 3A. This comparative analysis between experimental data and those obtained by multiplying the R.G. Smith constant by an integer is shown in

Table 3. Data provided by the experimental configuration using HR-FBGs vs theoretical data obtained using Equation (4).

	Experimental Pump Powers [W]		Pump Powers Obtained with Equation (4). [W]
Fiber Span	$P_{Max}^{1st}$	$P_{Max}^{2nd}$	$P_{Max}^{1Stokes}$	$P_{Max}^{2Stokes}$	$\left|\frac{P_{Max}^{1Stokes}}{P_{Max}^{1st}}-1\right|$	$\left|\frac{P_{Max}^{2Stokes}}{P_{Max}^{2nd}}-1\right|$
1 Km 1060-XP	5.50	-------	5.33	-------	~3%	-------
5 Km TrueWave	1.12	~2.5	1.26	~2.27	~12.5%	~9%

.

Based on experimental results of the free running and cascade Raman fiber laser configurations of Figure 1A,B, we propose that the coupled pump power, to estimate the maximum energy level of the first and second Stokes before generating the following Stokes, is expressed by the following equation:

$${\mathrm{P}}_{\mathrm{Max}}^{\mathrm{NStokes}}=\left(\mathrm{N}+1\right)\times \ln \left(\mathsf{\epsilon }\right)\frac{1}{{\mathrm{g}}_{\mathrm{RN}}\times {\mathrm{L}}_{\mathrm{effN}}}$$

(4)

where ${\mathrm{P}}_{\mathrm{Max}}^{\mathrm{NStokes}}$ is the coupled pump power at which a Stokes has its maximum power level; N is zero for the critical power 1 for the first Stokes, and 2 for the second Stokes; and $\ln \left(\mathsf{\epsilon }\right)$ is the R.G. Smith constant for the Raman threshold.

For the 1 Km 1060-XP fiber, between the experimental and theoretical value, there is an approximation of ~3% of the maximum pump powers. However, for the 5 Km TrueWave fiber at the first Stokes, this value is slightly overestimated ~12.5%, and, comparatively to the second Stokes, this variation is acceptable ~9%.

4. Conclusions

The experimental findings from our presented configurations have unveiled a remarkable correlation between the maximum energy output of the Stokes signals and the critical powers in conjunction with the R.G. Smith constant, as originally proposed by R.G. Smith [9]. This relationship has been succinctly captured in a simplified equation, which necessitates knowledge of key parameters such as the Raman gain coefficient, effective fiber length for signals interactions, and critical power.

Notably, our results have demonstrated consistent agreement with our established relationship for long fibers in the free-running configuration, while the resonant cavity configuration employing HR-FBGs aligns with our Equation (4) for short fibers. This compelling agreement underscores the potential of utilizing our formulae for accurate estimations of the coupled pumping powers required for maximum Stokes generations.