Dispersion Caused by the Penetration Effect in X-ray Compressors
Abstract
1. Introduction
2. GDD Caused by Angular Dispersion
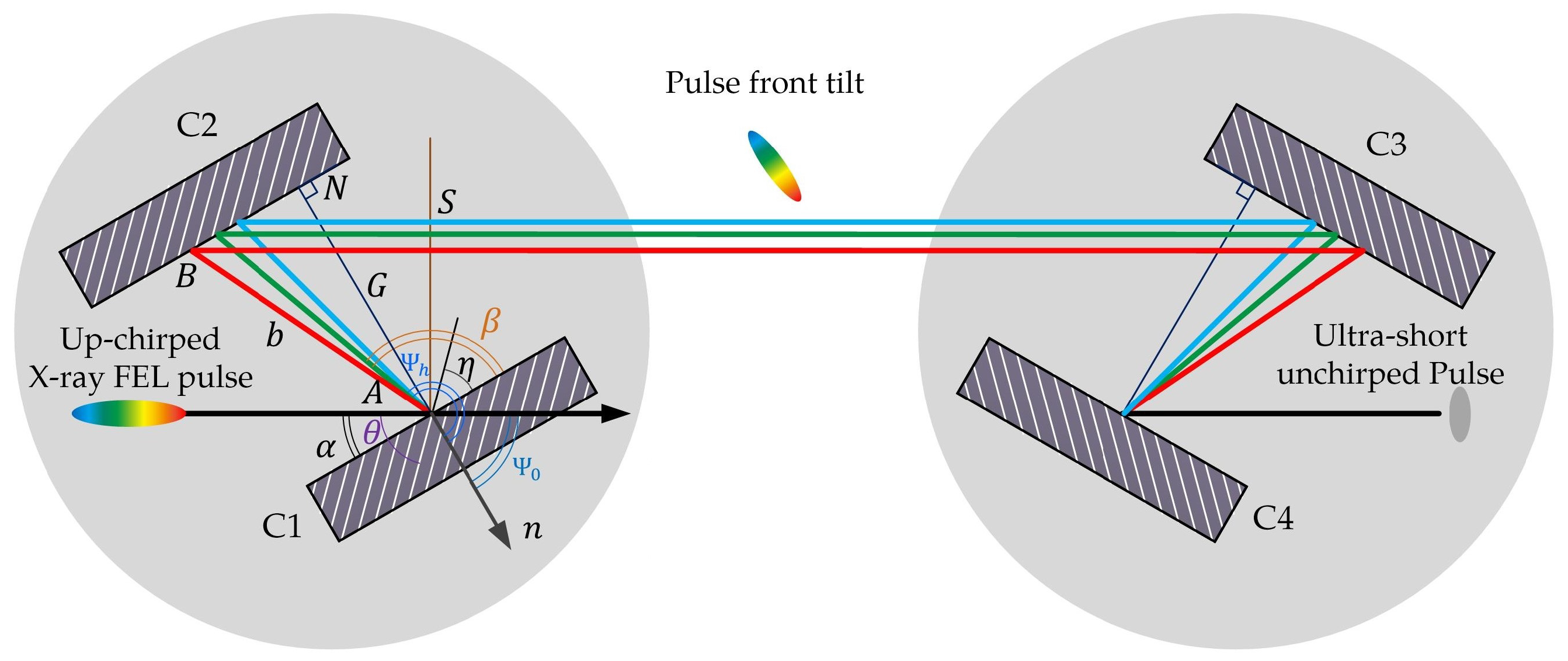
2.1. Angular Dispersion of Asymmetry-Cut Crystals and Multilayers
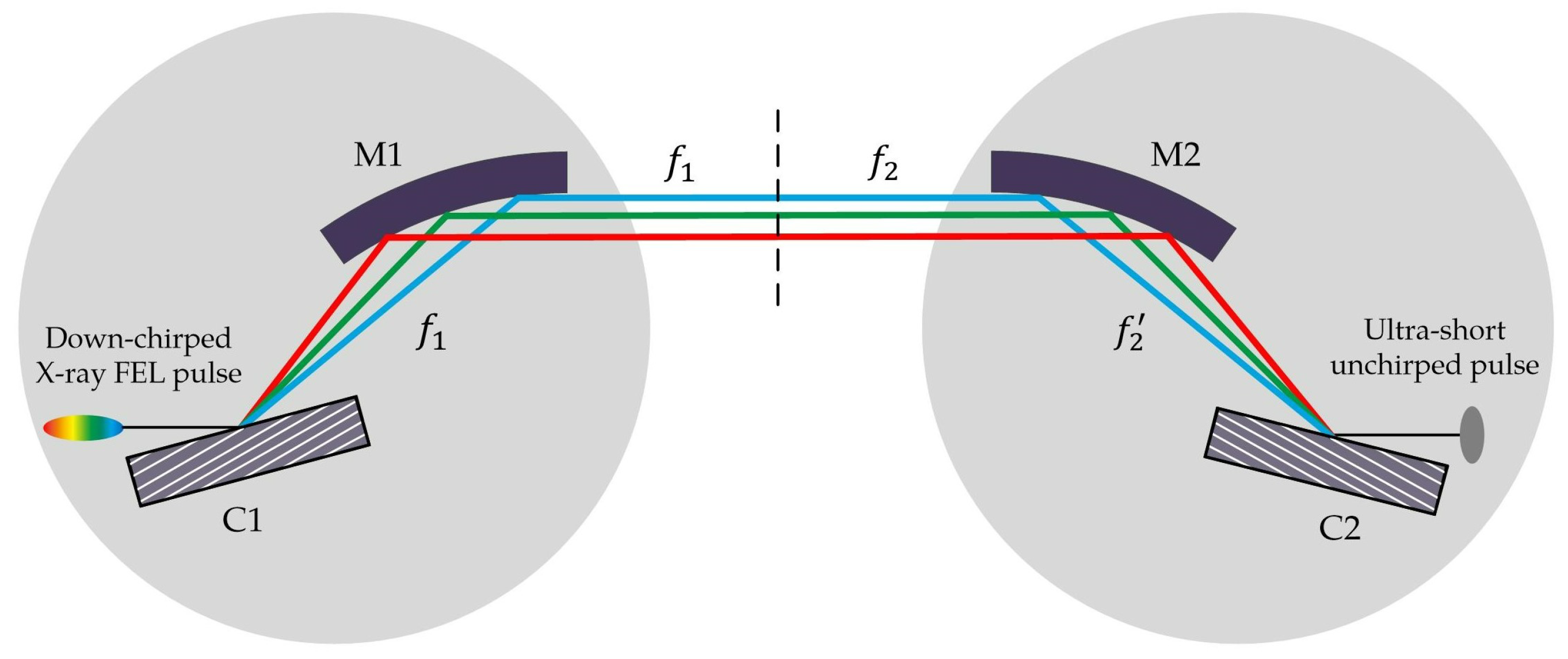
2.2. Two Typical X-ray Pulse Compressors
3. Dispersion of X-ray Penetration Effect
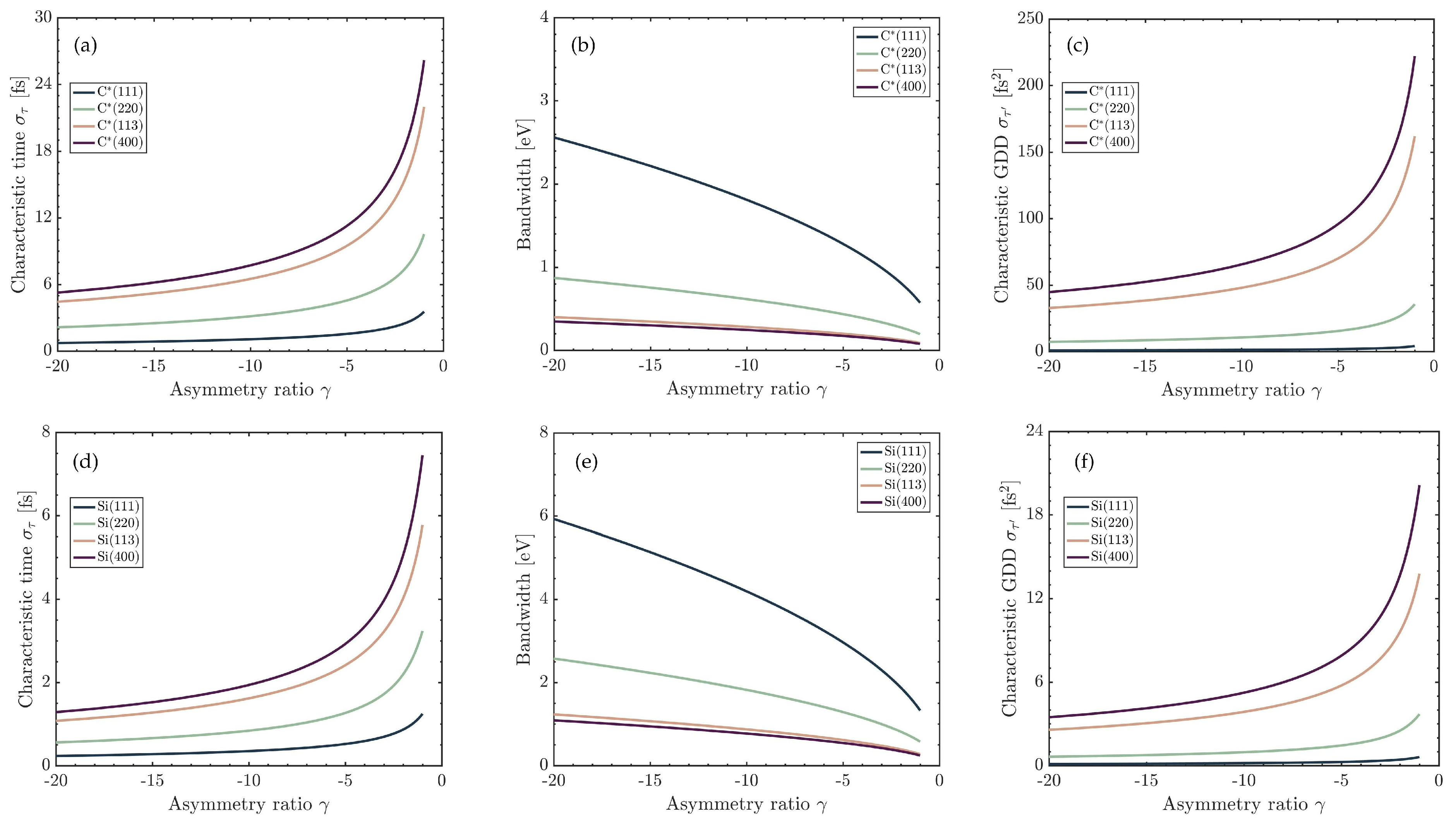
3.1. Penetration Dispersion
3.2. Intrinsic Pulse Stretching
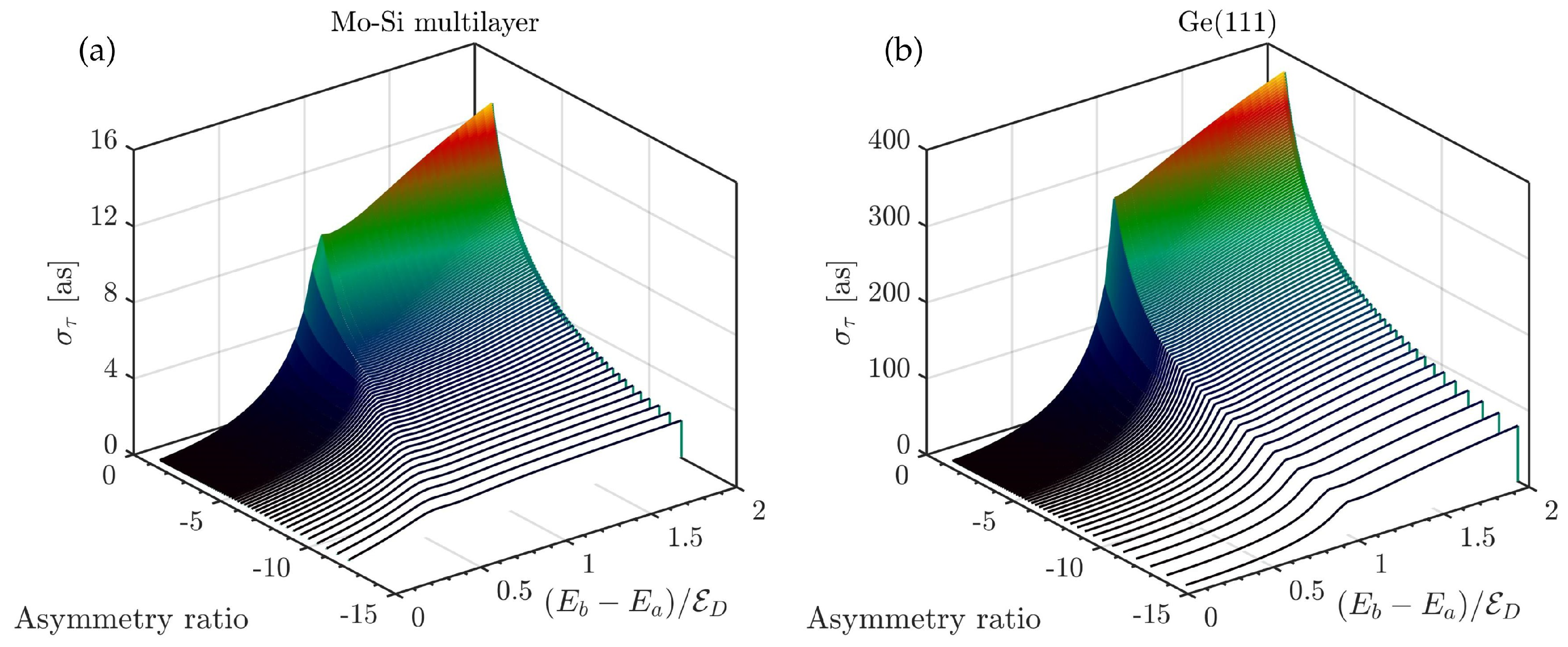
4. Compressor Configuration Optimization
4.1. Optimization Method
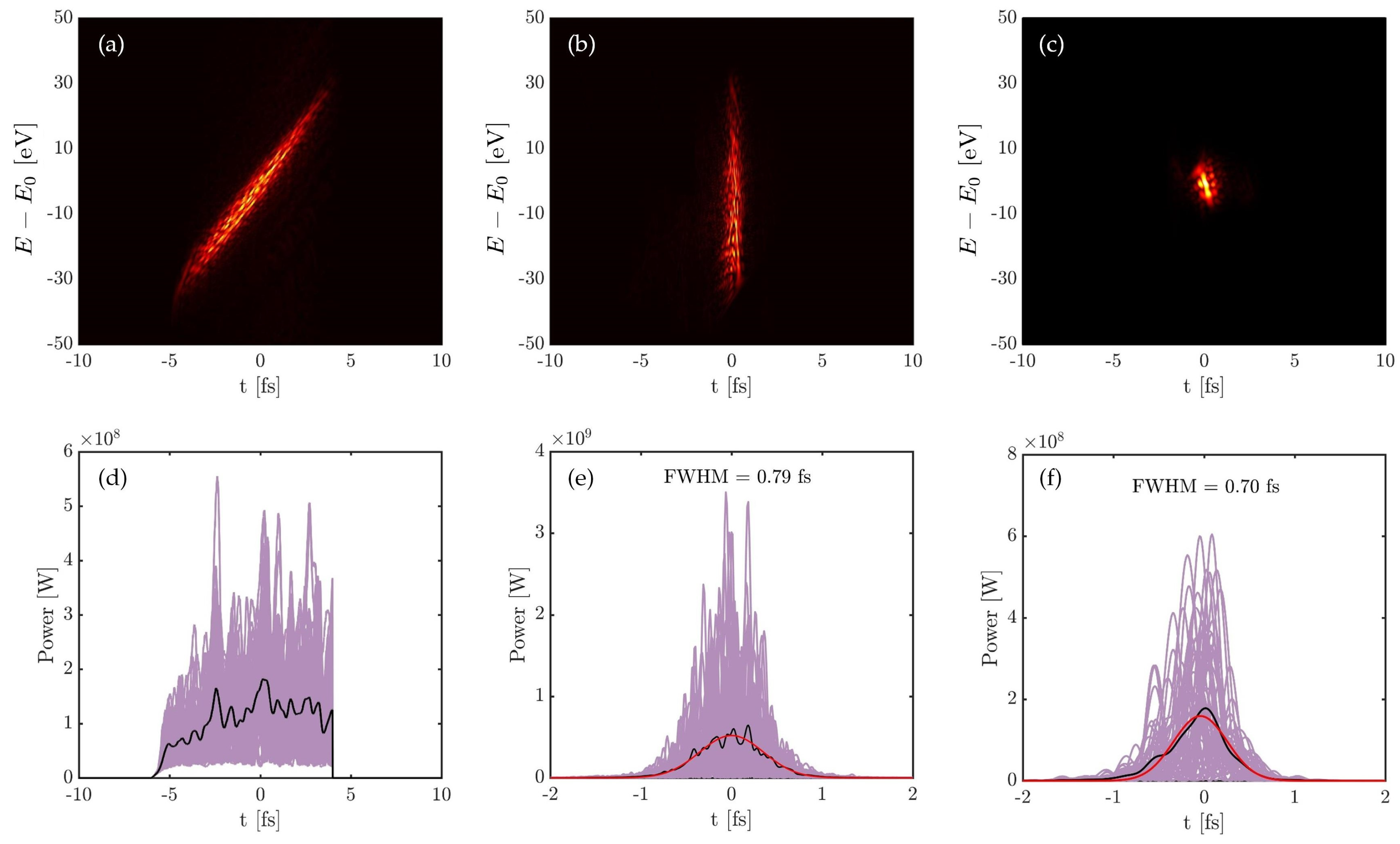
4.2. Application in Chirped XFEL Pulse Compression
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Notation Convention of Angles

Appendix B. Dynamical Theory of X-ray Diffraction
Appendix C. Asymmetry-Cut Multilayer
References
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Drescher, M.; Hentschel, M.; Kienberger, R.; Tempea, G.; Spielmann, C.; Reider, G.A.; Corkum, P.B.; Krausz, F. X-ray Pulses Approaching the Attosecond Frontier. Science 2001, 291, 1923–1927. [Google Scholar] [CrossRef] [PubMed]
- Chang, Z.; Corkum, P. Attosecond photon sources: The first decade and beyond [Invited]. J. Opt. Soc. Am. B 2010, 27, B9–B17. [Google Scholar] [CrossRef]
- Sansone, G.; Poletto, L.; Nisoli, M. High-energy attosecond light sources. Nat. Photonics 2011, 5, 655–663. [Google Scholar] [CrossRef]
- Krausz, F.; Stockman, M. Attosecond metrology: From electron capture to future signal processing. Nat. Photonics 2014, 8, 205–213. [Google Scholar] [CrossRef]
- Kraus, P.M.; Mignolet, B.; Baykusheva, D.; Rupenyan, A.; Horný, L.; Penka, E.F.; Grassi, G.; Tolstikhin, O.I.; Schneider, J.; Jensen, F.; et al. Measurement and laser control of attosecond charge migration in ionized iodoacetylene. Science 2015, 350, 790–795. [Google Scholar] [CrossRef] [PubMed]
- Baker, S.; Robinson, J.S.; Haworth, C.A.; Teng, H.; Smith, R.A.; Chirilă, C.C.; Lein, M.; Tisch, J.W.G.; Marangos, J.P. Probing Proton Dynamics in Molecules on an Attosecond Time Scale. Science 2006, 312, 424–427. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163. [Google Scholar] [CrossRef]
- Schultze, M.; Bothschafter, E.M.; Sommer, A.; Holzner, S.; Schweinberger, W.; Fiess, M.; Hofstetter, M.; Kienberger, R.; Apalkov, V.; Yakovlev, V.S.; et al. Controlling dielectrics with the electric field of light. Nature 2014, 493, 75–78. [Google Scholar] [CrossRef]
- Seres, J.; Seres, E.; Verhoef, A.J.; Tempea, G.; Streli, C.; Wobrauschek, P.; Yakovlev, V.; Scrinzi, A.; Spielmann, C.; Krausz, F. Source of coherent kiloelectronvolt X-rays. Nature 2005, 433, 596. [Google Scholar] [CrossRef]
- Popmintchev, T.; Chen, M.; Popmintchev, D.; Arpin, P.; Brown, S.; Ališauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; et al. Bright Coherent Ultrahigh Harmonics in the keV X-ray Regime from Mid-Infrared Femtosecond Lasers. Science 2012, 336, 1287–1291. [Google Scholar] [CrossRef]
- Chang, Z.; Rundquist, A.; Wang, H.; Murnane, M.M.; Kapteyn, H.C. Generation of Coherent Soft X Rays at 2.7 nm Using High Harmonics. Phys. Rev. Lett. 1997, 79, 2967–2970. [Google Scholar] [CrossRef]
- Chen, M.C.; Arpin, P.; Popmintchev, D.; Gerrity, M.; Zhang, B.; Seaberg, M.; Murnane, M.M.; Kapteyn, H. Bright, Coherent, Ultrafast Soft X-ray Harmonics Spanning the Water Window from a Tabletop Light Source. Phys. Rev. Lett. 2010, 105, 173901. [Google Scholar] [CrossRef] [PubMed]
- Emma, P.; Akre, R.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; et al. A compact X-ray free-electron laser emitting in the sub-ångstrom region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Allaria, E.; Castronovo, D.; Castronovo, D.; Cinquegrana, P.; Craievich, P.; Dal Forno, M.; Danailov, M.; D’Auria, G.; Demidovich, A.; De Ninno, G.; et al. Two-stage seeded soft-X-ray free-electron laser. Nat. Photonics 2013, 7, 913–918. [Google Scholar] [CrossRef]
- Kang, H.S.; Min, C.K.; Heo, H.; Kim, C.; Yang, H.; Kim, G.; Nam, I.; Baek, S.Y.; Choi, H.-J.; Mun, G.; et al. Hard X-ray free-electron laser with femtosecond-scale timing jitter. Nat. Photonics 2017, 11, 708–713. [Google Scholar] [CrossRef]
- Altarelli, M. The European X-ray free-electron laser facility in Hamburg. Nucl. Instruments Methods Phys. Res. Sect. Beam Interact. Mater. Atoms 2011, 269, 2845–2849. [Google Scholar] [CrossRef]
- Milne, C.J.; Schietinger, T.; Aiba, M.; Alarcon, A.; Alex, J.; Anghel, A.; Arsov, V.; Beard, C.; Beaud, P.; Bettoni, S.; et al. SwissFEL: The Swiss X-ray Free Electron Laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Kondratenko, A.M.; Saldin, E.L. Generation of coherent radiation by a relativistic electron beam in an undulator. Part. Accel. 1980, 10, 207–216. [Google Scholar]
- Bonifacio, R.; Pellegrini, C.; Narducci, L. Collective instabilities and high-gain regime in a free electron laser. Opt. Commun. 1984, 50, 373–378. [Google Scholar] [CrossRef]
- Feldhaus, J.; Saldin, E.; Schneider, J.; Schneidmiller, E.; Yurkov, M. Possible application of X-ray optical elements for reducing the spectral bandwidth of an X-ray SASE FEL. Opt. Commun. 1997, 140, 341–352. [Google Scholar] [CrossRef]
- Geloni, G.; Kocharyan, V.; Saldin, E. A novel self-seeding scheme for hard X-ray FELs. J. Mod. Opt. 2011, 58, 1391–1403. [Google Scholar] [CrossRef]
- Amann, J.; Berg, W.; Blank, V.; Decker, F.-J.; Ding, Y.; Emma, P.; Feng, Y.; Frisch, J.; Fritz, D.; Hastings, J.; et al. Demonstration of self-seeding in a hard-X-ray free-electron laser. Nat. Photonics 2012, 6, 693–698. [Google Scholar] [CrossRef]
- Yu, L.H. Generation of intense uv radiation by subharmonically seeded single-pass free-electron lasers. Phys. Rev. A 1991, 44, 5178–5193. [Google Scholar] [CrossRef]
- Stupakov, G. Using the Beam-Echo Effect for Generation of Short-Wavelength Radiation. Phys. Rev. Lett. 2009, 102, 074801. [Google Scholar] [CrossRef]
- Di Mitri, S.; Allaria, E.; Appio, R.; Badano, L.; Bassanese, S.; Bencivenga, F.; Borga, A.; Bossi, M.; Busetto, E.; Callegari, C.; et al. Commissioning and Initial Operations of FERMI@Elettra. In Proceedings of the 2nd International Particle Accelerator Conference, San Sebastian, Spain, 4–9 September 2011; pp. 918–922. [Google Scholar]
- Zholents, A.; Fawley, W. Proposal for Intense Attosecond Radiation from an X-Ray Free-Electron Laser. Phys. Rev. Lett. 2004, 92, 224801. [Google Scholar] [CrossRef]
- Zholents, A. Method of an enhanced self-amplified spontaneous emission for x-ray free electron lasers. Phys. Rev. Spec. Top. Accel. Beams 2005, 8, 040701. [Google Scholar] [CrossRef]
- Ding, Y.; Huang, Z.; Ratner, D.; Bucksbaum, P.; Merdji, H. Generation of attosecond x-ray pulses with a multicycle two-color enhanced self-amplified spontaneous emission scheme. Phys. Rev. Spec. Top. Accel. Beams 2009, 12, 060703. [Google Scholar] [CrossRef]
- Zholents, A.; Penn, G. Obtaining attosecond X-ray pulses using a self-amplified spontaneous emission free electron laser. Phys. Rev. Spec. Top. Accel. Beams 2005, 8, 050704. [Google Scholar] [CrossRef]
- Emma, P.; Bane, K.; Cornacchia, M.; Huang, Z.; Schlarb, H.; Stupakov, G.; Walz, D. Femtosecond and Subfemtosecond X-Ray Pulses from a Self-Amplified Spontaneous-Emission-Based Free-Electron Laser. Phys. Rev. Lett. 2004, 92, 074801. [Google Scholar] [CrossRef] [PubMed]
- Xiang, D.; Huang, Z.; Stupakov, G. Generating Intense Attosecond X-ray Pulses Using Ultraviolet-Laser-Induced Microbunching in Electron Beams. Phys. Rev. Spec. Top. Accel. Beams 2009, 12, 060701. [Google Scholar] [CrossRef]
- Huang, S.; Ding, Y.; Feng, Y.; Hemsing, E.; Huang, Z.; Krzywinski, J.; Lutman, A.A.; Marinelli, A.; Maxwell, T.J.; Zhu, D. Generating Single-Spike Hard X-Ray Pulses with Nonlinear Bunch Compression in Free-Electron Lasers. Phys. Rev. Lett. 2017, 119, 154801. [Google Scholar] [CrossRef] [PubMed]
- Bane, K.; Stupakov, G. Corrugated pipe as a beam dechirper. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2012, 690, 106–110. [Google Scholar] [CrossRef]
- Emma, P.; Venturini, M.; Bane, K.L.F.; Stupakov, G.; Kang, H.-S.; Chae, M.S.; Hong, J.; Min, C.-K.; Yang, H.; Ha, T.; et al. Experimental Demonstration of Energy-Chirp Control in Relativistic Electron Bunches Using a Corrugated Pipe. Phys. Rev. Lett. 2014, 112, 034801. [Google Scholar] [CrossRef] [PubMed]
- Lutman, A.; Maxwell, T.J.; MacArthur, J.P.; Guetg, M.; Berrah, N.; Coffee, R.N.; Ding, Y.; Huang, R.N.C.Z.; Marinelli, A.; Moeller, S.; et al. Fresh-slice multicolour X-ray free-electron lasers. Nat. Photonics 2016, 10, 745–750. [Google Scholar] [CrossRef]
- Guetg, M.W.; Lutman, A.A.; Ding, Y.; Maxwell, T.J.; Huang, Z. Dispersion-Based Fresh-Slice Scheme for Free-Electron Lasers. Phys. Rev. Lett. 2018, 120, 264802. [Google Scholar] [CrossRef]
- Pellegrini, C. High power femtosecond pulses from an X-ray SASE-FEL. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 2000, 445, 124–127. [Google Scholar] [CrossRef]
- Poletto, L.; Frassetto, F. Grating configurations to compress free-electron laser pulses. J. Synchrotron Radiat. 2018, 25, 52–58. [Google Scholar] [CrossRef]
- Bajt, S.; Chapman, H.N.; Aquila, A.; Gullikson, E. High-efficiency X-ray gratings with asymmetric-cut multilayers. J. Opt. Soc. Am. A 2012, 29, 216–230. [Google Scholar] [CrossRef]
- Prasciolu, M.; Haase, A.; Scholze, F.; Chapman, H.N.; Bajt, S. Extended asymmetric-cut multilayer X-ray gratings. Opt. Express 2015, 23, 15195–15204. [Google Scholar] [CrossRef] [PubMed]
- Chapman, H.; Nugent, K. X-ray pulse compression using strained crystals. Opt. Commun. 2002, 205, 351–359. [Google Scholar] [CrossRef]
- Shvyd’ko, Y.V.; Lerche, M.; Kuetgens, U.; Rüter, H.D.; Alatas, A.; Zhao, J. X-ray Bragg Diffraction in Asymmetric Backscattering Geometry. Phys. Rev. Lett. 2006, 97, 235502. [Google Scholar] [CrossRef] [PubMed]
- Hrdy, J.; Oberta, P. Possibility of X-ray pulse compression using an asymmetric or inclined double-crystal monochromator. J. Synchrotron Radiat. 2013, 20, 550–554. [Google Scholar] [CrossRef]
- Li, H.; MacArthur, J.; Littleton, S.; Dunne, M.; Huang, Z.; Zhu, D. Femtosecond-Terawatt Hard X-Ray Pulse Generation with Chirped Pulse Amplification on a Free Electron Laser. Phys. Rev. Lett. 2022, 129, 213901. [Google Scholar] [CrossRef] [PubMed]
- Weiner, A.M. Ultrafast Optics. 2009, Chapter 4. Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9780470473467 (accessed on 26 March 2023).
- Reiche, S. GENESIS 1.3: A fully 3D time-dependent FEL simulation code. Nucl. Instrum. Methods Phys. Res. Sect. 1999, 429, 243–248. [Google Scholar] [CrossRef]
- Authier, A. Dynamical Theory of X-ray Diffraction; Oxford University: Oxford, UK, 2001. [Google Scholar]
- Yuri, S. X-ray Optics—High-Energy-Resolution Applications; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Sears, V.F. Dynamical Diffraction in Periodic Multilayers. Acta Crystallogr. Sect. 1997, 53, 649–662. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: 60th Anniversary Edition, 7th ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Windt, D.L. IMD—Software for modeling the optical properties of multilayer films. Comput. Phys. 1998, 12, 360–370. [Google Scholar] [CrossRef]

| d [nm] | [∘] | [as] | [fs] | G [mm] | |||
|---|---|---|---|---|---|---|---|
| Ge(111) | 0.3266 | - | −10.5 | 31 | 1.03 × | 28.0 | 0.2% |
| Mo-Si | 2.0000 | 0.25 | −1.0 | 2 | 1.85 × | 27.4 | 0.7% |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| Electron energy | 8.0 | GeV | Undulator period | 2.6 | cm |
| Energy spread | 0.6 | MeV | Pulse duration | 10 | fs |
| Peak current | 800 | A | Average beta function | 20 | m |
| Photon energy | 10 | keV | Normalized emittance | 0.35 | mm-mrad |
| FEL parameter | 3.8 × | - | Undulator parameter | 1.632 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Hu, K.; Zhu, Y.; Wang, X.; Li, Q.; Xu, Z.; Wu, J.; Zhang, W. Dispersion Caused by the Penetration Effect in X-ray Compressors. Photonics 2023, 10, 484. https://doi.org/10.3390/photonics10050484
Yang C, Hu K, Zhu Y, Wang X, Li Q, Xu Z, Wu J, Zhang W. Dispersion Caused by the Penetration Effect in X-ray Compressors. Photonics. 2023; 10(5):484. https://doi.org/10.3390/photonics10050484
Chicago/Turabian StyleYang, Chuan, Kai Hu, Ye Zhu, Xiaofan Wang, Qinming Li, Zhongmin Xu, Juhao Wu, and Weiqing Zhang. 2023. "Dispersion Caused by the Penetration Effect in X-ray Compressors" Photonics 10, no. 5: 484. https://doi.org/10.3390/photonics10050484
APA StyleYang, C., Hu, K., Zhu, Y., Wang, X., Li, Q., Xu, Z., Wu, J., & Zhang, W. (2023). Dispersion Caused by the Penetration Effect in X-ray Compressors. Photonics, 10(5), 484. https://doi.org/10.3390/photonics10050484






