Abstract
We propose a perfectly vertical coupling scheme based on metasurface deflectors (meta-deflectors) and grating couplers (GCs). An approach for optimizing the GCs based on the Gaussian-fitting using the genetic algorithm is proposed. An meta-deflector based on amorphous silicon (a-Si) pillars is designed to the optimal coupling angle of the GC to ensure good coupling efficiency (CE). Simulations predict peak vertical CE to be 78% at the wavelength of 2 μm, with 1 dB bandwidth ≥35 nm. The design process of GC and meta-deflector is provided in detail, and the influence of fabrication error on the CE is analyzed.
1. Introduction
Silicon photonic integrated chips (PICs) based on silicon-on-insulator (SOI) platforms have been widely used in optical communication, computing, and sensing [1,2,3] due to their large-scale integration possibility, low cost, and low power consumption [4,5]. However, as the demand for high-speed data transmission continues to grow, the channel capacity of communication systems that rely on telecommunication wavelength bands has nearly reached its theoretical limit. To address this issue, novel technologies need to be developed to meet the ever-increasing demand for data transmission. Fortunately, the mature SOI platform has been shown to be transparent to the 2 μm band, making it an emerging window for communication [6]. In addition, the 2 μm band is a promising spectral window for chemical sensing, as it includes the absorption bands of varios of gas molecules (such as CO2, CO, and CH4) [7] and biological molecules (such as glucose) [8]. Due to these advantages, there has been a growing interest in PICs operating within the 2 μm band. Many advanced devices based on this band, including tunable array waveguide gratings [9], modulators [10], optical switches [11], and mode multiplexers [12], have been demonstrated on SOIs. Grating couplings (GCs) are one of the most convenient and efficient ways to interface off-chip components and PICs. Compared to edge couplers (ECs), GCs offer several advantages, including increased alignment tolerance, compatibility with wafer-scale testing, and the elimination of the need for deep facet etching or facet polishing [13]. These advantages make GCs a highly attractive option for integrating off-chip components with PICs.
Traditional GCs tend to deviate from the perfectly vertical direction to reduce the effect of second-order reflection. This requires angled polishing of the fiber facet and mounting the fiber ferrule with an angle to the photonics circuit plane. However, this packaging process can be complicated and expensive. Perfectly vertical GCs (PVGCs) with high coupling efficiency (CE) can be used to avoid these issues. Additionally, PVGCs can be used for implementing hybrid integrated surface-emitting lasers [14] and coupling with multi-core optical fibers [15]. Therefore, the development of a perfectly vertical coupled scheme is essential. Several schemes have been proposed for C-band, in terms of bi-directional coupling [16], polymer prism [17], tilted waveguide grating [18], blazing grating [19], multilayer structures [20], and L-shaped gratings [21]. However, the implementation of these schemes is limited by the fabrication complexity and the CE.
Metamaterials have emerged as a rapidly developing branch of materials science in recent decades [22,23,24,25]. A special class of metamaterials, metasurfaces [26,27,28,29], have garnered significant attention in optics due to their exceptional modulation capabilities in modulating the phase, amplitude, and polarization of light. Various metasurface materials have been explored, such as plasmonic metasurfaces [30], dielectric metasurfaces [31], and liquid crystal metasurfaces [32]. Among them, silicon metasurfaces, a type of dielectric metasurface, possess the advantages of high refractive index, low loss, and compatibility with CMOS technology. They have been widely used in beam deflection [33], color display [34], and holograms [35]. The ongoing development of metasurface devices, and in particular the proposal of metasurface deflectors (meta-deflectors), provides a new approach to achieving perfect vertical coupling.
In this work, a novel PVGC, working at 2 μm, consisting of a meta-deflector and a GC is proposed. The meta-deflector is designed with amorphous silicon (a-Si) pillars that can effectively deflect the vertically incident light to a desired angle. Based on the 340 nm SOI platform, a high efficiency GC is designed by using the genetic algorithm to optimize the Gaussian-fitting GC, which can couple the deflected light into the waveguide. By properly designing the structural parameters of the meta-deflector and the GC, the deflection angle of the meta-deflector can meet the optimal coupling angle of the GC, thereby achieving high efficiency perfect vertical coupling. The GC and the meta-deflector are designed by 2D finite different time domain (FDTD) and 3D-FDTD separately and then combined using the 3D FDTD to validate the effectiveness of this scheme. The FDTD simulation settings are introduced below. First, the GC and meat-deflector are set with enough size (with 24 periods of the GC and 33 periods of meta-deflector) making the size of the PVGC larger than the beam diameter. Then, a Gaussian source (TE mode) with a waist diameter of 11.6 μm is used to simulate the single-mode fiber of 2 μm band. Finally, perfectly matched layers are used to determine the simulation area. and the simulation grid accuracy is set to 10 nm for the optimal balance between simulation time and accuracy. The results demonstrate that the meta-deflector can deflect the beam by 18.5° at a wavelength of 2 μm. At this angle, the GC can achieve a coupling efficiency of 83%. Furthermore, combining the meta-deflector with the GC yielding a perfectly vertical coupling efficiency of 78%. In addition, the effect of fabrication deviation on the performance is analyzed.
2. Design of Grating Coupler and Metasurface Deflector
The proposed PVGC is presented in Figure 1a, which contains mainly two components, the GC and the meta-deflector. Figure 1b provides a cross-sectional view and parameters information, where Tm, Tc, Tw, and Tb denote the thickness of the meta-deflector, cladding, waveguide, and buried oxide (BOX) layer, respectively. The PVGC is designed using an SOI wafer with a 340 nm thick top silicon layer and a 2 μm thick BOX layer. The period and radius of the pillars are denoted by P and r, respectively. Λ represents the period of the GC, and the lengths of the unetched and etched parts are indicated by Lo and Le. The etch depth is denoted by Det.
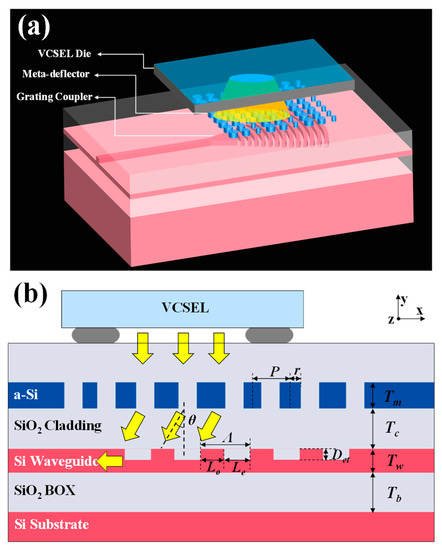
Figure 1.
(a) Three-dimensional structure of proposed PVGC. (b) Cross-sectional schematic of proposed PVGC (the arrows mark the direction of light).
The CE of the proposed PVGC is limited by two primary factors: the transmission of the meta-deflector and the CE of the GC. Theoretically, the meta-deflector can be specially designed to deflect the beam at any angle [33], making the coupling angle (θ) a key parameter for optimizing the GC to achieve higher CE. Once the optimal angle is determined, it is used to design the meta-deflector. The main design flow can be divided into the following three sections:
The first section is the design of the GC. The etch depth, coupling angle, period, and duty cycle (DC, defined as the ratio of Lo to Λ) are optimized by the 2D-FDTD simulations. A new design method based on Gaussian-fitting GC is developed to achieve higher CE and a proper optimal coupling angle corresponding to maximum CE. Additionally, a genetic algorithm is utilized to mitigate the deleterious effects introduced by the approximate value of the effective refractive index.
The second section is the design of the meta-deflector. First, the phase and transmission of a-Si pillars with different heights, radii, and periods are calculated by the parameter sweeping function of FDTD. After that, the target phase distribution is calculated using the optimal coupling angle obtained in the first section. Finally, the meta-deflector is constructed based on the target phase distribution and the results of parametric sweeping by interpolation.
The final section is to combine the GC with the meta-deflector for simulation, using 3D-FDTD to verify the correctness of the proposed scheme and analyze the impact of fabrication errors on the CE.
2.1. Design of Grating Coupler
The working principle of the GC is based on the Bragg condition [36]:
where represents the diffraction order of the grating, and 1 is taken here. is the coupling wavelength, represents the period of grating, is the refractive index of the cladding on the grating, is the diffraction angle, is the effective refractive index of the grating and can be expressed as [37]
where and represent the effective refractive index of the grating teeth and groove. The Λ can be derived from Equations (1) and (2):
When the grating is working as an out-coupling device, diffraction light in four directions will be generated when the light input from the waveguide passes through the GC, as illustrated in Figure 2a. Where a fundametal-mode (TE-mode) source is set to the right of the GC. Two frequency-domain power monitors (M1 and M2) positioned above and below the GC are employed to measure the amount of optical power in upward and downward diffraction, and two additional power monitors (M3 and M4) positioned along the waveguide are used to assess the grating’s reflection and transmission. The CE can be expressed as:
where , and represent the normalized power diffracted to the substrate and the normalized power reflected and transmitted in the waveguide. represents the directionality (the ratio of upward diffracted power to the total input power). is defined as the matching degree between the output mode field of GC and the mode field of source. As indicated in Equation (4), the CE is predominantly affected by and , and can be improved by optimizing and . Therefore, we divided the design process of GC into following three steps.
- (i).
- Improve the directionality by optimizing the etch depth and coupling angle.
- (ii).
- Improve by adjusting the output mode field of GC by Gaussian fitting.
- (iii).
- To search for the final structure using the genetic algorithm.
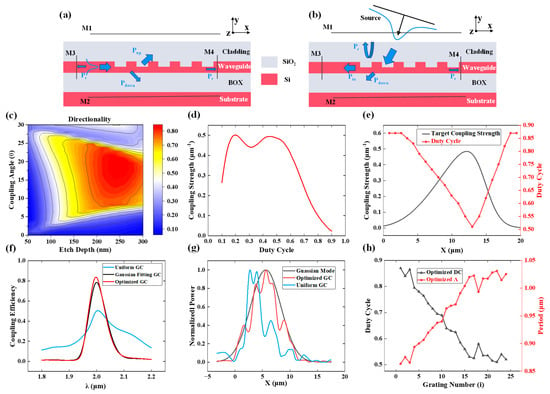
Figure 2.
The working mode of the GC (a) as an out-coupling device and (b) as an in-coupling device. (c) The relationship between directionality with etch depth and coupling angle. (d) The relationship between coupling strength and DC. (e) The relationship between target coupling strength (α) and DC with position (f) The CE comparison of uniform GC, Gaussian-fitting GC, and optimized GC at the wavelength of 1.8–2.2 μm. (g) The output mode field of uniform GC and Optimized GC compared with Gaussian field profile along the X axis. (h) The structural parameters of each unit of the optimized GC.
According to Reference [38], the directionality of a fixed-thickness waveguide grating is influenced by both the coupling angle and the etch depth. Starting from the basic structure of a uniform GC (with the DC of 0.5), we conduct a simultaneous sweep of the etch depth (in increments of 10 nm) and the coupling angle (in increments of 1°) to evaluate the directionality of various grating configurations. It is important to highlight that Λ is a function of DC, as shown in Equation (3), to satisfy the Bragg condition for each grating element and simplify the optimization process. Figure 2c shows the simulation results, which suggest that directionality is a function of the etch depth and coupling angle. Additionally, the maximum directionality which is 84% comes from the etch depth of 250 nm and coupling angle of 18.5°.
In the second step, the effect of apodization on the parameter was examined while keeping the values of Det and θ that correspond to the maximum directionality. It is well established that the each unit of the uniform GC has the same diffracting ability for light. Thus, the output mode field of uniform GC is exponentially decreasing along the grating direction (x-axis). There is a large mismatch with the Gaussian mode field of the source, resulting in a low values of . The can be improved by adjusting the coupling strength (α) along the x-axis through the variation of DC to get a Gaussian-fitting GC. The coupling strength is a measure of the power attenuation rate in the grating region. It can be defined by the following Equation [39]:
where L is the length of the GC, is the input power from the waveguide, and is the transmitted power after the GC. Figure 2d shows how the coupling strength (x = 0 is located at the start of the GC) varies with different values of DC. Gaussian-fitting output mode field can be obtained by varying the distribution of the coupling strength to meet the requirement below [40]
where represents a normalized Gaussian distribution with a standard deviation corresponding to the mode field diameter of l source.
The calculated correlation between and DC with the target position (the position of the center of the grating unit on the x-axis) is illustrated in Figure 2e, which is obtained by combining the DC and values illustrated in Figure 2c. A Gaussian-fitting GC is designed based on this correlation. It’s worth noting that, considering the limitations of DUV lithography, the DC is limited to between 0.5 and 0.87, to ensure the minimum feature size is greater than 100 nm. To complete the GC analysis the GC is also simulated as an out-coupling device to calculate the CE, as shown in Figure 2b. Where a Gaussian source (TE-mode) with a waist diameter of 11.6 μm is placed above the GC. The highest CE of Gaussian-fitting GC (with the source center at x = 7.3 μm) is achieved at 78%, as illustrated in Figure 2f, which is 28% higher than that of the uniform GC (with the source center at x = 4 μm).
To further improve the CE, the DC of each units of the Gaussian-fitting GC obtained in the second step are finely optimized by the genetic algorithm. Genetic algorithms have been widely used for the design of photonic devices [41]. However, in the optimization process of the GCs, the traditional genetic algorithm is very time-consuming and prone to getting stuck in local optima. This is because each grating unit has at least two parameters that need to be optimized, which leads to more calculations and more randomness. Therefore, a method is proposed that employs genetic algorithm optimization on a relatively idealized structure. Furthermore, Λ is used as a function of DC in our design, significantly reducing computational complexity and optimization process duration while still producing high-quality solutions. The optimization process comprises the following steps:
- (i).
- A random perturbation ΔDCi is introduced to the structural parameters of the Gaussian-fitting GC to generate a genetic material population.
- (ii).
- The fitness metric for the population was the CE, and it is used to evaluate the fitness of each population through FDTD simulation.
- (iii).
- Based on their fitness, populations are selected using the roulette-wheel selection method.
- (iv).
- The reproduction of the generation is accomplished through crossover and mutation. Each selected population has an 80% probability of intermixing with another population at a random crossover point, resulting in two child populations.
- (v).
- The obtained child populations has a 10% probability of mutation, which involve randomly modifying the selected structural parameters.
- (vi).
- This establishes an optimization loop that repeat steps (ii) to (v) until the convergence criteria are met.
To evaluate the effectiveness of our optimization procedure, we compare the CE of the uniform GC, the Gaussian-fitting GC, and the optimized GC (with the source center at x = 7.3 μm). The results are depicted in Figure 2f, which shows that the peak CE of the Gaussian-fitting GC (black curve) is improved by 28% compared to the uniform GC (blue curve). The proposed optimization algorithm further improves the CE by an additional 5% (red curve), resulting in a final efficiency of 83%. Figure 2g provides the comparison of the output mode field of the uniform GC (blue curve) and the output mode field of the optimized GC (red curve) with the Gaussian mode field (black curve). It is evident that the optimized GC closely matches the mode field of the source, as demonstrated by the overlap of their intensity profiles in Figure 2g. The final parameters of the optimized GC are displayed in Figure 2h, where the grating number represents the ordinal number of the grating cells sorted from x = 0.
2.2. Design of Metasurface Deflector
Since the optical properties of a metasurface are mainly determined by its subwavelength structures, it is possible to achieve a desired optical response (amplitude, phase, polarization state, etc.) by optimizing their geometry, size, direction, and arrangement [33]. Among various architectures of metasurfaces, the nanopillar-based metasurface is preferred due to its simplicity and ease of fabrication. For the meta-deflector design, we employ a periodic structure composed of a-Si pillars as the building blocks. In order to achieve the 0–2π phase control and high transmission in the 2 μm band, we use the 3D-FDTD method to analyze the transmission and phase for the pillars with different radii, heights, and periods. Figure 3a illustrates that sweeping the radii of the pillars from 100 nm to 350 nm, pillars with a period of 950 nm and a height of 1 μm can achieve high transmission across the entire range of phases from 0 to 2π.
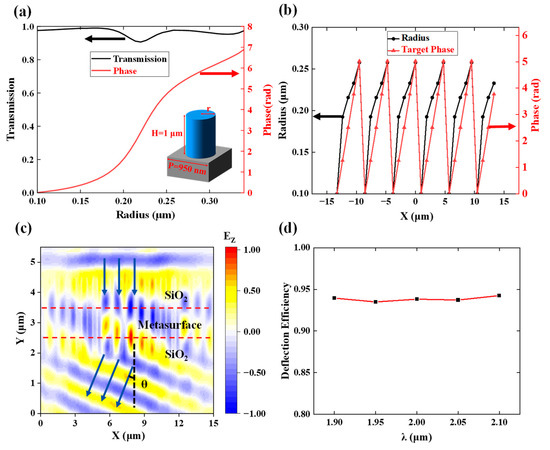
Figure 3.
(a) Transmission and phase of the periodic a−Si pillars with 950 nm unit cell size and 1 μm height for different radii. (b) The relationship between the target phase and target radius with position (c) The Ez field propagation at the wavelength of 2 μm (the arrows mark the direction of light). (d) The transmission of meta-deflector at the 1.9~2.1 μm band.
The principle of the meta-deflector is based on the generalized Snell law [27]:
where and are the refractive index of material above and below the meta-deflector, in our design . is the deflection angle, is the incidence angle (0° is taken). represents the phase gradient.
According to the design results of the GC, when the deflection angle is 18.5°, the CE is the highest. can be expressed as:
According to Equation (8), the distribution of the target phase in the x-axis is calculated, as shown in Figure 3b red curve. Based on the correlation between phase and radius depicted in Figure 3a, we use the interpolation method to construct the meta-deflector with pillars of appropriate radii. The black curve in Figure 3b shows the distribution of the radii used in the meta-deflector. Figure 3c depicts the propagation of light with the meta-deflector. It can be observed that vertically incident light is deflected at an angle of 18.5° after passing through the meta-deflector. Furthermore, we calculate the deflection efficiency (defined as the ratio of the power with a deflection of 18.5° to the total incident power) of the meta-deflector at 18.5°, and the results are shown in Figure 3d. It can be seen that the deflection efficiency is close to 94% in the band range of 1.9 to 2.1 μm.
3. Analysis and Discussion
After designing the GC and the meta-deflector, we employ the 3D-FDTD solution to test different combinations of the GC and meta-deflector. As shown by the blue curve in Figure 4a, in the case of vertical coupling without the meta-deflector, the CE is almost negligible. However, the existence of the meta-deflector (black curve) makes it possible for the perfectly vertical coupling to have a CE of about 78% at the wavelength of 2 μm. This value is 5% lower than the CE achieved in the case of oblique incidence (18.5°), as shown in the red curve. The 5% reduction can be explained by the deflection efficiency of the meta-deflector, which is 94%. As a result, some light is lost as it passes through. Figure 4b illustrates the propagation of the light with the meta-deflector and the GC. Observably, the light that is vertically incident undergoes deflection via the meta-deflector and subsequently couples into the waveguide by the GC. These results confirm the feasibility of the proposed PVGC.
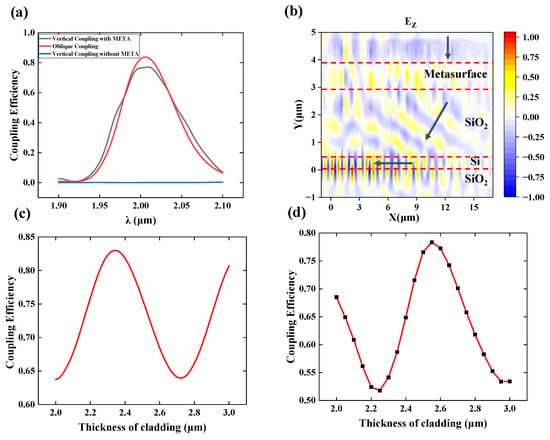
Figure 4.
(a) The CE of perfectly vertical coupling with meta-deflector, without meta-deflector, and oblique incidence coupling (18.5°). (b) The Ez field propagation of perfectly vertical coupling with meta-deflector at the wavelength of 2 μm (the arrows mark the direction of light). (c) The relationship between the Tc and the CE without meta-deflector. (d) The relationship between the Tc and the CE with meta-deflector.
Our design is based on a 340 nm SOI wafer. Although the waveguide thickness (Tw) and buried oxide layer thickness (Tb) are fixed at 340 nm and 2 μm, the cladding thickness (Tc) can be optimized to achieve the best performance. We sweep the relationship between the Tc and the CE with and without meta-deflectors, and the results are shown in Figure 4c,d. We find that the optimal Tc for the cases with and without meta-deflector are different, but both follow a trigonometric function relationship with the CE. When there is no meta-deflector, the optimal Tc is 2.34 μm, while with the deflector, due to the change in the refractive index above the cladding, this value change to 2.55 μm. It is worth noting that the design of the GC and the combination of meta-deflector and GC introduced above are based on different optimal Tc values. The final parameters are shown in Table 1.

Table 1.
Parameters of PVGC.
In practice, the light alignment inaccuracy and the fabrication errors (etch error of the GC, etch groove width error of the GC and the meta-deflector, and overlay shift error between the two layers) in the scheme may cause severe performance declines, especially the CE decrease. Therefore, we evaluate the effect of these factors on the CE. From Figure 5a, it not difficult to find that our proposed coupling scheme can still demonstrate a relatively high level of CE even if the light source shifts 4 μm from the center. Moreover, given by Figure 5b,c, the CE can be maintained well with an etch depth variation of ±30 nm or a width variation of ±40 nm. The correlation between the CE and the mask misalignment is illustrated in Figure 5d. When the latter is the range of −5 to 5 μm, the fluctuation of CE is only ±4%.
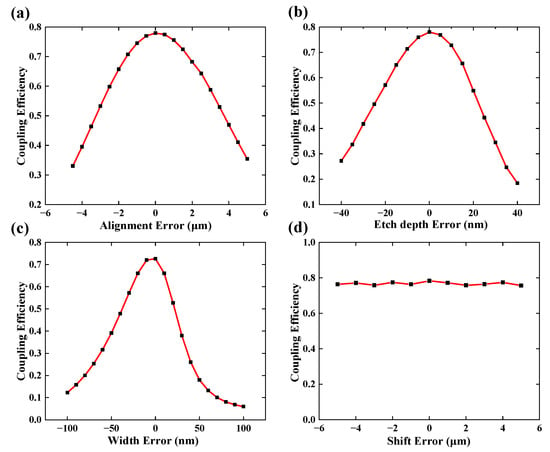
Figure 5.
Coupling efficiency versus fabrication errors. (a) The alignment error between the source and GC. (b) The etch depth error in the etching process of GC. (c) The width error in the etching process of the GC and the meta-deflector. (d) The overlay shift error between two layers.
4. Conclusions
In conclusion, we propose and numerically demonstrate a meta-deflector enhanced PVGC for perfectly vertical coupling at 2 μm band. A GC design method is also presented, which is optimized by using the genetic algorithm for a Gaussian-fitted GC. As a result, a high CE of 83% at an oblique angle of 18.5° is obtained. The meta-deflector is designed with an 18.5° deflection of the incident light to match the coupling angle of the GC. Finally, the proposed device achieves a total CE of 78% and a 1dB bandwidth of 35 nm at a wavelength of 2 μm. Furthermore, the impact of process deviations on performance is analyzed. The results show that the proposed scheme has a good tolerance to alignment error, etch depth error, and width error, and is insensitive to shift error. The proposed scheme offers a novel approach for realizing the hybrid integration of surface-emitting lasers and coupling with multi-core fibers.
Author Contributions
Conceptualization, Q.Z. and X.W.; methodology, X.W.; software, Q.Z.; validation, X.W.; writing—Original draft preparation, X.W.; writing—Review and editing, Q.Z., X.Z., Y.Q. and L.J.; supervision, T.H., S.Z., L.J. and Y.D.; project administration, T.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hu, T.; Dong, B.; Luo, X.; Liow, T.-Y.; Song, J.; Lee, C.; Lo, G.-Q. Silicon photonic platforms for mid-infrared applications. Photonics Res. 2017, 5, 417–430. [Google Scholar] [CrossRef]
- Xie, W.; Komljenovic, T.; Huang, J.; Tran, M.; Davenport, M.; Torres, A.; Pintus, P.; Bowers, J. Heterogeneous silicon photonics sensing for autonomous cars. Opt. Express 2019, 27, 3642–3663. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, R.; Li, X.; Li, T. Development trends in silicon photonics for data centers. Opt. Fiber Technol. 2018, 44, 13–23. [Google Scholar] [CrossRef]
- Bogaerts, W.; Baets, R.; Dumon, P.; Wiaux, V.; Beckx, S.; Taillaert, D.; Luyssaert, B.; Van Campenhout, J.; Bienstman, P.; Van Thourhout, D. Nanophotonic waveguides in silicon-on-insulator fabricated with CMOS technology. J. Light. Technol. 2005, 23, 401. [Google Scholar]
- Tsuchizawa, T.; Yamada, K.; Fukuda, H.; Watanabe, T.; Takahashi, J.-I.; Takahashi, M.; Shoji, T.; Tamechika, E.; Itabashi, S.; Morita, H. Microphotonics devices based on silicon microfabrication technology. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 232–240. [Google Scholar] [CrossRef]
- Petrovich, M.N.; Poletti, F.; Wooler, J.P.; Heidt, A.M.; Baddela, N.K.; Li, Z.; Gray, D.R.; Slavik, R.; Parmigiani, F.; Wheeler, N.V.; et al. Demonstration of amplified data transmission at 2 microm in a low-loss wide bandwidth hollow core photonic bandgap fiber. Opt. Express 2013, 21, 28559. [Google Scholar] [CrossRef] [PubMed]
- Schliesser, A.; Picqué, N.; Hänsch, T.W. Mid-infrared frequency combs. Nat. Photonics 2012, 6, 440. [Google Scholar] [CrossRef]
- Estevez, M.C.; Alvarez, M.; Lechuga, L.M.J.L.; Reviews, P. Integrated optical devices for lab-on-a-chip biosensing applications. Laser Photonics Rev. 2011, 6, 463–487. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Li, D.; Yao, Y.; Du, J.; He, Z.; Xu, K. Thermo-Optic Tunable Silicon Arrayed Waveguide Grating at 2-μm Wavelength Band. IEEE Photonics J. 2020, 12, 1–8. [Google Scholar] [CrossRef]
- Cao, W.; Hagan, D.; Thomson, D.J.; Nedeljkovic, M.; Littlejohns, C.G.; Knights, A.; Alam, S.-U.; Wang, J.; Gardes, F.; Zhang, W.; et al. High-speed silicon modulators for the 2 μm wavelength band. Optica 2018, 5, 1055–1062. [Google Scholar] [CrossRef]
- Yu, T.; Liu, Y.; Li, Z.; Xu, K.; Du, J. Integrated Thermo-optic Switch for 2-µm Spectral Band. In Optoelectronic Devices and Integration; Optica Publishing Group: Washington, DC, USA, 2019; p. OTu2B-4. [Google Scholar]
- Zheng, S.; Huang, M.; Cao, X.; Wang, L.; Ruan, Z.; Shen, L.; Wang, J.J.P.R. Silicon-based four-mode division multiplexing for chip-scale optical data transmission in the 2 μm waveband. Photonics Res. 2019, 7, 1030. [Google Scholar] [CrossRef]
- Cheng, L.; Mao, S.; Li, Z.; Han, Y.; Fu, H.J.M. Grating couplers on silicon photonics: Design principles, emerging trends and practical issues. Micromachines 2020, 11, 666. [Google Scholar] [CrossRef] [PubMed]
- Jahed, M.; Caut, A.; Goyvaerts, J.; Rensing, M.; Karlsson, M.; Larsson, A.; Roelkens, G.; Baets, R.; O’Brien, P. Angled Flip-Chip Integration of VCSELs on Silicon Photonic Integrated Circuits. J. Light. Technol. 2022, 40, 5190–5200. [Google Scholar] [CrossRef]
- Tong, Y.; Zhou, W.; Wu, X.; Tsang, H.K. Efficient Mode Multiplexer for Few-Mode Fibers Using Integrated Silicon-on-Insulator Waveguide Grating Coupler. IEEE J. Quantum Electron. 2019, 56, 1–7. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Cheng, Q.; Khokhar, A.Z.; Yan, X.; Huang, B.; Chen, H.; Liu, H.; Li, H.; Thomson, D.J.; et al. High-efficiency apodized bidirectional grating coupler for perfectly vertical coupling. Opt. Lett. 2019, 44, 5081–5084. [Google Scholar] [CrossRef] [PubMed]
- Kaur, K.; Subramanian, A.; Cardile, P.; Verplancke, R.; Van Kerrebrouck, J.; Spiga, S.; Meyer, R.; Bauwelinck, J.; Baets, R.; Van Steenberge, G. Flip-chip assembly of VCSELs to silicon grating couplers via laser fabricated SU8 prisms. Opt. Express 2015, 23, 28264–28270. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Hong, Y.; Zhu, Y.; Chen, J.; Gao, S.; Cai, X.; Shi, Y.; Liu, L. Compact high-efficiency perfectly-vertical grating coupler on silicon at O-band. Opt. Express 2017, 25, 22032–22037. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, Z.; Jia, H.; Zhang, X.; Qin, S. High-performance and compact binary blazed grating coupler based on an asymmetric subgrating structure and vertical coupling. Opt. Lett. 2011, 36, 2614–2617. [Google Scholar] [CrossRef] [PubMed]
- Dai, M.; Ma, L.; Xu, Y.; Lu, M.; Liu, X.; Chen, Y. Highly efficient and perfectly vertical chip-to-fiber dual-layer grating coupler. Opt. Express 2015, 23, 1691–1698. [Google Scholar] [CrossRef] [PubMed]
- Xiong, B.; Ma, W.; Wang, W.; Hu, X.; Chu, T.J.O.E. Compact vertical grating coupler with an achromatic in-plane metalens on a 220-nm silicon-on-insulator platform. Opt. Express 2022, 30, 36254. [Google Scholar] [CrossRef]
- Kadic, M.; Milton, G.W.; van Hecke, M.; Wegener, M.J.N.R.P. 3D metamaterials. Nat. Rev. Phys. 2019, 1, 198. [Google Scholar] [CrossRef]
- Kumar, A.; Solanki, A.; Manjappa, M.; Ramesh, S.; Srivastava, Y.K.; Agarwal, P.; Sum, T.C.; Singh, R. Excitons in 2D perovskites for ultrafast terahertz photonic devices. Sci. Adv. 2020, 6, eaax8821. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.; Mitra, A.; Aïssa, B.J.N. Metamaterials and metasurfaces: A review from the perspectives of materials, mechanisms and advanced metadevices. Nanomaterials 2022, 12, 1027. [Google Scholar] [CrossRef] [PubMed]
- Nadell, C.C.; Watts, C.M.; Montoya, J.A.; Krishna, S.; Padilla, W.J. Single Pixel Quadrature Imaging with Metamaterials. Adv. Opt. Mater. 2015, 4, 66–69. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Arbabi, E.; Horie, Y.; Kamali, S.M.; Faraon, A. Planar metasurface retroreflector. Nat. Photonics 2017, 11, 415–420. [Google Scholar] [CrossRef]
- Hu, J.; Bandyopadhyay, S.; Liu, Y.-H.; Shao, L.-Y. A Review on Metasurface: From Principle to Smart Metadevices. Front. Phys. 2021, 8, 586087. [Google Scholar] [CrossRef]
- Choudhury, S.; Wang, D.; Chaudhuri, K.; DeVault, C.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Material platforms for optical metasurfaces. Nanophotonics 2018, 7, 959–987. [Google Scholar] [CrossRef]
- Overvig, A.C.; Shrestha, S.; Malek, S.C.; Lu, M.; Stein, A.; Zheng, C.; Yu, N. Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light. Sci. Appl. 2019, 8, 1–12. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Wróbel, J.; Kula, P. Ultrafast electrical switching of nanostructured metadevice with dual-frequency liquid crystal. Sci. Rep. 2019, 9, 20367. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Li, J.; Su, R.; Yao, B.; Fang, H.; Li, K.; Zhou, L.; Liu, J.; Stellinga, D.; Reardon, C.P.; et al. Efficient Silicon Metasurfaces for Visible Light. ACS Photonics 2017, 4, 544–551. [Google Scholar] [CrossRef]
- Shu, F.; Yu, F.; Peng, R.; Zhu, Y.; Xiong, B.; Fan, R.; Wang, Z.; Liu, Y.; Wang, M. Dynamic Plasmonic Color Generation Based on Phase Transition of Vanadium Dioxide. Adv. Opt. Mater. 2018, 6, 1700939. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Tamir, T.; Peng, S.T. Analysis and design of grating couplers. Appl. Phys. A 1977, 14, 235–254. [Google Scholar] [CrossRef]
- Rytov, S. Electromagnetic properties of a finely stratified medium. Sov. Phys. JEPT 1956, 2, 466–475. [Google Scholar]
- Zhang, C.; Sun, J.-H.; Xiao, X.; Sun, W.-M.; Zhang, X.-J.; Chu, T.; Yu, J.-Z.; Yu, Y.-D. High Efficiency Grating Coupler for Coupling between Single-Mode Fiber and SOI Waveguides. Chin. Phys. Lett. 2013, 30, 014207. [Google Scholar] [CrossRef]
- Zhao, Z.; Fan, S. Design Principles of Apodized Grating Couplers. J. Light. Technol. 2020, 38, 4435–4446. [Google Scholar] [CrossRef]
- Waldhäusl, R.; Schnabel, B.; Dannberg, P.; Kley, E.-B.; Bräuer, A.; Karthe, W. Efficient Coupling into Polymer Waveguides by Gratings. Appl. Opt. 1997, 36, 9383–9390. [Google Scholar] [CrossRef]
- Bozzola, A.; Carroll, L.; Gerace, D.; Cristiani, I.; Andreani, L.C. Optimising apodized grating couplers in a pure SOI platform to −0.5 dB coupling efficiency. Opt. Express 2015, 23, 16289. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).